1 引言

合成孔径雷达(Synthetic Aperture Radar,SAR)具有全天时、全天候执行遥感监视任务的能力，其可以通过相干积累目标的多次回波得到目标的2维SAR图像^{[1, 2]}。一幅SAR图像通常由感兴趣目标和杂波组成。在实际环境中，由于较强的海杂波或地杂波的影响，使得感兴趣目标与杂波背景间的分界更不明显，这种弱分界增加了目标分割的难度。精确的目标分割结果有利于提高后续图像处理的有效性，如根据分割得到的目标轮廓可更精确地估计目标所处的姿态，进而提高姿态矫正的有效性。

图像分割算法主要包括两类：基于局部的分割算法和基于全局的分割算法。传统分割算法的通过计算阈值的方式，根据阈值将给定图像分割为前景和背景两部分，即大于阈值的一部分和小于阈值的另一部分。通过选取合适的阈值可得到感兴趣目标(前景图像)^[3]。更具体地讲，对于SAR图像，前景分割的主要目的是选择能够分割感兴趣目标像素点和背景杂波像素点的合适阈值。

基于全局的方法相对容易实现且计算复杂度较低。文献^[4]通过遍历的方法，寻找使图像前景和背景两部分方差最大的阈值以达到分割的目的，但需要前景和背景有较明显的不同。文献^[5]提出了一种基于全局的简便二值化分割方法，其直接选取累积直方图二阶导数的第1个拐点作为分割阈值，但只能应用于背景像素值较低的场景。不难发现，基于全局的方法对待分割图像有较严格的要求，即待分割图像的背景应相对简单，且前景和背景间有明显对比。因此，学者们的研究重心逐渐由基于全局的分割方法转至基于局部的分割方法。

与基于全局的方法相比，基于局部的分割方法更能有效解决困难场景下的分割问题。如被广泛使用的恒虚警率(Const False Alarm Rate,CFAR)算法已被应用于解决SAR图像的前景分割问题^[6-9]。更详细地讲，CFAR的本质是保证即使测试单元(Cell Under Test,CUT)内杂波/噪声水平有所改变时仍保持恒定的虚警率，这时的分割阈值(Threshold Value,TV)是通过分析CUT的近邻单元得到的。目前，研究CFAR的学者已提出较多改进版本的CFAR算法。如单元平均最大CFAR(Cell Averaging Greatest of CFAR)算法通过求单元平均值的方式计算TV，然后将CUT内大于TV的像素点归类为感兴趣目标的像素点。有序统计CFAR(Ordered Statistic CFAR)算法选择近邻单元内一个相对大的值作为TV，然后只保留CUT内大于TV的像素。然而，基于CFAR的算法都需要对近邻单元大小、乘积因子和累加因子等多个参数进行设置，并针对不同的环境仔细调节。

除选择TV进行图像分割的传统方法外，基于马尔科夫随机场(Markov Random Field,MRF)的SAR图像分割算法也被提出。基于MRF的分割算法为图像像素构建联合概率分布模型，然后计算像素点属于某一特定类别的概率，并根据概率完成图像分割^{[10, 11]}。文献^[10]提出最小化Gibbs能量函数以避免MRF中计算密集的全局优化问题。文献^[11]提出先使用k均值算法获得初始分割，然后使用MRF算法优化分割结果。尽管目前已有较多基于MRF方法的研究，但基于MRF算法的分割结果仍在很大程度上受初始分割结果及潜在分割类数的影响。

另一类在SAR图像分割领域被广泛研究的算法是基于聚类的算法^{[12, 13]}。此类算法能在特定条件下获得较好的性能，例如k均值算法针对球形簇才能获得最好的分割效果，谱聚类方法需要计算关联矩阵的特征向量来衡量成对像素间的相似度，而这需要较高的计算效能才能足够快地获得计算结果。

为实现更精确的SAR图像目标分割，该文认为目标与杂波在图像中的空间模式(像素能量强度和空间分布规律)并不相同且是相互可区分的，并基于表征转换机(Appearance Conversion Machine,ACM)理论提出一种有效的SAR图像目标分割算法，该算法的本质是分析给定图像中的像素空间模式，然后根据图像中像素空间模式的分布规律相应地改变像素值反映其与参考杂波图像的相似程度，最后根据衡量结果构建蒙版图像并完成分割。

本文组织结构如下：第2节介绍ACM理论；第3节提出本文的目标分割算法，并介绍算法的实现方法和原理；第4节给出本文算法对仿真和真实数据的实验处理结果；第5节总结全文。

2 表征转换机原理

对任一个被采集目标，令${{{G}}_{{\theta _i}}} \in {\mathbb {R}^{R \times C}}$和${{{G}}_{{\theta _j}}} \in {\mathbb {R}^{R \times C}}$分别代表采集条件为θ_i和θ_j时相应得到的图像，两幅图像展现目标的不同表征。则可定义转换机${M_{{\theta _i},{\theta _j}}}$，令其在给定采集条件为θ_i的表征时，可相应获得采集条件为θ_j时的表征，即

${{{G}}_{{\theta _j}}} = {M_{{\theta _i},{\theta _j}}}({{{G}}_{{\theta _i}}})$

(1)

对同一目标在不同采集条件下获得的不同表征图像，在没有获得足够信息的情况下完美地获取另外一种采集条件下的表征图像是非常困难的。即基于目标的任意单幅表征图像，难以提供足够的信息来获取目标在另一种采集条件下的相应表征图像。然而，若允许存在一定的误差，则可近似获取另一采集条件的对应表征图像^{[14, 15]}。可将式(1)改写为：

$\mathop {\min }\limits_{{M_{{\theta _i},{\theta _j}}}} \parallel{{{G}}_{{\theta _j}}} - {M_{{\theta _i},{\theta _j}}}({{{G}}_{{\theta _i}}})\parallel_F^2$

(2)

式(2)可以理解为估计映射函数y=f(x)，其中$x = {{{G}}_{{\theta _i}}}$,$y = {{{G}}_{{\theta _j}}}$和$f(*) = {M_{{\theta _i},{\theta _j}}}(*)$，这是一个回归问题并可以使用极限学习机求解，这样得到的映射函数即为表征转换机(Appearance Conversion Machine,ACM)^[15]。

不难理解，${{{G}}_{{\theta _j}}}$的像素点并不均与${{{G}}_{{\theta _i}}}$的某一个像素点${{{G}}_{{\theta _i}}}(r,c)$相关。因此，基于表征图像${{{G}}_{{\theta _i}}}$获得表征图像${{{G}}_{{\theta _j}}}$时，只需提供表征图像${{{G}}_{{\theta _i}}}$中与表征图像${{{G}}_{{\theta _j}}}$相关的像素点。更详细地讲，对于表征图像${{{G}}_{{\theta _j}}}$中的任意像素点，均可在允许误差出现的情况下，基于表征图像${{{G}}_{{\theta _i}}}$中与此像素点相关的一组像素点来求解。至此，上述ACM中的一个回归问题已经转化为M×N个回归问。

$\quad\quad {M_{{\theta _i},{\theta _j}}} = \left( {\begin{array}{*{20}{c}} {{\mathop{m}\nolimits} _{{\theta _i},{\theta _j}}^{1,1}}& \cdots &{{\mathop{m}\nolimits} _{{\theta _i},{\theta _j}}^{1,C}}\\ \vdots &{{\mathop{m}\nolimits} _{{\theta _i},{\theta _j}}^{r,c}}& \vdots \\ {{\mathop{m}\nolimits} _{{\theta _i},{\theta _j}}^{R,1}}& \cdots &{{\mathop{m}\nolimits} _{{\theta _i},{\theta _j}}^{R,C}} \end{array}} \right)$

(3)

$\quad\quad {\mathop{m}\nolimits} _{{\theta _i},{\theta _j}}^{r,c} = \mathop {\min }\limits_{{\mathop{m}\nolimits} _{{\theta _i},{\theta _j}}^{r,c}} {[{\mathop p\nolimits_{{\theta _j}} }(r,c) - {\mathop{m}\nolimits} _{{\theta _i},{\theta _j}}^{r,c}({\mathop {{q}}\nolimits_{{\theta _j}} }(r,c))]^2}$

(4)

其中，$\mathop p\nolimits_{{\theta _j}}(r,c)$为表征图像${{{G}}_{{\theta _j}}}(r,c)$中需要估计的目标像素点，$\mathop {{q}}\nolimits_{{\theta _j}}(r,c)$为表征图像${{{G}}_{{\theta _i}}}$中与$\mathop p\nolimits_{{\theta _j}}(r,c)$相关的一组像素。

3 基于表征转换机的目标分割方法

在一幅SAR图像中，属于不同目标的像素点通常呈现明显不同的空间模式，如能量强度和像素分布方式等。因此，通过分析图像空间模式的方式可辨别像素的归属，进而完成目标分割。本文提出基于ACM理论的目标分割方法，该算法首先衡量目标图像与参考杂波图像的相似程度，然后基于相似程度构建蒙版图像并完成分割。

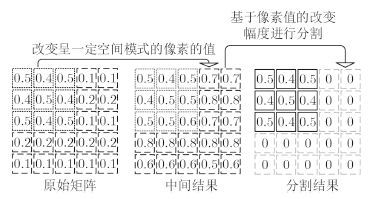
本文算法的基本原理如图 1所示，图中的每个方块指代矩阵的一个元素，方块内的数字为相应元素的值。矩阵左上角的3×3区域与右下角区域具有明显不同的空间模式。若对此矩阵进行一定处理后，可不改变左上角3×3区域像素的值并令其余区域的元素值有较大提升，通过对比中间结果与原始图像各元素相对改变的幅度即可识别出各元素的归属，进而达到图像分割的目的。实际上，图 1中的原始矩阵和中间结果分别为ACM的两个可相互转化的表征图像，基于ACM理论可构建一组回归函数，它们根据目标图像与参考杂波图像的相似程度改变目标图像的像素强度并构成一幅相似程度图。相似程度图内像素值的大小代表了相应区域与杂波空间模式的相似程度，基于相似程度图擦除与杂波相似程度较高的区域后即可获得分割后的目标图像。

3.1 增强非相干模式

本节讨论如何获得图 1的中间结果(相似程度图)以衡量SAR图像与参考杂波图像的相似程度。给定一幅杂波模式为P_b，目标模式为P_t的SAR图像${{I}} \in \mathbb {R}{^{M \times N}}$(M和N分别为方位维和距离维分辨单元的个数)。则可以定义由vec(I)到vec(I)的映射函数${{\mathop{s}\nolimits} _1}( \cdot )$：

${\rm{vec}}({{I}}) \leftarrow {s_1}({\rm{vec}}({{I}}))$

(5)

其中，vec(I)代表向量化的I，即将I中各行数据首尾相连获得单个行向量。

类似地，对只含杂波背景且杂波模式为P_b的SAR图像${{B}} \in \mathbb {R}{^{M \times N}}$，可定义一个由vec(B)到vec(B)的映射函数${{\mathop{s}\nolimits} _2}( \cdot )$：

${\rm{vec}}({{B}}) \leftarrow {s_2}({\rm{vec}}({{B}}))$

(6)

此外，还可定义一个函数${{\mathop{s}\nolimits} _3}( \cdot )$将图像B中的所有元素映射为1，即

${\rm{vec}}({{E}}) \leftarrow {s_3}({\rm{vec}}({{B}}))$

(7)

式中，E为全1矩阵。

结合式(5)和式(7)后可构建一个函数f (·)，输入向量化的杂波图像vec(B)时，输出为向量化的全1矩阵vec(E)，输入向量化的目标图像vec(I)时输出为向量化的矩阵vec(I)。则有映射函数f (·)可表示为：

$\mathop {\min }\limits_{f( \cdot )} \parallel {{\rm{vec}}({{{Q}}_i}) - f({\rm{vec}}({{{P}}_i}))} \parallel_F^2$

(8)

式中，$\big\{ {{{P}}_i} \! \in \! \mathbb {R}{^{M \times N}}\big\} _{i = 1}^2 \!=\! \{ {{I}},{{B}}\} $,$\big\{ {{{Q}}_i} \! \in \! \mathbb {R}{^{M \times N}}\big\} _{i = 1}^2 $ $ = \{ {{I}},{{E}}\} $分别为f(·)的变量和因变量，式(8)可根据目标图像与参考杂波图像的相似程度改变相应区域的像素值，并按解回归函数的方式求解。通过将I分为多幅子图像${ \rm{\{ }} {{ROI}}(m,n):1 \! < \! m \! < \! M,1 \! < \! n \! < \! N\} $的方式，可将求解单一回归函数的问题转化为求解一组回归函数的问题以获得更精确的局部映射。其中，r和c分别为距离维和方位维的单元索引。

$\begin{aligned} {{ROI}}(m,n) = & \{ t{(1,1)}{ \ ··· \ }t{({x_i},{y_i})}{ \ ··· \ }t(\mathop x\nolimits_{{N_{\large{s}}}} ,\mathop y\nolimits_{{N_{\large{s}}}} \} \\ & m - d < {x_i} < m + d,\\ & n - d < {y_i} < n + d \end{aligned}$

(9)

式中，t(x_i,y_i)为I中子图像中的第i个像素点；N_s=(2d+1)²为子图像中的像素个数；d为尺度因子。

令q(m,n)为ROI(m,n)的因变像素点，即输入为ROI(m,n)时的相应输出。针对这组输入和输出可构建一组回归函数s_mn为：

${s_{m,n}} = \mathop {\min }\limits_{s( \cdot )} \parallel {{q_i}(m,n) - s({\rm{vec}}({{{ROI}}_i}(m,n)))} \parallel_F^2$

(10)

式中，q_i(m,n)为围绕Q_i第m行第n列的像素，ROI_i(m,n)为围绕P_i第m行第n列像素的子图像，i为输入输出图像的序号。

至此，式(8)求解的单一回归函数问题已经转化为求解一组回归函数的问题：

$\begin{aligned} {{{Q}}_i} = & \left[{\begin{array}{*{20}{c}} {{q_i}(1,1)}& \!\cdots\! &{{q_i}(1,n)}\\ \vdots &\! \ddots & \!\vdots \\ {{q_i}(m,1)}& \!\cdots \!&{{q_i}(m,n)} \end{array}} \right]\\ = & \left[\!\! {\begin{array}{*{20}{c}} {{s_{1,1}}({{{ROI}}_i}(1,1))}& \cdots &{{s_{1,m}}({{{ROI}}_i}(1,n))}\\ \vdots & \ddots & \vdots \\ {{s_{n,1}}({{{ROI}}_i}(m,1))}& \cdots &{{s_{m,n}}({{{ROI}}_i}(m,n))} \end{array}} \!\!\!\right] \end{aligned}$

(11)

3.2 构建蒙版图像

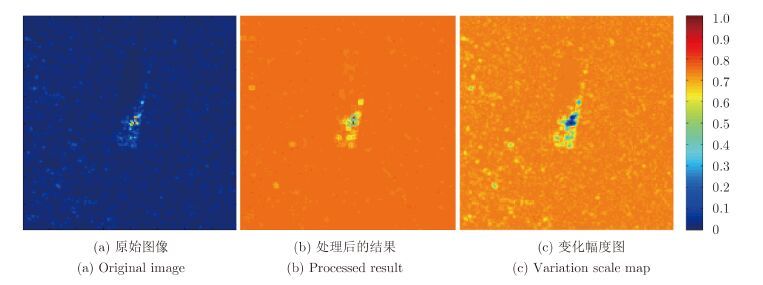
将原图像I输入计算得到的回归函数后，可计算得到新图像I'，新图像如图 2(b)所示。不难发现，处理后的图像中杂波背景的像素值被显著提高了，而待分割目标区域像素的值却没有显著改变。PIP处理后的图像I'减去原始图像I后可得到像素值的变化幅度图(相似程度图)，如图 2(c)所示。分析变化幅度图可知各区域与杂波背景的相似程度，基于此可以生成一幅蒙版图像${{M}} \in \mathbb {R}{^{M \times N}}$ ，将此蒙版图像与原图像按位与操作即可完成目标分割。

图 2(c)的变化幅度图反映了图像的各个区域与杂波的相似程度。不难理解，通过统计变化幅度图分布在各个灰度区间的像素个数，可以计算得到存在大部分杂波像素的最小相似阈值。实际上，这可以通过统计变化幅度图的灰度累积直方图来实现。灰度累积直方图反映了灰度区间相对前一个灰度区间的像素个数的改变程度，因此像素数量急剧增加的灰度区间(即灰度直方图曲率最大的点)将被选做分割阈值。

为获得灰度累积直方图，首先将图像的像素值按灰度区间分为R份，则对于第r个区间有式(12)成立

${p_r} = \sum\limits_{i = 1}^r {\frac{{{n_r}}}{n}} ,\ \ 1 \le r \le R$

(12)

式中，n为图像的像素总数，n_r为第r个灰度区间内的像素个数。在直角坐标系中做出的r与p_r的关系图形即为灰度累积直方图。

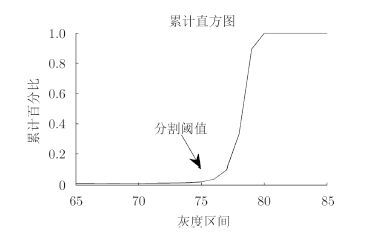
图 3是基于图 2(c)计算获得的累积直方图，这100份灰度区间内第76个灰度区间的曲率最大。

为满足更精细的分割需求，也可用基于微调参数的方式使用具体公式计算。此时，计算蒙版图像的数学表达式为：

$\ \,{{M}}(m,n) = \left\{ {\begin{array}{*{20}{c}} {1,\ {{T}}(m,n) < {a_k} - \beta }\\ {0,\ {{T}}(m,n) \ge {a_k} - \beta } \end{array}} \right.$

(13)

$\begin{aligned} k= & \mathop {\max }\limits_i {\rm{\big(\{ }}c{\rm{|}}{c_i}{\rm{ = num\{ }}{{T}}{\rm{|}}{a_i}{\rm{ < }}{{T}}(m,n){\rm{ < }}{a_{i + 1}}\} ,\\ & i = 1,\cdots ,l\} \big) \end{aligned}$

(14)

式中，1/l为采样间隔，$a \in A{\rm{ = \{ }}0 \ 1{\rm{/}}l \ \,2{\rm{/}}l \ ··· \ 1{\rm{\} }}$,β为偏移因子，c_i统计落在灰度区间(a_i,a_i+1)内的像素数量。计算得到的a_k为存在大部分杂波像素的最小阈值。

3.3 完整实现

本文基于ELM算法求解算法中的回归问题，这是因为ELM能以较低的计算复杂度获得有效的图像特征，这主要归因于ELM使用随机核和更少的优化参数，因此更易实现且拥有更强的扩展性^[16]。

根据ELM学习理论^[17-19]，正则化后的图像像素值位于欧几里德空间的一个有界可测紧凑子集上$[0, 1] \in \mathbb {R}{^d}$ ，对于任意给定的连续目标函数s(x)都存在较多映射函数${{h}}(x) = [{h_1} ··· {h_L}]$和相应的输出权重${{β}} = [{\beta _1} ··· {\beta _L}]$ 使

$\mathop {\lim }\limits_{L \to \infty } \left\| {{s_L}(x) - s(x)} \right\| = 0$

(15)

式中，L为ELM特征空间的维数，有大部分非线性分段连续函数都可用于特征映射^[18]

${{\mathop{s}\nolimits} _L}(x) = \mathop \sum \limits_{i = 1}^L {\beta _i}{h_i}(x) = {{h}}(x){{β}} $

(16)

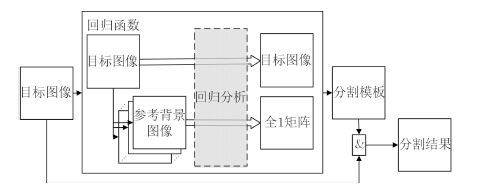
总地来讲，对任意给定SAR图像，可相应获得一组参考图像。为保证空间模式的有效分析，参考区域的最小尺寸应大于式(11)中的ROI尺寸。由于杂波背景以相似的分布模式遍布几乎整幅图像，即处于不同空间位置的杂波也可具有相似的分布模式。因此，参考背景区域空间位置的选择对算法的影响较小，对目标图像中任意只含有杂波背景的区域，通过平移和复制的方式即可生成与目标图像等尺寸的多幅参考杂波图像。基于这组图像数据，可相应构建一组回归函数计算给定目标SAR图像与杂波背景的相似程度，进而构建掩模图像并完成目标分割。本文算法的流程图如图 4所示，具体实现步骤如下：

输入：ELM的成本参数C、核参数P和数据集

$\begin{aligned} \aleph = & \{ ({{{ROI}}_i}(m,n),{q_i}(m,n))|{{{ROI}}_i}(m,n) \in {\mathbb {R}^{{N_s}}},\\ & {q_i}(m,n) \in {\mathbb {R}^1},i = 1,\cdots ,{N_C}\} \end{aligned}$

其中，N_s为${{{ROI}}_i}(m,n)$中的变量个数(图像像素数)；N_C为输入的图像数(参考杂波图像的数量加1张原SAR图像)。

步骤1  为M×N个回归函数分别计算隐藏层输出矩阵H

${{H}}\! = \!\left[\!\!\! {\begin{array}{*{20}{c}} {h({{{ROI}}_1}(m,n))}& \cdots &{h({{{ROI}}_1}(m,n))}\\ \vdots & \ddots & \vdots \\ {h({{{ROI}}_N}(m,n))}& \cdots &{h({{{ROI}}_N}(m,n))} \end{array}}\!\!\! \right]$

(17)

步骤2  为M×N个回归函数分别计算输出权重${{β}} = {{{H}}^\dagger }{{Q}}$，式中${{Q}} = {[{q_1}{(m,n)} \ ··· \ {q_N}(m,n)]^{\rm{T}}}$,${{{H}}^\dagger }$为Moore-Penrose广义逆；

步骤3  将原始图像输入得到的函数，计算变化幅度图；

步骤4  根据变化幅度图选择分割阈值，构建蒙版图像完成图像分割。

4 实验结果

本节测试算法的性能，并将本文算法与多个具有代表性的方法对比，如k-means算法和马尔科夫随机场算法^[10]。实验环节使用多种实验数据测试算法在不同场景下的目标分割效果，实验数据包括MSTAR公开数据集中的高分辨SAR图像，MSTAR数据集数据的分辨率为0.3 m×0.3 m，均由X波段的聚束式SAR雷达采集得到。此外，还基于OKTAL获得目标在不同SCR环境下的仿真SAR图像。OKTAL基于射线追踪技术针对目标的CAD模型计算生成相应目标的仿真SAR图像，仿真参数载频35 GHz，斜距23.6 km，生成SAR图像的分辨率为0.3 m×0.3 m。

在算法衡量方面使用模版图像来衡量本文算法对目标细节的分割精度，感兴趣目标和杂波区域均基于原始图像人工标记获得^[20]。在衡量参数方面，被正确分割的前景像素数(正确率)、被误判为背景的前景像素数(虚警率)和被正确分割的总像素数(精度)分别被定义为P_tp,P_fa和P_c。在实验参数方面，基于MRF模型方法的潜在分割类别数为2，期望值为0.4，最大循环数为50。本文涉及的所有算法均基于Matlab R2013a编程实现，测试电脑主机的内存为4 GB,CPU主频为1.8 GHz。

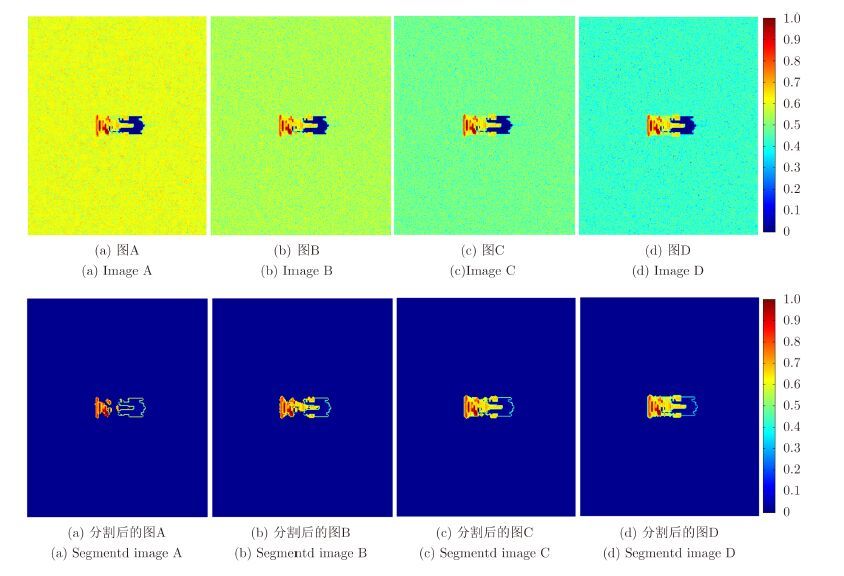
4.1 仿真SAR图像实验对比

本节使用OKTAL生成不同SCR环境下的仿真SAR图像，以测试本文算法在各种SCR环境下的目标分割性能。测试时共使用了4种SCR环境下的仿真SAR图像，它们的SCR分别为–2.3861 dB,–1.6118 dB,–0.7058 dB和0.3323 dB并分别用图A，图B，图C和图D表示，如图 5所示。处理结果如表 1所示，分析对比后不难发现，即使在原SAR图像SCR较低，目标与杂波间分界不明显的情况下也能得到较好的目标分割效果。但由于在SCR较低的图像中，目标的部分区域已被湮没在杂波中(如图 5(a)中目标的上下边缘)，因此分割后的图像中的目标也在一定程度上残缺了。随着待分割SAR图像SCR的提高则可相应地获得更好的分割效果，如图C和图D中的SAR图像均在分割后可得到保存较完好的目标。

4.2 真实SAR图像实验对比

本节使用MSTAR数据集内的高分辨SAR图像更进一步地测试算法的分割性能，并与其它算法对比分割结果。高分辨SAR图像详尽地展现了目标的细节信息，因此适合衡量算法对图像前景和背景的精确分割能力。原SAR图像和处理结果见图 6。

分割结果方面，基于MRF模型的算法和本文算法均得到了较好的目标分割结果。然而，对于能量相对强的背景杂波，基于MRF模型的算法有一定背景像素被误判。分析表 2中数据可知，本文算法的虚警率则相对较低，这意味着其在防止误判背景像素这方面有较好的表现。值得注意的是，尽管k-means算法的虚警率为最低的0%，但这是以擦除部分感兴趣目标为代价才得到的。此外，本文算法获得了最高的正确率和分割精度。这是因为本算法擅长分析图像像素的空间模式，即使对能量较强的杂波背景也可通过分析空间模式的方式得到更好的处理结果。在计算复杂度方面，k-means算法需要处理0.04 s，基于MRF模型的方法需要处理0.31 s，本文算法需要处理4.85 s。

总地来讲，本文算法处理后图像的正确率为93.08%，虚警率为0.62%，证明了本文算法在分析SAR图像空间模式方面的有效性及在SAR图像目标分割任务中的优势。

5 结论

(1) 本文提出一种有效的目标分割算法，此算法分割时也不会削弱与参考杂波不同的模式(空间分布规律)。

(2) 实验结果表明本文方法达到了预期的效果，在不同的信杂比下均有较好的目标分割效果和可靠性。

(3) 使用OKTAL软件获得了多种信杂比条件下的仿真数据，用于验证算法的有效性，为未来研究提供了更多可用的实验数据。