1 引言

合成孔径雷达(Synthetic Aperture Radar,SAR)具有目标定位能力，在军事应用方面如军事目标侦察、沿海岸军事部署等，机载SAR目标定位是其中的关键环节；在民用方面如地图测绘、地质勘探等，机载SAR目标定位也起着至关重要的作用。而衡量机载SAR目标定位精确程度的物理量是SAR定位精度，随着SAR在高分辨率方面的迅速发展，SAR的用户对定位精度的要求也越来越高^[1]。

高精度的运动补偿是提高定位精度的关键，现阶段通常选用基于IMU/GPS(Inertial Measurement Unit,IMU/Global Positioning System,GPS)测量数据的运动补偿方法。这种运动补偿方法受3个因素的限制^[2-5]：数据获取时天线相位中心(Antenna Phase Center,APC)的测量精度；运动补偿时因地形变化导致的平地假设不成立；CS算法、波数域算法等频域成像算法中的波束中心近似^[6-8]。其中第1个因素主要引入残余运动误差，可利用高精度的定位定向系统(Position and Orientation System,POS)^[9]来降低其对定位精度的影响，第2个因素可利用外部数字高程模型(Digital Elevation Model,DEM)进行基于地形的运动补偿^{[10, 11]}，最后一个因素主要引入残余的运动补偿误差，对该类误差目前还没有合适的算法可以完全消除，只能通过子孔径运动补偿算法^[12-14]降低其影响。

在使用高精度POS进行运动补偿时，SAR的几何定位精度主要受平地假设和波束中心近似的影响。德国宇航中心(DLR)的研究者针对这一问题相继提出了考虑地形的重轨干涉SAR 运动补偿算法^[10]和PTA(Precise Topography and Aperture-dependent motion compensation)算法^[14]。但这两种算法都存在一定的不足，前者在时域和频域分辨率上存在矛盾，并且精度不够高，对于合成孔径时间较长的系统在地形起伏剧烈、载机运动轨迹偏移较大的情况下不能实现高精度的运动补偿；后者精度高但运算量大，无法应用于数据的批量处理^[11]。

本文提出了一种快速几何精校正算法，该算法能够在满足精度的同时实现快速处理。本文的内容安排如下：第1节简单介绍了影响几何定位的误差来源和研究现状，明确了本文的研究范畴；第2节分析了平地假设和波束中心近似引起的相位误差及其对几何定位的影响，以及本文提出的算法原理和算法运算量分析；第3节和第4节分别进行了仿真分析和实测数据验证；最后对本文内容进行了总结概括。

2 算法原理

文献^{[3, 4]}详细研究了残余运动误差对已聚焦SAR图像影响，方位向几何定位误差直接与合成孔径时间内残余运动误差的线性项相关：

$\Delta x = - {r_0}\frac{{\partial \delta \Delta r}}{{\partial x}}$

(1)

其中，Δx表示方位向定位误差，r₀表示最近斜距，δΔr表示残余运动误差。为进一步说明残余运动误差对方位向几何定位的影响程度，将式(1)作如下调整：

$\Delta x=-{{r}_{0}}\frac{\delta \Delta {{r}_{L}}}{L}=-\frac{\delta \Delta {{r}_{L}}}{2\tan ({{\theta }_{\text{bw}}}/2)}$

(2)

其中，L表示合成孔径长度，$\delta \Delta {{r}_{L}}$表示合成孔径时间内δΔr的变化量，θ_bw表示方位向波束宽度。对于文献^[9]使用的高精度POS而言，位置精度可达0.05 m，当θ_bw为12°时，Δx的最大误差为0.24 m，但由于POS的测量误差随时间缓慢变化，在合成孔径时间内的线性漂移量要小于最大误差，从而在使用高精度POS进行运动补偿时，残余运动误差对方位向几何定位误差造成的影响可以忽略。除了基于POS数据的运动补偿算法外，还有一类基于SAR数据的运动补偿算法，该类算法通过重建运动误差或APC运动轨迹来实现运动补偿，然而该类算法的APC重建精度与高精度POS相比还有很大的差距，因此本文所提算法仅考虑高精度POS测量的运动数据。接下来重点分析平地假设和波束中心近似对SAR方位向几何定位精度的影响。

2.1 平地假设和波束中心近似导致的相位误差

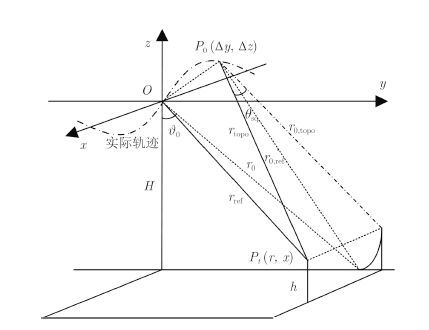
图 1是基于POS测量数据的机载SAR系统运动补偿几何关系示意图。其中x轴表示理想轨迹，xOz 表示交轨平面，点划线表示载机实际轨迹，Δy和Δz分别表示切航向水平和垂直运动误差，P₀(Δy,Δz)和P_t(r,x)分别表示天线相位中心(Antenna Phase Center,APC)和地面目标点的位置，θ_sq表示目标点斜视角，$\vartheta \!$₀表示波束中心的雷达视角，H和h分别表示飞行高度和目标点高程(相对参考平面高度)，r₀表示目标点的最近斜距，r_ref和r_topo分别表示目标点的参考斜距和实际斜距，r_0,ref和r_0,topo分别表示交轨平面内目标点的参考最近斜距(平地假设)和实际最近斜距。

传统的运动补偿(Motion Compensation,MoCo)方法为两级运动补偿方法^[6]，该方法为保证运动补偿的效率，一方面对不同目标点使用同一参考高度进行补偿，这一操作称为平地假设；另一方面在同一方位时刻，对波束照射范围内的所有目标均按照波束中心目标的运动补偿量进行补偿，这一操作称为波束中心近似。根据图 1所示的运动补偿几何关系，该方法的相位补偿量可表示为：

$\begin{align} & {{\phi }_{\text{ref}}}(r,x)=\frac{4\pi }{\lambda }\Delta {{r}_{0,\text{ref}}}(r,x)= \\ & \frac{4\pi }{\lambda }({{r}_{0,\text{ref}}}(r,x)-{{r}_{0}}(r,x)) \\ \end{align}$

(3)

其中λ表示波长。由于地面目标的高程不是平坦不变的，并且运动误差存在方位空变性，采用两级运动补偿方法进行运动补偿将导致残余相位误差。根据SAR的运动补偿几何关系，实际相位补偿量应为：

$\begin{aligned} {\phi _{{\rm{topo}}}}(r,x) = & \frac{4\pi }{\lambda }\Delta {r_{{\rm{topo}}}}(r,x)\\ = & \frac{4\pi }{\lambda }({r_{{\rm{topo}}}}(r,x) - {r_{{\rm{ref}}}}(r,x)) \end{aligned}$

(4)

式(4)中Δr_topo(r,x)可近似表示为：

$\begin{aligned} \Delta {r_{{\rm{topo}}}}(r,x) = & {r_0}\sqrt {{{\bigg(\frac{{\Delta {r_{0,{\rm{topo}}}}}}{{{r_0}}} + 1\bigg)}^2} + {{\tan }^2}{\theta _{{\rm{sq}}}}(x)} \\ & - {r_0}\sqrt {1 + {{\tan }^2}{\theta _{{\rm{sq}}}}(x)} \\ \approx & \Delta {r_{0,{\rm{topo}}}} \cdot \cos {\theta _{{\rm{sq}}}}(x) \end{aligned}$

(5)

平地假设和波束中心近似导致的相位误差表达式如下：

$\begin{aligned} {\phi _{{\rm{err,topo}}}}(r,x) = & {\phi _{{\rm{topo}}}}(r,x) - {\phi _{{\rm{ref}}}}(r,x)\\ \approx & \frac{4\pi }{\lambda }({r_{{\rm{0,topo}}}} - {r_{\rm{0}}}) \cdot \cos {\theta _{{\rm{sq}}}}(x)\\ & - \frac{4\pi }{\lambda }({r_{0,\; {\rm{ref}}}} - {r_{\rm{0}}}) \end{aligned}$

(6)

当波束宽度θ_bw较小时，式(6)可进一步简化为：

${\phi _{{\rm{err,topo}}}}(r,x) \approx \frac{4\pi }{\lambda }({r_{{\rm{0,topo}}}} - {r_{0,{\rm{ref}}}})$

(7)

其中r_0,ref和r_0,topo可根据几何关系表示为：

${r_{0,{\rm{ref}}}} \!=\! \sqrt {{{(H + \Delta z)}^2} + {{\Big(\sqrt {r_0^2 - {H^2}} + \Delta y\Big)}^2}}$

(8)

${r_{0,{\rm{topo}}}} \!=\! \sqrt {{{(H \!-\! h \!+\! \Delta z)}^2} \!+\! {{\Big(\sqrt {r_0^2 \!-\! {{(H \!-\! h)}^2}} \!\!+\! \!\Delta y\Big)}^2}}$

(9)

2.2 方位向快速几何精校正

2.1小节分析了平地假设和波束中心近似导致的相位误差，并通过推导获得了相位误差的表达式Φ_err,topo(r,x)。由于方位向几何定位误差与残余运动误差导致的残余相位误差线性项成正比^{[3, 4]}，可通过计算Φ_err,topo(r,x)的线性项系数来校正方位向几何定位误差。

$\begin{aligned} \frac{{d{\phi _{{\rm{err,topo}}}}}}{{dx}} = & \frac{{\partial \phi }}{{\partial \Delta y}}\frac{{d\Delta y}}{{dx}} + \frac{{\partial \phi }}{{\partial \Delta z}}\frac{{d\Delta z}}{{dx}}\\ \approx & \frac{{4{{π}} \Big(\sqrt {r_0^2 - {{(H - h)}^2}} - \sqrt {r_0^2 - {H^2}} \Big)}} {{\lambda {r_0}}}\\ & \cdot \frac{{d\Delta y}}{{dx}} - \frac{{4{{π}} h}}{{\lambda {r_0}}}\frac{{d\Delta z}}{{dx}} \end{aligned}$

(10)

式(10)表明，线性运动误差和地形起伏耦合是引起方位向几何定位误差的关键因素，线性运动误差和地形起伏越大，引起的方位向几何定位误差越大。水平误差Δy和高度误差Δz的线性项系数可通过对目标点在合成孔径时间内对应的运动误差进行线性拟合获得，最终通过式(11)计算SAR图像的方位向定位误差Δx。得到Δx之后即可通过方位向插值实现快速几何精校正。

$\Delta x=-\frac{1}{2\pi }\frac{d{{\phi }_{\text{err},\text{topo}}}}{dx}$

(11)

进一步总结快速几何精校正算法的流程，如图 2所示。

根据图 2可知，本算法通过POS数据获得的运动补偿数据、SAR的图像参数和外部DEM，根据式(10)和(11)来计算方位向定位误差Δx，然后通过方位向插值完成几何精校正。算法流程的关键点在于快速计算式(10)中的运动误差线性项系数$\frac{{d\Delta y}}{{dx}}$和$\frac{{d\Delta z}}{{dx}}$。为降低线性拟合的计算量，可考虑以下两点：由于合成孔径时间随r₀缓慢变化，在距离向可由逐距离门计算改为每隔N_k个距离门计算一次；在方位向逐点线性拟合时可充分利用前一点的中间结果，从而最大限度地降低线性拟合的计算量。通过最小二乘线性拟合公式可得$\frac{{d\Delta y}}{{dx}}$计算式，见式(12)：

$\frac{{d\Delta y}}{{dx}} = \frac{{{\Large{\sum}} {x_i^2} \cdot {\Large{\sum}} {\Delta {y_i}} - {\Large{\sum}} {{x_i}} \cdot {{{\Large{\sum}} {{x_i}\Delta y} }_i}}}{{N \cdot {\Large{\sum}} {x_i^2} - \Big({\Large{\sum}} {{x_i}{\Big)^2}} }}$

(12)

其中，N表示合成孔径时间内对应运动误差数据的点数，一般取64或128点即可。式(12)中$\sum {x_i^2}$,$\sum {{x_i}}$和$N \cdot \sum {x_i^2} - \Big(\sum {{x_i}{\Big)^2}}$为定值，只需要计算一次；而在计算当前点的$\sum {{y_i}}$和${\sum {{x_i}y} _i}$ 时，可利用上一点的中间结果，如式(13)所示：

$\left. \begin{gathered} \sum {{\text{ }}y_i^{{\text{cur}}}} = \sum {{\text{ }}y_i^{{\text{pre}}}} - {\text{ }}y_1^{{\text{pre}}} + {\text{ }}y_N^{{\text{cur}}} \hfill \\ \sum {x_i}{y_i}^{{\text{cur}}} = \sum {{x_i}{\text{ }}y_i^{{\text{pre}}}} - {x_1}{\text{ }}y_1^{{\text{pre}}} + {x_N}{y_N}^{{\text{cur}}} \hfill \\ \end{gathered} \right\}$

(13)

其中，cur标识当前点计算，pre标识上一点运算。通过以上两步可大大降低线性拟合的计算量，从而实现快速几何精校正。

2.3 快速算法运算量分析

为进一步说明本文提出的快速算法的高效性，表 1列出了PTA算法和快速算法的运算量表达式。其中N_a和N_r分别表示SAR图像方位向和距离向像素点数，W表示PTA算法FFT点数，K表示拉格朗日插值点数。W可取64或128,K一般取8。通过两种算法的运算量表达式不难看出，PTA算法因为要进行两次FFT和一次复乘运算，运算量较大，而本文提出的快速算法只需插值即可完成几何校正，运算量较小。

3 仿真分析

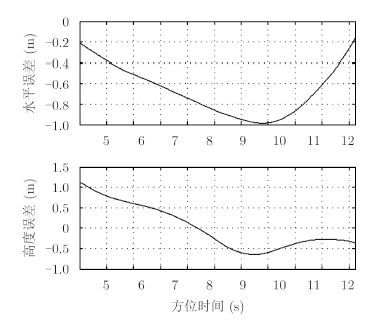
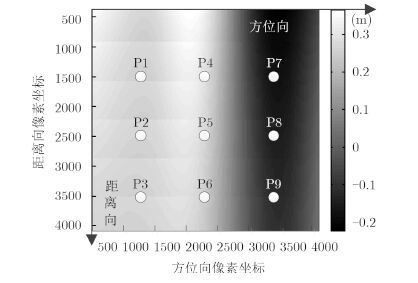
仿真系统为机载Ku波段调频连续波(Frequency Modulated Continuous Wave,FMCW)体制SAR，仿真参数如表 2所示。在几何误差产生机理方面，脉冲体制SAR与FMCW体制SAR是相同的，本文所提算法对脉冲体制SAR同样适用。生成回波数据时使用的运动误差数据(水平误差Δy和高度误差Δz)如图 3所示，该运动误差数据来自某次飞行实验采集的实测数据。在不同距离向和方位向均匀设定9个点目标，点目标设定位置如图 4所示。点目标高度在[-20, 20] m区间内等间隔选取。

仿真回波数据经过两步运动补偿和成像处理之后获得点目标图像，图像大小为方位向2048像素点距离向4096像素点。分别使用PTA算法和本文提出的快速算法对点目标成像数据进行几何校正处理，PTA算法耗时13 min 1 s，快速算法耗时2 min 17 s，效率提高4.7倍，验证了快速算法的效率。表 3给出了仿真条件下点目标方位向定位误差的仿真值和PTA算法与快速算法处理后的方位向定位残余误差。通过表 3可验证快速算法同样能够精确校正点目标的方位向定位误差，验证了快速算法的有效性。

快速算法求得的方位向定位误差Δx分布如图 4所示。在表 2所示的仿真参数和图 3所示的运动误差下，Δx在[-0.2,0.3] m范围内变化。Δx的变化范围表明：在波长较短，飞行高度偏低，运动误差较大，地形存在一定程度的起伏，由运动误差和地形起伏耦合造成的SAR图像方位向定位误差量级已达一到两个像素，当几何定位精度要求较高时不容忽略(1:2000制图下要求地图平面定位精度为0.2 m)，验证了几何精校正的必要性。

4 实测数据验证

对中国科学院电子学研究所的Ku波段机载FMCW SAR系统获取的SAR数据利用快速算法进行处理，以验证该算法的有效性，并从精度和效率两方面与现有算法进行比较。

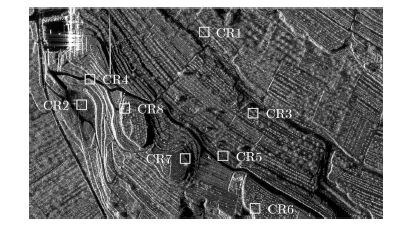
实测数据经过两步运动补偿和成像处理之后获得单视复图像(Single Look Complex,SLC)，如图 5所示。图 5标注了8个三面角反射器在SAR图像中的位置，角反射器的海拔高度和平地假设使用的参考高度之间的高程差见表 4。通过SAR的成像几何、SAR天线相位中心的运动轨迹、角反射器在大地坐标系中的位置(经纬高)和定标点在SAR图像中的位置可计算出定标器在SAR图像中的方位向几何定位误差定标值也在表 4中给出。

SAR图像尺寸为方位向4096像素点距离向8192像素点。分别使用PTA算法和本文提出的快速算法对SLC进行几何校正处理，PTA算法耗时53 min 20 s，快速算法耗时9 min 28 s，效率提高4.6倍，再次验证了快速算法的效率。经过两种算法处理后，方位向几何定位残余误差见表 4。

实测数据处理结果表明在保证效率的同时，本文提出的快速几何精校正算法能够达到和PTA算法同样的校正精度，进一步验证了该算法的有效性。值得说明的是经过几何精校正之后，两种算法在一些定标点上的残余误差较大，如CR5达到了0.05 m，其原因是定标点测量时存在一定量级的误差。

5 结论

本文针对基于DEM数据的机载SAR几何精校正进行了深入研究，推导了传统的两级运动补偿采用平地假设和波束中心近似在地形存在起伏时造成的残余相位误差表达式，并分析了其对SAR方位向几何定位的影响，从而说明高分辨率机载SAR基于高精度DEM的几何精校正的必要性。分析了现有基于DEM的高精度运动补偿算法在效率方面的不足，提出一种基于高精度DEM的快速几何精校正算法。该算法在残余相位误差表达式的基础上，推导了线性相位误差的近似表达式，利用FFT的时移性质，将线性相位误差进一步表示成方位向几何定位误差，从而通过方位向插值快速完成几何精校正。利用本文提出的快速算法进行了仿真和实测数据处理，结果验证了本文方法在方位向几何校正方面的有效性，并通过与PTA算法进行对比验证了快速算法在处理效率方面的优势。