(北京市嵌入式实时信息处理技术重点实验室 北京 100081)
(Beijing Key Laboratory of Embedded Real-time Information Processing Technology, Beijing 100081, China)
作为人类探测环境的重要工具,雷达已经经历了上百年的发展史,并形成了完善的雷达信号处理学科体系,对目标的信息获取能力越来越强大,极大地提高了战争中搜索、跟踪目标的能力[1]。然而随着隐身技术、反辐射导弹(ARM)、综合电子干扰(ECM)和低空突防技术的发展,特别是隐身技术的迅速发展,对雷达提出了新的要求和新的挑战[2]。传统雷达已经难以应付这种挑战,雷达的生存构成受到严重威胁,必须寻找新的技术发展途径。人们提出并研制了多种新体制雷达,例如超宽带雷达、长波段雷达、组网雷达和双基地雷达等。其中双基地雷达因其收发分置的几何配置特点带来了许多传统单基地雷达所无法拥有的优势。
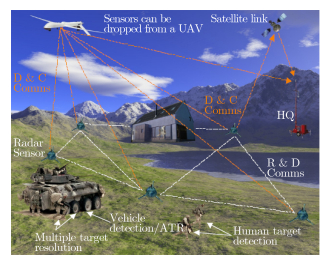
双基地雷达可以定义为发射机和接收机互相分离的雷达系统,而其双基地角定义为发射机到目标连线和接收机到目标连线的夹角。如果双基地角大于135°,则接收机位于目标的前向散射区,在这个区域内,目标的雷达散射截面积(Radar Cross Section,RCS)随双基地角的增大而迅速增大,通常比单基地RCS大十几到几十dB,当双基地角等于180°时,目标RCS达到最大值。我们将接收机工作于目标前向散射区的雷达称为前向散射雷达(Forward Scatter Radar,FSR)[3, 4],其典型系统结构如图 1所示。FSR利用了目标RCS在前向散射区所体现出的诸多特性,对反隐身和小型目标探测具有重要意义。

|
图 1 前向散射雷达系统结构 Fig.1 Configuration of FSR system |
FSR通常利用目标穿越基线时的前向散射信号来进行动目标的检测、跟踪、成像和识别。与传统的单基地雷达和双基地雷达不同,FSR的工作是基于目标对电磁波的衍射效应,而非散射效应。由电磁场理论知,当目标被电磁波照射时,其自身表面电流会感应产生自散射场,同时如果目标尺寸大于或等于波长,由于目标边缘对电磁波的衍射效应,在目标的后面会产生阴影场[5, 6]。阴影场主要存在于双基地角为180°附近的区域内,也叫做前向散射场。在这个区域阴影场通常远大于目标的自散射场,可以近似忽略自散射场的影响。很重要的一点是阴影区域的目标散射截面积(Radar Cross Section,RCS)仅由目标的轮廓决定,而与它的3维形状或材料无关。
当前的雷达隐身技术主要通过减弱、抑制、吸收和偏转目标的雷达回波来降低目标RCS,使其在一定范围内难以被敌方雷达发现和识别。但考虑到目标前向散射RCS不受目标形状和材料影响的特点,传统的隐身技术在前向散射区将完全失效。同时目标RCS在前向散射区迅速增强,通常比单基地雷达大十几到几十dB,也有效地提高了系统的敏感性[7],因此隐身目标探测是FSR的重要应用方向之一。此外,基于目标在前向散射区较强的RCS,也可利用FSR组网探测低空飞行的小型飞行器及行人、车辆等地面运动目标,在要地防空和战场势态感知方面发挥重要作用。由此可以看出前向散射雷达在目标探测方面的重大优势所在。本文首先简要回顾了双基地前向散射雷达国内外发展历程和研究现状。在此基础上,对双基地前向散射运动目标探测和双基地前向散射阴影逆合成孔径成像这两个关键技术进行了着重的展开描述,详细介绍了一些关键问题的解决方法以及最新的研究成果。进一步地,对基于卫星信号的双基地前向散射探测技术的发展进行了展望。最后一节给出结束语。
2 研究历史与现状 2.1 国外研究历史与现状虽然前向散射区RCS的增强效应很早就被发现,并且一些早期的双基地雷达也具备在前向散射区工作的能力,如著名的AN/FPS-23 Flutter雷达等,但是由于FSR的信号处理技术在此期间并没有得到相应的发展,造成前向散射效应对目标探测带来的优点一直没有被充分利用起来。直到20世纪80年代末期,随着双基地雷达目标检测与跟踪技术的迅速发展,才极大地推动了前向散射雷达的研究步伐,使得前向散射雷达的研究进入了一个新的阶段。
最初设计研制FSR的目的主要是为利用前向散射区较强的RCS和其反隐身的潜力,探测隐身目标和低空飞行的飞机、导弹等目标。上世纪八九十年代,俄国人对FSR进行长时间的研究,并开发了大型的实验系统。其FSR系统工作于UHF波段(波长0.77 m),发射天线和接收天线立于30 m高的杆上,两者相距40 km。实验目标包括Jak-52教练机、L-29喷气飞机和米-2直升机等,其飞行高度都在100~200 m。实验结果表明,当目标穿越基线上方且双基地角大于135°时都可以获得20 dB以上回波信噪比,而回波信噪比最大可达到60 dB以上[8]。鉴于系统采用了阵列接收天线以获得多通道回波,俄国人同时研究了基于匹配滤波的检测算法[9]、基于空时处理的量测参数估计算法[10]和基于高斯牛顿迭代的跟踪算法[11]。
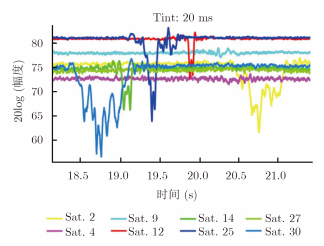
考虑到前向散射效应带来的强RCS可以弥补无源探测较弱的发射信号功率,利用导航卫星作为发射源,地面布置接收机构成前向散射配置来探测空中目标也是FSR的发展方向之一。最早的,德国的GmbH 公司的V. Koch和R. Westphal于1995年在IEEE上发表文章[12],提出使用全球导航卫星系统(GNSS)进行无源多基地探测。对所采集的4组实验信号数据的信噪比做了对比,实验目标为小型螺旋桨飞机和轻型喷气式飞机,分析结果表明所获得的散射信号与目标之间是相关的。2012年,德国弗劳恩霍夫集成电路研究所的研究人员发表了利用GPS信号探测空中目标的最新成果[13],实验利用GPS卫星作为发射机,利用右旋极化的半球天线作为接收机,在纽伦堡机场跑道附近的不同位置观测飞机穿越时的GPS前向散射信号。由于积累时间较短(处理间隔变短),其数据率较Koch的结果有所改善。分析结果表明,依据飞机穿越位置、卫星信号和接收位置的不同,接收信号会出现不同程度的衰减、提升或震荡。图 2是飞机穿越基线时同一位置接收到的不同卫星的前向散射信号,可以看出由于飞机的遮挡效应,可以明显观测到最大约30 dB的衰减,但同时也有一定提升产生,但最大不超过2 dB,这是由于飞机位置不同引起弗朗禾费衍射所导致。
|
图 2 利用不同卫星观测到的前向散射信号(20 ms非相参积累)[13] Fig.2 Forward scatter signal observed by different satellites (20 ms non-coherent accumulation)[13] |
近些年来隐身技术也开始广泛应用于地面/海面运动目标(如战车、坦克、舰船等)。考虑到FSR对弱RCS目标探测的优势,通过设计体积小、功耗低、易于布置且难以被发现的小型FSR并组网布置,可以实现对特定区域的势态感知,如图 3所示,在对地面车辆、海面舰艇探测方面具有一定优势[14]。进入21世纪以来,在英国伯明翰大学,由M. Cheniakov带领的MISL(Microwave Integrated Systems Laboratory)实验室开展了一系列有关前向散射雷达地面/海面运动目标探测的研究工作,并通过国际合作交流的方式发展了马来西亚、保加利亚、意大利及中国的科研人员参与到FSR的研究中来。伯明翰大学开发的小型多频FSR系统可以工作于VHF和UHF波段,使用包络检波从直达波中提取目标的散射信号[15]。
在地面目标探测方面,伯明翰大学的研究主要是针对车辆分类识别开展。其中,R. Abdullah等在2006年给出了基于回波功率谱的车辆目标识别方法[16],其采用估计过零点数的方法求解目标速度,并利用主成分分析和最近邻法进行分类,对实验数据的处理结果表明正确分类率可达60%以上。此外,R. Abdullah还给出了一种基于神经网络的车辆分类方法[17]。在海面目标探测方面,主要由L. Daniel领导的小组进行研究,其采用的系统频段较高(7.5 GHz),架设于海峡两侧,基线长度约数百米。对不同大小的舰船目标,其观测到了形式差别较大的回波[18]。
FSR不仅可以对隐身目标进行有效的检测与跟踪,而且在应用阴影逆合成孔径雷达(Shadow Inverse Synthetic Aperture Radar,SISAR)理论后,可以增加对目标成像和目标识别的能力,为目标分类识别提供了一种非常有效的新途径,也使得FSR的研究进入了一个新的阶段。上世纪80年代俄国人V. V. Chapursky发现前向散射阴影场与目标侧影轮廓之间存在一定数学对应关系,进而提出了SISAR成像技术。
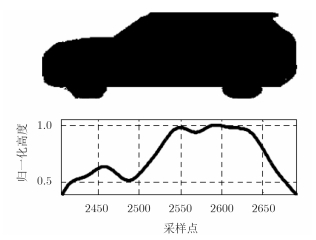
早期关于前向散射SISAR成像研究主要是以空中运动目标为研究对象。文献[19]基于小衍射角假设、夫琅禾费近似,首次提出了SISAR信号处理方法,使前向散射雷达具备了运动目标成像与识别能力。文献[20]在文献[19]基础上,基于小衍射角假设、菲涅耳近似,对信号模型和成像算法进行了改进,克服了夫琅禾费近似条件不满足的情况。虽然这一时期的理论研究成果对前向散射雷达意义重大,但并未引起较多关注。直至2000年,V. V. Chapurskiy在国际雷达会议上公布了SISAR研究成果,并给出了实验结果,SISAR信号处理方法才得到了广泛的关注[21]。V. V. Chapurskiy在文章中指出利用目标前向散射信号功率谱函数差异,可对运动目标进行识别;并给出了小观测角度下MiG-21、MiG-31及An-26三种不同形状飞机的前向散射雷达实验回波信号的功率谱函数,其形状各异且与飞机的轮廓函数一一对应,首次实验验证了SISAR 理论用于空中运动目标成像的正确性及目标识别的潜力。2015年,伯明翰大学发表了基于收发相参同步的FSR对地面车辆的SISAR成像结果[22](如图 4所示),验证了收发同步条件下的SISAR成像能力。
2.2 国内研究历史与现状国内方面,早期有关FSR的研究主要由西安电子科技大学开展,其研究工作主要是在俄罗斯人研究基础上,对空中运动目标成像技术进行理论分析与实验验证[23,24,25,26,27,28,29]。文献[23]提出利用小波分析的方法,抑制杂波对SISAR成像的影响;文献[24]分析了空中目标高度及位置对侧影像的影响,提出了利用目标侧影像归一化极点相对位置作为特征量的目标识别方法。文献[25]对文献[23]和文献[24]中信号模型进行改进,考虑了时间二次项对信号相位的影响。文献[26]对空中目标轮廓中线提取方法进行了研究,用侧影像相邻分辨单元幅度及相位关联特征判断相位的卷绕,应用条件约束重构目标中线。文献[27]利用地面车辆进行了L波段前向散射实验,获得了目标高度差像。文献[28]和文献[29]分别给出了两种成像参数估计方法,适用于小衍射角SISAR成像运动补偿。
北京理工大学自2006年起与英国伯明翰大学MISL实验室的FSR小组开展联合研究,在前向散射雷达杂波特性分析、运动目标参数估计与多目标分辨特性方面取得了丰富的研究成果。主要对地表杂波的幅度和频谱统计特性进行了详细研究,给出了地面运动目标速度的最优估计方法,并开展了多角度联合参数估计的实验研究。在此基础上,基于我国新一代导航卫星系统(北斗二代),开展了基于导航卫星信号进行空中目标探测的可行性验证实验,成功获取了民航客机的前向散射信号[30]。此外,北京理工大学从2010年起陆续发表了一系列有关SISAR成像技术的文章,其主要侧重于大衍射角SISAR成像和SISAR成像实验验证,对SISAR成像技术的进展起到了重要的推动作用。
3 双基地前向散射运动目标探测与传统单基地雷达相比,FSR的突出特点主要体现在两个方面:独特的散射机理及无距离向分辨能力。考虑到FSR系统是基于电磁波的衍射特性,而不是传统的后向散射特性,因此无论是信号模型还是杂波模型都与传统形式存在较大差异。同时,FSR距离分辨能力的缺失也给信号处理带来很多困难:首先雷达覆盖的大范围区域的杂波都会进入接收机,杂波强度非常大;其次无距离分辨能力导致系统无法直接定位,只能依靠回波多普勒等信息非线性求解目标运动参数。因此,前向散射杂波统计特性分析与高精度目标运动参数估计是前向散射雷达运动目标检测与跟踪的技术基础。这一节将从目标前向散射特性、杂波统计特性、运动目标参数估计方法及实验验证4个方面进行论述。
3.1 双基地前向散射RCS计算双基地前向散射RCS大于后向散射 RCS很早即被观察到,并应用到了双基地雷达的设想中。最早的R. E. Hiatt等在1960年给出了双基地角为180°时前向散射RCS的计算公式(1),并通过实验进行了验证[31]:
| $ {\sigma _{{\text{FS}}}} = \frac{{4\pi {A^2}}}{{{\lambda ^2}}} $ | (1) |
其中,A为目标在入射波方向的投影面积,$\lambda $为波长。式(1)表明,目标前向散射RCS仅与投影面积和波长有关,与目标3维形状和涂覆材料无关。进一步基于巴比涅原理,J. I. Glaser指出目标散射场与入射场照射一个其上开口形状与目标投影轮廓相同的无限大不透明屏是相同的[32]。因此,在双基地角接近180°时,前向散射RCS可以写为:
| $ {\sigma _{{\text{FS}}}} = \frac{{4\pi }}{{{\lambda ^2}}}{\left| {\iint {{\text{exp}}\left( {{\text{j}}\;k \cdot {\text{ }}\rho } \right){\text{d}}s}} \right|^2} $ | (2) |
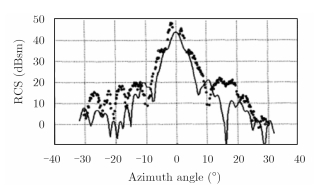
其中,k为波数矢量,ρ为目标侧影平面的坐标矢量,ds为微分表面积。当双基地角等于180°时,式(2)就退化为式(1)。式(2)表明,前向散射RCS随角度的变化与相同形状且均匀照射的天线方向图相同。随后,J. I. Glaser在1989年也给出了一些双基地在180°时的实测前向散射RCS结果[33]。1999年,A. B. Blyakhman等首次公开发表了真实飞机的前向散射回波功率的实测结果[8],如图 5所示,其中点线表示根据实测回波信噪比换算得到的RCS,实线表示利用式(2)得到的仿真值。
3.2 前向散射杂波特性分析与物理建模杂波背景中的信号检测通常要获知杂波的统计特性,以此确定最优检测策略及杂波抑制方法。针对前向散射杂波特性分析与物理建模这一问题,北京理工大学与伯明翰大学合作开展了一系列研究[34,35,36,37,38]。
研究首先针对杂波的统计特性进行分析,其主要包括幅度特性和谱特性。对幅度统计特性,3个载波频率的杂波数据统计显示:单通道杂波信号的统计特性曲线在小幅度时非常接近高斯概率密度函数,这也说明了在弱风时,杂波强度较弱且为各均匀散射体的回波数据,因此其统计特性接近高斯分布;而在强风时,由于强散射体(如树干等)的摆动,出现了强散射体杂波,因此杂波的均匀性被破坏,在特性曲线的尾部与高斯曲线有一定的差距,反而更接近于指数分布。
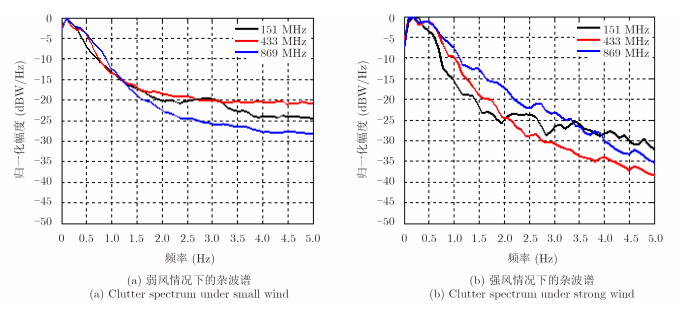
对谱特性,通过对不同风速、频率杂波功率谱的分析发现了前向散射情况下杂波的谱扩展对风速极不敏感这一特殊现象,风速的增加主要是对杂波强度的影响较大;并且同样的风速情况下,杂波的谱扩展与载波频率也不再是载波频率之比的比例关系,杂波的谱扩展也几乎相同,只有在强风的时候略有差异不同强度的杂波谱信号几乎相同,也即杂波谱特性并没有随着风速的增加而成比例的增加。例如图 6中的实测数据处理完全看不到433 MHz载波频率下的杂波谱宽是151 MHz载波频率下的杂波谱宽3倍的结果。
|
图 6 弱风和强风情况下不同载波频率的杂波谱特征[34] Fig.6 Clutter spectrum characters under different carrier frequencies and wind intensity[34] |
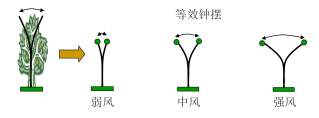
为解释杂波统计分析中一些独特的现象,结合前向散射雷达回波多普勒信号的形成条件,提出了利用钟摆模型对植被杂波的强度和谱扩展特性进行定性的解释。如图 7所示,前向散射雷达的植被杂波可以采用单摆振子模型来建模分析解释,等效为大量的单摆振子进行无规则的单摆振动,摆动幅度随风速变化;每个单摆振子具有自己固定的摆动周期,也即具有自己固定的振荡频率,在接收端形成具有接近各自振荡频率的整个杂波信号。钟摆模型下定性解释和理论分析得到的结果与实测数据处理结果的一致性充分表明了模型的有效性[34]。
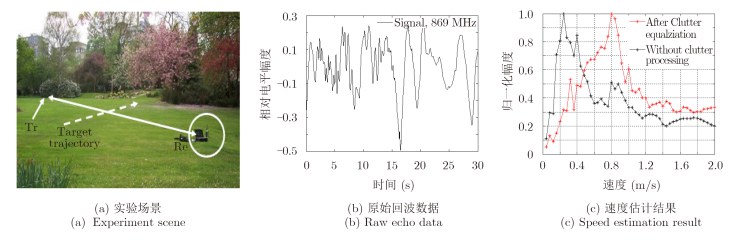
此外,基于功率谱模型拟合的方法对杂波信号的功率谱进行了估计,对比了各种经典的功率谱模型与真实杂波数据功率谱形状的差异,选定AR模型拟合实际功率谱密度函数;利用拟合的功率谱数学模型进行了杂波抑制的处理,而实测数据的处理结果充分地验证了杂波抑制方法的有效性。图 8给出了一组经过杂波抑制处理的目标运动速度估计结果,实验目标为人,载波频率869 MHz。可以看出,在较高的载波频率下,杂波信号太强,目标信号完全被淹没。杂波抑制前和杂波抑制后的速度估计处理结果差异非常明显:在杂波抑制前,无法进行有效的目标速度估计,而在杂波抑制后,其速度估计曲线较为平滑,存在明显的峰值,并得到了精确的速度估计结果,充分表明了在高载波频率杂波抑制的必要性,也证明了估计的杂波功率谱模型的有效性。
3.3 目标运动参数估计与杂波分析相类似,FSR中的目标运动参数估计也是研究的难点与重点之一。按照目标的不同划分,FSR中的运动参数估计主要分为地面/海面目标运动参数估计和空中目标运动参数估计。前者目标较小且速度较低,受雷达限制,一般只能获取单通道回波数据;后者目标较大且速度较快,一般通过阵列天线获取多通道回波数据,可以进行多普勒和波达角的估计。这些诸多的差异也决定了两者信号处理方法的不同。
北京理工大学自2008年起与MISL实验室联合发表了一系列有关FSR地面目标运动参数估计的文章[39,40,41,42,43]。研究首先在考虑多径影响、发射极化类型、球面波效应、观测角度非线性变化及面目标模型的基础上建立了地面运动目标的精确信号模型,并对接收回波功率进行了分析计算[40]。在信号建模和功率分析的基础上,基于最优信号处理理论,提出了一种速度参数估计方法,并详细地分析了各种非理想因素(非正交轨迹、非中点位置穿越基线及非零加速度情况)对速度估计性能的影响,并通过仿真数据和实测数据的处理对估计方法和非理想因素的影响进行了验证[42]。考虑到实际情况中目标穿越基线中点的情况较少,并且穿越的位置点严重影响目标的多普勒信号,从而造成目标速度估计的偏差较大。因此在最大似然估计理论框架下,提出了任意情况下的多参数联合非线性估计方法,该方法可以同时得到目标运动速度和穿越点位置的估计,并推导获得了解析的克拉美罗界,进一步扩充了系统的工作区域和提高了系统的参数估计精度[43]。
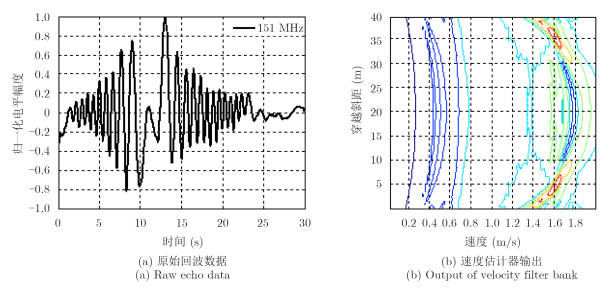
图 9给出了一组多参数联合非线性估计的结果。在实验的设计中,目标(人)垂直穿越基线,穿越点离发射机距离10 m,基线长度50 m,载波频率为151 MHz。从图 9中的处理结果可以看出,目标的估计速度为1.62 m/s,目标的穿越位置估计值为10 m和40 m,与真实值基本一致。多参数联合的估计方法能够精确地估计出目标的基线穿越位置,为沿基线方向提供一定的分辨能力奠定了基础。
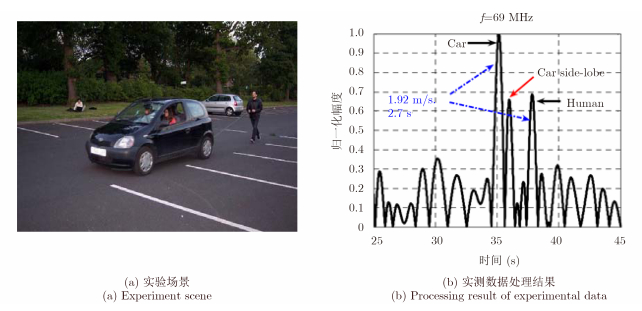
除此之外,也基于实验数据对FSR对地面编队目标的分辨能力进行了验证。图 10是一大一小两目标编队情况,大目标为车辆,小目标为人。在实验中,两目标的距离设置为5 m,目标之间通过细绳相连保持固定的间距和相同的速度。通过对实测信号的估计处理,速度估计值为1.92 m/s,峰值之间的时间间隔为2.65 s,因此估计的目标隔离度约为5.08 m,非常接近设置值,同时两个目标峰值清晰可见,表明两目标得到了较好的分辨。
在FSR空中目标运动参数估计方面,北京理工大学在俄国人研究的基础上进行了诸多改进,进一步提高了目标的初值估计和跟踪精度[44,45,46,47]。其中针对传统FSR目标跟踪中存在的初始状态估计误差太大、跟踪保持阶段数据率低、计算量大、稳定性差的问题,在2013年提出了一种修正的FSR 3维跟踪算法,算法基于解析推导和Levenberg-Marquardt算法提出了一种新的初始状态估计方法,在相同参数估计精度下,初值估计误差比经典方法降低了一个数量级,并使用修正的扩展卡尔曼滤波算法进行跟踪保持[44]。最近在2015年IEEE雷达会议上发表的文章给出了一种基于最小二乘的FSR跟踪初值估计算法[46],该方法在对观测噪声和不同航迹的适应能力上都远优于现有算法。
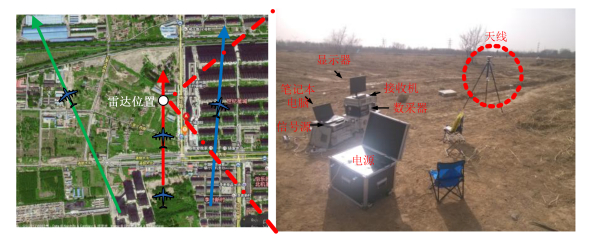
3.4 基于北斗导航卫星信号的前向散射目标探测北京理工大学在2015年自主开展了一系列基于北斗导航卫星信号探测空中运动目标的验证实验。实验利用北斗导航卫星作为发射源,地面布置接收机,构成前向散射配置探测首都机场附近起降的民航客机目标。实验场地上方有数条民航客机飞行通道。采用全向天线接收导航卫星信号,如图 11所示。
|
图 11 民航客机探测实验场景与实验设备 Fig.11 Experiment scene and equipment for civil airbus detection |
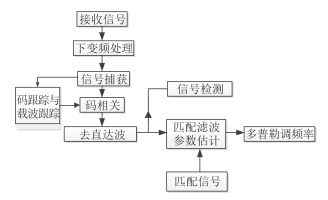
对接收回波,采用导航星信号处理中的码相关技术提取前向散射信号。理论分析表明,相参积累后的信号包络可以看作直达波信号与前向散射信号的一路正交分量相参叠加的结果,这样可以去除直达波的影响,利用抽取的前向散射信号进行目标检测及参数估计等后续信号处理操作。具体信号处理流程如图 12所示。
基于实验数据处理结果,首次观察到了北斗导航卫星对飞机目标的前向散射信号。如图 13所示,可以明显观察到前向散射场对回波信号的相位和幅度调制,主要表现为近似线性调频多普勒及阴影遮挡现象。
|
图 12 导航卫星前向散射信号处理流程 Fig.12 Processing flow of GNSS forward scatter signal |

|
图 13 北斗导航卫星前向散射信号提取结果 Fig.13 Forward scatter signal extraction of BeiDou navigation satellites |
当目标位于近似远场时,如图 13(a)所示,此时回波多普勒近似为线性调频信号,可以利用回波信号进行相关参数估计。根据理论推导可以给出目标平飞假设下前向散射回波多普勒Kr的表达式[30]:
| $ {K_r} \approx - {v^2}{\text{cos}}{\theta _{{\text{SV}}}}\left( {1 - {\text{co}}{{\text{s}}^2}{\theta _v}\;{\text{si}}{{\text{n}}^2}{\theta _{{\text{SV}}}}} \right)/\left( {\lambda H} \right) $ | (3) |
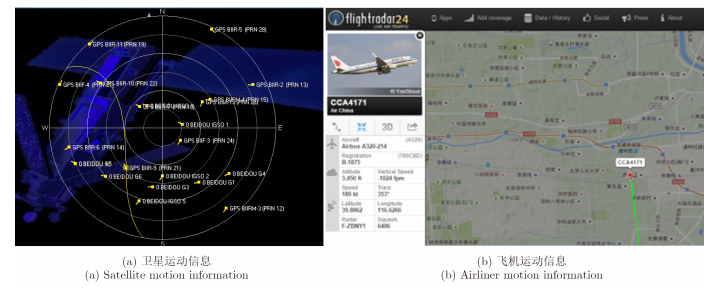
其中,v表示目标绝对运动速度,θSV表示卫星仰角,表示目标运动方向与基线在地面投影之间的夹角,λ表示信号波长,H表示目标距地面垂直高度。上述参数可以通过星历软件和网络查询获得,实际中我们使用了星历软件Obitron来获取卫星运动轨迹,输入接收机经纬度116.637552E,39.899809N和模拟时间,即可以获得此时北斗卫星相对于接收机的位置(俯仰角和方位角),如图 14(a)所示。同时利用航班查询网站Flightradar24获取飞机的运动信息,包括速度、高度、航向及位置等,如图 14(b) 所示。
|
图 14 目标及卫星信息获取 Fig.14 Information acquisition for targets and satellites |
对图 13(a)中的信号,根据Obitron获得其对应的卫星方位角为356.8°,俯仰角为73.8°;根据Flighradar24获得飞机型号为波音747,飞行高度1044 m,飞行速度103 m/s,航向角354°。将上述参数代入式(3)可以计算得到其调频率约为36 Hz/s。同时基于信号匹配的方法可以获得对该信号调频率的估计[42],其调频率估计结果约为31 Hz/s,误差约为14%。考虑到估计误差及航班信息的延迟性,作为理论验证该参数估计结果的精度可以接受。
4 双基地前向散射SISAR成像原理与方法在SISAR成像理论提出后相当长一段时间内对此项技术的研究都处于停滞状态,其原因主要有两点,其一是SISAR成像技术利用了类似于光学中的衍射理论而不是传统雷达成像的后向散射理论,这一点不太容易被接受;其二是一直缺乏适于成像的实验数据作为理论研究的支撑。实际上作为FSR特殊的目标识别技术,SISAR成像在FSR信号处理理论中占有重要地位。北京理工大学自2010年起,一直致力于SISAR成像技术的研究,在成像方法及实验验证方面开展了较多的研究工作[48,49,50,51,52,53,54,55,56,57,58,59,60]。这一节将从SISAR成像原理、成像方法及成像验证3个方面进行论述。
4.1 SISAR成像原理[21]SISAR信号建模及成像方式与传统雷达信号建模及成像方式有很大差异。其中,SISAR成像的目标前向散射信号模型可以通过黑体近似、巴比涅原理以及菲涅尔-基尔霍夫衍射理论得到[4]。
在双基地情况下,当目标被电磁波照射时,散射场由两部分组成:一部分是由入射波在目标表面形成的感应电流产生,被称为目标的自散射场;另一部分是由目标对入射波前的部分遮挡产生,被称为目标的阴影场。在前向散射雷达工作区域内,自散射场比阴影场弱很多,通常可以忽略其影响,这相当于把真实的目标看作一个绝对的黑体,在黑体的前向散射区域仅有阴影场存在。由于阴影场与目标3维形状无关,仅由目标的阴影轮廓形状决定,因此分析目标阴影场时,3维形状目标可近似为一个具有目标阴影轮廓形状的2维面目标,该面目标同时也是一个不透光屏。
假设存在一个无限大的屏,该屏透光部分(孔径)的形状恰好与2维面目标形状一致。${\dot E_t}$和${\dot E_s}$分别代表电磁波单独照射面目标和孔径时,前向散射雷达接收机处的电磁波信号。根据巴比涅原理可知,前向散射雷达接收信号${\dot E_t}$可以认为是直达波${\dot E_0}$和孔径衍射信号${\dot E_s}$之差:
| $ {\dot E_t} = {\dot E_0} - {\dot E_s} $ | (4) |
孔径的衍射信号${\dot E_s}$,可以根据目标阴影轮廓形状,利用菲涅耳-基尔霍夫衍射公式计算获得。为方便描述,下面将${\dot E_s}$称为目标的前向散射信号。SISAR技术正是利用目标前向散射信号包含的丰富的目标轮廓信息对运动目标进行成像与识别。
4.2 SISAR成像方法由菲涅耳-基尔霍夫衍射公式给出的理想前向散射信号模型形式较为复杂,无法直接根据其求解目标侧影轮廓。而SISAR成像方法则是在一定假设或近似的条件下将菲涅耳-基尔霍夫衍射公式进行化简,使其中包含的目标侧影轮廓信息易于数值求解。
俄国人最早提出的SISAR成像算法是在小衍射角条件下将目标斜距作关于基线斜距的泰勒展开[21],这样前向散射信号与目标复轮廓函数(包含高度差像和中线像信息)是一个菲涅尔变换对的关系。如果考虑用FFT进行快速成像,前向散射信号在补偿掉多普勒相位后与目标复轮廓函数是一个傅里叶变换对的关系[28],但这样中线像会出现误差。
考虑到传统小衍射角SISAR成像算法受衍射角和斜距近似的限制,相参角度和成像精度都有限,因此,文献[54]提出了一种高精度的大衍射角SISAR成像方法,该方法基于真实斜距历程的2阶近似方法获得了精确的前向散射信号模型。
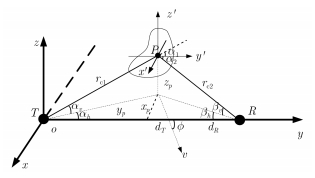
前向散射雷达成像系统结构如图 15所示,在大衍射角信号模型中,对目标侧影轮廓上任一点的收发斜距rR,T作如下近似表示:
|
图 15 前向散射雷达成像系统结构示意图 Fig.15 Illustration of FSR imaging system structure |
| $ {r_{R,T}} \approx {r_{c1,c2}} + \frac{{\left( {{{x'}^2} + 2x'{x_p}} \right) + \left( {{{z'}^2} + 2z'{z_p}} \right)}}{{2{r_{c1,c2}}}} $ | (5) |
其中,rc1,c2表示目标中心点的收发斜距,$x'$和$z'$为目标侧影轮廓上任一点的2维坐标,xp和zp表示目标中心点在全局坐标系下的位置坐标。式(5)是采用基于目标真实斜距历程的2阶近似方法,精确地描述了目标中心点位置,在大衍射角情况下,精度高于原小衍射角斜距近似方法。
在此基础上,大衍射角运动目标前向散射信号模型可简写为:
| $ E\left( t \right) = Q\int_{ - \infty }^{ + \infty } H\left( {x'} \right)\exp \left( {\frac{{{\text{j}}\gamma {{x'}^2}}}{{2{v^2}}}} \right)\exp \left( {\frac{{{\text{j}}\gamma x't}}{v}} \right){\text{d}}x' $ | (6) |
其中,v为目标运动速度;Q为幅度和相位皆与rc1,c2有关的复数项,表示目标与雷达几何关系对前向散射信号的影响;γ近似表示目标中心点的多普勒频率变化率,它描述了多普勒频率变化率随时间的非线性变化情况;$H\left( {x'} \right)$是目标复轮廓函数,描述了不同时刻目标高度轮廓对前向散射信号的影响。
对大衍射角前向散射信号模型进行逆变换可得到大衍射角成像算法:
| $ H\left( {x'} \right) = {{\text{e}}^{ - {\text{j}}\frac{{\gamma {{x'}^2}}}{{2{v^2}}}}}\int_{ - {T_s}/2}^{{T_s}/2} {\frac{\gamma }{{2\pi vQ}}E\left( t \right)} \exp \left( { - \frac{{{\text{j}}\gamma x't}}{v}} \right){\text{d}}t $ | (7) |
其中Ts为相参积累时间。在大衍射角成像算法中,由于精确补偿了目标中心点多普勒相位、目标轮廓长度二次相位以及目标沿基线方向运动速度引入的相位,得到的复轮廓函数的相位可以精确地反映目标中线高度信息,这使得FSR可以精确提取地面运动目标的中线高度像。在大衍射角SISAR成像算法的基础上,针对非垂直穿越目标轮廓投影面不与基线垂直的问题,文献[53]提出了一种改进的大衍射角SISAR成像方法,可以对非垂直穿越目标更精确地恢复轮廓像;针对地面运动目标成像中存在的多径干扰问题,文献[54]研究了多径干涉对目标前向散射RCS的影响以及对应的地面运动目标SISAR成像方法,并给出了车辆等地面目标的成像结果。
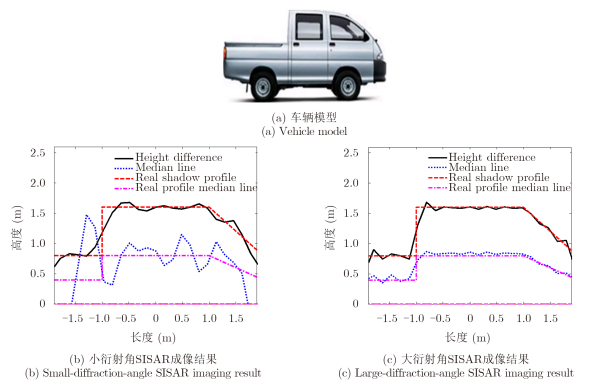
4.3 SISAR成像验证考虑到收发不同步的情况下利用包络检波方法一般只能提取单通道回波信号[4],并不适用于SISAR成像,因此早期关于SISAR成像的验证都是基于仿真开展的。为保证仿真结果的精确性和有效性,一般情况下都采用未经近似处理的菲涅尔-基尔霍夫衍射模型构造回波信号,并进一步利用回波信号进行SISAR成像。图 16给出了一组车辆目标的小衍射角SISAR成像与大衍射角SISAR成像的对比结果[52],用于成像的信号对应接收方位角为–28°~28°。对比可以看出,在衍射角较大时,大衍射角SISAR成像算法可以精确恢复目标的高度差像和中线像,而小衍射角SISAR成像算法分辨率较低,中线像也出现了较大误差。
为验证SISAR技术在实际应用中的能力,进一步开展了地面运动目标SISAR成像的验证实验,实验主要参数如表 1所示。
| 表 1 SISAR成像验证实验参数 Tab.1 Parameters of SISAR imaging experiment |
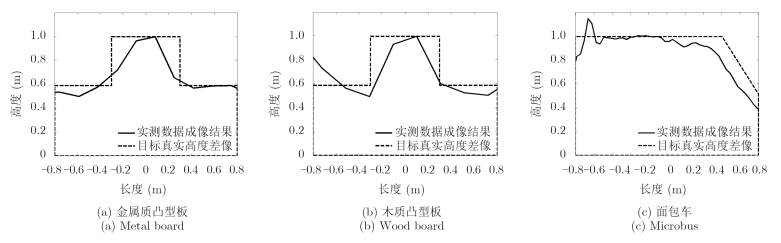
实验目标主要包括金属质凸形板、木质凸形板及面包车等,如图 17所示。考虑到包括检波只能提取单路实信号,因此在数据处理中采用了一种基于分段希尔伯特变换的复信号恢复方法[60],并利用恢复的正交复信号进行SISAR成像,其结果如图 18所示。由于目标中心相对天线的高度近似为0,因此只提取了高度差像结果。可以看出,所提取的高度差像和目标真实高度差像间有较强的一致性,验证了SISAR技术对运动目标成像和识别的作用。

|
图 17 SISAR成像实验目标 Fig.17 Targets in SISAR imaging experiment |
近年来,随着新一代隐身技术的发展(如“X-37B”的空天战机),常规军用雷达无法对其有效探测,受到越来越严重的威胁。双基地及前向散射探测技术作为一种有效的对抗手段受到越来越多的重视。特别是随着新一代卫星技术的发展,如新一代通信卫星(世广卫星)、导航卫星(北斗二代)及遥感卫星(地球同步轨道合成孔径雷达),其系统覆盖能力、平台和载荷能力都有大幅度的提升(采用大天线和大发射功率)。若在地面和空中布置接收平台,极易构成双基地配置或前向散射配置,使得目标的雷达散射截面积显著增大,从而实现对隐身目标的探测。
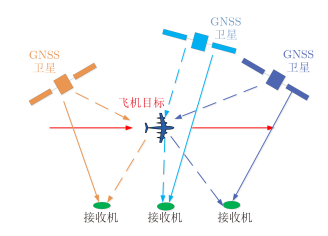
目前可以考虑的发射源有导航卫星和地球同步轨道合成孔径雷达(GEO SAR)卫星等,如图 19所示。其中导航卫星数目众多,覆盖区域广,任意时刻任意地点可见多颗卫星(4颗及以上),但导航星的等效全向辐射功率(EIRP)相对较弱,即使在前向散射配置下目标的RCS可以增大50~60 dB,但仍然亟需突破如下关键问题:高增益接收机及长时间信号积累技术、时频同步技术、高精度参数估计技术。
|
图 19 基于导航卫星的前向散射雷达组网 Fig.19 Netted FSR based on GNSS satellites |
地球同步轨道合成孔径雷达(GEO SAR)卫星是运行在36000 km高度地球同步轨道上的SAR卫星,通过轨道参数的合理设计,一颗GEO SAR卫星就可以保证对我国及部分周边国家的感兴趣区域每天观测一次到两次,对重点区域甚至可以实现不间断监视(图 20)。

|
图 20 GEO SAR对中国及邻近区域的重访时间 Fig.20 Revisit time of GEO SAR to China and neighboring regions |
目前,GEO SAR已被列入我国“高分辨率对地观测”国家科技重大专项的重点攻关项目之一,并且已经完成背景立项。基于GEO SAR卫星照射(EIRP值可达73~81 dBW),在地面/空中布置多个接收天线以形成天-地双基地前向散射雷达网络,可以实现对特定区域内隐身目标或低可见目标的全天时、全天候远距离监测,具有极大的应用潜力。但GEO SAR卫星数量受限且功率资源分配受限,因此亟需突破如下问题:最优卫星编队设计技术、波束扫描与波束管理技术、时频同步技术及高精度参数估计技术。
此外,如何利用FSR回波信息进行目标识别也是亟待研究的核心问题之一。当采用FSR组网探测时,基于多节点探测可以获得目标的多角度回波信号,从而获取多角度的目标参数信息。考虑如何利用多角度回波信号提高参数估计性能,如何借助多角度参数估计信息和多角度侧影轮廓像获得目标的3维轮廓信息,则可以大大提高对隐身目标的识别能力,可为隐身目标的识别提供一种有效的技术手段。
6 结束语FSR因其特殊的目标衍射效应而受到重视,其探测与成像技术也已由纯理论的研究阶段逐步开始转向实验验证阶段,应用方向也由早期的空中目标探测扩展到了地面及海面目标探测。本文首先介绍了近30年来FSR技术在地面、海面及空中目标的应用现状与趋势,并着重讨论了FSR的杂波特性与参数估计问题,通过建立新颖的钟摆物理模型,合理地解释了前向散射杂波谱宽对风速和波长不敏感这一特殊现象;同时,首次给出了基于北斗导航卫星的前向散射信号提取流程及民航飞机前向散射探测实验结果;最后,重点讨论了前向散射SISAR成像这一新技术,提出了基于非线性时变参数补偿的大衍射角SISAR成像新方法,并通过实验验证获取了多种目标的阴影轮廓像,为隐身目标的识别提供了一种重要技术手段。
同时,随着隐身技术的快速发展,新一代雷达与隐身目标的对抗会愈加剧烈,FSR技术因其优越的反隐身性能而将越来越受到重视。因此,FSR技术与双多基地雷达体制或组网雷达体制的结合,将弥补前向散射覆盖区域受限的缺点,充分发挥FSR技术的优势,进一步完善隐身目标的探测与识别体系,为隐身目标的探测与识别提供新的研究方向和更为广阔的发展前景。
| [1] |
Skolnik M I.
RADAR Handbook-2nd Edition[M]. New York: McGraw Hill, 1990 .
( 0) 0)
|
| [2] |
郦能敬. 雷达反对抗的新领域—反隐身飞机与对抗反雷达导弹[J].
电子学报,1987, 15 (2) : 98 –104.
Li N J. Radar ECCM's new area: anti-stealth and anti-ARM[J].
Acta Electronica Sinica,1987, 15 (2) : 98 –104.
( 0) 0)
|
| [3] |
Willis N J.
Bistatic Radar[M]. Boston, MA: Artech House Inc, 1991 .
( 0) 0)
|
| [4] |
Cherniakov M.
Bistatic Radar: Principles and Practice[M]. Chichester: John Wiley and Sons Ltd, 2007 : 395 -408.
( 0) 0)
|
| [5] |
杨振起, 张永顺, 骆永军.
双/多基地雷达系统[M]. 北京: 国防工业出版社, 1998 .
Yang Z Q, Zhang Y S, Luo Y J.
Bistatic (Multistatic) Radar Systems[M]. Beijing: National Defense Industry Press, 1998 .
( 0) 0)
|
| [6] |
Max B, Emil W.
Principle of Optics 6th Editon[M]. New York: Pergamon Press Inc, 1980 : 375 -380.
( 0) 0)
|
| [7] |
Li N J. Radar EECMs new area: anti-stealth and anti-ARM[J].
IEEE Transactions on Aerospace and Electronic Systems,1995, 31 (3) : 1120 –1127.
( 0) 0)
|
| [8] |
Blyakhman A B and Runova I A. Forward scattering radiolocation bistatic RCS and target detection[C]. IEEE International Radar Conference, Waltham, USA, 1999: 203-208.
( 0) 0)
|
| [9] |
Myakinkov A V. Optimal detection of high-velocity targets in forward scattering radar[C]. 5th International Conference on Antenna Theory and Techniques, Kyiv, Ukraine, 2005: 345-347.
( 0) 0)
|
| [10] |
Myakinkov A V and Ryndyk A G. Space-time processing in three-dimensional forward scattering radar[C]. 4th International Conference on Antenna Theory and Techniques, Sevastopol, Ukraine, 2003: 355-358.
( 0) 0)
|
| [11] |
Blyakhman A B, Ryndyk A G, and Sidorov S B. Forward scattering radar moving object coordinate measurement[C]. IEEE International Radar Conference, Washington, DC, VA, 2000: 678-682.
( 0) 0)
|
| [12] |
Koch V and Westphal R. A new approach to a multistatic passive radar sensor for air defense[C]. IEEE International Radar Conference, Alexandria, USA, 1995: 22-28.
( 0) 0)
|
| [13] |
Suberviola I, Mayordomo I, Mendizabal J. Experimental results of air target detection with a GPS forward-scattering radar[J].
IEEE Geoscience and Remote Sensing Letters,2012, 9 (1) : 47 –51.
( 0) 0)
|
| [14] |
Antoniou M, Sizov V, Hu C, et al.. The concept of a forward scattering micro-sensors radar network for situational awareness[C]. 2008 IEEE Radar Conference, Rome, Italy, 2008: 171-176.
( 0) 0)
|
| [15] |
Sizov V, Cherniakov M, Antoniou M. Forward scattering radar power budget analysis for ground targets[J].
IET Radar, Sonar & Navigation,2007, 1 (6) : 437 –446.
( 0) 0)
|
| [16] |
Cherniakov M, Abdullah R, Jancovic P, et al. Automatic ground target classification using forward scattering radar[J].
IEE Proceedings-Radar, Sonar and Navigation,2006, 153 (5) : 427 –437.
( 0) 0)
|
| [17] |
Abdullah R, Saripan M I, and Cherniakov M. Neural network based for automatic vehicle classification inforward scattering radar[C]. IET International Conference on Radar Systems, Edinburgh, UK, 2007: 1-5.
( 0) 0)
|
| [18] |
Marina G, Liam D, Vladimir S, et al. Phenomenology of Doppler forward scatter radar for surface targets observation[J].
IET Radar, Sonar & Navigation,2013, 7 (4) : 422 –432.
( 0) 0)
|
| [19] |
Chapurskiy V V. Restoration of images of object from one-dimensional radio holograms synthesized at small diffraction angles[J].
Radiotekhnika i Elektronika,1988, 33 (8) : 1747 –1756.
( 0) 0)
|
| [20] |
Surikov B S, Khasina E A, Chapurskiy V V. Correlation and spectral functions of one-dimensional radio holograms synthesized at small diffraction angles[J].
Radiotekhnika i Elektronika,1989, 34 (2) : 409 –419.
( 0) 0)
|
| [21] |
Chapurskiy V V and Sablin V N. SISAR: shadow inverse synthetic aperture radiolocation[C]. IEEE International Radar Conference, Washington, DC, USA, 2000: 322-328.
( 0) 0)
|
| [22] |
Stanislav H, Liam D, and Edward H. Target shadow profile reconstruction in ground-based forward scatter radar[C]. IEEE International Radar Conference, Arlington, USA, 2015: 846-851.
( 0) 0)
|
| [23] |
张涛, 张群, 罗斌凤, 等. 基于时频分析的双基地前向散射雷达侧影成像[J].
电子学报,2001, 29 (6) : 726 –731.
Zhang T, Zhang Q, Luo B F, et al. Shadow imaging for bistatic radar based on forward scattering by joint time frequency analysis[J].
Acta Electronica Sinica,2001, 29 (6) : 726 –731.
( 0) 0)
|
| [24] |
张涛, 罗永健, 张群, 等. SISAR侧影像的校正及特征提取[J].
电子与信息学报,2002, 24 (11) : 1634 –1640.
Zhang T, Luo Y J, Zhang Q, et al. Calibration and extraction of features for SISAR shadow image[J].
Journal of Electronics and Information Technology,2002, 24 (11) : 1634 –1640.
( 0) 0)
|
| [25] |
罗斌凤, 张冠杰, 张守宏. SISAR中运动目标全息信号的表达及仿真研究[J].
电子与信息学报,2003, 25 (10) : 1315 –1320.
Luo B F, Zhang G J, Zhang S H. The expression and simulation of radio hologram signal for the moving object in SISAR[J].
Journal of Electronics & Information Technology,2003, 25 (10) : 1315 –1320.
( 0) 0)
|
| [26] |
罗斌凤, 张守宏, 张涛, 等. SISAR侧影轮廓中线相位重构及其识别特征提取[J].
电子学报,2004, 32 (3) : 368 –372.
Luo B F, Zhang S H, Zhang T, et al. Shadow profile midline phase reconstruction and its identification features extraction for SISAR[J].
Acta Electronica Sinica,2004, 32 (3) : 368 –372.
( 0) 0)
|
| [27] |
曹运合, 张涛, 罗斌凤, 等. 前向散射雷达目标成像实验研究[J].
现代雷达,2009, 31 (1) : 18 –21.
Cao Y H, Zhang T, Luo B F, et al. Experimental imaging results for forward scattering hedge radar[J].
Modern Radar,2009, 31 (1) : 18 –21.
( 0) 0)
|
| [28] |
Luo Y, Hu D L, Luo B F, et al.. Motion compensation for SISAR based on contrast maximization[C]. 1st Asian and Pacific Conference on Synthetic Aperture Radar, Huangshan, China, 2007: 431-434.
( 0) 0)
|
| [29] |
Cao Y H, Zhang T, Luo B F, et al.. Experimental results for shadow inverse synthetic aperture radar[C]. 2009 IET Radar Conference, Guilin, China, 2009: 1-3.
( 0) 0)
|
| [30] |
胡程, 王力, 刘长江. 基于GNSS信号的前向散射无源探测系统研究[C]. 中国电子学会第二十一届青年学术年会, 西安, 2015: 273-281.
Hu C, Wang L, and Liu C J. Forward scatter radar for passive detection based on GNSS signal[C]. 21st CIE-youth Conference, Xi'an, China, 2015: 273-281.
( 0) 0)
|
| [31] |
Hiatt R E, Siegel K M, Weil H. Forward scattering of coated objects illuminated by short wavelength radar[J].
Proceedings of the IRE,1960, 48 (9) : 1630 –1635.
( 0) 0)
|
| [32] |
Glaser J I. Bistatic RCS of complex objects near forward scatter[J].
IEEE Transactions on Aerospace and Electronics Systems,1985, 21 (1) : 70 –78.
( 0) 0)
|
| [33] |
Glaser J I. Some results in the bistatic Radar Cross Section (RCS) of complex objects[J].
Proceedings of the IRE,1989, 77 (5) : 639 –648.
( 0) 0)
|
| [34] |
胡程. 短基线前向散射雷达系统理论与信号处理方法研究[D]. [博士论文], 北京理工大学, 2009.
Hu C. Research on system theory and signal processing method in short baseline forward scattering radar[D]. [Ph.D. dissertation], Beijing Institute of Technology, 2009.
( 0) 0)
|
| [35] |
Hu C, Long T, Zeng T, et al. Physical modeling and spectrum spread analysis of surface clutter in forward scattering radar[J].
SCIENCE CHINA Information Sciences,2010, 53 (11) : 2310 –2322.
( 0) 0)
|
| [36] |
Hu C, Long T, Zeng T. Statistic characteristic analysis of forward scattering surface clutter in bistatic radar[J].
SCIENCE CHINA Information Sciences,2010, 53 (12) : 2675 –2686.
( 0) 0)
|
| [37] |
Zhang C F, Liu C J, Hu C, et al.. Statistical analysis and simulation method of forward scattering clutter in bistatic radar[C]. 2013 IET Radar Conference, Xi'an, China, 2013: 1-6.
( 0) 0)
|
| [38] |
胡程, 刘长江, 曾涛, 等. 双基地前向散射雷达杂波分析与模拟方法[J].
信号处理,2013, 29 (3) : 293 –303.
Hu C, Liu C J, Zeng T, et al. Statistical analysis and simulation method of forward scattering clutter in bistatic radar[J].
Journal of Signal Processing,2013, 29 (3) : 293 –303.
( 0) 0)
|
| [39] |
Hu C, Antoniou M, Cherniakov M, et al.. Quasi-optimal signal processing in ground forward scattering radar[C]. IEEE Radar Conference, Rome, Italy, 2008: 1-6.
( 0) 0)
|
| [40] |
Long T, Hu C, Cherniakov M. Ground moving target signal model and power calculation in forward scattering micro radar[J].
SCIENCE CHINA Information Sciences,2009, 52 (9) : 1704 –1714.
( 0) 0)
|
| [41] |
Hu C, Li X L, and Cherniakov M. Analysis of signal characteristic and resolution in ground forward scattering radar[C]. IEEE International Conference on Signal Processing, Beijing, China, 2010: 1969-1972.
( 0) 0)
|
| [42] |
Hu Cheng, Sizov V, Antoniou M, et al. Optimal signal processing in ground-based forward scatter micro radars[J].
IEEE Transactions on Aerospace and Electronic Systems,2012, 48 (4) : 3006 –3026.
( 0) 0)
|
| [43] |
Zeng T, Hu C, Cherniakov M, et al. Joint parameter estimation and Cramer-Raobound analysis in ground-based forward scatter radar[J].
EURASIP Journal on Advances in Signal Processing,2012 .
doi: 10.1186/1687-6180-2012-80.
( 0) 0)
|
| [44] |
Hu C, Zeng T, Zhou C, et al. Accurate three-dimensional tracking method in bistatic forward scatter radar[J].
EURASIP Journal on Advances in Signal Processing,2013 .
doi: 10.1186/1687-6180-2013-66.
( 0) 0)
|
| [45] |
Zhou C, Hu C, Liu X R, et al.. Analysis of primary parameters estimation with space time processing in forward scatter radar[C]. 2013 IET Radar Conference, Xi'an, China, 2013: 1-5.
( 0) 0)
|
| [46] |
Liu C J, Hu C, Zhang K, et al.. A method for robust track initialization in forward scatter radar[C]. 2015 IEEE Radar Conference, Arlington, USA, 2015: 450-454.
( 0) 0)
|
| [47] |
Liu C J, Wang L, Wang M Q, et al.. Measurement estimation in forward scatter radar with a planar array[C]. 2015 IET International Radar Conference, Hangzhou, China, 2015: 1-6.
( 0) 0)
|
| [48] |
刘长江, 胡程, 曾涛, 等. 一种基于相位补偿的前向散射雷达阴影逆合成孔径快速成像方法[J].
电子与信息学报,2015, 37 (10) : 2294 –2299.
Liu C J, Hu C, Zeng T, et al. Fast forward scatter shadow inverse synthetic aperture radar imaging algorithm based on phase compensation[J].
Journal of Electronics & Information Technology,2015, 37 (10) : 2294 –2299.
( 0) 0)
|
| [49] |
Zhou C, Zhu C Y, Hu C, et al.. Accuracy analysis of SISAR imaging algorithm in forward scatter radar[C]. International Conference on Wireless Communication and Signal Processing, Huangshan, China, 2012: 1-5.
( 0) 0)
|
| [50] |
胡程, 周超. 前向散射阴影逆合成孔径雷达成像误差分析[J].
电子与信息学报,2013, 35 (5) : 1103 –1107.
Hu C, Zhou C. Analysis of forward scattering shadow inverse synthetic aperture radar imaging algorithm[J].
Journal of Electronics & Information Technology,2013, 35 (5) : 1103 –1107.
( 0) 0)
|
| [51] |
Li X L, Hu C, Zhu Y, et al.. The imaging research of the ground moving targets in forward scattering radar[C]. IEEE International Conference on Signal Processing, Beijing, China, 2010: 2019-2022.
( 0) 0)
|
| [52] |
Zeng T, Li X, Hu C, et al. Investigation on accurate signal modeling and imaging of the moving target in ground-based forward scatter radar[J].
IET Radar, Sonar & Navigation,2011, 5 (8) : 862 –870.
( 0) 0)
|
| [53] |
Liu C J, Hu C, Xu J, et al.. Modified signal modeling and imaging method of non-perpendicular crossing targets in forward scatter radar[C]. 2014 IEEE Radar Conference, Cincinnati, USA, 2014: 291-295.
( 0) 0)
|
| [54] |
Li X L, Hu C, Zeng D Z, et al.. Investigation of the SISAR imaging of the ground moving target under multipath interference[C]. 2011 IEEE Radar Conference, Kansas, America, 2011: 157-161.
( 0) 0)
|
| [55] |
Hu C, Li X L, Long T, et al. An accurate SISAR imaging method of groundmoving target in forward scatter radar[J].
SCIENCE CHINA Information Sciences,2012, 55 (10) : 2269 –2280.
( 0) 0)
|
| [56] |
陈新亮, 胡程, 曾涛. 一种基于前向散射雷达的车辆目标自动识别方法[J].
中国科学: 信息科学,2012, 42 (11) : 1471 –1480.
Chen X L, Hu C, Zeng T. Automatic vehicle classification based on forward scattering radar[J].
Scientia Sinica (Informationis),2012, 42 (11) : 1471 –1480.
( 0) 0)
|
| [57] |
Zeng D Z, Li X L, and Hu C. Effect of the polarization on SISAR imaging and feature recognition in forward scattering radar[C]. IEEE International Geoscience and Remote Sensing Symposium, Hawaii, USA, 2010: 1613-1616.
( 0) 0)
|
| [58] |
李晓良, 胡程, 曾涛. 多极化前向散射RCS分析及其对目标分类识别的影响[J].
电子与信息学报,2010, 32 (9) : 2191 –2196.
Li X L, Hu C, Zeng T. The analysis of multi-polarization forward scattering RCS and the effect on target classification and identification[J].
Journal of Electronics & Information Technology,2010, 32 (9) : 2191 –2196.
( 0) 0)
|
| [59] |
Hu C, Zhou C, Zhu C Y, et al.. Forward scatter radar SISAR imaging: theory and primary experimental results analysis[C]. 14th International Radar Symposium, Dresden, Germany, 2013: 643-648.
( 0) 0)
|
| [60] |
Hu C, Zhou C, Zeng T, et al. Radio holography signal reconstruction and shadow inverse synthetic aperture radar imaging in ground-based forward scatter radar: theory and experimental results[J].
IET Radar, Sonar & Navigation,2014, 8 (8) : 907 –916.
( 0) 0)
|