逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)可在远距离、全天候条件下对运动目标进行成像,因而在战略预警、目标识别以及空中交通管制等军事和民用领域发挥着重要的作用,并得到了广泛的应用[1]。ISAR能够同时获得目标距离向和方位向的高分辨,从而可使雷达目标呈现2维图像。其中,距离向高分辨率取决于信号的带宽,带宽越大,距离分辨率越高;方位向高分辨率则通过提高方位向的积累时间(目标沿雷达视线方向的转角)获得。然而,各种不利条件对传统ISAR成像带来了挑战,比如回波被强噪声污染或由于敌方干扰需要人为地删除部分数据造成回波缺损时,如何保证高分辨率及高质量成像效果。
近年来压缩感知(Compressive Sensing,CS)理论[2]的出现为上述问题的解决提供了一种新思路。由于ISAR成像满足稀疏性机理[3],可以将CS理论应用于ISAR成像。自Baraniuk将CS理论应用于雷达成像以来[3],国内外众多学者开展了基于CS理论3个关键环节(雷达回波稀疏表示、量测矩阵构造和重构算法设计)的ISAR成像研究。文献[4]针对ISAR 信号在传统傅里叶基下稀疏表示时出现的能量泄露和频谱展宽的问题,提出了一种改进的傅里叶基,并通过仿真表明改进稀疏基的成像效果优于传统傅里叶基。文献[5]研究了基于ISAR信号的参数化稀疏表示模型,利用求解该模型的稀疏性算法既能补偿目标旋转速度又能进行ISAR成像,从旋转速度估计的准确度、ISAR成像的效果和计算的复杂度3个方面比较了4种参数化稀疏重构算法,给出了每种算法的优点和缺点。文献[6]考虑到散射点之间的相关性,联合局部稀疏性约束和非局部全变分提出一种ISAR成像方法,该方法能够有效地压制噪声及去除虚假点,缺点是算法运算量较大。文献[7] 基于CS提出了一种2维联合超分辨ISAR成像算法, 由于该方法有效利用了2维耦合信息,因此提高了2维分辨率。基于CS理论的ISAR成像方法已涌现出很多成果,但是,目前CS理论在ISAR成像中的应用大多数都是基于单量测向量(Single Measurement Vector,SMV)模型,即将ISAR回波数据按照距离单元划分,对每一距离单元重构后组合得到最终的成像结果。由于SMV模型下,基于CS理论的ISAR 成像重构算法效率较低及实时性较差,使得CS理论距离实际应用还有较大差距;而近年来出现的基于多量测向量(Multiple Measurement Vectors,MMV) 模型[8]的CS理论可在一定程度上减少重构时间,提高重构质量。但是MMV模型需要信号满足联合稀疏的假设,文献[9]将相位自聚焦模型等效为MMV 模型,基于多任务贝叶斯模型提出了一种相位自聚焦ISAR成像算法,取得了较好的成像效果。文献[10] 将SAR回波在距离向上等效为MMV模型,实现了快速SAR成像。而这在ISAR信号模型中一般是不满足的。因此研究符合ISAR回波信号特点的MMV 模型,提高ISAR成像效率是一个值得研究的问题。
本文针对这一问题,首先依据多量测向量的ISAR成像模型,研究了基于线性Bregman迭代(Linearized Bregman Iteration,LBI)的一类多量测向量成像算法。全文安排如下:第2节介绍基于多量测向量的ISAR成像模型;并针对该模型研究了一类基于LBI的多量测向量成像算法,给出了此类算法的整体构架和应用条件,然后给出了收敛性和抗噪性分析;第3节通过仿真结果分析了算法的良好性能,分析了正则化参数对算法性能的影响,并通过实测数据的实验结果验证了所提算法的有效性及优势;最后给出总结。
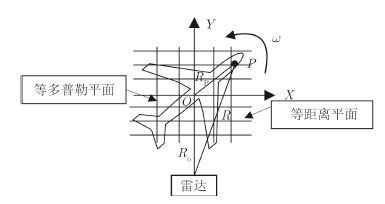
2 基于线性Bregman迭代类的多量测向量成像算法 2.1 基于多量测向量的ISAR成像模型本文的研究重点是ISAR方位向成像,假设已对回波数据完成了脉冲压缩、平动补偿[11]。假设目标在X-Y 2维平面内绕自身重心原点O以角速度w逆时针匀速转动,如图 1所示。
|
图 1 雷达转台成像模型 Fig.1 Turntable imaging model of radar |
设雷达距目标坐标系原点O的距离为Ro,目标上某一散射点P在初始时刻位于目标直角坐标系的坐标为(xP,yP),散射点P到目标坐标系原点O的距离为
| $\begin{align} &R({{t}_{\text{P}}})=\sqrt{R_{\text{o}}^{2}+R_{\text{P}}^{2}+2\cdot {{R}_{\text{o}}}\cdot {{R}_{\text{P}}}\cdot \sin (\theta +\omega {{t}_{\text{P}}})} \\ &\approx {{R}_{\text{o}}}+{{x}_{\text{P}}}\omega {{t}_{\text{P}}}+{{y}_{\text{P}}} \\ \end{align}$ | (1) |
假设雷达发射线性调频信号
| $s(t)=\text{rect}\left( \frac{{{t}_{\text{f}}}}{{{T}_{\text{p}}}} \right)\cdot \text{exp}\left( \text{j}2\pi \left( {{f}_{\text{c}}}t+\frac{1}{2}{{k}_{\text{r}}}t_{\text{f}}^{2} \right) \right)$ | (2) |
其中, μ>0为矩形函数,fc为载频,Tp为脉宽,kr为调频率,tf=t–nT为距离向快时间,tn=nT为方位向慢时间,T为脉冲重复周期。则P点的回波经距离向脉压后为:
| $\begin{align} &{{s}_{\text{r}}}({{t}_{\text{f}}},{{t}_{n}})=\sigma \text{rect}\left( \frac{{{t}_{n}}}{{{T}_{\text{a}}}} \right)\text{sinc}\left[ {{T}_{\text{p}}}{{k}_{\text{r}}}\left( {{t}_{\text{f}}}-\frac{2\left( {{R}_{\text{o}}}+{{y}_{\text{P}}} \right)}{c} \right) \right] \\ &\cdot \exp \left[ -\text{j}4\pi \frac{\left( {{R}_{\text{o}}}+{{y}_{\text{P}}} \right)}{\lambda } \right]\exp \left( -\text{j}2\pi {{f}_{d}}{{t}_{n}} \right) \\ \end{align}$ | (3) |
其中, σ为P点的散射系数,c为光速, λ为波长,多普勒频率fd=2 wxP/ λ。此时即实现了距离向分辨。将经过距离对准后的回波按距离单元排列,假设共取D个距离单元,若第d个距离单元内有K个强散射点,则此距离单元的回波信号可表示为:
| ${{s}_{d}}\left( {{t}_{n}} \right)=\sum\limits_{k=1}^{K}{{{\sigma }_{k}}}\cdot \text{rect}\left[ \frac{{{t}_{n}}}{{{T}_{\text{a}}}} \right]\exp \left( -\text{j}2\pi {{f}_{k}}{{t}_{n}} \right)$ | (4) |
其中,fk为第k个散射点的多普勒频率。由式(4)可知,与整个多普勒域相比,目标所占的多普勒成分仅有K个,满足稀疏性,因此可以构建基于CS的ISAR模型。
定义慢时间间隔为 Δt以及多普勒频率分辨率为 Δfd,假设脉冲重复频率为fr,则慢时间序列tn可以表示为
| $\begin{align} &\min {{\left\| {{x}_{d}} \right\|}_{0}}, \text{s}.\text{t}. {{y}_{d}}\text{=}\Phi {{s}_{d}}\left( {{t}_{n}} \right)=\Phi \Psi {{x}_{d}}=\Theta {{x}_{d}}, \\ &d=1,2,\cdots ,D \\ \end{align}$ | (5) |
其中, Φ为M×Na的量测矩阵,M为量测数, Θ= Φ Ψ为M×N的感知矩阵。文献[2]证明了当感知矩阵 Θ满足RIP条件时,信号可以从量测值yd中精确重构出来,此时可以利用CS重构算法求解,对D个距离单元逐一重构,然后组合即可获得ISAR 图像。由于对每个距离单元都需要重构,将会产生大量的冗余计算,增加不必要的计算负担[12]。
为减少冗余计算,缩短成像时间,本文研究基于多量测向量的ISAR成像模型,即
| $Y=\Theta X$ | (6) |
其中,Y=[y1 y2 ··· yD]为回波数据矩阵,X=[x1 x2 ··· xD]为待重构的散射点矩阵。若求得解X,即可得到ISAR图像。与传统MMV模型不同,这里不同距离单元散射点的稀疏度和支撑集都不需要相同。令kd表示xd的稀疏度,向量K=[k1 k2 ··· kD]表示X的稀疏度,称为X的稀疏度向量,即X为K稀疏的,此时X不再是联合稀疏的。首先利用X的稀疏特性约束,将求解式(6)的稀疏解问题描述为如下优化问题:
| $\underset{X\in {{C}^{N\times D}}}{\mathop{\min }}\,{{\left\| X \right\|}_{0,q}}, \text{s}.\text{t}. Y=\Theta X$ | (7) |
其中,
式(7)是NP难的问题,在感知矩阵 Θ满足RIP条件时,可以将式(7)转化为以下凸优化问题:
| $\underset{X\in {{C}^{N\times D}}}{\mathop{\min }}\,{{\left\| X \right\|}_{1}}, \text{s}.\text{t}. Y=\Theta X$ | (8) |
其中,矩阵的1-范数定义为
有关LBI理论的详细内容可参考文献[13],文献[13]首先提出Bregman迭代方法,并提出LBI。此后,文献[14-16]深入研究了LBI的性能,取得了一系列的研究成果。
本节首先根据多量测向量ISAR成像模型,然后利用LBI理论的基本原理,推导出了多量测向量线性Bregman算法(Multiple measurement vectors Linearized Bregman,MLB)算法。针对MLB算法存 在 “停滞现象 ”,收敛速度慢的问题,研究了多量测向 量快速线性Bregman算法(Multiple measurement vectors Fast Linearized Bregman,MFLB)算法、多量测向量改进线性Bregman算法(Multiple measurement vectors Improved Linearized Bregman,MILB)算法和多量测向量快速改进型线性Bregman算法(Multiple measurement vectors Fast Improved Linearized Bregman,MFILB)算法以加快收敛速度,减少迭代次数,缩短成像时间。为便于理解,本文首先给出这4种算法的相互关系及适用条件,如表 1所示,然后进一步分析各类算法特征。从表中可以看出,基于LBI理论得到MMV-ISAR模型的成像算法,即得到MLB算法后,首先判断感知矩阵的条件数是否为1,若为1,则继续判断是否存在停滞,若不存在,则此时使用MLB算法进行成像,若存在停滞,则此时使用MFLB算法进行成像;若感知矩阵条件数不为1,则继续判断是否存在停滞,若不存在,则此时使用MILB算法进行成像,若存在停滞,则此时使用MFILB算法进行成像。
| 表 1 4种算法相互关系及适用条件 Tab.1 The relationship and conditions of application of the four algorithms |
为从含有噪声回波数据矩阵中恢复X,放松式(8)的约束项,利用正则化参数 m控制稀疏度和误差,转化为如下正则化形式:
| $\widehat{X}\text{=}\underset{X\in {{C}^{N\times D}}}{\mathop{\text{argmin}}}\,\mu {{\left\| X \right\|}_{1}}\text{+}\frac{1}{2}\left\| \Theta X-Y \right\|_{\text{F}}^{2}$ | (9) |
其中,
| ${{\left\| A \right\|}_{\text{F}}}=\sqrt{\left( \sum\limits_{i,j=1}^{N}{{{\left| {{a}_{ij}} \right|}^{2}}} \right)}=\sqrt{\text{tr}\left( {{A}^{\text{H}}}A \right)}$ | (10) |
其中,tr(·)为矩阵的迹,即对角线元素之和。
2.2.1 MLB 算法本文成像模型与文献[17]中的求解模型是一致的,我们在文献[17]中详细推导了算法原理,下面给出MLB算法的迭代格式:
| $\left\{ \begin{array}{*{35}{l}} {{V}^{k+1}}={{V}^{k}}+{{\Theta }^{\text{H}}}(Y-\Theta {{X}^{k}}) \\ {{X}^{k+1}}\text{=}\delta \text{sof}{{\text{t}}_{\mu }}({{V}^{k+1}}) \\ \end{array} \right.$ | (11) |
其中,soft(·)为复数矩阵条件的软阈值算子,定义如下:
| $\begin{align} &\text{sof}{{\text{t}}_{\mu }}\left( V \right)=\frac{\max \left\{ \left| {{V}_{ij}} \right|-\mu ,0 \right\}}{\max \left\{ \left| {{V}_{ij}} \right|-\mu ,0 \right\}+\mu }{{V}_{ij}} \\ &=\left\{ \begin{matrix} \frac{{{V}_{ij}}}{\left| {{V}_{ij}} \right|}\left( \left| {{V}_{ij}} \right|-\mu \right),&\left| {{V}_{ij}} \right|>\mu \\ 0,&\left| {{V}_{ij}} \right|\le \mu \\ \end{matrix} \right. \\ \end{align}$ | (12) |
其中,Vij为复数矩阵V中第i行第j列的元素,|Vij|表示Vij的模。从软阈值算子soft的定义中可以看出,MLB算法的软阈值算子从点收缩拓展为面收缩,平面阈值比原始的线阈值具有更好的压制噪声效果,因为平面阈值考虑到了全局数据,而线阈值仅考虑到当前一列的数据,基于实测数据的成像实验将验证这一结论。
此外,由于MLB算法只是最基本的迭代格式,一方面,存在 “停滞 ”现象,即几次迭代时,算法输出保持不变;另一方面,MLB算法在感知条件数较大时,收敛速度将会较慢。为解决这两方面的问题,研究3种算法,下面具体分析。
2.2.2 MFLB 算法文献[14]通过估计迭代步长的方 法减少了LB算法的 “停滞 ”现象带来的迭代次数变大的影响,下面利用这一思想对MLB算法实现快速迭代。在停滞时间内,假设发生m步停滞,第k次迭代时停滞开始,第k+m次迭代时停滞终止,第k+m+1次迭代时Vk+m+1突破了闭区间[– μ, μ],产生一个新的Xk+m+1(Xk+m+1≠X*),因为Xk+m最终能够收敛到一个极限值X*[14],因此有Xk
| $\left\{ \begin{array}{*{35}{l}} {{X}^{k+j}}\equiv {{X}^{k}} \\ {{V}^{k+j}}\text{=}{{V}^{k}}+j\cdot \Delta V,\ j=1,\cdots ,m \\ \end{array} \right.\ \ $ | (13) |
在停滞期间内,每次迭代Vk仅以固定的增量 ΔV进行积累,第j次迭代的积累量为j· ΔV,Vk+j不足以突破闭区间[–μ, μ],第k+m+1次迭代的Vk+m+1才能突破闭区间[–μ, μ]。因此,要想终止停滞,需要将Vk的积累量增大为(k+m+1)· ΔV,才能使Vk+m+1能够突破闭区间[–μ, μ]的限制。
为计算停滞步长,首先对Xk,Vk,Xk+j,Vk+j 和 ΔV进行矩阵向量化处理,即
| $\left\{ \begin{matrix} \widetilde{X}_{i}^{k+j}\equiv \widetilde{X}_{i}^{k},&\forall i \\ \widetilde{V}_{i}^{k+j}\text{=}\widetilde{V}_{i}^{k}+j\cdot \Delta {{\widetilde{V}}_{i}},\ &i\in {{I}_{0}} \\ \widetilde{V}_{i}^{k+j}\equiv \widetilde{V}_{i}^{k},\ &i\in {{I}_{1}} \\ \end{matrix} \right.$ | (14) |
当且仅当I0中
| $s=\text{min}\left\{ {{s}_{i}}\left| {{s}_{i}}=\left\lceil \frac{\mu \cdot \text{sign}\left( \Delta \widetilde{V}{{}_{i}} \right)-\widetilde{V}_{i}^{k}}{\Delta {{\widetilde{V}}_{i}}} \right\rceil ,\forall i\in {{I}_{0}} \right| \right.$ | (15) |
其中,
| $\left\{ \begin{array}{*{35}{l}} {{X}^{k+s}}\equiv {{X}^{k}} \\ {{V}^{k+s}}\text{=}{{V}^{k}}+s\cdot \Delta V \\ \end{array} \right.$ | (16) |
因此,当Xk在两步迭代保持不变时,认为其处于迭代停滞状态,此时可通过增加Vk的变化量以突破[–μ, μ],从而使Xk加速到停滞的临界点,以此减少积累时间,加快算法运行速度。
注意到,MFLB算法虽然通过估计迭代步长加快了算法收敛,但依然没有解决感知条件数较大时,收敛速度将较慢的问题。
2.2.3 MILB 算法文献[15]指出,感知矩阵条件数越小,则LB算法收敛越快。因此,需要对感知矩阵的条件数进行优化以减少迭代次数,具体的优化方法在文献[17]中进行了详细的介绍。下面介绍关键的步骤。
首先在式(6)两边乘以( Θ ΘH)–1/2,得到
| ${{(\Theta {{\Theta }^{\text{H}}})}^{-1/2}}Y={{(\Theta {{\Theta }^{\text{H}}})}^{-1/2}}\Theta X$ | (17) |
令
| ${{Y}_{1}}={{\Theta }_{1}}X$ | (18) |
对式(18)采用MLB算法求解,将Y1, Q1代入,可得MIBL算法迭代公式
| $\left\{ \begin{array}{*{35}{l}} {{V}^{k+1}}={{V}^{k}}+{{\Theta }^{\text{H}}}{{(\Theta {{\Theta }^{\text{H}}})}^{-1}}(Y-\Theta {{X}^{k}}) \\ {{X}^{k+1}}=\delta \text{sof}{{\text{t}}_{\mu }}({{V}^{k+1}}) \\ \end{array} \right.$ | (19) |
其中,
由式(18)可知此时感知矩阵为 Θ1,计算 Θ1条件数
| ${{\Theta }_{1}}\Theta _{1}^{\text{H}}=({{(\Theta {{\Theta }^{\text{H}}})}^{-1/2}}\Theta ){{({{(\Theta {{\Theta }^{\text{H}}})}^{-1/2}}\Theta )}^{\text{H}}}=I$ | (20) |
| $\text{cond}({{\Theta }_{1}})={{[{{\lambda }_{\max }}({{\Theta }_{1}}\Theta _{1}^{\text{H}})/{{\lambda }_{\min }}({{\Theta }_{1}}\Theta _{1}^{\text{H}})]}^{1\text{/2}}}=1$ | (21) |
可以看出MILB算法对感知矩阵的条件数进行了优化,达到了加快收敛速度的目的。
2.2.4 MFILB 算法MFLB算法和MILB算法在一定程度上能够减少迭代次数,但这两种算法都存在缺陷:一是MFLB算法虽然通过估计迭代步长减少了迭代次数,但是该算法的感知矩阵条件数不是最优的,所以迭代次数不是最快的;二是MILB算法虽然将感知矩阵条件数优化到最小,但该算法依然存在 “停滞 ”现象。因此本节从这两方面考虑,首先对感知矩阵的条件数进行优化,从整体上加快了收敛的速度,然后对停滞步长进行估计,以进一步提高收敛速度,具体内容可参考文献[18]。
优化感知矩阵条件数的方法与MILB算法相同,估计迭代步长的方法与MFLB的思想大体一致, 需要注意的是MFILB算法中 ΔV= Θ+(Y– QXk)。 具体过程与MFLB算法类似,得到s,也就是停滞的长度,然后利用式(23)终止停滞。
| $s\text{=min}\left\{ {{s}_{i}}\left| {{s}_{i}}\text{=}\left\lceil \frac{\mu \cdot \text{sign}\left( \Delta \widetilde{V}{{}_{i}} \right)-\widetilde{V}_{i}^{k}}{\Delta \widetilde{V}{{}_{i}}} \right\rceil ,\ \forall i\in {{I}_{0}} \right. \right\}$ | (22) |
| $\left\{ \begin{array}{*{35}{l}} {{X}^{k+s}}\equiv {{X}^{k}} \\ {{V}^{k+s}}\text{=}{{V}^{k}}+s\cdot \Delta V \\ \end{array} \right.$ | (23) |
MLB算法、MFLB算法、MILB算法和MFILB算法是LBI在MMV模型下的拓展,因此分析算法收敛性时,重点分析其是否依然满足收敛性结论。MMV模型下,可将迭代格式改写为如下形式:
| $\left\{ \begin{array}{*{35}{l}} \left[ \begin{matrix} V_{1}^{k+1}&\cdots &V_{D}^{k+1} \\ \end{matrix} \right] \\ =\left[ \begin{matrix} V_{1}^{k}&\cdots &V_{D}^{k} \\ \end{matrix} \right]+C(\left[ \begin{matrix} Y{{}_{1}}&\cdots &Y{{}_{D}} \\ \end{matrix} \right] \\ \quad -\Theta \left[ \begin{matrix} X_{1}^{k}&\cdots &X_{D}^{k} \\ \end{matrix} \right]) \\ \left[ \begin{matrix} X_{1}^{k+1}&\cdots &X_{D}^{k+1} \\ \end{matrix} \right] \\ =\delta \text{sof}{{\text{t}}_{\mu }}\left( \left[ \begin{matrix} V_{1}^{k+1}&\cdots &V_{D}^{k+1} \\ \end{matrix} \right] \right) \\ \end{array} \right.$ | (24) |
其中,当C= QH时,迭代式(24)为MLB和MFLB;当C= Q+时,迭代式(24)为MILB和MFILB。则式(24)的第j列为:
| $\left\{ \begin{array}{*{35}{l}} \left[ V_{j}^{k+1} \right]=\left[ V_{j}^{k} \right]+C\left( \left[ {{Y}_{j}} \right]-\Theta \left[ X_{j}^{k} \right] \right) \\ \left[ X_{j}^{k+1} \right]=\delta \text{sof}{{\text{t}}_{\mu }}(\left[ V_{j}^{k+1} \right]) \\ \end{array} \right.$ | (25) |
式(25)是SMV模型的LBI算法,每一列满足收敛性结论,因此拓展到MMV后,依然满足收敛性结论。
2.3.2 抗噪性分析下面对所提4种算法的抗噪性能进行分析,由于3种改进算法只是在收敛速度得到了加快,因此4种算法具有相同的抗噪性能,下面进行统一分析。
下面对抗噪性能进行具体分析。为方便解释抗噪性能,将迭代式(11)改写为如下等价形式:
| $\left\{ \begin{array}{*{35}{l}} {{Y}^{k+1}}=Y+{{Y}^{k}}-\Theta {{X}^{k}} \\ {{X}^{k+1}}=\delta \text{sof}{{\text{t}}_{\mu }}({{\Theta }^{\text{H}}}{{Y}^{k+1}}) \\ \end{array} \right.$ | (26) |
当k=0,Y0=0,X0=0时,Y1=Y,将迭代式(26) 中的含噪输入Y1分解为两部分:Y1= QX1+ QB1,其中X1可看作为原始纯净信号X的一部分,收缩算子soft可将 ΘHY1中的小信号成分过滤掉,因此X1是过平滑的且不含任何噪声;B1包含两部分:一是原始纯净信号X中未恢复的信号X-X1;二是噪声分量Ω,可表示为 ΘB1= Θ(X-X1)+ Ω,又有Y1= ΘX1+ ΘB1,所以Y1= Θ(X-X1)+ Ω+ ΘX1。若期望从B1中恢复出未恢复信号X-X1,则需要在第2次迭代时将 ΘB1反馈到原始含噪量测输入Y中,所以第2次迭代新的输入Y2为:
| $\begin{align} &{{Y}^{2}}=Y+\Theta {{B}^{1}}=2\Theta {{X}^{1}}+2\Theta {{B}^{1}}-\Theta {{X}^{1}} \\ &=2\Theta \left( \overline{X}-{{X}^{1}} \right)+2\Omega +\Theta {{X}^{1}} \\ \end{align}$ | (27) |
和第1次迭代含噪量测输入Y1相比,未恢复信号X-X1变为两倍,同时Y2包含的噪声分量也变为两倍。由于第2次迭代新的含噪量测输入Y2可分解为Y2= ΘX2+ ΘB2,利用Y2求解X2时,Y2中的信号成分不仅使X2继承了X1,而且重构了未恢复信号X-X1的部分信息,因此X2比X1更逼近X。那么经过k次迭代后,有
| $\left\| Y-\Theta {{X}^{k}} \right\|>\left\| Y-\Theta \overline{X} \right\|={{\sum }^{2}}$ | (28) |
本文所有实验数据处理都是在操作系统为Windows7的个人计算机上实现的,仿真平台为Matlab R2008b,计算机主要参数如下:处理器为Intel酷睿E7500,主频为2.93 GHz,内存为2 GB。
仿真 1 迭代次数及运算时间比较
本仿真的主要目的是比较LB,FLB,ILB和FILB 4种算法迭代次数及运算时间的关系。参数设置:稀疏信号长度为400,稀疏度为40,量测矩阵为200行400列的随机高斯矩阵,停止准则为

|
图 2 相对重构误差与迭代次数的关系 Fig.2 Relationship between relative reconstruction error and iteration number |
| 表 2 迭代次数与运算时间比较 Tab.2 Comparison of iteration number and CPU time |
由图 2及表 2可以看出,4种算法的相对重构误差随迭代次数的增加,最终都能减小到设定的停止门限。同时MLB算法存在明显的 “停滞现象 ”;MFLB算法通过估计迭代步长的方式有效地缓解了 “停滞现象 ”;MILB算法通过优化感知矩阵条件数的方式有效地减少了迭代次数,加快了收敛;MFILB 算法在优化感知矩阵条件数的基础上估计迭代步长,进一步减少了迭代次数,体现出MFILB算法的优势。
仿真 2 正则化参数对算法性能的影响
本仿真主要验证正则化参数对4种线性Bregman 算法性能的影响。根据文献[15]的收敛性定理和本文的收敛性分析可知,0< d<1
|
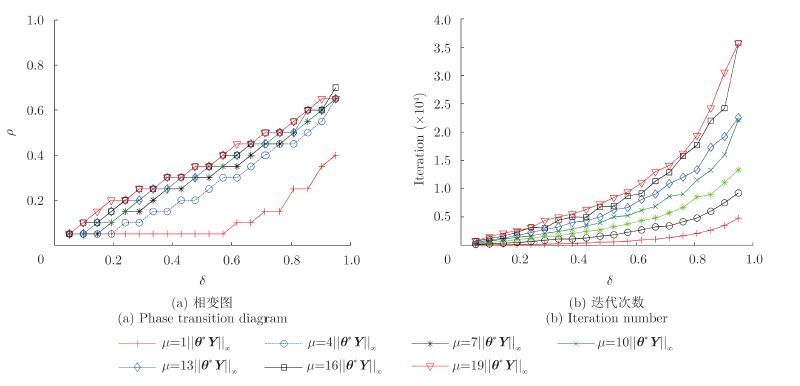
图 3 MLB算法不同m的相变图及所需迭代次数 Fig.3 Phase transition diagram and iteration number of MLB algorithm with different μ |
|
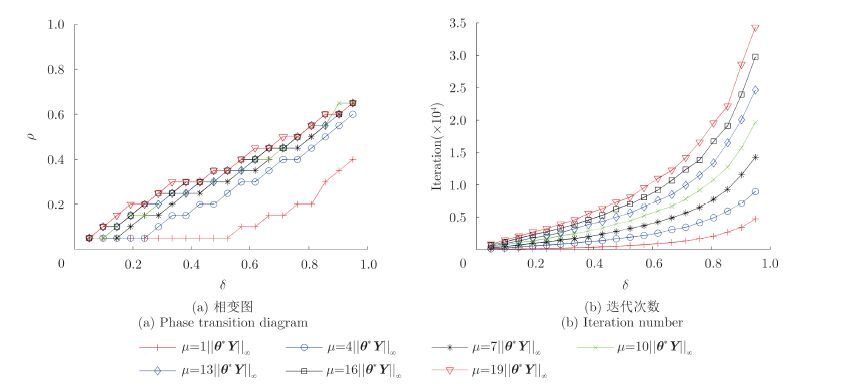
图 4 MFLB算法不同m的相变图及所需迭代次数 Fig.4 Phase transition diagram and iteration number of MFLB algorithm with different μ |
|
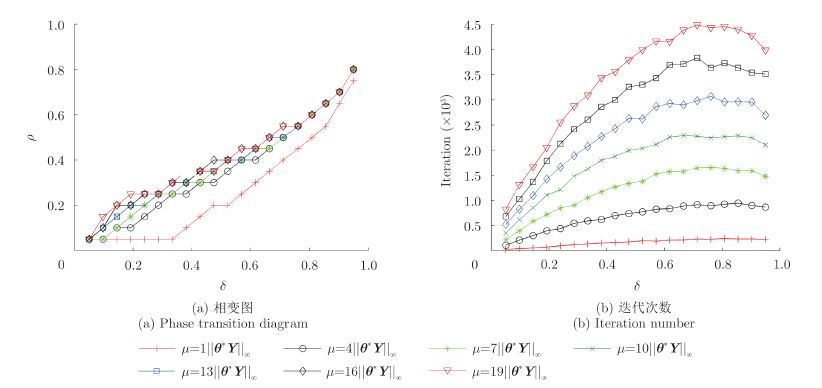
图 5 MILB算法不同m的相变图及所需迭代次数 Fig.5 Phase transition diagram and iteration number of MILB algorithm with different μ |
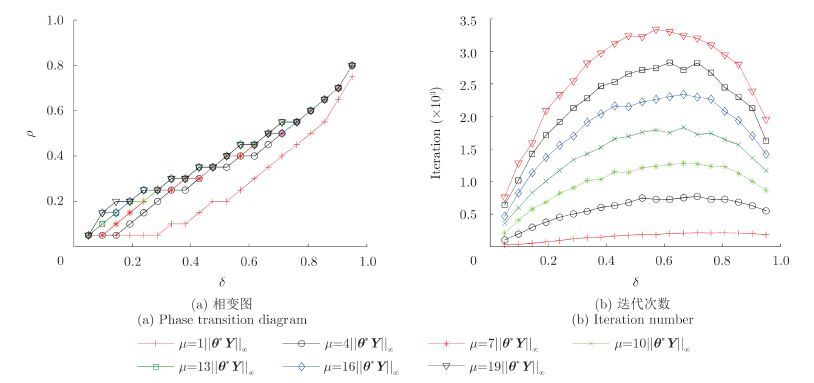
|
图 6 MFILB算法不同m的相变图及所需迭代次数 Fig.6 Phase transition diagram and iteration number of MFILB algorithm with different μ |
根据图 3~图 6, m较小时,4种线性Bregman 算法重构性能都较差,随着 m越大,4种算法重构性能都越好,但所需迭代次数也越多,因此,在选择 m时既不能过小( m过小导致重构性能较差),又不能过大( m过大导致所需迭代次数过多,可行性较差), 在实际中可依据具体的需求选择不同的正则化参数。同时。可以看出,所需平均迭代次数的关系为:MFILB<MILB<MFLB<MLB,此结论与仿真1也是一致的。
仿真 3 与其他算法的比较
本仿真将4种线性Bregman算法与正交匹配追踪(Orthogonal Matching Pursuit,OMP)算法[21]、IST[22]和IHT[23]算法进行比较。信号模型参数设置与仿真2相同,OMP算法中稀疏度冗余设置为2K; 本文方法设置 m=19
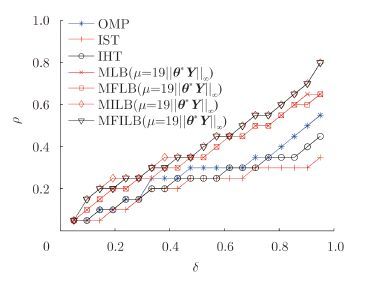
|
图 7 4种线性Bregman算法与OMP, IST和IHT算法比较结果 Fig.7 Comparison of four linearized Bregman algorithms with OMP, IST and IHT algorithms |
从图 7可以看出,IHT算法性能优于IST算法;OMP算法性能优于IHT算法;MLB和MFLB算法的性能优于OMP算法;MILB和MFILB算法的性能优于MLB和MFLB算法。
3.2 实测数据成像实验为进一步验证算法性能,下面利用实测数据进行不同信噪比的ISAR成像实验。部分雷达参数如下:雷达发射信号为LFM信号,带宽为100 MHz, 工作频段为S波段。图 8(a)为512脉冲RD成像结果,也是后续超分辨重建算法的参考模板,超分辨重建算法利用128脉冲,然后进行4倍超分辨成像;图 8(b)为目标支撑区,是通过合适的门限将图 8(a) 划分为目标支撑区和背景支撑区,对比算法得到的超分辨图像若落在目标支撑区则判定为目标,反之则判定为噪声。实验中通过以下3个评价指标对成像质量进行定量分析。
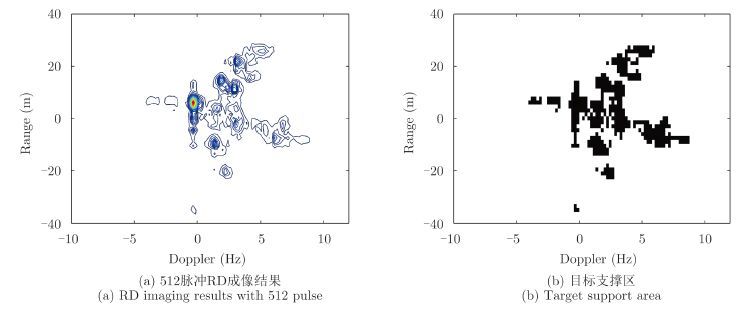
|
图 8 512脉冲RD成像结果和目标支撑区 Fig.8 RD imaging results with 512 pulse and target support area |
(1) 目标背景比(Target-to-Background Ratio,TBR)。定义为:
| $\text{TBR}=10\log 10\left( \frac{\sum\limits_{\left( i,j \right)\in T}{{{\left| {{\widehat{X}}_{i,j}} \right|}^{2}}}}{\sum\limits_{\left( i,j \right)\in B}{{{\left| {{\widehat{X}}_{i,j}} \right|}^{2}}}} \right)$ | (29) |
其中,T和B分别表示目标支撑区和背景支撑区,
(2) 噪声能量(Noise energy)。定义为:
| $\text{Noise}\ \text{energy}=\sum\limits_{\left( i,j \right)\in B}{{{\left| {{\widehat{X}}_{i,j}} \right|}^{2}}}$ | (30) |
噪声能量表示落入背景支撑区的虚假散射点和残余噪声能量水平,噪声能量越大,目标识别率越低。
(3) 相关系数(Coherence)。定义为:
| $\text{Coherence}=\frac{\left\langle \left| X \right|\cdot \left| \widehat{X} \right| \right\rangle }{\sqrt{{{\left| X \right|}_{2}}}\sqrt{{{\left| \widehat{X} \right|}_{2}}}}$ | (31) |
其中,
此外,通过计算机仿真时间来衡量成像时间,算法所需时间越短则成像效率越高,算法所需时间越长则可行性越差。
为得到不同信噪比的实测数据,对回波数据添加高斯白噪声。CS重构算法的性能和噪声水平密切相关,而噪声水平是未知的,因此利用能量门限选择噪声单元,然后利用清洁区估计噪声水平[1]。
阈值的取法,取
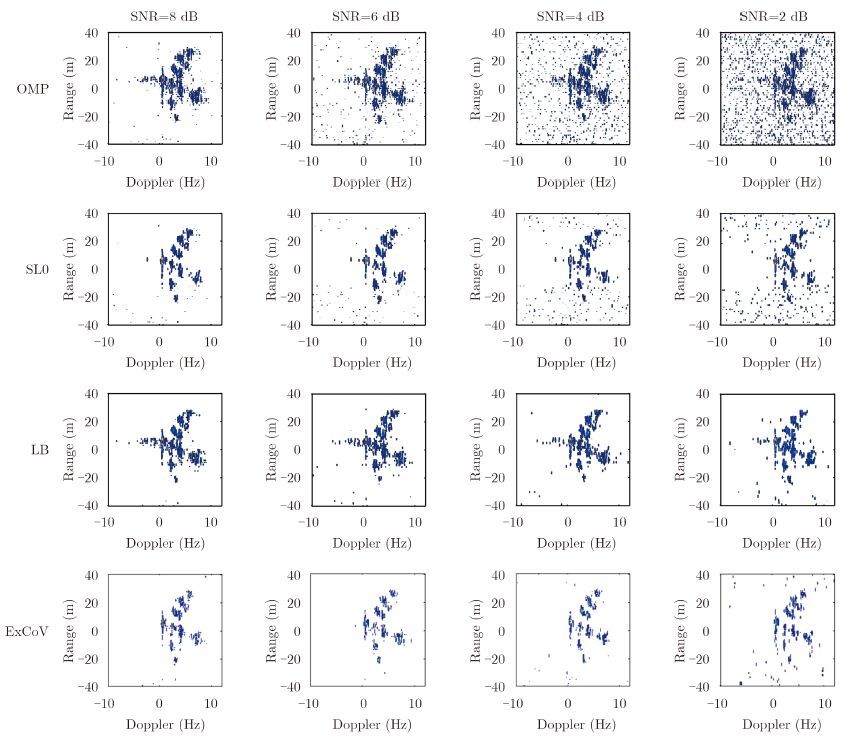
|
图 9 信噪比为8 dB, 6 dB, 4 dB, 2 dB时的4种单量测向量算法成像结果 Fig.9 Imaging results of four SMV algorithms under 8 dB, 6 dB, 4 dB, and 2 dB SNRs |
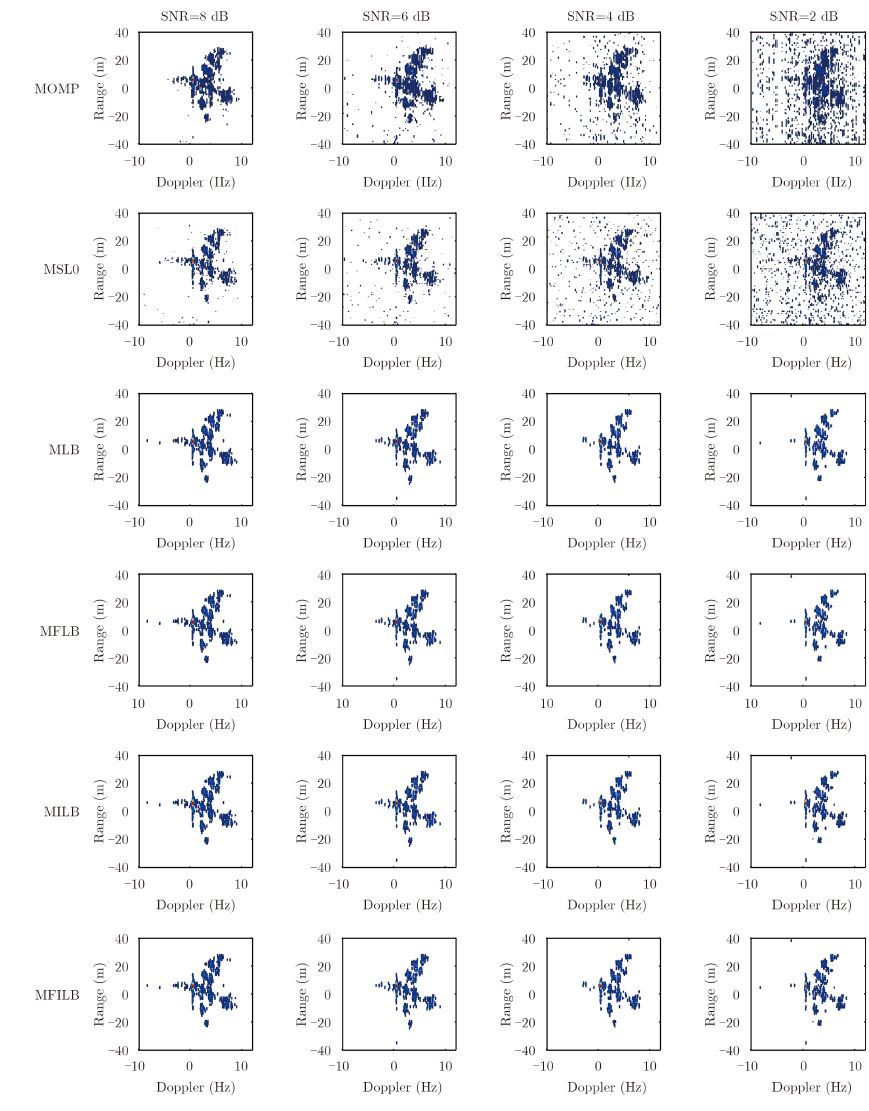
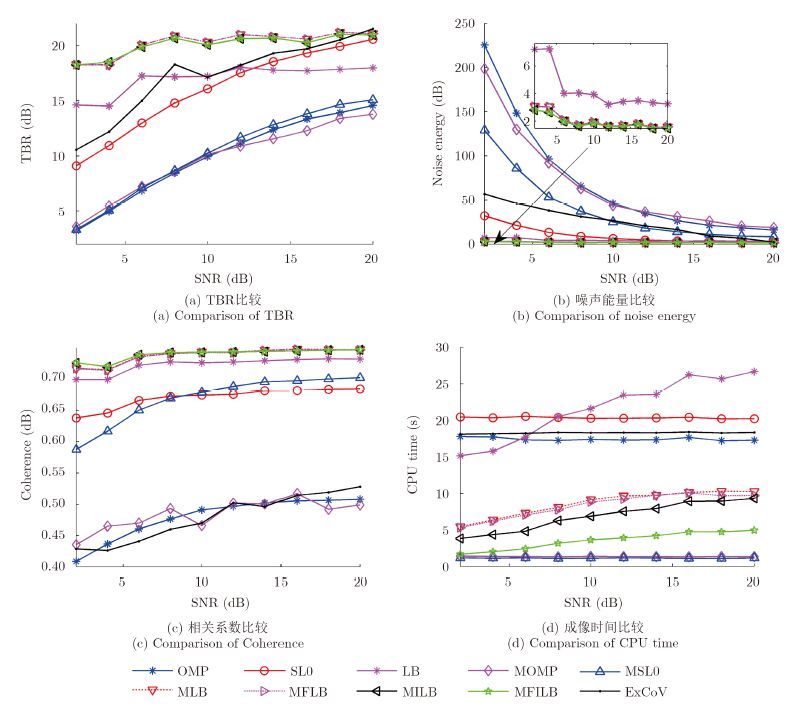
图 10为不同信噪比条件下MOMP[27],MSL0[28], MLB,MFLB,MILB和MFILB算法对多量测向量ISAR模型的成像结果,其中MOMP算法稀疏度冗余设置为40。可以看出,随着信噪比的降低,MOMP 算法和MSL0算法受信噪比影响严重,低信噪比时出现大量虚假散射点,而本文研究的4种算法受信噪比影响较小,成像效果较好,且优于LB算法,原因在于本文算法使用的平面阈值比LB算法的线阈值具有更好的压制噪声效果,因为平面阈值考虑到了全局数据,而线阈值仅考虑到当前一列的数据。 为进一步定量评价算法的成像性能,下面给出评价指标随信噪比的变化曲线。图 11(a)为不同算法TBR 比较,图 11(b)为不同算法噪声能量比较,图 11(c) 为不同算法相关性比较,图 11(d)为不同算法成像时间比较。通过对比可以看出,相比单量测向量ISAR 模型成像算法以及MOMP算法和MSL0 算法,本文所研究的算法具有更大的TBR,更小的噪声能量, 更大的相关系数,以及更短的成像时间。说明本文算法结果具有更高的识别率,更好的抑制噪声能力,以及较高的可行性。实测数据进一步验证了本文算法的有效性以及成像质量和成像时间的优势。
|
图 10 信噪比为8 dB, 6 dB, 4 dB, 2 dB时的6种多量测向量算法成像结果 Fig.10 Imaging results of six MMV algorithms under 8 dB, 6 dB, 4 dB, and 2 dB SNRs |
|
图 11 不同信噪比条件下成像性能比较 Fig.11 Curves of imaging performance under different SNRs |
本文针对单量测向量CS-ISAR成像时间长的问题,研究了多量测向量ISAR成像模型,并基于LBI 理论研究了一类多量测向量成像算法,给出了此类算法的整体构架和各种算法的应用条件,然后给出了正则化参数选取方法,在实际中可依据具体的需求选择不同的正则化参数,通过仿真结果表明所提算法具有良好的重构性能及速度优势,基于实测数据的ISAR成像实验也验证了本文算法的有效性,体现出成像时间和成像质量方面的优势。
| [1] |
张龙, 张磊, 邢孟道. 一种基于改进压缩感知的低信噪比ISAR高分辨成像方法[J].
电子与信息学报,2011, 32 (9) : 2263 –2267.
Zhang Long, Zhang Lei, Xing Meng-dao. Development and prospect of compressive sensing[J].
Journal of Electronics&Information Technology,2011, 32 (9) : 2263 –2267.
( 0) 0)
|
| [2] |
Donho D L. Compressed sensing[J].
IEEE Transactions on Information Theory,2006, 52 (4) : 1289 –1306.
( 0) 0)
|
| [3] |
Baraniuk R and Steeghs P. Compressive radar imaging[C]. IEEE Radar Conference, Boston, USA, 2007: 128-133.
( 0) 0)
|
| [4] |
Zhang S S, Xiao B, and Zong Z L. Improved compressed sensing for high-resolution ISAR image reconstruction[J].
SCIENCE CHINA Information Sciences,2014, 59 (23) : 2918 –2926.
( 0) 0)
|
| [5] |
Rao W, Li G, Wang X Q, et al. Comparison of parametric sparse recovery methods for ISAR image formation[J].
SCIENCE CHINA Information Sciences,2014, 57 (2) : 11 –12.
( 0) 0)
|
| [6] |
Zhang X H, Bai T, Meng H Y, et al. Compressive sensing-based ISAR imaging via the combination of the sparsity and nonlocal total variation[J].
IEEE Geoscience and Remote Sensing Letters,2014, 11 (5) : 990 –994.
( 0) 0)
|
| [7] |
吴敏, 邢孟道, 张磊. 基于压缩感知的二维联合超分辨ISAR成像算法[J].
电子与信息学报,2014, 36 (1) : 187 –193.
Wu Min, Xing Meng-dao, Zhang Lei. Two dimensional joint super-resolution ISAR imaging algorithm based on compressive sensing[J].
Journal of Electronics&Information Technology,2014, 36 (1) : 187 –193.
( 0) 0)
|
| [8] |
Davies M E and Eldar Y C. Rank awareness in joint sparse recovery[J].
IEEE Transactions on Information Theory,2012, 58 (2) : 1135 –1146.
( 0) 0)
|
| [9] |
Zhao L F, Wang L, Bi G A, et al. An autofocus technique for high-resolution inverse synthetic aperture radar imagery[J].
IEEE Transactions on Geoscience and Remote Sensing,2014, 52 (10) : 6392 –6403.
( 0) 0)
|
| [10] |
陈一畅, 张群, 陈校平, 等. 多重测量矢量模型下的稀疏步进频率SAR成像算法[J].
电子与信息学报,2014, 36 (12) : 2987 –2993.
Chen Yi-chang, Zhang Qun, Chen Xiao-ping, et al. Imaging algorithm of sparse stepped fequency SAR based on multiple measurement vectors model[J].
Journal of Electronics&Information Technology,2014, 36 (12) : 2987 –2993.
( 0) 0)
|
| [11] |
俞翔, 朱岱寅, 张劲东, 等. 基于设计结构化Gram矩阵的ISAR运动补偿方法[J].
电子学报,2014, 42 (3) : 442 –461.
Yu Xiang, Zhu Dai-yin, Zhang Jing-dong, et al. A motion compensation algorithm based on the designing structured Gram matrices[J].
Acta Electronica Sinica,2014, 42 (3) : 442 –461.
( 0) 0)
|
| [12] |
李少东, 陈文峰, 杨军, 等. 任意稀疏结构的多量测向量快速稀疏重构算法研究[J].
电子学报,2015, 43 (4) : 708 –715.
Li Shao-dong, Chen Wen-feng, Yang Jun, et al. Study on the fast sparse recovery algorithm via multiple measurement vectors of arbitrary sparse structure[J].
Acta Electronica Sinica,2015, 43 (4) : 708 –715.
( 0) 0)
|
| [13] |
Yin W, Osher S, Goldfarb D, et al. Bregman iterative algorithms for l1-minimization with applications to compressed sensing[J].
SIAM Journal on Imaging Sciences,2008, 1 (1) : 143 –168.
( 0) 0)
|
| [14] |
Osher S, Mao Y, Dong B, et al. Fast linearized Bregman iteration for compressive sensing and sparse denoisng[J].
Communications in Mathematical Sciences,2011, 8 (1) : 93 –111.
( 0) 0)
|
| [15] |
Cai J F, Osher S, and Shen Z W. Linearized Bregman iterations for frame-based image deblurring[J].
SIAM Journal on Imaging Sciences,2009, 2 (1) : 226 –252.
( 0) 0)
|
| [16] |
Yin W. Analysis and generalizations of the linearized Bregman method[J].
SIAM Journal on Imaging Sciences,2010, 3 (4) : 856 –877.
( 0) 0)
|
| [17] |
陈文峰, 李少东, 杨军. 任意稀疏结构的复稀疏信号快速重构算法及其逆合成孔径雷达成像[J].
光电子·激光,2015, 26 (4) : 797 –804.
Chen Wen-feng, Li Shao-dong, Yang Jun. Fast recovery algorithm for complex sparse signal with arbitrary sparse structure and its inverse synthetic aperture radar imaging[J].
Journal of Optoelectronics · Laser,2015, 26 (4) : 797 –804.
( 0) 0)
|
| [18] |
李少东, 陈文峰, 杨军, 等. 一种快速复数线性Bregman迭代算法及其在ISAR成像中的应用[J].
中国科学: 信息科学,2015, 45 (9) : 1179 –1196.
Li Shao-dong, Chen Wen-feng, Yang Jun, et al. A fast complex linearized Bregman iteration algorithm and its application in ISAR imaging[J].
Scientia Sinica (Informationis),2015, 45 (9) : 1179 –1196.
( 0) 0)
|
| [19] |
Donoho D L. High-dimensional centrally symmetric polytopes with neighborliness proportional to dimension[J].
Discrete&Computational Geometry,2006, 35 (4) : 617 –652.
( 0) 0)
|
| [20] |
田野, 毕辉, 张冰尘, 等. 相变图在稀疏微波成像变化检测降采样分析中的应用[J].
电子与信息学报,2015, 37 (10) : 2335 –2341.
Tian Ye, Bi Hui, Zhang Bing-chen, et al. Application of phase diagram to sampling ratio analysis in sparse microwave imaging change detection[J].
Journal of Electronics&Information Technology,2015, 37 (10) : 2335 –2341.
( 0) 0)
|
| [21] |
Tropp J A and Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J].
IEEE Transactions on Information Theory,2007, 53 (12) : 4655 –4666.
( 0) 0)
|
| [22] |
Daubechies I, Defrise M, and De M C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J].
Communications on Pure and Applied Mathematics,2004, 57 (11) : 1413 –1457.
( 0) 0)
|
| [23] |
Blumensath T and Davies M E. Iterative hard thresholding for compressed sensing[J].
Applied and Computational Harmonic Analysis,2009, 27 (3) : 265 –274.
( 0) 0)
|
| [24] |
张磊. 高分辨率SAR/ISAR成像及误差补偿技术研究[D]. [博士论文], 西安电子科技大学, 2012.
Zhang Lei. Study on high resolution SAR/ISAR imaging and error correction[D]. [Ph.D. dissertation], Xidian University, 2012.
( 0) 0)
|
| [25] |
Mohimani G H, Zadeh M B, and Jutten C. A fast approach for over-complete sparse decomposition based on smoothed l0 norm[J].
IEEE Transactions on Signal Processing,2009, 57 (1) : 289 –301.
( 0) 0)
|
| [26] |
苏伍各, 王宏强, 邓彬, 等. 基于方差成分扩张压缩的稀疏贝叶斯ISAR成像方法[J].
电子与信息学报,2014, 36 (7) : 1525 –1531.
Su Wu-ge, Wang Hong-qian, Deng Bin, et al. Sparse Bayesian representation of the ISAR imaging method based on ExCoV[J].
Journal of Electronics&Information Technology,2014, 36 (7) : 1525 –1531.
( 0) 0)
|
| [27] |
Tropp J A, Gilbert A C, and Strauss M J. Simultaneous sparse approximation via greedy pursuit[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Ann Arbor, USA, 2005: 721-724.
( 0) 0)
|
| [28] |
Liu Z, You P, Wei X Z, et al. Dynamic ISAR imaging of maneuvering targets based on sequential SL0[J].
IEEE Geoscience and Remote Sensing Letter,2013, 10 (5) : 1041 –1045.
( 0) 0)
|


