先进的有源干扰是近几年来雷达对抗的研究热点之一,通过时域、相位或运动调制,有源干扰能对雷达系统形成压制或欺骗干扰[1, 2]。但另一方面,有源干扰也存在着结构复杂、反应时间延迟等固有缺点。相比之下,采用无源材料实现对抗有着结构简单、反应速度快等显著优点,也一直是雷达隐身、战场防护的有效途径[3]。Salisbury屏(简称:S屏)是一种干涉型雷达吸波材料,其基本结构是在导体平板前四分之一波长处放置一块具有特定阻值的阻抗层来减缩电磁波垂直入射情况下平板的后向散射[4];自提出S屏的概念后,对单层和多层S屏的反射特性及性能优化方法的研究成为热点[5, 6];此后,文献[7]首次给出S屏雷达散射截面近似的物理光学解释,并分析了不同尺寸S屏的后向散射性能;为扩展S屏的吸波频宽和角度稳定性,国内外学者分别提出基于高阻抗表面的多频带Salisbury屏设计方法[8]以及基于频率选择表面的S屏吸波体[9],并从仿真和实验两个方面验证了设计的可行性。现有研究表明,S屏能显著减小目标的后射散射,因而在雷达隐身、电子对抗等方面具备较好的应用价值。
二面角是雷达目标中的强散射结构,常用于构成假目标对雷达实施诱骗,新型二面角反射器的设计和分析成为研究热点。文献[10]设计了一种基于超材料吸波体的新型二面角反射器,这种角反射器可有效对抗X波段变频雷达对角反射器假目标的探测与识别;文献[11]将雷达吸波材料涂覆于金属二面角表面,实现减缩金属二面角反射器的后向RCS至期望水平。此外,旋转型角反射器的设计方法也层出不穷[12, 13],在尺寸固定的情况下有效改变了二面角反射器的雷达散射截面;值得一提的是,作为定标体,二面角的极化散射特性也被广泛研究,其极化散射矩阵经常被用来进行目标识别。有文章提出了基于Krogager的目标分解方法[14],将各距离分辨单元的极化散射矩阵分解为球形、二面角和螺旋体的散射矩阵,并提取出反应目标散射中心和物理结构的特征进行目标识别。
作为众多雷达目标中的典型二次散射结构,二面角的雷达散射特征对于复杂目标的探测和识别具有重要的意义。目标特性是特征提取和目标识别的基础,如果目标本身的特性发生改变,将使其具备天然的反识别能力。利用S屏雷达目标特征变换的性能,本文设计了一种基于S屏的二面角结构,进行了理论分析,并应用FEKO仿真分析了该新型二面角结构的电磁散射特性,给出其极化散射矩阵。在此基础上,分析了雷达工作频率和目标姿态对其极化散射特性的影响。
2 基于Salisbury屏的新型二面角结构典型的S屏通过在导体平板前放置一块具有特定阻值的阻抗层来消除电磁波垂直入射情况下平板的后向散射,其基本原理是利用进入RAM并经目标表面反射的回波和直接由RAM表面反射的反射波相互干涉而抵消[15],使得在特定频率处的反射回波大幅衰减。当导体背板和阻抗层之间的距离为0.25l,即阻抗层阻值与空气中自由波阻抗相等时,S屏在该波长所对应的频率处反射回波衰减性能最好。同时,研究表明S屏具有雷达目标特征变换的效果。
本文利用S屏所设计的新型的二面角结构可以改变矩形金属二面角结构的RCS特性和极化特性。类似于金属二面角,基于S屏的矩形二面角结构(简称S屏二面角)由两个正方形面组成,不同的是将金属二面角的两个金属面替换为两个标准的S屏,图 1为S屏二面角示意图,其中S0为二面角两个S屏的边长,预定张角为2g,j和q为电磁波入射角度。该新型二面角可以等效成两个S屏按照预定角度组合而成的一种双层结构,第1层是阻抗层,第2层为金属背板,且阻抗层和导体背板由厚度为d的各向同性低损耗介质或空气分开。
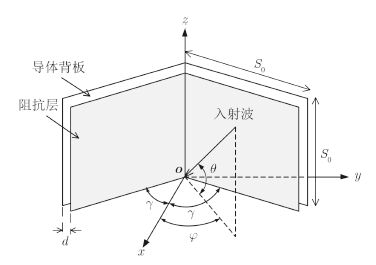
|
图 1 S屏二面角结构示意图 Fig.1 Diagram of a Salisbury screen dihedral |
与金属二面角反射器相似,S屏二面角所能支持的反射次数取决于预定张角2g。当2g ≥ 90°时,仅1次和2次反射回波对散射场有贡献;当60° ≤ 2g ≤ 90°时,决定散射场特性的因素的则包含1次、2次和3次反射回波,随着夹角2g的减小,必须考虑更多次反射[16]。本文仅考虑到3次反射,即60° ≤ 2g ≤ 90°情况,故本文以90°和60°的二面角为例进行分析。
3 S屏二面角后向RCS分析下面对正交S屏二面角结构进行分析,考虑两种电磁波入射情况:①电磁波垂直于其中一面入射(θ=0°,φ=45°);②电磁波与其中一面的夹角为45°(θ=0°,φ=0°)。如图 2所示为两种电磁波入射情况示意图。
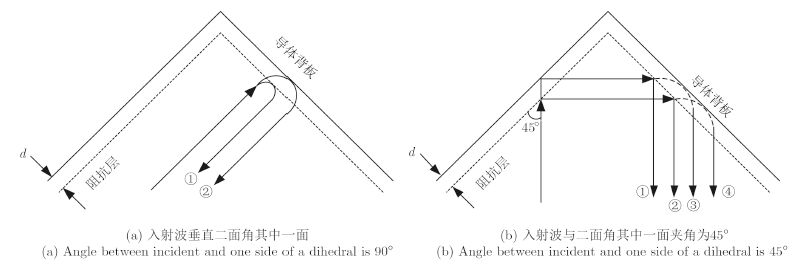
|
图 2 电磁波入射到S屏二面角示意图 Fig.2 Diagram of electromagnetic wave is incident on Salisbury screen dihedral |
(1) 电磁波垂直于其中一面入射(θ=0°,φ=45°)
当电磁波垂直入射到S屏二面角结构的其中一面时,不会发生2次反射,入射电磁波接触到S屏二面角会产生两束反射回波,即回波①和②,此时表现为S屏的特性,两束回波可以相互抵消,如果入射电磁波频率为f0,对应波长为λ0,d=0.25λ0,那么由S屏的特性可知,散射回波的能量几乎为零,可以预测,这种情况下S屏二面角将表现出很低的后向RCS。
(2) 电磁波与其中一面的夹角为45°(θ=0°,φ=0°)
当入射电磁波与二面角的其中一面呈45°夹角时,会发生2次反射,即入射到其中一面的电磁波经过第1次反射后入射到另外一面产生2次反射,分析可知这种情况下会产生4束回波,分别为回波①、②、③、④,且波束①和③、波束②和④之间分别都存在2d/cos(45°)的波程差,且波束之间仍彼此存在着其他不同的波程差,导致回波之间存在复杂的干涉现象,致使S屏二面角的后向散射和极化散射特性会与金属二面角有所不同。
4 S屏二面角结构的电磁散射特性分析考虑到S屏可以实现雷达目标特征变换,可以预见,基于S屏的新型二面角结构能够有效地改变金属二面角的后向散射和极化散射特性。为研究该新型二面角结构的电磁散射特性,利用FEKO软件对其进行建模和仿真,并根据仿真结果对其后向散射特性和极化散射特性进行分析。FEKO是针对电磁辐射、散射、EMC等确定性问题而开发的专业电磁场分析软件,从严格的电磁场积分方程出发,以经典矩量法为基础,采用多层快速多级子算法,并与高频分析方法完美结合,在保持精度的前提下提高计算效率,是目前国内外比较先进可靠的电磁场分析软件。
仿真参数设置如下,基于S屏的二面角结构为双层结构,第1层为阻抗层,设置为Impedance边界,其中电阻值377 Ω/m2,电抗值0 Ω/m2;第2层为导体背板,设置为PEC边界,对于入射的平面电磁波,PEC边界相当于“一面墙”,电磁波遇到PEC边界后会直接反射;入射波是频率f0=10 GHz (λ0=3 cm)的线极化平面电磁波,入射角度-45°≤φ≤45°,θ=0°;低损耗介质成份设置为“空”(εr=1,tanδ=) d=0.25λ0=0.75 cm,S0=5λ0=15 cm,其中θ,φ,d和S0的含义如图 1所示,且分别设置S屏二面角结构的张角为90°和60°进行仿真分析。
4.1 后向散射特性分析
假设电磁波入射角度为φ0,电磁波会在二面角的两个面之间发生多次反射,且存在多组相位差为
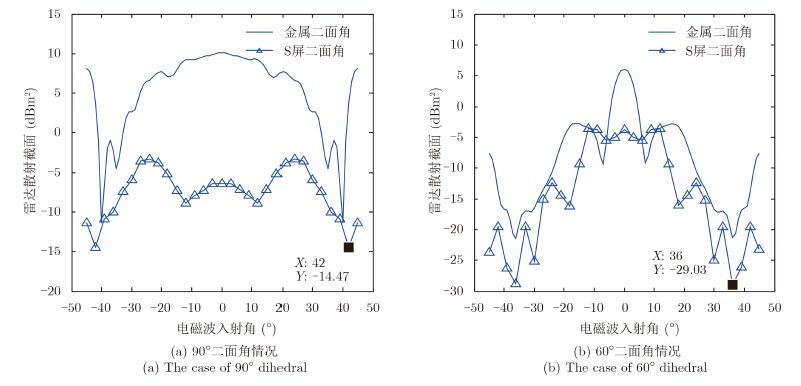
|
图 3 S屏二面角和金属二面角的后向RCS曲线 Fig.3 Backscattering curve of a Salisbury screen dihedral and a metal dihedral |
对比图 2中的两组RCS曲线,可以得到两点分析结果:
首先,基于S屏的二面角改变了金属二面角的RCS特性。相比于金属二面角,张角为90°和60°的S屏二面角后向RCS峰值点发生了变化,峰值点分别从0°偏移到了±25°和±12°左右,且RCS峰值全部低于金属二面角的RCS峰值。正交S屏二面角的RCS特性整体变化较大,而60°S屏二面角的后向RCS除峰值点发生偏移和扩展外,总体趋势与金属二面角相近。
其次,与金属二面角相比,S屏二面角在改变金属二面角后向散射特性的同时,全面减缩二面角结构的后向RCS值。表 1为电磁波不同入射角度下S屏二面角相比金属二面角的后向RCS减缩值。
| 表 1 不同入射角度下S屏二面角相比金属二面角的后向RCS减缩值 Tab.1 The reduced value of Salisbury screen dihedral backscattering compared with metal dihedral at different incident angles |
依据表 1中数据可知正交S屏二面角相比正交金属二面角在5个角度下的RCS平均减缩值为13.2 dBm2,60°情况下的RCS平均减缩值为8.9 dBm2,两种S屏二面角均较好地实现了二面角结构的后向RCS减缩,且正交S屏二面角的后向RCS减缩效果更优。
此外,从表 1也可以看出两种S屏二面角都在入射角度|φ|=45°时的RCS减缩效果十分明显,这是因为当|φ|=45°时,可以等效成电磁波只入射到二面角的其中一面,此时几乎不会发生二次反射,呈现出S屏的特性,故后向RCS减缩效果明显,仿真结果和理论分析相吻合。
4.2 极化散射特性分析
由前文可以看到,雷达散射截面只表征雷达目标散射的幅度特性,缺乏对诸如极化和相位等目标特性的表征。而极化散射矩阵可完整描述目标在特定姿态、入射频率下的包括极化、相位以及能量特性在内的全部雷达目标电磁散射信息。极化散射矩阵S也将散射场与入射场联系起来[17],表示为
| $\left[{\begin{array}{*{20}{l}} {\mathop E\nolimits_1^{\rm{s}} }\\ {\mathop E\nolimits_2^{\rm{s}} } \end{array}} \right]{\rm{ = }}\left[{\begin{array}{*{20}{c}} {{S_{\rm{1}}}_{\rm{1}}}& {{S_{\rm{1}}}_{\rm{2}}}\\ {{S_{\rm{2}}}_{\rm{1}}}& {{S_2}_{\rm{2}}} \end{array}} \right]\left[{\begin{array}{*{20}{l}} {\mathop E\nolimits_1^{\rm{i}} }\\ {\mathop E\nolimits_2^{\rm{i}} } \end{array}} \right]$ | (1) |
极化散射矩阵S一般为复数形式,矩阵元素可以表示为
| $\left| {{S_{ij}}} \right|{\rm{ = 20log}}\left| {\frac{{\mathop E\nolimits_i^{\rm{s}} }}{{\mathop E\nolimits_j^{\rm{i}} }}} \right|$ | (2) |
S屏二面角可以改变金属二面角结构的极化特性,下面以张角为90°的两种二面角结构为例,求解不同电磁波入射角度下的极化散射矩阵,并分析S屏二面角结构的极化散射特性。
(1) 入射角φ=0°时,金属二面角和S屏二面角极化散射矩阵分别如下:
| $\begin{align} & {{S}_{-\text{dihedral}}}=\left[ \begin{matrix} \text{-0}.\text{1090}\text{+}\text{0}.\text{8775i} & \text{-0}.\text{0000}\text{+}\text{0}.\text{0000i} \\ \text{0}.\text{0000}\text{+}\text{0}.\text{0000i} & \text{0}.\text{2089}\text{-}\text{0}.\text{8516i} \\ \end{matrix} \right] \\ & \left| {{S}_{-\text{dihedral}}} \right|=\left[ \begin{matrix} \text{0}.\text{8842} & \text{0}.\text{0000} \\ \text{0}.\text{0000} & \text{0}.\text{8769} \\ \end{matrix} \right] \\ & {{S}_{\text{S}}}_{-\text{dihedral}}=\left[ \begin{matrix} \text{-0}.\text{1048-0}.\text{0435i} & \text{0}.\text{0000}\text{+}\text{0}.\text{0000i} \\ \text{0}.\text{0000+0}.\text{0000i} & \text{-0}.\text{0630}\text{+}\text{0}.\text{0122i} \\ \end{matrix} \right] \\ & \left| {{S}_{\text{S}}}_{-\text{dihedral}} \right|=\left[ \begin{matrix} \text{0}.\text{1135} & \text{0}.\text{0000} \\ \text{0}.\text{0000} & \text{0}.\text{0641} \\ \end{matrix} \right] \\ \end{align}$ |
(2) 入射角φ=25°时,金属二面角和S屏二面角极化散射矩阵分别如下:
| $\begin{align} &{{S}_{-\text{dihedral}}}=\left[ \begin{matrix} \text{-0}.\text{0470}\text{+}\text{0}.\text{5097i}&\text{-0}.\text{0000}\text{-}\text{0}.\text{0002i} \\ \text{-0}.\text{0000}\text{-}\text{0}.\text{0002i}&\text{-0}.\text{0715}\text{-}\text{0}.\text{4202i} \\ \end{matrix} \right] \\ &\left| {{S}_{-\text{dihedral}}} \right|=\left[ \begin{matrix} \text{0}.\text{5119}&\text{0}.\text{0002} \\ \text{0}.\text{0002}&\text{0}.\text{4263} \\ \end{matrix} \right] \\ \end{align}$ |
| $\begin{align} &{{S}_{\text{S}}}_{-\text{dihedral}}=\left[ \begin{matrix} \text{-0}.\text{1292}\text{-}\text{0}.\text{0949i}&\text{0}.\text{0001}\text{-}\text{0}.\text{0000i} \\ \text{0}.\text{0002}\text{+}\text{0}.\text{0000i}&\text{-0}.\text{0213}\text{-}\text{0}.\text{0233i} \\ \end{matrix} \right] \\ &\left| {{S}_{\text{S}}}_{-\text{dihedral}} \right|=\left[ \begin{matrix} \text{0}.\text{1603}&\text{0}.\text{0001} \\ \text{0}.\text{0002}&\text{0}.\text{0316} \\ \end{matrix} \right] \\ \end{align}$ |
(3) 入射角j=45°,金属二面角和S屏二面角极化散射矩阵分别如下:
| $\begin{align} & {{S}_{-\text{dihedral}}}=\left[ \begin{matrix} \text{0}.\text{0050+0}.\text{7430i} & \text{0}.\text{0000-0}.\text{0000i} \\ \text{0}.\text{0000-0}.\text{0000i} & \text{-0}.\text{0653+0}.\text{6330i} \\ \end{matrix} \right] \\ & \left| {{S}_{-\text{dihedral}}} \right|=\left[ \begin{matrix} \text{0}.\text{7430} & \text{0}.\text{0000} \\ \text{0}.\text{0000} & \text{0}.\text{6363} \\ \end{matrix} \right] \\ & {{S}_{\text{S-}}}_{\text{dihedral}}=\left[ \begin{matrix} \text{-0}.\text{0182}\text{-}\text{0}.\text{0258i} & \text{-0}.\text{0000}\text{+}\text{0}.\text{0000i} \\ \text{-0}.\text{0000}\text{+}\text{0}.\text{0000i} & \text{-0}.\text{0258}\text{-}\text{0}.\text{0004i} \\ \end{matrix} \right] \\ & \left| {{S}_{\text{S-}}}_{\text{dihedral}} \right|=\left[ \begin{matrix} \text{0}.\text{0315} & \text{0}.\text{0000} \\ \text{0}.\text{0000} & \text{0}.\text{0258} \\ \end{matrix} \right] \\ \end{align}$ |
从图 4能够看出,随着电磁波入射角度|φ|的变化,金属二面角散射矩阵两个主极化通道幅度值呈等比例变化,且变化趋势与其同条件下的后向RCS趋势一致,即0°≤|φ|≤45°时,两个主极化通道幅值先下降之后上升,在|φ|=39°时同时达到最低,分别为HH通道-17.3 dBm2和VV通道-15.8 dBm2。S屏二面角散射矩阵的HH通道幅度值始终强于VV通道幅度值,当0°≤|φ|≤45°时,随着|φ|的增大,HH通道幅度值先下降后上升,在|φ|=25°时达到最大-15.9 dBm2,相比之下,VV通道幅度值则波动式下降,波动周期大约为5°,由此可见电磁波入射角度是影响S屏二面角极化散射特性的重要因素之一。在相同的电磁波入射角度下,S屏二面角有效地改变了金属二面角的极化散射特性,两种二面角结构极化散射特性相差如此明显正是由于S屏二面角的双层结构所导致的,这实质上是S屏对金属平板结构雷达目标特征变换的原因。从以上分析可以看出,倘若用S屏二面角对雷达实施欺骗干扰,能够起到良好的掩护和伪装效果,且S屏二面角制作工艺简单,成本低,易于实现。
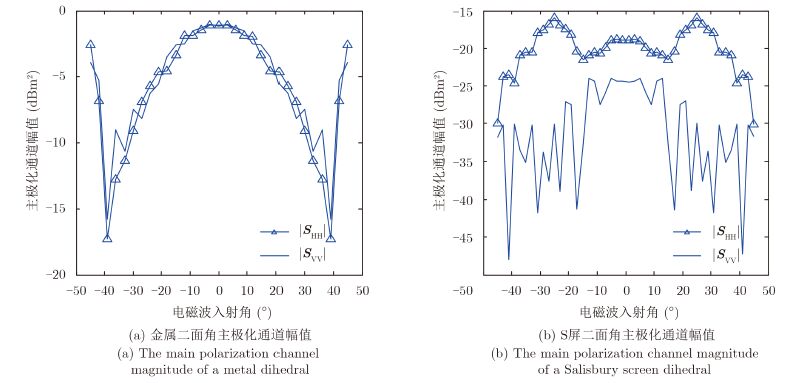
|
图 4 金属二面角和S屏二面角极化散射矩阵主极化通道幅值 Fig.4 The main polarization channel magnitude of a metal dihedral and a Salisbury screen dihedral |
由电磁散射理论可知,极化散射矩阵能够完整地表征目标对电磁波的散射特性,且极化散射矩阵随雷达工作频率与目标姿态而变化[18],雷达工作频率和目标姿态是影响雷达目标极化特性的关键因素,下面具体分析关键参数对新型二面角结构的极化特性的影响。
5.1 雷达工作频率对S屏二面角极化特性影响分析下面从雷达目标极化散射矩阵的角度,以正交金属二面角和正交S屏二面角为例,依据仿真结果具体分析频率对S屏二面角极化特性影响。设置入射波是频率f (5~15 GHz)的线极化平面电磁波,入射角度φ=0°,θ=0°,距离d=0.75 cm,S0= 5λ0=15 cm,二面角张角2γ=90°,其中φ,θ,λ,d和S0的含义如图 1所示,其余参数设置同第4节。分别在入射电磁波频率为7 GHz和13 GHz下求得S屏二面角的极化散射矩阵如下,其中SS-7 GHz和SS-13 GHz代表入射频率为7 GHz和13 GHz下求解的极化散射矩阵。
| $\begin{align} & {{S}_{\text{S-}}}_{\text{7}\text{GHz}}=\left[ \begin{matrix} \text{0}.\text{0885}\text{-}\text{0}.\text{1538i} & \text{0}.\text{0000}\text{-}\text{0}.\text{0000i} \\ \text{0}.\text{0000}\text{-}\text{0}.\text{0000i} & \text{-0}.\text{1289}\text{-}\text{0}.\text{0080i} \\ \end{matrix} \right] \\ & \left| {{S}_{\text{S}}}_{\text{-7}\text{GHz}} \right|=\left[ \begin{matrix} \text{0}.\text{1775} & \text{0}.\text{0000} \\ \text{0}.\text{0000} & \text{0}.\text{1291} \\ \end{matrix} \right] \\ & {{S}_{\text{S}}}_{\text{-13}\text{GHz}}=\left[ \begin{matrix} \text{-0}.\text{0386}\text{+}\text{0}.\text{0690i} & \text{0}.\text{0001}\text{+}\text{0}.\text{0001i} \\ \text{0}.\text{0001}\text{+}\text{0}.\text{0000i} & \text{-0}.\text{0053}\text{+}\text{0}.\text{0089i} \\ \end{matrix} \right] \\ & \left| {{S}_{\text{S}}}_{\text{-13}\text{GHz}} \right|=\left[ \begin{matrix} \text{0}.\text{0791} & \text{0}.\text{0001} \\ \text{0}.\text{0001} & \text{0}.\text{0104} \\ \end{matrix} \right] \\ \end{align}$ |
分析这两组极化散射矩阵,并与4.2小节中入射电磁波频率为10 GHz,φ=0°时的散射矩阵对比,可以得到以下几点分析结果:(1) 交叉极化通道分量的幅度值基本不随入射电磁波频率变化,相对稳定。(2) 主极化通道分量幅度值随入射电磁波频率的变化比较明显。图 5给出S屏二面角散射矩阵两个主极化通道幅度和相位频变特性曲线,从图 5(a)可以看出,在大部分的入射频率处,散射矩阵HH通道幅值都高于VV通道幅值,且随着入射频率的增大,两者均呈下降趋势,HH通道幅度值平稳缓慢下降,VV通道幅度值呈振荡式下降,且下降速度更快,可见对于S屏二面角反射器的应用应在特定的频率范围之内。图 5(b)显示散射矩阵VV通道相位比HH通道相位对随频率的变化更加敏感,HH通道相位除在频率1.05 GHz处出现一次翻转外,总体处于下降状态,VV通道相位在频率低于0.8 GHz时基本保持平稳,但频率高于0.8 GHz后开始振荡式变化,振荡周期逐渐增大,相位绝对值逐渐减小。
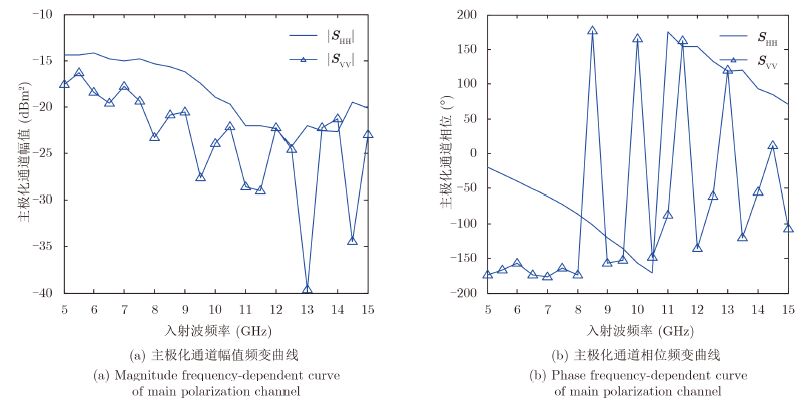
|
图 5 S屏二面角极化散射矩阵主极化通道频变特性曲线 Fig.5 Main polarization channel frequency-dependent characteristic curve of Salisbury screen dihedral |
综上分析,在电磁波入射角度一定的情况下,S屏二面角的极化特性随频率变化较大,并非像金属二面角一样极化散射矩阵稳定在
S屏二面角的空域极化特性主要表现在自身姿态对其极化特性的影响,下面以正交二面角为例,分析在特定入射频率和角度下,分析S屏二面角姿态对其极化散射特性的影响。不失一般性,S屏二面角的姿态角定义为二面角的折线分别在yoz和xoz平面内旋转的角度(w0和p0),如图 6所示。设定入射波频率f=10 GHz,目标姿态角w0=45°,p0=0°,电磁波入射角度-45°≤φ≤45°,其余参数设置与4.1小节相同。根据仿真数据,求得电磁波入射角分别为φ=0°和φ=25°极化散射矩阵如下,其中SS-0°和SS-25°分别代表入射角度为0°和25°下求解的极化散射矩阵。
|
图 6 二面角结构目标姿态角定义 Fig.6 The definition for target pose angle of the dihedral structure |
| $\begin{align} & {{S}_{\text{S}}}_{\text{-}{{\text{0}}^{\text{o}}}}=\left[ \begin{matrix} \text{-0}.\text{0839-0}.\text{0157i} & \text{-0}.\text{0212-0}.\text{0284i} \\ \text{-0}.\text{0208-0}.\text{0278i} & \text{-0}.\text{0837-0}.\text{0149i} \\ \end{matrix} \right] \\ & \left| {{S}_{\text{S-}{{0}^{\text{o}}}}} \right|=\left[ \begin{matrix} \text{0}.\text{0853} & \text{0}.\text{0354} \\ \text{0}.\text{0347} & \text{0}.\text{0850} \\ \end{matrix} \right] \\ & {{S}_{\text{S}}}_{\text{-2}{{\text{5}}^{\text{o}}}}=\left[ \begin{matrix} \text{0}.\text{0009+0}.\text{0083i} & \text{-0}.\text{0000+0}.\text{0125i} \\ \text{0}.\text{0002+0}.\text{0129i} & \text{-0}.\text{0011+0}.\text{0083i} \\ \end{matrix} \right] \\ & \left| {{S}_{\text{S}}}_{\text{-2}{{\text{5}}^{\text{o}}}} \right|=\left[ \begin{matrix} \text{0}.\text{0084} & \text{0}.\text{0125} \\ \text{0}.\text{0129} & \text{0}.\text{0083} \\ \end{matrix} \right] \\ \end{align}$ |
将这两组S屏二面角的极化散射矩阵与4.2小节目标姿态角w0=0°,电磁波入射角分别为0°和25°时的散射矩阵对比,能够看出S屏二面角的姿态对其极化散射矩阵影响较大,完全改变了金属二面角的极化散射特性。对比两种不同姿态下S屏二面角的极化散射矩阵,可以发现,由于目标姿态角的改变导致其极化散射矩阵中交叉极化分量的幅值大幅提高,主极化分量幅值则有所下降。当姿态角w0=0° 时,任何入射角度下,主极化通道幅值全部高于交叉极化通道幅值,而在w0=45°时,两类极化通道(主极化和交叉极化)的相对幅值大小则取决于电磁波的入射角度,不能一概而论。由文献[17]可知,当金属二面角反射器的姿态角w0=45°时,理论上其散射矩阵的两个交叉极化通道幅值为1,两个主极化通道幅值则为0,这种情况下,可以通过极化滤波的方式消除二面角反射器干扰和诱骗,相比之下S屏二面角在4个通道都会有能量穿过,同时也提高了二面角结构抗极化识别的能力。
6 小结二面角结构是雷达目标中常见的结构,由于其目标特征比较明显,经常被雷达用来探测和分类识别目标,如果其散射特性发生改变,将具备天然的电子对抗能力。新材料的出现为新型二面角设计提供了可能,本文根据S屏独特的电磁散射特性,设计了一种新型的S屏二面角,从理论和仿真两个角度分析了其后向散射特性和极化特性。研究结果表明,基于Salisbury屏的二面角在改变普通金属二面角的极化特性方面效果显著,达到了目标特征变换的目的。可以预见,拥有Salisbury屏二面角结构的目标,在特定的照射频率附近和适合的姿态角下或具备天然抗识别能力,并兼具隐身的作用,这种新型结构在无源电子对抗中具备较强的应用前景。
| [1] |
Xu Le-tao, Feng De-jun, and Wang Xue-song. Improved synthetic aperture radar micro-Doppler jamming method based on phase-switched screen[J].
IET Radar, Sonar & Navigation , 2016, 10 (3) : 525-534 ( 0) 0)
|
| [2] |
吴晓芳, 代大海, 王雪松, 等. 基于微动调制的SAR新型有源干扰方法[J].
电子学报 , 2010, 38 (4) : 954-959 Wu Xiao-fang, Dai Da-hai, Wang Xue-song, et al. A novel method of active jamming for SAR based on micro motion modulation[J].
Acta Electronica Sinica , 2010, 38 (4) : 954-959 ( 0) 0)
|
| [3] |
贾菲, 鲍红权, 徐铭. 吸收型雷达无源干扰材料研究进展与应用[J].
舰船电子对抗 , 2015, 38 (2) : 7-10 Jia Fei, Bao Hong-quan, and Xu Ming. Research development and application of absorptive passive jamming material of radar[J].
Shipboard Electronic Countermeasure , 2015, 38 (2) : 7-10 ( 0) 0)
|
| [4] |
Salisbury W W. Absorbent body for electromagnetic waves[P]. US: 259994 A.
( 0) 0)
|
| [5] |
Fante R L and Mccormack M T. Reflection properties of the Salisbury screen[J].
IEEE Transactions on Antennas and Propagation , 1988, 36 (10) : 1443-1454 DOI:10.1109/8.8632 ( 0) 0)
|
| [6] |
Chambers B. Optimum design of a Salisbury screen radar absorbers[J].
Electronics Letters , 1994, 30 (16) : 1353-1354 DOI:10.1049/el:19940896 ( 0) 0)
|
| [7] |
Haupt R L. Scattering from small Salisbury screens[J].
IEEE Transactions on Antennas and Propagation , 2006, 54 (6) : 1807-1810 DOI:10.1109/TAP.2006.875921 ( 0) 0)
|
| [8] |
党可征, 时家明, 李志刚, 等. 基于高阻抗表面的多频带Salisbury屏设计[J].
物理学报 , 2015, 64 (11) : 114101(1)-114101(6) Dang Ke-zheng, Shi Jia-ming, Li Zhi-gang, et al. Design of multiband Salisbury screen based on high impedance surfaces[J].
Acta Physica Sinica , 2015, 64 (11) : 114101(1)-114101(6) ( 0) 0)
|
| [9] |
Seman F C, Cahill R, Fusco1 V F, et al. Design of a Salisbury screen absorber using frequency selective surfaces to improve bandwidth and angular stability performance[J].
IET Microwaves, Antennas & Propagation , 2011, 5 (2) : 149-156 ( 0) 0)
|
| [10] |
祝寄徐, 裴志斌, 屈绍波, 等. 一种加载超材料吸波体的新型二面角反射器的设计[J].
空军工程大学学报(自然科学版) , 2013, 14 (6) : 85-88 Zhu Ji-xu, Pei Zhi-bin, Qu Shao-bo, et al. A design of a new dihedral corner reflector loaded with meta-material absorbing layer[J].
Journal of Air Force Engineering University (Natural Science Edition) , 2013, 14 (6) : 85-88 ( 0) 0)
|
| [11] |
史庆藩, 闫学群. 材料涂覆非正交金属二面角反射器的后向散射[J].
北京理工大学学报 , 2002, 22 (6) : 668-671 Shi Qing-fan and Yan Xue-qun. Backscattering from nonorthogonal dihedral corner reflectors coated by radar absorbing materials[J].
Journal of Beijing Institute of Technology , 2002, 22 (6) : 668-671 ( 0) 0)
|
| [12] |
祝寄徐, 裴志斌, 屈绍波, 等. 一种旋转型的角反射器的设计[J].
现代电子技术 , 2013, 36 (11) : 1-4 Zhu Ji-xu, Pei Zhi-bin, Qu Shao-bo, et al. Design of rotary- type corner reflector[J].
Modern Electronics Technique , 2013, 36 (11) : 1-4 ( 0) 0)
|
| [13] |
李有才, 郑春弟, 黄强. 旋转式RCS可变角反射器的结构设计与可行性研究[J].
舰船电子对抗 , 2011, 34 (3) : 106-109 Li You-cai, Zheng Chun-di, and Huang Qiang. Structural design and feasibility study of rotary corner with variable RCS[J].
Shipboard Electronic Countermeasure , 2011, 34 (3) : 106-109 ( 0) 0)
|
| [14] |
李莹, 任勇, 山秀明. 基于目标分解的极化雷达飞机识别法[J].
清华大学学报(自然科学版) , 2001, 41 (7) : 32-35 Li Ying, Ren Yong, and Shan Xiu-ming. Target decomposition-based polarimetric radar aircraft recognition method[J].
Journal of Tsinghua University (Science & Technology) , 2001, 41 (7) : 32-35 ( 0) 0)
|
| [15] |
熊勇. 基于相位调制表面的雷达吸波材料的电磁特性研究[D]. [硕士论文], 南京航空航天大学, 2008: 6-7.
( 0) 0)
|
| [16] |
郭辉萍, 刘学观, 殷红成, 等. 各向异性材料涂覆金属二面角反射器的RCS分析[J].
电子与信息学报 , 2003, 25 (9) : 1255-1260 Guo Hui-ping, Liu Xue-guan, Yin Hong-cheng, et al. RCS analysis of anisotropic coating dihedral corner reflectors[J].
Journal of Electronics & Information Technology , 2003, 25 (9) : 1255-1260 ( 0) 0)
|
| [17] |
黄培康, 殷红成, 许小剑.
雷达目标特性[M]. 北京: 电子工业出版社, 2010 : 174 -185.
Huang Peikang, Yin Hongcheng, and Xu Xiaojian.
Radar Target Characteristic[M]. Beijing: Publishing House of Electronics Industry, 2010 : 174 -185.
( 0) 0)
|
| [18] |
庄钊文, 肖顺平, 王雪松.
雷达极化信息处理及其应用[M]. 北京: 国防工业出版社, 1999 : 1 -28.
Zhuang Zhaowen, Xiao Shunping, and Wang Xuesong.
Radar Polarization Information Processing and Application[M]. Beijing: National Defense Industry Press, 1999 : 1 -28.
( 0) 0)
|
| [19] |
黄培康.
雷达目标特征信号[M]. 北京: 中国宇航出版社, 2009 : 42 -45.
Huang Peikang.
Radar Target Signature Signal[M]. Beijing: China Astronautic Publishing House, 2009 : 42 -45.
( 0) 0)
|




