② (中国科学院大学 北京 100049)
② (University of Chinese Academy of Sciences, Beijing 100049, China)
合成孔径雷达(Synthetic Aperture Radar, SAR)是一种通过孔径合成实现方位向高分辨率的雷达遥感技术。尽管SAR的概念自提出至今已经几十年,但由于涉及到了微波、电子、信号处理、地球物理、地形测绘、航空航天等多个领域,学术界对SAR的研究一直热情不减。不同于传统光学遥感,SAR一般工作在微波频段,具备全天时、全天候的测绘能力,在军事领域和民用领域均有广泛应用。随着近些年来计算机技术的飞速发展,信号处理能力持续增强,SAR在朝着更高分辨率更宽测绘带不断发展[1]。
滑动聚束(Slide Spotlight)模式是一种兼顾方位向高分辨率和方位向幅宽的工作模式。这种模式在雷达平台飞行过程中通过不断地调整雷达波束指向(机械转动或者馈电扫描),来增大方位向多普勒合成带宽,从而提升SAR的方位向分辨率。当前众多SAR系统已经采用了滑动聚束模式,比如TerraSAR-X[2, 3]。滑动聚束模式的成像一般先进行一步去斜(Deramp)操作,然后用常用的频域成像算法进行聚焦[4, 5]。然而,当成像要求的分辨率不断提高,方位向幅宽不断增大时,频域成像方法难以保证可靠的成像性能,尤其是在边缘区域,目标性能会恶化得更为严重。
BP(Back-Projection,后向投影)成像算法[6, 7],是一种适用于多种SAR工作模式的时域成像方法。这种成像方法源自于计算机层析成像技术(Computed Tomography),它可以综合不同角度对一个物体的X射线扫描结果,反演物体的内部结构。当BP算法应用于SAR成像时,由于它是时域的,所以可以适应方位向多普勒中心的时变性,适用于包括滑动聚束在内的多种SAR工作模式,除此之外,BP算法可以通过增大减小方位向的累加区间方便地调整方位向处理带宽,还可以灵活地选取成像区域的像素间隔。不过,由于BP算法是逐像素处理算法,因此算法复杂度较高,为O(N3),而一般频域算法的算法复杂度为O(N2logN),较高的计算负担成为了BP算法广泛应用的障碍。
近些年来,GPU(Graphics Processing Unit, 图形处理器)[8]作为一种高性能的并行浮点处理器,实现了从传统单一的3D图形处理到图形处理、通用计算兼备的重大转变,大大推进了GPGPU (General-Purpose computing on Graphics Processing Units, GPU通用计算)的发展,降低了GPGPU的使用门槛。得益于海量的核心数目,GPU通常拥有十几倍到数十倍于CPU的浮点计算能力,应用于不同领域的越来越多的程序,比如电磁仿真、计算化学、机器学习等[9, 10],被迁移到GPU平台以实现算法加速,同样BP成像算法的GPU实现也被多次提出[11, 12]。目前,随着GPU使用越发广泛,更多的注意力转移到如何实现CPU和GPU的异构并行程序设计,在SAR成像相关领域已经有了一些尝试,并取得了不错的效果[13, 14]。
本文主要内容有两点:一是,利用BP成像算法克服频域成像算法的局限性,实现滑动聚束方位向宽测绘带情况下,中心区域以及场景边缘区域的良好聚焦;二是,当前CPU仍然是不可忽视的计算力量,通过线程协调,给GPU和CPU合理分配计算任务,发挥GPU强大计算能力的同时,不闲置CPU的计算能力,本文设计并实现了CPU/GPU异构平台的BP成像算法,使计算资源得到充分利用,并提高了成像灵活性。
2 滑动聚束模式滑动聚束模式是一种介于条带SAR和聚束SAR的工作模式,它同时兼顾了方位向高分辨率和方位向幅宽,图 1是滑动聚束模式SAR斜距平面的几何关系图,雷达平台沿x正方向飞行,起点为x1,终点为x2,场景中心目标位于

|
图 1 滑动聚束模式斜距平面几何关系图 Fig.1 Slant plane geometry of slide spotlight mode |
滑动聚束SAR一般先进行一步Deramp操作,实现方位向各目标多普勒中心的一致化,同时Deramp操作也降低了滑动聚束SAR对PRF的要求。在方位向幅宽不大或者说滑动聚束模式的扫描角变化不大的情况下,Deramp结合常规成像算法可以很好地实现聚焦,但当扫描角变化较大时,尤其是在星载情形下,上述处理方案就很难保证在整个方位向幅宽范围达成一致的良好聚焦效果。比如TerraSAR-X的滑动聚束模式[15],它的扫描角控制在-2.2°~2.2°范围之间,如果范围过大,边缘处的聚焦效果就会恶化。这是因为,当扫描角过大时,一方面会遇到类似于大斜视角成像的问题,即距离徙动变大,距离徙动矫正比较困难,且方位向和距离向耦合强烈,加剧了成像处理的复杂性;另一方面,由于数据获取时间内轨道弯曲及地球自转效应会更明显,将导致成像参数如方位向调频率等发生变化,也加剧了成像的困难性[16]。
3 BP成像算法BP成像算法是一种适用性很强的时域成像算法。假设s(τ, u)为距离向压缩后的回波信号,τ为距离向时间,u为方位向时间,R(u)为成像目标位置x到SAR天线相位中心xorbit(u)的斜距,x处的成像结果g(x)如式(1) 所示。
| $ \left. \begin{align} & g\left( \pmb{x} \right)=\int{s\left( \frac{2R\left( u \right)}{c},u \right)}\exp \left( \text{j}\frac{4\pi R\left( u \right)}{\lambda }\text{d}u \right) \\ & R\left( u \right)=\left| {{\pmb{x}}_{\text{orbit}}}\left( u \right)-\pmb{x} \right| \\ \end{align} \right\} $ | (1) |
从公式可以看出BP成像的基本步骤如下:
步骤1 对回波进行距离向压缩,通过卷积相应的匹配滤波器,实现回波的距离向聚焦。在文献[7]中也给出了2维的BP成像方法,即不进行距离向压缩,对距离向和方位向都进行后向投影操作,但是2维的计算复杂度过高,为
O(N4),一般不采用这种方法。
步骤2 对于一个成像目标,计算其到每一个PRF时刻雷达天线相位中心的斜距,并根据该斜距在相应的回波数据中进行插值。一般常用的插值操作有两种,一是利用FFT作升采样后取值,另一种是利用sinc函数进行插值,本文采用FFT升采样的方法,这样就可以使用现有的FFT数学库进行快速计算[17]。
步骤3 对每一个插值得到的数据,根据其斜距补偿相应的相位。由于回波数据接收过程中进行了混频操作,混频之后,数据中残留了沿方位向变化的相位,因此需要对该相位进行相应的补偿。
步骤4 将补偿后的值进行累加,就完成了该目标的成像,重复以上步骤,就可以实现对成像区域每个像素点的成像。
将BP算法用流程图表示,即如图 2所示。

|
图 2 BP算法流程图 Fig.2 BP algorithm flowchart |
由于BP算法是时域算法,它很好地避免了频域成像算法遇到的一些问题。
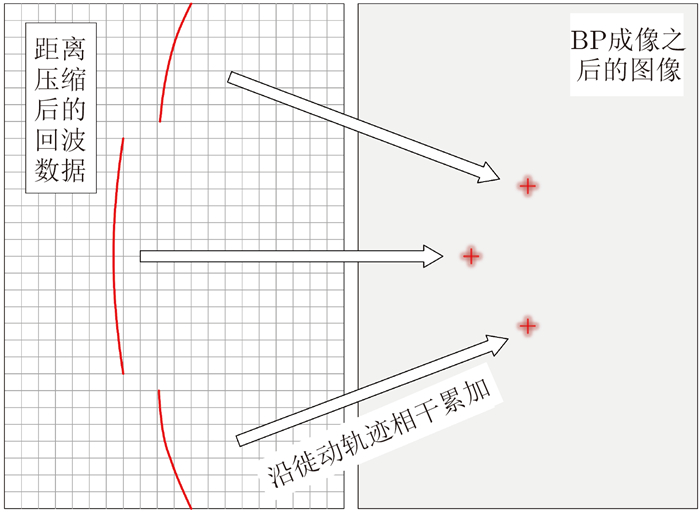
(1) 距离徙动问题:BP算法不需要将数据变换到频域,因此可以根据目标各个时刻的斜距精确确定目标的徙动轨迹,图 3展示了BP成像算法通过对斜距的计算可以很好地适应目标的徙动轨迹。
|
图 3 BP算法精确沿徙动轨迹相干累加 Fig.3 BP algorithm adds values coherently along the accurate trajectory of range migration |
(2) 方位向调频率问题:方位向调频率沿方位向和距离向都是时变的,频域算法很难适应时变信号的处理。而BP算法是时域算法,它针对每个像素的斜距计算,本质上就是在适应方位向调频率的时变性。
(3) 方位向和距离向耦合:耦合的出现,本身来自于处理域的变换,BP本身在时域进行处理,不需要进行处理域的变换,因此也不存在频域算法所遇到的耦合问题。
综上可知,BP成像算法理论上可以在更大的方位向幅宽内实现一致的点目标聚焦性能。然而BP成像算法的最大障碍来自于其算法复杂度。对于N×N个像素的成像区域,假设其合成孔径的点数也是N,那么每一个像素需要进行N次斜距计算,N次插值,N次相位补偿,最后需要将得到的N个值进行累加。所以,算法的整体计算复杂度为
O(N3)。而频域算法一般使用FFT进行计算,其算法复杂度为O(N2logN),相比而言,BP算法的算法复杂度更高,其运算速度成为研究领域广泛关注的问题。
近些年来,GPU以及基于GPU平台提出的GPGPU技术得到了研究人员的广泛关注。GPU本是3D图形处理器,用来进行3D场景的加速渲染,早期其内部指令是固定的,被称作固定管线,只能实现3D图形的顶点、深度、纹理、栅格化等固定渲染功能。后来,固定管线发展成为可编程管线,管线的处理功能可以通过相应的着色语言(如GLSL, HLSL)进行着色编程,之后Nvidia公司还开发了CG语言,简化了着色程序的编程负担。这个时期,GPU通用计算的概念GPGPU已经初步提出,很多通用计算程序将数据等效为3D图形处理中的顶点信息,配合着色编程,实现通用计算的目的[18]。
随着越来越多通用计算的需求被提出,GPU生产厂商在可编程管线的通用计算方面投入了大量精力。其中Nvidia公司的CUDA(Compute Unified Device Architecture)架构无疑是最受瞩目的划时代产品,随之推出的CUDA C语言,引起大规模并行计算相关领域的强烈反响。CUDA C使得GPGPU编程彻底摆脱了3D图形的束缚,极大降低了GPGPU的编程门槛[19]。
GPU强大的计算能力源自于几个方面,最主要的两点,一是海量的计算核心,一般CPU只有几个或者十几个计算核心,而GPU的计算核心可以达到上千个,虽然主频不及CPU,但上千核心并行工作的计算能力也远在CPU之上;二是,GPU的显存吞吐能力惊人,现在的GPU普遍采用GDDR5显存,其时钟频率数倍于CPU用的内存时钟频率,而且GPU使用的显存位宽很大,保证了与GPU计算能力相匹配的存取能力。表 1给出了Nvidia一款专业计算卡Tesla K20c的主要参数。
| 表 1 Nvidia Tesla K20c及Intel Xeon E5620主要参数 Tab.1 Parameters of Nvidia Tesla K20c and Intel Xeon E5620 |
尽管,GPU的计算能力超出CPU很多,但CPU的计算能力依然不可忽视,表 1中给出了后面仿真中使用的Intel Xeon E5620的主要参数,其双精度浮点性能为85.12 Gflops,工作站中配备了两颗CPU,那么约有GPU双精度浮点性能的7.3%。而且,GPU在计算机中一般是通过PCIE2.0或者3.0总线和CPU及内存进行数据传输,因此GPU一般很难达到计算能力的峰值,另外,相比于动辄几十甚至上百个GB的主机内存,GPU的显存容量要小很多,当处理大规模数据的时候,频繁的数据传输使得GPU的计算能力打了折扣。总之,需要将计算任务合理分配给CPU和GPU,使得CPU和GPU并行工作,最大可能地挖掘工作站的计算能力,一般将这种计算平台称为CPU/GPU异构计算平台。
5 异构平台下的BP算法异构平台的BP算法需要解决的问题是CPU和GPU的协同工作问题。根据前面对于BP算法的讨论可知,成像平面内各个像素的成像过程是彼此独立的,因此可以实现以像素为单位的并行计算,如此一来,可以将成像平面内所有像素的成像看成待分配的计算任务的集合,CPU和GPU的协同工作就是将这些需要成像的像素合理地分配给CPU和GPU进行计算。
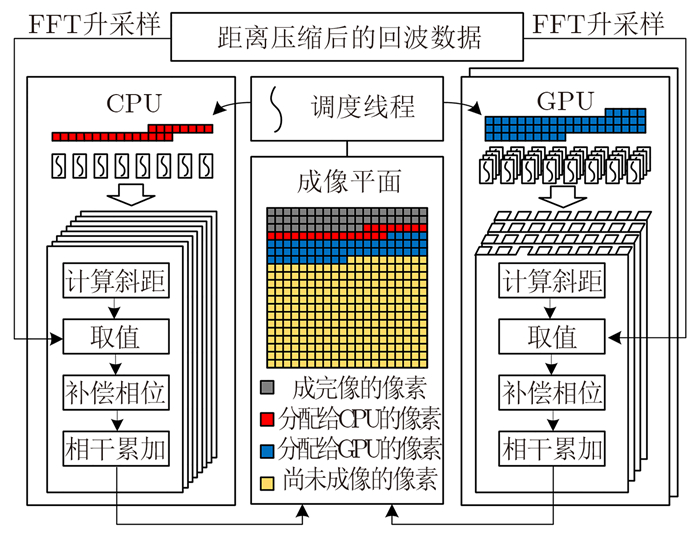
若每个像素是一项计算任务,那么每个线程就是CPU和GPU进行计算的一个实体,所有任务都要落实到线程才能完成相应的计算。这里将异构BP涉及到的线程分为以下几种:
(1) 调度线程,此线程用于给CPU和GPU分配若干像素,分配的像素个数依赖于CPU和GPU的计算能力,调度线程可以控制只使用CPU或GPU,或者二者同时参与计算,提高了成像的灵活性,另外对于GPU显存的有限性,调度线程也可以控制传递给GPU的数据量,提高程序的稳健性;
(2) GPU控制线程,GPU的控制独占一个CPU线程,如果有多个GPU,那么就占据多个CPU线程,虽然此线程可以和GPU实现异步操作,但是在GPU计算过程中需要多次和GPU进行数据交换与同步,因此不适合进行成像计算,这里只用做GPU的控制,负责和GPU相互传输数据以及启动GPU计算核函数。考虑到此线程并不参与计算,所以图 4中并没有展示出GPU控制线程;
|
图 4 CPU/GPU异构平台BP算法流程图 Fig.4 BP algorithm flowchart on a CPU/GPU heterogeneous platform |
(3) CPU计算线程,除却一个调度线程和若干GPU控制线程,剩余的CPU核心可以开辟线程参与成像计算任务;
(4) GPU计算线程,该线程由GPU控制线程通过调用计算核函数启动,可以同时启动数百或上千GPU线程进行成像计算。
异构BP的算法流程如图 4所示,其基本步骤为,调度线程根据CPU和GPU的计算能力,分配数目与之匹配的像素,此外还需要考虑GPU的显存大小。像素分配完成后,调度线程一方面通知CPU计算线程进行成像计算,另一方面通知GPU控制线程启动GPU成像核函数。CPU和GPU的成像计算过程基本一致,即将调度线程分配进来的像素分配给各自的计算线程,计算线程依次进行计算斜距、升采样数据取值、相位补偿、相干累加4个步骤完成像素的成像,其中升采样这一步,CPU和GPU可以调用各自相应的FFT库函数,最后将成像结果放置到成像平面中的正确位置,并向调度线程请求新的计算任务。不断地重复以上过程,直到成像平面内的所有像素都计算完毕,至此成像结束。
相比于仅使用CPU或者仅使用GPU计算,异构平台BP成像算法可以让二者并行执行,互不干扰,充分挖掘了计算资源,提高了成像效率。
6 实验结果 6.1 成像有效性为了对BP算法在高分宽测滑动聚束模式下的有效性进行验证,这里设计了一组X波段星载滑动聚束模式的参数,并进行了仿真,参数如表 2所示。
| 表 2 星载滑动聚束SAR仿真参数 Tab.2 Spaceborne slide spotlight SAR simulation parameters |
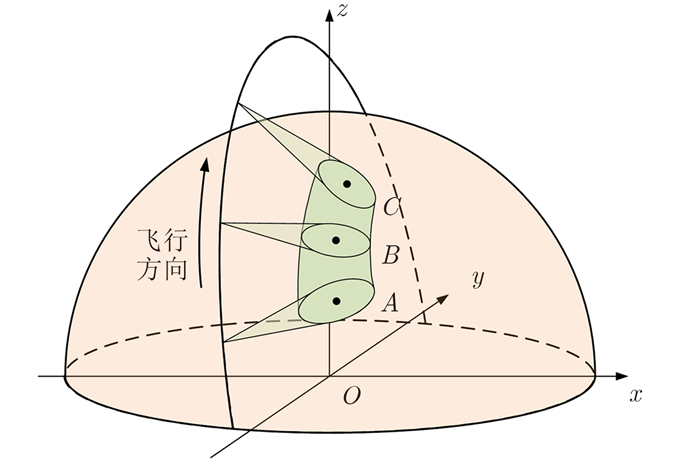
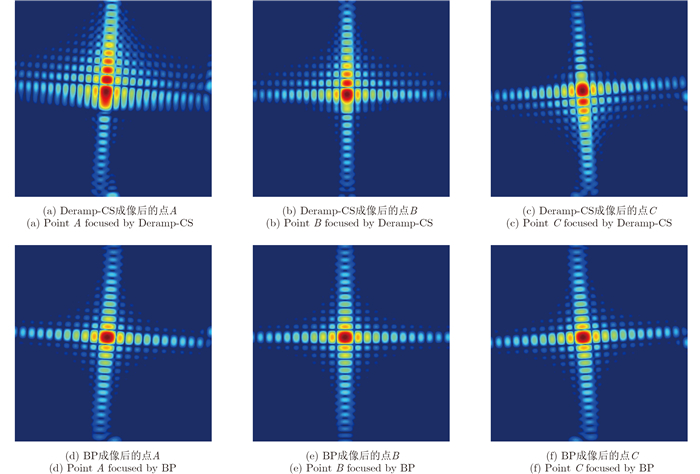
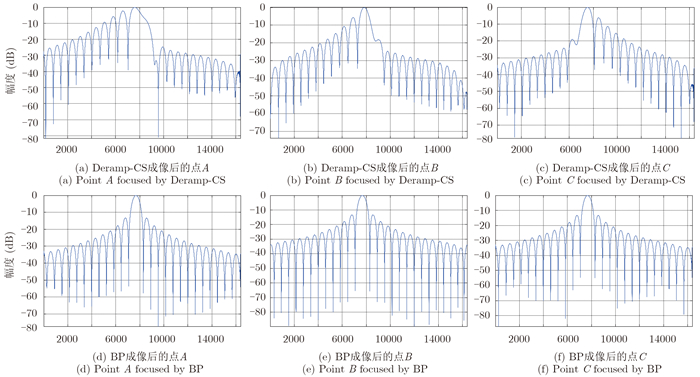
仿真场景的方位向中心和两端位置共设置了3个点目标A, B, C,如图 5所示,从A到C,雷达波束从前侧视、正侧视逐步过渡到后侧视,由于方位向0.3 m的分辨率比较高,点目标的方位向合成孔径的点数很多,达到了24000个点。我们分别采用Deramp-CS算法以及BP算法对仿真数据进行了成像,图 6给出了各点目标的成像结果,图 6(a),图 6(b),图 6(c)分别为使用Deramp-CS算法处理的A, B, C 3点的点目标结果,图 6(d),图 6(e),图 6(f)分别为使用BP算法处理的A, B, C 3点的点目标结果,很直观地可以看出Deramp-CS算法没有能够很好地实现方位向聚焦,而BP算法聚焦效果很好。进一步,图 7给出了各点目标方位向的幅度剖面图,图 7(a),图 7(b),图 7(c)分别为使用Deramp-CS算法处理的A, B, C 3点的方位向幅度剖面,图 7(d),图 7(e),图 7(f)分别为使用BP算法处理的A, B, C 3点的方位向幅度剖面。仿真中使用的方位向的天线方向图为矩形窗,因此方位向的第1旁瓣应该在-13.2 dB附近,可以看出Deramp-CS算法成的点目标旁瓣过高而且严重不对称,无法达到成像要求,而BP算法所成的3个位置的点目标均能满足成像要求。
|
图 5 星载滑动聚束SAR仿真模型 Fig.5 Spaceborne slide spotlight SAR simulation model |
|
图 6 分别使用Deramp-CS和BP算法的点目标成像结果 Fig.6 Point targets processed with Deramp-CS and BP algorithm |
|
图 7 分别使用Deramp-CS和BP算法的点目标方位向幅度剖面图 Fig.7 Azimuth magnitude lines of the point targets processed with Deramp-CS and BP algorithm |
以上滑动聚束仿真的BP成像部分使用了本文提出的异构并行BP算法,表 1给出了成像所使用的工作站CPU和GPU的主要参数:两颗Intel Xeon E5620 CPU,工作主频2.66 GHz, 4核8线程,两颗可同时运行16个线程;GPU型号为Nvidia Tesla K20c, 2496个CUDA核心,双精度峰值计算能力1.17 Tflops。在算法的实际运行中,包含一个调度线程,一个GPU控制线程,剩余的闲置线程作为CPU计算线程参与成像计算,由于CPU的计算速度慢于GPU,为了平衡CPU和GPU的计算负载,尽量避免GPU任务完成后等待CPU的情况出现,我们按每次10:1的比例将像素分配给GPU和CPU,这是在CPU和GPU多次计算任务中得出的比较合适的分配比例。
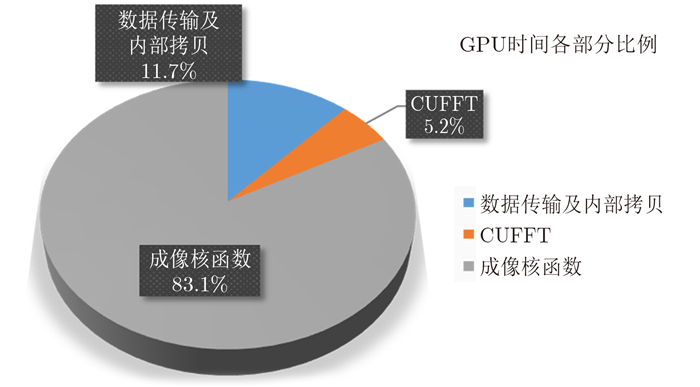
在算法的具体实现中,我们选取的回波尺寸为方位向24000个点,距离向25550个点,该数据为双精度复数据,需要存储空间9.14 GB,而且数据在GPU中需要使用CUFFT进行16倍的升采样,这样一来数据量达到了146 GB,远超出了Tesla K20c的5 GB显存空间,因此,回波数据只能分批多次进入GPU,数据的传输一定程度上造成了GPU计算效率的下降。另一方面,对于距离向25550个点且需要升采样16倍的回波来说,显存中同时最多能够存储800条左右的回波,除去成像点需要占用的空间则会更少一些。在GPU内部存储的使用上,CUFFT之后将升采样数据绑定到纹理内存,这样在取值插值过程中,就可以使用GPU自带的纹理拾取函数,提高插值效率。在线程网格分配上,由于调度线程已经将2维成像平面中的像素进行了1维线性化处理,因此降低了线程网格分配难度,只需要将足够多的像素线性地分配到线程网格上,使得GPU尽可能地满载运行即可。图 8给出了GPU各部分时间所占用的比例,综合来看,GPU的计算瓶颈在于其显存容量有限,无法容纳高分辨率下升采样的回波数据。目前Nvidia已经推出了具有更大显存的专业计算卡,相信今后会有很大改观。
|
图 8 GPU时间各部分所占比例 Fig.8 GPU time propotions of each part |
对于CPU计算部分,内存容量达到192 GB,相对于GPU来说宽松很多,在仅使用CPU的情况下,可以实现全部核心满载运行,当CPU和GPU进行联合异构计算时,GPU需要占用一个控制线程,此时CPU无法满载运行,但仍然可以达到95%左右。
我们对成像速度进行了统计对比,选取的成像平面的点数分别为128×128, 256×256, 512×512, 1024×1024,成像所用的时间、加速比以及满载情况如表 3所示,单独使用GPU的成像速度约为单独使用CPU的9.07倍,而CPU和GPU同时使用的成像速度约为单独使用CPU的9.90倍,可见,CPU已经参与到了成像计算当中,发挥了闲置核心的计算能力。在本实验中CPU发挥的作用较小,这是因为工作站采用的GPU是Nvidia专业计算卡,CPU和该卡的计算能力相差较为悬殊(可以参考表 1),当使用一些普通消费级的GPU,比如Nvidia Geforce系列,CPU的计算能力就会占据更大的比重了。
| 表 3 不同尺寸SAR图像在不同平台下的成像时间 Tab.3 The imaging time of different size on different platforms |
本文对方位向宽测绘带滑动聚束模式的成像方法进行了讨论,由于在高分辨率宽测绘带情况下存在调频率时变、距离徙动较大、距离向和方位向耦合强烈的问题,导致频域算法难以实现良好聚焦。而BP成像算法作为时域算法可以很好地避免以上3个问题,因此在场景中心及边缘区域均可以实现良好聚焦,实验结果也对此进行了验证。然而,BP算法的算法复杂度为O(N3),再加上滑动聚束模式分辨率高,合成孔径长度长,数据量大,对计算能力提出了巨大挑战。为此,本文提出了一种基于CPU/GPU异构平台的并行BP算法,这种算法相比于只运行在CPU或GPU上的算法来说,充分利用了计算资源,提高了成像效率,另一方面,调度线程的存在使得成像更加灵活,既可以让CPU和GPU同时工作,也可以单独只使用CPU或GPU,另外调度线程的设计也充分考虑了当前GPU显存较为有限的现状,合理分配计算任务,提高了程序的实用性。
| [1] |
邓云凯, 赵凤军, 王宇. 星载SAR技术的发展趋势及应用浅析[J].
雷达学报, 2012, 1(1): 1-10. Deng Yun-kai, Zhao Feng-jun and Wang Yu. Brief analysis on the development and application of spaceborne SAR[J]. Journal of Radars, 2012, 1(1): 1-10. (  0) 0)
|
| [2] |
Werninghaus R. TerraSAR-X mission[C]. SAR Image Analysis, Modeling, and Techniques Ⅵ, Barcelona, Spain, 2003:9-16.
http://spie.org/Publications/Proceedings/Paper/10.1117/12.511500?origin_id=x4325&start_volume_number=05200 ( 0) 0)
|
| [3] |
Mittermayer J, Lord R, and Borner E. Sliding spotlight SAR processing for TerraSAR-X using a new formulation of the extended chirp scaling algorithm[C]. 2003 IEEE International Geoscience and Remote Sensing Symposium, 2003, 3:1462-1464.
http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1294144 ( 0) 0)
|
| [4] |
Lanari R, Tesauro M, Sansosti E, et al.. Spotlight SAR data focusing based on a two-step processing approach[J].
IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(9): 1993-2004. DOI:10.1109/36.951090 ( 0) 0)
|
| [5] |
Xu Wei, Huang Ping-ping and Deng Yun-kai. TOPSAR data focusing based on azimuth scaling preprocessing[J].
Advances in Space Research, 2011, 48(2): 270-277. DOI:10.1016/j.asr.2011.03.024 ( 0) 0)
|
| [6] |
Desai M D and Jenkins W K. Convolution backprojection image reconstruction for spotlight mode synthetic aperture radar[J].
IEEE Transactions on Image Processing, 1992, 1(4): 505-517. DOI:10.1109/83.199920 ( 0) 0)
|
| [7] |
Ozdemir C. Inverse Synthetic Aperture Radar Imaging with MATLAB Algorithms[M]. John Wiley & Sons, 2012.
( 0) 0)
|
| [8] |
Owens J D, Houston M, Luebke D, et al.. GPU computing[J].
Proceedings of the IEEE, 2008, 96(5): 879-899. DOI:10.1109/JPROC.2008.917757 ( 0) 0)
|
| [9] |
Krakiwsky S E, Turner L E, and Okoniewski M M. Acceleration of Finite-Difference Time-Domain (FDTD) using Graphics Processor Units (GPU)[C]. 2004 IEEE MTT-S International Microwave Symposium Digest, 2004, 2:1033-1036.
http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1339160 ( 0) 0)
|
| [10] |
Cireşan D, Meier U, Masci J, et al.. Multi-column deep neural network for traffic sign classification[J].
Neural Networks, 2012, 32: 333-338. DOI:10.1016/j.neunet.2012.02.023 ( 0) 0)
|
| [11] |
Fasih A and Hartley T. GPU-accelerated synthetic aperture radar backprojection in CUDA[C]. 2010 IEEE Radar Conference, Washington, DC, 2010:1408-1413.
http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5494395 ( 0) 0)
|
| [12] |
Capozzoli A, Curcio C and Liseno A. Fast GPU-based interpolation for SAR backprojection[J].
Progress In Electromagnetics Research, 2013, 133: 259-283. DOI:10.2528/PIER12071909 ( 0) 0)
|
| [13] |
丁金闪, OtmarL, HolgerN, 等. 异构平台双基SAR成像的RD算法[J].
电子学报, 2009, 37(6): 1170-1173. Ding Jin-shan, Otmar L, Holger N, et al.. Focusing bistatic SAR data from herterogeneous platforms using the range Doppler algorithm[J]. Acta Electronica Sinica, 2009, 37(6): 1170-1173. (  0) 0)
|
| [14] |
Song Ming-cong, Liu Ya-bo, Zhao Feng-jun, et al..Processing of SAR data based on the heterogeneous architecture of GPU and CPU[C]. 2013 IET International Radar Conference, Xi'an, China, 2013:1-5.
http://ieeexplore.ieee.org/document/6624464/ ( 0) 0)
|
| [15] |
Mittermayer J, Wollstadt S, Prats-Iraola P, et al.. The TerraSAR-X staring spotlight mode concept[J].
IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3695-3706. DOI:10.1109/TGRS.2013.2274821 ( 0) 0)
|
| [16] |
Cumming I G and Wong F H. Digital Processing of Synthetic Aperture Radar Data:Algorithms and Implementation[M]. Artech House, 2005.
( 0) 0)
|
| [17] |
Gorham L R A and Moore L J. SAR image formation toolbox for MATLAB[C]. Algorithms for Synthetic Aperture Radar Imagery XVⅡ, Orlando, USA, 2010:769906.
http://spie.org/Publications/Proceedings/Paper/10.1117/12.855375 ( 0) 0)
|
| [18] |
Nickolls J and Dally W J. The GPU computing era[J].
IEEE Micro, 2010, 30(2): 56-69. DOI:10.1109/MM.2010.41 ( 0) 0)
|
| [19] |
Kirk D. NVIDIA CUDA software and GPU parallel computing architecture[C]. Proceedings of the 6th International Symposium on Memory Management, New York, USA, 2007, 7:103-104.
http://dl.acm.org/citation.cfm?id=1296909 ( 0) 0)
|




