1 引言

正交频分复用^[1](Orthogonal Frequency-Division Multiplexing,OFDM)技术首先成熟应用于通信领域，Jankiraman等人^{[2, 3]}于1998年将OFDM技术引入到雷达系统中，他们设计了名叫“PANDORA”的雷达，采用了OFDM-LFM信号体制。近几年来，OFDM新体制雷达引起了包括美、德等多国在内的世界范围内研究者的兴趣，在国际期刊和会议上涌现出不少高水平的相关论文，从不同角度和背景研究了相关的技术和理论，推动着OFDM雷达向前发展。

OFDM雷达同时发射多个相互正交的子载频来获得大的时宽带宽积，具有距离高分辨能力和多普勒分辨能力。与传统的雷达相比，OFDM雷达具有波形设计灵活、易于数字化、强抗干扰能力和环境适应能力等优点^[4–6]。但它在应用上还存在一些技术难点，例如发射波形的包络峰均比(Peak to Mean Envelope Power Ratio,PMEPR)较高^[7–10]、多普勒频偏导致的邻道干扰^{[11, 12]}等。

相位编码^{[13, 14]}是OFDM雷达研究最为广泛的一种信号形式，因为它具有低截获、设计灵活等特点，并且为降低PMEPR提供了较好的条件。然而相位编码OFDM也有其自身的问题，其中最主要的是如何设计具有良好性质的编码。现有已知的具有良好自相关性质的编码数目有限，例如理想的巴克码、Huffman码等自相关旁瓣较低，但是其长度受限且序列固定，容易被截获，安全性较差；互补编码集^[13]自相关和互相关性能都很好，但其数量有限，寻码过程复杂。因此，设计出一种PMEPR满足发射需求、编码数目和长度灵活多样、自相关性质优良、生成方案简单的信号就成为制约相位编码OFDM雷达走向实际应用的瓶颈问题之一。通过定义以PMEPR和模糊函数性能为指标的优化函数，并通过优化算法求解编码集，Sebt等人^[15]，Alimosaymer等人^[16]，Guo等人^[17]提出了相应的相位编码OFDM信号优化算法。

本文针对相位编码OFDM雷达的上述问题，提出了一种基于Bernoulli混沌的相位编码OFDM信号设计方法，综合考虑编码数目和长度灵活度、PMEPR、自相关性质等因素，形成一套简单易行的编码生成方案，得到的编码方式灵活，长度任意且具有初值敏感性，具有很好的低截获和抗干扰性能，并且PMEPR小于2，自相关性质优良。目前，已有较多文献研究将混沌理论应用到单载频相位编码信号中^[18]，但确切研究混沌应用于相位编码OFDM雷达的文献较少，中国科学院的丁凯^[19]在博士论文中研究了混沌码OFDM-SAR系统，在OFDM-SAR系统成像、抗干扰性能等方面开展了工作，西北工业大学的Huang等人^[20]提出了一种混沌相位编码多载频步进频脉冲串信号，并研究了这种信号的特性。但在混沌相位编码波形设计、编码生成方案等关键问题上未开展深入研究。

本文首先简单介绍了相位编码OFDM雷达信号及其特点，然后提出基于Bernoulli混沌的四相编码OFDM雷达信号生成方案，重点分析了信号的各种特性，最后对这种新的信号体制的应用前景进行了展望。

2 相位编码OFDM雷达信号及其特点

OFDM雷达实质上是一种采用了多载频发射信号体制的雷达，它同时发射多个相互正交的子载频，每个子载频上可采用各种调制方式获得大的时宽带宽积。

设雷达发射信号为：

$ s\left( t \right) = \exp \left( {{\rm{j}}2\pi {f_0}t} \right)\sum\limits_{m = 0}^{M - 1} {u\left( {t - m{T_{\rm{r}}}} \right)} $

(1)

其中，f₀为发射中心载频，M是脉冲个数，T_r是脉冲重复周期，u(t)为OFDM多载频信号的复包络：

$ u\left( t \right) = \sum\limits_{n = 0}^{N - 1} {{w_n}{\rm{rect}}\left[{\frac{{t - {T_{\rm{p}}}/2}}{{{T_{\rm{p}}}}}} \right]{\rm{exp}}\left( {{\rm{j}}2\pi n\Delta ft} \right)} $

(2)

其中，N是子载频个数，w_n是第n个子载频的频率加权系数，rect(·)为单位矩形窗函数，T_p是脉冲宽度，Δf是相邻子载频之间的频率间隔，满足OFDM条件：

$ \Delta f = 1/{T_{\rm{p}}} $

(3)

此处，第n个子载频与第m个子载频之间正交是指：

$ \frac{1}{{{T_{\rm{p}}}}}\int_0^{{T_{\rm{p}}}} {\rm{exp}}\left( {{\rm{j}}2\pi n\Delta ft} \right){\rm{exp}}\left( { - {\rm{j}}2\pi m\Delta ft} \right) = \left\{ {\begin{array}{*{20}{c}} {1,}&{m = n}\\ {0,}&{m \ne n} \end{array}} \right. $

(4)

若T_r=T_p，则OFDM雷达为连续波体制。

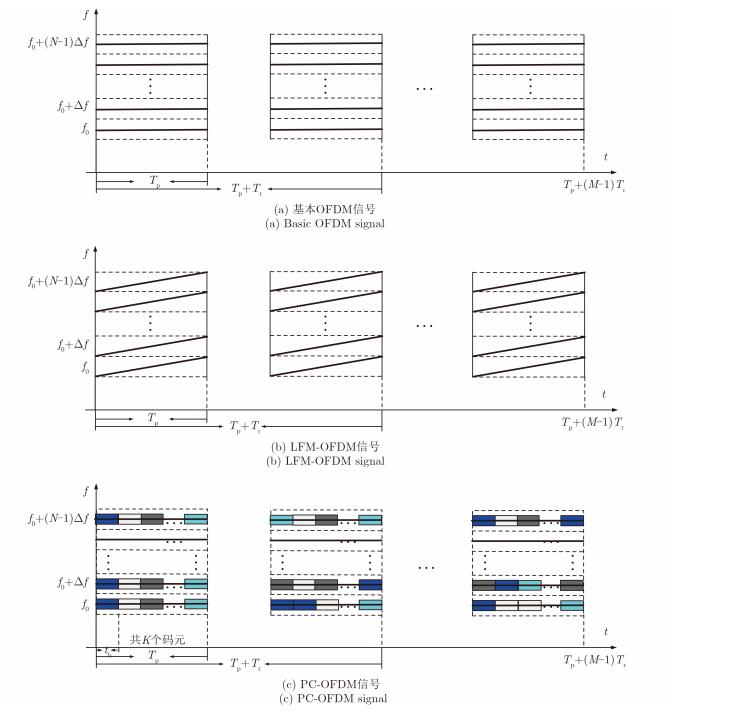
OFDM雷达的子载频上可以进行任何形式的调制，最常见的有线性调频调制(Linear Frequency Modulation,LFM)和相位编码(Phase Coded,PC)调制，分别称为LFM-OFDM和PC-OFDM，其与基本OFDM信号的区别如图 1所示。图 1(a)是基本的OFDM信号，每个子载频是单载频，子载频之间的频率间隔为Δf；图 1(b)是LFM-OFDM信号，每个子载频采用线性调频，带宽均为Δf；图 1(c)是PC-OFDM信号，每个子载频上采用相位编码调制，且子载频频率间隔Δf和码元宽度t_b满足Δf= 1/t_b。这种PC-OFDM信号脉内、脉间子载频上编码可以相同也可以不同，设计非常灵活，而且还具备一些独特优点，如抗干扰能力强、易于数字化、通信雷达一体化等，因此这种信号是OFDM雷达研究的热点。

PC-OFDM雷达信号的复包络可表示为^[7]：

$ \begin{array}{l} u\left( t \right) = \sum\limits_{p = 0}^{P - 1} {\sum\limits_{n = 0}^{N - 1} {\sum\limits_{k = 0}^{K - 1} {{w_{n,m}}{\rm{exp}}\left( {{\rm{j}}{a_{n,k,m}}} \right)} } } \\ \;\;\;\;\;\; \cdot {\rm{exp}}({\rm{j}}2\pi n\Delta f(t - p{T_{\rm{r}}}))\\ \;\;\;\;\;\; \cdot {\rm{rect}}\left( {\frac{{t - \left( {k - 1} \right){t_{\rm{b}}}}}{{{t_{\rm{b}}}}} - \frac{1}{2}} \right) \end{array} $

(5)

其中，P为发射脉冲数，N为子载频数，K为编码长度，w_n,m为第m个脉冲内第n个子载频的加权系数，包括幅度及初相加权，a_n,k,m为第m个脉冲内第n个子载频的第k个相位编码。t_b为码元宽度，Δf= 1/t_b为子载频间隔，则脉冲宽度T_p=Kt_b，而带宽B=NΔf=N/t_b，因此PC-OFDM信号的时间-带宽积表示为BT=KN，为基本OFDM信号时间-带宽积K倍，且与传统的线性调频信号(Linear Frequency Modulation,LFM)信号时间-带宽积受限于调频率不同，PC-OFDM信号时间-带宽积可以通过改变子载频数N和编码长度K灵活设计。

PC-OFDM雷达信号在各类OFDM雷达信号中具有独特的优势：首先，它继承了相位编码信号的低截获的特点，信号被侦收复制的概率小，安全性能高；其次，它的设计最灵活，由于编码种类繁多、长度各异，因此其各种参数设计自由度大；再次，PC-OFDM信号体制支持通信功能的开发，有利于实现雷达、通信一体化。

PC-OFDM雷达信号也存在一些不足：首先是发射波形的包络峰均比(Peak-to-Mean Envelope Power Ratio,PMEPR)问题，由于A/D采样、放大器等硬件有一定的动态范围，限制了发射信号的PMEPR不能过高，文献[13]表明采用合适的相位编码可以使OFDM雷达发射波形的PMEPR降低到实用要求的2以内，因此如何找到满足条件的相位编码方式就成为一个必须面对的问题；其次现有已知的具有良好自相关性质的编码数目有限，无法满足OFDM雷达实际应用时对编码数目和长度的要求，因此如何设计编码数目和长度灵活多样、具有良好自相关性质的编码是另外一个重要的问题；另外，PC-OFDM雷达信号的处理比较复杂，需要针对不同应用寻求不同的处理方法。

3 基于Bernoulli混沌的四相编码OFDM雷达信号

混沌是指可通过确定性系统产生的，貌似随机的不规则运动^[21]。时域混沌信号为对初始值敏感的非周期随机信号，变换到频域为类噪声的宽带连续功率谱，具有很好的信号隐身和保密性能。相比于传统的伪随机信号，混沌信号具有数量众多、可选择性强、长度不受限、且不存在周期性的优点；相比于随机噪声信号，混沌信号可控、易于产生、存储和恢复。因此，选择混沌序列作为相位编码的基础，可以保证编码信号的随机性、安全性，而且编码数据和长度要求可以满足。

用混沌相位编码调制OFDM信号，在多载频技术的基础上结合了相位编码技术，它的编码类型和长度将更加灵活，除了宽带所带来的高的距离分辨能力，还具有较低的自相关函数旁瓣，高的频谱利用率，图钉型模糊函数。根据混沌信号的初值敏感性可生成大量的随机噪声信号，同时又可根据其初始条件和映射规则确定再生同样的随机噪声信号。因此在对雷达回波信号进行压缩处理时，可根据混沌初始条件重生混沌相位编码OFDM信号，可省去体积庞大、电路复杂的延时线部件。由于混沌相位编码OFDM信号的每一个发射脉冲信号都根据不同的初始条件和映射规则产生混沌序列，所以不同脉冲信号具有正交性，因此，将该信号用于成像雷达，可获得低的截获概率，同时在抗干扰、抗衰落、抑制多径与杂波干扰等方面有优越的性能。

对于闭区间J=^{[0, 1]}$ \subset $R，当连续映射$f:J \to J$满足^[22]：

(1) f 周期点周期无上界，

(2) 存在不可数集$S \! \subset \! J$,S不含周期点，对$ \forall p,q \in S,p \ne q $ ，使得

$ \begin{array}{*{20}{l}} {\mathop {\lim }\limits_{n \to \infty } \sup \left| {{f^n}\left( p \right) - {f^n}\left( q \right)} \right| > 0,}\\ {\mathop {\lim }\limits_{n \to \infty } \inf \left| {{f^n}\left( p \right) - {f^n}\left( q \right)} \right| = 0} \end{array} $

(6)

(3) 对任意$p \in S$以及任意周期点$q \in J$，有

$\mathop {\lim }\limits_{n \to \infty } \sup \left| {{f^n}\left( p \right) - {f^n}\left( q \right)} \right| > 0$

(7)

这意味着，存在一个不可数集合，此集合中只含有混沌轨道，任意两个轨道之间既不趋近也不趋远，且任意轨道不趋于周期轨道。这样的不可数区间称为混沌吸引域。混沌一般分为两种：一是连续混沌，通过微分或积分获得；一是离散混沌，通过差分迭代获得。考虑到混沌产生、处理的简便，以及混沌相位编码的性质，本文选取Bernoulli混沌作为产生相位编码的基础，它是离散混沌序列的一种，可由下式产生：

$ \begin{array}{l} {x_{k + 1}} = \left\{ {\begin{array}{*{20}{c}} {b{x_k} + a,\;{x_k} < 0}\\ {b{x_k} - a,\;{x_k} \ge 0} \end{array}} \right.,\;{x_k} \in [- 0.5,0.5),\\ \;\;\;\;\;\;\;\;\;\;a = 0.5,\;b = 2 - \varepsilon \end{array} $

(8)

其中，x_k为过程变量，a,b为混沌映射参数，ε为一接近于0的极小正值，混沌吸引域为[–0.5,0.5)。b值越接近2，混沌序列值在混沌吸引域[–0.5,0.5)的遍历性越好。

通过设置x₀和a,b后，式(8)可以产生Bernoulli混沌序列。然后对Bernoulli混沌序列进行量化编码，得到四相编码序列，量化规则为：

$ {a_k} = 2\pi \cdot {\rm{ceil}}\left( {{N_{\rm{p}}}{x_k} + 0.5} \right)/{N_{\rm{p}}} $

(9)

其中，x_k为截取的Bernoulli混沌序列，N_p为相位编码数，这里取N_p=4。实际上按照本文的设计方法，N_p取不同值可以获得二相及多相相位编码。由于相位编码数N_p越大，信号安全性越好，自相关旁瓣越低，但信号的复杂度越大，综合考虑安全性能和实现复杂度，优选四相编码，即N_p=4；然后，用得到的一个四相编码序列对第m个OFDM雷达脉冲信号各子载频进行相位调制，若每个子载频上编码都相同，则a_n,k,m=a_k，如图 1(c)中第1个脉冲所示；若每个子载频上编码不同，则重复生成四相编码序列的过程N次，得到a_n,k，并令a_n,k,m=a_n,k，如图 1(c)中第2个脉冲所示。考虑到实现简单，并且后续需要进行初相加权以控制PMEPR，本文只研究每个子载频上用的混沌相位编码序列相同，即a_n,k,m=a_k。最后对每个子载频进行初相加权等手段控制PMEPR，即可获得混沌相位编码OFDM雷达信号。具体步骤如下图 2所示。

步骤1 设定混沌初值x₀以及混沌映射参数b，根据1维离散Bernoulli迭代映射方程式(8)产生混沌序列x₀,x₁,···,x_K–1,···，可取x₀$ \in $[–0.5,0.5),a=0.5,1.5 < b < 2，这里b的取值应接近2，但不能等于2，最好取1.9 < b < 2，这样混沌的遍历性较好；

步骤2 剔除前C个序列点，C的取值范围是C ≥ 1，取K个Bernoulli混沌序列点{$\mathop x\nolimits_k^\prime $|k=1,2,···,K; $\mathop x\nolimits_k^\prime $=x_k+C}进行量化编码，量化规则如式(9)，这里剔掉前C个序列点是为了使选取的混沌序列性质更好，为了获得随机性更好的混沌序列，还可以采用其它选取方式，如采用固定采样率抽取等，不会影响选取序列的性质；

步骤3 对N个子载频进行w_n加权。令w_n= $\left| {{w_n}} \right|{{\rm{e}}^{{\rm{j}}{\theta _n}}}$，其中$\left| {{w_n}} \right|$为幅度加权，θ_n为初相加权，若取$\left| {{w_n}} \right| = 1$，则表示只进行初相加权，若取q_n=0，则表示只进行幅度加权；令a_n,k,m=a_k，得到各行均相等的相位编码矩阵{a_n,k,m|a_n,k,m=a_k}_N×K；用该矩阵对加权后的各子载频进行相位编码调制，得到PC-OFDM信号第m个脉冲上的复包络u(t)。对于脉冲串，可重复上述操作获得每个脉冲互不相同的脉冲串，也可以重复发射这一个脉冲，获得相同脉冲的脉冲串。最终得到的混沌四相编码OFDM雷达脉冲的包络可表示为：

$ \begin{array}{l} u\left( t \right) = \sum\limits_{n = 0}^{N - 1} {\sum\limits_{k = 0}^{K - 1} {{w_n}{\rm{exp}}\left( {{\rm{j}}{a_k}} \right)} } \\ \;\;\;\;\;\;\;\;\; \cdot {\rm{exp}}\left( {{\rm{j}}2\pi n\Delta ft} \right){\rm{rect}}\left[{\frac{{t - {t_{\rm{b}}}/2 - \left( {k - 1} \right){t_{\rm{b}}}}}{{{t_{\rm{b}}}}}} \right] \end{array} $

(10)

其中，w_n=$\left| {{w_n}} \right|{{\rm{e}}^{{\rm{j}}{\theta _n}}}$,a_k表示四相位编码序列，对混沌序列按式(9)进行量化编码得到。

上述过程中，产生基于Bernoulli混沌的多相编码序列并用于PC-OFDM雷达信号的调制是本文方法的关键，相对于常用的编码序列和随机编码序列，这种方法下产生的编码序列有以下主要优势，第一，基于Bernoulli混沌的四相编码序列长度任意，例如，相关性能良好的二相Barker码，比K=13长的二相Barker码全部未知，而多相Barker码序列长度可以更长，但寻码过程复杂，而基于Bernoulli混沌的四相编码序列长度基本不受限制，一般而言，随着编码序列长度增加，混沌特性更加明显，相关性能更好；第二，基于Bernoulli混沌的四相编码序列值更加灵活且易于保存、复现，与Barker码、Frank码、P3、P4码序列值相对固定不同，由于Bernoulli混沌所具有的类随机性，其序列值灵活多变近似于随机编码，但是与随机编码存储较难、基本无法复现的缺点相比，基于Bernoulli混沌的四相编码序列，仅混沌初值是随机选取的，因此只须保存混沌初值，经过相同的混沌映射及量化编码就可以复现性质良好的编码序列。当然，必须看到基于Bernoulli混沌的四相编码序列的相关性能很大程度上受到混沌初值选择的影响，不同混沌初值所产生的混沌序列量化编码序列在相关性能上的差异是很大的，因此需要进一步研究混沌初值选择算法，来获得满足应用需要的编码序列，一种可行的思路是预先设置编码序列峰值旁瓣比(Peak-to-Side-Lobe Ratio,PSLR)的阈值，再在混沌吸引域中随机产生混度初值，并按式(8)、式(9)得到编码序列，计算PSLR，若满足预先设置的阈值条件，则输出序列和对应的混沌初值，否则重复上述步骤。这样的方法保证了编码序列的随机性，但是同时增加了寻码时间，尽管产生一个混沌编码序列的过程算法复杂度很低，但是当阈值条件设置较高时，迭代过程平均耗时势必增加。因此，需要根据实际需要，权衡寻码时间和编码序列PSLR，进行设置。其他混沌初值选择算法是进一步优化该种编码序列的方向之一。

另外，对于PC-OFDM雷达信号而言，子载频数N和编码长度K是其较为重要的两个参数。在码元宽度t_b保持不变(相应地，子载频间隔Δf也保持不变)的情况下，子载频数N越大，信号带宽越大，距离分辨率越高，且包络的起伏越小；编码长度K与信号的PMEPR无关，但编码长度越长，信号脉宽越长，速度分辨率越高，且信号的自相关函数旁瓣相对越低。基于Bernoulli混沌的四相编码，由于其编码长度K没有限制，可以自由选择，因此用于PC-OFDM雷达信号的调制可以增加信号设计的灵活性，优化其时间-带宽积，使得信号同时具备高的测距、测速精度，降低脉冲压缩旁瓣，且信号抗干扰、抗截获性能有所提高。

4 信号特性分析

下面从信号PMEPR、模糊函数两方面对基于Bernoulli混沌的四相编码OFDM雷达信号特性进行分析，得出信号综合优化方案。

4.1 发射信号PMEPR

信号u(t)的PMEPR可定义为^[7]：

$ {\rm{PMEPR}} = \frac{{{P_{{\rm{peak}}}}}}{{{P_{{\rm{mean}}}}}} = \frac{{{{\left[{\mathop {\max }\limits_{t \in \left[{0,T{\kern 1pt} } \right]} \left\{ {\left| {u\left( t \right)} \right|} \right\}} \right]}^2}}}{{\left( {1/T{\mkern 1mu} } \right)\int_0^T {{{\left| {u\left( t \right)} \right|}^2}} {\rm{d}}t}} $

(11)

其中，T为一个信号周期。

对于式(10)定义的混沌四相编码OFDM雷达脉冲的包络，由|a_k|=1，且采用均一化载频加权系数，即有$\sum\nolimits_{n = 0}^{N - 1} {{{\left| {{w_n}} \right|}^2} = 1} $，包络功率均值为：

$ \begin{array}{l} {P_{{\rm{mean}}}} = \frac{1}{{{T_{\rm{p}}}}}\int_0^{{T_{\rm{p}}}} {\left| {u\left( t \right)} \right|^2}{\rm{d}}t = \frac{1}{{T{\mkern 1mu} }}\sum\limits_{k = 0}^{K - 1} {\int_{k{t_{\rm{b}}}}^{\left( {k + 1} \right){t_{\rm{b}}}} {{\left| {{u_k}\left( t \right)} \right|}^2}{\rm{d}}t} \\ = \frac{1}{{{T_{\rm{p}}}}}\sum\limits_{k = 0}^{K - 1} {\int_{k{t_{\rm{b}}}}^{\left( {k + 1} \right){t_{\rm{b}}}} {{{\left| {{a_k}} \right|}^2}\sum\limits_{N = 0}^{N - 1} {{{\left| {{w_n}} \right|}^2}} {\rm{d}}t} } = \frac{{K{t_{\rm{b}}}}}{{{T_{\rm{p}}}}} = 1 \end{array} $

(12)

因此，降低信号峰值旁瓣比的问题变为降低信号峰值功率，且信号各码元包络是相同的，因此降低整个混沌四相编码OFDM信号峰值的问题可以简化为降低一个码元内信号包络的峰值，且仅与子载频数N与子载频加权系数的选择有关。对于相位编码OFDM信号，常用的降低PMEPR的载频加权方式有3种：一种是幅度加权，采用各种窗函数调制各子载频幅度，即频域加窗处理；二是相位加权，即各子载频加上不同的初相；三是幅度加权和相位加权同时使用。针对混沌四相编码OFDM雷达信号，我们研究了不同途径的效果。

(1) |w_n|幅度加权

只对各子载频幅度进行加权，首先令θ_n=0，所用窗函数如表 1所示，并对表 1中的窗函数进行归一化处理，使得$\sum\nolimits_{n = 0}^{N - 1} {{{\left| {{w_n}} \right|}^2} = 1} $。

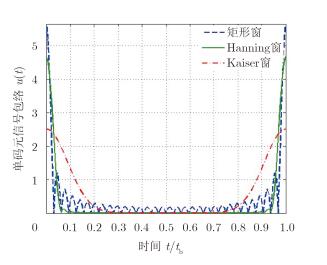
只考虑单码元信号包络，图 3所示为不同窗函数幅度加权条件下，32个子载频合成OFDM单码元信号包络，过采样率为2,Kaiser窗形状参数β=75。由图可得，当各子载频采用矩形窗函数加权时，包络峰值达到$\sqrt N $，此时PMEPR为最大值N；对于广义余弦窗Hanning窗而言，包络主瓣峰值及旁瓣略有降低，主瓣展宽并不明显，包络形状没有明显改变，PMEPR降低不明显；对于Kaiser窗而言，由于选取了较大的形状参数值β，主瓣明显展宽，峰值降低明显，能量分布更加均匀。

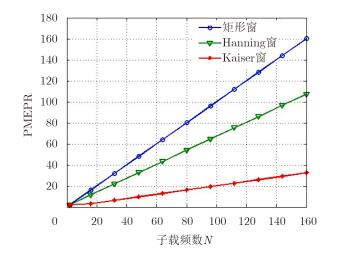
进一步地，设置子载频数N为不同数值，分别计算信号PMEPR，可以得到不同窗函数的PMEPR随N变化的曲线如图 4所示。从图中看出，PMEPR随子载频个数N的增大近乎直线增加，尽管经过Kaiser窗加权，PMEPR大大降低，但仍未达到技术指标要求，说明单一采用幅度加权不能控制信号的PMEPR。

(2) 初相加权

首先设置|w_n|=1/$\sqrt N $,θ_n采用不同的初相(如表 2所示)。

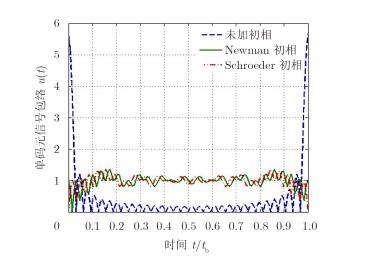
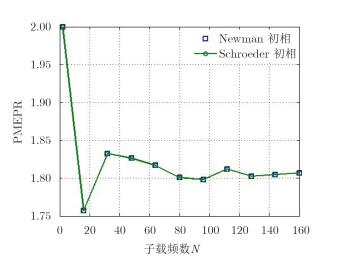
32个子载频合成单码元OFDM信号包络见图 5。由图可得，初相加权完全改变了信号包络形状，且大大降低了包络峰值，且Newman初相加权和Schroeder初相加权信号包络形状完全一样，只是平移了一个采样点。对不同子载频个数OFDM单码元信号包络，分别计算PMEPR，可以得到不同初相加权信号PMEPR随N变化的曲线如图 6所示。从图中看出，表 2中的两种初相单独加权是等效的，均可以将PMEPR控制在2左右，并且随着N增大，PMEPR趋于稳定在1.8左右，若要得到更低的PMEPR，则需要将初相加权与幅度加权相结合。

(3) 幅度和初相加权

选取|w_n|为表 1中的不同窗函数，θ_n采用表 2中的不同初相。

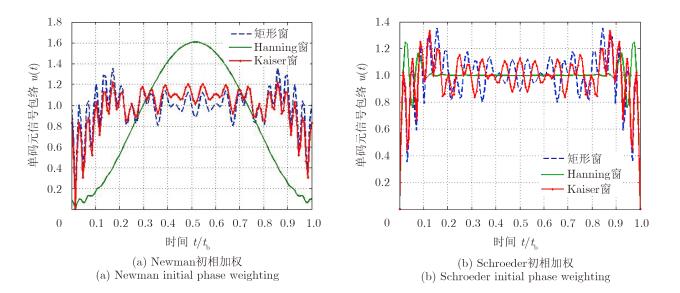
图 7为32个子载频OFDM单码元信号包络。图 7(a)中，对于Newman初相，经过比较，优选Kaiser窗形状参数选为β=1.2，此时Kaiser窗近似于矩形窗，但是旁瓣水平相对于矩形窗较低，组合上Newman初相可进一步降低信号包络峰值水平，能量分布更加平均，而组合Hanning窗，信号包络峰值反而有所升高。对于Schroeder初相，其值与加权幅度之间存在耦合，图 7(b)中仍选择β=75的Kaiser窗，可以看到，相对于矩形窗情况，无论是Hanning窗还是Kaiser窗，其包络形状大致不变，而波形进一步平滑，幅值降低。

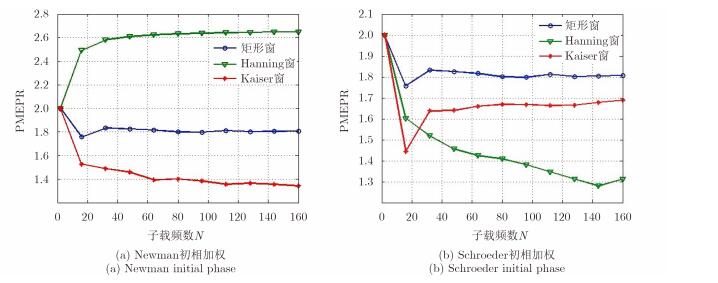
由图 8得到两种具有较好效果的组合加权方式：β=1.2的Kaiser窗组合Newman初相加权，Hanning窗组合Schroeder初相加权。且随着N增加，PMEPR值略有降低，且渐趋于平稳。

信号包络峰均比(PMEPR)仅与子载频个数及加权方式有关。以上3种子载频加权方式中，单独使用幅度加窗，信号包络形状未见明显变化，降低PMEPR的效果有限；单独使用初相加权，可以有效降低信号PMEPR；幅度组合初相加权，当选择合适的窗函数与初相进行加权时，可进一步降低信号PMEPR，其中，两种较为有效的方式为形状参数β=1.2的Kaiser窗函数组合Newman初相加权和Hanning窗组合Schroeder初相加权。这两种加权方式下，随着子载频数的增加，信号PMEPR略有下降，渐趋于平稳，均在1.5以下，达到了雷达发射机的技术指标。

4.2 模糊函数及特性分析

模糊函数是分析、比较雷达信号特性的有力工具，它可以用来衡量波形的分辨力、模糊度、测量精度以及抑制杂波能力。其定义为^[23]：

$ \chi (\tau ,\upsilon ) = \int_{ - \infty }^{ + \infty } {s(t){s^*}(t - \tau )\exp \left( {{\rm{j}}2\pi \upsilon t} \right){\rm{d}}t} $

(13)

PC-OFDM单脉冲信号的模糊函数表达式：

$ \begin{array}{l} \chi (\tau ,\upsilon ) = \int_{ - \infty }^{ + \infty } {u(t){u^*}(t + \tau )\exp \left( {{\rm{j}}2\pi \upsilon t} \right){\rm{d}}t} \\ \;\;\;\;\;\;\;\;\;\;\;\;\; = \sum\limits_{n = 0}^{N - 1} {\sum\limits_{l = 0}^{N - 1} {{w_n}w_l^*\exp \left( { - {\rm{j}}2\pi l\frac{\tau }{{{t_{\rm{b}}}}}} \right)} } {\chi _{n,l}}\left( {\tau ,\upsilon } \right) \end{array} $

(14)

其中，${\chi _{n,l}}\left( {\tau ,\upsilon } \right)$表示n,l两个子载频上相位编码信号的互模糊函数，令τ=it_b+η，其表达式为：

$ \begin{array}{l} {\chi _{n,l}}\left( {\tau ,\upsilon } \right)\\ = \int_{ - \infty }^{ + \infty } {\rm{exp}}\left( {{\rm{j}}2\pi \left( {\upsilon + \;\frac{{n - l}}{{{t_{\rm{b}}}}}} \right)t} \right)\sum\limits_{k = 0}^{K - 1} {a_k}{\rm{rect}}\left( {\frac{{t - k{t_{\rm{b}}}}}{{{t_{\rm{b}}}}}\; - \;\frac{1}{2}} \right)\;\;\\ \cdot \sum\limits_{m = 0}^{K - 1} {a_m^*{\rm{rect}}\left( {\frac{{t - m{t_{\rm{b}}} + i{t_{\rm{b}}} + \eta }}{{{t_{\rm{b}}}}} - \frac{1}{2}} \right){\rm{d}}t} \\ = \sum\limits_{k = 0}^{K - 1} {{a_k}a_{k + i}^*\int_{k{t_{\rm{b}}}}^{\left( {k + 1} \right){t_{\rm{b}}} - \eta } {\rm{exp}}\left( {{\rm{j}}2\pi \left( {\upsilon + \;\frac{{n - l}}{{{t_{\rm{b}}}}}} \right)t} \right){\rm{d}}t} \\ + \sum\limits_{k = 0}^{K - 1} {{a_k}a_{k + i + 1}^*\int_{\left( {k + 1} \right){t_{\rm{b}}} - \eta }^{\left( {k + 1} \right){t_{\rm{b}}}} {\rm{exp}}\left( {{\rm{j}}2\pi \left( {\upsilon + \;\frac{{n - l}}{{{t_{\rm{b}}}}}} \right)t} \right){\rm{d}}t} \end{array} $

(15)

当k < 0或k>K–1时，a_k=0。因此，信号模糊函数性能与子载频加权及编码序列的自相关函数有关。

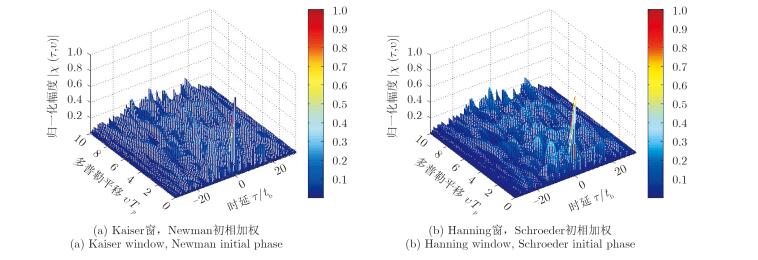
实验采用上一节中讨论的，包络峰均比控制较好的两种加权方式对N=32个子载频进行加权，并用同一个K=32长的Bernoulli混沌量化四相编码序列对信号各载频进行调制，在混沌吸引域[–0.5,0.5)中随机产生Bernoulli混沌初值为0.3147。信号码元宽度t_b=0.2 μs，则脉冲宽度T_p=6.4 μs，带宽B= 160 MHz，发射基带频率f₀=10 GHz。求取两种信号模糊函数如图 9所示。两种加权方式下，信号的模糊函数均呈图钉状，具有单一的峰值，其余能量较为均匀地分布于距离-多普勒平面，较为狭窄的中心峰值意味着该种信号具有距离、多普勒高分辨，因而同时具有高精度测速和宽带成像的潜力。

(1) 距离分辨率

令$\upsilon = 0$，得到模糊函数零多普勒截线，即自相关函数表达式如下：

$ \begin{array}{l} \chi (\tau ,0) = \sum\limits_{n = 0}^{N - 1} {\sum\limits_{l = 0}^{N - 1} {{w_n}w_l^*\exp \left( { - {\rm{j}}2\pi l\frac{\eta }{{{t_{\rm{b}}}}}} \right)} } {\chi _{n,l}}\left( {\tau ,0} \right)\\ \;\;\;\;\;\;\;\;\;\;\; = \sum\limits_{n = 0}^{N - 1} {\sum\limits_{l = 0}^{N - 1} {{w_n}w_l^*\exp \left( { - {\rm{j}}2\pi l\frac{\eta }{{{t_{\rm{b}}}}}} \right)} } \\ \;\;\;\;\;\;\;\;\;\;\;\; \cdot \left( {{t_{\rm{b}}} - \eta } \right){\rm{sinc}}\left( {\frac{{n - l}}{{{t_{\rm{b}}}}}\left( {{t_{\rm{b}}} - \eta } \right)} \right){R_{\rm{a}}}\left( i \right)\\ \;\;\;\;\;\;\;\;\;\;\;\; + \eta {\rm{sinc}}\left( {\frac{{n - l}}{{{t_{\rm{b}}}}}\eta } \right){R_{\rm{a}}}\left( {i + 1} \right) \end{array} $

(16)

其中R_a(i)为相位编码序列非周期自相关函数。特别地，令η=0，整倍码元延迟处，自相关函数表达式进一步写为：

$ \chi (i{t_{\rm{b}}},0) = {t_{\rm{b}}}\sum\limits_{n = 0}^{N - 1} {{{\left| {{w_n}} \right|}^2}{R_{\rm{a}}}\left( i \right)} = {t_{\rm{b}}}{R_{\rm{a}}}\left( i \right) $

(17)

因此，整码元延迟处的旁瓣水平仅由相位编码编码序列的旁瓣水平决定，而子载频加权、子载频数仅影响码元间的旁瓣水平。

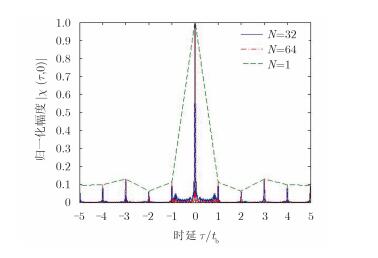
图 10中给出了子载频数分别为N=32,N=64的相位编码OFDM信号与单频相位编码信号归一化自相关函数值对比。由图可见，在码元的整倍延迟处，相位编码OFDM信号自相关函数旁瓣值与所用相位编码序列的自相关函数旁瓣值是一致的，这与式(17)的结论是一致的。雷达信号的距离分辨率与其带宽成反比，而相位编码OFDM雷达信号通过增加子载频数N，可以增大带宽，从而提高距离分辨率，从图中可得，随着子载频数N的增加，主瓣更窄，且整倍码元之间的旁瓣宽度和高度变低。

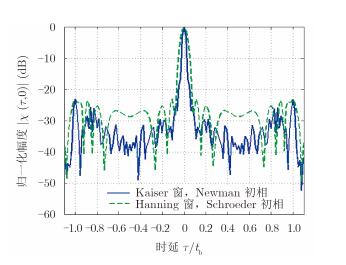
为了进一步分析子载频加权方式的影响，图 11比较了图 9中两种加权信号的自相关函数。为了分析两种加权方式对信号距离分辨的影响，截取延迟为一个码元长度内的曲线，可以明显看出，Kaiser窗组合Newman初相加权，主瓣更窄，码元内部旁瓣更低。综合信号PMEPR、距离分辨考虑，Kaiser窗、Newman初相加权是一种较为理想的子载频加权方式。

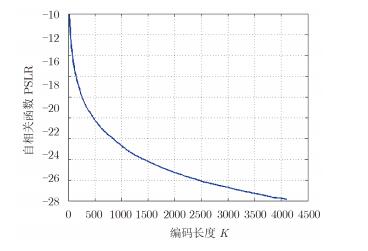
最后，考虑编码序列长度对相位编码序列自相关函数旁瓣水平的影响。以峰值旁瓣比(Peak-to-Side Lobe Ratio,PSLR)作为指标衡量信号的相关函数旁瓣水平，以相同的混沌初值产生不同长度的Bernoulli混沌量化编码，产生不同相位编码数的子载频数N=32的相位编码OFDM信号，并求取自相关函数PSLR值。重复上述步骤并求最终的平均值，以消除混沌初值对结果的影响。由图 12可知，随着编码长度K的增加，信号自相关函数PSLR不断降低，相关性能更加优良。这是由于Bernoulli量化相位编码序列自身的相关性能随着序列长度的增加趋于优良所决定的。然而，相位编码序列长度也不能无限增加，在脉冲宽度的一定的情况下，码元宽度随着序列长度增加而减小，而在现有硬件环境下，相位跳变的速率是有限的，序列长度过长，势必导致误差的产生，且后续处理较为复杂。

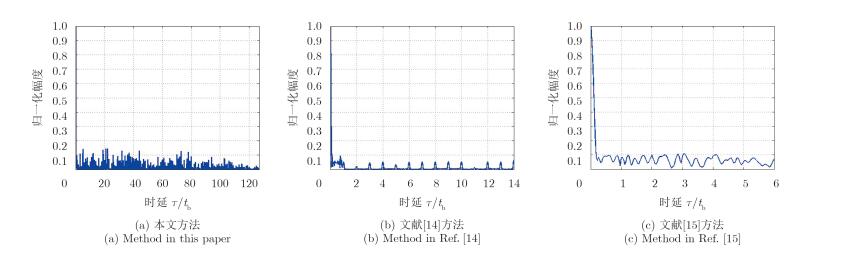
图 13为本文方法与现有的经典算法^{[14, 15]}在距离分辨率上的比较。其中图 13(a)为子载频数N=15，相位编码长度K=128，随机产生混沌初值x₀= –0.332746454505278,β=1.2 Kaiser窗、Newman初相加权四相编码OFDM信号，图 13(b)为采用15位多相Barker码调制，同样为β=1.2 Kaiser窗、Newman初相加权的IS PC-OFDM信号，图 13(c)则为最小二乘准则下同时最优化模糊函数、PMEPR的PC-OFDM信号。其中，图 13(a)，图 13(b)中信号PMEPR均等于1.7107，而图 13(c)中信号PMEPR等于1.8949。经过比较，我们可以看到，本文方法通过增长编码序列的长度使得自相关函数旁瓣水平与其他两种方法相当。信号时间-带宽积更大，但是相应地信号处理复杂度有所提高，且旁瓣水平略高于另两种方法，并依赖于初值选择和编码长度。然而，相对于图 13(b)中采用相对固定的序列进行编码，本文方法抗截获、抗干扰性能更好，且参数设置更为灵活；图 13(c)中的最小二乘准则下的优化算法原则上可以优化设计任意子载频数和编码长度的PC-OFDM信号，而其迭代次数也随着这两个参数的增大而增大，相对而言，本文方法算法复杂度较低，且信号PMEPR控制得也更好。

(2) 多普勒分辨率

令τ=0，得到模糊函数零时延截线，即多普勒模糊函数

$ \begin{array}{l} \chi (0,\upsilon ) = \sum\limits_{n = 0}^{N - 1} {\sum\limits_{l = 0}^{N - 1} {{w_n}w_l^*} } {\chi _{n,l}}\left( {0,\upsilon } \right)\\ \;\;\;\;\;\;\;\;\;\;\; = \sum\limits_{n = 0}^{N - 1} {\sum\limits_{l = 0}^{N - 1} {{w_n}w_l^*} } \int_0^{{T_{\rm{p}}}} \exp \left( {{\rm{j}}2\pi \left( {\upsilon + \frac{{n - l}}{{{t_{\rm{b}}}}}} \right)t} \right){\rm{d}}t\\ \;\;\;\;\;\;\;\;\;\;\; = {T_{\rm{p}}}\sum\limits_{n = 0}^{N - 1} {\sum\limits_{l = 0}^{N - 1} {{w_n}w_l^*} } {\rm{sinc}}\left( {\left( {\upsilon + \frac{{n - l}}{{{t_{\rm{b}}}}}} \right){T_{\rm{p}}}} \right)\\ \;\;\;\;\;\;\;\;\;\;\; \approx {T_{\rm{p}}}{\rm{sinc}}\left( {\upsilon {T_{\rm{p}}}} \right) \end{array} $

(18)

因此，零时延截线主瓣宽度为$\upsilon = 1/{T_{\rm{p}}}$，即脉宽的倒数，而与加权方式、编码序列无关。因此相位编码OFDM信号的多普勒分辨率与脉冲宽度成正比。

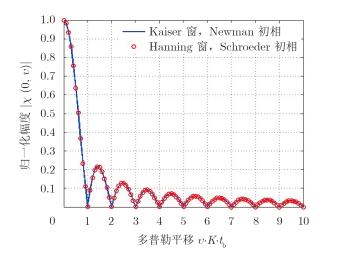
图 14所示为两种加权信号模糊函数零时延截线，与式(18)中的推导一致，加权方式对零时延截线没有影响，主瓣宽度等于1/T_p，且随着多普勒频移$\upsilon $的增大，幅度下降明显。

图 15为$\upsilon {T_{\rm{p}}}$取不同值时，信号的脉冲压缩结果。由图中可得，当$\upsilon {T_{\rm{p}}} = 0.6$时，即目标运动相对径向速度约为1400 m/s时，相对于静止情况下，脉冲压缩结果形状未发生改变，但峰值幅度有所下降，约下降6 dB左右，而当$\upsilon {T_{\rm{p}}} = 1$时，即目标运动相对径向速度约为2340 m/s时，由于对应零时延截线的零点处，脉冲压缩结果形状完全改变，在零时延处没有取得峰值。通过多次试验可以得出结论，相位编码OFDM信号对于多普勒频偏较为敏感，在$\upsilon {T_{\rm{p}}}$较小(目标低速)情况下，多普勒频偏影响不大；在$\upsilon {T_{\rm{p}}}$<0.5(目标中速)情况下，多普勒频偏将会导致脉冲压缩性能变差，峰值下降；在$\upsilon {T_{\rm{p}}}$较大(目标高速)情况下，多普勒频偏将导致脉冲压缩结果恶化，必须通过其它方式，例如多普勒频偏估计和补偿加以改善。

由本节的分析，基于Bernoulli混沌，通过量化编码产生大量序列长度任意、相关性能较为优良、易于存储与复现的相位编码序列，使得雷达波形设计更加灵活，且具有保密性、抗干扰性，优势明显；经过窗函数和初相组合加权，解决了相位编码OFDM信号包络起伏较大的问题，PMEPR降至1.5左右，且进一步地，压缩了信号自相关函数码元内部的旁瓣值。相位编码OFDM雷达信号模糊函数近似图钉型，同时具有距离、多普勒高分辨，应用前景广阔；而另一方面，相位编码OFDM雷达信号对于多普勒频偏较为敏感，需要在后续处理时加以补偿。综合信号PMEPR和模糊函数特性及后续处理算法的复杂度，一般优选N > 32,64≤K≤128,Kaiser窗混合Newman初相加权。

结束语

相位编码OFDM雷达符合雷达多功能、智能化、数字化、网络化的发展潮流，具有广泛的应用前景，值得我们展开深入研究。本文介绍了相位编码OFDM雷达信号及其特点，提出了基于Bernoulli混沌的四相编码OFDM雷达信号生成方案，并分析了信号的各种特性，得出了一些初步的结论。相对于目前常用的相位编码OFDM信号波形优化算法，基于Bernoulli混沌的四相编码OFDM雷达信号波形参数设计更加灵活，包络起伏控制良好，易于产生，存储、保密性、抗干扰性优良，但是相对而言自相关旁瓣水平较高，依赖于混度初始值选取，且编码长度要求较长，仍需进一步研究改进。