低RCS的弱目标检测是当前雷达领域面临的一个技术难题[1]。增加信号相参积累时间能够提高弱目标检测信噪比,但目标运动引起的距离走动会严重影响目标能量的积累和检测。因此,必须减小或消除距离走动对目标能量积累的影响。研究目标包络距离走动问题的雷达信号积累方法有很多[2],其中积分类方法是一个研究热点。积分类方法包括相参Hough变换[3]、相参Radon变换[4, 5]等,文献[6-8]已将这类方法统一为Radon-Fourier变换(RFT),其本质是对目标运动参数决定的直线进行积分的同时增加对目标的多普勒滤波。
然而,现有的相参积累算法多数以单基地雷达目标检测为应用背景,单基地雷达主要接收目标后向散射回波进行相参积累,除时间滤波外很难增加其他空间信息,对弱目标的检测效果和前景有限。双基地雷达能够利用目标侧向或前向散射进行探测[9, 10],有优于单基地雷达的目标信息获取能力。此外,增加接收站组成双基地雷达系统还能够增大探测范围和作用距离,增强系统抗干扰和战场生存能力。
本文提出了双基地雷达RFT弱目标积累检测方法,其中第2节介绍了双基地雷达回波模型,第3节分析了双基地雷达RFT算法的特点,给出了在距离-速度域的具体实现方法,第4节为仿真验证结果。
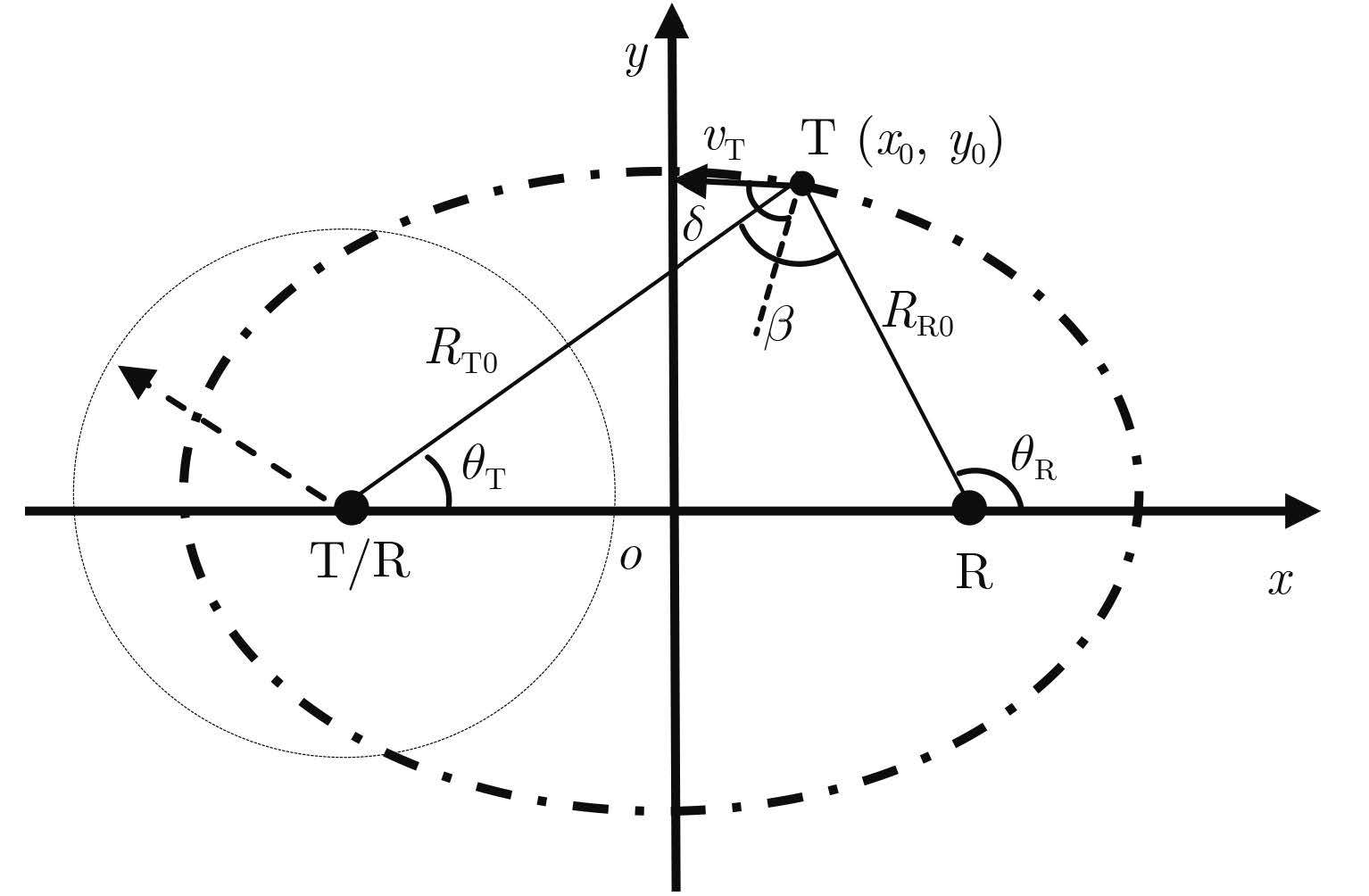
2 双基地雷达信号模型本文主要讨论T/R-R类型的双基地雷达,这种双基地雷达容易在现有雷达基础上,通过增加一个独立接收站构成。其模型如图 1所示,雷达T/R位置(–L,0),独立接收站R位置(L,0),β为双基地角,δ为目标方向角。
|
图 1 T/R-R双基地雷达几何模型 Fig.1 T/R-R bistatic radar geometric model |
设系统工作在侧向区,雷达发射线性调频信号
| $p(\tau ) = {\rm{rect}}\Big(\frac{\tau }{{{T_{\rm{p}}}}}\Big){\rm{exp}}({\rm{j}} \pi \gamma {\tau ^2})$ | (1) |
其中${\rm{rect}}(u) = \left\{ {\matrix{ {1,\;\left| u \right| \le {1 \over 2}} \cr {0,\;{\rm{其他}}} \cr } } \right.$。式(1)中,τ为时间;Tp是脉冲时宽;γ=B/Tp是线性调频率,B为脉冲带宽;脉压比D=TpB。
目标以恒速vT运动,初始时刻与发射站、接收站的斜距分别为RT0,RR0。将接收站接收的直达波作为参考信号[11],那么瞬时双基地距离和可定义为:
| $\begin{align} & {{R}_{\text{s}}}(t)=\sqrt{R_{\text{T}0}^{2}+v_{\text{T}}^{2}{{t}^{2}}-2{{R}_{\text{T}0}}{{v}_{\text{T}}}t\cos (-\frac{\beta }{2})}+ \\ & \sqrt{R_{\text{R}0}^{2}+v_{\text{T}}^{2}{{t}^{2}}-2{{R}_{\text{R}0}}{{v}_{\text{T}}}t\cos (\delta +\frac{\beta }{2})}-2L \\ \end{align}$ | (2) |
为便于分析,忽略目标起伏特性影响,接收站接收到的目标基带回波信号可表示为
| $\begin{align} & {{s}_{\text{r}}}(\tau ,t)={{\sigma }_{0}}p(\tau -{{R}_{\text{s}}}(t)/\text{c}) \\ & \cdot \text{exp}(-\text{j}2\pi {{f}_{0}}{{R}_{\text{s}}}(t)/\text{c})+w(t) \\ \end{align}$ | (3) |
其中,τ=nTs为快时间,Ts是快时间采样周期,n=0,1,···,Nr–1,Nr为距离窗采样数。t=mTr为慢时间,Tr为脉冲重复周期,m=0,1,···,M–1,M为相参积累时间内发射的脉冲数。f0为发射信号载频,c为光速,σ0为目标双基地后向散射系数,w(t)为白噪声。
忽略目标距离的2阶以上分量,式(2)可近似为:
| $\begin{align} & R_{\text{s}}^{\prime }(t)\approx {{R}_{\text{T}0}}+{{R}_{\text{R}0}}-2L-2{{v}_{\text{T}}}\text{cos}\delta \text{cos}(\frac{\beta }{2})t \\ & +\frac{1}{2}(\frac{\text{si}{{\text{n}}^{2}}(\delta -\frac{\beta }{2})}{{{R}_{\text{T}0}}}+\frac{\text{si}{{\text{n}}^{2}}(\delta +\frac{\beta }{2})}{{{R}_{\text{R}0}}})v_{\text{T}}^{2}{{t}^{2}} \\ \end{align}$ | (4) |
上式中,令${r_0} = {R_{{\rm{T}}0}} + {R_{{\rm{R}}0}} - 2L$,为起始时刻目标双基地距离;${v_0} = - 2{v_{\rm{T}}}{\rm{cos}}{\delta} {\rm{cos}}(\beta /2)$,为起始时刻目标双基地径向速度;${a_0} = \bigg(\frac{{{{\rm{sin}}^2}\Big({\delta} - {{\frac{\beta }{2}}}\Big)}}{{{R_{{\rm{T}}0}}}} + $ $\frac{{{{\rm{sin}}^2}\Big({\delta} + {{\frac{\beta }{2}}}\Big)}}{{{R_{{\rm{R}}0}}}}\bigg)\mathop v\nolimits_{\rm{T}}^2 $,为起始时刻目标双基地加速度。此时
| ${f_{\rm{d}}} = - \frac{1}{\lambda }\frac{{{\rm{d}}{R'_{\rm{s}}}(t)}}{{{\rm{d}}t}} = - \frac{{{v_0} + {a_0}t}}{\lambda }$ | (5) |
双基地雷达的距离分辨单元和多普勒分辨单元分别为:
| $\quad \; \,{\rho _{\rm{r}}} \approx \frac{{\rm{c}}}{{2B{\cos^2}(\beta /2)}}$ | (6) |
| ${\rho _{\rm{d}}} = \frac{1}{T\;} = \frac{1}{{M{T_{\rm{r}}}}}$ | (7) |
若积累时间T内不发生多普勒扩展和距离弯曲,即满足
| $T < \min(\sqrt {\lambda /{a_0}} ,\sqrt {8{\rho _{\rm{r}}}/{a_0}} ) = \sqrt {\lambda /{a_0}} $ | (8) |
其中
| $\begin{align} & {{a}_{0}}=\max \{(\frac{\text{si}{{\text{n}}^{2}}(\delta -\frac{\beta }{2})}{{{R}_{\text{T}0}}}+\frac{\text{si}{{\text{n}}^{2}}(\delta +\frac{\beta }{2})}{{{R}_{\text{R}0}}})\text{ }v_{\text{T}}^{2}, \\ & (\frac{\text{si}{{\text{n}}^{2}}(\delta +\frac{\beta }{2})}{{{R}_{\text{T}0}}}+\frac{\text{si}{{\text{n}}^{2}}(\delta -\frac{\beta }{2})}{{{R}_{\text{R}0}}})\text{ }v_{\text{T}}^{2}\} \\ \end{align}$ |
则目标与雷达间的瞬时距离和可表示为瞬时斜距rs(t)=r0+v0t。忽略指数常数项,回波快时间域的匹配滤波输出为:
| $\begin{align} & {{s}_{\text{MF}}}(\tau ,t)={{\sigma }_{0}}\text{sinc}(\pi B(\tau -{{r}_{\text{s}}}(t)/\text{c})) \\ & \cdot \text{exp}(-\text{j}2\pi {{v}_{0}}t/\lambda ) \\ \end{align}$ | (9) |
令r=cτ为目标距离搜索参数,上式可重写为:
| $\begin{align} & {{s}_{\text{MF}}}(\tau ,t)={{\sigma }_{0}}\text{sinc}(\frac{\pi B(r-{{r}_{\text{s}}}(t))}{\text{c}}) \\ & \cdot \text{exp}(-\text{j}2\pi {{v}_{0}}t/\lambda ) \\ \end{align}$ | (10) |
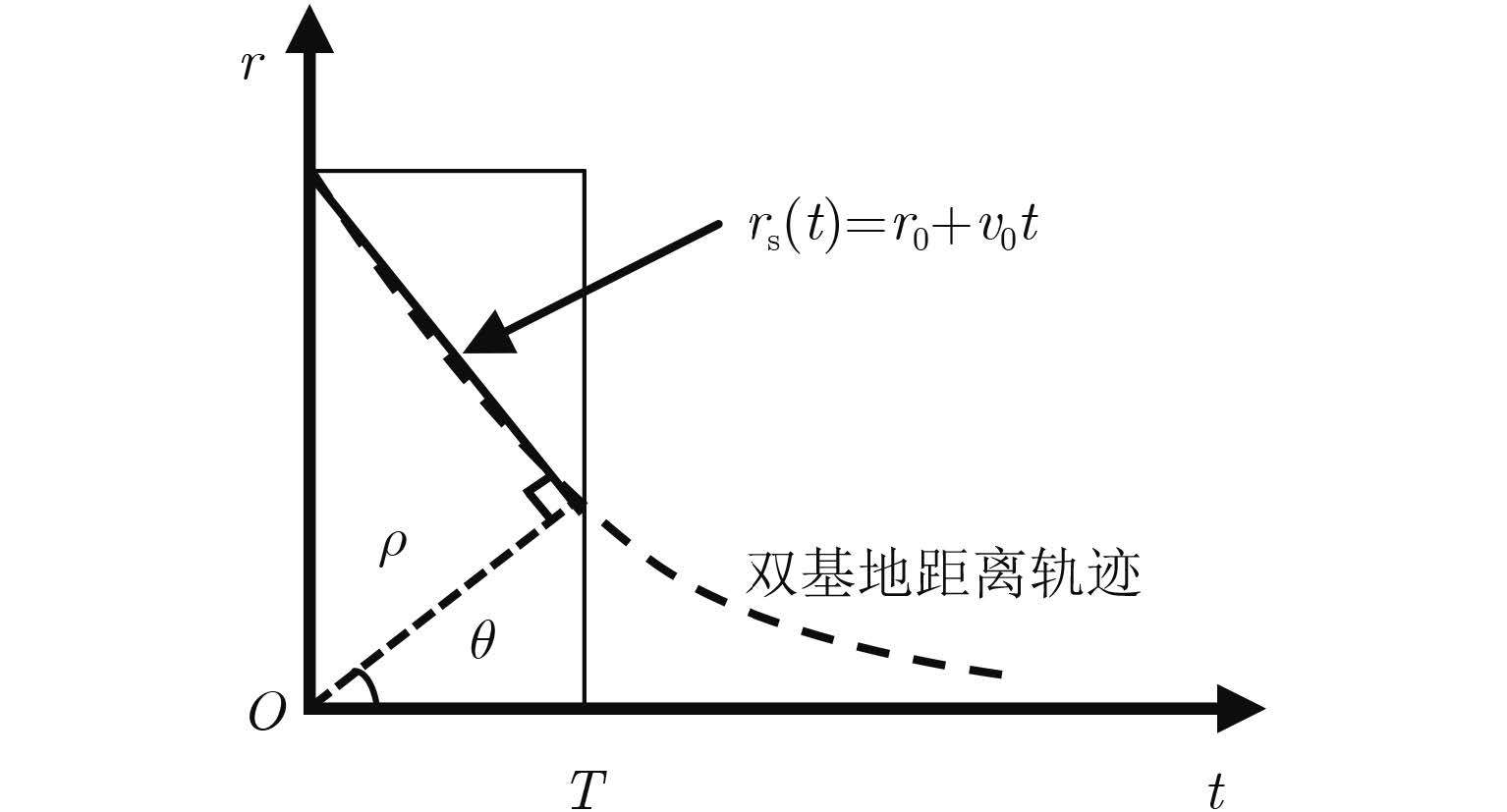
由式(10)可知,经过脉冲压缩处理后目标回波包络走动是一条由目标运动参数(r0,v0)决定的斜线,如图 2所示。当目标在Δts时间内移动距离和Δr>ρr时,即产生跨距离单元问题。
|
图 2 双基地距离轨迹 Fig.2 Bistatic distance trajectory |
标准RFT用于信号检测的基本思想是将距离-脉冲域空间带有相位信息的直线信号轨迹映射成某参数空间的一个点。由回波模型推导过程可知,双基地雷达可在规定的积累时间内采用标准RFT变换实现相参积累。利用不同的速度搜索值构造多普勒滤波器
| ${H_{\rm{v}}}(t) = {\rm{exp}}({\rm{j}}2 \pi vt/\lambda ) = {\rm{exp}}( - {\rm{j}}2 \pi {f_{\rm{d}}}t)$ | (11) |
双基地RFT变换可表示为:
| $\begin{align} & G(\rho ,\theta )=\int_{-\infty }^{\infty }{\int_{-T/2}^{T/2}{{{s}_{\text{MF}}}(r,t)}} \\ & \cdot \delta (\rho -t\text{cos}\theta -r\text{sin}\theta ){{H}_{\text{v}}}(t)\text{d}t\text{d}r \\ & =\int_{-T/2}^{T/2}{{{s}_{\text{MF}}}(\frac{\rho }{\text{sin}\theta }-t\text{cot}\theta ,t)}{{H}_{\text{v}}}(t)\text{d}t \\ \end{align}$ | (12) |
与标准RFT算法参数(fd,v,θ)在信号空间中构成一组映射关系相似,双基地系统中,如果目标近似具有1阶运动特性,直线的截距r0与极距ρ的关系仍可表述为ρ=r0sinθ,斜率v0与极角θ的关系表述为v0=–cotθ。因此,可将式(12)从(ρ,θ)域变换到(r,v)域,即
| $G(r,v) = \int_{ - T/2}^{T/2} {{s_{{\rm{MF}}}}(t,{r_0} + {v_0}t){H_{\rm{v}}}(t)} {\rm{d}}t$ | (13) |
双基地RFT变换距离-速度域离散表达式为:
| $\begin{align} & G(r,v)=\sum\limits_{m=1}^{M}{{{s}_{\text{MF}}}(t,r+vt)}{{H}_{\text{v}}}(t) \\ & =\sum\limits_{m=1}^{M}{\text{sinc}}(\pi B[(r-{{r}_{0}})+(v-{{v}_{0}})m{{T}_{\text{r}}}]/\text{c}) \\ & \cdot \text{exp}(\text{j}2\pi (v-{{v}_{0}})m{{T}_{\text{r}}}/\lambda ) \\ \end{align}$ | (14) |
其中,$r \in [{r_{{\rm{min}}}},{r_{{\rm{max}}}}]$为双基地距离搜索范围,$v \in [{v_{{\rm{min}}}},{v_{{\rm{max}}}}]$为双基地速度搜索范围,M为积累脉冲数。定义距离搜索步长Δr=c/fs,速度搜索步长Δv=λ/T,则
| $r = {r_{{\rm{min}}}} + i\Delta r,\begin{array}{*{20}{c}} {} & {i = 1,\cdots ,{N_{\rm{r}}}} & {} \end{array}$ | (15) |
| $\ v = {v_{{\rm{min}}}} + q\Delta v,\begin{array}{*{20}{c}} {} & {q = 1,\cdots ,{N_{\rm{v}}}} & {} \end{array}$ | (16) |
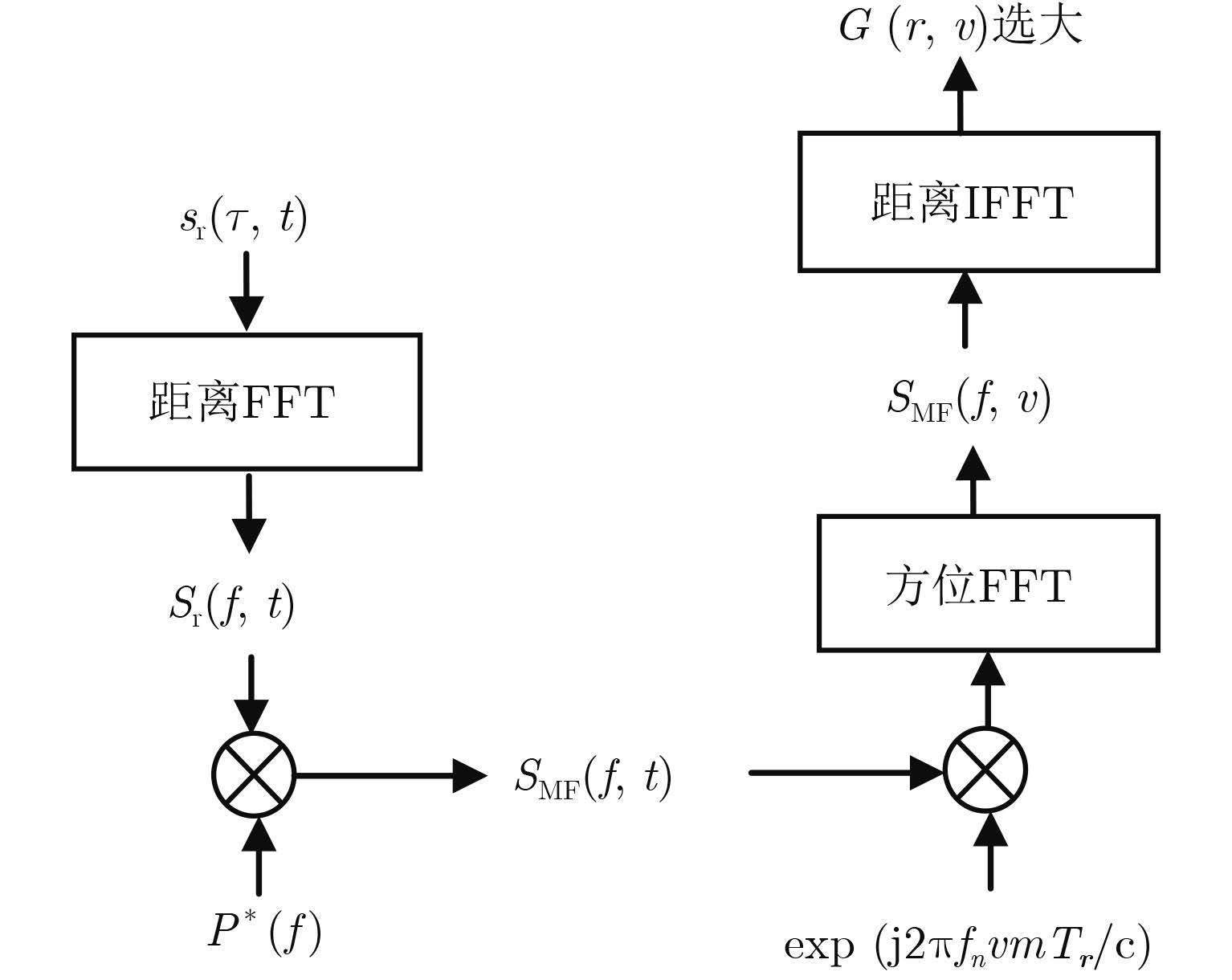
在式(14)中RFT变换通过联合搜索参数空间中目标参数,解决了距离走动(弯曲)与相位调制耦合的问题。由于雷达数据为离散值,参数空间搜索步长通常为整数,这种方法会引入由量化误差带来的能量损失。本节结合频域匹配滤波技术,提出一种计算式(14)的方法,如图 3所示。该方法在不采用插值运算的条件下也能显著减小由量化误差引起的积累损失。
步骤1 对接收到的M个基带回波脉冲进行FFT 处理;
步骤2 产生距离匹配滤波器的频率响应函数P*(f)并与基带回波脉冲相乘;
步骤3 在频域乘以引起距离走动的指数项的共轭exp(j2πfnvmTr/c),将斜率为v的直线运动轨迹校正为垂直于t轴的直线;
步骤4 通过FFT变换对脉间相位差进行补偿并沿方位维对每一距离频率单元进行累加;
步骤5 对步骤4的结果进行IFFT处理可得G(r,v),峰值检测得到目标结果。
该算法基于FFT和IFFT实现,运算复杂度较低。设距离域采样点数为Nr,速度域采样点数为Nv,相参积累脉冲数为M。
按图 3频域算法需要复乘次数分别为:步骤1:$(1/2)M{N_{\rm{r}}}{\rm{lo}}{{\rm{g}}_2}({N_{\rm{r}}})$,步骤2:MNr,步骤3、步骤4:[2(M+Nv)+4(M+Nv)log2(M+Nv)]Nr,步骤5:$(1/2)[M{N_{\rm{r}}}{\rm{lo}}{{\rm{g}}_2}({N_{\rm{r}}}) + {N_{\rm{r}}}{N_{\rm{v}}}]$。
|
图 3 双基地RFT变换频域算法流程 Fig.3 Process of bistatic RFT algorithm in frequency domain |
距离搜索范围。双基地雷达工作于侧向区,由参考文献[10]可知,此时双基地角范围β$ \in $(30°,135°),基线长度范围2L$ \in $(0.7RM,$ \sqrt 2 $RM),RM为单基地雷达最大作用距离。由双基地雷达三角关系,最大双基地搜索距离为:
| ${r_{{\rm{max}}}} = \frac{{2\sqrt 2 L}}{{\sqrt {1 - {\rm{cos}}{\beta _{{\rm{min}}}}} }} - 2L$ | (17) |
速度搜索范围。由起始时刻目标双基地径向速度可知,对所有的β值,当δ$ \in $(–90°,90°)时,多普勒频移为正;当δ$ \in $(90°,270°)时,多普勒频移为负。双基地搜索速度最大值为:
| ${v_{{\rm{max}}}} = \left| {2{v_{{\rm{Tmax}}}}{\rm{cos}}\Big(\frac{{{\beta _{{\rm{min}}}}}}{2}\Big)} \right|$ | (18) |
其中,vTmax为观测目标的最大速度。
4 仿真实验结果雷达载频fc=3 GHz,脉冲重复频率fr=1500 Hz,最大作用距离RM=100 km,发射LFM脉冲时宽Tp=10 站位置(50 km,0),观测区域内有一目标位于(20 km,50 km)处,其双基地后向散射系数σ0=1,以恒速vT=200 m/s运动,目标方向角δ=45°。忽略波束影响,此时初始双基地距离r0=44.33 km,初始双基地速度v0=–208 m/s,最大可相参积累脉冲数为573个,积累时间内目标运动跨7个搜索步长。
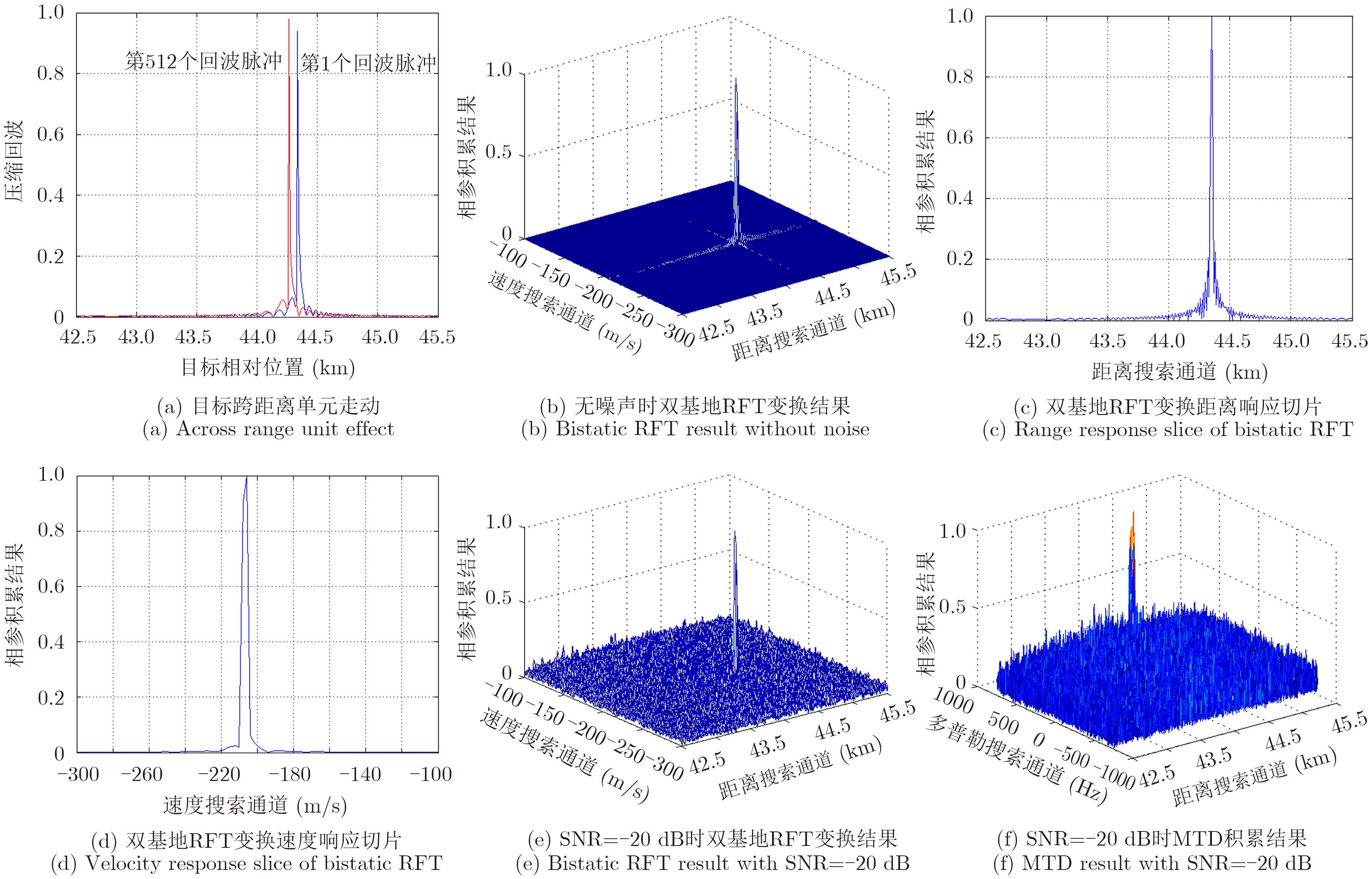
仿真时,距离搜索范围r$ \in $(42.5 km,45.5 km),速度搜索范围v$ \in $(–300 m/s,–100 m/s);脉压SNR增益为10lg(D)≈24 dB,脉冲积累数为512个,故RFT变换的SNR增益为101g(M)≈27 dB,噪声为高斯白噪声。其结果如图 4所示,图 4(a)显示了积累时间内目标距离单元走动情况,图 4(b)为无噪声时RFT变换结果,图 4(c),图 4(d)表明距离-速度域RFT变换可以近似为距离、速度两维脉冲压缩结果。图 4(e),图 4(f)对比说明,该算法比传统MTD方法有更高的积累增益。
|
图 4 双基地RFT变换仿真 Fig.4 Simulation of bistatic RFT |
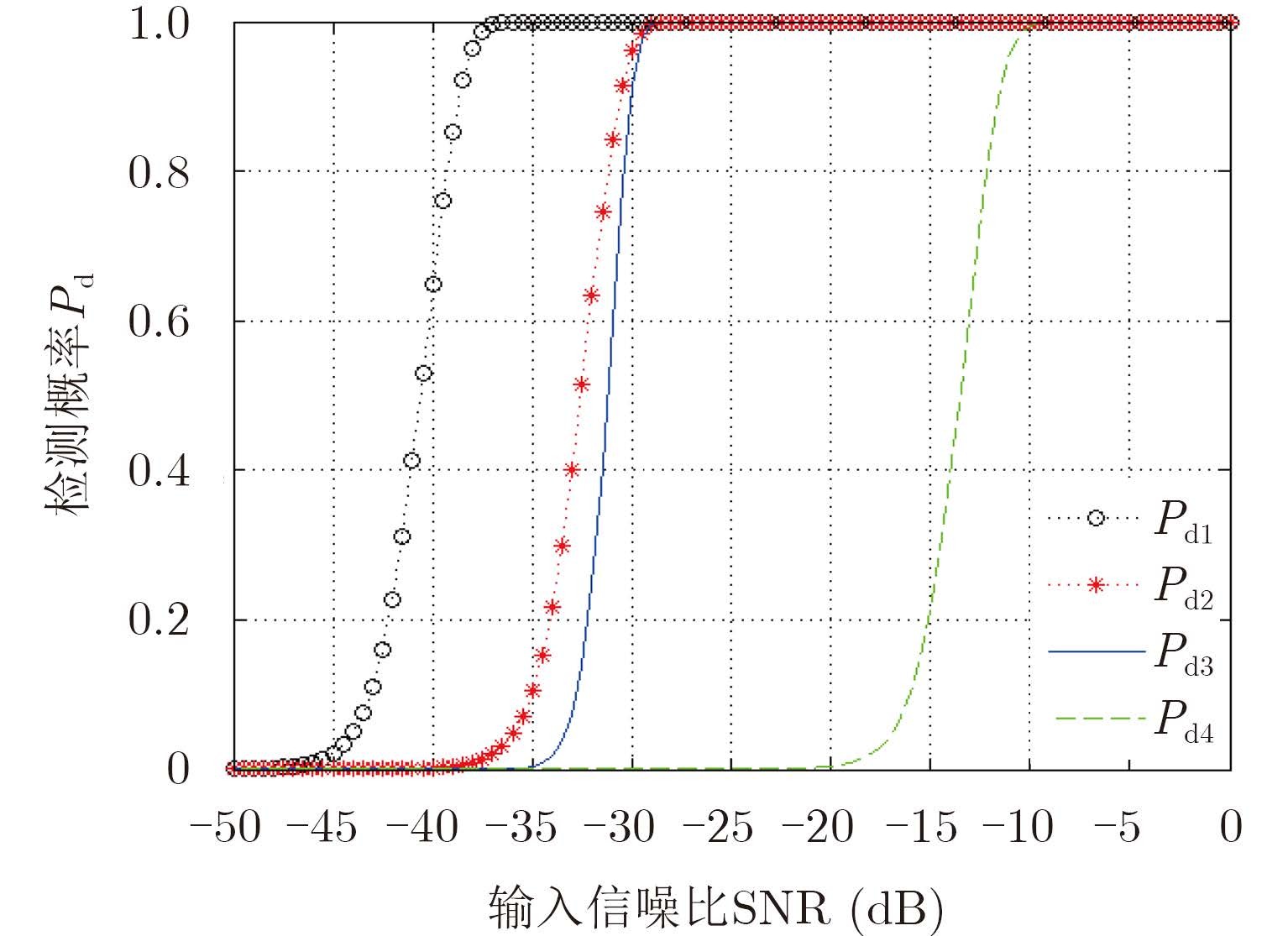
图 5给出了不同SNR条件下的RFT算法检测性能曲线(Pd1),仿真中虚警概率为Pfa=10–6。作为比较,同时给出了MTD相参积累时的检测性能曲线(Pd2)、跨距离单元非相参积累时的检测性能曲线(Pd3)和单个脉冲检测性能曲线(Pd4)。可以看出,Pd=0.9时,本文方法所需SNR最低,为–38.7 dB,它比MTD方法和非相参积累方法分别小8.1 dB和8.6 dB。
|
图 5 双基地RFT算法检测性能 Fig.5 Detection performance of bistatic RFT |
本文提出了基于RFT变换的双基地雷达相参积累方法,该算法能够在频域实现,且运算复杂度较低。在目标相参积累角内,增加接收机数量,雷达系统能够获得更多的积累脉冲数,从而为弱目标检测提供一条有益的途径。
| [1] |
许稼, 彭应宁, 夏香根, 等. 空时频检测前聚焦雷达信号处理方法[J].
雷达学报 , 2014, 3 (2) : 129-141 Xu Jia, Peng Ying-ning, Xia Xiang-gen, et al. Radar signal processing method of space-time-frequency focus-before detects[J].
Journal of Radars , 2014, 3 (2) : 129-141 ( 0) 0)
|
| [2] |
田静. 雷达机动目标长时间积累信号处理算法研究[D]. [博士论文], 北京理工大学, 2014: 9-20.
Tian Jing. Study on long-time coherent integration for radar maneuvering targets[D]. [Ph.D. dissertation], Beijing Institute of Technology, 2014: 9-20.
( 0) 0)
|
| [3] |
Zeng Jian-kui, He Zi-shu, Mathini S, et al. Modified Hough transform for searching radar detection[J].
IEEE Geoscience and Remote Sensing Letters , 2008, 5 (4) : 683-686 ( 0) 0)
|
| [4] |
Carretero-Moya J, Gismero-Menoyo J, Asensio-Lopez A, et al.. A coherent radon transform for small target detection[C]. IEEE Radar Conference, California, USA, 2009: 1-4.
( 0) 0)
|
| [5] |
战立晓, 刘润华, 汤子跃, 等. 基于相参Radon变换的米波相控阵雷达弱目标检测[J].
现代雷达 , 2013, 35 (9) : 30-35 Zhan Li-xiao, Liu Run-hua, Tang Zi-yue, et al. Target detection for metric-band phased array radar based on coherent radon transform[J].
Modern Radar , 2013, 35 (9) : 30-35 ( 0) 0)
|
| [6] |
Xu J, Yu J, Peng Y, et al. Radon-Fourier transform for radar target detection Ⅰ: Generalized Doppler filter bank[J].
IEEE Transactions on Aerospace and Electronic Systems , 2011, 47 (2) : 1186-1202 ( 0) 0)
|
| [7] |
Xu J, Yu J, Peng Y, et al. Radon-Fourier transform for radar target detection Ⅱ : Blind speed sidelobe suppression[J].
IEEE Transactions on Aerospace and Electronic Systems , 2011, 47 (4) : 2473-2489 ( 0) 0)
|
| [8] |
Yu J, Xu J, Peng Y, et al. Radon-Fourier transform for radar target detection Ⅲ : Optimality and fast implementations[J].
IEEE Transactions on Aerospace and Electronic Systems , 2012, 48 (2) : 991-1004 ( 0) 0)
|
| [9] |
Baker C J, Lhume A, and Qineti Q. Netted radar sensing[J].
IEEE Aerospace & Electronic Systems Magazine , 2003, 18 (2) : 3-6 ( 0) 0)
|
| [10] |
杨振起, 张永顺, 骆永军.
双(多)基地雷达系统[M]. 北京: 国防工业出版社, 1998 : 20 -22.
Yang Zhen-qi, Zhang Yong-shun, and Luo Yong-jun.
Bistatic (Multistatic) Radar Systems[M]. Beijing: National Defence Industry Press, 1998 : 20 -22.
( 0) 0)
|
| [11] |
Guan Xin, Zhong Li-hua, Hu Dong-hui, et al. An extended processing scheme for coherent integration and parameter estimation based on matched filtering in passive radar[J].
Journal of Zhejiang University-Science C (Computers & Electronics) , 2014, 15 (11) : 1071-1085 ( 0) 0)
|
| [12] |
RichardsM A.
雷达信号处理基础[M]. 北京: 电子工业出版社, 2008 : 229 -248.
Richards M A.
Fundamentals of Radar Signal Processing[M]. Beijing: Publishing House of Electronics Industry, 2008 : 229 -248.
( 0) 0)
|
| [13] |
KayS M.
统计信号处理基础[M]. 北京: 电子工业出版社, 2014 : 448 -452.
Kay S M.
Fundamentals of Statical Signal Processing[M]. Beijing: Publishing House of Electronics Industry, 2014 : 448 -452.
( 0) 0)
|




