随着民用航空技术的不断发展,机载气象雷达技术的应用极大地提高了气象预报的实时性和准确性,为民航飞机的安全运行提供了可靠的保障。一般认为,雷达反射率越高的区域越危险。实际上,只有会造成飞机结冰和存在湍流的高反射率区域才是危险的[1]。目前的机载气象雷达仍然是单极化体制,尚不具备降水类型区分功能,飞行员只能采取绕行的方式避开雷达指示的高反射率区域。2012年美国国家公务航空协会(NBAA,National Business Aviation Association)召开的年会上,Collins航电市场部主管Craig Peterson指出气象雷达新功能可借助多极化工作模式、电子扫描天线和新的信号处理算法等实现[2]。机载气象雷达的主要生产厂商柯林斯公司(Collins)和霍尼韦尔公司(Honeywell)等也已经开始了相应技术的开发。2012年Collins申请了适用于机载气象雷达系统的双极化天线的专利[3]。借助多极化技术增强机载气象雷达的目标检测能力,实现精细的降水分类(诸如冰雹、雨、雪)与危险级别判断[4, 5, 6],必将是机载气象雷达未来的发展方向,这将对保障飞行安全和进一步降低由天气引起的航班延误具有重要意义。
目前,气象目标极化仿真主要通过数值天气预报模式(Numerical Weather Prediction,NWP)输出原始气象数据,在该数据的基础上构建气象目标的微物理特性(粒子的轴向分布,粒径分布和雨滴谱等),最后通过电磁散射计算获得气象目标的双极化信息。1965年,Waterman等人[7]提出了一种计算非球形颗粒光散射的计算方法,称为T矩阵法,该方法采用积分方程求解一个有界,封闭面包裹的目标散射场,根据其散射体表面的边界条件以及入射场、散射场和面场关系得到T矩阵的解。T矩阵法是目前计算椭球形粒子电磁散射特性的常用方法。1996年,Yee提出了有限差分时域法[8](Finite Difference Time Domain method,FDTD),该方法广泛地应用于求解包括冰晶粒子、雪晶等目标的电磁散射特性。除上述方法,电磁散射计算的方法还包括:分离变量法(Separation of Variables Method,SVM),点匹配法(Point Matching Method,PMM),离散偶极子近似法(Discrete Dipole Approximation,DDA)和矩量法(Method of Moments,MoM)等[9],但随着算法的精确度越来越高,也带来了运算耗时过长的问题,而考虑到气象场景计算本身含有大量的粒子,采用T矩阵法进行气象领域的研究工作是目前较为常用的方法。
2011年,Li等人[10]采用先进的区域预报系统(The Advanced Regional Prediction System,ARPS)仿真得到气象目标的微物理特性,利用T矩阵法模拟了1977年5月20日的超级单体风暴极化信息;同年,Lupidi等人[11]通过天气预报模式(Weather Research Forecast,WRF)对2010年3月8日一次严重的冬季风暴的极化特性进行了仿真,该仿真结果适用于地基天气雷达;Clotilde Augros[12]于2013年采用中尺度非静力模式(The Non-Hydrostatic Mesoscale Atmospheric Model,Meso-NH)对2012年9月24日的“弓状回波”进行地基气象雷达极化仿真,并通过真实地基极化雷达回波数据对仿真参数进行校正;Lischi等人[13]在2014年通过WRF输出的气象数据实现了混合气象目标在地基气象雷达系统的极化参数仿真。
综上,为开展双极化多普勒天气雷达的理论研究和设计应用,提供带有极化信息的气象目标仿真显得尤为重要。目前,机载双极化气象雷达的理论研究正处于发展阶段,为了给机载双极化气象雷达的技术研究提供数据来源,本文提出了一种基于数值天气预报模式的机载气象雷达降雨目标极化特性仿真方法。该方法利用数值天气预报模式可获得温度、粒子浓度、混合比等降雨目标的气象参数,从而实现气象场景的建模与仿真。在分析降雨目标微物理特性的基础上,利用T矩阵法计算降雨目标的电磁散射矩阵,从而实现降雨目标的极化特性仿真。不同微物理特性参数下的仿真结果表明:该方法可实现降雨目标的气象建模,与实测数据对比分析,该方法的双极化仿真结果有效、可靠。
2 数值天气预报模式数值天气预报模式是一门综合性应用科学,其也可简称为数值预报模式。常用的数值预报模式的业务产品包括WRF、ARPS、Meso-NH、第5代中尺度数值模式(Mesoscale Model version 5,MM5)和区域大气模式系统(Region Atmosphere Model System,RAMS)等。其中,WRF模式是由美国环境预测中心(National Centers for Environmental Prediction,NCEP)和美国国家大气研究中心(National Center for Atmospheric Research,NCAR)等科研机构和相关大学共同参与、研发的新一代中尺度数值天气预报系统。该模式着重考虑1~10 km的水平网格,结合先进的数值方法和资料同化技术,是从云尺度到天气尺度等不同尺度的重要天气特征预报精度工具。WRF模式采用改进的物理方案,同时具有多重嵌套和方便定位不同地理位置的能力。本文利用WRF模式实现降雨目标的场景建模。
WRF模式分为供研究使用的ARW(The Advanced Research WRF)模式和供业务使用的NMM(The Non-hydrostatic Mesoscale Model)模式。WRF模式主要由3部分组成:模式预处理、主模式和模式产品后处理。本文选用ARW3.6版本,该模式不仅可以用于真实天气的个案模拟,也可以用于理想天气环境的个例研究。WRF模式的物理过程包含了大气的水平涡动扩散、垂直涡动扩散,积云对流参数化方案、云物理方案,太阳短波辐射和大气长波辐射方案等,其水平分辨率、垂直层次、积分区域及各种物理过程等均可根据需求进行调整。WRF模式的基本配置方案,如表 1所示。
| 表 1 WRF模式的基本配置方案 Tab. 1 The basic configuration of WRF model |
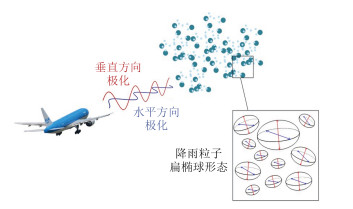
雨滴的尺度大小、形状分布、轴比特性、空间取向和谱分布等微物理特性是揭示降雨物理本质的重要特征参量,其与雷达回波的相互关系是气象雷达定量估计降雨强度的基础。本文在分析降雨目标微物理特性的基础上,利用T矩阵法计算降雨目标的电磁散射矩阵,从而实现降雨目标的极化特性仿真。机载双极化气象雷达探测降雨目标的原理示意图,如图 1所示。
|
图 1 机载双极化气象雷达探测降雨目标的原理示意图 Fig. 1 The schematic diagram of rainfall detection with airborne dual polarization weather radar |
降雨目标的微物理特性主要由目标的轴比特性,轴向分布和粒子浓度分布决定。轴比特性主要描述单个气象微粒的体积与其形态的关系,轴向分布用于描述大量气象微粒在下落过程中的主轴方向分布,而粒子浓度分布则用于描述气象场景中大量宏观粒子不同体积的数量分布情况。
(1) 轴比特性
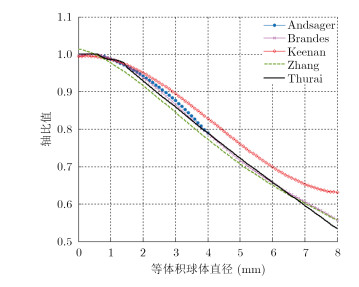
雨滴在下落过程中并非为常见的椭球体形态。在下落过程中,雨滴受到空气阻力及自身表面张力的影响,会产生一定程度的扭曲,只有直径很小的雨滴会成为球体形态。随着雨滴体积的增大,其形态逐渐从球体变化到近似扁椭球体的形态。本文用等体积球体直径来表示雨滴的等效体积。为了便于计算,一般情况下,把雨滴的不规则形状等效为椭球体,用椭球体的长轴和短轴对其形态进行描述。1999年,Andsager等人[14]通过观测中到大雨滴在下落中的振动情况来拟合轴比函数;2001年,Zhang等人[15]在对极化雷达的变量估计中开始考虑雨滴轴向对电磁散射的影响,在计算中加入了轴比函数进行仿真计算;同年,Keenan等人[16]研究轴比函数,雨滴谱分布对5 cm极化雷达的影响;2002年,Brandes等人[17]则考虑轴比函数对极化雷达的变量估计的影响;2007年,美国科罗拉多州立大学的Thurai M等人[18]通过实际观测采用了分段拟合雨滴的轴比函数来表示雨滴的形态与等体积球直径的关系。上述轴比函数的分布情况,如图 2所示。
|
图 2 轴比函数分布示意图 Fig. 2 The axis ratio function distribution |
图 2表示不同的轴比函数分布情况,除了Keenan的轴比函数在大雨滴的估计值偏高以外,其它轴比函数分布均比较接近。本文采用Thurai M等人提出的轴比函数,其采用分段函数拟合的形式,对不同体积的雨滴采用不同方式拟合,提高了雨滴轴比的精确性。其表达式如下:
| $b/a = \left\{ \begin{array}{l} 1,\quad\,D \lt 0.7\,\rm{mm}\\ 1.173 - 0.5165D + 0.4698D_{}^2 - 0.1317D_{}^3 - 8.5 \times {10^{ - 3}}D_{}^4,\\ \quad\quad 0.7 \le D \le 1.5\,\rm{mm}\\ 1.065 - 6.25 \times {10^{ - 2}}D - 3.99 \times {10^{ - 3}}D_{}^2 + 7.66 \times {10^{ - 4}}D_{}^3 - 4.095 \times {10^{ - 5}}D_{}^4 ,\\ \quad\quad D \gt 1.5\,\rm{mm} \end{array} \right.$ | (1) |
式中,D表示等体积球体直径,b/a表示扁椭球体的短轴与长轴之比。通过对实际雨滴的观察,通过轴比函数将雨滴的体积与其形态关系一一对应,更利于为后续的极化雷达提供雨滴形态的研究数据。
(2) 轴向分布
雨滴数据获取主要通过2维视频雨滴计量仪(2D Video Distrometer,2DVD)的观测获得,在完全稳定的空气条件下,雨滴下落的主轴倾角基本不发生改变。在实际情况中,雨滴下落的主轴方向会受到空气扰动的影响。统计数据表明,雨滴在下落过程中其主轴倾角服从高斯分布,表达式如下:
| $P\left( \delta \right) = \frac{1}{{{\sigma _\delta }\sqrt {2{\rm{\pi }} } }}{{\rm{e}}^{ - \frac{{{{\left( {\delta - \bar \delta } \right)}^2}}}{{2\sigma _\delta ^2}}}}$ | (2) |
式中,$\bar \delta $表示倾角平均值,${\sigma _\delta }$表示统计标准差。通过选取不同的$\bar \delta $和${\sigma _\delta }$值,可以用来描述不同场景下的雨滴的轴向分布。一般情况下,在较为稳定的空气中,雨滴不会发生较大的倾角,$\bar \delta $接近于垂直下落,且${\sigma _\delta }$的取值较小;在空气扰动较大的情况下,${\sigma _\delta }$的取值较大。
(3) 雨滴谱函数
一般的降雨过程中包含很多不同直径大小的雨滴,为了描述降雨中雨滴数量和雨滴大小的统计特性,常用雨滴谱函数描述其分布的统计特性。常见的雨滴谱函数有M-P分布和 Gamma 分布等。M-P分布是Gamma分布的特殊形式,采用Gamma分布拟合雨滴谱,能灵活地描述不同场景下的雨滴分布的特征[10],其表达式如下:
| $ N(D) = {N_{\rm{0}}}{D^\mu }{{\rm{e}}^{ - {\rm{ }} \wedge D}} $ | (3) |
式中,D表示等体积球体直径;μ表示形状因子,该参数决定雨滴谱的分布形状;N0表示截距参数,其表达式如下:
| $ {N_0} = {N_{\rm{t}}}\frac{{{\Lambda ^{\mu + 1}}}}{{\Gamma (\mu + 1)}} $ | (4) |
式中,$ \Gamma $表示gamma函数;Nt表示粒子数,$\Lambda $表示斜率参量,其表达式如下:
| $\Lambda {\rm{ = }}{\left[{\frac{{{\rm{\pi }} {\rho _{\rm{w}}}{N_{\rm{t}}}\Gamma (\mu + 4)}}{{6\Gamma (\mu + 1){\rho _{\rm{a}}}q}}} \right]^{\frac{1}{3}}}$ | (5) |
式中,ρa表示空气密度,单位为kg·m-3; ρw表示降雨密度,单位为kg·m-3。q表示水汽混合比,单位为g/kg。上式中ρa,q和Nt均由WRF输出数据获得。
由于不同地区,不同时间的降雨过程具有不同的雨滴谱分布,故通过调整Gamma分布中的截距参数N0,斜率参量$\Lambda $和形状因子μ来拟合不同地区的降雨特点,是目前作为气象目标研究的主要方法之一。其中,截距参数N0和斜率参量$\Lambda $由WRF输出的气象参数计算获得,形状因子μ一般根据降雨过程的不同选取不同的经验值,因此需要对不同的形状因子μ进行讨论分析。
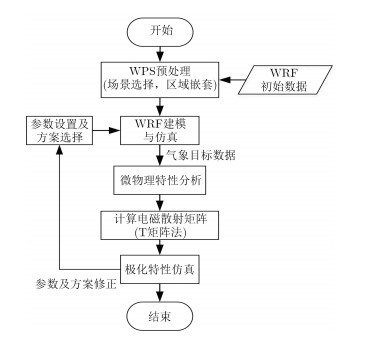
3.2 降雨目标的极化特性仿真本文首先通过WRF预处理系统(The WRF Pre-processing System,WPS)对WRF初始数据进行仿真场景的选取和区域嵌套设置,预处理后的数据经由天气预报模式WRF进行气象场景建模与仿真。利用WRF产生的气象目标数据构建降雨目标的微物理特性,通过T矩阵法计算降雨目标的电磁散射矩阵,从而实现降雨目标的极化特性仿真。本文方法的仿真流程图,如图 3所示。
|
图 3 本文方法的仿真流程图 Fig. 3 The simulation flow chart of the proposed method |
本文利用T矩阵法计算降雨目标的电磁散射矩阵,从而实现降雨目标的极化特性仿真。电磁散射特性计算时通常需要确定粒子的介电常数,粒子取向,直径的关系以及轴比函数等,利用上述参数可确定散射矩阵$\left[{\begin{array}{*{20}{c}}{{S_{{\rm{hh}}}}} & {{S_{{\rm{hv}}}}}\\ {{S_{{\rm{vh}}}}} & {{S_{{\rm{vv}}}}}\end{array}} \right]$,从而保证后续极化特性的仿真[19]。
极化特性参数是目前通过雷达参数对气象目标反演研究的主要参数,其中包括了水平反射率因子Zh,垂直反射率因子Zv,差分反射率因子Zdr和差分传播相移率Kdp等。其中,差分传播相移率则用于比较接收水平和垂直电磁波上的相位关系[20]。
(1) 雷达反射率因子
雷达反射率因子是用于描述气象目标降雨强度大小的一个重要参数,该参数用于表征降雨目标反射电磁波的能力。一般情况下,降雨强度越强,雷达接收目标的回波功率越强,反射率因子也越大。不同极化方向下的反射率因子Zij可以表示为:
| $ {Z_{ij}} = \frac{{{\lambda ^4}}}{{{{\rm{\pi }} ^5}{{\left| {{K_{\rm{w}}}} \right|}^2}}}\int_0^\infty {{\sigma _{ij}}(D)N(D){\rm{d}}D} ,\;i,j = h,v\; $ | (6) |
式中,i和j分别表示雷达电磁波的极化方向,可以取值水平方向h和垂直方向v,$\Lambda $为电磁波波长,D表示等体积球体直径,N(D)表示雨滴谱函数,${\left| {{K_{\rm{w}}}} \right|^2}$为液态水的离子积常数,一般取0.93。${\sigma _{ij}}$为粒子的后向散射截面积,其中${\sigma _{ij}}{\rm{ = 4}}{\rm{\pi }} {\left| {{S_{ij}}} \right|^2}$,Sij表示电磁散射矩阵系数。
利用水平反射率因子和垂直反射率因子可计算得到差分反射率因子,其数值大小主要受粒子形态和介电常数两种因素共同决定。当气象目标均为降雨粒子时,由于介电常数相同,差分反射率因子与粒子轴比一一对应。随着雨滴体积的增大,雨滴逐渐由圆球体扭曲为扁椭球形态。因此差分反射率因子不仅可以用于表征粒子形态,还可以用来表征粒子的体积,其表达式为:
| $ {Z_{{\rm{dr}}}} = 10{\lg }\frac{{{Z_{{\rm{hh}}}}}}{{{Z_{{\rm{vv}}}}}} = 10{\lg}\frac{{{{\left| {{S_{{\rm{hh}}}}} \right|}^2}}}{{{{\left| {{S_{{\rm{vv}}}}} \right|}^2}}} $ | (7) |
式中,Zhh为水平反射率因子,Zvv为垂直反射率因子。Zdr的取值随着雨滴扁平程度的加剧而增加,扁平程度与雨滴大小有关,所以可由Zdr判断雨滴的形态和雨滴的大小。当观测的气象目标为体积较小的球形雨滴时,Zdr的数值接近于0,另一方面,在实际观测中,由冰雹和霰的翻滚作用而造成了Zhh和Zvv的平均值接近,也会使Zdr的数值趋近于0。因此差分反射率因子Zdr可以作为区别冰雹和霰存在的辅助工具。
(2) 差分传播相移率
由于降雨粒子并非正规球体,前向散射会因入射方向的不同产生不同的散射特性,所以在极化方向上会产生不同的相位差,且该相位差会随着电磁波在降雨区域传播的距离增加而变化。一般情况下,在降雨较强的区域,相位差积累较大,在降雨强度较小的区域,积累较小[21]。由于雷达是通过目标反射到雷达的电磁波来侦测相位差,因此雷达探测到的总相位差称为差分传播相移Φdp,则定义差分传播相移率Kdp(或称为比差分相位)为Φdp随距离r的变化率,即:
| $ {\phi _{{\rm{dp}}}} = 2\int_0^r {K_{{\rm{dp}}}}{\rm{d}}r $ | (8) |
式中,r表示雷达距离气象目标的距离。在瑞丽散射的近似条件下,差分传播相移率可以表示为[21]:
| $ {K_{{\rm{dp}}}} = {10^3}\frac{{2{\rm{\pi }} }}{{{K_0}}}{\rm{Re}}\left[{{S_{{\rm{vv}}}} - {S_{{\rm{hh}}}}} \right] $ | (9) |
式中,K0表示自由空间传播常数,Shh和Svv表示散射矩阵中的元素。
4 仿真结果对比分析在UTC时间2015年6月16日至21日期间,热带风暴“比尔”经过美国德克萨斯州东部和俄克拉荷马州最后抵达大西洋。该热带风暴具有典型的热带气旋特征,并伴有大面积降雨,是降雨目标仿真较为合适的研究对象。约在UTC时间2015年6月17日15:00左右,热带风暴“比尔”正处于美国地基气象雷达(编号KWFS,纬度32°34′19.20″北,经度97°18′7.20″西)附近。为模拟本次的热带风暴降雨特性,选取仿真时间范围为UTC时间2015年6月17日0:00至23:59,WRF初始数据选取每日4次的1°×1°全球再分析资料(Final Operational Global Analysis,FNL),该数据由美国国家环境预测中心(NCEP)和国家大气研究中心(NCAR)提供。
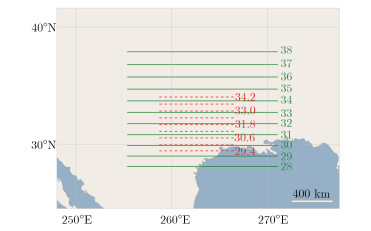
4.1 基于WRF模式的降雨目标建模及仿真结果仿真中心区域经纬度为32.78°N,-96.80°E,物理方案采用Milbrandt 2-mom,该方案可以产生极化仿真需要的水汽混合比和粒子数浓度等参数。采用地面加密观测资料对当天发生于美国的热带风暴“比尔”进行仿真,并采用2层嵌套网格进行建模。设置母网格分辨率为15000 m×15000 m,子网格分辨率为5000 m×5000 m,垂直方向上按气压分为27层。WRF嵌套结构示意图,如图 4所示。
|
图 4 WRF嵌套结构示意图 Fig. 4 The schematic diagram of WRF nested structure |
图 4中绿色实线表示母网格仿真区域,红色虚线表示子网格仿真区域,线条右侧标注表示仿真区域的纬度。基于WRF模式的降雨目标建模通过初始数据得到母网格的粗精度数据,在该数据的基础上利用子网格进行模拟仿真。为了保证数据的输出精度,采用子网格的输出数据作为研究对象。基于WRF模式的降雨目标建模结果,如图 5所示。
图 5表示基于WRF模式的降雨目标建模结果。图 5(a)表示水汽混合比,图 5(b)表示粒子浓度。如图 5(a)所示,WRF输出的水汽混合比,用于描述仿真场景中空气的含水量,单位为g/kg。从图中可以看出,在该时刻热带风暴在中心处产生涡旋,在涡旋中心及左侧区域含水量较大,最高时含水量达到了1.71 g/kg。如图 5(b)所示,该图表示降雨粒子浓度分布,在涡旋附近,降雨粒子浓度较大。对比图 5(a)和图 5(b)相同区域,区域1实线部分处于热带风暴核心区附近,水汽混合比数值较高而粒子浓度也相对较高,符合热带风暴中心区域分布特征;区域2虚线部分处于热带风暴漩涡边缘,水汽混合比相对中心区域有较为明显的降低,但粒子浓度并没有减小。通过对比图 5(a)和图 5(b)可以初步判断WRF仿真热带风暴基本符合热带气旋特性,可用于极化特性计算与分析。
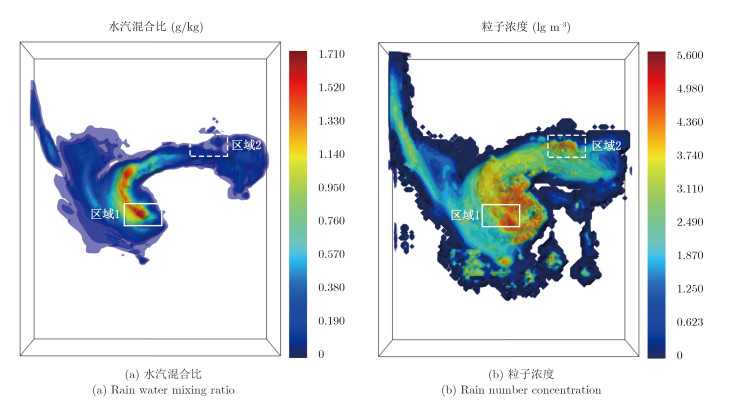
|
图 5 基于WRF模式的降雨目标建模结果 Fig. 5 The modeling results of precipitation target based on WRF model |
一般情况下,轴向分布符合高斯型分布。为了分析轴向分布对极化参数计算的影响,选取WRF仿真中风暴核心区域附近网格位置为(32,118,12)的数据,设定形状因子μ为0,信号波长$\Lambda $为3.33 cm(X波段),分别选取高斯分布的标准差${{\sigma _\delta }}$为1,5,10,15和20进行极化参数计算,不同标准差下极化参数的仿真结果,如表 2所示。
| 表 2 不同标准差下的极化参数仿真结果 Tab. 2 The results of polarization parameters under different standard deviation |
从表 2中可以看出,随着轴向分布标准差的增大,水平反射率因子,差分反射率因子和差分传播相移率等极化参数的取值逐渐降低。一般情况下,气象场景越复杂,场景气象变化越剧烈,选取的标准差数值越高。考虑到本文仿真场景为一次热带风暴,设定轴向分布服从$\left( {\bar \delta ,{\sigma _\delta } = 30} \right)$的高斯分布。
4.3 不同形状因子下的极化特性仿真结果根据霍尼韦尔公司RDR-4B型机载气象雷达在气象方式下的工作参数,选取脉冲重复频率为380 Hz,波束宽度为3°,扫描角度±45°。为考虑形状因子μ对降雨目标雨滴谱的分布影响,本文选取不同的形状因子μ来描述降雨目标的雨滴谱函数,并计算其对应的极化参数。不同形状因子下的水平反射率因子,差分反射率因子和差分传播相移率的仿真结果,如图 6-图 8所示。与美国国家气候数据中心(National Climatic Data Center,NCDC)的实测雷达数据的对比分析表明,本文方法的双极化仿真结果有效、可靠。
计算不同形状因子下的水平反射率因子Zh,差分反射率因子Zdr和差分传播相移率Kdp,其数值变化范围如表 3所示。
图 6(a)-图 6(c)分别表示形状因子μ=0,1,2时,水平反射率因子的分布情况,图 6(d)表示地基气象雷达探测到的水平反射率因子的分布情况。同理,图 7(a)-图 7(c)分别表示形状因子μ=0,1,2时,差分反射率因子的分布情况,图 7(d)表示地基气象雷达探测到的差分反射率因子的分布情况。图 8(a)-图 8(c)分别表示形状因子μ=0,1,2时,差分传播相移率的分布情况,图 8(d)表示地基气象雷达探测到的差分传播相移率的分布情况。
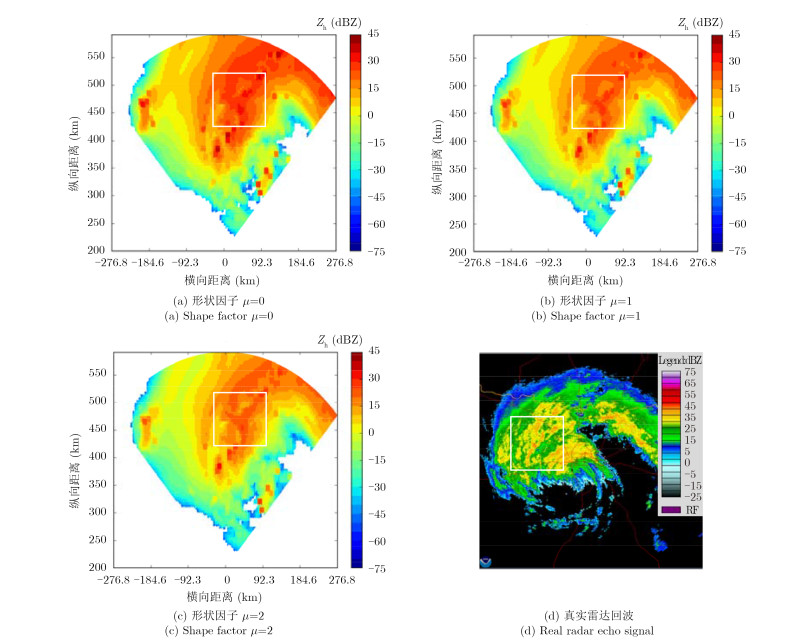
|
图 6 不同形状因子下的水平反射率因子对比结果 Fig. 6 The results of horizontal reflectivity factor in different shape factors |
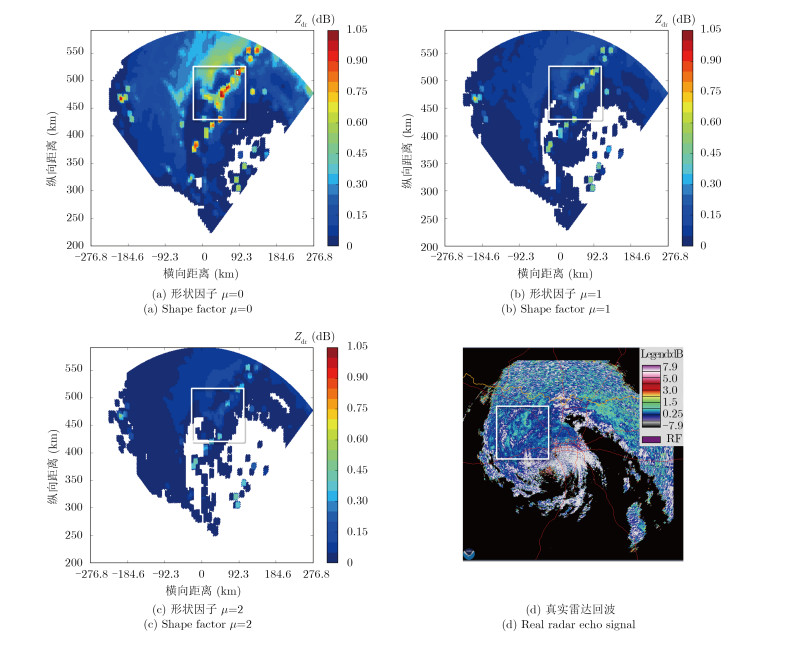
|
图 7 不同形状因子下的差分反射率因子对比结果 Fig. 7 The results of differential reflectivity factor in different shape factors |
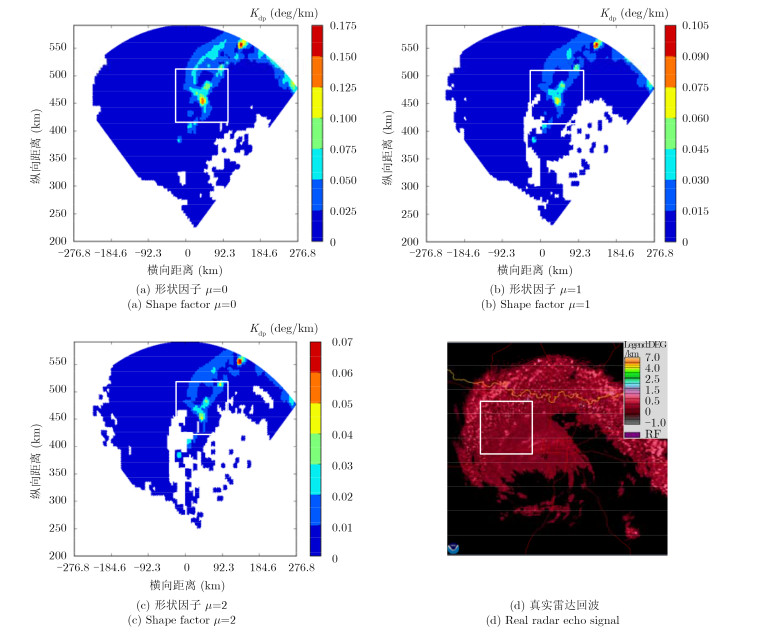
|
图 8 不同形状因子下的差分传播相移率对比结果 Fig. 8 The results of differential propagation phase in different shape factors |
如图 6(a)-图 6(c)所示,飞机正前方450~500 km左右(白色方框标注区域)为热带风暴的核心区域。对比不同的形状因子的仿真结果可知,当μ=0时,水平反射率因子回波能量最高,μ=1次之,μ=2最低。对比表 3中不同形状因子下Zh的取值范围,可以看出,随着μ的增大,降雨的回波强度逐渐减小。从同一区域地基雷达的实际数据可以看出,热带风暴在图中标注区域的反射率因子最大值约为40 dB,说明当形状因子μ=0时,仿真结果与真实情况较为接近。
| 表 3 仿真极化参数输出范围 Tab. 3 Polarization simulation parameters range |
同理,对比图 7中不同形状因子下的差分反射率因子仿真结果可知,在热带风暴的核心区域(白色方框标注区域),差分反射率因子较大,说明这里存在有尺寸较大的扁椭圆形态雨滴,周围则以小椭球雨滴为主。从表 3中的统计数据可以看出,差分反射率因子在μ=0时其值达到了1,这说明该区域雨滴粒径较大,雨滴扭曲较为严重。随着μ值的增大,差分反射率因子的值逐渐减小。当μ=2时,差分反射率因子最大值仅为0.51。对比真实地基气象雷达输出的差分反射率因子可以看出,当形状因子μ=0时,仿真结果比较接近真实情况。
不同形状因子下差分传播相移率的对比结果,如图 8所示。在差分传播相移率较高的区域表明该地区降雨较强,随着μ值的增大,差分传播相移率随之减小。对比真实地基气象雷达数据的输出数据可知,当形状因子μ=0时,仿真结果与真实情况较为接近。虽然相对于实测数据,仿真结果的取值偏小,但其整体分布情况仍符合热带风暴的形态规律。
5 结论带有极化信息的气象目标仿真是双极化多普勒天气雷达的理论研究和设计应用的基础。目前,机载双极化气象雷达的理论研究正处于发展阶段,为了给机载双极化气象雷达的技术研究提供数据来源,本文提出了一种基于数值天气预报模式的机载气象雷达降雨目标极化特性仿真方法。以全球再分析资料的实测数据作为气象目标建模的初始数据,通过WRF数值预报模式模拟了一次热带风暴的发生过程。改变雨滴谱的形状因子来调整降雨目标的微物理特性,并利用T矩阵法计算气象目标的电磁特性,从而实现降雨目标的极化特性仿真。不同微物理特性参数下的仿真结果表明:该方法可实现降雨目标的气象建模,与实测数据对比分析,该方法的双极化仿真结果有效、可靠。
| [1] | Lupidi A, Moscardini C, Garzelli A, et al. Polarimetry applied to avionic weather radar: improvement on meteorological phenomena detection and classification[C]. 2011 Tyrrhenian International Workshop on Digital Communications-Enhanced Surveillance of Aircraft and Vehicles (TIWDC/ESAV), Capri, 2011: 73-77.( 1) 1) |
| [2] | Craig Peterson. Weather radar: the Next 10 Years[OL].http://www.ral.ucar.edu/general/fpaw2012/Presentations/Peterson.pdf,2012.( 1) 1) |
| [3] | Woodell D L, West J B, Elsallal W A, et al. Weather radar system and method using dual polarization antenna[P]. US, 008098189B1, 2012.( 1) 1) |
| [4] | Bunch B P and Christianson P. System and method to identify regions of airspace having ice crystals using an onboard weather radar system[P]. US, 20130234884A1, 2013.( 1) 1) |
| [5] | Khatwa R and Mathan S. Enhanced alerting of characteristic weather hazards[P]. US, 008395541B2, 2013.( 1) 1) |
| [6] | Ratan K and Dave P. Methods and systems for presenting weather hazard information on an in-trial procedures display[P]. EP, 2354805A1, 2011.( 1) 1) |
| [7] | Waterman P C. Matrix formulation of electromagnetic scattering[J]. Proceedings of the IEEE, 1965, 53(8): 805-812.( 1) 1) |
| [8] | Yee K S. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media[J].IEEE Transactions on Antennas and Propagaction, 1966, 14(3): 302-307.( 1) 1) |
| [9] | 许丽生, 陈洪滨, 丁继烈, 等. 非球形粒子光散射计算研究的进展综述[J]. 地球科学进展, 2014, 29(8): 903-912.Xu Li-sheng, Chen Hong-bin, Ding Ji-lie, et al. Summary of non-spherical particles in progress calculation of light scattering[J]. Advances in Earth Science, 2014, 29(8): 903-912.( 1) 1) |
| [10] | Li Z Z, Zhang Y, Zhang G, et al. A microphysics-based simulator for advanced airborne weather radar development[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(4): 1356-1373.( 2) 2) |
| [11] | Lupidi A, Moscardini C, Berizzi F, et al. Simulation of X-band polarimetric weather radar returns based on the Weather Research and Forecast Model[C]. 2011 IEEE Radar Conference (RADAR), Kansas, 2011: 734-739.( 1) 1) |
| [12] | Augros C, Caumont O, Ducrocq V, et al. Development and validation of a full polarimetric radar simulator[C]. 36 th Conference on Radar Meteorology, Breckenridge, 2013: 387.( 1) 1) |
| [13] | Lischi S, Lupidi A, Martorella M, et al. Advanced polarimetric Doppler weather radar simulator[C]. IEEE 2014 15th International Radar Symposium (IRS), Gdansk, 2014: 1-6.( 1) 1) |
| [14] | Andsager K, Beard K V, and Laird N F. Laboratory measurements of axis ratios for large raindrops[J]. Journal of the Atmospheric Sciences, 1999, 56(15): 2673-2683.( 1) 1) |
| [15] | Zhang G, Vivekanandan J, and Brandes E. A method for estimating rain rate and drop size distribution from polarimetric radar measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(4): 830-841.( 1) 1) |
| [16] | Keenan T D, Carey L D, Zrnic D S, et al. Sensitivity of 5-cm wavelength polarimetric radar variables to raindrop axial ratio and drop size distribution[J]. Journal of Applied Meteorology, 2001, 40(3): 526-545.( 1) 1) |
| [17] | Brandes E A, Zhang G, and Vivekanandan J. Experiments in rainfall estimation with a polarimetric radar in a subtropical environment[J]. Journal of Applied Meteorology, 2002, 41(6): 674-685.( 1) 1) |
| [18] | Thurai M, Huang G J, Bringi V N, et al. Drop shapes, model comparisons, and calculations of polarimetric radar parameters in rain[J]. Journal of Atmospheric and Oceanic Technology, 2007, 24(6): 1019-1032.( 1) 1) |
| [19] | Leinonen J. High-level interface to T-matrix scattering calculations: architecture, capabilities and limitations[J]. Optics Eexpress, 2014, 22(2): 1655-1660.( 1) 1) |
| [20] | Bringi V N and Chandrasekar V. Polarimetric Doppler Weather Radar: Principles and Applications[M]. Cambridge University Press, 2001: 161-210.( 1) 1) |
| [21] | Jameson A R and Mueller E A. Estimation of propagation-differential phase shift from sequential orthogonal linear polarization radar measurements[J]. Journal of Atmospheric and Oceanic Technology, 1985, 2(2): 133-137.( 2) 2) |


