②(航天飞行器生存技术与效能评估实验室 北京 100085
②(The Institute of Effectiveness Evaluation of Flying Vehicle, Beijing 100085, China
现代条件下,飞机面临着复杂的威胁电磁环境,例如防空警戒雷达、地面跟踪制导雷达、机载火控雷达、雷达末制导的寻的导弹等,遂行任务的飞机此时必须采取适当的电子对抗措施以躲避威胁。目前,大部分地对空导弹或空空导弹普遍采用雷达导引头对空中目标进行末制导[1]。为了阻止进攻方的有效探测,防御方(例如飞机)会携带干扰机,施放噪声压制干扰或欺骗干扰,使机载雷达产生错误的速度、距离测量信息。为此,雷达导引头普遍采用了跟踪干扰源(HOJ)技术,该技术是将目标发射的干扰信号作为信号源,被动接收干扰信号,从而实现无源被动角度跟踪与精确测量。跟踪干扰源技术能够有效对付施放自卫式噪声压制干扰的飞机。多路径干扰(也称为对映体干扰)是一种新型的对抗机载火控雷达或弹载雷达的有效自卫干扰方式之一[2, 3, 4]。多路径干扰借助多路径传播策略来阻碍雷达截获干扰机平台所在的准确位置。干扰机发射信号照射到地面上,并发生了反弹,此时,通过地面反射的干扰信号和真实目标回波都能够进入导引头天线,使得导引头视场角内存在两个角跟踪信号,当干扰信号与真实目标回波信号在速度、角度之间的差别难以区分时,就能够同时形成多维度的欺骗干扰效果,对雷达末制导寻的带来很大威胁,目前对多路径干扰未见到有效的对抗措施。雷达极化技术是通过测量天线特性、目标回波、干扰回波和杂波的极化特性,进而提高目标识别和干扰抗干扰能力的一种新型信号与信息处理技术[5, 6],是除了传统时域、频域、空域信号处理以外一个新的可资利用和发展的技术领域,逐渐受到重视和发展。文献[7, 8]从极化敏感的角度分析了空间两点源对单脉冲雷达测角系统的影响模型,采用同时极化发射同时接收的体系结构和极化滤波处理可能有助于抑制转发式干扰。上述极化处理方法并未考虑低空突防的外部环境以及电波传播路径的影响,更多考虑的是直达干扰信号在完全极化条件下信号滤波的问题。本文首先分析了多路径干扰对雷达导引头作用机理,设计了一种双极化导引头的结构,建立了多路径干扰和直达干扰信号的正交极化回波信号模型,根据杂波的后向散射理论,提出了基于信号极化相位统计特性差异的多路径干扰检测方法。该方法不仅可以判断是否受到干扰,快速识别多路径干扰信号,还能够鉴别干扰信号的极化。通过仿真试验,验证了方法的可行性,为有效对抗多路径干扰提供了有益参考。
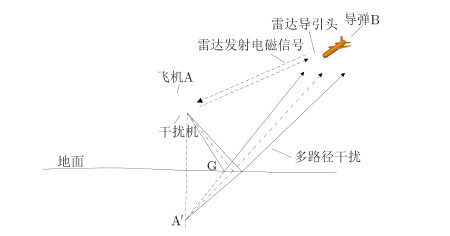
2 多路径干扰机理多路径干扰原理如图 1所示,是作战飞机在进行低空突防时如果遭遇雷达制导的硬杀伤武器,为了自卫防护常采用的一种自卫式有源电子干扰。雷达制导武器在末制导阶段多采用主动脉冲多普勒体制的导引头,在多路径干扰释放之前,作战飞机主动降低自身高度,迫使雷达导引头波束工作于下视状态。假设干扰信号在地面发生反射,当雷达导引头B向目标(A)方向发射电磁波信号,飞机A携带的机载自卫干扰设备接收、复制、放大导引头雷达信号并调制后形成干扰信号,由专用天线向地面发射,到达地面后发生反弹,产生多路径干扰。多路径干扰信号进入导引头接收系统。同时进入导引头雷达系统的信号还有目标的真实反射回波信号或 直达干扰信号。如果干扰信号功率强于目标真实反射回波信号功率,且干扰信号与目标真实反射回波所携带的一种以上信息(距离、速度、角度)之间的差别不足以使导引头雷达将干扰信号和真实反射回波信号区别开,雷达自动增益控制系统就会跟踪较强回波信号,也就是把目标回波方向判断为功率较强的BG方向,将目标确定为飞机A在地面下的镜像机A',则制导导弹的命中点将会是图 1中G点。
|
图 1 多路径干扰的原理示意图 Fig. 1 Schematic diagram of multipath interference |
多路径干扰信号从地面方向进入雷达导引头,导引头的天线波束一般都比较窄,当目标位于导引头下视或正视方向时,进入的干扰信号强度足够大。同时,多路径干扰效果除由干扰机发射功率决定外,还由地面对干扰信号的反射特性决定,在不同季节、时间、温度、照射方向条件下,其干扰效果也存在差异。可以推断,A释放干扰的时候,进入B系统的信号有两个:真实回波信号和多路径干扰信号。干扰信号是雷达发射信号经过射频存储延迟转发生成的,则干扰信号与雷达发射信号保持相干,并且当满足一定空间关系时,可以实现对速度、距离、角度3个通道的同时干扰。因此,导引头B或火控雷达就面临真假目标回波识别的问题。极化域是时域、频域、空域之外又一个可以挖掘利用的信息域,第3节给出一种新颖的基于极化技术的多路径干扰信号识别方法。
3 双极化导引头对多路径干扰的极化识别方法 3.1 多路径干扰回波信号建模干扰机发射信号照射到地面上,产生多路径干扰。发射的干扰信号最初可以是任何极化方式。但是由于地面不是像金属、玻璃一样的光滑表面,照射到地面上的任何信号都将被去极化,因此多路径干扰信号的极化相位差通常是随机的。
对于直达干扰信号,主极化和交叉极化通道的接收信号如式(1)所示:
| $\left[{\begin{array}{*{20}{c}} {{S_1}}\\ {{S_2}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\;\cos \theta }&{{\mkern 1mu} \sin \theta } \end{array}}\\ {\begin{array}{*{20}{c}} { - \sin \theta }&{\cos \theta } \end{array}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{E_y}}\\ {{E_x}} \end{array}} \right] + \left[{\begin{array}{*{20}{c}} {{n_1}}\\ {{n_2}} \end{array}} \right]$ | (1) |
式中,Ex,Ey是干扰机发射的水平和垂直极化分量信号;n1,n2是两个分量的热噪声分量;θ 是导弹的横滚角,当θ =0时,天线照射方向与导引头发射极化方向一致。一般而言,Ex,Ey是同相的线极化信号,不考虑热噪声的影响,S1,S2也应是同相的。
对于多路径干扰信号,主极化和交叉极化通道的接收信号可表示为
| $ \left[{\begin{array}{*{20}{c}} {S_1^c}\\ {S_2^x} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\;\cos \theta }&{{\mkern 1mu} \sin \theta } \end{array}}\\ {\begin{array}{*{20}{c}} { - \sin \theta }&{\cos \theta } \end{array}} \end{array}} \right]\;\left[{\begin{array}{*{20}{c}} {{c_{yy}}}&{{c_{yx}}}\\ {{c_{xy}}}&{{c_{xx}}} \end{array}} \right]\;\left[{\begin{array}{*{20}{c}} {{E_y}}\\ {{E_x}} \end{array}} \right] + \left[{\begin{array}{*{20}{c}} {{n_1}}\\ {{n_2}} \end{array}} \right] $ | (2) |
式中,cyy,cyx,cxy,cxx为地形杂波后向散射系数,系数下标的第1个字母代表发射极化,第2个字母代表接收极化。在满足互易性条件下:cyx=cxy。
根据杂波的后向散射理论可知,杂波后向散射以非相干散射为主[9],即电磁波的相位是随机的,并且在2π 区间均匀分布的,称之为非相干。杂波的散射截面积可以表示如下:
| $ \sigma = {\left| {\sum\limits_{i = 1}^n {\sqrt {{\sigma _i}} {{\rm e}^{{\rm j} \phi _i}}} } \right|^2} $ | (3) |
其中,σ i是独立散射体的RCS,Φ i是各独立散射体的相位。相位因子 ${{\rm e}^{{\rm j}{\phi _i}}}$ 包含了反射造成的相位变化,以及雷达距离导致的相位延迟。举一个简单的例子,如果所有的散射体具有同样的散射能量(即σ i=σ ),
对非相干散射,得到:
| $ \overline {{\sigma }} _{c} = \sum\limits_{i = 1}^n \sigma = n\sigma $ | (4) |
对相干散射,当所有散射体同相时,
| $ \overline \sigma = {\left| {\sum\limits_{i = 1}^n {\sqrt \sigma }} \right|^2} = {\left| {n\sqrt \sigma } \right|^2} = {n^2} \sigma $ | (5) |
因此,如果杂波区域有10个散射截面积为σ =1 m2的散射体,根据杂波的散射类型,最终杂波区的RCS会在10 m2~100 m2区间随机变化。
总的来说,杂波的散射特性取决于入射电磁波的极化,以及散射体的表面特性。杂波的极化散射矩阵用RCS表示如下:
| $ {S_c} \! = \!\! \left[\!\!\!\! {\begin{array}{*{20}{c}} {{c_{yy}}} & {{c_{yx}}} \\ {{c_{xy}}} & {{c_{xx}}} \end{array}} \!\!\! \right] \!\! = \!\! \left( \!\!\! {\begin{array}{*{20}{c}} {{{\left( {{\sigma _{\rm{HH}}}} \right)}^{1/2}} \! {\rm{e}^{{\rm j}{\phi _{\rm{HH}}}}}} & {{{\left( {{\sigma _{\rm{HV}}}} \right)}^{1/2}} \! {\rm{e}^{{\rm j}{\phi _{\rm{HV}}}}}} \\ {{{\left( {{\sigma _{\rm{VH}}}} \right)}^{1/2}} \! {\rm{e}^{{\rm j}{\phi _{\rm{VH}}}}}} & {{{\left( {{\sigma _{\rm{VV}}}} \right)}^{1/2}} \! {\rm{e}^{{\rm j}{\phi _{\rm{VV}}}}}} \end{array}} \!\!\! \right) $ | (6) |
其中,下标表示水平和垂直极化的发射和接收,单基地雷达满足收发互易性,${\left( {{\sigma _{\rm{HV}}}} \right)^{1/2}} = {\left( {{\sigma _{\rm{VH}}}} \right)^{1/2}}$ ,${\phi _{\rm{HV}}} = {\phi _{\rm{VH}}}$ ,因此该矩阵是一个对称矩阵。通常,散射表面对入射电磁波起到一定的去极化作用,例如落叶林和松树林的极化比测量值 ${\overline \sigma _{\rm{HH}}}/{\overline \sigma _{\rm{HV}}}$ 和 ${\overline \sigma _{\rm{VV}}}/{\overline \sigma _{\rm{VH}}}$ 位于3~10 dB的范围内。
地杂波参量模型提供了一种适用于有大量地面杂波试验采样数据的经验模式,可用于平均后向散射系数(σ 0),参量模型如下:
| $ {{\overset{\_}{\mathop{\sigma }}\,}^{0}}=A{{(\psi +C)}^{B}}\exp \left[\frac{-D}{(1+\frac{0.1{{\sigma }_{h}}}{\lambda })} \right] $ | (7) |
式中,Ψ 为掠射角(rad),σ h为地表面标准方差(cm),λ 为雷达波长,A,B,C和D为经验常数[10, 11]。该模型提供的 ${{\overset{\_}{\mathop{\sigma }}\,}^{0}}$ 是擦地角、表面粗糙度和频率的函数,可用于包括土壤、草地、树林、沙地、岩石、城市、雪地等多种类型的地杂波[12]。参数A,B,C和D的值可参考文献[11]。
从上述分析可以看出,多路径干扰信号的回波幅度、相位与地形特性有关,并且干扰信号主极化和交叉极化分量间的相位差是随机的,而直达干扰信号的极化相位差是确定的。通过分析接收信号的极化相位差是否服从一定的随机分布,就可以判断雷达接收信号是否受到干扰,且干扰信号是直达干扰还是多路径干扰,有助于雷达采取进一步的抗干扰措施。
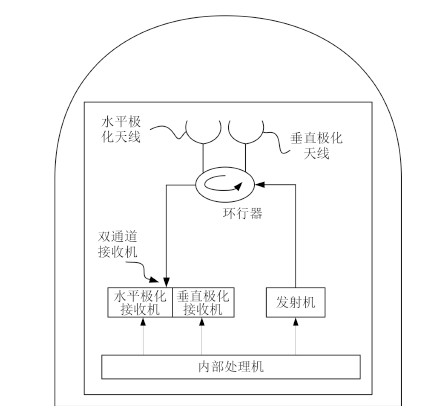
3.2 多路径干扰信号的极化识别方法利用极化相位特性,来进行多路径干扰检测,需要在雷达系统中安装正交双极化天线和双通道接收机。双极化通道接收机与正交双极化天线相连,能够同时接收回波信号的水平极化和垂直极化分量,如图 2所示。接收机的主极化通道允许接收与发射信号极化方式近似一致的回波信号,交叉极化通道接收与主极化通道相正交的信号。
|
图 2 双极化雷达导引头结构示意图 Fig. 2 Structure of dual polarization radar seeker |
将主极化和交叉极化两个接收通道的回波信号分成多个距离单元,每个距离单元相当于一个特殊的时间窗,代表目标的距离。处理器对每个距离单元进行时间采样,并对每个距离单元内的信号进行多普勒滤波组处理。类似于大多数脉冲多普勒雷达,多普勒滤波器组补偿了信号回波由于目标与雷达系统相对运动产生的多普勒频移。内部处理器根据两个通道每个距离单元的多普勒滤波器组输出的相位值,计算对应滤波器组输出的相位差;然后计算该距离单元的相位差均值和标准差。假设 ${\phi _{di}}$ 为距离单元内第i个多普勒滤波器输出的相位差,m为距离单元内多普勒滤波器个数,n为每个通道的距离单元个数,那么两接收通道在各个距离单元上的相位差均值和标准差可以通过下式计算得到:
| $ {\bar \phi _j} = {\rm{ }}\frac{{\sum\limits_{i = 1}^m {{\phi _{di}}} }}{m},\quad j = 1,2,\cdots ,n $ | (8) |
| $ {s_j} = \sqrt {\frac{{\sum\limits_{i = 1}^m {{{\left( {{\phi _{di}} - {{\bar \phi }_j}} \right)}^2}} }}{{m - 1}}} ,\quad j = 1,2,\cdots ,n $ | (9) |
然后,对所有距离单元求得的相位差均值和相位差标准差再取均值,如下式所示:
| $ \bar \phi = \left( {\sum\limits_{j = 1}^n {{{\bar \phi }_j}} } \right)/n $ | (10) |
| $ \bar s = \left( {\sum\limits_{j = 1}^n {{s_j}} } \right)/n $ | (11) |
建立如下干扰识别原则:
| $ \left\{ \begin{array}{l} \bar \phi \to 0\;{\rm{and}}\;\;\;\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\bar s \le {s_e}} \end{array}\;线极化直达干扰} \end{array}\\ \bar \phi \to 90\;{\rm{and}}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\;\;\;\bar s \le {s_e}} \end{array}{\rm{圆极化直达干扰}}} \end{array}\\ \bar s \ge m{s_e}\quad \quad \quad \quad \quad \;\;{\mkern 1mu} {\rm{地形反弹干扰}} \end{array} \right. $ | (12) |
式中,se为直达干扰相位差判定精度的经验值,m=2或3。当$\bar s $ 小于判定精度时,若 $\bar \phi $ 接近0°,则判定干扰信号为直达干扰,极化方式为线极化;若 $\bar \phi $ 接近90°,则判定干扰信号为直达干扰,极化方式为圆极化。反之,如果$\bar s $ 很大,达到了判定精度的2~3倍,则判定干扰信号为多路径干扰。
3.3 多路径干扰的识别流程设计(1) 记录发射信号极化方式
雷达导引头向期望目标发射雷达探测信号的同时其内部处理器记录发射信号的极化特性。
(2) 接收回波信号
雷达导引头通过正交双极化天线以及双通道接收机接收回波信号。接收到的回波信号可能包括真实目标回波,干扰机发射的直达干扰信号以及多路径干扰信号。接收机的主极化通道允许接收与发射信号极化方式一致的回波信号,交叉极化通道接收与主极化通道相正交的信号。
(3) 判定是否存在干扰
雷达导引头中的处理器分析接收机通道接收到信号的极化方式。期望目标的表面回波应保留发射信号的极化特征,如果交叉极化通道接收到可测的交叉极化回波信号,处理器就认为接收信号与发射信号的极化方式不同,确定存在干扰信号,并进一步判定干扰类型。否则,处理器就判定干扰不存在,继续对回波进行常规的信号处理。
(4) 确定干扰类型
一旦发现干扰存在,处理器根据接收信号的极化相位特性来识别多路径干扰。如果处理器分析接收信号相位差是随机的,就判定存在多路径干扰,否则处理就判定存在直达干扰。然后处理器启动相应的抗干扰程序,重新获取目标的真实回波。
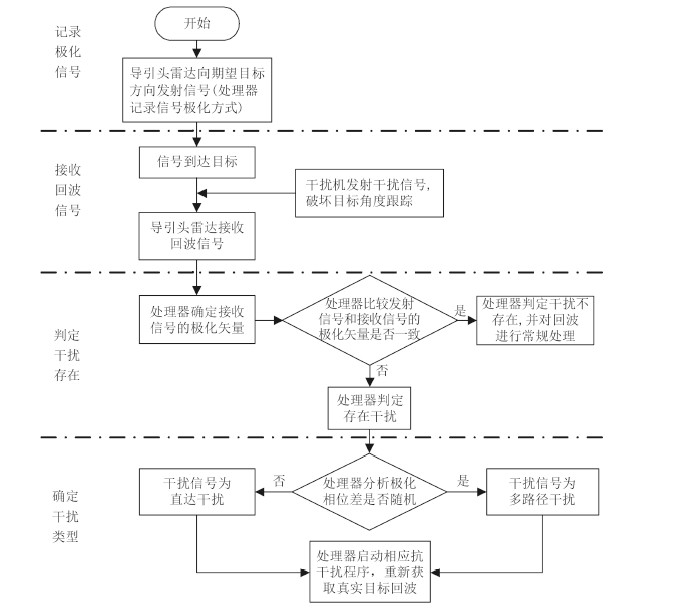
图 3所示为雷达多路径干扰极化识别方法的仿真流程。
|
图 3 极化雷达导引头对多路径干扰识别处理流程 Fig. 3 Identification processing flow of multi path jamming for polarization radar seeker |
根据本文提出的方法,进行了不同类型干扰信号下的仿真对比试验。仿真试验中,X波段雷达导引头采用高重频模式,PRF=300 kHz,脉宽为3 μs,最大占空比为0.44,迎头飞机目标RCS约为10 m2,采用数字式多普勒滤波器组,对每一个回波脉冲采用8点FFT处理,干扰机发射功率是雷达导引头发射功率的2倍,分别采用圆极化,45°线极化。弹目的水平投影距离约为20 km,图 4,图 5,图 6,图7 ,图 8,图 9为试验结果。通过试验结果对比可以看出,直达干扰信号和多路径信号的极化特征具有明显的统计特性差异,在不同的距离单元,对于直达干扰,垂直极化与水平极化信号的相位差更加集中,分布标准差较小,而对于多路径干扰,垂直极化与水平极化信号的相位差分布较广,标准差较大,可以通过本文发明方法区分这两种信号。
|
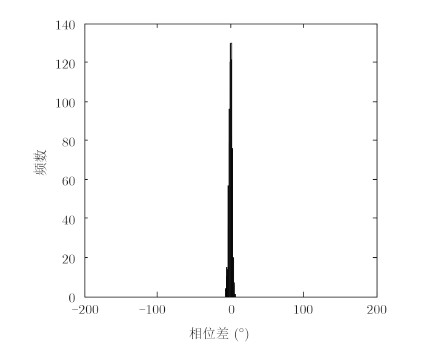
图 4 45°斜线极化直达干扰极化均值统计直方图 Fig. 4 Polarization mean histogram of 45° oblique polarization direct interference |
|
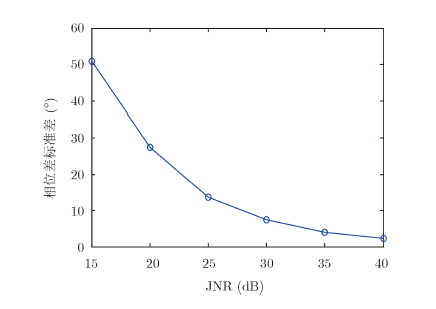
图 5 45°斜线极化直达干扰极化标准差性能曲线 Fig. 5 Standard deviation performance curve of 45° oblique polarization direct jamming |
|
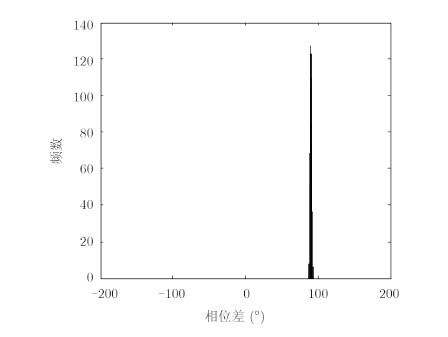
图 6 圆极化直达干扰极化均值统计直方图 Fig. 6 Polarization means histogram of circular polarization direct interference |

|
图 7 圆极化直达干扰极化标准差性能曲线 Fig. 7 Standard deviation performance curve of circular polarization direct jamming |
|
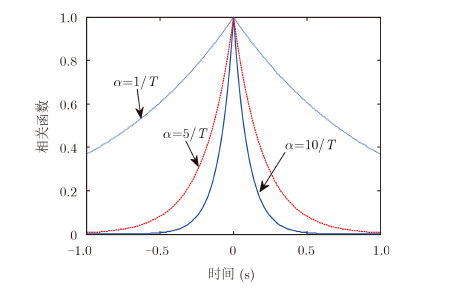
图 8 地面杂波散射系数 Fig. 8 Ground clutter scattering coefficient |

|
图 9 45°斜线极化多路径干扰极化均值统计直方图 Fig. 9 Polarization mean histogram of 45° oblique polarization multipath jamming |
图 4、图 6分别为45°斜线极化直达干扰、圆极化直达干扰在干噪比JNR=30 dB、导引头的横滚角θ =30°时,计算机仿真得到的1024个距离单元的相位差统计分布。其中,45°斜线极化时仿真结果为:相位差均值0.0153°,相位差标准差为7.4432°; 圆极化时仿真结果为:相位差均值为90.1088°,相位差标准差为3.5787°。可以看出,在1024个距离单元,直达干扰的垂直极化与水平极化信号的相位差更加集中,分布标准差较小。
图 5、图 7分别为45°斜线极化直达干扰、圆极化直达干扰相位差标准差统计值与干噪比的关系曲线,其中JNR=15~40 dB,随着干扰信号功率的不断增大,标准差统计值也由大到小逐渐趋于稳定,在5°范围内。
图 8为某地形条件下,地面杂波后向散射系数仿真结果。其中,杂波散射系数cyy,cxy,cxx服从相干复高斯分布,系数cyy幅度服从瑞利分布 $f\left( A \right) = A\exp \left( { - {A^2}/2} \right)$ ,相位服从[-π ,π]内的均匀分布 $f\left( \varphi \right) = \left\{ \begin{array}\[\frac{{\rm{1}}}{{{\rm{2\pi }}}},\; - {\rm{\pi }} \le \varphi \le {\rm{\pi }}\ 0,\;\;\;\;{\rm{else}} \end{array} \right.$ ,cyy的相关函数为 $\gamma \left( \tau \right) = {{\rm{e}}^{ - {\rm{ }}\alpha \left| \tau \right|}}$ ,$\alpha = 10/T\;$ ; cxy的相关函数为 $\gamma \left( {\tau } \right) = {{\rm{e}}^{ - {\rm{ }}\alpha \left| \tau \right|}}$ ,$\alpha = 5/T\;$ ; cxx的相关函数为 $\gamma \left( {\tau } \right) = {{\rm{e}}^{ - {\rm{ }}\alpha \left| \tau \right|}}$ ,$\alpha = 1/T\;$ 。
图 9为45°斜线极化在图 8所示地形时产生的多路径干扰。干噪比JNR=30 dB,导引头的横滚角 $\theta = {30^ \circ }$ ,计算机仿真得到的1024个距离单元的相位差统计分布,相位差均值为4.1829°,相位差标准差为87.9125°。可以看出,在1024个距离单元,多路径干扰的垂直极化与水平极化信号的相位差分布范围广,分布标准差较大。
图 10为多路径干扰相位差标准差统计值与干噪比的关系曲线,其中,JNR=15~40 dB,随着干扰信号功率的不断增大,标准差的统计值很大,且变化范围不大,保持在87°左右。
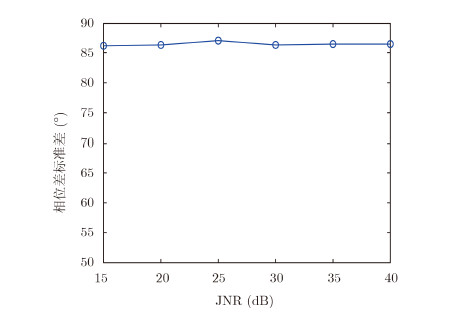
|
图 10 45°斜线极化多路径干扰极化标准差性能曲线 Fig. 10 Standard deviation performance curve of 45° oblique polarization multipath jamming |
通过大量仿真试验结果对比可以看出,直达干扰信号和多路径信号的极化相位差特征具有明显的统计特性差异,在不同的距离单元,无论是45°线极化的直达干扰,还是圆极化的直达干扰信号,其垂直极化分量与水平极化分量的相位差更加集中,且分布标准差较小。而对于多路径干扰,垂直极化与水平极化分量的相位差分布较广,标准差较大,通过本文给出的方法可以较好地识别出多路径干扰信号,并且能够识别出直达干扰信号的极化方式,这就能够改善雷达导引头适应复杂电磁环境的能力,特别是为多路径干扰条件下正确跟踪真实目标提供了有效的技术手段。
5 结论本文围绕多路径干扰展开研究,分析了多路径干扰对雷达的作用机理,建立了多路径干扰和直达干扰信号的回波信号正交极化信号模型,提出了基于信号极化相位统计特性差异的多路径干扰检测方法。该方法物理内涵清晰,算法实现简单,不仅可以判断是否受到干扰,并判断干扰信号的类型方式,还能够鉴别干扰信号的极化。通过仿真试验,验证了方法的可行性,为有效对抗多路径干扰提供了有益参考。该方法可以应用于飞机火控雷达、巡航导弹末制导雷达以及多种信号探测、识别、跟踪装置中,快速识别多路径干扰信号,提高系统的抗干扰能力。
| [1] | Wang Liandong, Dai Huanyao, and Yang Hui. A novel pulsed Doppler radar seeker modeling method used for closed loop trajectory simulation[J]. IEICE Electronics Express, 2014, 11(22): 1–10.( 1) 1) |
| [2] | 平殿发, 张伟, 苏峰. 机载对映体干扰有效性分析[J]. 雷达科学与技术, 2014, 12(3):235-239. Ping Dianfa, Zhang Wei, and Su Feng. Airborne imagejamming efficiency analysis[J]. Radar Science and Technology, 2014, 12(3):235-239.( 1) 1) |
| [3] | 李勇, 叶志铨. 对映体干扰原理及影响干扰效果的因素分析[J]. 电子信息对抗技术, 2006, 21(5):29-32. Li Yong and Ye Zhiquan. Analysis of image-jamming rationale and factors effecting the effectiveness[J]. Electronic Information Warfare Technology, 2006, 21(5):29-32.( 1) 1) |
| [4] | 高彬, 毛士艺, 孙进平, 等. 对映体干扰作战效能仿真评估[J]. 弹箭与制导学报, 2010, 30(4):223-226. Gao Bin, Mao Shiyi, Sun Jinping, et al.. Simulation measures of efficiency for terrain bounce jamming[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2010, 30(4):223-226.( 1) 1) |
| [5] | Dai H Y, Wang X S, and Li Y Z. Main-lobe jamming suppression method of using spatial polarization characteristics of antenna[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3):2167-2179.( 1) 1) |
| [6] | Dai H Y, Wang X S, Luo J, et al.. A new polarimetric method by using spatial polarization characteristics of scanning antenna[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(3):1653-1656.( 1) 1) |
| [7] | 张思远, 李永祯, 肖顺平. 空间两点源的单脉冲测角极化响应研究[J]. 雷达科学与技术, 2015, 13(5):467-472. Zhang Siyuan, Li Yongzhen, and Xiao Shunping. Polarimetric response for dual-point sources in monopulse angular measurement system[J]. Radar Science and Technology, 2015, 13(5):467-472.( 1) 1) |
| [8] | 李永祯, 胡万秋, 陈思伟, 等. 有源转发式干扰的全极化单脉冲雷达抑制方法研究[J]. 电子与信息学报, 2015, 37(2):276-282. Li Yongzhen, Hu Wanqiu, Chen Siwei, et al.. Active repeater jamming suppression using polarimetric monopulse radar[J]. Journal of Electronics & Information Technology, 2015, 37(2):276-282.( 1) 1) |
| [9] | Morris G V. Airborne Pulse Doppler Radar[M]. Beijing:Aviation Industry Publishing House, 1990, 12.( 1) 1) |
| [10] | Eaves J and Reedy E. Principles of Modern Radar[M]. New York:Van Nostrand Reinhold, 1987.( 1) 1) |
| [11] | 戴幻尧, 申绪涧, 赵晶, 等. 动目标显示与脉冲多普勒雷达[M]. 国防工业出版社, 2016, 1. Dai Huanyao, Shen Xujian, Zhao Jing, et al.. MTI and Pulsed Doppler Radar with MATLAB[M]. National Defend Industry Press, 2016, 1.( 2) 2) |
| [12] | 韦顺军, 师君, 张晓玲, 等. 基于曲面投影的毫米波InSAR数据成像方法[J]. 雷达学报, 2015, 4(1):49-59. Wei Shunjun, Shi Jun, Zhang Xiaoling, et al.. Millimeterwave interferometric synthetic aperture radar data imaging based on terrain surface projection[J]. Journal of Radars, 2015, 4(1):49-59.( 1) 1) |


