合成孔径雷达(Synthetic Aperture Radar,SAR)是当前对地观测的重要手段之一。由于具有全天候、全天时和一定的穿透成像能力,SAR已经被广泛应用于战场侦查和情报获取等领域。SAR图像自动目标识别(Automatic Target Recognition,ATR)技术可以有效获取目标信息,提高军队自动化水平。目前识别技术上常用的方法包括模板匹配法[1],支持向量机(Support Vector Machine,SVM)法[2],文献[3]中提出的基于Gabor滤波器和局部纹理特征提取的方法,文献[4]中提出的多信息字典学习和稀疏表示相结合的方法等等。但是这些方法都需要人工凭借经验进行特征提取,具有一定的盲目性和不确定性。
近年来,深度学习(Deep Learning)理论在模式识别领域掀起了一股浪潮,相关的理论和实验成果不断出现。2006年,Hinton等人[5]提出了非监督的逐层贪婪训练方法,解决了深度增加所带来的“梯度耗散”问题,使神经网络能够朝着更深的方向进行发展。随后许多学者根据不同的应用背景提出了多种DL模型,如深度置信网络(Deep Belief Network,DBN)[6]、栈式消噪自动编码机(Stacked Denoising Autoencoders,SDA)[7]和卷积神经网络(Convolutional Neural Network,CNN)[8]等。由于可以直接处理2维图像,卷积神经网络在图像识别领域取得了较多的应用,如人脸识别[9],人体行为识别[10],医学图像识别[11]等。
CNN主要有以下特点:采用原始图像作为网络输入,避免了复杂的特征提取过程;局部感受域获取的特征与图像的平移、缩放和旋转无关;权值共享结构降低了网络模型的复杂度;下采样利用局部相关性原理,在有效减少数据处理量的同时保留了结构信息[12]。CNN作为一种特征学习方法,通过非线性的简单模型将原始数据转化为更为抽象的表达,在特征学习过程中不需要过多的人工参与[13]。
本文主要研究将CNN应用于SAR图像目标识别领域,减少特征选取中的人工操作。为了进一步增强CNN所提取特征的可分性,本文尝试将类别可分性度量引入代价函数之中。为了提高CNN对特征的分类能力,利用支持向量机对CNN模型中的Softmax分类器进行替换。实验结果表明,该方法具有良好的识别分类效果,证明了其有效性。
2 卷积神经网络卷积神经网络是一种多层神经网络结构,主要由输入层、卷积层、下采样层、输出层等组成,其中卷积层和下采样层为隐含层。在卷积神经网络中,输入层用于接收原始图像;卷积层用于提取图像特征,并降低噪声的影响;下采样层利用图像局部相关性原理,减少需要处理的数据量;输出层将提取特征映射为最终所得到的标签。
图像在CNN中的映射过程是一个前向传播过程,上一层的输出作为当前层的输入。为了避免线性模型表达能力不够的问题,各层在传递时需要加入非线性的激活函数。第l层的输出可以表示为:
| $\left. \begin{array}{l} {{u}^l} = {{W}^l}{{x}^{l - 1}} + {{b}^l}\\ {{x}^l} = f\left( {{{u}^l}} \right) \end{array} \right\}$ | (1) |
式中,l表示层数,x为特征图,W为当前网络层的映射权值矩阵,b为当前网络的加性偏置项,f为激活函数。
CNN模型常用后向传播(Back Propagation,BP)算法[14]来对参数进行迭代更新。BP算法是一种常见的监督式学习方法。该算法首先利用样本的实际输出与期望输出求得代价函数,然后将代价函数反向传播至各层,最后利用梯度下降法(Gradient Descent,GD)沿着代价函数的负梯度方向调整网络中的权值和偏置等参数。
首先假设输出的目标类别维数为B,即共有B类样本,网络以均方误差作为代价函数。第n个样本的代价函数E0为:
| ${E_0} = \frac{1}{2}\sum\limits_{k = 1}^B {{{\left( {t_k^n - y_k^n} \right)}^2}} = \frac{1}{2}\left\| {{{t}^n} - {{y}^n}} \right\|_2^2$ | (2) |
式中,$t_k^n$表示第n个样本中第k个神经元所对应的期望值,$y_k^n$表示第k个神经元的实际输出值。
然后定义${{\delta }^l} = \frac{{\partial {E_0}}}{{\partial {{u}^l}}}$为第l层的灵敏度,设第L层为输出层,根据式(1)、式(2)可得输出层的灵敏度为:
| ${{\delta }^L} = f'({{u}^L}) \circ ({{y}^n} - {{t}^n})$ | (3) |
在反向传播过程中,可由第l+1层的灵敏度δl+1和式(1)得到第l层的灵敏度为:
| ${{\delta }^l} = {{W}^{l + 1}}{{\delta }^{l + 1}} \circ f'({{u}^l})$ | (4) |
完成了代价函数的反向传播之后,需要利用梯度下降法根据代价函数对网络中参数的偏导数对参数进行更新,最终使代价函数达到极小值。偏导数在此处就是$\frac{{\partial {E_0}}}{{\partial {{W}^l}}}$和$\frac{{\partial {E_0}}}{{\partial {{b}^l}}}$。
分别求E0对Wl和bl的偏导,由式(1)可得:
| $\left. \begin{array}{l} \frac{{\partial {E_0}}}{{\partial {{W}^l}}} = \frac{{\partial {E_0}}}{{\partial {{u}^l}}} \circ \frac{{\partial {{u}^l}}}{{\partial {{W}^l}}} = {{\delta }^l} \circ {{x}^{l - 1}}\\ \frac{{\partial {E_0}}}{{\partial {{b}^l}}} = \frac{{\partial {E_0}}}{{\partial {{u}^l}}} \circ \frac{{\partial {{u}^l}}}{{\partial {{b}^l}}} = {{\delta }^l} \end{array} \right\}$ | (5) |
根据梯度下降法,可以得出第l层神经元权值的更新变化量为:
| $\left. \begin{array}{l} \Delta\! {{W}^l} = - \eta \frac{{\partial {E_0}}}{{\partial {{W}^l}}}\\ \Delta \!{{b}^l} = - \eta \frac{{\partial {E_0}}}{{\partial {{b}^l}}} \end{array} \right\}$ | (6) |
为了使CNN模型所提取的特征具有更好的类别可分性,代价函数在式(2)的基础上,增加了样本的类别可分性度量[15],即类内距离与类间距离:
| ${E_1} = \frac{1}{2}\left\| {{y}_c^n - {{M}_c}} \right\|_2^2 \quad \quad \ $ | (7) |
| ${E_2} = \frac{1}{2}\sum\limits_{c' = 1}^B {\left\| {{{M}_c} - {{M}_{c'}}} \right\|_2^2} $ | (8) |
| $E = {E_0} + \alpha {E_1} - \beta {E_2}$ | (9) |
对代价函数进行修正的目的是在调整权值参数时,使网络向着有利于分类的方向进行调整,提高最终训练结果的可分性。为了使代价函数能够反向传播,需要求得修正后代价函数的灵敏度。
对于类内距离函数E1,其输出层的灵敏度为:
| $\delta _{1}^{L}=\frac{\partial {{E}_{1}}}{\partial {{u}^{L}}}=\frac{\partial }{\partial {{u}^{L}}}\frac{1}{2}\left\| y_{c}^{n}-{{M}_{c}} \right\|_{2}^{2}=\left( 1-\frac{1}{{{n}_{c}}} \right){f}'\left( {{u}^{L}} \right){}^\circ (y_{c}^{n}-{{M}_{c}})$ | (10) |
对于类间距离函数E2,其输出层的灵敏度为:
| $\begin{align} & \delta _{2}^{L}=\frac{\partial {{E}_{2}}}{\partial {{u}^{L}}}=\frac{\partial }{\partial {{u}^{L}}}\frac{1}{2}\sum\limits_{{c}'=1}^{B}{\left\| {{M}_{c}}-{{M}_{{{c}'}}} \right\|_{2}^{2}}= \\ & \frac{1}{{{n}_{c}}}{f}'({{u}^{L}}){}^\circ \sum\limits_{{c}'=1}^{B}{\left( {{M}_{c}}-{{M}_{{{c}'}}} \right)} \\ \end{align}$ | (11) |
根据式(3)、式(9)、式(10)和式(11)可以得到修正后的输出层灵敏度为:
| $\begin{align} & {{\mathbf{\delta }}^{\prime }}={{\delta }^{L}}+\alpha \delta _{1}^{L}-\beta \delta _{2}^{L}= \\ & {f}'({{u}^{L}}){}^\circ ({{y}^{n}}-{{t}^{n}})+\alpha \left( 1-\frac{1}{{{n}_{c}}} \right)\cdot \\ & {f}'({{u}^{L}}){}^\circ (y_{c}^{n}-{{M}_{c}}) \\ & -\beta \frac{1}{{{n}_{c}}}{f}'({{u}^{L}}){}^\circ \sum\limits_{{c}'=1}^{B}{\left( {{M}_{c}}-{{M}_{{{c}'}}} \right)} \\ \end{align}$ | (12) |
得到了输出层的灵敏度之后,根据式(4)即可迭代得到各层的灵敏度,再根据式(5)和式(6),可以得到各层参数的更新量。
3.2 支持向量机的使用在CNN模型中,通常利用Softmax回归模型作为分类器。该分类器通过全连接方式将CNN模型所提取特征映射为最终输出标签。这种分类方法在训练时可以有效地与反向传播过程结合,方便模型中参数的更新,但是Softmax单层全连接的方式并不能很好地解决非线性分类问题。
支持向量机[16]是Vapnik等人于1995年首先提出的,主要利用核函数将原始特征空间中的非线性分类界面隐式地映射到更高维的变换特征空间中产生线性分类界面,达到更好的分类效果[17]。SVM在解决非线性分类问题上表现优良。为解决Softmax 对非线性样本特征的支持问题,本文利用SVM代替Softmax作为CNN模型的分类器,对样本通过所有隐含层后所得特征进行分类。
4 实验结果 4.1 实验数据集为了验证本文方法的有效性,采用美国国防研究规划局(DARPA)和空军研究实验室(AFRL)联合资助的运动和静止目标获取与识别(Moving and Stationary Target Acquisition and Recognition,MSTAR)数据库进行实验。数据库中的SAR图像分辨率为0.3 m×0.3 m,目标图像大小为128×128像素。MSTAR数据库中包含了BMP2、BRDM2、BTR60、BTR70、D7、T62、T72、ZIL131、ZSU234、2S1等10类目标的SAR图像数据。实验采用17°俯仰角下的图像作为训练样本,15°俯仰角下的图像作为测试样本。
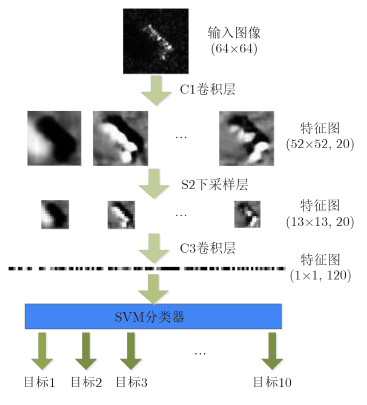
4.2 实验模型实验中用于SAR图像识别的CNN模型如图 1所示。该模型包括输入层,输出层,2个卷积层和1个下采样层。由于目标在图像中仅占据较小的部分,为了减少输入维数,我们选择截取图像中央64×64大小的部分作为模型的输入,除裁剪外,未进行其他预处理操作。卷积层采用的卷积核大小为13×13,C1卷积层神经元个数为20个,输出特征图大小为52×52。C3卷积层神经元有120个,输出特征图大小为1×1。S2下采样层局部感受域的大小为4×4,神经元个数为20个,输出特征图大小为13×13。激活函数采用的是sigmoid函数,偏置初始值设为0,学习率为1。各层权值的初始值在区间$\left[{ - 4\sqrt {\frac{6}{{{\rm{fa}}{{\rm{n}}_{{\rm{in}}}} \!+\! {\rm{fa}}{{\rm{n}}_{{\rm{out}}}}}}} ,4\sqrt {\frac{6}{{{\rm{fa}}{{\rm{n}}_{{\rm{in}}}} \!+\! {\rm{fa}}{{\rm{n}}_{{\rm{out}}}}}}} } \right]$内随机生成[18],其中fanin为各层的输入特征图个数,fanout为输出特征图个数。式(9)中的参数设置为α=0.03,β=2。实验平台为Windows 764bit+Matlab 2010。
|
图 1 本文卷积神经网络结构示意图 Fig. 1 CNN structural plan of the method |
实验中,训练样本为17°俯仰角下BMP2_SN9563、BTR70_C71、T72_SN132的SAR图像数据,测试数据为15°俯仰角下BMP2_SNC21、BMP2_SN9563、BMP2_SN9566、BTR70、T72_SN132、T72_SN812和T72_SNS7的SAR图像数据。3类目标的识别结果如表 1所示。
| 表 1 3类MSTAR目标识别结果 Tab. 1 The recognition results of three types of MSTAR targets |
从表 1可以看出,对于相同型号目标的SAR图像,本文方法的正确识别率达到了98.97%以上。对于相同类别不同型号的变体,正确识别率也都在91.62%以上。本文方法整体的平均识别率达到了95.90%。表 2中可以看出本文方法识别率优于SVM、ELM以及稀疏表示等方法。实验中,在相同条件下利用相同结构但未经改进的CNN模型进行了识别测试,得到的平均识别率为93.63%,说明本方法相较于改进前CNN模型也有一定提高。
| 表 2 与其他方法的效果对比 Tab. 2 The recognition performance compare with >other methods |
在10类目标的识别实验中,目标包括BRDM2、BMP2(BMP2_SNC21、BMP2_SN9563、BMP2_SN9566)、BTR60、BTR70、D7、ZIL131、ZSU234、T62、T72(T72_SN132、T72_SN812、T72_SNS7)、2S1等10类。训练样本为17°俯仰角下不包括变体(即不包括BMP2_SNC21、BMP2_SN9566、T72_SN812、T72_SNS7等型号)的SAR图像数据,测试样本为15°俯仰角下的包含变体的各目标SAR图像数据。识别结果如表 3。
从表 3的分类结果可以看出,本文方法10类目标分类结果仍然较好,平均识别率仍能达到93.76%。
| 表 3 10类MSTAR目标识别结果 Tab. 3 The recognition results of ten types of MSTAR targets |
针对SAR图像目标识别问题,本文提出了一种基于卷积神经网络的目标识别方法。通过在代价函数中引入类别可分性度量以及使用支持向量机代替Softmax分类器,对卷积神经网络进行了改进。利用MSTAR图像数据对该方法进行验证。结果表明,在不需要人工进行特征提取的情况下,该方法在3类目标分类实验中,达到了95.90%的识别率,在10类目标分类实验中,平均识别率仍然能达到93.76%。实验结果说明本文方法的有效性以及卷积神经网络在SAR图像目标识别上具有一定的应用潜力。
| [1] | Ross T D, Worrell S W, Velten V J, et al.. Standard SAR ATR evaluation experiments using the MSTAR public release data set[C]. Aerospace/Defense Sensing and Controls, International Society for Optics and Photonics, 1998: 566-573.( 1) 1) |
| [2] | Tao W, Xi C, Xiangwei R, et al.. Study on SAR target recognition based on support vector machine[C]. 2009 2nd Asian-Pacific Conference on Synthetic Aperture Radar, 2009: 856-859.( 1) 1) |
| [3] | 王璐, 张帆, 李伟, 等. 基于 Gabor 滤波器和局部纹理特征提取的 SAR 目标识别算法[J]. 雷达学报, 2015, 4(6): 658-665. DOI: 10.12000/JR15076. Wang Lu, Zhang Fan, Li Wei, et al.. A method of SAR target recognition based on Gabor filter and local texture feature extraction[J]. Journal of Radars, 2015, 4(6); 658-665. DOI: 10.12000/JR15076.( 1) 1) |
| [4] | 齐会娇, 王英华, 丁军, 等. 基于多信息字典学习及稀疏表示的SAR目标识别[J]. 系统工程与电子技术, 2015, 37(6): 1280-1287. Qi Huijiao, Wang Yinghua, Ding Jun, et al.. SAR target recognition based on multi-information dictionary learning and sparse representation[J]. System Engineering and Electronics, 2015, 37(6): 1280-1287.( 1) 1) |
| [5] | Hinton G E and Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507.( 1) 1) |
| [6] | Hinton G E, Osindero S, and Teh Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527-1554.( 1) 1) |
| [7] | Vincent P, Larochelle H, Lajoie I, et al.. Stacked denoisingautoencoders: learning useful representations in a deep network with a local denoisingcriterion[J]. The Journal of Machine Learning Research, 2010, 11: 3371-3408.( 1) 1) |
| [8] | Lecun Y, Bottou L, Bengio Y, et al.. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324.( 1) 1) |
| [9] | Ma Y, He J, Wu L, et al.. An effective face verification algorithm to fuse complete features in convolutional neural network[C]. MultiMedia Modeling. Springer International Publishing, 2016: 39-46.( 1) 1) |
| [10] | Ijjina E P and Mohan C K. Human action recognition based on motion capture information using fuzzy convolution neural networks[C]. 2015 Eighth International Conference on Advances in Pattern Recognition (ICAPR), Kalkata, 2015: 1-6.( 1) 1) |
| [11] | Ciompi F, de Hoop B, van Riel S J, et al.. Automatic classification of pulmonary peri-fissural nodules in computed tomography using an ensemble of 2D views and a convolutional neural network out-of-the-box[J]. Medical Image Analysis, 2015, 26(1): 195-202.( 1) 1) |
| [12] | 尹宝才, 王文通, 王立春. 深度学习研究综述[J]. 北京工业大学学报, 2015, 41(1): 48-59. Yin Bao-cai, Wang Wen-tong, and Wang Li-chun. Review of deep learning[J]. Journal of Beijing University of Technology, 2015, 41(1): 48-59.( 1) 1) |
| [13] | Lecun Y, Bengio Y, and Hinton G. Deep Learning[J]. Nature, 2015, 521(7553): 436-444.( 1) 1) |
| [14] | Rumelhart D E, Hinton G E, and Williams R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323(6088): 533-536.( 1) 1) |
| [15] | 孙艳丰, 齐光磊, 胡永利, 等. 基于改进 Fisher 准则的深度卷积神经网络识别算法[J]. 北京工业大学学报, 2015, 41(6): 835-841. Sun Yanfeng, Qi Guanglei, Hu Yongli, et al.. Deep convolution neural network recognition algorithm based on improved fisher criterion[J]. Journal of Beijing University of Technology, 2015, 41(6): 835-841.( 1) 1) |
| [16] | Cortes C and Vapnik V. Support-vector networks[J]. Machine Learning, 1995, 20(3): 273-297.( 1) 1) |
| [17] | 孙即祥, 等. 现代模式识别[M]. 北京: 高等教育出版社, 2008: 624-625. Sun Jixiang, et al.. Pattern Recognition[M]. Beijing: Higher Education Press, 2008: 624-625.( 1) 1) |
| [18] | Glorot X and Bengio Y. Understanding the difficulty of training deep feedforward neural networks[J]. Journal of Machine Learning Research, 2010, 9: 249-256. ( 1) 1) |


