目标极化散射矩阵能够完整地描述雷达目标电磁散射特性,通常具有复数形式,并随着工作频率和目标姿态而变化[1]。从目标极化散射矩阵出发,可以得到一系列用于目标分类与识别的极化特征量,能够有效地提高雷达目标分类和识别等能力。高精度的目标极化散射矩阵测量是提高极化信息应用潜力的前提和基础。
近年来,全极化相控阵雷达成为气象探测、防空预警和舰载多功能等雷达的重要发展趋势。2006年,美国联邦航空局、国家海洋与大气局和海军研究局三家联合资助并起草了全极化多功能相控阵雷达的研制计划[2, 3],用以气象监测、空中交通管制和服务于国家安全等。在全极化相控阵雷达发展需求牵引下,国内外相关学者开始关注相控阵雷达的极化测量技术研究[4, 5, 6, 7, 8, 9, 10, 11]。2009年,俄克拉荷马州立大学的Zhang等人[4, 5]采用正交电偶极子阵元模型,研究了分时和同时极化测量体制下的气象目标极化参数估计误差的校准方法;2011年,在Zhang 的正交偶极子理论模型基础上,Zrnic等人[7]研究了气象目标极化参数估计与多普勒参数的耦合问题;2013年,Lei等人[6]将Zhang的正交偶极子平面相控阵理论模型进一步扩展为理想的口径天线和全极化微带阵元。上述研究大多以理想的全极化阵元为天线模型,并假设目标的极化散射特性不随相控阵雷达波束指向的变化而改变,其极化测量方法的适用范围有限。
实际上,相控阵雷达波束指向角的变化会给雷达极化测量方程带来两个方面的影响:一方面,雷达坐标下的极化基会随波束指向角的变化而改变,导致目标呈现在雷达坐标系下的极化散射特性会发生变化;另一方面,全极化相控阵雷达天线的极化特性同样会随着波束指向角的变化而改变[10, 11]。上述两个方面的影响将导致相控阵雷达目标观测极化散射矩阵成为波束指向角的函数。论文将综合考虑上述两个因素,结合准确的全极化相控阵雷达天线空域极化特性和目标极化散射特性模型,建立更为精确的全极化相控阵雷达目标观测方程,利用典型的简单形体目标和阵元模型,分析波束扫描角对目标极化散射特性、天线极化特性和雷达观测极化散射矩阵的影响。
2 全极化相控阵雷达目标观测方程假设全极化相控阵雷达天线水平(H)和垂直(V)极化端口的发射信号分别为xh和xv,那么,雷达的接收信号可以表示为:
| $ \begin{array}{l} r = \left[ {\begin{array}{*{20}{c}} {{r_{\rm{h}}}}\\ {{r_{\rm{v}}}} \end{array}} \right] = {G_r}(\theta ,\phi )S(\theta ,\phi ){G_t}(\theta ,\phi )x\;\; = \;\tilde S(\theta ,\phi )x = \left[ {\begin{array}{*{20}{c}} {{{\tilde s}_{{\rm{hh}}}}(\theta ,\phi )}&{{{\tilde s}_{{\rm{hv}}}}(\theta ,\phi )}\\ {{{\tilde s}_{{\rm{vh}}}}(\theta ,\phi )}&{{{\tilde s}_{{\rm{vv}}}}(\theta ,\phi )} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_{\rm{h}}}}\\ {{x_{\rm{v}}}} \end{array}} \right] \end{array} $ | (1) |
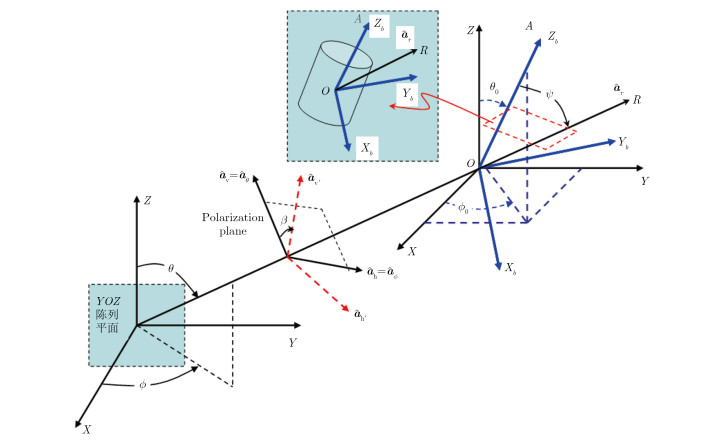
其中,θ和φ分别为天线波束指向的俯仰角和方位角(如图 1所示),S是定义在雷达坐标系下的目标极化散射矩阵,包含了目标局部坐标系和雷达坐标系下的角度和极化基变换,rh和rv分别为H和V极化通道的接收信号,$\tilde S = {G_r}S{G_t}$是包含了雷达天线响应的目标极化散射矩阵,Gr和Gt分别为全极化相控阵雷达接收和发射天线的极化辐射矩阵,通常假设两者互易相等,即${{G}}_{r}^{} = {{G}}_t^{\rm{T}}$。
|
图 1 目标与雷达阵面坐标系 Fig. 1 Target and radar coordinate systems |
对于分时极化测量,采用连续两个发射脉冲完成对目标极化散射矩阵所有元素的测量,则连续两个发射脉冲信号分别为${{{x}}_1} = {[\begin{array}{*{20}{c}} \!\! {{x_{\rm{h}}}} \! & \! 0 \!\! \end{array}]^{\rm{T}}}$和${{{x}}_2} = {[\begin{array}{*{20}{c}} \!\! 0 \! & \! {{x_{\rm{v}}}} \!\! \end{array}]^{\rm{T}}}$,每个脉冲测量得到极化散射矩阵的一列元素;对于同时极化测量,采用两正交极化天线同时发射、同时接收的工作方式,通过两发射信号之间的正交性来实现散射矩阵中不同元素的分离,能够在一个脉冲内完成目标极化散射矩阵所有元素的测量,即单个脉冲发射的信号为${{x}} = {[\begin{array}{*{20}{c}} \!\! {{x_{\rm{h}}}} \!\! & \! {{x_{\rm{v}}}} \!\! \end{array}]^{\rm{T}}}$。
式(1)仅仅为相控阵雷达的电压接收方程,实际上雷达的极化测量性能还与发射波形、发射和接收通道特性等因素有关[12]。论文重点考虑全极化相控阵雷达波束扫描对雷达观测方程的影响,而忽略极化测量体制、发射波形、通道一致性等不随波束扫描而改变的影响因素,将全极化相控阵雷达的目标观测极化散射矩阵定义为:
| $ \tilde S(\theta,\phi) = {{{G}}^{\rm{T}}}(\theta,\phi){{S}}(\theta,\phi){{G}}(\theta,\phi) $ | (2) |
其中,${{G}}(\theta,\phi)$为全极化相控阵雷达天线的极化辐射矩阵,${{S}}(\theta,\phi)$是与雷达天线极化基定义相同的目标极化散射矩阵。${{G}}(\theta,\phi)$和${{S}}(\theta,\phi)$都是雷达波束指向角的函数,将随波束扫描角度的变化而变化,这一变化特性在传统相控阵雷达目标极化信息的获取与应用中通常被忽略。随着目标极化识别等应用的深入开展,雷达对目标极化特性的获取精度要求越来越高。全极化相控阵雷达的目标观测极化散射矩阵随波束指向角的变化规律是建立极化精密测量方程的基本依据,将成为影响目标极化测量性能的重要因素。
3 波束指向角对目标观测极化散射矩阵的影响由式(2)可知,目标观测极化散射矩阵$\tilde S(\theta,\phi)$ 由${{G}}(\theta,\phi)$和${{S}}(\theta,\phi)$两部分共同决定,下面将建立统一的雷达观测坐标系,对两者分别进行分析。
3.1 目标极化散射矩阵以目标质心O为原点,建立雷达发射坐标系OXYZ,全极化相控阵天线阵列位于YOZ平面内,雷达视线方向为OR,其球坐标系的单位矢量为$ ({{{\hat {{a}}}}_r},{{{\hat {{a}}}}_\theta },{{{\hat {{a}}}}_\phi })$,如图 1所示。将相控阵雷达的垂直和水平极化分别定义为:${{\hat {{a}}}_{\rm{v}}} = - {{{\hat {{a}}}}_\theta}$,$ {\hat {a}}_{\rm{h}} = {\hat {a}}_\phi $。假设目标的对称轴OA与Z轴的夹角为q0,其在OXY平面的投影与X轴的夹角为f0。现以对称轴OA为Zb轴,建立目标坐标系OXbYbZb,它是由OXYZ坐标系经过两次欧拉角旋转得到的:首先将OXYZ绕Z轴旋转φ0,再将新坐标系绕Y轴旋转θ0。
根据目标与雷达坐标系之间的变换关系,可以得到雷达视线OR在球坐标系下的单位矢量$ ({{{\hat {{a}}}}_r},{{{\hat {{a}}}}_\theta },{{{\hat {{a}}}}_\phi })$与$({{{\hat {{a}}}}_{xb}},{{{\hat {{a}}}}_{yb} },{{{\hat {{a}}}}_{zb}})$的关系可表示为[9]:
| $ \left[{\begin{array}{*{20}{c}} {{\rm{ }}{{\hat a}_r}}\\ {{{\hat a}_\theta }}\\ {{{\hat a}_\phi }} \end{array}} \right] = {\bf{Q}} \left[{\begin{array}{*{20}{c}} {{{\hat a}_{xb}}}\\ {{{\hat a}_{yb}}}\\ {{{\hat a}_{zb}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{q_{11}}}&{{q_{12}}}&{{q_{13}}}\\ {{q_{21}}}&{{q_{22}}}&{{q_{23}}}\\ {{q_{31}}}&{{q_{32}}}&{{q_{33}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{{\hat a}_{xb}}}\\ {{{\hat a}_{yb}}}\\ {{{\hat a}_{zb}}} \end{array}} \right] $ | (3) |
其中
| $ {\begin{array}{*{20}{c}} {q_{11}} = {\rm{sin}} \theta {\rm{cos}}{\theta _0}{\rm{cos}} (\phi - {\phi _0}) {\rm{ - cos}}\theta {\rm{sin}}{\theta _0} \hspace{25pt} \\ {q_{12}} = {\rm{sin}} \theta {\rm{sin}} (\phi - {\phi _0}) \hspace{98pt} \\ {q_{13}} = {\rm{sin}} \theta {\rm{sin}}{\theta _0}{\rm{cos}} (\phi - {\phi _0}) {\rm{ + cos}}\theta {\rm{cos}}{\theta _0} \hspace{23pt}\\ {q_{21}} = {\rm{cos}} \theta {\rm{cos}}{\theta _0}{\rm{cos}} (\phi - {\phi _0}) + {\rm{sin}}\theta {\rm{sin}}{\theta _0}\hspace{17pt}\\ {q_{22}} = {\rm{cos}}\theta \sin (\phi - \phi _0) \hspace{93pt} \\ {q_{23}} = {\rm{cos}}\theta {\rm{sin}}{\theta _0}{\rm{cos}} (\phi - {\phi _0}) - {\rm{sin}}\theta {\rm{cos}}{\theta _0} \hspace{17pt} \\ {q_{31}} = - {\rm{cos}}{\theta _0}{\rm{\sin}} (\phi \! - \! {\phi _0}),\ \,{q_{32}} = {\rm{cos}} (\phi \! - \! {\phi _0})\\ {q_{33}} = - {\rm{sin}}{\theta _0} {\rm{\sin}} (\phi - {\phi _0}) \hspace{82pt} \\ \end{array}} $ |
将目标对称轴OA方向的单位矢量${{{\hat {{a}}}}_{OA}}$表示为${{{\hat {{a}}}}_{OA}} = {{{\hat {{a}}}}_{zb}}$,那么,雷达视线OR与目标对称轴OA的夹角$\psi $为:
| $ \begin{align} \cos \psi & = {{\hat {a}}_{OA}}{{\hat {a}}_r} = {q_{13}}\\ & = {\rm{sin}}\theta {\rm{sin}}{\theta _0}{\rm{cos}} (\phi - {\phi _0}) + {\rm{cos}}\theta {\rm{cos}}{\theta _0} \end{align} $ | (4) |
如图 2所示,${{OA'}}$为目标对称轴OA在极化平面的投影,其单位矢量${{{\hat {{a}}}}_{OA'}}$与${{{\hat {{a}}}}_\theta}$的夹角b可表示为:

|
图 2 雷达观测极化基与目标对称轴之间的关系 Fig. 2 The relationship between radar observation polarization bases with symmetry axis of target |
| $ \tan \beta = \frac{{{{\hat {a}}}_{OA'}}\cdot{{\hat {a}}_\phi}}{{{{\hat {a}}}_{OA'}}\cdot{{{\hat {a}}}_\theta}} = \frac{{{\rho _\phi }}}{{{\rho _\theta}}} $ | (5) |
其中
| $ {\begin{array}{1} {\rho _\theta} \! = \! {q_{21}}{\rho \! _{xb}} \! + \! {q_{22}}{\rho \! _{yb}} \! + \! {q_{23}}{\rho \! _{zb}} ,\ {\rho _\phi} \! = \! {q_{31}}{\rho \! _{xb}} \! + \! {q_{32}}{\rho \! _{yb}} \! + \! {q_{33}}{\rho \! _{zb}}\\ {\rho \! _{xb}} \! = \! \frac{- \! {q_{11}}\cos \! \psi }{\sin \! \psi } \! ,\ {\rho \! _{yb}} \! = \! \frac{- \! {q_{12}}\cos \! \psi }{\sin \! \psi } \! ,\ {\rho \! _{zb}} \! = \! \frac{1 \! - \! {q_{13}}\cos \! \psi }{\sin \! \psi } \ \end{array}} $ |
现将雷达观测极化基$({{{\hat {{a}}}}_{\rm{v}}},{{{\hat {{a}}}}_{\rm{h}}})$旋转角度β,得到新的一组极化基$({{{\hat {{a}}}}_{{\rm{v'}}}},{{{\hat {{a}}}}_{{\rm{h'}}}})$,其中${{{\hat {{a}}}}_{{\rm{v'}}}} = {{{\hat {{a}}}}_{{{OA'}}}}$。假设目标旋转对称,那么,在$({{{\hat {{a}}}}_{{\rm{v'}}}},{{{\hat {{a}}}}_{{\rm{h'}}}})$极化基的观测下,目标的极化散射矩阵为:
| $ {{{{{S}}'}}\!_{{\rm{h'v'}}}}(\psi ) = \left[{\begin{array}{*{20}{c}} {{{s'}\!_{{\rm{h'h'}}}}(\psi )} & 0\\ 0 & {{{s'}_{{\rm{v'v'}}}}(\psi )} \end{array}} \right]$ | (6) |
根据极化基变换可以得到目标在雷达观测极化基$({{{\hat {{a}}}}_{\rm{v}}},{{{\hat {{a}}}}_{\rm{h}}})$下的散射矩阵:
| $\begin{aligned} {{{S}}_{{\rm{hv}}}}(\theta,\phi) = & {{{S}}_{{\rm{hv}}}}(\psi ,\beta ) = \left[\!\! {\begin{array}{*{20}{c}} {{s_{{\rm{hh}}}}} & {{s_{{\rm{hv}}}}}\\ {{s_{{\rm{vh}}}}} & {{s_{{\rm{vv}}}}} \end{array}} \!\! \right]\\ = & \! {{R}}( - \beta ) \!\! \left[\!\! {\begin{array}{*{20}{c}} {{{s'}_{{\rm{h'h'}}}}(\psi )} & 0\\ 0 & {{{s'}_{{\rm{v'v'}}}}(\psi )} \end{array}} \!\! \right] \! {{R}}(\beta ) \end{aligned}$ | (7) |
其中
| $ {{R}}(\beta ) = \left[{\begin{array}{*{20}{c}}{\cos \beta } & { - \sin \beta }\\{\sin \beta } & {\cos \beta }\end{array}} \right],\ \beta = {\rm{atan}} ({{{\rho _\phi }} \mathord{\left/ {\vphantom {{{\rho _\phi }} {{\rho _\theta }}}} \right.} {{\rho _\theta }}}),$ |
| $\psi = {\rm{acos}} (\sin\theta \sin{\theta _0}\cos(\phi - {\phi _0})+ \cos \theta \cos {\theta _0}),$ |
R(β)为雷达测量极化基$({{{\hat {{a}}}}_{\rm{v}}},{{{\hat {{a}}}}_{\rm{h}}})$ 与目标本地极化基$({{{\hat {{a}}}}_{{\rm{v'}}}},{{{\hat {{a}}}}_{{\rm{h'}}}})$之间的旋转转换矩阵,并且有${{{R}}^{ - 1}}(\beta ) = {{{R}}^{\rm{T}}}(\beta ) = {{R}}( - \beta )$。
由上述分析可知,目标在相控阵雷达坐标系下的极化散射矩阵Shv(θ,φ)的求解过程为:
步骤1 已知目标姿态角为(θ0,φ0),雷达波束扫描角为(θ,φ),由式(4)和式(5)分别求解得到雷达视线OR与目标对称轴OA的夹角y和极化基旋转角度β。
步骤2 已知旋转对称目标在本地目标坐标系下的极化散射矩阵$ {{{{{S}}'}}_{{\rm{h'v'}}}}(\psi )$,根据式(7)和步骤1求解得到的(φ,β),得到目标在相控阵雷达坐标系下的极化散射矩阵Shv(θ,φ)。
3.2 全极化相控阵天线极化辐射矩阵对于全极化平面相控阵天线,根据迭加原理可以得到其合成的全极化方向图特性为:
| $\begin{aligned} {{G}}(\theta,\phi) = & \left[\!\! {\begin{array}{*{20}{c}} {g_{{\rm{hh}}}^{} (\theta,\phi)} & {g_{{\rm{hv}}}^{} (\theta,\phi)}\\ {g_{{\rm{vh}}}^{} (\theta,\phi)} & {g_{{\rm{vv}}}^{} (\theta,\phi)} \end{array}} \!\! \right]\\ = & \sum\limits_{m = 1}^M \sum\limits_{n = 1}^N {w_{m,n}^{} \exp ({\rm{j}}k{{{{\hat {{a}}}}}_r}} \cdot {{{R}}_{m,n}})\\ & \cdot {{{G}}_{m,n}}(\theta,\phi) \end{aligned}$ | (8) |
其中,${{{R}}_{m,n}} = {{{\hat {{a}}}}_y}(m - 1){d_y} + {{{\hat {{a}}}}_z}(n - 1){d_z}$为第m行、n列阵元的位置矢量,dy和dz分别为阵元沿y轴和z轴方向的间距,Gm,n(θ,φ)为雷达坐标系下第m行、n列阵元的极化辐射矩阵,wm,n为阵元端口的激励系数(这里假设全极化阵元的H和V极化端口加权系数相同)。
忽略阵元间的互耦影响,并假设所有阵元的极化辐射矩阵都是相同的,即${{{G}}_{m,n}}(\theta,\phi) = {{{G}}_e}(\theta,\phi)$,全极化相控阵天线极化辐射矩阵可以进一步表示为:
| ${{G}}(\theta,\phi) = AF(\theta,\phi){{{G}}_e}(\theta,\phi) \hspace{55pt}$ | (9) |
| $\begin{aligned} AF(\theta,\phi) = & \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {\exp \left( {{\rm{j}}k\left( {{d_y}V\left( {m - 1} \right)} \right.} \right.} } \\ & \left. {\left. { + {d_z}W\left( {n - 1} \right)} \right)} \right)w_{m,n}^{} \end{aligned}$ | (10) |
其中,AF(θ,φ)为阵列因子,$ V = \sin \theta \sin \phi $和$ W = \cos \theta $是方向余弦,${{{G}}_e}(\theta,\phi)$为阵元的极化辐射矩阵。由式(10)可以看出,如果所有阵元的辐射特性相同,全极化相控阵天线极化辐射矩阵可以简化为阵列因子和阵元极化辐射矩阵的乘积。在这种情况下,由于阵列因子为标量,对矩阵${{{G}}_e}(\theta,\phi)$中所有元素的影响相同,因此,全极化相控阵天线合成波束的极化特性可以等效为阵元的极化特性。
对于沿y轴和z轴方向放置的半波长正交电偶极子阵元,理想情况下的阵元极化辐射矩阵${{{G}}_e}(\theta,\phi)$可以表示为[9]:
| $ {{{G}}_e}(\theta,\phi) \!=\! \left[\!\!\! {\begin{array}{*{20}{c}} {\cos \phi {f_y}(\theta,\phi)} & 0\\ { -\! \cos \theta \sin \phi {f_y}(\theta,\phi)} & {\sin \theta {f_z}(\theta,\phi)} \end{array}} \!\!\! \right]$ | (11) |
其中,fy(θ,φ)和fz(θ,φ)分别为y和z轴方向电流元辐射电场的空间因子,分别可以表示为:
| $\begin{aligned} {f\!_y}(\theta,\phi) \! = \! \frac{{\cos \! \left( {{\Large\frac{\rm{\pi }}{2}} \sin \! \theta \sin \! \phi } \right)}}{{1 - {{\sin }^2} \! \theta {{\sin }^2} \! \phi}},\ {f\!_z}(\theta,\phi) \! = \! \frac{{\cos \! \left( {{\Large\frac{\rm{\pi }}{2}}\cos \! \theta } \right)}}{{1 - {{\cos }^2} \! \theta }} \end{aligned}$ |
下面选取雨滴为目标,半波长正交电偶极子阵元为全极化相控阵阵元,分析波束指向角对目标极化散射矩阵、全极化相控阵天线极化辐射矩阵和雷达观测极化散射矩阵的影响。
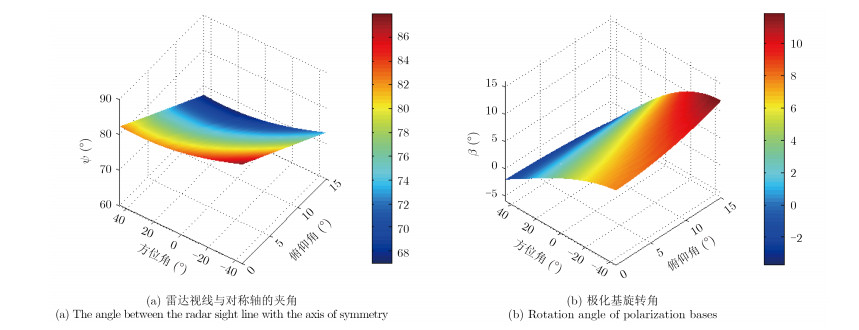
4.1 雨滴目标极化散射特性分析将雨滴目标的的姿态角设置为(θ0,φ0)=(8°,30°),俯仰角定义为90°-θ,方位角定义为φ。图 3给出了(φ,β)随雷达波束指向角的变化规律。由图可见,在不同雷达波束扫描角度下的(y,b)各不相同,将导致在相控阵雷达观测极化基下,不同波束指向角下的目标极化散射特性各不相同。
|
图 3 (Ψ, β)随波束指向角的变化关系 Fig. 3 The changes of angles (Ψ, β) in the relationship with the beam pointing angle |
下面以雨滴为例,分析相控阵雷达观测坐标系下的目标极化散射特性。对于单个雨滴粒子目标,差分反射率(differential reflectivity)定义为${Z_{{\rm{dr}}}} = 10{\lg}$ $\left( {{{{{\left| {{s_{{\rm{hh}}}}} \right|}^2}} \mathord{\left/ {\vphantom {{{{\left| {{s_{{\rm{hh}}}}} \right|}^2}} {{{\left| {{s_{{\rm{vv}}}}} \right|}^2}}}} \right.} {{{\left| {{s_{{\rm{vv}}}}} \right|}^2}}}} \right)$,线性去极化比(linear depolarization ratio)定义为${\rm{LD}}{{\rm{R}}_{{\rm{vh}}}} = 10\lg \left( {{{\left| {{s_{{\rm{vh}}}}} \right|}^2}/{{\left| {{s_{{\rm{hh}}}}} \right|}^2}} \right)$
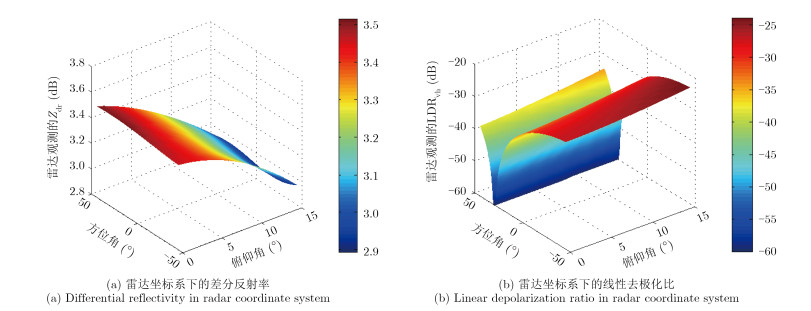
假设在目标坐标系下,当电磁波的入射角φ=90°时,雨滴的极化散射参数为Zdr=3.6 dB和svh=0 (LDRvh=-$\infty $),雨滴的姿态角仍设置为(θ0,φ0)= (8°,30°)。图 4给出了在雷达坐标系下,单个雨滴粒子的Zdr和LDRvh随相控阵雷达波束扫描角的变化情况。由图可见,在雷达观测坐标系下,俯仰角0°~15°,方位角-45°~45°范围内雨滴的Zdr取值范围为2.9~3.5 dB,LDRvh的最大值为-25 dB。
|
图 4 雷达坐标系下雨滴极化散射矩阵随波束扫描角的变化规律 Fig. 4 Raindrops polarization scattering matrix variation with beam scanning angle in radar coordinate system |
当阵列中所有阵元的辐射特性相同时,全极化相控阵天线极化辐射特性可以等效为阵元的极化辐射特性。图 5所示为理想情况下、沿y轴和z轴方向放置的半波长正交电偶极子的全极化辐射电场随俯仰角和方位角的变化情况,其中俯仰角的扫描范围为0°~15°,方位角的范围为-45°~45°。y方向电偶极子的交叉极化方向图gvh随着方位角和俯仰角的增大而逐渐增大,在上述波束扫描角度范围内,最大的交叉极化达到-20 dB。两主极化方向图ghh和gvv在俯仰角0°~15°和方位角-45°~45°内的变化较小,其起伏量分别为4.0 dB和0.7 dB。

|
图 5 半波长正交电偶极子的极化辐射电场 Fig. 5 The polarized radiation field of orthogonal half-wavelength dipole |
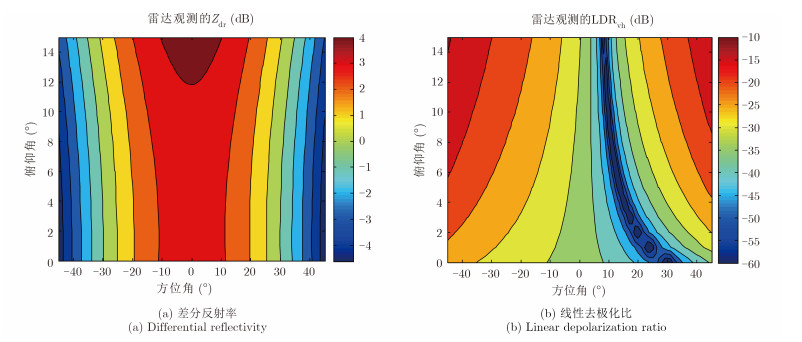
仍然选取雨滴在目标自身坐标系下的极化散射参数为Zdr=3.6 dB和svh=0 (LDRvh=-$\infty $),雨滴的姿态角(θ0,φ0)=(8°,30°),全极化相控阵天线同样采用半波长正交电偶极子为阵元。图 6给出了在雷达坐标系下,全极化相控阵雷达观测得到的单个雨滴粒子的Zdr和LDRvh随相控阵雷达波束扫描角的变化情况,其中俯仰角的扫描范围为0°~30°,方位角的范围为-45°~45°。由图可见,在全极化相控阵雷达探测条件下,雨滴的观测极化散射矩阵将受目标本身极化散射特性和雷达天线极化特性两方面的影响(如4.1节和4.2节分析),雷达观测得到的雨滴Zdr取值范围为-4~4 dB,LDRvh的最大值为-10 dB。可以看出,在全极化相控阵雷达观测条件下,就算目标的姿态固定,在不同波束指向角得到的目标观测极化散射特性会各不相同,与定义在目标本身坐标系的极化散射特性差异明显,这给全极化相控阵雷达极化信息的精确获取和应用带来了很多困难。
|
图 6 相控阵雷达观测得到的雨滴极化散射特性(θ0,φ0)= (8°, 30°) Fig. 6 Raindrops polarization scattering characteristics observed by phased array radar when (θ0,φ0)= (8°, 30°) |
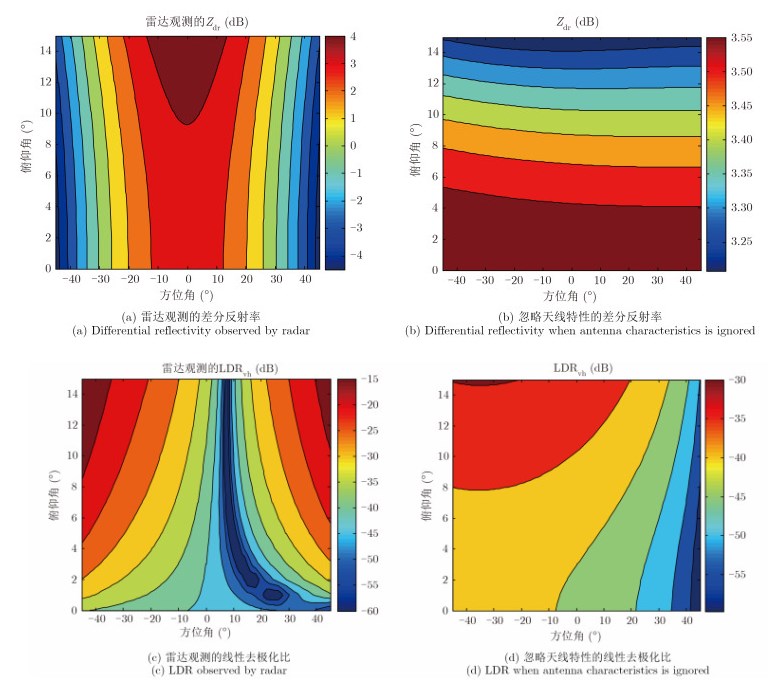
现将雨滴的姿态角设置为(θ0,φ0)=(2°,50°),图 7(a)和图 7(c)分别给出了雷达观测得到的Zdr和LDRvh随方位角和俯仰角的变化情况,与倾斜角(θ0,φ0)= (8°,30°)相比,目标的倾斜角度改变对雷达观测的Zdr取值范围影响不大,而LDRvh的最大值减小为-15 dB。
|
图 7 相控阵雷达观测得到的雨滴极化散射特性(θ0,φ0)=(2°, 50°) Fig. 7 Raindrops polarization scattering characteristics observed by phased array radar when (θ0,φ0)=(2°, 50°) |
如果忽略相控阵雷达天线的极化特性对雷达目标观测极化散射矩阵的影响,仅仅考虑波束指向角改变引起的极化基旋转,得到雷达观测的Zdr和LDRvh分别如图 7(b)和图 7(d)所示。可以看出,在俯仰角0°~15°和方位角-45°~45°内,如果忽略全极化相控阵天线极化特性的影响,Zdr离真值3.6 dB的差值小于0.4 dB,LDRvh最大值也仅仅为-30 dB,远远小于考虑天线极化特性的-15 dB。由此可见,对于雨滴这种简单形体目标,当目标的初始姿态角较小时,全极化相控阵天线的极化特性对目标观测极化散射矩阵的影响起主要作用。总体而言,随着波束扫描角度的增大,相控阵天线的交叉极化将逐渐增大,加之受雷达观测极化基变化的影响,全极化相控阵雷达得到的目标观测极化散射矩阵将越偏离目标极化散射矩阵的真实值。
5 结束语目标极化散射矩阵的精确测量是全极化相控阵雷达极化信息处理的前提和基础。相控阵雷达天线的极化特性随波束扫描角度的变化而改变,天线交叉极化会随方位角和俯仰角的增大而显著增大,将严重影响相控阵雷达极化测量的性能。另外,在不同的波束指向下,定义在雷达坐标系下的目标极化散射矩阵同样会发生变化。针对上述问题,论文从目标坐标系和雷达坐标系的转换关系出发,结合目标极化散射矩阵和雷达天线极化特性,建立了全极化相控阵雷达目标极化测量方程,分析了目标极化散射特性、雷达天线极化特性和雷达目标观测极化散射特性随波束指向角的变化规律,为全极化相控阵雷达极化信息的精确获取及应用提供了更为准确的数学模型。
| [1] | 黄培康, 殷红成, 许小剑. 雷达目标特性[M]. 北京: 电子工业出版社, 2003: 155–159.Huang Pei-kang, Yin Hong-cheng, and Xu Xiao-jian. Radar Target Characteristics[M]. Beijing: Publishing House of Electronics Industry, 2003: 155–159.( 1) 1) |
| [2] | Weadon M, Heinselman P L, Forsyth D, et al. Multifunction phased-array radar[J]. Bulletin of the American Mathematial Society, 2009, 90(3): 385–389.( 1) 1) |
| [3] | Weber M E, Cho J Y N, Herd J S, et al. The next generation multi-mission U. S. surveillance radar network[J]. Bulletin of the American Mathematial Society, 2007, 88(11): 1739–1751.( 1) 1) |
| [4] | Zhang G, Doviak R J, Zrnic D S, et al. Phase array radar polarimetry for weather sensing: a theoretical formulation for bias corrections[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(11): 3679–3689.( 2) 2) |
| [5] | Zhang G, Doviak R J, Zrnic D, et al. Phased array radar polarimetry for weather sensing: challenges and opportunities[C]. 2008 IEEE IGARSS, Boston, MA, 2008: 449–452.( 2) 2) |
| [6] | Lei L, Zhang G, and Doviak R J. Bias correction for polarimetric phased-array radar with idealized aperture and patch antenna elements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1): 473–486.( 2) 2) |
| [7] | Zrnic D S, Zhang G, and Doviak R J. Bias correction and Doppler measurement for polarimetric phased-array radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(2): 843–853.( 2) 2) |
| [8] | 李棉全, 李永祯, 董健, 等. 正交偶极子阵列天线的空域极化特性[J]. 电波科学学报, 2012, 27(2): 396–401.Li Mian-quan, Li Yong-zhen, Dong Jian, et al. Polarization characteristics analysis of crossed dipoles[J]. Chinese Journal of Radio Science, 2012, 27(2): 396–401.( 1) 1) |
| [9] | 李棉全. 全极化相控阵雷达精密测量技术[D]. [博士论文], 国防科技大学, 2013: 122–160.Li Mian-quan. Precision measurement technology for fully polarimetric phased array radar[D]. [Ph.D. dissertation], National University of Defense Technology, 2013: 122–160.( 3) 3) |
| [10] | 罗佳, 王雪松, 李永祯, 等. 天线空域极化特性的表征及分析[J]. 电波科学学报, 2008, 23(4): 620–628.Luo Jia, Wang Xue-song, Li Yong-zhen, et al. Description and analysis of spatial polarization charateritics of antenna[J]. Chinese Journal of Radio Science, 2008, 23(4): 620–628.( 2) 2) |
| [11] | 戴幻尧, 李永帧, 薛松, 等. 相控阵天线空域极化特性的高频仿真分析[J]. 电波科学学报, 2011, 26(2): 316–322.Dai Huan-yao, Li Yong-zhen, Xue Song, et al. High frequency simulation analysis of spatial polarization characteristic of phased arra[J]. Chinese Journal of Radio Science, 2011, 26(2): 316–322.( 2) 2) |
| [12] | 何密. 同时极化测量体制雷达的校准方法研究[D]. [博士论文], 国防科技大学, 2012: 60–88.He Mi. The study of calibration methods for simultaneously polarization measurement radar[D]. [Ph.D. dissertation], National University of Defense Technology, 2012: 60–88.( 1) 1) |


