② (中国传媒大学信息工程学院 北京 100024)
③ (电子科技大学电子工程学院 成都 610054)
② (Information Engineering School, Communication University of China, Beijing 100024, China)
③ (School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu 610054, China)
极化散射矩阵(PSM)是用于雷达目标分类识别的一项重要目标散射特性。由于雷达观测目标的种类、结构和材料日益复杂,其极化散射特性随之复杂,使得现实目标,尤其是复杂材质飞行器的宽带极化特性数据获取需求日益迫切,但是对此类目标极化散射的定量研究却未见报道。
不同于金属目标,复杂材质目标会产生更为特殊的退极化效应,这一现象对于雷达目标分类识别具有潜在的应用价值。然而复杂材质目标极化散射特性的理论建模、计算存在诸多难点,此时实验测量成为主要研究手段。目前,室内目标全极化定量测量可以实现复杂目标多姿态、多站角的极化散射特性信息精确获取[1,2,3,4,5,6,7,8]。本实验室利用紧缩场暗室进行目标全极化散射测量已有较为可靠的技术体系,可以开展复杂材质无人机极化散射特性定量研究工作。
本文以复杂材质无人机为研究对象,旨在研究复杂材质目标与金属目标的极化散射特性差异,揭示复杂目标交叉极化散射来源。文中将利用实验测量手段,得到无人机及其部件全极化散射特性数据,与金属化目标的理论仿真结果进行对比,完成研究分析。第2节介绍了宽带极化散射特性数据的测量及校准方法,通过标准体实测数据验证了测量精度。第3节给出无人机整机及部件的全极化测量结果,并结合金属参考目标的仿真结果进行了讨论,发现复杂材质构成的无人机机身部位是主要的交叉极化散射来源。
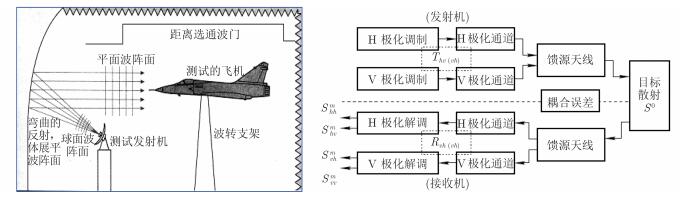
2 复杂目标极化散射测量方法复杂材质无人机的极化测量在紧缩场暗室中进行,实验测量原理如图 1所示。
|
图 1 实验测量原理 Fig.1 Diagrammatic sketch of measurement experiment |
进行目标全极化测量时,需要完成测量信号极化调制、发射、散射信号接收和解调4个主要过程。当电磁信号在一个极化的发射通道和接收通道中传输时,由于泄露现象的存在,会对另一个极化通道产生影响,形成影响极化测量精度的主要乘性误差。系统发射通道和接收通道存在电磁信号的泄露,加之目标区固有的背景散射,构成了重要的加性耦合误差[9]。为了准确获取复杂材质无人机的极化散射特性数据,需要采用极化校准测量的方法开展实验,以修正上述误差。
同时,由于缺乏真实无人机的理论仿真数据作为对比,为了保证测量数据的准确性,我们采用了两种不同的测量校准方法,基于标准体进行互标定验证。此两种方法分别是单定标体极化散射测量校准方法和三定标体极化散射测量校准方法[1, 10]。
图 2所示为直径300 mm金属定标球8.5~10.5 GHz扫频全极化散射特性测量结果。分析对比两种校准测量得到的结果,可知实验系统对直径300 mm金属定标球校准后的测量极化纯度优于35 dB,且不同方法的结果一致性较好。

|
图 2 直径300 mm定标球扫频测量结果 Fig.2 The sweep frequency test result of sphere with 300 mm in diameter |
图 3所示为两种校准方法互标定验证后的菱形二面角全极化数据与理论值对比。菱形二面角边长为200 mm,横滚角为22.5°。分析图中曲线,可知8.5~10.5 GHz范围内,测量值与理论值差异为±1 dB。同时,因为测量值经过校准两种方法标定传递后获得,故可以说明目标交叉极化测量精度差异不超过±1 dB。

|
图 3 菱形二面角(22.5°)测量与计算值对比 Fig.3 Comparison between measurement and theory result of rhombic dihedral with 22.5° in roll angle |
一般复杂飞行器目标的交叉极化散射和同极化散射的幅值差在-20 dB至8 dB之间[1],上述两种标准体的实验结果可以说明,测量的极化纯度与精度能够满足无人机测量研究的需要。
3 实验结果与分析本部分内容给出了复杂材质无人机整机及部件的测量结果,并针对结果进行了讨论,包括无人机实测数据与其金属化精确数值计算结果的对比分析,整机与部件极化散射特性关系分析。
无人机的实测结果在紧缩场暗室中获得,实验设备采用基于矢量网络分析仪构建的散射测试系统,测试频率8.5~10.5 GHz。用于对比的金属化模型理论计算数据通过并行多层快速多极子方法求解混合场积分方程获得,此方法有利于电磁场数值问题的快速求解,且求解精度较高。
3.1 无人机整机研究中使用的复杂材质无人机由玻璃钢、碳纤维、木材和金属等多种材料构成,结构形式主要为轻质骨架外覆蒙皮,包含机身、机翼、尾翼、发动机和螺旋桨等主要部件。
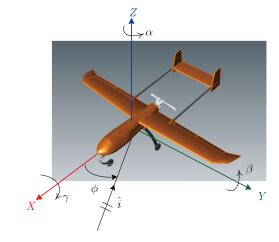
无人机姿态定义如图 4所示,其中$\alpha $, $\beta $, $\gamma $分别定义为方位角、俯仰角和横滚角。测量实验中无人机状态如图 5所示。我们测量了$\beta $=0时,X波段无人机整机360°方位角内的全极化散射数据。
|
图 4 无人机姿态定义 Fig.4 Coordinate of UAV |

|
图 5 无人机测试状态 Fig.5 Condition of UAV in measuring |
无人机10 GHz全极化散射测试结果和仿真计算结果如图 6所示,由图中可以看出此型无人机及其金属化模型:(1) 同极化散射在部分角度位置差异明显,但大角域内均值差异不大;(2) 都存在一定强度的交叉极化散射,但曲线表现出的起伏特性完全不同。无人机的交叉极化测量结果随角度变化存在明显的快起伏特性,小角域内幅度统计均值变化不大,这说明此目标在不同方位处都存在退极化效应且效果相当。金属化模型交叉极化仿真结果则表现出了明显的慢起伏特性,在0°, ±50°, ±90°和±180°存在较强的交叉极化散射,其他角度则明显减小。两组数据的统计结果如表 1所列。频带内其他频点的测量结果分析均表现出了与10 GHz处相同的结论,故不再对点频数据逐一展示。

|
图 6 无人机在f=10 GHz, 0°俯仰角RCS测量值与计算值对比 Fig.6 RCS comparison between measurement and theory result of UAV with 10 GHz in frequency and 0° in pitch angle |
| 表 1 真实无人机与金属化模型的散射均值统计(f=10 GHz,统计角域20°) Tab.1 Statistical mean comparison between real and metal UAV at 10 GHz in 20° angular range |
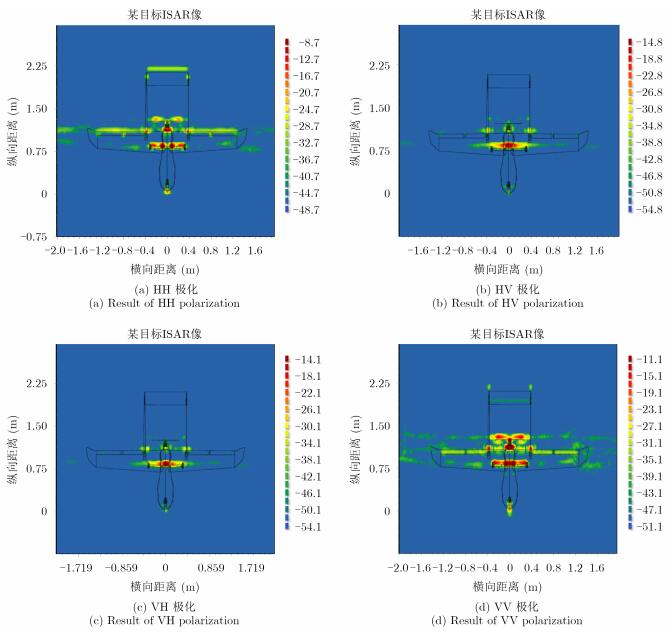
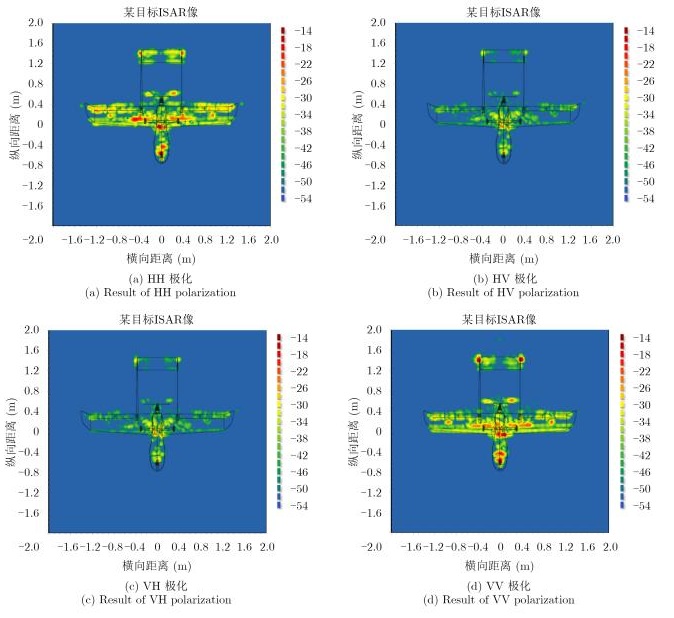
两类结果的宽带2维ISAR成像分别如图 7(计算结果)和图 8(测量结果)所示,并嵌套了无人机的几何外形作为比对,成像中心角0°,孔径角30°,可以看出真实无人机与其金属化模型的成像特征存在较大的差异。无人机实测成像结果包含较强的散射中心和连续的高散射区域,4个极化下目标几何外形清晰,表现出了明显的体散射特征;金属化模型则以集中的强散射中心为主,且与真实目标强散射点位置不同,在图像中没有体现目标的几何外形特征。特别,对比图 7与图 8中交叉极化成像结果,真实无人机存在散射强点扩展,大量强散射分布在飞机结构轮廓内部,而金属化模型则在结构表边缘处体现出很强的散射中心特征,说明实际无人机内部结构是其产生交叉极化散射的重要因素,散射机理与全金属目标差异明显。
|
图 7 金属化无人机X波段0°俯仰、0°方位ISAR计算图像 Fig.7 Calculational ISAR of metal UAV in X band with 0° in pitch and azimuth angle |
|
图 8 无人机X波段0°俯仰、0°方位2维ISAR测量图 Fig.8 Measurement ISAR of UAV in X band with 0°in pitch and azimuth angle |
由于入射角度对目标散射特性的影响较大,图 9和图 10分别给出了45°方位角和90°方位角无人机ISAR成像结果。通过对比分析可知,在不同入射条件下,各部件对无人机全极化散射的贡献是不同的,侧视时有一种散射机理明显占优,但其机身轮廓内部始终体现了较为明显全极化散射特性,其他部位则随角度变化体现出了较大差异。故此可通过分别研究主要部件的全极化散射特性来确认无人机交叉极化散射的真实来源。
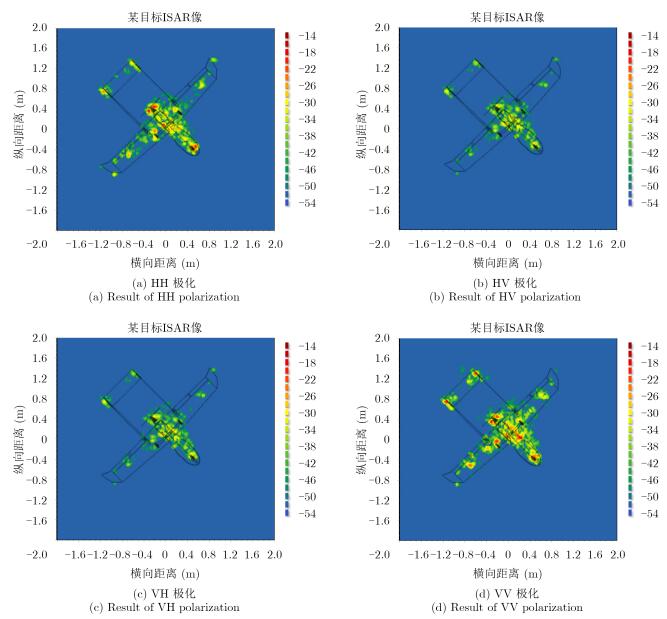
|
图 9 无人机X波段0°俯仰、45°方位2维ISAR测量图 Fig.9 Measurement ISAR of UAV in X band with 0° in pitch angle and 45° in azimuth angle |
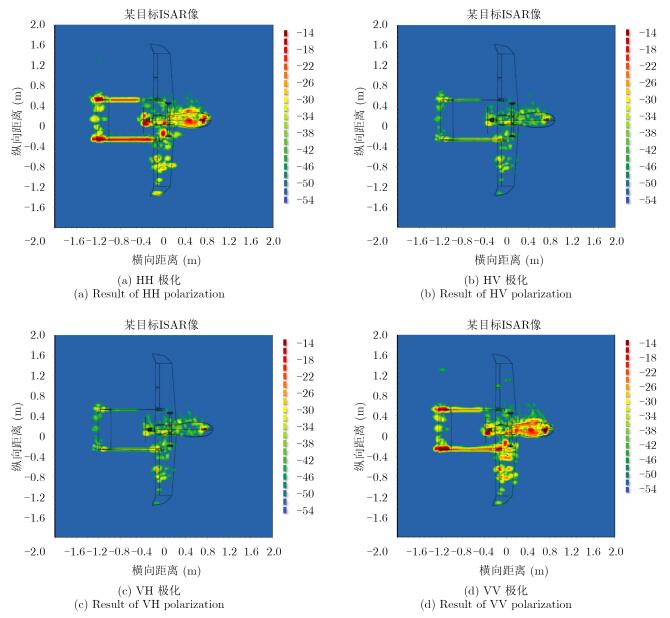
|
图 10 无人机X波段0°俯仰、90°方位2维ISAR测量图 Fig.10 Measurement ISAR of UAV in X band with 0° in pitch angle and 90° in azimuth angle |
此外,借助2维成像结果,我们对无人机测量结果进行了散射中心提取和分类比重分析,结果如表 2所列。从表中数据可以看出,构成无人机交叉极化分量的强散射中心体现出了多种结构类型,且随角度变化明显,说明此型无人机的极化散射特性与其复杂的内部结构有一定的关联性,这种特性可用于对本型无人机全极化特征提取与分类识别研究。
| 表 2 无人机散射中心的提取与分类分析(f=10 GHz) Tab.2 Extract and analyze on scattering center of UAV at 10 GHz |
由上节无人机测量结果可以看到,机身和机翼部分对整机的4个极化散射分量都有明显的贡献,本节将通过分解测量的方法,主要借助成像特征研究部件与整机全极化散射特性的联系。由于部件缺少可靠的金属化模型计算结果作为比对,故这部分研究采用两种校准测量对比的方法,以保证结果的准确性。
(1) 机身
无人机机身在10 GHz处的全极化测量结果如图 11所示。分析测量结果可知机身同极化散射曲线的起伏特征与整机相似,强散射位置幅度较小;交叉极化散射量级与整机相似,与同极化分量差异为10 dB左右。机身的2维ISAR成像结果如图 12所示,其交叉极化图像中散射分布特征与整机图像对应区域基本一致,体现出了相同的退极化效应。分析原因,由于机身为中空结构且蒙皮比较复杂,蒙皮材料为多层复合材料,最外层为玻璃钢材质,中间层为轻木材质的蜂窝状结构,最内层为玻璃钢材质,机身与其他部件的连接结构较多,导致空隙结构丰富,从而导致机身的退极化效应比较明显,成为整机交叉极化散射的主要来源。
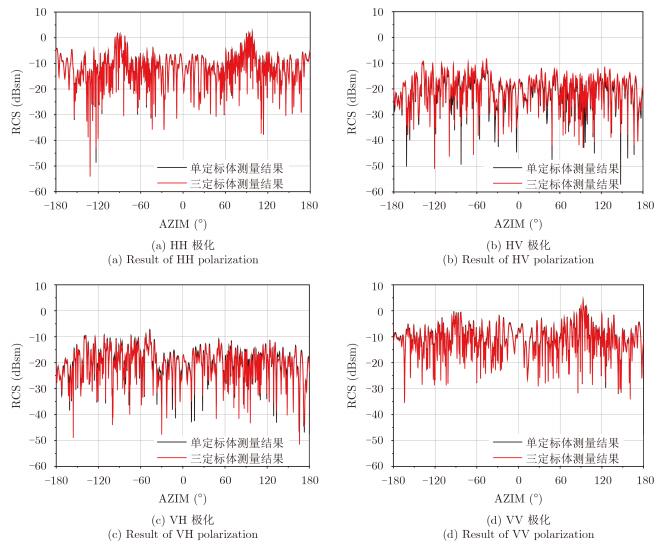
|
图 11 无人机机身俯仰角0°全方位RCS (f=10 GHz) Fig.11 Azimuth RCS, both single and tri-calibration, of UAV's body at 10 GHz with 0° in pitch angle |
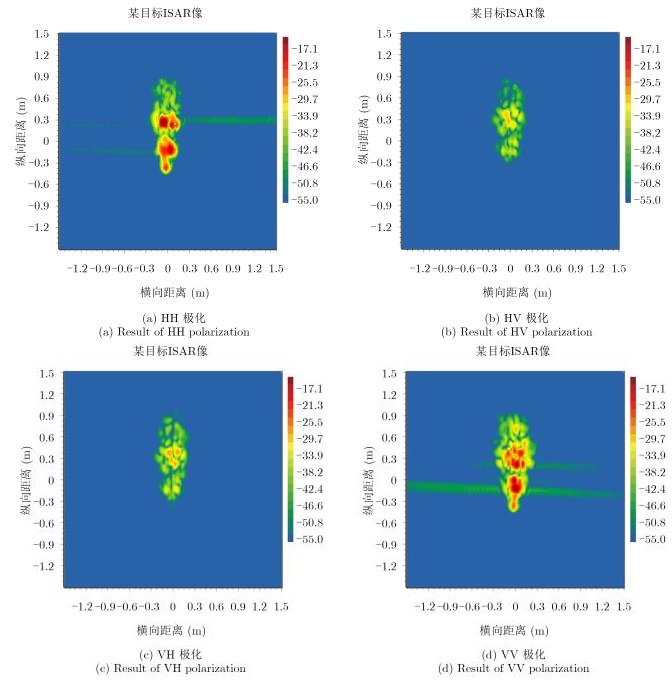
|
图 12 无人机机身X波段0°俯仰、0°方位全极化2维ISAR图 Fig.12 Measurement ISAR of UAV's body in X band with 0° in pitch and azimuth angle |
(2) 机翼
无人机机翼在10 GHz处的全极化测量结果如图 13所示,其同极化与交叉极化散射幅度差约为10 dB。2维ISAR成像结果如图 14所示,表现出的同极化与交叉极化散射特征差异同整机基本一致,为10 dB左右。特别交叉极化图像中机翼端部的散射强点,以及前缘、后缘的散射区域分布也符合整机成像中机翼部分的特点。分析机翼的结构特点,主要为玻璃钢纤维网织材质蒙皮,内部包含了一些金属部件和孔洞结构,造成其存在明显的体散射效应和材料内部的复杂耦合关系,使得机翼的交叉极化散射较明显,构成了整机交叉极化散射的来源之一。但金属化整机模型的计算图像基本无法分辨机翼部分。

|
图 13 无人机机翼俯仰角0°全方位RCS (f=10 GHz) Fig.13 Azimuth RCS, both single and tri-calibration, of UAV's wing at 10 GHz with 0° in pitch angle |
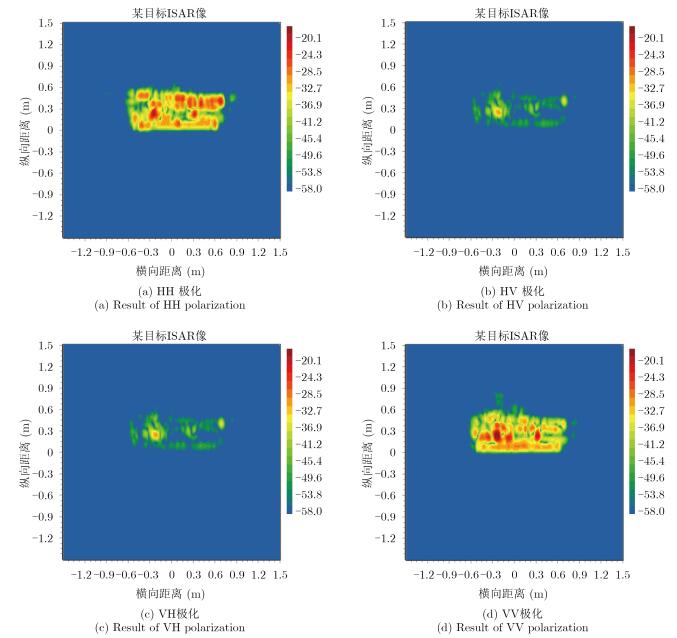
|
图 14 无人机机翼X波段0°俯仰、0°方位全极化2维ISAR图 Fig.14 Measurement ISAR of UAV's wing in X band with 0° in pitch and azimuth angle |
对于其他部件,如螺旋桨,交叉极化散射在-40~-50 dBsm量级,参考金属球的测量结果,此量级己接近本次测量的极小值,故认为此类部件的实际交叉极化散射很弱,对整机的退极化效应贡献很小。
4 结论复杂材质目标会表现出与全金属目标差异较大的全极化散射特性。本文以复杂材质无人机为研究对象,通过实验测量的手段,定量化地揭示了整机与其金属化模型交叉极化散射来源、表现特征与产生机理的差异。利用分部件测量分析的方式,在缺乏计算结果对比的情况下,采用两种校准测量比对验证的方法,证明此无人机整机与主要部件的极化散射数值特征与成像特征是一致的,部件的全极化特性直接影响整机的全极化特性,机身部位是整机交叉极化散射的主要来源,且与其内部结构有着较强的关联性。
| [1] |
黄培康, 殷红成, 许小剑.
雷达目标特性[M]. 北京: 电子工业出版社, 2005 .
Huang Pei-kang, Yin Hong-cheng, Xu Xiao-jian.
Characteristics of Radar Target[M]. Beijing: Publishing House of Electronics Industry, 2005 .
( 0) 0)
|
| [2] |
Alexander N T, Currie N C, and Tuley M T. Calibration of bistatic RCS measurements[C]. Proceedings of Antenna and Propagation Techniques Association 1995 Symposium, Columbus, USA, 1995:13-17.
( 0) 0)
|
| [3] |
Jersak B D B. Bistatic, fully polarimetric radar cross-section calibration techniques and measurement error analysis[D].[Ph.D. dissertation], University of Texas at Arlington, 1993:116-128.
( 0) 0)
|
| [4] |
Eigel R L. Bistatic radar cross section characterization of complex objects[D].[Master dissertation], Air Force Institute of Technology, 1999:25-33.
( 0) 0)
|
| [5] |
Saraband I K, Ulaby F T, Tassoudji M A. Calibration of polarimetric radar systems with good polarization isolation[J].
IEEE Transactions on Geoscience and Remote Sensing , 1990, 28 (1) : 70-75 DOI:10.1109/36.45747 ( 0) 0)
|
| [6] |
Mortensen H B. Implementation of bistatic polarimetric calibration procedure for the EMSL[R]. European Microwave Signature Laboratory, Internal memorandum, 1995.
( 0) 0)
|
| [7] |
Riegger S, Wiesbeck W. Wide-band polarimetry and complex radar cross section signatures[J].
Proceedings of the IEEE , 1989, 77 (5) : 649-658 DOI:10.1109/5.32055 ( 0) 0)
|
| [8] |
Monzon J C. A cross-polarized bistatic calibration device for RCS measurements[J].
IEEE Transactions on Antennas and Propagation , 2003, 51 (4) : 833-839 DOI:10.1109/TAP.2003.811071 ( 0) 0)
|
| [9] |
Huang Pei-kang, Ning Chao, Xu Xiao-jian, et al. Solution for polarimetric radar cross section measurement and calibration[J].
Journal of Systems Engineering and Electronics , 2014, 25 (2) : 211-216 DOI:10.1109/JSEE.2014.00025 ( 0) 0)
|
| [10] |
庄钊文, 袁乃昌, 莫锦军, 等.
军用目标雷达散射截面预估与测量[M]. 北京: 科学出版社, 2007 .
Zhuang Zhao-wen, Yuan Nai-chang, Mo Jin-jun, et al.
Estimation and Measurement of Radar Cross Section of Military Targets[M]. Beijing: Science Press, 2007 .
( 0) 0)
|




