雷达目标极化散射特性是近年来研究的热点。由于目标全极化散射回波中有着与目标相关的丰富信息,例如目标的几何形状、材料、介电常数等[1],因此随着电磁波极化特性的加入,使得处理接收到的目标回波信号时扩展了信息维度,能够对目标进行更加精细的识别和分析[2]。目前在电磁波极化的科学研究和工程应用中,全极化SAR研究取得了较大进展,技术较为成熟[3]。对于全极化雷达对空探测的研究则主要集中在极化信息处理,例如极化滤波[4],相干斑去噪[5],极化目标特征提取等[6]。相关研究仍然面临着较大的挑战,如通常情况下,雷达目标散射回波中的交叉极化分量电平远小于主极化电平,这使得雷达难以接收到全极化信息;另外,对于目标极化散射机理研究不够深刻,传统的研究通常将电磁散射归结为平面、二面角、球标等标准体目标的散射[7, 8],而人造目标的复杂性导致的变极化效应难以进行准确的描述。根据电磁散射理论,对于常规飞行目标,米波频段为电磁散射的谐振区,目标的散射截面积(RCS)剧烈震荡,回波得以增强[9]。因此在谐振频段目标的极化散射特性是需要进一步研究的内容。
本文首先分析了典型结构的极化散射机理;然后采用基于积分方程——多层快速多极子算法(MultiLevel Fast Multipole Algorithm,MLFMA)对隐身和非隐身飞机目标在米波频段开展了极化散射数值建模计算;分析对比了隐身和非隐身飞机目标的结构和远场极化散射特性的差异,揭示全极化回波特别是强交叉极化回波的产生机理,为目标全极化信息利用和特征识别提供了一定的参考。
2 典型结构全极化散射机理从雷达极化学的角度,电磁波与目标的作用可以表示为[10]:
| $ {E^{\rm{s}}} = S{E^{\rm{i}}} $ | (1) |
| $ {S}=\left[\begin{matrix} {{s}_{xx}} & {{s}_{xy}} \\ {{s}_{yx}} & {{s}_{yy}} \\ \end{matrix} \right] $ | (2) |
式(1)中,S表示全极化散射矩阵,为目标的固有属性并且是与目标姿态角有关的参量,其中下标x,y代表任意的正交极化基,矩阵中的每个元素刻画了目标对不同极化电磁波的散射特性;主对角线元素的模值反映了主极化散射分量电平强度,次对角线元素模值反映了交叉极化散射分量电平强度。Ei为入射波,Es为散射波。给定散射矩阵,入射波方向改变,RCS也会变化。同样目标姿态变化也会引起RCS的波动,这种波动会在某些角度上达到最大值,实现雷达目标极化自适应匹配照射[11]。此时如果接收天线极化方向与散射电场极化方向相同,可以使得接收到的目标散射回波功率最大,满足极化自适应匹配接收条件[12]。极化信息利用的一大难点在于目标全极化散射回波中,通常情况下主极化散射分量远大于交叉极化散射分量,这使得全极化信息利用遇到了极大的限制。但是由于目标运动时具有不同的姿态,雷达波照射角度也不尽相同,交叉极化散射回波在某些照射条件下较大,可以实现极化信息的有效应用。
针对交叉极化的产生机理,考察了典型结构,如金属二面角和偶极子的极化散射特性。如图 1所示的垂直放置二面角散射回波中,主极化分量占绝对优势,交叉极化为零。将二面角旋转一定角度后,入射波方向不变,交叉极化散射回波可以得到显著增强[13]。图 1(a)到图 1(b)中二面角散射矩阵变换关系为:
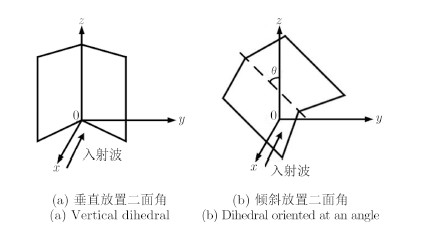
|
图 1 二面角 Fig. 1 Dihedrals |
| $ \begin{array}{l} {S_{Rot}} = R\left( \theta \right)\left[ {\begin{array}{*{20}{c}} 1&0\\ 0&{ - 1} \end{array}} \right]{R^{ - 1}}\left( \theta \right)\\ \;\;\;\;\; = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1&0\\ 0&{{\rm{ - }}1} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta }\\ { - \sin \theta }&{\cos \theta } \end{array}} \right]\\ \;\;\;\;\;{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\cos 2\theta }&{\sin 2\theta }\\ {\sin 2\theta }&{ - \cos 2\theta } \end{array}} \right] \end{array} $ | (3) |
这里的R(θ)为旋转矩阵,旋转角θ=${\rm{\pi }}$/4时,散射回波中只有交叉极化分量,主极化分量为零。对金属偶极子也能得到类似的结论。图 2(a)到图 2(b)中金属偶极子散射矩阵变换过程为[14]:
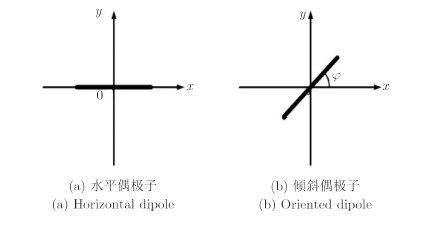
|
图 2 金属偶极子 Fig. 2 Mental dipole |
| $ \begin{array}{l} {S_{Rot}} = R\left( \varphi \right)\left[ {\begin{array}{*{20}{c}} 0&0\\ 0&1 \end{array}} \right]{R^{ - 1}}\left( \varphi \right)\\ \;\;\;\;\; = \left[ {\begin{array}{*{20}{c}} {\cos \varphi }&{ - \sin \varphi }\\ {\sin \varphi }&{\cos \varphi } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 0&0\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\cos \varphi }&{\sin \varphi }\\ { - \sin \varphi }&{\cos \varphi } \end{array}} \right]\\ \;\;\;\; = \left[ {\begin{array}{*{20}{c}} {{{\sin }^2}\varphi }&{ - \cos \varphi \sin \varphi }\\ { - \cos \varphi \sin \varphi }&{{{\cos }^2}\varphi } \end{array}} \right] \end{array} $ | (4) |
旋转角$\varphi = {\rm{\pi }}$时,散射回波中交叉极化分量大小等于主极化分量。以上分析说明了典型结构在电磁波倾斜照射时,散射矩阵与旋转矩阵相乘,使得次对角线元素不为零,从而大大增强了交叉极化散射。该结论可以推广至由多种几何结构组成的复杂目标,其强散射源散射更多,极化散射特性对于目标姿态敏感,交叉极化信息会更加丰富。
3 基于积分方程的极化散射数值分析为准确分析目标全极化散射特性,采用了基于积分方程MLFMA的数值分析方法。对于3维导体目标,首先建立电场积分方程[15]:
| $t \cdot \int_s {\left[ {J\left( {r'} \right) + \frac{1}{{{r^2}}}\nabla ' \cdot J\left( {r'} \right)\nabla } \right]} \frac{{{e^{ikR}}}}{R}dS' = \frac{{4\pi i}}{{k\eta }}t \cdot {E^i}\left( r \right) $ | (5) |
式(5)中,S表示目标表面,r和r'表示场点和源点位置矢量;t表示目标表面S上切向矢量,Ei表示入射电场,R=|r–r'|。并矢格林函数为:
| $ \begin{array}{l} G\left( {{r_j},{r_i}} \right) = \frac{{ik}}{{4\pi }}\int {{d^2} \cdot k\left( {I - \cdot k \cdot k} \right){e^{ik\left( {{r_{jm}} - {r_{im}}'} \right)}}} \\ \;\;\;\;\;\;\;\;\;\;\;\;\; \cdot {\alpha _{mm'}}\left( {{r_{mm'}} \cdot k} \right) \end{array} $ | (6) |
其中,ri和rj表示场点和源点矢量,rjm,rim'表示场点和源点所在组的组中心矢量,αmm'为转移因子。在采用迭代方法求解以上的积分方程中,涉及大量的矩矢相乘运算。MLFMA将矩矢运算按照一定互耦关系分组分层,层间嵌套,逐层递推实现快速运算。MLFMA将传统矩量法的计算复杂度从O(N2) 量级降低至O(NlogN)[16]。
4 飞机目标全极化散射分析如图 3所示隐身和非隐身飞机目标几何示意图,目标均为全尺寸模型,飞机机头正对x轴正方向。频率450 MHz雷达波照射角度为:($\theta ,\phi $$\in $[45°,135°]×[0°,180°]。其中θ和Φ为球坐标系下的坐标变量。
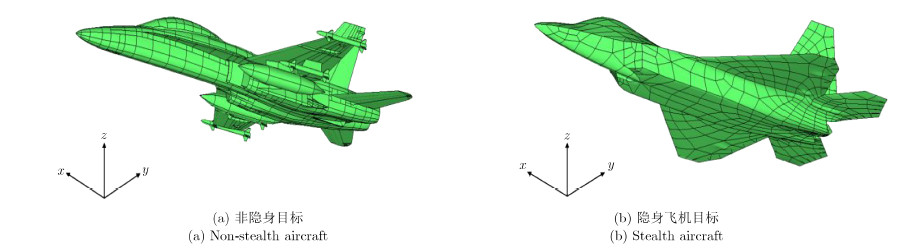
|
图 3 飞机目标几何示意图 Fig. 3 Airplanes |
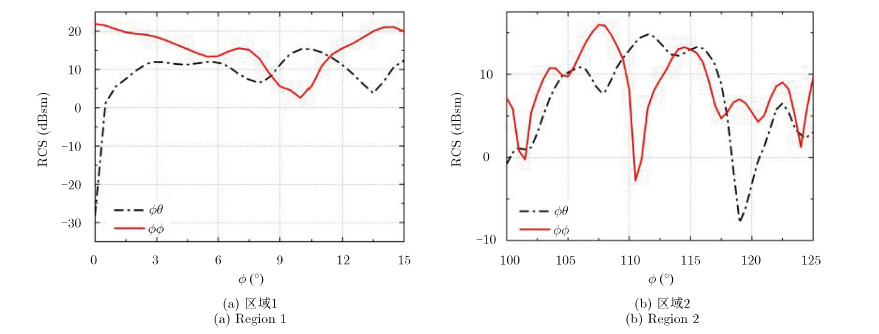
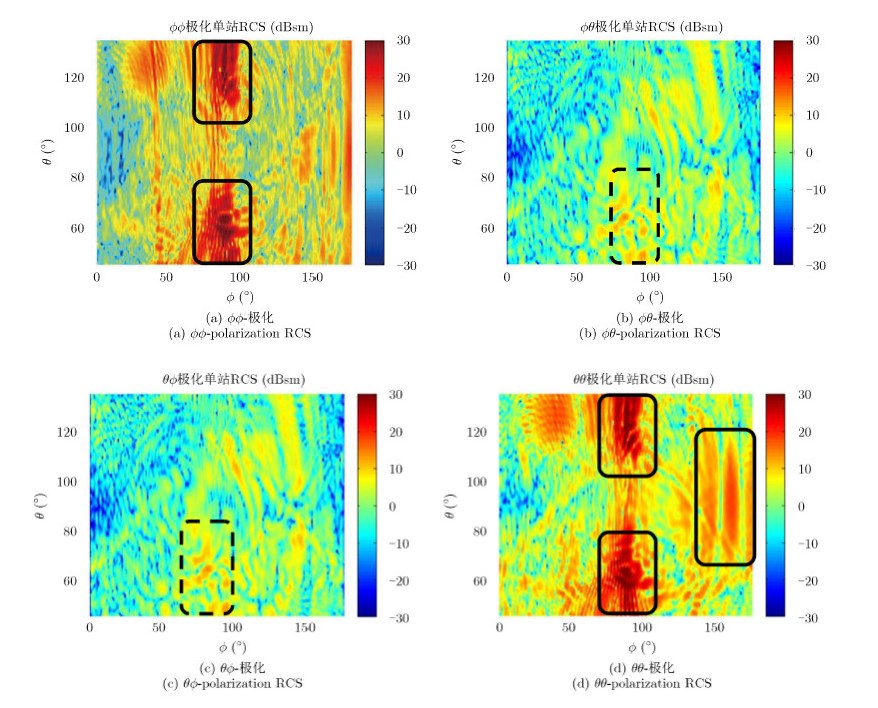
图 4给出给定角度域内不同极化雷达波照射时的单站RCS。可以看出,主极化散射较强的区域对应于目标前下方、侧向和后向侧照射等,如图 4(a)和图 4(d)中Φ$\in $[70°,110°]——侧面照射时RCS达到峰值;相对而言交叉极化散射分量小于主极化分量。但是对应于飞机前下方和侧下方照射,在($\theta ,\phi $)$\in $[95°,130°]×[0°,40°](区域1)和($\theta ,\phi $)$\in $[100°,135°]×[100°,140°](区域2)范围内,对应于飞机侧下方照射时,交叉极化散射分量也达到了15 dBsm;而且 $\phi \theta $和 $ \theta \phi $极化回波RCS分布相同。如图 5所示,选取θ=100°,Φ$\in $[0°,15°](区域1内)和θ=114°,Φ$\in $[110°,125°](区域2内)作图,可以看出在该角度范围内,交叉极化分量与主极化大小相当。
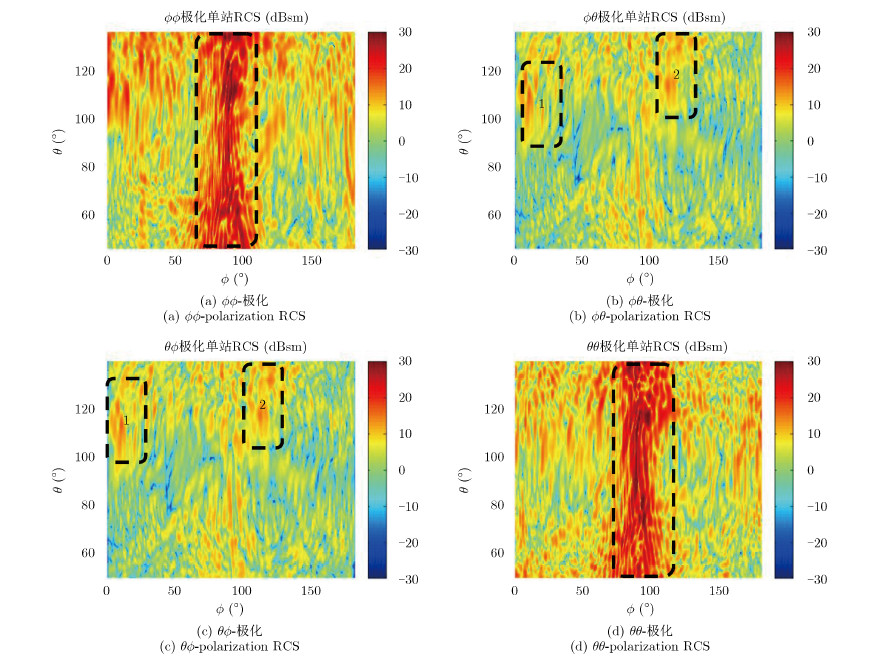
|
图 4 非隐身目标的全极化散射特性 Fig. 4 Fully polarimetric scattering characteristics of non-stealth aircraft |
|
图 5 较强交叉极化散射区域雷达散射回波 Fig. 5 Cross-polarimetric RCS curves |
|
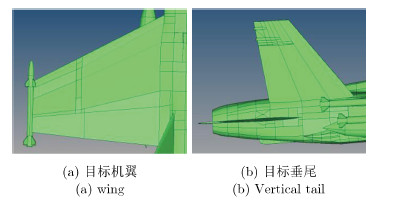
图 6 目标翼面 Fig. 6 Wings |
非隐身飞机具有较多的典型强散射源:进气道、挂弹、翼面边缘等,飞机的整体散射由各结构散射共同产生。以下对其极化散射特性进行分析[17]:
(1) 边缘散射
目标机翼和垂尾对不同极化的电磁波照射非常敏感。入射波电场矢量与机翼前缘平行时会产生强散射,电场矢量与翼面垂直时在机翼后缘的散射较强。电磁波斜入射时,电场可以矢量分解为平行和垂直于翼面的两个分量。散射回波经过矢量叠加后在与入射波垂直的极化方向上有一定的投影,产生交叉极化。
(2) 面结构散射
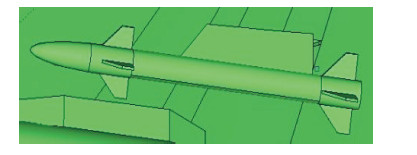
目标表面法向与入射波方向平行时会产生极大的面散射。目标翼面、机身部分都会有面散射而产生强主极化分量。如图 7所示,外挂物上的翼面会产生角反射器,外挂物与机翼也会形成多次反射,同样形成角反效应。随着目标姿态的变化,角反射器旋转,从而产生很强的交叉极化。
|
图 7 目标外挂物(导弹) Fig. 7 Cruise missle |
(3) 表面电磁缺陷散射
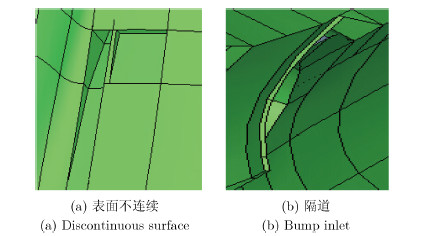
金属目标表面不连续结构截断电流从而产生电磁波反射。由于电流矢量方向受到目标介质或者结构的影响,产生变极化效应,如图 8(a)所示的不连续结构。
|
图 8 目标表面不连续结构和隔道 Fig. 8 Discontinuous surface and bump inlet |
(4) 进气道和隔道散射
目标进气道和进气道与机身之间存在的隔道也会产生较强的后向散射回波。机身与进气道之间的隔道实际上形成了一个腔体,容易产生谐振引起回波。随着腔体内表面曲率的变化,从而产生复杂的回波极化分量。
以上的强散射源在雷达波照射下产生很强的主极化散射回波。目标在空中运动时,其相对于雷达的空间位置会不断改变。类似之前分析的二面角和金属偶极子产生交叉极化的原理,这些强散射源旋转后,雷达波入射后产生较强的交叉极化回波。
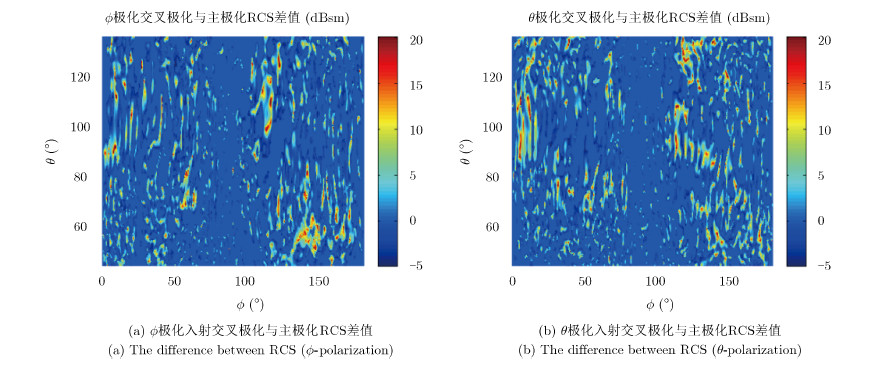
为了进一步分析主极化散射和交叉极化散射关于目标姿态照射角度的关系,将交叉极化RCS值与主极化RCS值相减。仅选取主极化RCS值大于–20 dBsm的结果进行作图。从图 9中可以看出,非隐身飞机的交叉极化较强区域的分布较广。
|
图 9 交叉极化与主极化RCS差值(主极化大于–20 dBsm)
Fig. 9 The difference between the cross-polarimetric and the main-polarimetric RCS of non-stealth aircraft (The strength of main-polarimetric RCS is greater than –20 dBsm) |
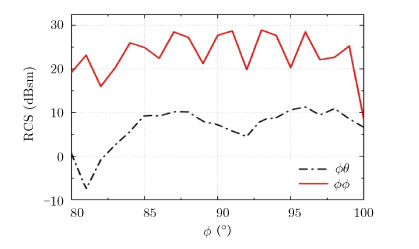
对于图 3(b)中的隐身飞机目标采用同样的方法进行分析,得到如图 10所示的全极化散射回波结果。可以看出,经过外形隐身设计,威胁角度范围内的回波RCS得到了较大缩减,即使在米波频段的主极化分量也在0 dBsm左右。强散射分布在侧向和尾向,如图 10(a)和图 10(d)中的黑框部分角度。对于交叉极化散射分量,较强交叉极化散射点相比非隐身飞机大为减少,仅在($\theta ,\phi $)$\in $[0°,80°]×[60°,100°](图 10(b)和图 10(c)中虚线框部分)等侧向以及斜后方角度范围内分布,主要是由机翼、垂尾与机身形成的二面角在电磁波斜入射时产生。同时强交叉极化散射点分布比较离散,数目较少并且强度比非隐身飞机弱。如图 11所示,在θ=46°,Φ$\in $[80°,100°]的角度内,交叉极化较高,但是其仍然不超过主极化RCS值。经过外形隐身优化的目标,其强散射源较少,即使目标位置变化,产生的交叉极化分量比非隐身目标小很多。
|
图 10 隐身目标的全极化散射特性 Fig. 10 Stealth aircraft full-polarimetric scattering characteristics |
|
图 11 隐身目标RCS曲线(θ=46°,Φ$\in $[80°, 100°]) Fig. 11 Stealth aircarft RCS curves |
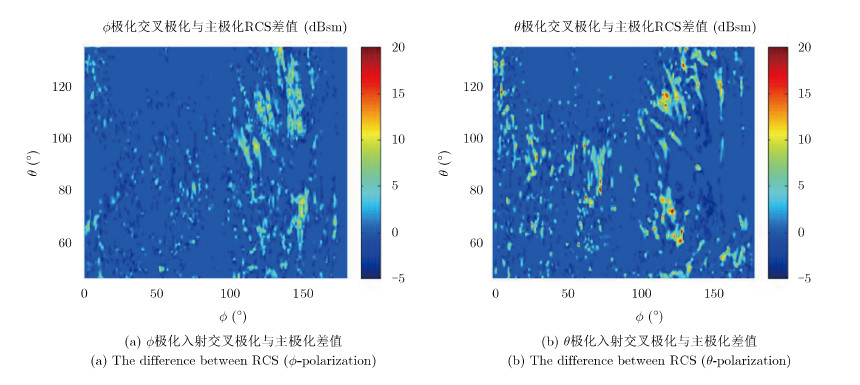
图 12对隐身飞机的交叉极化与主极化分量差值进行分析。可以看出,隐身目标在前向和侧向(主要威胁方向)几乎没有形成强的交叉极化散射,特别是对于Φ极化。较强交叉极化散射多数集中在目标侧后向区域。
|
图 12 隐身目标交叉极化与主极化RCS差值(主极化大于–20 dBsm) Fig. 12 The difference between the cross-polarimetric and the main-polarimetric RCS of steath aircraft (The strength of main-polarimetric RCS is greater than –20 dBsm) |
从两类飞机极化散射仿真结果可以看出,非隐身目标外形结构复杂,构成多种强散射源。在其运动姿态角度变化时能够激励起较强的全极化回波,其中产生强交叉极化的原因可以认为是典型散射结构在电磁波斜入射时等效为原散射矩阵与旋转因子相乘,使得次对角线元素不为零,增强了交叉极化散射。对于隐身目标,气动外形结构简单平滑,强散射结构较少。不仅威胁方向RCS极低,交叉极化分量也仅在目标侧向和上、下侧后方向有一定分布。
5 结论本文首先分析了典型结构的极化散射产生机理,运用积分方程数值方法对隐身和非隐身飞机目标在米波频段进行极化散射仿真计算。可以看出,通常情况下目标散射场的主极化分量大于交叉极化分量。但是对于非隐身目标,电磁波在一定角度照射时,其交叉极化散射回波较强。而经过外形优化设计的隐身目标,减少了能够引起强散射的几何结构,交叉极化散射特性较弱。本文研究内容为目标全极化信息利用和特征识别提供重要参考。
| [1] | 陈强. 雷达极化中若干理论问题研究[D]. [博士论文], 国防科技大学, 2010. Chen Q. Study on theoretical problems in radar polarimetry[D]. [Ph.D. dissertation], National University of Defense Technology, 2010.( 1) 1) |
| [2] | 李金梁, 李永祯, 王雪松. 米波极化雷达的反隐身研究[J]. 雷达科学与技术, 2005, 3(6): 321-326. Li J L, Li Y Z, and Wang X S. Study on anti-stealth with meter-band polarimetric radar[J]. Radar Science and Technology, 2005, 3(6): 321-326.( 1) 1) |
| [3] | 邢世其. 人造目标极化雷达三维成像理论与方法研究[D]. [博士论文], 国防科技大学, 2013: 3-4. Xing S Q. Study on the 3D imaging of manmade targets based on polarimetric radar[D]. [Ph.D. dissertation], National University of Defense Technology, 2013: 3-4.( 1) 1) |
| [4] | 王雪松. 宽带极化信息处理的研究[D]. [博士论文], 国防科技大学, 1999: 4-6. Wang X S. Study on wideband polarization information processing[D]. [Ph.D. dissertation], National University of Defense Technology, 1999: 4-6.( 1) 1) |
| [5] | 崔一. 基于SAR图像的目标检测研究[D]. [博士论文], 清华大学, 2011: 37-57. Cui Y. Study on target detection in synthetic aperture radar images[D]. [Ph.D. dissertation], Tsinghua University, 2011: 37-57.( 1) 1) |
| [6] | 代大海. 极化雷达成像及目标特征提取的研究[D]. [博士论文], 国防科技大学, 2008: 49-71. Dai D H. Study on polarimetric radar imaging and target feature extration[D]. [Ph.D. dissertation], National University of Defense Technology, 2008: 49-71.( 1) 1) |
| [7] | Jakob Van Zyl. Synthetic Aperture Radar Polarimetry[M]. Hoboken, NJ, USA: Wiley, 2011.( 1) 1) |
| [8] | 安文韬. 基于极化SAR的目标极化分解与散射特征提取研究[D]. [博士论文], 清华大学, 2010: 11-24.n An W T. The polarimetric decomposition and scattering charasteristic extraction of polarimetric SAR[D]. [Ph.D. dissertation], Tsinghua University, 2010: 11-24.( 1) 1) |
| [9] | 刘俊. 米波雷达低仰角估计方法研究[D]. [博士论文], 西安电子科技大学, 2012: 3-5. Liu J. Study on low-angle estimation in vhf radar[D]. [Ph.D. dissertation], Xidian University, 2012: 3-5.( 1) 1) |
| [10] | 李谦, 林昌禄. 雷达极化理论中常见极化散射矩阵特性分析[J]. 电子科技大学学报, 1993, 22(5): 490-500. Li Q and Lin C L. Analysis of characteristic properties of the common polarization scattering matrices in radar polarization theory[J]. Journal of University of Electronic Science and Technology of China, 1993, 22(5): 490-500.( 1) 1) |
| [11] | 刘志文, 柯有安. 雷达反隐身的若干问题与技术途径[J]. 现代雷达, 1992, 14(3): 1-8. Liu Z W and Ke Y A. On radar anti-stealth techniques and its problems[J]. Modern Radar, 1992, 14(3): 1-8.( 1) 1) |
| [12] | 林世明, 杨健. 目标散射矩阵的特征值理论和雷达天线的最优极化[J]. 电波科学学报, 1995, 10(1/2): 11-15. Lin S M and Yang J. Eigenvalue theory of scattering matrix and optimal polarization of radar antenna[J]. Chinese Journal of Radio Science, 1995, 10(1/2): 11-15.( 1) 1) |
| [13] | 常宇亮, 文玲, 戴幻尧. 目标交叉极化散射特性的强度分析[J]. 雷达科学与技术, 2012, 10(5): 544-548. Chang Y L, Wen L and Dai H Y. Analysis of cross-polarization scattering strength from target[J]. Radar Science and Technology, 2012, 10(5): 544-548.( 1) 1) |
| [14] | Jong-Sen Lee and Eric Pottier. Polarimetric Radar Imaging: From Basis to Applications[M]. Taylor & Francis Group, 2012: 93-95.( 1) 1) |
| [15] | 聂在平, 胡俊, 姚海英, 等. 用于复杂目标三维矢量散射分析的快速多极子方法[J]. 电子学报, 1999, 27(6): 104-109. Nie Z P, Hu J, Yao H Y, et al.. The fast multipole methods for vector analysis of scattering from 3-Dimensional objects with complex structure[J]. Acta Electronica Sinica, 1999, 27(6): 104-109.( 1) 1) |
| [16] | 盛新庆. 计算电磁学要论[M]. 第2版, 合肥: 中国科学技术大学出版社, 2008: 31-39. Sheng X Q. A Brief Treatise on Computational Electronmagnetics[M]. The Second Edition, Hefei: Press of University of Science and Technology of China, 2008: 31-39.( 1) 1) |
| [17] | 桑建华. 飞行器隐身技术[M]. 北京: 航空工业出版社, 2013: 63-68. Sang J H. Low-Obserbable Technologiese of Aircraft[M]. Beijing: Aviation Industry Publishing House, 2013: 63-68.( 1) 1) |


