②(北京跟踪与通信技术研究所 北京 100094)
②(Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, China)
雷达目标电磁散射机理研究是目标分类识别的基石[1]。高分辨成像和全极化测量都是现代雷达系统的重要发展趋势,研究高分辨全极化成像条件下雷达目标的极化散射机理,已成为雷达极化信息处理领域的热点问题。
目标总的电磁散射可以等效为某些局部位置上的电磁散射的合成,这些局部的散射源通常称为散射中心[1]。目标的散射中心主要产生于目标的边缘、棱角、尖端等曲率不连续点的部位,代表了目标的精细物理结构。通过分析散射中心的不同的散射机理,可为目标分类识别提供依据。基于散射中心特征来实现目标分类识别,相较于传统的自动目标识别方法,具有表述简洁,计算高效的优点。
对于散射中心散射机理的分析,目前主要针对极化SAR数据展开[2, 3, 4, 5, 6],例如:徐牧[3, 4]提出一种基于空频域极化特征的极化SAR图像人造目标几何结构反演方法,基于Cameron分解对散射机理进行分析,并反演出散射中心的几何特征。Fuller[5]针对极化SAR数据,将Krogager分解与GTD模型的频率依赖因子结合,对典型结构进行了更细致的划分,实现复杂目标各散射中心的类型判别。Michael[6]在此基础上,针对汽车的极化SAR数据,分析了散射结构类型特征对目标具有较强的可分性。
HRRP (High Resolution Range Profile)可以反映目标散射中心在纵向距离上的分布情况,而且其不要求目标相对于雷达平台有一定的转角,因而,HRRP的获取更加容易,对雷达平台有更大的适应性,在雷达目标识别中占据重要地位[7, 8]。因此,本文针对全极化HRRP,展开人造目标全极化HRRP散射机理的研究。本文首先基于极化分解技术,对全极化HRRP散射中心的散射机理进行分类,并分析了在几何结构判别时存在的问题。针对因目标方位角度不同而造成的几何结构误判,文中分析了极化方位角补偿方法对误判性能的改善。而针对几何结构反演中存在的不确定性,文中结合散射中心的频率色散性来提高判别的准确性。最后,通过对组合目标电磁仿真计算数据的实验,验证本文方法的有效性并分析了方法的应用条件。
2 散射中心空域极化特性分析GTD模型[9, 10]能精确描述雷达目标的高频电磁散射特性,并通过频率依赖因子反映散射中心的几何特征。而适用于全极化条件下的相干极化GTD模型,简称CP-GTD模型,是在GTD模型的基础上得到的[11]。该模型不仅能给出频率依赖因子,还能给出表征散射中心极化特性的散射矩阵,二者相互结合,能更完整地给出雷达目标的高分辨极化散射特性。
雷达目标的CP-GTD模型如下:
| ${x_l}\left( n \right) = {\rm{ }}{\rm{ }}\sum\limits_{m = 1}^d {s_{m,l}^{}{{\left( {{\rm{j}}\frac{{{f_n}}}{{{f_{\rm{c}}}}}} \right)}^{{\alpha _m}}}{{\rm{e}}^{ - {\rm{j}}\frac{{4{r_m}}}{c}{f_n}}}} + {u_l}\left( n \right),\qquad \quad \quad \;n = 1,2, \cdots ,N$ | (1) |
其中,${s_{m,l}}$为m 散射中心在 l极化测量下的复散射系数,它对应着散射矩阵的一个元素。 fn为信号频率,fc为载频。 a为散射中心对频率的依赖因子,其值由对应典型结构形状的曲率决定,通常是0.5的整数倍。采用P-MUSIC估计方法可对式(1)中的散射矩阵以及频率依赖因子进行估计,具体估计过程参见文献[11],这里不再赘述。
2.1 基于极化分解的散射机理分类极化分解技术利用极化信息,能够揭示目标的散射机理,增强对目标散射特性的理解。本文主要针对确定的人造目标进行分类识别,因此采用相干极化分解中的Krogager分解方法[12, 13]。相干极化分解的目的是将散射矩阵表示为几个典型散射机理的组合,其中Krogager分解方法将对称的散射矩阵分解为3个有具体物理意义的相干分量之和,分别为球散射、二面角散射和螺旋体散射,其表达式如下所示:
| $\begin{array}{*{35}{l}} {{\bf{S}}_{\left( {{\rm{H}},{\rm{V}}} \right)}}{\rm{ = }}{{\rm{e}}^{{\rm{j}}\phi }}\left\{ {{{\rm{e}}^{{\rm{j}}{\phi _s}}}{k_{\rm{S}}}\left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right] + {k_{\rm{D}}}\left[ {\begin{array}{*{20}{c}} {\cos 2\theta }&{\sin 2\theta }\\ {\sin 2\theta }&{ - \cos 2\theta } \end{array}} \right]} \right.\quad \quad \quad \;\left. { + {k_{\rm{H}}}{{\rm{e}}^{ \mp {\rm{j}}2\theta }}\left[ {\begin{array}{*{20}{c}} 1&{ \pm {\rm{j}}}\\ { \pm {\rm{j}}}&{ - 1} \end{array}} \right]} \right\} \end{array}$ | (2) |
式中,kS,kD和kH为实数,分别表示球散射,二面角散射和螺旋体散射分量的贡献,q是取向角,f是散射矩阵的绝对相位。显然,球散射代表了奇次散射的散射机理,二面角散射为偶次散射。
不同的散射中心对应一种主要的散射机理,为了更清楚地显示占优势的散射机理,计算奇次散射、偶次散射以及螺旋体散射的相对大小:${\kappa _{\rm{o}}} = \frac{{\left| {{k_{\rm{S}}}} \right|}}{{\left| {{k_{\rm{S}}}} \right| + \left| {{k_{\rm{D}}}} \right| + \left| {{k_{\rm{H}}}} \right|}},{\kappa _{\rm{e}}} = \frac{{\left| {{k_{\rm{D}}}} \right|}}{{\left| {{k_{\rm{S}}}} \right| + \left| {{k_{\rm{D}}}} \right| + \left| {{k_{\rm{H}}}} \right|}},{\kappa _{\rm{h}}} = 1 - {\kappa _{\rm{o}}} - {\kappa _{\rm{e}}}$。其中,${\kappa _{\rm{o}}}$,${\kappa _{\rm{e}}}$分别为奇次散射与偶次散射归一化的散射强度,而螺旋体散射的相对大小kh,由奇次与偶次散射的相对大小来决定。这3个由Krogager分解得到的特征参数,简称Krogager特征参数,表明了3种散射机理在总体散射中占的比例大小。
几何结构作为雷达目标的本质属性之一,它对目标的描述更加贴近人类视觉系统的感知方式。用典型的几何结构描述目标的外形轮廓,有利于对目标的属性类别做出判断。分析目标散射中心的散射机理,研究其对应的几何结构,对于雷达目标识别具有重要意义。一些典型的几何结构与散射机理以及Krogager特征参数的对应关系如表 1所示[2]。
| 表 1 Krogager特征参数与典型结构对应关系 Tab. 1 Krogager parameters for canonical scattering geometries |
目标的极化散射特性除了与自身属性密切相关外,还依赖于目标与雷达之间的位置关系。位置的不同,目标的极化散射矩阵产生变化,从而同一目标结构可能呈现出不同的散射机理,这将导致基于散射机理的几何结构判别出现误判。这种位置关系包括目标的俯仰角与方位角。由于成像识别时,目标的俯仰角通常较为固定,而目标的极化散射特性随方位角的变化通常更为显著,影响较大。因此下文研究典型结构方位角度变化时,对散射机理类型判别的影响。
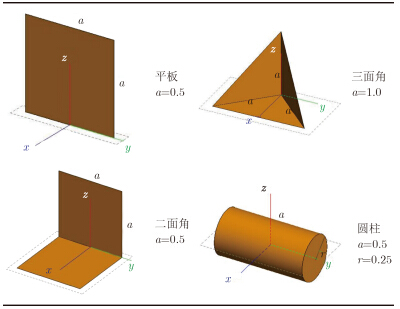
采用电磁仿真计算软件,计算典型结构目标在不同方位角下的全极化回波,并对数据展开2.1节所述的散射机理分析。由于方位变化对旋转对称性结构的极化特性不产生影响,且本文只研究人造目标包含的主要几何结构,因此,此处对平板、二面角、三面角以及水平放置的圆柱体这4类典型结构体展开研究,各几何结构的尺寸如表 2所示。雷达频率范围1.0~1.3 GHz,俯仰角为45°,方位角由0°~90°变化。各典型性结构的Krogager特征参数随方位角的变化情况如图 1所示。
| 表 2 典型几何结果尺寸(m) Tab. 2 Size of canonical scattering geometries (m) |

|
图 1 典型结构的Krogager特征参数随方位角变化关系 Fig.1 Variation of Krogager parameters of canonical scattering geometries with azimuth |
图 1中,随着典型几何结构方位角度的改变,呈现的散射机理有明显变化。其中三面角在0°~30°的方位角度范围内,保持奇次散射的机理,而平板、二面角以及圆柱维持散射机理不变的方位角度范围则相对较小。由此可见,基于散射机理来判定散射中心对应的几何结构,存在一定的姿态角限制,大于角域范围的姿态变化,将导致几何结构的误判。因此,在目标识别时,建立目标模型库,应以一定的角度范围划分区间,存储各角度区间中目标相应的模板。
2.3 极化方位角补偿对空域极化特性的影响目标方位角的变化,导致了目标极化方位角的旋转,使得相同的目标具有不同的散射矩阵,从而导致提取的散射机理不准确,影响目标的几何结构判定。而Kimura[14]研究了旋转的建筑体墙面导致极化方位角的变化,并推得极化方位角与目标方位角的关系式为:$\tan \theta = \frac{{ - \tan \alpha }}{{\cos \phi }}$,也说明了这一问题,其中q为极化方位角,a为目标方位角,f为雷达入射角。
极化方位角补偿是通过将不同极化方位角的散射矩阵围绕雷达视线方向旋转到同一极化方位角下,使具有不同极化方位角的同一散射体的散射矩阵变换到同一基准下,即达到同一散射目标具有相同的散射矩阵的目的,从而消除极化方位角对散射矩阵的影响。极化方位角补偿的关键就是对目标极化方位角的估计,目前极化方位角估计的方法主要有基于极化响应的方位角估计,基于圆极化方法极化方位角估计和基于极化目标分解的极化方位角估计等[15]。本文采用适应性较好、计算简洁、被广泛应用的基于圆极化的极化方位角的估计方法[16, 17],在H,V线极化基下的极化方位角q的估计公式为:
| $\begin{array}{*{35}{l}} \theta \text{=}\frac{1}{4}\left[ \arctan \left( \frac{-4\text{Re}\left( \left\langle \left( {{S}_{\text{HH}}}-{{S}_{\text{VV}}} \right)S_{\text{HV}}^{*} \right\rangle \right)}{-\left\langle {{\left| {{S}_{\text{HH}}}-{{S}_{\text{VV}}} \right|}^{2}} \right\rangle +4\left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle } \right)+{\rm{\pi }} \right], \\ \quad \ \theta >{\rm{\pi }} /4,\quad \theta =\theta -{\rm{\pi }} /2 \\ \end{array}$ | (3) |
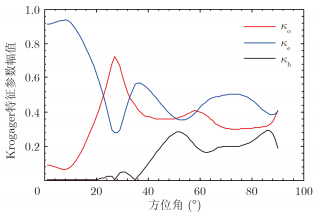
由此估计得到的极化方位角的范围为$\text{ }\!\![\!\!\text{ }-{\rm{\pi }} /4,{\rm{\pi }} /4\text{ }\!\!]\!\!\text{ }$。对2.2节中的实验数据,进行极化方位角补偿后,再进行Krogager分解,其中二面角的结果如图 2所示。
|
图 2 极化方位角补偿后的二面角极化分解结果 Fig.2 Krogager parameters of dihedral after polarization orientation angle compensation |
与图 1(c)比较可以看出,进行方位角补偿后,误判螺旋结构的概率有所降低,但奇、偶散射机理的误判仍然存在。可见,采用基于圆极化的极化方位角估计方法,不能准确估计出目标方位姿态变化引起的极化方位角旋转,从而不能有效消除目标姿态变化对散射机理分类的影响。分析其估计不准的原因,基于圆极化方法的极化方位角估计方法中,估计的极化方位角指的是目标偶次散射绕雷达视线的旋转角度[18],而这一角度并不能完全表征由于目标方位姿态角的变化,引起的极化方位角旋转,因此,该方法不能准确估计出该情况下的极化方位角。其起到的主要作用为降低了目标的交叉极化分量,从而减小了极化分解中螺旋散射分量的贡献。基于以上分析,为了通过补偿极化方位角来实现类型误判概率的进一步降低,还需要研究在该情况下更准确的极化方位角估计方法。
3 散射中心散射机理分类 3.1 散射中心频率色散特性由前文可以看到,单独依靠Krogager特征参数进行散射中心类型判别,存在较大的不确定性。因此,本文进一步分析散射中心的频率色散特性,并将其与极化特性结合,以达到降低类型判别的不确定性。Moghaddar 等人首先研究了散射中心的频率色散特性,在散射中心模型中引入了频率依赖关系${f^\alpha }$,这里a值由对应的几种典型散射机理(如镜面、边缘、尖顶等)及其多重绕射所决定,并结合导体平板的紧缩场数据进行了研究。Potter 等人提出的GTD模型,认为在高频光学区目标散射中心幅度具有明显的频率依赖性,因此GTD模型包含散射中心的类型因子,该因子考虑了频率色散所引起的目标散射特性变化,可以反映散射中心的几何特征[11]。频率依赖因子与典型散射结构具有如表 3所示的对应关系[9]。
| 表 3 频率依赖因子与典型结构对应关系 Tab. 3 Frequency response parameter for canonical scattering geometries |
从表中可以看到,频率依赖因子反映了散射中心的几何特征,但也存在不确定性,如:平板、二面角以及三面角的频率依赖因子均为1,仅依赖该特征参数,不能进行区分。
3.2 散射机理分类将Krogager特征参数与频率依赖因子这两类参数结合起来,对散射中心类型判别的不确定性将大大地降低[5]。为降低特征维数,Krogager特征参数仅取${\kappa _{\rm{o}}}$,${\kappa _{\rm{e}}}$这两个参数,形成了[a ${\kappa _{\rm{o}}}$ ${\kappa _{\rm{e}}}$]3维特征矢量。其具体求解方法为:首先采用P-MUSIC方法估计各散射中心的频率依赖因子与散射矩阵,之后对极化方位角补偿后的散射矩阵进行极化分解,得到Krogager特征参数,进而获得各散射中心对应的3维特征矢量。表 4中列出了各典型结构与特征矢量的对应关系,基于此可判定各散射中心的结构类型。
| 表 4 3维特征矢量与典型结构对应关系 Tab. 4 3-Dimensional parameter for canonical scattering geometries |
由表 4可见,该特征矢量可区分9类典型结构,不确定性降低。但是,在参数估计中,实际值与理论值存在一定偏差。因此采用最小二乘的方法,将实际值与理论值进行比较,来判定散射中心的类型:
| $d = \mathop {\arg \min }\limits_k {\left\| {{w_k} - v} \right\|^2}$ | (4) |
其中,wk为第k类典型结构对应的特征矢量的理论值,v为特征矢量的实际值,d则指示了使距离最小的理论值所对应的典型结构。
另外,由于频率依赖因子一般估计偏差较大,且敏感于模型误差、噪声和杂波,Krogager特征参数相较而言更准确。因此,在基于上述3维特征矢量进行分类而存在模糊时,依据Krogager特征参数来解模糊[5]。例如,对于特征矢量[-1, 1, 0],其与曲边特征矢量[-0.5,0.5,0.5]以及球体特征矢量[0, 1, 0] 均相距较近。但是由于其Krogager特征参数与球的严格匹配,将其判定为球更为合适。由此进一步定义特征矢量[-0.5,1,0]、[-1, 1, 0]为球体特征矢量,[0, 0, 1]、[-0.5,0,1]、[-1, 0, 1]为帽形结构特征矢量。
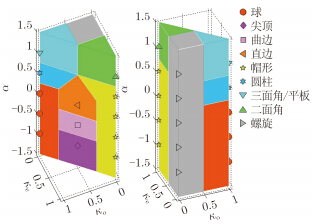
基于最小二乘方法以及以上设定,特征空间被划分为9个区域,分别对应9类典型结构,如图 3所示。由HRRP的散射中心提取的特征矢量,落于空间中某一区域中,就将其判定为该区域对应的典型结构类型。
|
图 3 典型结构在特征空间中的分布图 Fig.3 Feature space partitioned into scatterer classes |
实验1 为验证文中方法的可行性与有效性,本文应用Feko电磁计算软件对目标的回波进行仿真,得到相应的全极化HRRP。目标由不同散射机理的结构体组成,如图 4所示。仿真计算条件设为:雷达频率1.0~1.3 GHz,入射波俯仰角45°,以沿xoz平面入射为方位角0°。

|
图 4 组合体目标 Fig.4 Structure of the combined target |
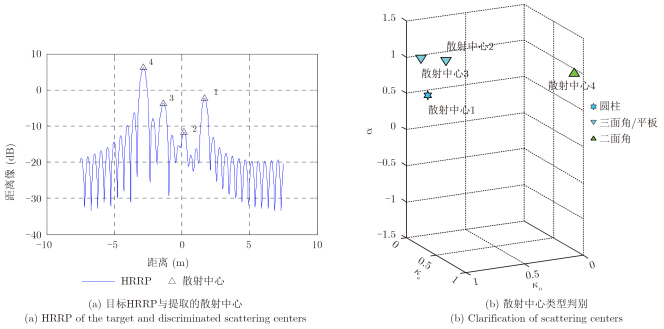
方位角为0°时的目标回波数据得到的HRRP,作为测试样本,进行散射机理类型判别实验,结果如图 5所示。
|
图 5 散射中心类型判别结果 Fig.5 Results of the classification of scattering centers |
图 5(a)为目标HH通道的HRRP,以及采用P-MUSIC方法提取得到的散射中心。4个散射中心,分别对应组合目标的4个散射结构。而提取各散射中心的频率依赖因子与Krogager特征参数,其值如图 5(b)所示。根据散射中心在该3维特征空间中的分布,判定各散射中心对应的散射结构分别为圆柱,三面角/平板以及二面角,与目标相一致。
实验2 该实验的目的为测试本文方法适用的角度域范围。以0.2°角度间隔,计算上述组合目标方位角-40°~40°间的全极化回波。并分别以10°到80°不等的角度范围,测试相应范围内正确判别散射中心类型的概率,以此研究不同的角度域大小对目标散射机理类型判别的影响。
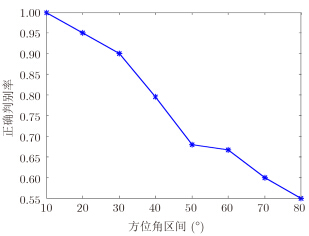
从图 6可见,当角域范围小于30°时,对目标正确类型判别的概率大于90%。因此,在建立目标的模板库时,以小于这个角度范围为间隔存储目标的特征模板,能对目标更准确地进行描述,从而得到更高的识别概率。
|
图 6 散射机理分类正确率随角域大小的变化 Fig.6 Variation of correct probability of scattering mechanism identification with angle bound |
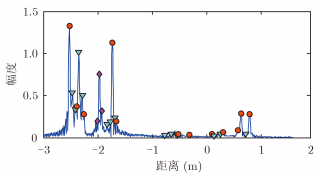
实验3 该实验以汽车(MazdaMPV)的电磁仿真计算数据进行实验,汽车模型如图 7所示。数据来自AFRL 民用汽车数据集[19],为中心频率9.6 GHz,带宽5.35 GHz时,3类汽车在俯仰角30°,全方位角条件下,全极化回波的电磁仿真计算数据。以汽车后视,即方位角180°时的1维距离像,进行散射机理的分类,结果如图 8所示。

|
图 7 MazdaMPV模型 Fig.7 MazdaMPV model |
|
图 8 MazdaMPV汽车HRRP与散射中心分类结果 Fig.8 HRRP of MazdaMPV and results of the classification of scattering centers |
图 8中,各散射中心处的图标,指示了散射中心的类型,图标定义与图 3中一致。由图可见,汽车后视时,平板与球(双曲面)散射结构较多,也存在部分尖顶结构。其中在距离像中的汽车尾部以及中间位置,主要呈平板结构。而由汽车模型看,车尾与车顶,符合平板散射机理的分类。
5 结论本文针对人造目标的全极化HRRP,研究了基于散射中心的散射机理分类判别方法。文中首先分析了基于极化分解技术的目标散射机理分类判别,此后,针对目标方位角变化导致的类型误判问题,研究了极化方位角补偿技术对误判性能的改善。随后,文中结合目标的频率色散特性,构造了散射中心类型判别的特征矢量,该特征矢量与典型结构的对应关系大大降低了类型判别的不确定性。经实验验证,在一定的角域范围内,本文提出的方法能有效实现目标散射中心散射机理的分类。
| [1] | 黄培康, 殷红成, 许小剑, 等. 雷达目标特性[M]. 北京: 电子工业出版社, 2005. Huang P K, Yin H C, Xu X J, et al.. Radar Target Signature[M]. Beijing: Publishing House of Electronics Industry, 2005.( 2) 2) |
| [2] | Jackson J A. Three-dimensional feature models for synthetic aperture radar and experiments in feature extraction[D]. [Ph.D. dissertation], Ohio State University, 2009.( 2) 2) |
| [3] | 徐牧, 王雪松, 肖顺平, 等. 基于散射机理分类与方位对称性判决的极化SAR人造目标提取[J]. 国防科技大学学报, 2008, 30(5): 68–72. Xu M, Wang X S, Xiao S P, et al.. Man-made target extraction based on scattering mechanism identification and azimuthal symmetry decision of POLSAR images[J]. Journal of National University of Defense Technology, 2008, 30(5): 68–72.( 1) 1) |
| [4] | 徐牧. 极化 SAR 图像人造目标提取与几何结构反演研究[D]. [博士论文], 国防科学技术大学, 2008. Xu M. Extraction and geometrical structure retrieval of man-made target in POLSAR imagery[D]. [Ph.D. dissertation], National University of Defense Technology, 2008.( 1) 1) |
| [5] | Fuller D F. Phase history decomposition for efficient scatterer classification in SAR imagery[D]. [Ph.D. dissertation], Air Force Institute of Technology, 2011.( 4) 4) |
| [6] | Saville M A, Jackson J A, and Fuller D F. Rethinking vehicle classification with wide-angle polarimetric SAR[J]. IEEE Aerospace and Electronic Systems Magazine, 2014, 29(1): 41–49.( 2) 2) |
| [7] | 冯博, 陈渤, 王鹏辉, 等. 利用稳健字典学习的雷达高分辨距离像目标识别算法[J]. 电子与信息学报, 2015, 37(6): 1457–1462. Feng B, Chen B, Wang P H, et al.. Radar high resolution range profile target recognition algorithm via stable dictionary learning[J]. Journal of Electronics & Information Technology, 2015, 37(6): 1457–1462.( 1) 1) |
| [8] | Wang J, Li Y, and Chen K. Radar high-resolution range profile recognition via geodesic weighted sparse representation[J]. IET Radar, Sonar & Navigation, 2015, 9(1): 75–83.( 1) 1) |
| [9] | Potter L C, Chiang D-M, Carriere R, et al.. A GTD-based parametric model for radar scattering[J]. IEEE Transactions on Antennas and Propagation, 1995, 43(10): 1058–1067.( 2) 2) |
| [10] | Potter L C and Moses R. Attributed scattering centers for SAR ATR[J]. IEEE Transactions on Image Processing, 1997, 6(1): 79–91.( 1) 1) |
| [11] | 代大海. 极化雷达成像及目标特征提取研究[D]. [博士论文], 国防科学技术大学, 2008. Dai D H. Study on polarimetric radar imaging and target feature extraction[D]. [Ph.D. dissertation], National University of Defense Technology, 2008.( 3) 3) |
| [12] | Krogager E. New decomposition of the radar target scattering matrix[J]. Electronics Letters, 1990, 26(18): 1525–1527.( 1) 1) |
| [13] | Lee J-S and Pottier E. Polarimetric Radar Imaging: From Basics to Applications[M]. Taylor & Francis Group, CRC Press, 2009.( 1) 1) |
| [14] | Kimura H, Papathanassiou K P, and Hajnsek I. Polarization orientation effect in urban areas on PolSAR data[C]. Proceedings of IGARSS 2005, Seoul, 2005, 7: 4863–4867. .( 1) 1) |
| [15] | 龙江平, 丁晓利, 汪长城. 极化方位角补偿信息支持下的植被参数反演[J]. 测绘学报, 2014, 43(10): 1051–1060. Long J P, Ding X L, and Wang C C. Forest parameters inversion with the support of compensation information of radar polarization orientation angle[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1051–1060.(  1) 1) |
| [16] | Lee J S, Krogag er E, Schuler D L, et al.. On the estimation of polarization orientation angles induced from azimuth slopes using polarimetric SAR data[C]. IEEE 2000 Processing of International Geoscience and Remote Sensing Symposium, Honolulum, HI, 2000, 3: 1310–1312.( 1) 1) |
| [17] | Lee J S, Schuler D L, Ainworth T L, et al.. On the estimation of radar polarization orientation shifts induced by terrain slopes[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(1): 30–41.( 1) 1) |
| [18] | Lee J-S, Schuler D L, and Ainworth T L. Polarimetric SAR data compensation for terrain azimuth slope variation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(5): 2153–2163.( 1) 1) |
| [19] | Dungan K E, Austin C, Nehrbass J, et al.. Civilian vehicle radar data domes[C]. Proceedings of the SPIE, Orlando, 2010, 7699. doi: 10.117/12.850151.( 1) 1) |