② (哈尔滨工业大学信息感知技术协同创新中心 哈尔滨 150001)
② (Collaborative Innovation Center of Information Sensing and Understanding at Harbin Institute of Technology, Harbin 150001, China)
利用高频频段(3~30 MHz)的垂直极化电磁波远超过微波雷达探测范围的传播优势,高频地波雷达可实现对海面舰船和超低空飞行器的超视距探测。基于这一特点,高频地波雷达被认为是一种能实现濒海国家管控和监督海上专属经济区的主要技术手段。特别是当高频地波雷达工作在高频频段中的低频部分(3~6 MHz)时,其可以更低的损耗实现更远的作用距离[1, 2]。
然而,在获取超视距探测这一优势时,高频地波雷达不可避免地受到电离层杂波、海杂波、电台干扰和其他工业干扰的影响,这制约了高频地波雷达的探测性能。其中,电离层杂波以其能量强、存在时间长、覆盖连续多个距离单元和多普勒单元等众多特点,成为了影响高频地波雷达探测性能的主要因素[3]。因此,研究有效的电离层杂波抑制措施来降低其对高频地波雷达的影响,是当前研究高频雷达抗干扰的一个重点。
目前电离层杂波抑制的方法主要集中在空域自适应波束形成方法[4, 5, 6, 7, 8]、旁瓣对消抗干扰方法[9, 10, 11, 12]和极化域抗干扰方法[13, 14, 15, 16]上。其中,空域自适应波束形成方法主要是通过自适应地调节阵列的权值,在保留期望信号的同时最大限度地抑制电离层杂波干扰;旁瓣对消方法则是加一系列辅助天线,将主瓣波束对准目标信号,并在干扰副瓣上形成零点,以达到在空间和时间上良好的抑制效果;而极化域抗干扰则是利用一对或一组正交极化天线获取回波信号的极化特性再加以滤波。虽然这些方法是基于高频地波雷达不同的接收阵列和接收条件而提出来的,但都利用了电离层杂波与目标信号在空域或极化域上参数的差异,并能取得不错的抑制效果。然而,若电离层杂波与目标信号的来波方向相近甚至相同时,在空域上抑制杂波将很难取得更好的效果;特别地,当前实际应用的高频地波雷达的接收阵列以线阵为主,因而无法同时提供方位角和俯仰角上的分辨力[3],这就导致即使电离层杂波与目标信号在方位角和俯仰角上都有较大的差异,也可能因为空间频率的值近似甚至相同,无法在空域上提供良好的电离层杂波抑制效果。类似地,若电离层杂波的极化状态与目标信号的极化状态相近时,在极化域上抑制杂波也难以取得理想的效果。同时,一些抑制电离层杂波的算法未讨论在实际情况中如何准确地估计杂波的参数,并将其运用到杂波抑制算法当中。另一些算法给出了参数估计方法,但运用到实测数据中存在困难或局限性。例如有人提出用多重信号分类(Multiply Signal Classification, MUSIC)算法对电离层杂波测角[12],但MUSIC算法需获取大量的快拍数并需要已知信号个数,而在现实情况中这些条件难以全部满足。
为了解决上述问题,本文首先以L型阵列作为高频地波雷达接收阵列,将空域极化域协同滤波算法[17]运用到电离层杂波抑制中。然后在距离-多普勒域上将基于压缩感知(Compressive Sensing, CS)的DOA测角方法[18]用于电离层杂波的空域参数估计,并提出在距离-多普勒域上基于统计特性的极化参数估计方法。最后通过对实测数据的处理,给出实测数据的空域参数估计和极化域参数估计,并通过参数估计后的滤波结果对比验证参数估计方法和空域极化域协同滤波算法的有效性。
2 接收阵列模型及基本信号处理 2.1 高频地波雷达接收阵列模型本文中高频地波雷达接收阵列为16个阵元组成的L型极化敏感阵列,如图 1所示。其中,平行于海岸线的8个阵元为主阵,垂直于海岸线的8个阵元为辅阵。主阵的阵元间距为d1=12 m,辅阵的阵元间距为d2=12 m,主阵与辅阵相距d3=10 m。图 1中辅阵里方框代表水平极化天线,其余圆圈均表示为垂直极化天线。另外,图 1中的$\theta$∈[0, 90°]表示俯仰角,定义指向天顶时为0°; $\phi$∈[-180°, 180°]表示方位角,定义指向正前方(主阵法线方向)时为0°。

|
图 1 接收阵列模型 Fig.1 Receive array model |
需要指出的是,图 1所示的接收阵列中垂直极化阵元数较多,可在空域上对杂波进行抑制。而水平极化通道则与垂直极化通道做极化信息处理,在极化域上实现杂波抑制。
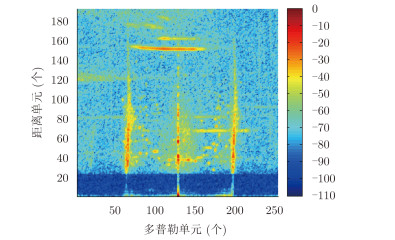
2.2 信号模型及基本信号处理过程各个通道接收到的远场回波信号一般在经过混频、采样、正交双通道处理和相干积累后,先得到距离域信息,然后将距离域的信号做快速傅里叶变换(FFT),得到信号的频域信息。为了更好地表现回波信号的多普勒效应及其信息,一般将频域转变到信号的多普勒域,最后得到距离-多普勒谱(Range-Doppler spectrum, RD谱)。一个垂直极化通道形成的RD谱如图 2所示。图中横坐标表示多普勒单元,纵坐标表示距离单元,各个距离-多普勒单元的功率根据数值大小用不同的颜色表征。
|
图 2 垂直极化通道的RD谱 Fig.2 The Range-Doppler spectrum of vertical polarization chennal |
在极化敏感阵列中,信号的极化信息表现为阵元中两正交极化通道(即由一个垂直极化通道和一个水平极化通道组成)之间的相关特性。假设信号S(ri, fj)是极化角为ε、极化角相差为η的完全极化平面波,于是有[15]:
| $ \begin{align} & \mathit{\boldsymbol{S}}\left( {{r}_{i}}, {{f}_{j}} \right)=\left[\begin{matrix} \cos \theta & \cos \phi \sin \theta \\ 0 &-\sin \phi \\ \end{matrix} \right]\left[\begin{matrix} s\left( {{r}_{i}}, {{f}_{j}} \right)\cdot \cos \varepsilon \\ s\left( {{r}_{i}}, {{f}_{j}} \right)\cdot \sin \varepsilon {{\rm{e}}^{\rm{j}\eta }} \\ \end{matrix} \right] \\ &\;\;\;\;\;\;\;\;\;\;\;\; =\left[\begin{matrix} \cos \theta & \cos \phi \sin \theta \\ 0 &-\sin \phi \\ \end{matrix} \right]\left[\begin{matrix} \cos \varepsilon \\ \sin \varepsilon {{\rm{e}}^{\rm{j}\eta }} \\ \end{matrix} \right]s\left( {{r}_{i}}, {{f}_{j}} \right) \\ &\;\;\;\;\;\;\;\;\;\;\;\; ={{\mathit{\boldsymbol{a}}}_{\rm{p}}}s\left( {{r}_{i}}, {{f}_{j}} \right) \\ \end{align} $ | (1) |
同时,阵列中的各垂直极化通道经过上述信号处理后可将接收的数据展示成如下形式,即:
| $ \begin{align} & \mathit{\boldsymbol{x}}\left( {{r}_{i}}, {{f}_{j}} \right)=\mathit{\boldsymbol{a}}\left( {{r}_{i}}, {{\theta }_{\rm{i}}}, {{\phi }_{\rm{i}}} \right){{\mathit{\boldsymbol{S}}}_{\rm{i}}}\left( {{r}_{i}}, {{f}_{j}}, 2 \right) \\ &\;\;\;\;\;\;\;\;\;\;\;\; +\mathit{\boldsymbol{a}}\left( {{r}_{i}}, {{\theta }_{\rm{t}}}, {{\phi }_{\rm{t}}} \right){{\mathit{\boldsymbol{S}}}_{\rm{t}}}\left( {{r}_{i}}, {{f}_{j}}, 2 \right)+\mathit{\boldsymbol{n}}\left( {{r}_{i}}, {{f}_{j}} \right) \\ \end{align} $ | (2) |
| $ {\tau _1} =-2{\rm{ \mathsf{ π} }}{d_1}\sin \theta \left( {-\cos \phi } \right)/\lambda $ | (3) |
| $ {\tau _2} =-2{\rm{ \mathsf{ π} }}{d_2}\sin \theta \sin \phi /\lambda $ | (4) |
| $ \begin{array}{l} {\mathit{\boldsymbol{a}}_{\rm{s}}} = \mathit{\boldsymbol{a}}\left( {{r_i},\theta ,\phi } \right)\\ \;\;\; = \left[ {\begin{array}{*{20}{c}} {1\; \cdots \;{{\rm{e}}^{{\rm{j}}\left( {{M_1} - 1} \right){\tau _1}}}\;{{\rm{e}}^{{\rm{j}}2{\rm{ \mathsf{ π} }}{d_3}\sin \theta \left( { - \cos \phi } \right)/\lambda }}\; \cdots } \end{array}} \right.\\ {\left. {\;\;\;\;\;\;\;\;\begin{array}{*{20}{c}} {{{\rm{e}}^{{\rm{j}}2{\rm{ \mathsf{ π} }}{d_3}\sin \theta \left( { - \cos \phi } \right)/\lambda }} \cdot {{\rm{e}}^{{\rm{j}}{M_2}{\tau _2}}}} \end{array}} \right]^{\rm{T}}} \end{array} $ | (5) |
设远场信号s经L型极化敏感阵列接收并经基本信号处理后的输出为:
| $ z\left( {{r_i}, {f_j}} \right) = {\mathit{\boldsymbol{a}}_{{\rm{sp}}}} \cdot s\left( {{r_i}, {f_j}} \right) $ | (6) |
| $ {\mathit{\boldsymbol{a}}_{{\rm{sp}}}} = {\mathit{\boldsymbol{a}}_{\rm{s}}} \otimes {\mathit{\boldsymbol{a}}_{\rm{p}}} $ | (7) |
| $ {\mathit{\boldsymbol{a}}_{{\rm{sp}}}} = \left[{\begin{array}{*{20}{c}} {({\rm{- }}\sin \phi \sin \varepsilon {{\rm{e}}^{{\rm{j}}\eta }}) \cdot {\rm{1}}}\\ \vdots \\ {({\rm{- }}\sin \phi \sin \varepsilon {{\rm{e}}^{{\rm{j}}\eta }}) \cdot {{\rm{e}}^{{\rm{j}}\left( {{M_1}{\rm{- }}1} \right){\tau _1}}}}\\ \vdots \\ {({\rm{ - }}\sin \phi \sin \varepsilon {{\rm{e}}^{{\rm{j}}\eta }}) \cdot {{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}{d_3}\sin \theta \left( { - \cos \phi } \right)/\lambda }} \cdot {{\rm{e}}^{{\rm{j}}{M_2}{\tau _2}}}}\\ {(\cos \theta \cos \varepsilon + \cos \phi \sin \theta \sin \varepsilon {{\rm{e}}^{{\rm{j}}\eta }}) \cdot {{\rm{e}}^{{\rm{j}}[\left( {m-1} \right){\tau _2}{\rm{ + }}\tau ']}}} \end{array}} \right] $ | (8) |
| $ z\left( {{r_i},{f_j}} \right) = {\mathit{\boldsymbol{a}}_{{\rm{sp}},{\rm{t}}}}{s_{\rm{t}}}\left( {{r_i},{f_j}} \right){\rm{ + }}{\mathit{\boldsymbol{a}}_{{\rm{sp}},{\rm{i}}}}{s_{\rm{i}}}\left( {{r_i},{f_j}} \right) + \mathit{\boldsymbol{n}}\left( {{r_i},{f_j}} \right) $ | (9) |
考虑列满秩矩阵A∈
| $ {\mathit{\boldsymbol{E}}_{{\bf{AB}}}} = \mathit{\boldsymbol{A}}{\left( {{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{P}}_B^ \bot \mathit{\boldsymbol{A}}} \right)^{-1}}{\mathit{\boldsymbol{A}}^{\rm{H}}}\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{B}}^ \bot $ | (10) |
| $ \mathit{\boldsymbol{P}}_\mathit{\boldsymbol{B}}^ \bot = \mathit{\boldsymbol{I}}-\mathit{\boldsymbol{B}}{({\mathit{\boldsymbol{B}}^{\rm{H}}}\mathit{\boldsymbol{B}})^{-1}}{\mathit{\boldsymbol{B}}^{\rm{H}}} $ | (11) |
| $ {\mathit{\boldsymbol{E}}_{{\bf{AB}}}}\mathit{\boldsymbol{A}} = \mathit{\boldsymbol{A}} $ | (12) |
| $ {\mathit{\boldsymbol{E}}_{{\bf{AB}}}}\mathit{\boldsymbol{B}} = 0 $ | (13) |
| $ {\mathit{\boldsymbol{w}}_{{\rm{sp}}}} = {\left( {{\mathit{\boldsymbol{A}}_{{\rm{sp}}}}{\mathit{\boldsymbol{a}}_{{\rm{sp}},{\rm{t}}}}{{\left( {\mathit{\boldsymbol{a}}_{{\rm{sp}},{\rm{t}}}^{\rm{H}}\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{a}}_{{\rm{sp}},{\rm{i}}}}}^ \bot {\mathit{\boldsymbol{a}}_{{\rm{sp}},{\rm{t}}}}} \right)}^{ - 1}}\mathit{\boldsymbol{a}}_{{\rm{sp}},{\rm{t}}}^{\rm{H}}\mathit{\boldsymbol{P}}_{{\mathit{\boldsymbol{a}}_{{\rm{sp}},{\rm{i}}}}}^ \bot } \right)^{\rm{H}}} $ | (14) |
| $ \begin{array}{l} {{\hat s}_{\rm{t}}}\left( {{r_i},{f_j}} \right)\\ = \mathit{\boldsymbol{w}}_{{\rm{sp}}}^{\rm{H}}\left( {{\mathit{\boldsymbol{a}}_{{\rm{sp}},{\rm{t}}}}{s_{\rm{t}}}\left( {{r_i},{f_j}} \right) + {\mathit{\boldsymbol{a}}_{{\rm{sp}},{\rm{i}}}}{s_{\rm{i}}}\left( {{r_i},{f_j}} \right) + \mathit{\boldsymbol{n}}\left( {{r_i},{f_j}} \right)} \right)\\ = \mathit{\boldsymbol{w}}_{{\rm{sp}}}^{\rm{H}}{\mathit{\boldsymbol{a}}_{{\rm{sp}},{\rm{t}}}}{s_{\rm{t}}}\left( {{r_i},{f_j}} \right) + \mathit{\boldsymbol{w}}_{{\rm{sp}}}^{\rm{H}}{\mathit{\boldsymbol{a}}_{{\rm{sp}},{\rm{i}}}}{s_{\rm{i}}}\left( {{r_i},{f_j}} \right) + \mathit{\boldsymbol{n}}\left( {{r_i},{f_j}} \right)\\ = {s_{\rm{t}}}\left( {{r_i},{f_j}} \right) + \mathit{\boldsymbol{w}}_{{\rm{sp}}}^{\rm{H}}\mathit{\boldsymbol{n}}\left( {{r_i},{f_j}} \right) \end{array} $ | (15) |
电离层杂波和目标信号的特征区别首先表现在距离-多普勒域上。电离层的高度大致是已知的。白天,E层可能出现在离地高度为90~140 km中的某一高度上;F层白天常分为2层,其中F1层可能出现在170~220 km中的某一高度上,F2层可能出现在220~450 km中的某一高度上。电离层具体出现的位置主要取决于当时该电离层内最大电子浓度所在的高度[3],各电离层在白天形成的杂波常出现在RD谱内大致相似的距离上并占据若干距离单元,同时在多普勒域上有明显的展宽。夜间,随着太阳辐射的减弱,电离层中的E层会消失;F1层上升,与F2层合成一片F层区域。相应地,晚上录取的数据形成的RD谱上一般不会出现E层杂波,同时会出现一大片F层杂波,但其在RD谱上出现的距离比白天要远。例如图 2所示的RD谱是某年1月下午录取的数据,图中距离单元大于150且有多普勒展宽的高能量区域即为明显的F层杂波干扰。而目标信号在RD谱内通常表示为占据不超过5个距离-多普勒单元的十字形式。因而电离层杂波和目标信号在RD谱上的特征差异十分明显,可用于完成距离域参数和速度域参数的提取。
根据RD谱中估计出的电离层杂波位置,在滤波前需要对出现电离层杂波的区域估测出电离层杂波的空域参数和极化参数。然后利用RD谱中多普勒频率处于两个由海杂波形成的Bragg峰之间、距离域上小于90 km的区域内确定的目标信号,估测出目标信号的空域参数和极化参数。
3.3 空域参数估计由3.1节滤波的过程可知,对目标信号和电离层杂波的参数估计很大程度影响滤波的效果。特别地,由于电离层杂波在时域上的非平稳性,在保证高频地波雷达输出信噪比的情况下很难获得多个快拍,故需要在单快拍下获取杂波的来波方向。
基于CS的DOA估计理论在来波信号稀疏的情况下,可以用较少的快拍数以较高的概率重构回波信号。由于在单个距离-多普勒单元上,电离层杂波的来波方向非常少,符合CS的应用条件。故本文使用基于CS的单快拍测角算法[18]进行电离层杂波测向。具体地,对L型阵列中主阵接收到的回波信号和辅阵接收到的回波信号分别用上述方法测角,得到在直角坐标系下的回波信号与主阵的夹角∠TOB及回波信号与辅阵的夹角∠TOA,如图 1所示。为方便起见,记α=∠TOA, β=∠TOB。
根据图 1, α和β与信号的俯仰角$\theta$和方位角$\phi$有如下关系:
| $ \cos \alpha = \sin\theta \left( { - \cos \phi } \right) $ | (16) |
| $ \cos \beta = \sin\theta \sin \phi $ | (17) |
根据式(16)和式(17),可解出信号的俯仰角和方位角如下:
| $ \theta = \arcsin \left( {\sqrt {{{\cos }^2}\alpha + {{\cos }^2}\beta } } \right) $ | (18) |
| $ \phi {\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {\arctan (cos\beta /\cos \alpha ),}&{\cos \alpha > 0}\\ {\arctan (cos\beta /\cos \alpha ) + {{180}^ \circ },}&{\cos \alpha < 0} \end{array}} \right. $ | (19) |
当前对信号极化参数的估计大多出现在基于极化敏感阵列的空域极化域多参数联合估计方法中,例如子空间理论中的极化Root-MUSIC方法[20],基于稀疏重构的联合估计方法[21]和基于张量理论的联合估计方法[22]。对高频地波雷达而言,由于快拍数的限制,利用实测数据进行极化参数估计的有效方法还不是很多。同时由于目标信号的回波来自海面,其回波的水平极化分量被海水吸收,所以高频地波雷达想要探测的目标信号的极化角一般非常大(接近90°);而发射的垂直极化电磁波经电离层反射后既有垂直极化波,也有水平极化波,因而极化角不会非常大,于是我们只需对电离层杂波的极化参数进行估计。
由于电离层杂波聚集在有限的连续相邻的距离-多普勒单元上可使得干噪比较高,洪泓等人[16]提出了一种基于距离-多普勒域的电离层杂波极化参数估计方法,即在判定电离层杂波存在的若干连续距离单元上,逐距离单元计算每个距离-多普勒单元上的极化参数,将上述每个距离单元内能量最大的距离-多普勒单元的极化参数作为该距离单元的极化参数估计值,故可被称为能量最大极化参数估计方法。实测数据处理结果显示,利用该估计方法获得的极化参数进行极化域抑制电离层杂波能取得较好的效果,这说明该极化参数估计方法能较为有效地估计杂波的极化参数。
但是,如果能量最大的距离-多普勒单元内存在目标信号,则目标信号不同于电离层杂波的极化特性会导致上述估计方法得到的极化参数不精确甚至失效。
在距离域上可被分离出来且只占据若干连续距离单元(不超过6~7 km)的电离层杂波被视为镜面反射杂波[3],在较小的相干积累时间内具有较大的平稳性。同时其在相邻的距离单元和多普勒单元上具有一定的相似性[3],于是本文提出一种在距离-多普勒域上基于统计特性的极化参数估计方法,来解决上述估计极化参数方法受目标信号影响这一问题。首先,为避免噪声的影响,设定信号功率门限,将出现镜面反射杂波且满足功率大于该门限的距离-多普勒单元保留下来;接着,将保留下来的距离-多普勒单元的极化参数统计起来取平均值,作为这片杂波的极化估值,从而可极大地降低被电离层杂波覆盖的目标信号对该杂波极化参数估计的影响。这一估计方法与能量最大极化参数估计方法对实测数据处理的结果将在第4节展示。
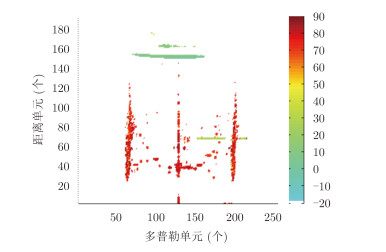
4 实测数据处理结果 4.1 空域参数估计结果为验证基于CS的单快拍测角算法用于电离层杂波测向的有效性,我们对沿海某高频地波雷达的实测数据进行了处理。该数据的原始RD谱如图 2所示,设定能量门限对该图中的距离-多普勒单元做能量上的提取,将大于门限的距离-多普勒单元做基于CS的测向,得到该单元的俯仰角和方位角,然后我们将得到的每个距离-多普勒单元上信号的俯仰角和方位角根据数值用不同的颜色表征,就得到信号在距离-多普勒域上的俯仰角谱和方位角谱,分别如图 3和图 4所示。图 3中俯仰角0°对应天顶方向,90°对应水平方向。图 4中0°对应主阵列法线方向,即指向海面正前方。
|
图 3 能量最大信号的俯仰角谱 Fig.3 The pitch angle spectrum of the signal with maximum power |
|
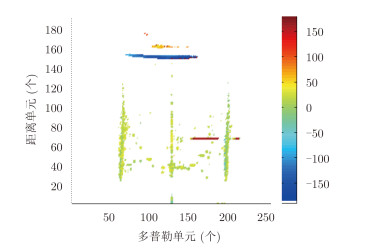
图 4 能量最大信号的方位角谱 Fig.4 The azimuth spectrum of the signal with maximum power |
从图 3所示的俯仰角谱可以看到,电离层杂波的俯仰角主要来自天顶方向和斜向,而海杂波和目标信号主要来自俯仰角很大的海面方向。从图 4所示的方位角可以看到,目标信号和海杂波的方位角主要集中在正负45°之间,而尽管在每个区域中的电离层杂波方位基本一致,不同区域的电离层杂波却对应于不同的方位角,表明不同区域的电离层杂波是由不同的电离层反射产生的,且各个电离层对应的方位角不同。
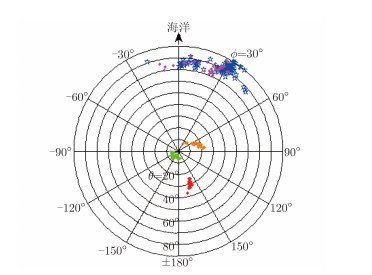
为了进一步表现出电离层杂波与目标信号及海杂波在方向上的差异,将电离层杂波和目标信号及海杂波的测角结果展现在图 5中。其中,红色点、绿色点和橘黄色点分别对应图 2中处于第69距离单元、第153距离单元和第163距离单元附近的电离层杂波;蓝色五角星对应距离单元在30到60之间的目标信号的测角结果;粉红色点代表距离单元在30到60之间的海杂波的测角结果。图 5中同心圆的半径由内到外表示从0°到90°的俯仰角$\theta$;每个同心圆的圆周表示方位角$\phi$,其0°指向主阵列法线方向,即海面正前方;每个点表示一个距离-多普勒单元中测到的信号的俯仰-方位角度。从图 5中可以更清晰地看到,电离层杂波以来自天顶附近方向为主,而目标信号主要来自海面。
|
图 5 电离层杂波和目标信号及海杂波的角度谱 Fig.5 The angle spectrum of the ionospheric clutter, target signal and sea clutter |
为了对比能量最大极化参数估计方法和本文所提的在距离-多普勒域上基于统计特性的极化参数估计方法,我们在第(153, 126)距离-多普勒单元添加了一个俯仰角为82°,方位角为30°的目标信号,该信号的俯仰角和方位角与第(59, 136)距离-多普勒单元的真实目标信号一致。同时由于基本信号处理中窗函数的运用,该信号对其相邻的上下左右4个距离-多普勒单元均有影响,并且该目标信号被F层杂波覆盖。
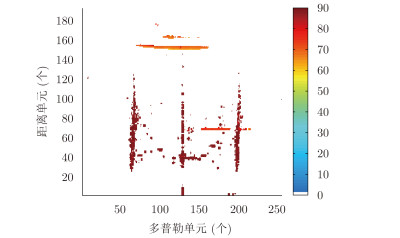
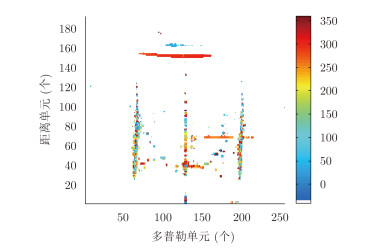
类似RD谱,我们将每个距离-多普勒单元上信号的极化角和极化角相差根据数值用不同的颜色表征,就得到信号在距离-多普勒域上的极化角谱和极化角相差谱。于是,我们对添加了目标信号后的距离-多普勒域上的信号作极化参数估计,其结果如图 6和图 7所示。
|
图 6 极化角谱 Fig.6 The spectrum of polarization angle |
|
图 7 极化角相差谱 Fig.7 The spectrum of polarization phase delay |
从图 6可以看到电离层杂波的极化角与海杂波及可能的目标信号差异明显,同时连续存在电离层杂波的距离单元上的极化角几乎一致。从图 7也可以看到每片电离层杂波的极化角相差也基本保持一致,并与海杂波和海面上的信号差异明显。这为下一步的滤波做好了参数准备。同时处理结果显示,当未加入目标信号时,能量最大极化参数估计方法得到的第153距离单元的极化角和极化角相差分别为67.6°和294.1°;基于统计特性极化参数估计方法得到的结果分别为67.4°和295.7°,两种方法估计的数值基本一致。而当加入目标信号后,能量最大极化参数估计方法得到的第153距离单元的极化角和极化角相差分别为81.7°和332.8°,与未加入目标信号相比估计值变化很大,这会影响到接下来的滤波;而基于统计特性极化参数估计方法得到的结果分别为67.4°和295.8°,与未加入目标信号时的估计值相比基本不变,避免了目标信号对电离层杂波的极化参数估计的影响。
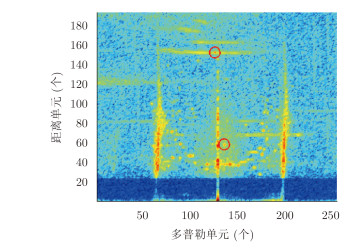
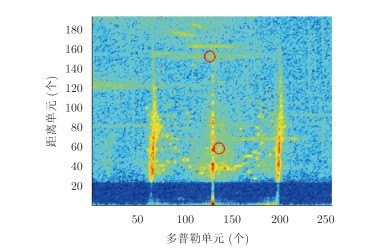
4.3 协同滤波处理结果图 8给出用能量最大极化参数估计电离层杂波极化信息后的空域极化域协同滤波结果。对比图 2我们可以看到除了距离单元153及其附近的电离层杂波,其他区域的电离层杂波都受到了较好的抑制,而153距离单元及其附近的电离层杂波由于极化参数估计不准确的影响,未能对该区域的电离层杂波形成很好的抑制效果。相应地,图 9给出的是在基于统计特性的极化参数估计后的空域极化域协同滤波结果。从图 9中我们可以看到各个不同区域的电离层杂波被较好地抑制,其总体抑制效果要好于图 8。同时,从图 8和图 9中红色圆圈内可以看到,第(153, 126)和第(59, 136)距离-多普勒单元中的仿真目标信号和真实目标信号都被保留下来。对比图 8和图 9,可以看到极化参数估计对后继滤波效果有较为明显的影响。
|
图 8 能量最大极化参数估计后的空域极化域协同滤波结果 Fig.8 The output of space-polarization collaborative filter after estimation of polarization parameter based on maximum power |
|
图 9 基于统计特性的极化参数估计后的空域极化域协同滤波结果 Fig.9 The output of space-polarization collaborative filter after estimation of polarization parameter based on statistical characteristics |
本文使用一种斜投影空域极化域协同滤波完成电离层杂波抑制。在距离-多普勒域上将基于CS的DOA测角方法应用于电离层杂波的方向估计,并提出一种基于统计特性的极化参数估计方法实现极化参数估计。这两种参数估计算法都利用了电离层杂波在距离-多普勒域上具有更高的干噪比的特性,估计性能的提升使基于空域极化域协同滤波的电离层杂波抑制算法取得更好的效果。实测数据处理结果表明了参数估计方法和滤波算法的有效性。
| [1] |
Chan H C. Iceberg detection and tracking using high frequency surface wave radar[R]. Defence Research Establishment Ottawa (ontario), 1997.
( 0) 0)
|
| [2] |
Chan H C. Detection and tracking of low-altitude aircraft using HF surface-wave radar[R]. Defence Research Establishment Ottawa (ontario), 1998.
( 0) 0)
|
| [3] |
Chan H C. Characterization of ionospheric clutter in HF surface-wave radar[R]. Defence R & D Canada-Ottawa, 2003.
( 0) 0)
|
| [4] |
Fabrizio G A, Gray D A, Turley M D. Experimental evaluation of adaptive beamforming methods and interference models for high frequency over-the-horizon radar systems[J].
Multidimensional Systems and Signal Processing , 2003, 14 (1) : 241-263 ( 0) 0)
|
| [5] |
Fabrizio G A, Gershman A B, Turley M D. Robust adaptive beamforming for HF surface wave over-the-horizon radar[J].
IEEE Transactions on Aerospace and Electronic Systems , 2004, 40 (2) : 510-525 DOI:10.1109/TAES.2004.1310001 ( 0) 0)
|
| [6] |
Wan Xian-rong, Cheng Feng, Ke Heng-yu. Experimental trials on ionospheric clutter suppression for high-frequency surface wave radar[J].
IEE Proceedings Radar, Sonar and Navigation , 2006, 153 (1) : 23-29 DOI:10.1049/ip-rsn:20050019 ( 0) 0)
|
| [7] |
Guo Xin, Sun Hong-bo, Yeo T S. Interference cancellation for high-frequency surface wave radar[J].
IEEE Transactions on Geoscience and Remote Sensing , 2008, 46 (7) : 1879-1891 DOI:10.1109/TGRS.2008.916482 ( 0) 0)
|
| [8] |
Riddolls R J and Adve R S. Two-dimensional adaptive processing for ionospheric clutter mitigation in high frequency surface wave radar[C]. Proceedings of Radar Conference, Pasadena, 2009: 1-4.
( 0) 0)
|
| [9] |
Wan Xian-rong, Ke Heng-yu, Wen Bi-yang. Adaptive ionospheric clutter suppression based on subarrays in monostatic HF surface wave radar[J].
IEE Proceedings Radar, Sonar and Navigation , 2005, 152 (2) : 89-96 DOI:10.1049/ip-rsn:20045020 ( 0) 0)
|
| [10] |
黄亮, 文必洋, 吴立明, 等. 高频地波雷达电离层干扰抑制研究[J].
电波科学学报 , 2007, 22 (4) : 626-630 Huang Liang, Wen Bi-yang, Wu Li-ming, et al. Ionospheric interference mitigation in HFSWR[J].
Chinese Journal of Radio Science , 2007, 22 (4) : 626-630 ( 0) 0)
|
| [11] |
Li Lei, Xu Rong-qing, Li Gao-peng. Robust ionospheric clutter mitigation method for high frequency surface wave radar[J].
Science in China Series F: Information Sciences , 2008, 51 (12) : 2087-2093 DOI:10.1007/s11432-008-0135-9 ( 0) 0)
|
| [12] |
Tian Wen-long, Li Gao-peng, Xu Rong-qing. Ionospheric clutter mitigation for high-frequency surface-wave radar using two-dimensional array and beam space processing[J].
IET Radar, Sonar & Navigation , 2012, 6 (3) : 202-211 ( 0) 0)
|
| [13] |
Mao Xing-peng, Liu Yong-tan. Null phase-shift polarization filtering for high-frequency radar[J].
IEEE Transactions on Aerospace and Electronic Systems , 2007, 43 (4) : 1397-1408 DOI:10.1109/TAES.2007.4441747 ( 0) 0)
|
| [14] |
Mao Xing-peng, Liu Ai-jun, Hou Hui-jun, et al. Oblique projection polarisation filtering for interference suppression in high-frequency surface wave radar[J].
IET Radar, Sonar & Navigation , 2012, 6 (2) : 71-80 ( 0) 0)
|
| [15] |
Mao Xing-peng, Hong Hong, Deng Wei-bo, et al. Research on polarization cancellation of nonstationary ionosphere clutter in HF radar system[J].
International Journal of Antennas and Propagation , 2015 : 1-12 ( 0) 0)
|
| [16] |
洪泓, 毛兴鹏, 果然, 等. 基于距离-多普勒域的电离层杂波极化抑制方法[J].
系统工程与电子技术 , 2014, 36 (12) : 2400-2405 Hong Hong, Mao Xing-peng, Guo Ran, et al. Method for polarization cancellation of ionospheric clutter based on range-Doppler domain[J].
Journal of Systems Engineering and Electronics , 2014, 36 (12) : 2400-2405 ( 0) 0)
|
| [17] |
Hong Hong, Mao Xing-peng, and Hu Cui. A multi-domain collaborative filter for HFSWR based on oblique projection[C]. Proceedings of Radar Conference, Atlanta, 2012: 0907-0912.
( 0) 0)
|
| [18] |
王秀红, 毛兴鹏, 张乃通. 基于DOA的脉冲压缩雷达单快拍DOA估计[J].
系统工程与电子技术 , 2014, 36 (9) : 1737-1743 Wang Xiu-hong, Mao Xing-peng, Zhang Nai-tong. Single-snap DOA estimation based on compressed sensing in pulse compression radar system[J].
Journal of Systems Engineering and Electronics , 2014, 36 (9) : 1737-1743 ( 0) 0)
|
| [19] |
Behrens R T, Scharf L L. Signal processing applications of oblique projection operators[J].
IEEE Transactions on Signal Processing , 1994, 42 (6) : 1413-1424 DOI:10.1109/78.286957 ( 0) 0)
|
| [20] |
Wong K T, Li Linshan, Zoltowski M D. Root-MUSIC-based direction-finding and polarization estimation using diversely polarized possibly collocated antennas[J].
IEEE Antennas and Wireless Propagation Letters , 2004, 3 (1) : 129-132 DOI:10.1109/LAWP.2004.831083 ( 0) 0)
|
| [21] |
田野.基于稀疏重构的阵列信号多参数估计[D].[博士论文], 吉林大学, 2014: 77-89.
Tian Ye. Multi-parameter estimation for array signals based on sparse reconstruction[D].[Ph.D. dissertation], Jilin University, 2014: 77-89.
http://cdmd.cnki.com.cn/Article/CDMD-10183-1014268090.htm ( 0) 0)
|
| [22] |
李阳.张量理论及其在阵列处理中的应用研究[D].[博士论文], 复旦大学, 2014: 147-151.
Li Yang. Tensor theory and its application to array signal processing[D].[Ph.D. dissertation], Fudan University, 2014: 147-151.
http://cdmd.cnki.com.cn/Article/CDMD-10246-1015411326.htm ( 0) 0)
|




