②(中国科学院大学 北京 100039)
②(University of Chinese Academy of Sciences, Beijing 100039, China)
合成孔径雷达(Synthetic Aperture Radar,SAR)是一种高分辨率成像的雷达,具有全天候、全天时、远距离以及穿透能力强等优点,目前已成为对地观测的重要手段[1]。极化SAR分类作为SAR图像分类的重要部分,在军事侦察、土地勘察和城市规划等领域都有着广泛的应用前景[2]。随着极化SAR系统与成像技术的不断发展和成熟,极化SAR地物分类成为国内外研究的热点。
发展到目前,国内外学者已经提出了很多关于极化分类的经典方法[3, 4, 5, 6, 7, 8, 9, 10]。经典的H/α分类方法[4]是基于Cloude分解[11]发展而来,利用Cloude分解得到相干矩阵的特征值,利用特征值的函数组成的散射熵H和α角对目标进行分类。该分类方法的基本思想是:利用极化熵能够反映目标散射特性随机性的特点,将极化熵H作为目标散射随机性的自然测度,然后再利用α角识别目标的基本散射机制,从而完成不同散射类型的分类[4, 12]。H/α分类方法对于不同区域的划分是通过直线进行划分的,分界线是根据经验主观决定的,因此只适合对目标区域的粗略分类,无法在目标结构分析中广泛应用。而且,目标具有一定的散射不均匀性,使得分类结果杂乱且各类之间界限模糊。针对这种问题,有学者基于极化分解分类方法设计了迭代分类方法。最常用的统计迭代分类算法是基于Wishart距离的H/α-Wishart迭代分类方法[6, 12]。这类方法的优点是它们可以方便地与地物散射类型机制相对应,实现非监督分类。但是这种基于H/α散射机制的方法只能区分散射类型不同的地物,而难以区分散射类型相近的地物类型。
本文主要从充分挖掘特征值的潜力,克服基于H/α的方法对于特征值使用方式的弱点,使之能够广泛地用于不同地物分类的角度出发,给出了一种基于特征值的极化SAR图像分类方法。首先,对极化相干矩阵做Cloude-Pottier分解,获得相干矩阵的特征值,并用一种自适应调整高斯分量个数的高斯混合模型(Gaussian Mixture Model,GMM)对特征值分布进行较为准确地拟合,用经k均值方法进行参数初始化的最大期望(Expectation Maximization,EM)算法求解GMM参数。然后,基于对特征值的分布拟合,使用朴素贝叶斯分类器进行初步分类。针对可能存在特征值分布较为相近导致错分的问题,计算每两类地物的特征值分布的相似度[13],将相似度大于给定阈值的类别对组成相似性表,对于初步结果中的这些相似对再用基于Wishart距离的K近邻分类器进行细分。综合分析在机载和星载SAR两个不同数据上的实验结果,表明这种方法能够克服基于H/α的非监督分类方法对于特征值利用的一些不足,且与常用的SVM方法效果相当。
2 基于特征值的极化分类方法 2.1 特征值获取与使用根据单站互易理论,极化散射矩阵可以表示如下[9]:
| ${S } = \left[\begin{gathered} {S_{\rm{hh}}}\;\;\;{S_{\rm{vh}}} \\ {S_{\rm{vh}}}\;\;\;{S_{\rm{vv}}} \\ \end{gathered} \right]$ | (1) |
其中,分量的第1个下标索引代表接收极化方式,第2个下标索引代表发射极化方式,利用Pauli基可以将散射矩阵转化为向量:
| ${{k}} = \frac{1}{{\sqrt 2 }}{\left[{{S_{\rm{hh}}} + {S_{\rm{vv}}},{S_{\rm{hh}}} - {S_{\rm{vv}}},2{S_{\rm{vh}}}} \right]^{\rm T} }$ | (2) |
n视极化相干矩阵为:
| ${{T}} = \frac{1}{{{n}} }\sum\limits_{i = 1}^{{n}} {{{{k}}_i}{{k}}_i^{*{\rm T} }} $ | (3) |
其中,n为视数,ki是第i个单视向量样本。Cloude-Pottier分解是对极化相干矩阵T基于特征值/特征向量的分析。因为T是Hermitian半正定矩阵,总是可以做如下特征值/特征向量分析:
| $ {T} = {\lambda _1}{{e}_1} \cdot {e}_1^{*{\rm T} } + {\lambda _2}{{e}_2} \cdot {e}_2^{*{\rm T} } + {\lambda _3}{{e}_3} \cdot {e}_3^{*{\rm T} }$ | (4) |
其中,λi是T的第i个特征值,且满足λ1≥λ2≥λ3≥0,ei是对应的正交特征向量。这样,T被分解成3项,每项都代表了一部分散射贡献,λi代表每项的贡献量,ei代表贡献的散射类型。每项的相对强度可以表示为:
| ${p_i} = {\lambda _i}{\Huge{/}}\sum\limits_{i = 1}^3 {{\lambda _i}} $ | (5) |
H/α的定义如下:
| $H = - \sum\limits_{i = 1}^3 {{p_i}{{\log }_3}{p_i}} ,\;\;\alpha = \sum\limits_{i = 1}^3 {} {p_i}{\alpha_i}$ | (6) |
在后文第3节实验结果与分析中,分别给出了两个实验数据的H/α平面分布情况。AIRSAR数据的9类地物中有大量地物被其他类别覆盖,区分性很差,而RADARSAT-2数据有相对较好的区分度。基于H/α模型的缺点,考虑到H和α都是特征值的函数,特征值应包含不少于H和α的信息,而专门针对特征值的分析研究还较少,本文给出了一种基于特征值的一整套分类方法,更充分地利用相干矩阵特征值提供的极化信息。
2.2 自适应GMM和EM算法求解通过2.1节的原理,得到每类地物样本集的特征值之后,使用GMM对其统计分布进行拟合。GMM是指具有式(7)的概率分布的模型[14]
| $P(x{\rm{|}} \theta ) = \sum\limits_{k = 1}^K {{\alpha_k} \phi (x|{\theta _k})} $ | (7) |
其中,${\alpha_k}$是权重系数,${\alpha_k} \ge 0$,$\sum\nolimits_{k = 1}^K {{\alpha_k}} = 1$; $\phi (x|{\theta _k})$是高斯分布概率密度,${\theta _k} = ({\mu _k},\mathop \sigma \nolimits_k^2 )$。
GMM通常的求解方法是EM算法,EM算法是一个局部最优算法,常常容易陷入局部最优解,使得它的初始值对算法的结果有着极其重要的影响,一般的初始化方法有:随机中心,层次聚类,k均值算法等[15]。由于k均值聚类算法也是一种动态迭代算法且分类个数人为确定,是已知因素,与EM算法用于有限混合模型参数估计有一定吻合性,故我们可以通过k均值聚类先给出混合数据的一个粗糙分组,得到参数的粗略估计值,作为迭代的初始值。
EM算法最初由Dempster. Laird. Rubin于1977年提出[14, 16],其重要应用之一是高斯混合模型的参数估计。本文使用的具体算法流程描述如下:
输入:建模数据${x_1},{x_2},\cdots ,{x_{N}}$及高斯分量个数K
输出:高斯混合模型各个分量参数${\alpha_k}$及${\theta _k} = ({\mu _k},\sigma _k^2)$
步骤 1 使用k均值来进行初始化。将数据使用k均值聚类成K类,取每类的均值、方差及在总样本中的比例为初始参数。
步骤 2 E步:根据当前参数,计算分模型k对数据${x_j}$的响应度:
| $\begin{array}\lambda {\gamma _{jk}} = \frac{{{\alpha _k}\phi \left( {{x_j}\left| {{\theta _k}} \right.} \right)}}{{\sum\limits_{k = 1}^K {{\alpha _k}\phi \left( {{x_j}\left| {{\theta _k}} \right.} \right)} }},\\ j = 1,2 \ldots ,N;k = 1,2, \ldots K \end{array}$ | (8) |
步骤 3 M步:计算新一轮迭代的模型参数
| $\begin{array}\lambda {\mu _k} = \frac{{\sum\limits_{j = 1}^N {{\gamma _{jk}}{x_j}} }}{{\sum\limits_{j = 1}^N {{\gamma _{jk}}} }},\sigma _k^2 = \frac{{\sum\limits_{j = 1}^N {{\gamma _{jk}}} \left( {{x_j} - {\mu _k}} \right)}}{{\sum\limits_{j = 1}^N {{\gamma _{jk}}} }},\\ {\alpha _k} = \frac{{\sum\limits_{j = 1}^N {{\gamma _{jk}}} }}{N},k = 1,2, \ldots ,N \end{array}$ | (9) |
步骤 4 重复步骤2和步骤3,直到收敛。
另一方面,直接固定个数K的GMM难以同时适应不同的地物类型的特征值分布。分布拟合不佳将直接导致后续分类错误。所以,本文使用了自适应调整高斯分量个数的GMM。经过前期实验,绝大多数地物的特征值都能用1-3个高斯分量较为准确地拟合出来,所以选择3为初始高斯分量个数,对数据拟合,得到权重,然后查看权重值大小,若出现小于阈值的权重,则分量个数减1,直到每个权重都大于预先设定的阈值。阈值过大,会导致欠拟合,阈值过小,会导致过拟合,并且增加不必要的计算量。综上所述,本文的自适应GMM及其求解流程如图 1所示。
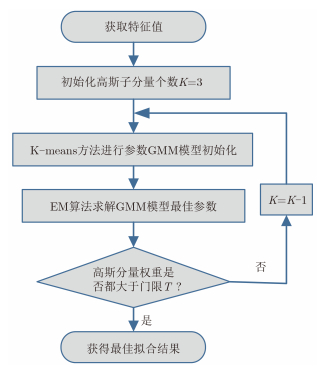
|
图 1 自适应GMM及其求解流程 Fig. 1 Flowchart of adaptive GMM |
贝叶斯分类是基于贝叶斯定理与特征条件独立的假设的分类方法。对于给定的训练数据集,首先基于特征条件独立假设学习输入/输出的联合概率分布,然后基于此模型,对于给定的输入,利用贝叶斯定理求出后验概率最大的输出[14]。贝叶斯分类器实现简单,学习和预测的效率都很高,是一种常用的方法。针对上文已求得的各类地物的3个特征值的概率分布,作为贝叶斯分类器的输入,实现基于特征值的初步分类。
在拟合了特征值的分布后,对于每个像素点,使用3个特征值的联合分布值作为其统计度量。输入${{X}} \subseteq {R^3}$为3维向量的集合(此处用X和x表示特征值λ),输出为类标记集合$Y = \{ {c_1},{c_2},\cdots ,{c_{K}}\} $。训练数据集为$N = \{ ({{{x}}_1},{y_1}),({{{x}}_2},{y_2}),\cdots ,({{{x}}_{{N}} },{y_{{N}} })\} $。朴素贝叶斯法通过训练数据集学习联合概率分布$P({{X}},Y\;)$。具体地,学习以下先验概率及条件概率分布。先验概率分布为$P(Y = {c_k})$,条件概率分布为:
| $P({{X}} = {{x}}|Y = {c_k})\; = \prod \limits_{j = 1}^3 {P({{{X}}^{(j)}} = {{{x}}^{(j)}}|Y = {c_k})} $ | (10) |
朴素贝叶斯法分类时,对于给定的输入x,通过学习到的模型计算后验概率分布$P(Y = {c_k}|{{X}} = {{x}})$,将后验概率最大的类作为x的类别,后验概率计算根据贝叶斯定理进行:
| $P(Y = {c_k}|X = x) = \frac{{P\left( {X = x\left| {Y = {c_k}} \right.} \right)P\left( {Y = {c_k}} \right)}}{{\sum\limits_k {P\left( {X = x\left| {Y = {c_k}} \right.} \right)P\left( {Y = {c_k}} \right)} }}$ | (11) |
将式(10)代入,又因本文各类的先验概率未知,于是$P(Y = {c_k})$作为等概率处理,得到:
| $P(Y = {c_k}|X = x) = \frac{{\prod\limits_{j = 1}^3 P \left( {{X^{\left( j \right)}} = {x^{\left( j \right)}}\left| {Y = {c_k}} \right.} \right)}}{{\sum\limits_k {\prod\limits_{j = 1}^3 P \left( {{X^{\left( j \right)}} = {x^{\left( j \right)}}\left| {Y = {c_k}} \right.} \right)} }}$ | (12) |
这是朴素贝叶斯方法的基本公式。式(12)中,分母对所有ck都是相同的,于是,本文所用的朴素贝叶斯分类器可表示为:
| $y \!= \!f({{x}})\! =\! \arg \mathop {\max }\limits_{{c_k}} \prod\limits_{j = 1}^3 {P({{{X}}^{(j)}} \!= \!{{{x}}^{(j)}}|Y \!=\! {c_k})} $ | (13) |
对于特征值分布较为相近的类别对,贝叶斯分类可能存在错分的情况。为了找出这些类别对,我们对每两类的分布计算其相似性。根据概率密度的性质$ P(a < x < b ) = \int_a^b {f(x){\rm{d}}x} $,$f(x) \ge 0\;$,$ \int_{ - \infty }^{ + \infty } {f(x){\rm{d}}x = 1\;\;} $,可以用两个概率密度分布组成的面积度量它们的相似性[13]。示意图如图 2所示。
| $ S = \int_{ - \infty }^{ + \infty } {\max ({f_1}(x),{f_2}(x)){\rm{d}}x},\;\,\,1 \le S \le 2$ | (14) |
| $ \ \ \;{\text{similarity}}({f_1},{f_2}) = 1 - 0.5 \times S$ | (15) |
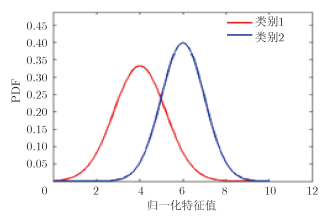
|
图 2 两分布相似度计算示意图 Fig. 2 Similarity calculation of two distributions |
其中,f1,f2分别代表两类地物的特征值分布,f1(x),f2(x)代表它们的概率密度函数。从上式可知,它们组成的面积越大,相似度越小,面积越小,相似度越大。
对于极化特征值的3维向量来说,相似度计算如下:
| ${\text{similar}}(a,b) = \prod\limits_{i = 1}^3 {{\text{similarity}}({\lambda _{ai}},{\lambda _{bi}})} $ | (16) |
其中,a和b代表不同的类别,λai和λbi分别代表它们第i个特征值的分布。由此,得到a和b两类的相似度similar(a,b)。根据这个度量计算出每两类之间的相似度,然后设定阈值,相似度小于阈值的判定为不相似对,相似度大于阈值的判定为相似对,并保存在相似性表中。
2.5 基于Wishart距离的K近邻分类器K近邻是一种简单直观的机器学习算法。给定训练数据集,对新的输入实例,在训练集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,就把该输入实例分为这个类。K近邻使用的模型实际上对应于对特征空间的划分。模型由3个基本要素决定,即距离度量、K值及分类决策规则[14]。此处,我们采用Wishart距离度量。经过实验,本文K值取20为佳,分类决策规则采用多数表决。
Lee等人在文献[3]中提出了基于最大似然判决准则的极化SAR图像Wishart监督分类方法,应用最大似然法可得到每个像素的相干矩阵与类中心相干矩阵的复Wishart距离,然后将该像素分类到与其距离最近的类别。Wishart距离度量的定义为:
| $d({{T}},{\omega _m}) = {\text{In}}|{{{T}}_m}| + {\rm Tr} ({{T}}_m^{ - 1}{{T}})$ | (17) |
其中,T表示初步分类标签出现在相似性表中的样本的相干矩阵,Tm表示相似对的某一类的参考值。对于在相似性表中的每个像素都计算其与当前相似性对中两类样本点的距离,然后按照距离由小到大排序,取最前面的K个标签值,则将当前像素归类到出现次数较多的那类标签中。
2.6 算法流程本实验算法流程如图 3所示,具体流程如下:
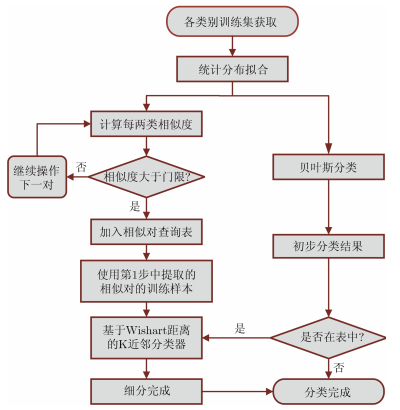
|
图 3 本文方法流程图 Fig. 3 Flowchart of the proposed method |
步骤 1 根据2.1节的原理对全极化数据相干矩阵做Cloude-Pottier分解,获得特征值。利用2.2节的拟合与求解方法对每类地物样本的特征值分布进行拟合。
步骤 2 根据2.4节的原理计算每两类地物的分布相似度,将相似度大于给定阈值的类别对加入相似性表。
步骤 3 利用2.3节的朴素贝叶斯分类方法,结合步骤1中得到概率分布进行初步的分类。
步骤 4 对于步骤3的分类结果中出现在相似表中的类别对,利用2.4节的基于Wishart距离的K近邻算法进一步分类,此处使用的训练样本集与步骤1中的相同。
3 实验结果与分析本节采用了两个全极化数据集对上文给出的算法进行实验。实验数据1选取的是1989 年由ARISAR 获取的荷兰Flevoland 地区的L 波段的4视全极化机载SAR数据,该数据大小为370× 420,数据的伪彩图、训练集位置、真实地物参照如图 4所示,其主要覆盖了具有平坦地形和均匀土壤的农田区域。数据2是C波段的RADARSAT-2星载数据,获取时间是2008年,地点是荷兰的Flevoland,选择区域大小为520×600,主要包括的地物类型有植被、城市、水域、农田等。数据的伪彩图及训练集位置如图 4(a)和图 4(c)所示,训练集为红框标出的区域。精度验证采用的样本集位置如图 4(b)所示[17]。本文中,实验数据都经过了窗口大小为5×5的精制Lee滤波预处理过程。

|
图 4 实验所用的数据 Fig. 4 The datasets used in the experiments |
图 5分别给出了两个数据集中的不同类别地物样本在H/α平面上的分布情况,其中AIRSAR数据的每类样本点均取1200个点,RADARSAT-2数据的样本点均取2000个点。可以看出,AIRSAR数据的9类地物中有大量地物被其他类别覆盖,区分性很差,而RADARSAT-2数据有相对较好的区分度。这将直接导致基于H/α的分类方法对这两种不同的数据集产生不同的效果,具体结果见后文的结果描述。
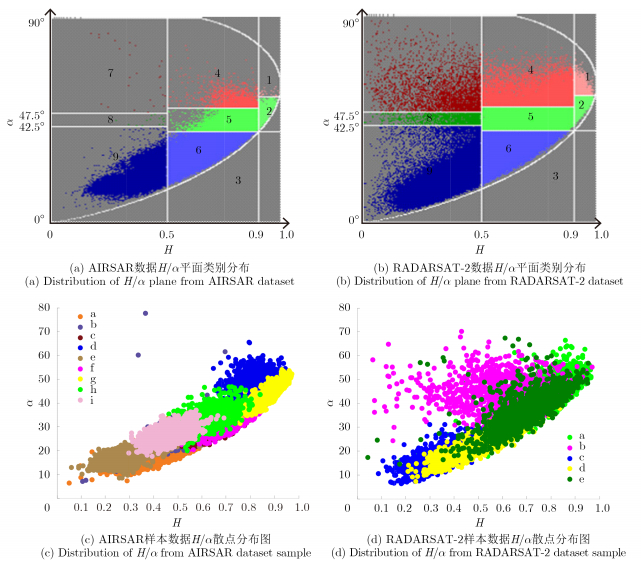
|
图 5 H/α散点分布图 Fig. 5 Distribution of H/α |
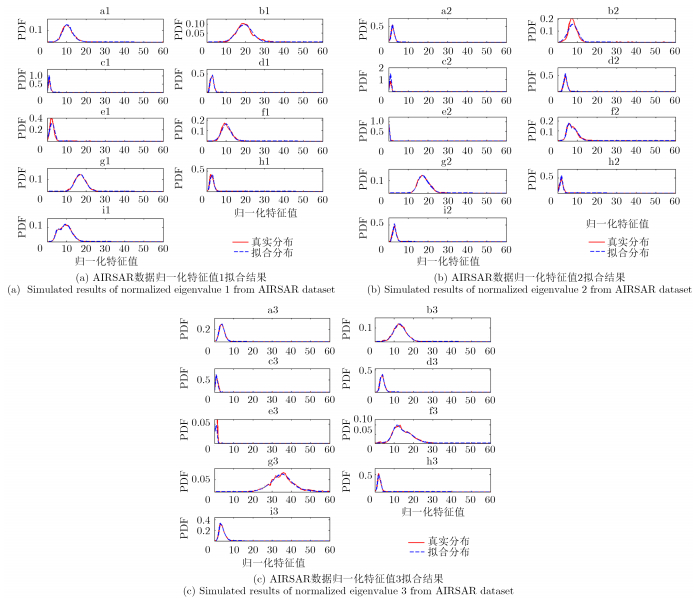
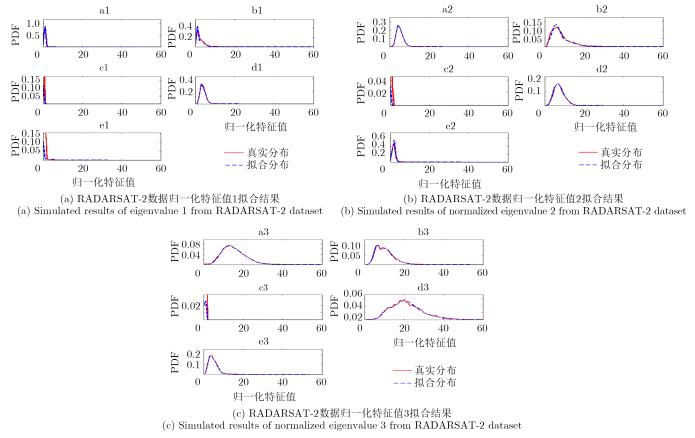
对两个数据集特征值进行自适应调整高斯分量个数的GMM拟合的高斯分量个数结果分别见表 1和表 2。对其每种地物样本对应的3个归一化特征值分布拟合结果如图 6和图 7所示。其中自适应GMM的权重阈值设置为T=0.05。由结果可以看出本文提出的自适应调整高斯分量个数的GMM可以准确地拟合不同类型的特征值分布,且对于不同类别有较好的可分性。
| 表 1 AIRSAR数据特征值GMM拟合的高斯子分量的个数 Tab. 1 Numbers of Gaussian components of eigenvalues from AIRSAR dataset |
|
图 6 AIRSAR数据归一化特征值分布 Fig. 6 Distribution of normalized eigenvalue from AIRSAR dataset |
|
图 7 RADARSAT-2数据归一化特征值分布 Fig. 7 Distribution of normalized eigenvalue from RADARSAT-2 dataset |
| 表 2 RADARSAT-2数据特征值GMM拟合的高斯子分量的个数 Tab. 2 Numbers of Gaussian components of eigenvalues from RADARSAT-2 dataset |
获得每种地物的特征值分布后,一方面使用朴素贝叶斯分类器进行初步分类,分类的结果分别如图 8(a),图 9(a)所示。其必要性和优点主要有3点。一是贝叶斯分类是本文对于特征值利用的核心思想的关键步骤,对相关问题对于特征值的使用研究有参考价值。二是贝叶斯分类已经取得不错的结果。对于某些情况(比如只能获取特征值特征),是一种很好的做快速地物分类的选择。三是在此基础上,下一步的细分只对那些特征值分布相近,贝叶斯分类器容易错分的类别对进行完善优化。另一方面对于每两种之间分布相似度进行计算,相似度阈值设置为T=0.0030。阈值设置是根据实验中得到的相似度数据选择了多个典型的阈值,通过实验发现此阈值对于两个数据都能有较好的实验结果,故作此设置。相似度大于给定阈值的类别对如表 3和表 4所示,可以看出存在于相似性表中的类别对在初步分类的结果中存在较多错分情况。对这些类别对进行进一步细分的最终结果如图 8(b),图 9(b)所示。因无法获得所有像素的真实对应类型,我们只利用图 4(b)中确定类别的像素进行准确率计算。表 5分别列出了这两步操作的正确率,由图 8(a),图 8(b)和图 9(a),9(b)及表 5可以看出进一步的Wishart-KNN细分提升了特征值分布相似对的分类准确率。为了说明本文“统计分布拟合”、“相似度计算”和“贝叶斯分类”的初步分类的有效性以及实验结果依赖于题目中的“特征值”,有必要单独使用相同的训练集进行基于Wishart距离的KNN分类器的对比实验。实验结果如图 8(d)和图 9(d)。从实验结果中,可以看到,其与本文方法的分类精度不相同,分别是87.93%和89.17%,本文得到的结果是题目中的“特征值”和“基于Wishart距离的K近邻分类器”共同达到的效果,说明了本文“统计分布拟合”、“相似度计算”和“贝叶斯分类”的初步分类的有效性。
| 表 3 AIRSAR数据的相似对表 Tab. 3 Similarity table of AIRSAR dataset |
| 表 4 RADARSAT-2数据的相似对表 Tab. 4 Similarity table of RADARSAT-2 dataset |
| 表 5 AIRSAR数据分类准确率(%) Tab. 5 Classification accuracy of AIRSAR dataset (%) |

|
图 8 AIRSAR数据不同方法分类结果比较 Fig. 8 Comparison of different methods for AIRSAR dataset |
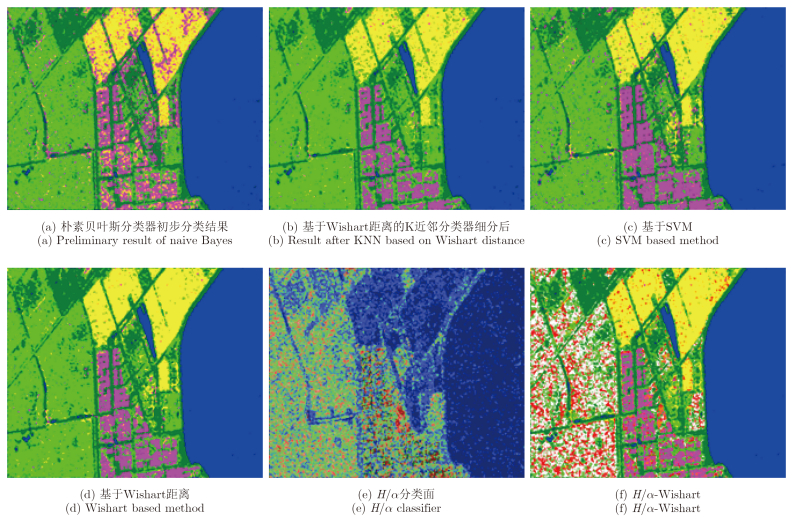
|
图 9 RADARSAT-2数据不同方法分类结果比较 Fig. 9 Comparison of different methods for RADARSAT-2 dataset |
下面通过实验结果来验证本文方法的有效性,由于本文方法是一种监督的分类方法,我们将其与典型的基于SVM的监督分类方法[10, 14]进行比较。在基于SVM的方法中,选取与本文方法相同的训练样本、相同的特征输入即极化特征值与T矩阵的元素、相同的精度验证样本,以保证比较的科学性。SVM分类器训练过程中需要选择核函数和设置模型参数,本文实验中使用RBF核函数,需寻优的参数包括惩罚参数C和核函数参数γ。一种实用的参数寻优方法是对指数式增长的序列进行实验,C的搜索范围一般为C=2-5,2-3,···,215,γ的搜索范围一般是γ=2-15,2-13,···,23[18]。在实验中,通过参数寻优,得到AIRSAR数据的实验参数为C=27和γ=2-1,RADARSAT-2数据的实验参数为C=213和γ=2-3。同时,我们也利用H/α分类器方法、H/α-Wishart方法进行了实验。所有分类结果见图 8和图 9。如前所述,单一的H/α分类器和H/α-Wishart方法对于具有相似散射类型的数据1的分类效果都很差,对于散射类型差异较大的数据2具有较好的区分能力。本文方法和基于SVM的方法对数据1和数据2都能取得较好的结果。此外,本文方法充分挖掘了特征值的利用,而且不需要SVM分类大量的参数寻优和交叉验证过程。综上所述,本文的方法能够克服基于H/α的方法对于散射类型较为相似的地物在特征值利用方面的缺陷,是一种较为通用的有效的基于特征值的极化分类方法。
4 结论本文针对如何更好地利用特征值进行极化分类的问题,给出了一整套方案,并且在方案中具有对一些问题的解决方法,充分地挖掘了特征值在极化分类中的潜力。该方法首先提出了一种自适应调整高斯分量个数的GMM对特征值分布进行较为准确地拟合,使用经k均值方法进行参数初始化的EM算法求解GMM模型,然后采用朴素贝叶斯分类器进行初步分类。针对可能存在特征值分布较为相近导致错分的问题,计算每两类地物的特征值分布的相似度,将相似度大于给定阈值的类别对组成相似性表,对于这些相似对再用基于Wishart距离的K近邻分类器进行细分。实验结果表明,对于具有相似散射类型的地物,本文方法克服了基于H/α的非监督分类方法对于特征值利用的不足,对于散射类型相差较大的地物,本文方法和基于H/α的方法都具有很好的分类效果。另外,两个数据的结果表明,本文方法能够取得与经典SVM方法相当的效果。本文仍然存在不足之处,对于如何利用特征值来完成第2步的细分过程,还有很大的提升空间与加深研究的价值。在接下来的工作中,我们将进一步研究利用特征值信息构建纹理描述子等方式来完成第2步的细分过程,以使对于特征值的使用价值得到更充分的体现。
| [1] | Lee J S and Pottier E. 极化合成孔径雷达成像基础与应用[M]. 北京: 电子工业出版社, 2013: 199-223. Lee J S and Pottier E. Polarimetric Radar Imaging: From Basics to Applications[M]. Beijing: Publishing House of Electronics Industry, 2013: 199-223.(  1) 1) |
| [2] | 滑文强, 王爽, 侯彪. 基于半监督学习的SVM-Wishart极化SAR图像分类方法[J]. 雷达学报, 2015, 4(1): 93-98 Hua Wen-qiang, Wang Shuang, and Hou Biao. Semi-supervised learning for classification of polarimetric SAR images based on SVM-Wishart[J]. Journal of Radars, 2015, 4(1): 93-98.(  1) 1) |
| [3] | Lee J S, Grunes M R, and Kwok R. Classification of multilook polarimetric SAR imagery based on complex Wishart distribution[J]. International Journal of Remote Sensing, 1994, 15(11): 2299-2311.( 2) 2) |
| [4] | Cloude S R and Pottier E. An entropy based classication scheme for land applications of polarimetric SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(1): 68-78.( 3) 3) |
| [5] | Tzeng Y C and Chen K S. A fuzzy neural network to SAR image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(1): 301-307.( 1) 1) |
| [6] | Lee J S, Grunes M R, Ainsworth T L, et al.. Unsupervised classification using polarimetricdecomposition and the complex Wishart classifier[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2249-2258.( 2) 2) |
| [7] | Famil L F, Pottier E, and Lee J S. Unsupervised classification of multifrequency and fully polarimetric SAR images based on the H/A/α-Wishart classifier[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(11): 2332-2342.( 1) 1) |
| [8] | Lee J S, Grunes M R, Pottier E, et al.. Unsupervised terrain classification preserving polarimetric scattering characteristics[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(4): 722-731.( 1) 1) |
| [9] | Cao F, Hong W, and Wu Y R. An unsupervised segmentation with an adaptive number of clusters using theSPAN/H/α/Aspace and the complex Wishart clusteringfor fully polarimetric SAR data analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3454-3467.( 2) 2) |
| [10] | Lardeux C, Frison P L, Tison C, et al.. Support vector machine for multifrequency SAR polarimetric data classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(12): 4143-4151.( 2) 2) |
| [11] | Cloude S R and Pottier E. A review of target decomposition theorems in radar polarimetry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(2): 498-518.( 1) 1) |
| [12] | 周伟, 孙艳丽, 许成斌, 等. 一种多极化SAR 舰船目标与方位向模糊鉴别方法[J]. 雷达学报, 2015, 4(1): 84-92. Zhou Wei, Sun Yan-li, Xu Cheng-bin, et al.. A method for discrimination of ship target and azimuth ambiguity in multi-polarimetric SAR imagery[J]. Journal of Radars, 2015, 4(1): 84-92.(  2) 2) |
| [13] | Gou S P, Qiao X, Zhang X R, et al.. Eigenvalue analysis-based approach for POL-SAR image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2): 805-818.( 2) 2) |
| [14] | 李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012: 37-53. Li Hang. Statistical Learning Methods[M]. Beijing: Tsinghua University Press, 2000: 37-53.(  5) 5) |
| [15] | 王鑫. 基于高斯混合模型的k均值初始化EM 算法的研究[J]. 商丘师范学院学报, 2012, 28(12): 11-14. Wang Xin. Gaussian mixture model based k-means to initialize the EM algorithm[J]. Journal of Shangqiu Normal University, 2012, 28(12): 11-14.(  1) 1) |
| [16] | Dempster A P, Laird N M, and Rubin D B. Maximum-likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society, 1977, 39(1): 1-38.( 1) 1) |
| [17] | Liu B, Hu H, Wang H Y, et al.. Superpixel-based classification with an adaptive number of classes for polarimetric SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(2): 907-924.( 1) 1) |
| [18] | Hsu C W, Chang C C, and Lin C J. A practical guide to support vector classication[OL]. http://www.csie.ntu.edu.tw/-cjlin/papers/guide/guide.pdf. 2010.( 1) 1) |


