以多输入多输出(Multiple Input and Multiple Output,MIMO)技术为基础体制的MIMO雷达系统,因其在目标检测、参数估计、杂波抑制等方面具有诸多优势[1, 2],已成为现代雷达发展趋势的综合体现,引起国内外学者的高度关注。根据信号处理方式的不同,MIMO雷达可以分为分布式MIMO雷达和集中式MIMO雷达;本文以集中式MIMO雷达为研究对象,重点研究单基地配置下的多目标参数估计问题。
单基地配置下的集中式MIMO雷达利用匹配滤波技术,能够在接收端综合收、发阵列孔径,获取比传统相控阵雷达更大的孔径扩展,因此在目标分辨能力和参数估计性能方面优势明显。为了获取目标参数的有效估计,传统基于相控阵雷达的高分辨算法被广泛应用于目标参数估计中。文献[3]通过设计相应的降维矩阵,将原始单基地MIMO雷达高维回波数据转换到了低维信号空间,去除了虚拟扩展中所有的冗余数据,因此降低了后续处理的数据维数,但其参数求解涉及1维Capon谱搜索;文献[4]在进行降维变换之后,直接利用ESPRIT算法进一步避免了谱搜索;文献[5, 6]在文献[4]的基础上进一步通过酉变换,充分利用复观测数据及其共轭数据来提高ESPRIT算法的参数估计精度,在不增加阵元的情况下,提高了算法的估计性能,同时通过实值运算,也进一步降低了整体的运算复杂度;但以上研究局限于1维线阵模型,无法获取多维方位信息实现目标方向的定位。
事实上,当收、发阵列均采用2维(或更高维)阵列配置时,目标参数维度的扩展意味着目标特征描述得更加准确,同时收、发阵列经过MIMO雷达虚拟扩展后整体天线流型也就更为复杂,因此深入研究2维天线配置下单基地MIMO雷达的虚拟扩展性能以及参数估计问题对目标的定位具有重要意义。文献[7, 8]基于单基地MIMO雷达3维阵列配置模型,对比分析了不同平面流型配置下基于最大似然估计算法的MIMO雷达天线位置敏感性和模糊限,重点考虑阵列几何形状对MIMO雷达虚拟阵列流形的影响,分析比较了不同阵列配置下MIMO雷达总的敏感性测度;文献[9]进一步通过MIMO虚拟阵列流形的微分几何性质,研究了MIMO雷达估计精度、检测及分辨的性能极限,并对比了几种典型天线几何配置下MIMO雷达系统的测向性能,为MIMO雷达系统的天线设计提供了依据。但文献[7, 8, 9]的研究集中在2维阵列配置对MIMO雷达测向性能的影响。文献[10]研究了双平行线阵配置下单基地MIMO雷达的2维参数估计问题,提出了降维(RD)ESPRIT算法,该模型尽管进行了降冗余处理,但只能实现1维方向上的阵列扩展;文献[11]研究了L型阵列配置下单基地MIMO雷达的2维参数估计问题,算法通过构造降维矩阵对回波数据进行降维预处理后,利用二次优化方法将2维DOA估计分解为两个1维DOA估计,一定程度上降低了运算复杂度,但降维矩阵的设计并没有最大程度地降低回波数据的维数,回波数据中仍存在冗余;同时参数求解过程中两次1维谱搜索仍存在较高的运算量;文献[12]针对文献[11]存在的问题,利用L型阵列配置对应的虚拟阵列的对称性,通过重新设计降维矩阵,去除了所有冗余数据,并利用ESPRIT算法在不牺牲阵列孔径的条件下实现2维DOA的有效估计,避免了谱搜索;文献[13]研究了平面阵配置下的单基地MIMO雷达的2维参数估计问题,通过降维矩阵的设计以及降维处理,并针对降维后阵列流型与双基地MIMO雷达的等效相似性,利用文献[14, 15]中的酉变换思想进行实数域信号子空间估计和2维参数求解,其降维矩阵的设计以及降维过程本质上为文献[3, 4, 5, 6]中1维降维变换在2维上的扩展应用,同时由于采用面阵配置,面临着巨大硬件成本和复杂代价。以上算法尽管能够实现单基地MIMO雷达1维/2维目标角度的有效估计,但大多要求收、发阵列阵元间距满足半波长的限制,本质上仍属于角度参量在短基线阵元间距上的度量。
众所周知,阵列的孔径决定着雷达的分辨性能和测向精度,阵元间的基线扩展(大于半波长)能够有效增大阵列的整体孔径,提高参数估计的性能和精度,但会带来方位估计的周期性模糊。本文针对单基地MIMO雷达的2维测向问题,提出一种具有2维双尺度平移不变特性的收、发十字型阵列设计,并针对传统DR-UESPRIT算法求解过程中存在的实数域旋转不变因子无法提取的问题,提出一种新的基于酉变换的高精度估计算法,算法利用收、发阵列中十字型阵列的中心对称性,通过酉矩阵设计及酉变换过程,将发射、接收阵列中存在得长、短基线平移不变关系映射到实数域,并基于双尺度酉ESPRIT(Dual-Resolution Unitary ESPRIT,DR-UESPRIT)算法实现2维参数的高精度无模糊估计,同时不牺牲阵列孔径,无需额外的配对算法和谱搜索,能够实现特征分解与参数求解完全实数化,具有更低的运算复杂度。
2 问题建模考虑单基地MIMO雷达系统,收、发阵列均为如图 1所示的交叉阵列,其中发射阵列由以参考点o为交叉点的两个垂直子阵构成,x轴与y轴均为等间距线阵,阵元间距分别为$\Delta _x^t\left( { \gg {\lambda \mathord{\left/ {\vphantom {\lambda 2}} \right.} 2}} \right)$和$ d_y^t\left( { = {\lambda\mathord{\left/ {\vphantom {\lambda2}} \right. } 2}} \right) $,并分别以参考点o(o点为x轴与y轴共用)对称分布着2Mtx-1和2Mty-1个发射阵元,即x轴与y轴的各个半轴(不含参考点o)的阵元数分别为Mtx-1和Mty-1;同样对应的接收阵列x轴与y轴方向分别等间距分布2Mrx-1和2Mry-1个接收阵元,阵元间距分别为$d_x^r\left( { = {\lambda \mathord{\left/ {\vphantom {\lambda2}} \right. } 2}} \right)$和$\Delta _y^r\left( { \gg {\lambda\mathord{\left/ {\vphantom {\lambda2}} \right.} 2}} \right)$。假设远场空域存在K个目标,第k(k=1,···,K)个目标的空间角度信息为$\left( {{\vartheta _k},{\phi _k}} \right)$,并满足$\cos \vartheta = \cos \theta \cos \varphi $,$\cos \phi = \cos \theta \sin \varphi$;其中$(\theta ,\varphi )$对应目标的俯仰角与方位角,$(\varphi ,\phi )$对应目标分别与x轴、y轴的夹角。发射端Mt=2Mtx+2Mty-3个发射阵元同时发射相同载频及带宽的一组正交波形信号$S = \left[ {{s_1}\left( t \right), \cdots ,} \right.{\left. {{s_{{M_t}}}\left( t \right)} \right]^{\rm{T}}}$,则第l{l=1,···,L}次脉冲下Mt个正交发射波形经过目标反射后在接收端的输出信号为:
\[l\{ l = 1,...,{\rm{L}}\} \]

|
图 1 单基地 MIMO 雷达收、发阵列结构示意图 Fig. 1 Transmit/receive array structure for monostatic MIMO radar |
| $ {{x}_l}\left( t \right) \! = \!\! {{A}_r}\left( {\vartheta ,\phi } \right) {\rm diag} \left( {{\beta _l}} \right){A}_t^ {\rm T}\left( {\vartheta ,\phi } \right) {S} \left( t \right) \! + \! {{w}_l} \left(t \right) $ | (1) |
符号(•)T表示矩阵的转置,diag(e)表示以向量e为元素的对角矩阵;$ {\beta _l} = \left[{\beta _1^l\exp \left( {{\rm j}2\pi {f_1}t} \right),\cdots,} \right. $
$ \left. { \beta _K^l\exp \left( {{\rm j}2\pi {f \! _K}t} \right)} \right]^{\rm T} $对应第l次脉冲下各个目标的散射系数(由目标的RCS决定)及多普勒频率参量;wl(t)为加性高斯噪声矢量;${A_t}\left( {\vartheta ,\phi } \right) = [{a_t}\left( {{\vartheta _1},{\phi _1}} \right),$$ \left.{ \cdots,\ {{a}_t}\left( {{\vartheta _K},{\phi _K}} \right)} \right] $,$ {{A}_r}\left( {\vartheta ,\phi } \right) = \left[{{{a}_r}\left( {{\vartheta _1},{\phi _1}} \right),\ \cdots,}\right. $$ \left.{ {{a}_r}\left( {{\vartheta _K},{\phi _K}} \right)} \right]$分别对应发射和接收导向矢量;发射、接收导向矢量分别满足:
| $ {{a}_t}\left( {\vartheta ,\phi } \right) = \left[{\begin{array}{*{20}{c}}{\bar {a}_{ty}^ + \left( \phi \right)}\\ {{{a}_{tx}}\left( \vartheta \right)}\\ {{\underline{a}}_{ty}^ - \left( \phi \right)} \end{array}} \right],\ {{a}_r}\left( {\vartheta ,\phi } \right) = \left[{\begin{array}{*{20}{c}} {\bar {a}_{ry}^ + \left( \phi \right)}\\ {{{a}_{rx}}\left( \vartheta \right)}\\ {{\underline{a}}_{ry}^ - \left( \phi \right)} \end{array}} \right] $ |
其中:
| $ {{a}_{tx}}\left( \vartheta \right) = \left[{\begin{array}{*{20}{c}}{{a}_{tx}^ + \left( \vartheta \right)}\\ {{\underline{a}}_{tx}^ - \left( \vartheta \right)}\end{array}} \right] = \left[{\begin{array}{*{20}{c}}{\bar {a}_{tx}^ + \left( \vartheta \right)}\\ {{a}_{tx}^ - \left( \vartheta \right)}\end{array}} \right] \\ {{a}_{rx}}\left( \vartheta \right) = \left[{\begin{array}{*{20}{c}} {{a}_{rx}^ + \left( \vartheta \right)}\\ {{\underline{a}}_{rx}^ - \left( \vartheta \right)}\end{array}} \right] = \left[{\begin{array}{*{20}{c}}{\bar {a}_{rx}^ + \left( \vartheta \right)}\\ {{a}_{rx}^ - \left( \vartheta \right)}\end{array}} \right] $ |
$ {\overline{a}}_{tx}^ + \left( \vartheta \right) $为$ {a}_{tx}^ + \left( \vartheta \right) $的前Mtx-1项,$ {\underline{a}} _{tx}^ - \left( \vartheta \right) $为$ {a}_{tx}^ - \left( \vartheta \right) $的后Mtx-1项,$ {a}_{tx}^ + \left( \vartheta \right) $和 $ {a}_{tx}^ - \left( \vartheta \right) $分别对应发射阵列x轴正、负半轴(含参考点o)的流型矢量; $ {\overline{a}}_{ty}^ + \left( \phi \right) $为 $ {a}_{ty}^ + \left( \phi \right) $的前Mty-1项,$ {\underline{a}}_{ty}^ - \left( \phi \right) $为 $ {a}_{ty}^ - \left( \phi \right) $的后Mty-1项,$ {a}_{ty}^ + \left( \phi \right) $和 $ {a}_{ty}^ - \left( \phi \right) $分别对应发射阵列y轴正、负半轴(含参考点o)的流型矢量; $ {\overline{a}}_{rx}^ + \left( \vartheta \right) $为 $ {a}_{rx}^ + \left( \vartheta \right) $的前Mrx-1项,$ {\underline{a}}_{rx}^ - \left( \vartheta \right) $为 $ {a}_{rx}^ - \left( \vartheta \right) $的后Mrx-1项,$ {a}_{rx}^ + \left( \vartheta \right) $和 $ {a}_{rx}^ - \left( \vartheta \right) $分别对应发射阵列x轴正、负半轴(含参考点o)的流型矢量; $ {\overline{a}}_{ry}^ + \left( \phi \right) $为 $ {a}_{ry}^ + \left( \phi \right) $的前Mry-1项,$ {\underline{a}}_{ry}^ - \left( \phi \right) $为 $ {a}_{ry}^ - \left( \phi \right) $的后Mry-1项,$ {a}_{ry}^ + \left( \phi \right) $和 $ {a}_{ry}^ - \left( \phi \right) $分别对应接收阵列y轴正、负半轴(含参考点o)的流型矢量;同时满足:
| $ \left. \begin{array}{l} a_{ty}^ + \left( \phi \right) = {\left[{\exp \left( {{\rm{j}}\kappa _{{M_{ty}} - 1}^{ty}} \right),\cdots ,\exp \left( {{\rm{j}}\kappa _0^{ty}} \right)} \right]^{\rm{T}}},\;a_{ty}^ - \left( \phi \right) = {\left[{\exp \left( {{\rm{j}}\kappa _0^{ty}} \right),\cdots ,\exp \left( {{\rm{j}}\kappa _{ - \left( {{M_{ty}} - 1} \right)}^{ty}} \right)} \right]^{\rm{T}}}\\ a_{tx}^ + \left( \vartheta \right) = {\left[{\exp \left( {{\rm{j}}\kappa _{{M_{tx}} - 1}^{tx}} \right),\cdots ,\exp \left( {{\rm{j}}\kappa _0^{tx}} \right)} \right]^{\rm{T}}},\;\;{\mkern 1mu} a_{tx}^ - \left( \vartheta \right) = {\left[{\exp \left( {{\rm{j}}\kappa _0^{tx}} \right),\cdots ,\exp \left( {{\rm{j}}\kappa _{ - \left( {{M_{tx}} - 1} \right)}^{tx}} \right)} \right]^{\rm{T}}}\\ a_{ry}^ + \left( \phi \right) = {\left[{\exp \left( {{\rm{j}}\kappa _{{M_{ry}} - 1}^{ry}} \right),\cdots ,\exp \left( {{\rm{j}}\kappa _0^{ry}} \right)} \right]^{\rm{T}}},\;{\mkern 1mu} \;a_{ty}^ - \left( \phi \right) = {\left[{\exp \left( {{\rm{j}}\kappa _0^{ry}} \right),\cdots ,\exp \left( {{\rm{j}}\kappa _{ - \left( {{M_{ry}} - 1} \right)}^{ry}} \right)} \right]^{\rm{T}}}\\ a_{rx}^ + \left( \vartheta \right) = {\left[{\exp \left( {{\rm{j}}\kappa _{{M_{rx}} - 1}^{rx}} \right),\cdots ,\exp \left( {{\rm{j}}\kappa _0^{rx}} \right)} \right]^{\rm{T}}},\;\;{\mkern 1mu} a_{rx}^ - \left( \vartheta \right) = {\left[{\exp \left( {{\rm{j}}\kappa _0^{rx}} \right),\cdots ,\exp \left( {{\rm{j}}\kappa _{ - \left( {{M_{rx}} - 1} \right)}^{rx}} \right)} \right]^{\rm{T}}} \end{array} \right\} $ | (2) |
其中
| $ \left. \begin{array}{l} {\kappa _{{m_{rx}}}^{rx} \,\!\! = {{ - 2\pi {m_{rx}}d_x^r\cos \vartheta } \mathord{\left/ {\vphantom {{ - 2\pi {m_{rx}}d_x^r\cos \vartheta } \lambda}} \right. } \lambda}; \ {m_{rx}} = - \left( {{M_{rx}} - 1} \right),\cdots ,0,\cdots ,{M_{rx}} - 1}\\ {\kappa _{{m_{ty}}}^{ty} = {{ - 2\pi {m_{ty}}d_y^t\cos \phi } \mathord{\left/ {\vphantom {{ - 2\pi {m_{ty}}d_y^t\cos \phi } \lambda}} \right. } \lambda}; \ {m_{ty}} = - \left( {{M_{ty}} - 1} \right),\cdots ,0,\cdots ,{M_{ty}} - 1}\\ {\kappa _{{m_{tx}}}^{tx} = {{ - 2\pi {m_{tx}}\Delta _x^t\cos \vartheta } \mathord{\left/ {\vphantom {{ - 2\pi {m_{tx}}\Delta _x^t\cos \vartheta } \lambda}} \right. } \lambda}; \ {m_{tx}} = - \left( {{M_{tx}} - 1} \right),\cdots ,0,\cdots ,{M_{tx}} - 1}\\ {\kappa _{{m_{ry}}}^{ry} = {{ - 2\pi {m_{ry}}\Delta _y^r\cos \phi } \mathord{\left/ {\vphantom {{ - 2\pi {m_{ry}}\Delta _y^r\cos \phi } \lambda}} \right. } \lambda}; \ {m_{ry}} = - \left( {{M_{ry}} - 1} \right),\cdots ,0,\cdots ,{M_{ry}} - 1} \end{array} \right\} $ | (3) |
由于发射正交波形,则接收的回波信号经过匹配滤波以及矢量化操作后,可得第 l 次快拍的接收数据:
| $ { {y}_l} = {G}\left( {\vartheta ,\phi } \right){\beta _l} + { {n}_l} $ | (4) |
对yl进行列堆栈,即可得到L次脉冲下十字型阵列MIMO雷达的回波接收数据 $ {Y} \in {{\mathbb C}^{{M_t}{M_r} \times L}} $:
| $ {Y} = \left[{{{y}_1},{{y}_2},\cdots ,{{y}_L}} \right] = {G}\left( {\vartheta ,\phi } \right) \eta + {N} $ | (5) |
式中,$ \eta = \left[{{\beta _1},\cdots ,{\beta _L}} \right] \in {{\mathbb C}^{K \times L}} $对应目标的散射系数及多普勒频率信息; $ {N} \! = \! \left[{{{n}_1},\cdots,{{n}_L}} \right] \in {{\mathbb C}^{{M_t}{M_r} \times L}} $为加性高斯白噪声,并服从 $ {N} \! \sim \! {N^c}\left( \ {0,\sigma_n^2{{I}_{{M_t}{M_r}}}} \ \right); $ $G\left( {\vartheta ,\phi } \right) = {A_r}\left( {\vartheta ,\phi } \right) \oplus {A_t}\left( {\vartheta ,\phi } \right) = \left[{g\left( {{\vartheta _1},{\phi _1}} \right),\; \cdots ,} \right.$ $ \left.{ {g}\left( {{\vartheta _K},{\phi _K}} \right)} \right]{{\mathbb C}^{{M_t}{M_r} \times K}} $对应联合导向矢量,其中 $ {g}\left( {\vartheta ,\phi } \right) = {{a}_r}\left( {\vartheta ,\phi } \right) \otimes {{a}_t}\left( {\vartheta ,\phi } \right) $,上式中 $ \oplus $和 $ \otimes $分别为Khatri-Rao积和Kronecker积。显然,由以上信号模型以及收、发阵列流型可知,收、发阵列中分别存在2维方向上的长、短基线,因此可以直接采用DR-ESPRIT(Dual-Resolution ESPRIT,DR-ESPRIT)算法,获取目标2维角度的高精度估计;同时鉴于发射、接收阵列在x,y轴向上均满足关于参考点o中心对称,因此可以基于酉变换实现算法由复数域向实数域的转换,进一步降低算法运算量,然而直接利用传统DR-UESPRIT算法,就会存在实数域旋转不变因子无法提取的问题(将在文中3.3.1节讨论分析),从而无法实现特征分解与参数求解完全实数化;针对这个问题,本文提出一种新的基于酉变换的DR-UESPRIT算法,实现MIMO雷达2维高精度DOA的联合估计。
3 基于酉变换的高精度2维角度联合估计 3.1 酉矩阵设计及实信号子空间估计由信号模型和式(5)可得,发射、接收对应的流型矢量满足:
| $ \left. \begin{array}{l} {{Q}_{{M_t}}^{\rm H}{{a}_t}\left( {\vartheta ,\phi } \right) = {Q}_{{M_t}}^{\rm H}\left[{\begin{array}{*{20}{c}} {\bar {a}_{ty}^ + \left( \phi \right)}\\ {{{a}_{tx}}\left( \vartheta \right)}\\ {\underline {a}_{ty}^ - \left( \phi \right)} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {\bar {h}_{ty}^ + \left( \phi \right)}\\ {{{h}_{tx}}\left( \vartheta \right)}\\ {\bar {h}_{ty}^ - \left( \phi \right)} \end{array}} \right] = {{h}_t}\left( {\vartheta ,\phi } \right)}\\ {{Q}_{{M_r}}^{\rm H}{{a}_r}\left( {\vartheta ,\phi } \right) = {Q}_{{M_r}}^{\rm H}\left[{\begin{array}{*{20}{c}} {\bar {a}_{ry}^ + \left( \phi \right)}\\ {{{a}_{rx}}\left( \vartheta \right)}\\ {\underline {a}_{ry}^ - \left( \phi \right)} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {\bar {h}_{ry}^ + \left( \phi \right)}\\ {{{h}_{rx}}\left( \vartheta \right)}\\ {\bar {h}_{ry}^ - \left( \phi \right)} \end{array}} \right] = {{h}_r}\left( {\vartheta ,\phi } \right)} \end{array} \right\} $ | (6) |
式中,$ {{h}_{tx}}\left( \vartheta \right) \! = \!\! \left[\!\! {\begin{array}{*{20}{c}} {\bar {h}_{tx}^ + \left( \vartheta \right)}\\ 1\\ {\bar {h}_{tx}^ - \left( \vartheta \right)}\end{array}} \!\! \right],$ $ {{h}_{rx}}\left( \vartheta \right) \! = \!\! \left[\!\! {\begin{array}{*{20}{c}}{\bar {h}_{rx}^ + \left( \vartheta \right)}\\ 1\\ {\bar {h}_{rx}^ - \left( \vartheta \right)}\end{array}} \!\! \right] $;其中 $ \bar {h}_{tx}^ + \left( \vartheta \right) $,$ \bar {h}_{tx}^ - \left( \vartheta \right) $分别为 $ {h}_{tx}^ + \left( \vartheta \right) $和 $ {h}_{tx}^ - \left( \vartheta \right) $的前${M_{tx}} - 1$项,$ \bar {h}_{ty}^ + \left( \phi \right) $,$ \bar {h}_{ty}^ - \left( \phi \right) $分别为 $ {h}_{ty}^ + \left( \phi \right) $和 $ {h}_{ty}^ - \left( \phi \right) $的前${{\rm{M}}_{{\rm{ty}}}} - 1$项; $ \bar {h}_{rx}^ + \left( \vartheta \right) $、 $ \bar {h}_{rx}^ - \left( \vartheta \right) $分别为 $ {h}_{rx}^ + \left( \vartheta \right) $和 $ {h}_{rx}^ - \left( \vartheta \right) $的前${{\rm{M}}_{{\rm{rx}}}} - 1$项,$ \bar {h}_{ry}^ + \left( \phi \right) $,$ \bar {h}_{ry}^ - \left( \phi \right) $分别为 $ {h}_{ry}^ + \left( \phi \right) $和 $ {h}_{ry}^ - \left( \phi \right) $的前${{\rm{M}}_{{\rm{ry}}}} - 1$项;并满足:
| $ \left. \begin{array}{l} {{h}_{ty}^ + \left( \phi \right) = \sqrt 2 {{\left[{\cos \left( {{k} _{{M_{ty}} - 1}^{ty}} \right),\cdots ,\cos \left( {{k} _0^{ty}} \right)} \right]}^{\rm T}},\ {h}_{ty}^ - \left( \phi \right) = \sqrt 2 {{\left[{ - \sin \left( {{k} _{{M_{ty}} - 1}^{ty}} \right),\cdots ,- \sin \left( {{k} _0^{ty}} \right)} \right]}^{\rm T}}}\\ {{h}_{tx}^ + \left( \vartheta \right) = \sqrt 2 {{\left[{\cos \left( {{k} _{{M_{tx}} - 1}^{tx}} \right),\cdots ,\cos \left( {{k} _0^{tx}} \right)} \right]}^{\rm T}},\quad \! {h}_{tx}^ - \left( \vartheta \right) = \sqrt 2 {{\left[{ - \sin \left( {{k} _{{M_{tx}} - 1}^{tx}} \right),\cdots ,- \sin \left( {{k} _0^{tx}} \right)} \right]}^{\rm T}}}\\ {{h}_{ry}^ + \left( \phi \right) = \sqrt 2 {{\left[{\cos \left( {{k} _{{M_{ry}} - 1}^{ry}} \right),\cdots ,\cos \left( {{k} _0^{ry}} \right)} \right]}^{\rm T}},\,\,\; \! {h}_{ry}^ - \left( \phi \right) = \sqrt 2 {{\left[{ - \sin \left( {{k} _{{M_{ry}} - 1}^{ry}} \right),\cdots ,- \sin \left( {{k} _0^{ry}} \right)} \right]}^{\rm T}}}\\ {{h}_{rx}^ + \left( \vartheta \right) = \sqrt 2 {{\left[{\cos \left( {{k} _{{M_{rx}} - 1}^{rx}} \right),\cdots ,\cos \left( {{k} _0^{rx}} \right)} \right]}^{\rm T}},\quad \! {h}_{rx}^ - \left( \vartheta \right) = \sqrt 2 {{\left[{ - \sin \left( {{k} _{{M_{rx}} - 1}^{rx}} \right),\cdots ,- \sin \left( {{k} _0^{rx}} \right)} \right]}^{\rm T}}} \end{array} \right\} $ | (7) |
酉变换矩阵${{Q}_{{M_t}}},{{Q}_{{M_r}}} $满足:
| $ \left. \begin{array}{l} {{Q}_{2N}} = \frac{1}{{\sqrt 2 }}\left[{\begin{array}{*{20}{c}} {{{I}_N}}& {{\rm j}{{I}_N}}\\ {{\Pi _N}}& {-{\rm j}{\Pi _N}} \end{array}} \right]\\ {{Q}_{2N + 1}} = \frac{1}{{\sqrt 2 }}\left[{\begin{array}{*{20}{c}} {{{I}_N}}& {{{{0}}_{N \times 1}}}& {{\rm j}{{I}_N}}\\ {{{0}}_{N \times 1}^{\rm T}}& {\sqrt 2 }& {{{0}}_{N \times 1}^{\rm T}}\\ {{\Pi _N}}& {{{{0}}_{N \times 1}}}& {-{\rm j}{\Pi _N}} \end{array}} \right] \end{array} \right\} $ | (8) |
式中${{\rm I}_{\rm{N}}}$,${\Pi _{\rm{N}}}$为N×N维的单位矩阵和反对角矩阵。由式(6)得,存在酉变换矩阵$ {\tilde {Q}_{{M_t}{M_r}}} = {{Q}_{{M_r}}} \otimes {{Q}_{{M_t}}} $满足:
| $ \begin{align} {\ \Large \tilde \!\!\!} {Q}_{{M_t}{M_r}}^{\rm H} {g}\left( {\vartheta ,\phi } \right) & \! = \! \left[{{Q}_{{M_r}}^{\rm H}{{a}_r}\left( {\vartheta ,\phi } \right)} \right] \! \otimes \! \left[{{Q}_{{M_t}}^{\rm H}{{a}_t}\left( {\vartheta ,\phi } \right)} \right]\\ & \! = \! {{h}_r}\left( {\vartheta ,\phi } \right) \! \otimes \! {{h}_t}\left( {\vartheta ,\phi } \right) = {h}\left( {\vartheta ,\phi } \right) \end{align} $ | (9) |
显然,${\rm{h}}(\vartheta ,\phi )$为$g(\vartheta ,\phi )$在实数域对应的流型矢量,同时由上式可以看出,通过酉变换转换为实数域后,发射与接收导向矢量Kronecker积的关系并没有改变,这就为后续在实数域分别通过发射与接收矢量,提取长短基线的平移不变关系提供了条件。在进行实数域信号子空间估计之前,需要构建相应的Centro-Hermitian矩阵,即通过回波数据协方差矩阵(Covariance Matrix,CM)的前后平滑构建可得:
| $ \begin{align} {{R}_f} = & {{\left( {{{R}_{Y}} + {\Pi _{{M_t}{M_r}}}{R}_{Y}^*{\Pi _{{M_t}{M_r}}}} \right)} \mathord{\left/{\vphantom {{\left( {{{R}_{Y}} + {\Pi _{{M_t}{M_r}}}{R}_{Y}^*{\Pi _{{M_t}{M_r}}}} \right)} 2}} \right.} 2}\\ = & {{\left( {{G}{{R}_\eta }{{G}^ {\rm H}} + {\Pi _{{M_t}{M_r}}}{{G}^*}{R}_\eta ^*{{G}^{\rm T}}{\Pi _{{M_t}{M_r}}}} \right)} \mathord{\left/{\vphantom {{\left( {{G}{R_\eta }{{G}^{\rm H}} + {\Pi _{{M_t}{M_r}}}{{G}^*}{R}_\eta ^*{{G}^T}{\Pi _{{M_t}{M_r}}}} \right)} 2}} \right.} 2}\\ & + \sigma _n^2{{I}_{{M_t}{M_r}}} \! = \! {G}{{\left( {{{R}_\eta } \!\! + \!\! {R}_\eta ^*} \right){{G}^{\rm H}}} \mathord{\left/ {\vphantom {{\left( {{{R}_\eta } \!\! + \!\! {R}_\eta ^*} \right){{G}^{\rm H}}} \!\! 2}} \right.} 2} \! + \! \sigma _n^2{{I}_{{M_t}{M_r}}} \end{align} $ | (10) |
式中,$ {{R}_{Y}} \! = \! E\left\{ {{Y}{{Y}^{\rm H}}} \right\} \! = \! {G}{{R}_\eta }{{G}^{\rm H}} \! + \! \sigma _n^2{{I}_{{M_t}{M_r}}} $对应复数域的回波数据协方差矩阵,其中$ {R}_{\eta } = E\left\{ {\eta {\eta ^{\rm H}}} \right\} $。上式化简用到了$ {\Pi _{{M_t}{M_r}}}{{G}^*} = $ $ {G},\ {{G}^{\rm T}}{\Pi _{{M_t}{M_r}}} = {{G}^{\rm H}} $ 。通过酉变换矩阵$ {\tilde Q_{{M_t}{M_r}}}$即可实现复数域向实数域的变换:
| $\begin{array}{l} {{\rm{R}}_{{\rm{CM}}}}{\rm{ = }}\tilde Q_{{M_t}{M_r}}^HR{{\tilde Q}_{{M_{\rm{t}}}{M_r}}} = \tilde Q_{{M_t}{M_r}}^HG[({R_\eta } + R_\eta ^*)/2]{G^H}{{\tilde Q}_{{M_t}{M_r}}}\\ + \sigma _n^2{I_{{M_t}{M_r}}} = H{\mathop{\rm Re}\nolimits} ({R_\eta }){H^H} + \sigma _n^2{I_{{M_t}{M_r}}} \end{array}$ | (11) |
式中,$ {H} \left( {\vartheta ,\phi } \right) = \left[{{h} \left( {{\vartheta _1},{\phi _1}} \right),\cdots ,{h} \left( {{\vartheta _K},{\phi _K}} \right)} \right] $对应实数域的流型矢量,满足$ {h} \left( { \vartheta ,\phi } \right) = $ $ {{h}_r}\left( { \vartheta ,\phi } \right) \otimes {{h}_t}\left( { \vartheta ,\phi } \right) $;显然通过对矩阵R酉变换后即可获取对应的实数域协方差矩阵RCM。在获得实数域协方差矩阵RCM后,通过对其特征分解即可获得对应实信号子空间的估计值US。则无噪条件下估计的信号子空间US与对应的流行矢量H张成相同的空间,即存在非奇异矩阵T满足:
| ${{\rm{U}}_s} = HT = \tilde Q_{{M_t}{M_r}}^HGT$ | (12) |
发射、接收阵列中x,y轴向上的短基线阵元间距可以获得2维角度的无模糊粗估计,同时发射、接收阵列中x,y轴向上的长基线阵元间距可以获得2维角度的高精度估计,对应的平移不变关系分别为:
| $ \left. \begin{array}{l} {\exp \! \left( {{\rm j}{k} _{ - 1}^{ty}} \right) \! {J}_y^{c1}{{J}_{ty}}{{a}_t}\left( {\vartheta ,\phi } \right) \! = \! {J}_y^{c2}{{J}_{ty}}{{a}_t}\left( {\vartheta ,\phi } \right)}\\ {\exp \! \left( {{\rm j}{k} _{ - 1}^{rx}} \right) \! {J}_x^{c1}{{J}_{rx}}{{a}_r}\left( {\vartheta ,\phi } \right) \! = \! {J}_x^{c2}{{J}_{rx}}{{a}_r}\left( {\vartheta ,\phi } \right)}\\ {\exp \! \left( {{\rm j}{k} _{ - 1}^{tx}} \right) \! {J}_x^{f1}{{J}_{tx}}{{a}_t}\left( {\vartheta ,\phi } \right) \! = \! {J}_x^{f2}{{J}_{tx}}{{a}_t}\left( {\vartheta ,\phi } \right)}\\ {\exp \! \left( {{\rm j}{k} _{ - 1}^{ry}} \right) \! {J}_y^{f1}{{J}_{ry}}{{a}_r}\left( {\vartheta ,\phi } \right) \! = \! {J}_y^{f2}{{J}_{ry}}{{a}_r}\left( {\vartheta ,\phi } \right)} \end{array} \right\} $ | (13) |
式中,
| $J_y^{c1} = \left[ {{I_{2{M_{ty}} - 2}},{0_{\left( {2{M_{ty}} - 2} \right) \times 1}}} \right]$ |
| $J_y^{c2} = \left[ {{0_{\left( {2{M_{ty}} - 2} \right) \times 1}},{I_{2{M_{ty}} - 2}}} \right]$ |
| $J_x^{c1} = \left[ {{I_{2{M_{rx}} - 2}},{0_{\left( {2{M_{rx}} - 2} \right) \times 1}}} \right]$ |
| $J_x^{c2} = \left[ {{0_{\left( {2{M_{rx}} - 2} \right) \times 1}},{I_{2{M_{rx}} - 2}}} \right]$ |
| $J_x^{f1} = \left[ {{I_{2{M_{tx}} - 2}},{0_{\left( {2{M_{tx}} - 2} \right) \times 1}}} \right]$ |
| $J_x^{f2} = \left[ {{0_{\left( {2{M_{tx}} - 2} \right) \times 1}},{I_{2{M_{tx}} - 2}}} \right]$ |
| $J_y^{f1} = \left[ {{I_{2{M_{ry}} - 2}},{0_{\left( {2{M_{ry}} - 2} \right) \times 1}}} \right]$ |
| $J_y^{f2} = \left[ {{0_{\left( {2{M_{ry}} - 2} \right) \times 1}},{I_{2{M_{ry}} - 2}}} \right]$ |
选择矩阵${{J_{rx}}}$,${{J_{tx}}}$,${{J_{ty}}}$及${{J_{ry}}}$分别满足:
| $ \left. {\begin{array}{*{20}{l}} {{J_{rx}} = \left[ {\begin{array}{*{20}{c}} {{0_{{M_{ry}} - 1}}}&{{I_{2{M_{rx}} - 1}}}&{{0_{{M_{ry}} - 1}}} \end{array}} \right]}\\ {{J_{tx}} = \left[ {\begin{array}{*{20}{c}} {{0_{{M_{ty}} - 1}}}&{{I_{2{M_{tx}} - 1}}}&{{0_{{M_{ty}} - 1}}} \end{array}} \right]}\\ {{J_{ty}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{I_{{M_{ty}} - 1}}}&{{0_{\left( {{M_{ty}} - 1} \right) \times \left( {2{M_{tx}} + {M_{ty}} - 2} \right)}}} \end{array}}\\ {\begin{array}{*{20}{c}} {{0_{\left( {{M_{ty}} + {M_{tx}} - 2} \right) \times 1}}}&1&{{0_{\left( {{M_{ty}} + {M_{tx}} - 2} \right) \times 1}}} \end{array}}\\ {\begin{array}{*{20}{c}} {{0_{\left( {{M_{ty}} - 1} \right) \times \left( {2{M_{tx}} + {M_{ty}} - 2} \right)}}}&{{I_{{M_{ty}} - 1}}} \end{array}} \end{array}} \right]}\\ {{J_{ry}} = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{I_{{M_{ry}} - 1}}}&{{0_{\left( {{M_{ry}} - 1} \right) \times \left( {2{M_{rx}} + {M_{ry}} - 2} \right)}}} \end{array}}\\ {\begin{array}{*{20}{c}} {{0_{\left( {{M_{ry}} + {M_{rx}} - 2} \right) \times 1}}}&1&{{0_{\left( {{M_{ry}} + {M_{rx}} - 2} \right) \times 1}}} \end{array}}\\ {\begin{array}{*{20}{c}} {{0_{\left( {{M_{ry}} - 1} \right) \times \left( {2{M_{rx}} + {M_{ry}} - 2} \right)}}}&{{I_{{M_{ry}} - 1}}} \end{array}} \end{array}} \right]} \end{array}} \right\} $ | (14) |
则式(13)对应的实数域平移不变关系为:
| $ \left. {\begin{array}{*{20}{l}} {\exp \left( {{\rm{j}}\kappa _{ - 1}^{ty}} \right)Q_{2{M_{ty}} - 2}^{\rm{H}}J_y^{c1}{J_{ty}}{Q_{{M_t}}}{h_t}\left( {\vartheta ,\phi } \right) = Q_{2{M_{ty}} - 2}^{\rm{H}}J_y^{c2}{J_{ty}}{Q_{{M_t}}}{h_t}\left( {\vartheta ,\phi } \right)}\\ {\exp \left( {{\rm{j}}\kappa _{ - 1}^{rx}} \right)Q_{2{M_{rx}} - 2}^{\rm{H}}J_x^{c1}{J_{rx}}{Q_{{M_r}}}{h_r}\left( {\vartheta ,\phi } \right) = Q_{2{M_{rx}} - 2}^{\rm{H}}J_x^{c2}{J_{rx}}{Q_{{M_r}}}{h_r}\left( {\vartheta ,\phi } \right)}\\ {\exp \left( {{\rm{j}}\kappa _{ - 1}^{tx}} \right)Q_{2{M_{tx}} - 2}^{\rm{H}}J_x^{f1}{J_{tx}}{Q_{{M_t}}}{h_t}\left( {\vartheta ,\phi } \right) = Q_{2{M_{tx}} - 2}^HJ_x^{f2}{J_{tx}}{Q_{{M_t}}}{h_t}\left( {\vartheta ,\phi } \right)}\\ {\exp \left( {{\rm{j}}\kappa _{ - 1}^{ry}} \right)Q_{2{M_{ry}} - 2}^{\rm{H}}J_y^{f1}{J_{ry}}{Q_{{M_r}}}{h_r}\left( {\vartheta ,\phi } \right) = Q_{2{M_{ry}} - 2}^{\rm{H}}J_y^{f2}{J_{ry}}{Q_{{M_r}}}{h_r}\left( {\vartheta ,\phi } \right)} \end{array}} \right\} $ | (15) |
同时易证得:
| $ \left. {\begin{array}{*{20}{l}} {Q_{2{M_{ty}} - 2}^{\rm{H}}J_y^{c2}{Q_{2{M_{ty}} - 1}} = {{\left( {Q_{2{M_{ty}} - 2}^{\rm{H}}J_y^{c1}{Q_{2{M_{ty}} - 1}}} \right)}^*},Q_{2{M_{tx}} - 2}^{\rm{H}}J_x^{f2}{Q_{2{M_{tx}} - 1}} = {{\left( {Q_{2{M_{tx}} - 2}^{\rm{H}}J_x^{f1}{Q_{2{M_{tx}} - 1}}} \right)}^*}}\\ {Q_{2{M_{rx}} - 2}^{\rm{H}}J_x^{c2}{Q_{2{M_{rx}} - 1}} = {{\left( {Q_{2{M_{rx}} - 2}^{\rm{H}}J_x^{c1}{Q_{2{M_{rx}} - 1}}} \right)}^*},Q_{2{M_{ry}} - 2}^{\rm{H}}J_y^{f2}{Q_{2{M_{ry}} - 1}} = {{\left( {Q_{2{M_{ry}} - 2}^{\rm{H}}J_y^{f1}{Q_{2{M_{ry}} - 1}}} \right)}^*}} \end{array}} \right\} $ | (16) |
将式(16)代入式(15)可得:
| $ \left. \begin{array}{l} {\exp \left( {{\rm j}\kappa _{ - 1}^{ty}} \right)\left( {{K}_y^{c1} - {\rm j}{K}_y^{c2}} \right){{T}_{ty}}{{h}_t}\left( {\vartheta ,\phi } \right) = \left( {{K}_y^{c1} + {\rm j}{K}_y^{c2}} \right){{T}_{ty}}{{h}_t}\left( {\vartheta ,\phi } \right)}\\ {\exp \left( {{\rm j}\kappa _{ - 1}^{rx}} \right)\left( {{K}_x^{c1} - {\rm j}{K}_x^{c2}} \right){{T}_{rx}}{{h}_r}\left( {\vartheta ,\phi } \right) = \left( {{K}_x^{c1} + {\rm j}{K}_x^{c2}} \right){{T}_{rx}}{{h}_r}\left( {\vartheta ,\phi } \right)}\\ {\exp \left( {{\rm j}\kappa _{ - 1}^{tx}} \right)\left( {{K}_x^{f1} - {\rm j}{K}_x^{f2}} \right){{T}_{tx}}{{h}_t}\left( {\vartheta ,\phi } \right) = \left( {{K}_x^{f1} + {\rm j}{K}_x^{f2}} \right){{T}_{tx}}{{h}_t}\left( {\vartheta ,\phi } \right)}\\ {\exp \left( {{\rm j}\kappa _{ - 1}^{ry}} \right)\left( {{K}_y^{f1} - {\rm j}{K}_y^{f2}} \right){{T}_{ry}}{{h}_r}\left( {\vartheta ,\phi } \right) = \left( {{K}_y^{f1} + {\rm j}{K}_y^{f2}} \right){{T}_{ry}}{{h}_r}\left( {\vartheta ,\phi } \right)} \end{array} \right\} $ | (17) |
其中
| $ {\begin{array}{*{20}{l}} {{T_{ty}} = Q_{2{M_{ty}} - 1}^{\rm{H}}{J_{ty}}{Q_{{M_t}}},{\mkern 1mu} {\kern 1pt} {T_{rx}} = Q_{2{M_{rx}} - 1}^{\rm{H}}{J_{rx}}{Q_{{M_r}}}}\\ {{T_{tx}} = Q_{2{M_{tx}} - 1}^{\rm{H}}{J_{tx}}{Q_{{M_t}}},{\mkern 1mu} {\kern 1pt} {T_{ry}} = Q_{2{M_{ry}} - 1}^{\rm{H}}{J_{ry}}{Q_{{M_r}}}} \end{array}} $ | (18) |
| $ {\begin{array}{*{20}{l}} {K_y^{c1} = {\rm{Re}}\left\{ {Q_{2{M_{ty}} - 2}^{\rm{H}}J_y^{c2}{Q_{2{M_{ty}} - 1}}} \right\},{\mkern 1mu} {\kern 1pt} K_y^{c2} = {\rm{Im}}\left\{ {Q_{2{M_{ty}} - 2}^{\rm{H}}J_y^{c2}{Q_{2{M_{ty}} - 1}}} \right\}}\\ {K_x^{c1} = {\rm{Re}}\left\{ {Q_{2{M_{rx}} - 2}^{\rm{H}}J_x^{c2}{Q_{2{M_{rx}} - 1}}} \right\},{\mkern 1mu} {\kern 1pt} K_x^{c2} = {\rm{Im}}\left\{ {Q_{2{M_{rx}} - 2}^{\rm{H}}J_x^{c2}{Q_{2{M_{rx}} - 1}}} \right\}}\\ {K_x^{f1} = {\rm{Re}}\left\{ {Q_{2{M_{tx}} - 2}^{\rm{H}}J_x^{f2}{Q_{2{M_{tx}} - 1}}} \right\},{\mkern 1mu} {\kern 1pt} K_x^{f2} = {\rm{Im}}\left\{ {Q_{2{M_{tx}} - 2}^{\rm{H}}J_x^{f2}{Q_{2{M_{tx}} - 1}}} \right\}}\\ {K_y^{f1} = {\rm{Re}}\left\{ {Q_{2{M_{ry}} - 2}^{\rm{H}}J_y^{f2}{Q_{2{M_{ry}} - 1}}} \right\},{\mkern 1mu} {\kern 1pt} K_y^{f2} = {\rm{Im}}\left\{ {Q_{2{M_{ry}} - 2}^{\rm{H}}J_y^{f2}{Q_{2{M_{ry}} - 1}}} \right\}} \end{array}} $ | (19) |
考虑收发联合导向矢量,进一步化简式(17)可得:
| $ \left. \begin{array}{l} {\tan \left( {{{\kappa _{ - 1}^{ty}} \mathord{\left/{\vphantom {{\kappa _{ - 1}^{ty}} 2}} \right.} 2}} \right)\left( {{K}_y^{c1}{{T}_{ty}} \otimes {{I}_{{M_r}}}} \right){h}\left( {\vartheta ,\phi } \right) = \left( {{K}_y^{c2}{{T}_{ty}} \otimes {{I}_{{M_r}}}} \right){h}\left( {\vartheta ,\phi } \right)}\\ {\tan \left( {{{\kappa _{ - 1}^{rx}} \mathord{\left/{\vphantom {{\kappa _{ - 1}^{rx}} 2}} \right.} 2}} \right)\left( {{K}_x^{c1}{{T}_{rx}} \otimes {{I}_{{M_t}}}} \right)\tilde {h}\left( {\vartheta ,\phi } \right) = \left( {{K}_x^{c2}{{T}_{rx}} \otimes {{I}_{{M_t}}}} \right)\tilde {h}\left( {\vartheta ,\phi } \right)}\\ {\tan \left( {{{\kappa _{ - 1}^{tx}} \mathord{\left/{\vphantom {{\kappa _{ - 1}^{tx}} 2}} \right.} 2}} \right)\left( {{K}_x^{f1}{{T}_{tx}} \otimes {{I}_{{M_r}}}} \right){h} \left( {\vartheta ,\phi } \right) = \left( {{K}_x^{f2}{{T}_{tx}} \otimes {{I}_{{M_r}}}} \right){h}\left( {\vartheta ,\phi } \right)}\\ {\tan \left( {{{\kappa _{ - 1}^{ry}} \mathord{\left/{\vphantom {{\kappa _{ - 1}^{ry}} 2}} \right.} 2}} \right)\left( {{K}_y^{f1}{{T}_{ry}} \otimes{{I}_{{M_t}}}}\right)\tilde {h}\left( {\vartheta ,\phi } \right) = \left( {{K}_y^{f2}{{T}_{ry}} \otimes {{I}_{{M_t}}}} \right)\tilde {h}\left( {\vartheta ,\phi } \right)} \end{array} \right\} $ | (20) |
式中,$ \tilde {h}\left( {\vartheta ,\phi } \right) \! = \! {{h}_t}\left( {\vartheta ,\phi } \right) \! \otimes \! {{h}_r}\left( {\vartheta ,\phi } \right) \! = \! {\Xi _{{M_t}{M_r}}}{h}\left( {\vartheta ,\phi } \right) $。$ {\Xi _{{M_t}{M_r}}} = \sum\nolimits_{m = 1}^{{M_r}} {\sum\nolimits_{n = 1}^{{M_t}} {\left( {\Xi _{m,n}^{{M_r} \times {M_t}} \otimes \Xi _{n,m}^{{M_t} \times {M_r}}} \right)} } $,其中$ \Xi _{i,j}^{{M_r} \times {M_t}} $表示第(m,n)元素为1,其余为0的Mr×Mt维矩阵,其余类似;进一步考虑K个目标,上式可得:
| $ \left. \begin{array}{l} (K_y^{c1}{T_{ty}} \otimes {I_{{M_r}}})H(\vartheta ,\phi )\Phi _y^c = (K_y^{c2}{T_{ty}} \otimes {I_{{M_r}}})H(\vartheta ,\phi )\\ (K_x^{c1}{T_{tx}} \otimes {I_{{M_t}}})\tilde H(\vartheta ,\phi )\Phi _x^c = (K_x^{c2}{T_{rx}} \otimes {I_{{M_t}}})\tilde H(\vartheta ,\phi )\\ (K_x^{f1}{T_{tx}} \otimes {I_{{M_r}}})H(\vartheta ,\phi )\Phi _x^f = (K_x^{f2}{T_{tx}} \otimes {I_{{M_r}}})H(\vartheta ,\phi )\\ (K_y^{f1}{T_{ry}} \otimes {I_{{M_t}}})\tilde H(\vartheta ,\phi )\Phi _y^f = (K_y^{f2}{T_{ry}} \otimes {I_{{M_t}}})\tilde H(\vartheta ,\phi ) \end{array} \right\} $ | (21) |
式中,$\tilde H(\vartheta ,\phi ) = [\tilde h({\vartheta _1},{\phi _1}), \cdots ,\tilde h({\vartheta _k},{\phi _k})]$,满足$\tilde H = {\Xi _{{M_t}{M_r}}}H$;并且:
| $ \left. {\begin{array}{*{20}{l}} {\Phi _y^c = {\rm{diag}}\left\{ {\tan \left( {\kappa _{ - 1}^{ty,1}/2} \right), \cdots ,\tan \left( {\kappa _{ - 1}^{ty,K}/2} \right)} \right\}}\\ {\Phi _x^c = {\rm{diag}}\left\{ {\tan \left( {\kappa _{ - 1}^{rx,1}/2} \right), \cdots ,\tan \left( {\kappa _{ - 1}^{rx,K}/2} \right)} \right\}}\\ {\Phi _x^f = {\rm{diag}}\left\{ {\tan \left( {\kappa _{ - 1}^{tx,1}/2} \right), \cdots ,\tan \left( {\kappa _{ - 1}^{tx,K}/2} \right)} \right\}}\\ {\Phi _y^f = {\rm{diag}}\left\{ {\tan \left( {\kappa _{ - 1}^{ry,1}/2} \right), \cdots ,\tan \left( {\kappa _{ - 1}^{ry,K}/2} \right)} \right\}} \end{array}} \right\} $ | (22) |
式中
| $ \left\{ {{k} _{ - 1}^{ty,k}} \right\}_{k = 1}^K = {{2\pi d_y^t\cos {\phi _k}} \mathord{\left/{\vphantom {{2 \pi d_y^t\cos {\phi _k}} {l} }} \right.} {l} },\\ \left\{ {{k} _{ - 1}^{rx,k}} \right\}_{k = 1}^K = {{2\pi d_x^r\cos {\vartheta _k}} \mathord{\left/{\vphantom {{2\pi d_x^r\cos {{q} _k}} {l} }} \right.} {l}},\\ \left\{ {{k} _{ - 1}^{tx,k}} \right\}_{k = 1}^K = {{2\pi {D} _x^t\cos {\vartheta _k}} \mathord{\left/{\vphantom {{2\pi {D} _x^t\cos {\vartheta _k}} {l} }} \right.} {l} },\\ \left\{ {{k} _{ - 1}^{ry,k}} \right\}_{k = 1}^K = {2\pi {D} _y^r\cos {\phi _k}} \mathord{\left/{\vphantom {{2\pi {D} _y^r\cos {\phi _k}} {l} }} \right.} {l} $ |
由式(12)和式(21)可得:
| $ \left. \begin{array}{l} \left( {K_y^{c1}{T_{ty}} \otimes {I_{{M_r}}}} \right){U_S}\Psi _y^c = \left( {K_y^{c2}{T_{ty}} \otimes {I_{{M_r}}}} \right){U_s}\\ \left( {K_x^{c1}{T_{rx}} \otimes {I_{{M_t}}}} \right){{\tilde U}_S}\Psi _x^c = \left( {K_x^{c2}{T_{rx}} \otimes {I_{{M_t}}}} \right){{\tilde U}_s}\\ \left( {K_x^{f1}{T_{tx}} \otimes {I_{{M_r}}}} \right){U_S}\Psi _x^f = \left( {K_x^{f2}{T_{tx}} \otimes {I_{{M_r}}}} \right){U_s}\\ \left( {K_y^{f1}{T_{ry}} \otimes {I_{{M_t}}}} \right){{\tilde U}_S}\Psi _y^f = \left( {K_y^{f2}{T_{ry}} \otimes {I_{{M_t}}}} \right){{\tilde U}_s} \end{array} \right\} $ | (23) |
式中,${\tilde U_S} = {\Xi _{{M_t}{M_r}}}{U_S}$, $\Psi _y^c = {T^{ - 1}}\Phi _y^cT$,
$\Psi _x^c = {T^{ - 1}}\Phi _x^cT$, $\Psi _x^f = {T^{ - 1}}\Phi _x^fT$,$\Psi _y^f = {T^{ - 1}}\Phi _y^fT$;其中
以上旋转不变因子的提取基于同一个信号子空间,也就是说获其中的角度信息是保持不变的,理论上同一目标的2维角参数间是一一对应的,但实际过程中特征分解是分开进行的,因此就无法保证2维角度间的参数配对以及后续周期性高精度估计值的解模糊。对$ \Psi _y^c $进行特征分解可得:
| $ \Psi _y^c = P\tilde \Phi _y^c{P^{ - 1}} $ | (24) |
对比可得P和T-1均由$ \Psi _y^c $的特征向量构成,只是位置顺序可能不一样,因此存在一个有限次列交换矩阵F,使得:
| $ P = {T^{ - 1}}F $ | (25) |
进一步代入式(24)可得:
| $ \tilde \Phi _y^c = {F^{ - 1}}\Phi _y^cF $ | (26) |
利用矩阵P进一步构造:
| $ \left. {\begin{array}{*{20}{l}} {\tilde \Phi _x^c = {P^{ - 1}}\Psi _x^cP = {F^{ - 1}}T\Psi _x^c{T^{ - 1}}F = {F^{ - 1}}\Phi _x^cF}\\ {\tilde \Phi _x^f = {P^{ - 1}}\Psi _x^fP = {F^{ - 1}}T\Psi _x^f{T^{ - 1}}F = {F^{ - 1}}\Phi _x^fF}\\ {\tilde \Phi _y^f = {P^{ - 1}}\Psi _y^fP = {F^{ - 1}}T\Psi _y^f{T^{ - 1}}F = {F^{ - 1}}\Phi _y^fF} \end{array}} \right\} $ | (27) |
此时,$\tilde \Phi _y^c$,$\tilde \Phi _x^c$,$\tilde \Phi _x^f$以及$\tilde \Phi _y^f$对角线元素即可自动配对到同一个目标,通过下式即可获得配对的2维空间角的粗估计和精估计。
| $ \left. {\begin{array}{*{20}{l}} {u_k^c = \cos \left( {\phi _k^c} \right) = {\rm{atan}}\left( {\tilde \Phi _{y,k}^c} \right)\lambda {\rm{/}}\pi d_y^t,{\mkern 1mu} {\kern 1pt} u_k^f = \cos \left( {\phi _k^f} \right) = {\rm{atan}}\left( {\tilde \Phi _{y,k}^f} \right)\lambda {\rm{/}}\pi \Delta _y^r}\\ {v_k^c = \cos \left( {\vartheta _k^c} \right) = {\rm{atan}}\left( {\tilde \Phi _{x,k}^c} \right)\lambda {\rm{/}}\pi d_x^r,{\mkern 1mu} {\kern 1pt} v_k^f = \cos \left( {\vartheta _k^f} \right) = {\rm{atan}}\left( {\tilde \Phi _{x,k}^f} \right)\lambda {\rm{/}}\pi \Delta _x^t} \end{array}} \right\} $ | (28) |
式中,$\tilde \Phi _{y,k}^c$,$\tilde \Phi _{x,k}^c$,$\tilde \Phi _{y,k}^f$以及$\tilde \Phi _{x,k}^f$分别对应特征值矩阵的第k(k=1,···,K)个特征值。阵元间短基线平移不变关系可以获得无模糊粗估计值($ u_k^c $,$ v_k^c $),对应的阵元间长基线平移不变关系获得的高精度估计值($ u_k^f $,$ v_k^f $)具有周期模糊,其对应的模糊值可表示为:
| $ \left. {\begin{array}{*{20}{l}} {u_k^{f,m} = u_k^f + m\lambda {\rm{/}}\Delta _y^r,\;}&{\left\lceil {\left( { - 1 - u_k^f} \right)\lambda {\rm{/}}\Delta _y^r{\rm{/}}\lambda } \right\rceil \le m \le \left\lfloor {\left( {1 - u_k^f} \right)\lambda {\rm{/}}\Delta _y^r{\rm{/}}\lambda } \right\rfloor }\\ {v_k^{f,n} = v_k^f + n\lambda {\rm{/}}\Delta _x^t,\;}&{\left\lceil {\left( { - 1 - v_k^f} \right)\lambda {\rm{/}}\Delta _x^t{\rm{/}}\lambda } \right\rceil \le m \le \left\lfloor {\left( {1 - v_k^f} \right)\lambda {\rm{/}}\Delta _x^t{\rm{/}}\lambda } \right\rfloor } \end{array}} \right\} $ | (29) |
则对应以($ u_k^c $,$ v_k^c $)为参考值,即可确定最优的周期模糊数$ \mathop m\limits^\frown,$ $ \mathop n\limits^\frown $,则对应的无模糊高精度2维角度估计值可以表示为:
| $ \left. {\begin{array}{*{20}{l}} {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over u} _k^f = u_k^f + \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over m} \lambda {\rm{/}}\Delta _y^r,}\\ {\quad \quad \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over m} = \mathop {\arg \min }\limits_m \left| {u_k^f - u_k^c - m\lambda {\rm{/}}\Delta _y^r} \right|}\\ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over u} _k^f = v_k^f + \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over n} \lambda {\rm{/}}\Delta _x^t,}\\ {\quad \quad \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over n} = \mathop {\arg \min }\limits_n \left| {v_k^f - v_k^c - n\lambda {\rm{/}}\Delta _x^t} \right|} \end{array}} \right\} $ | (30) |
则对应的无模糊高精度2维空间角以及对应的方位、俯仰估计值为:
| $ \left. \begin{array}{l} {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \phi } }_k} = \arccos \left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over u} _k^f} \right)\\ {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \theta } }_k} = {\rm{arc}}\cos \left( {\sqrt {{{\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over u} _k^f} \right)}^2} + {{\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over v} _k^f} \right)}^2}} } \right)\\ {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \vartheta } }_k} = \arccos \left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over v} _k^f} \right)\\ {{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \varphi } }_k} = \arctan \left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over u} _k^f/\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over v} _k^f} \right) \end{array} \right\} $ | (31) |
至此,将算法流程总结如下:
(1) 利用回波数据计算对应的协方差矩阵,并进一步通过前后向平滑构建相应的Centro-Hermitian矩阵;
(2) 根据式(9)构建对应的酉变换矩阵,并进行酉变换处理和特征分解,获得实数域的信号子空间;
(3) 根据3.2.1节利用估计的信号子空间,进行实数域粗估计和精估计的联合估计;
(4) 根据3.2.2节实现粗估计和精估计间参数的配对,并利用粗估计值来解对应高精度估计的周期性模糊,最终获得无模糊的2维高精度估计。
3.3 算法性能及运算复杂度分析 3.3.1 算法酉变换分析传统DR-UESPRIT算法[14, 15]主要是将收发导向矢量作为整体利用其中心对称性进行酉变换,即在构建如式(10)的Centro-Hermitian矩阵Rf后,通过酉变换矩阵${{Q}_{{M_t}{M_r}}}$实现将Rf整体从复数域向实数域变换:
| $ \begin{align} {{R}_{{R}_f}} & = {Q}_{{M_t}{M_r}}^{\rm H}{{R}_f}{{Q}_{{M_t}{M_r}}} = {{{Q}_{{M_t}{M_r}}^{\rm H}\left( {{{R}_{Y}} + {\Pi _{{M_t}{M_r}}}{R}_{Y}^*{\Pi _{{M_t}{M_r}}}} \right){{Q}_{{M_t}{M_r}}}} \mathord{\left/ {\vphantom {{{Q}_{{M_t}{M_r}}^{\rm H}\left( {{{R}_{Y}} + {\Pi _{{M_t}{M_r}}}{R}_{Y}^*{\Pi _{{M_t}{M_r}}}} \right){{Q}_{{M_t}{M_r}}}} 2}} \right. } 2}\\ & = {{\left( {{Q}_{{M_t}{M_r}}^{\rm H}{{R}_{Y}}{{Q}_{{M_t}{M_r}}} + {Q}_{{M_t}{M_r}}^{\rm H}{\Pi _{{M_t}{M_r}}}{R}_{Y}^*{\Pi _{{M_t}{M_r}}}{{Q}_{{M_t}{M_r}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{Q}_{{M_t}{M_r}}^{\rm H}{{R}_{Y}}{{Q}_{{M_t}{M_r}}} + {Q}_{{M_t}{M_r}}^{\rm H}{\Pi _{{M_t}{M_r}}}{R}_Y^*{\Pi _{{M_t}{M_r}}}{{Q}_{{M_t}{M_r}}}} \right)} 2}} \right. } 2}\\ & = {{\left( {{Q}_{{M_t}{M_r}}^{\rm H}{{R}_{Y}}{{Q}_{{M_t}{M_r}}} + {{\left( {{Q}_{{M_t}{M_r}}^*} \right)}^{\rm H}}{R}_{Y}^*{Q}_{{M_t}{M_r}}^*} \right)} \mathord{\left/ {\vphantom {{\left( {{Q}_{{M_t}{M_r}}^{\rm H}{{R}_Y}{{Q}_{{M_t}{M_r}}} + {{\left( {{Q}_{{M_t}{M_r}}^*} \right)}^{\rm H}}{R}_{Y}^*{Q}_{{M_t}{M_r}}^*} \right)} 2}} \right. } 2} = {\mathop{\rm Re}\nolimits} \left( {{Q}_{{M_t}{M_r}}^{\rm H}{{R}_{Y}}{{Q}_{{M_t}{M_r}}}} \right) \end{align} $ | (32) |
上式中用到$ {\Pi _{{M_t}{M_r}}}{{Q}_{{M_t}{M_r}}} = {Q}_{{M_t}{M_r}}^* $;此时对应复数域x轴向上短基线旋转不变性(其余轴向上长、短基线类似)可表示为:
| $ \begin{array}{*{20}{l}} {\exp \left( {{\rm{j}}\kappa _{ - 1}^{rx}} \right)\left( {J_x^{c1}{J_{rx}} \otimes {I_{{M_t}}}} \right)g\left( {\vartheta ,\phi } \right)}\\ {\quad \quad = \left( {J_x^{c2}{J_{rx}} \otimes {I_{{M_t}}}} \right)g\left( {\vartheta ,\phi } \right)} \end{array} $ | (33) |
对应的实数域旋转不变性为:
| $ \begin{array}{*{20}{l}} {\exp \left( {{\rm{j}}\kappa _{ - 1}^{rx}} \right)\left( {J_x^{c1}{J_{rx}} \otimes {I_{{M_t}}}} \right){Q_{{M_t}{M_r}}}{\rm{ }}\rho \left( {\vartheta ,\phi } \right)}\\ {\quad \quad = \left( {J_x^{c2}{J_{rx}} \otimes {I_{{M_t}}}} \right){Q_{{M_t}{M_r}}}{\rm{ }}\rho \left( {\vartheta ,\phi } \right)} \end{array} $ | (34) |
其中,$Q_{{M_t}{M_r}}^{\rm{H}}g\left( {\vartheta ,\phi } \right) = \rho \left( {\vartheta ,\phi } \right)$对应实导向矢量,显然上式对应的旋转不变关系在实数域是不存在的,也就是说复数域对应的旋转不变关系无法通过传统酉变换处理映射至实数域,这是由于本文信号模型中发射与接收矢量均由两维子阵构成,则Khatri-Rao积的耦合会使得实数域对应的流型矢量$ {Q}_{{M_t}{M_r}}^{\rm H} {G} $中2维角度的旋转不变关系变得更为复杂,实数域流型矢量中待求参量间就会产生的耦合,此时复数域中待求参量间的旋转不变特性在实数域也就不成立。而本文酉变换过程分别利用收、发阵列的中心对称性,等效将发射与接收导向矢量分别实数化,因此经本文酉变换转换为实数域后,发射与接收导向矢量Kronecker积的关系并没有改变,对应的发射与接收导向矢量中分别存在的长、短基线旋转不变特性经过酉变换映射到实数域后并没有改变,通过实数域的不同长、短基线对应的旋转不变因子的提取,即可实现多目标参量在不同阵元基线上的度量,获取参数的超分辨。与传统DR-UESPRIT算法相比,本文算法在利用多尺度旋转不变技术实现2维空间角度高精度估计的同时,能够实现参数求解的全实数化,具有更低的运算复杂度。
3.3.2 运算复杂度分析考虑到相同维数下,实数域进行特征值分解和矩阵运算的运算量约为在复数域进行运算的1/4[16],则本文2维高精度估计算法的运算复杂度主要集中在:(1)协方差矩阵构造及酉变换:$ O\left\{ {2M_t^2M_r^2L} \right\} $; (2)实数域特征分解以及信号子空间估计:$ O\left\{ {{{M_t^3M_r^3} \mathord{\left/{\vphantom {{M_t^3M_r^3} 4}} \right.} 4}} \right\} $; (3)实值矩阵$\tilde \Phi _{y,k}^c$,$\tilde \Phi _{x,k}^c$,$\tilde \Phi _{y,k}^f$以及$\tilde \Phi _{x,k}^f$的计算以及2维角度的求解与配对:$ O\left\{ {\left[{\left( {2{M_{tx}} - 2} \right){M_r} \! + \! \left( {2{M_{ty}} - 2} \right){M_r}} + \right. \left( {2{M_{rx}}} \right.} \right. $ $ \left. {{{\left. {\left. { - 2} \right){M_t} + \left( {2{M_{ry}} - 2} \right){M_t} + 3{K^2}} \right]} \mathord{\left/{\vphantom {\left. \left( {2{M_{rx}} - 2} \right){M_t} + \left( {2{M_{ry}} - 2} \right){M_t} + 3 \right]} {K^2}} \right.} 4}} \right\} $;因此算法总的运算复杂度为:$O\left\{ {2M_t^2M_r^2L + \left[ {M_t^3M_r^3 + } \right.} \right.\left( {2{M_{tx}}{\kern 1pt} - 2} \right){M_r}{\kern 1pt} + \left( {2{M_{ty}}{\kern 1pt} - 2} \right){M_r}{\kern 1pt}$${\kern 1pt} + \left( {2{M_{rx}}{\kern 1pt} - 2} \right){M_t} + \left. {\left. {\left( {2{M_{ry}} - 2} \right){M_t} + 3} \right]{K^2}/4} \right\}$。对应的直接采用DR-ESPRIT算法的运算复杂度为$ O\left\{ \! {M_t^2 \! M_r^2 \! L} \right. \! + \! M_t^3 \! M_r^3 \! + $ $ \left[\ {\left( {2{M_{tx}} - 2} \right){M_r} + \left( {2{M_{ty}} - 2} \right){M_r} + \left( {2{M_{rx}} - 2} \right){M_t} + } \right. $ $ \left. {\left( {2{M_{ry}} - 2} \right){M_t} + 3} \right]\left. {{K^2}} \right\} $;采用传统DR-UESPRIT算法[14, 15]求解,由于实值导向矢量对应的长、短基线的旋转不变特性不再满足,因此只能实现实数域的特征分解,在利用长、短基线实现超分辨的过程中仍需将估计的实信号子空间转换到复数域,因此算法复杂度为:$ O \! \left\{ \! {{{2M_t^2 \! M_r^2 \! L \! + \! M_t^3 \! M_r^3} \! \mathord {\left/{\vphantom {{2M_t^2 \! M_r^2 \! L \! + \!\! M_t^3 \! M_r^3} 4}} \right.} 4} } \right. $ $ + \left[{\left( {2{M_{tx}} \! - 2} \right){M_r} + \left( {2{M_{ty}} \! - 2} \right){M_r} + {\left( {2{M_{rx}} \! - 2} \right){M_t} + }} \right. $$ \left. {\left. {\left( {2{M_{ry}} - 2} \right){M_t} + 3} \right]{K^2}} \right\} $。对比显然本文算法能够有效克服了传统将收、发导向矢量整体酉变换算法(即DR-UESPRIT算法)中实数域旋转不变因子无法提取的问题,在实现特征分解与参数求解完全实数化的同时,具有更低的运算复杂度。此外,本文算法在采用最小二乘的方法估计$ \Psi _y^c,$ $ \Psi _x^c,$ $ \Psi _x^f $以及$ \Psi _y^f $时,应满足列满秩条件$ K \! \le \! \min \left[{\left( {2{M_{tx}} \! - \! 2} \right) \! {M_r}} \right. $,$ \left( {2{M_{ty}} - 2} \right){M_r} $,$ \left( {2{M_{rx}} - 2} \right){M_t} $,$ \left. \left( {2{M_{ry}} - 2} \right){M_t} \right] $;因此,理论上算法的最大可分辨目标数目为$ \min \! \left[\left( {2{M_{\! tx}} \!\! - \!\! 2} \right) \! {M_{\! r}} \!\! - \!\! 1,\right. $$ \left( {2{M_{\! ty}} \!\! - \!\! 2} \right) \! {M_{\! r}} \!\! - \!\! 1,$$ \left( {2{M_{\! rx}} \!\! - \!\! 2} \right) \! {M_{\! t}} \!\! - \!\! 1,$ $ \left. \left( {2{M_{ry}} - 2} \right){M_t} - 1 \right] $。
4 仿真实验与数据分析假设十字型阵列配置下的单基地MIMO雷达,雷达收发阵列结构如图 1所示,以Hadamard编码信号为发射波形,分别进行以下仿真实验。
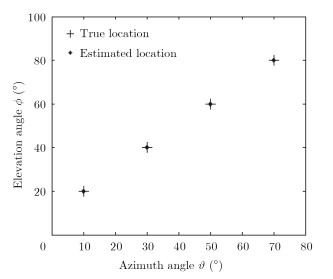
实验1 算法有效性验证 假设MIMO雷达收、发阵列配置满足Mtx=4,Mty=4,Mrx=4,Mry=4;收、发阵列中短基线阵元间距为$d_y^t = d_x^r = \lambda /2$,长基线阵元间距为$ \Delta _x^t = \Delta _y^r = 10\lambda$;远场空域存在4个独立目标,对应的2维空间角度满足$({\vartheta _1},{\phi _1}) = (10^\circ ,20^\circ )$,$({\vartheta _2},{\phi _2}) = (30^\circ ,40^\circ )$,$({\vartheta _3},{\phi _3}) = (50^\circ ,60^\circ )$,$({\vartheta _4},{\phi _4}) = (70^\circ ,80^\circ )$;信噪比为5 dB,数据快拍长度L=200,进行100次Monte-Carlo实验,仿真结果如图 2所示。由图 2可知,本文算法能够实现目标2维空间角度的有效估计及参数的自动配对,同时估计的2维空间角度比较集中而没有出现散布,一定程度上也反映了算法的稳健性。
|
图 2 本文算法的估计结果 Fig. 2 The estimation result of proposed method |
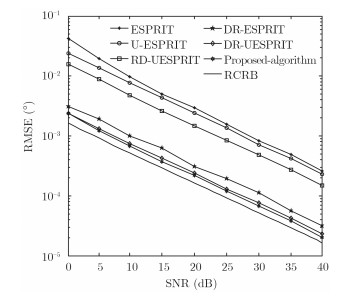
实验2 算法估计性能的比较 假设MIMO雷达收、发阵列配置不变,即Mt=Mr=13;收、发阵列中短基线阵元间距为$ d_y^t = d_x^r = {\lambda\mathord{\left/{\vphantom {\lambda2}} \right.} 2} $,长基线阵元间距为$ \Delta _x^t = \Delta _y^r = 10\lambda$;远场空域存在2个独立目标,对应的2维空间角度满足$({\vartheta _1},{\phi _1}) = (10^\circ ,20^\circ )$,$({\vartheta _2},{\phi _2}) = (50^\circ ,40^\circ )$;数据快拍长度L=200;信噪比为-10~40 dB;进一步与文献[13]RD-UESPRIT算法、文献[15]U-ESPRIT算法、文献[17, 18]ESPRIT算法传统DR-ESPRIT算法及传统DR-UESPRIT算法进行参数估计性能的比较,仿真结果如图 3所示。为保证对应孔径相同,ESPRIT算法、U-ESPRIT算法阵元配置为Mt=Mr=13; RD-UESPRIT算法中收、发阵列均采用方形阵,收、发阵列配置Mtx=7,Mty=7,Mrx=7,Mry=7,即Mt=Mr=49; DR-ESPRIT算法、传统DR-UESPRIT算法采用与本文相同的阵列配置;其中2维空间角参量估计性能的RCRB采用文献[14]的计算方法。
|
图 3 不同算法间空间角估计性能与信噪比的关系 Fig. 3 Spatial angles estimation performance versus SNR with different methods |
由图 3仿真结果可以看出,随着信噪比的增大,以上几种算法参数估计的RMSE逐渐变小,估计精度越来越高,这一点很好理解;同时与文献[15, 17, 18]算法仅利用短基线阵元间距(半波长)进行参数估计相比,本文算法长、短基线相结合的十字型阵列,利用双尺度法进行解周期模糊处理,实现长基线阵元间距的高精度无模糊估计,因此估计精度更优;特别地与文献[13]收发均采用方形阵列相比,本文对应的十字型阵列构型简单,在获得更高估计性能的同时不会造成阵列冗余,能够有效减少收发阵元数目及硬件开销。与DR-ESPRIT算法相比,传统DR-UESPRIT算法以及本文所提算法在利用双尺度进行方位高精度估计时,采用酉变换技术进行实协方差矩阵构造,均复用到了回波数据的共轭,因此对应的信号子空间估计也就更准确,对应的无模糊粗估计和高精度估计性能较优;与传统DR-UESPRIT算法相比,本文算法在估计精度及性能上与之相当,但在算法复杂度上更优,显然本文通过酉变换矩阵的设计,等效于将发射与接收导向矢量分别实数化,因此发射与接收导向矢量在实数化后Kronecker积的关系并没有改变,对应的长、短基线旋转不变特性经过酉变换映射到实数域后并没有改变,有效克服了传统DR-UESPRIT算法中收发流型矢量整体进行酉变换过程时,由于发射或接收矢量非理想造成的实数域流型矢量中待求参量间的耦合问题,因此与DR-UESPRIT算法相比,本文算法能够在保证估计精度的同时,实现回波矩阵特征分解和多参量联合估计求解的全部实数化,算法复杂度更优。
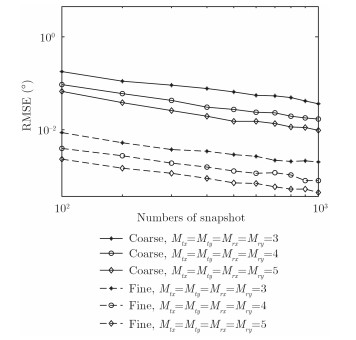
实验3 算法估计性能与参数之间的关系 收、发阵列配置满足Mtx=3,Mty=3,Mrx=3,Mry=3;信噪比为10 dB,其余不变,比较算法估计性能与基线长度$ (\Delta _x^t = \Delta _y^r) $之间的关系,仿真结果如图 4所示。目标2维空间角度不变,收、发阵列配置满足Mtx=Mty=Mrx=Mry=3,4,5;数据快拍长度L=100: 100: 1000变化,其余不变,比较算法估计性能与阵元数/快拍数之间的关系,仿真结果如图 5所示。由图 4可得,随着阵元间长基线长度的增大,粗估计误差几乎保持不变,显然阵元间短基线间距(半波长)是不变的,因此对应的方向估计是低精度无模糊的;而解模糊后的高精度估计误差随着长基线长度的增大存在基线模糊门限[19],即当基线长度小于模糊门限时,基线长度的增加会使得长基线对应的栅瓣宽度减小,从而改善参数估计精度;而当基线长度高于基线模糊门限时,栅瓣进一步减小会造成双尺度解模糊处理时正确解模糊的概率降低,进而使得估计性能恶化,终趋于无模糊粗估计对应的估计性能。同时,由文献[19]中可知造成估计精度恶化的最大基线长度满足$ {\delta _{\max }} = $ $\mathop {\min }\limits_{k = 1,\cdots ,K} \sqrt {\frac{1}{{2\sigma _k^2}}{{\left( {\frac{1}{{f_k^{ - 1}\left( \Upsilon \right)}}} \right)}^2} - 1} $,其中$ \sigma _k^2 $为目标方位粗估计误差,$ f(\Upsilon) $对应代价函数。即随着基线长度的变化,对应算法高精度估计性能是有界的。由图 5可以看出,随着阵元数及快拍数的增大,对应阵列雷达孔径也逐渐变大,对信号子空间的估计也就越准确,因此本文算法粗估计与精估计对应的估计性能也就越好。值得注意的是,阵元数的增大、快拍数的增加,意味着硬件成本及运算复杂度的增加,实际工程中满足需要精度的阵列配置即可。

|
图 4 本文算法估计性能与基线长度之间的关系 Fig. 4 Estimation performance of the proposed method versus long baseline |
|
图 5 本文算法估计性能与阵元数/快拍数间的关系 Fig. 5 Estimation performance of the proposed method versus numbers of array/snapshot |
本文针对单基地MIMO雷达的2维测向问题,提出一种具有2维双尺度平移不变特性的收、发十字型阵列设计,并针对传统DR-UESPRIT算法求解过程中存在的实数域旋转不变因子无法提取的问题,提出一种新的基于酉变换的高精度估计算法,理论分析与仿真结果表明:本文算法不牺牲阵列孔径,在获得2维空间角度无模糊高精度估计的同时,无需额外的配对算法和谱搜索;与传统酉变换过程相比,本文算法的酉变换过程等效将发射与接收导向矢量分别实数化,能够实现特征分解与参数求解完全实数化,具有更低的运算复杂度,更便于实际工程应用。
| [1] | Huleihel W, Tabrikian J, and Shavit R. Optimal adaptive waveform design for cognitive MIMO radar[J]. IEEE Transactions on Signal Processing, 2013, 61(20): 5075–5089.( 1) 1) |
| [2] | Wang P, Li H B, and Himed B. A parametric moving target detector for distributed MIMO radar in non-homogeneous environment[J]. IEEE Transactions on Signal Processing, 2013, 61(9): 2282–2294.( 1) 1) |
| [3] | Zhang X, Huang Y, Chen C, et al.. Reduced-complexity Capon for direction of arrival estimation in a monostatic multiple-input multiple-output radar[J]. IET Radar, Sonar & Navigation, 2012, 6(8): 796–801.( 2) 2) |
| [4] | Zhang X and Xu D. Low-complexity ESPRIT-based DOA estimation for colocated MIMO radar using reduced- dimension transformation[J]. Eletronics Letters, 2011, 47(4): 283–284.( 3) 3) |
| [5] | 文才, 王彤. 单基地MIMO雷达降维酉ESPRIT算法[J]. 系统工程与电子技术, 2014, 36(6): 1062–1067. Wen C and Wang T. Reduced-dimensional unitary ESPRIT algorithm for monostatic MIMO radar[J]. Systems Engineering and Electronics, 2014, 36(6): 1062–1067.(  2) 2) |
| [6] | Wang W, Wang X, Song H, et al.. Conjugate ESPRIT for DOA estimation in monostatic MIMO radar[J]. Signal Processing, 2013, 93(7): 2070–2075.( 2) 2) |
| [7] | Chen H W, Li X, Jiang W D, et al.. MIMO radar sensitivity analysis of antenna position for direction finding[J]. IEEE Transactions on Signal Processing, 2012, 60(10): 5201–5216.( 2) 2) |
| [8] | Chen H W, Zhou W, Yang J, et al.. Manifold sensitivity analysis for MIMO radar[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(5): 999–1003.( 2) 2) |
| [9] | Chen H W, Yang J, Zhou W, et al.. Manifold studies on fundamental limits of direction finding multiple-input multiple-output radar systems[J]. IET Radar, Sonar & Navigation, 2012, 6(8): 708–718.( 2) 2) |
| [10] | Li J F, Zhang X F, Chen W Y, et al.. Reduced-dimensional ESPRIT for direction finding in monostatic MIMO radar with double parallel uniform linear arrays[J]. Wireless Personal Communications, 2014, 77(1): 1–19.( 1) 1) |
| [11] | 王伟, 王晓萌, 李欣, 等. 基于MUSIC算法的L型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2014, 36(8): 1954–1959. Wang Wei, Wang Xiao-meng, Li Xin, et al.. Reduced-dimensional DOA estimation based on MUSIC algorithm in MIMO radar with L-shaped array[J]. Journal of Electronics & Information Technology, 2014, 36(8): 1954–1959.(  2) 2) |
| [12] | 梁浩, 崔琛, 代林, 等. 基于ESPRIT算法的L型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2015, 37(8): 1928–1935. Liang Hao, Cui Chen, Dai Lin, et al.. Reduced-dimensional DOA estimation based on ESPRIT algorithm in MIMO radar with L-shaped array[J]. Journal of Electronics & Information Technology, 2015, 37(8): 1928–1935.(  1) 1) |
| [13] | Li J F and Zhang X F. Unitary reduced-dimensional estimation of signal parameters via rotational invariance techniques for angle estimation in monostatic multiple-input-multiple-output radar with rectangular aarrays[J]. IET Radar, Sonar & Navigation, 2014, 8(6): 575–584.( 3) 3) |
| [14] | Zheng G M and Chen B X. Unitary dual-resolution ESPRIT for joint DOD and DOA estimation in bistatic MIMO radar[J]. Multidmensional Systems and Signal Processing, 2015, 26(1): 159–178.( 4) 4) |
| [15] | Zheng G M, Chen B X, and Yang M L. Unitary ESPRIT algorithm for bistatic MIMO radar[J]. Electronics Letters, 2012, 48(3): 179–181.( 5) 5) |
| [16] | Ren S, Ma X, Yan S, et al.. 2-D unitary ESPRIT-like Direction-Of-Arrival (DOA) estimation for coherent signals with a uniform rectangular array[J]. Sensors, 2013, 13(4): 4272–4288.( 1) 1) |
| [17] | Chen D F, Chen B X, and Guo D Q. Angle estimation using ESPRIT in MIMO radar[J]. Electronics Letters, 2008, 44(12): 770–771.( 2) 2) |
| [18] | Chen J L, Gu H, and Su W M. Angle estimation using ESPRIT without pairing in MIMO radar[J]. Electronics Letters, 2008, 44(24): 1422–1423.( 2) 2) |
| [19] | Lemma A N, Veen A J, and Deprettere E F. Multiresolution ESPRIT algorithm[J]. IEEE Transactions on Signal Processing, 1999, 47(6): 1722–1726.( 2) 2) |


