② (中国科学院大学 北京 100039)
② (University of Chinese Academy of Sciences, Beijing 100039, China)
合成孔径雷达(SAR)因其全天时全天侯的地球影像获取能力,被认为是一种有效的地球遥感手段[1]。由于距离向非模糊宽度对系统设计的限制,传统的SAR系统不能同时满足方位向高分辨率、距离向宽测绘带的要求。方位向高分辨率来自于直径较短的天线在长合成孔径时间内对目标进行照射,从而产生更高的多普勒带宽,需要足够高的脉冲采样频率(PRF)才能避免频谱混叠。相应地,非模糊距离要求子脉冲之间有较大的时间间隔,限制了PRF的取值。扫描SAR(ScanSAR)作为经典的宽测绘带SAR成像解决方案,通过牺牲方位向分辨率来增加测绘宽度。为了提高方位向分辨率,聚束/滑动聚束模式牺牲了波束的方位向覆盖范围。随着科技的进步,越来越多的科研任务及军事活动对SAR系统提出了新的需求,新的系统概念随之出现[2]。
Mosaic模式是一种新的SAR工作方式,通过将滑动聚束/聚束模式与ScanSAR相结合,实现高分宽测成像。在数据采集期间,雷达天线不仅像ScanSAR一样在距离向上扫描,而且像聚束/滑动聚束模式一样在方位向上扫描。根据雷达天线不同的方位向扫描方法,Mosaic模式可分为两种:方位向围绕场景中心扫描的聚束Mosaic模式[1],及方位向围绕更远的虚焦点扫描的滑动Mosaic模式[3-5]。以色列间谍卫星TECSAR首先采用了滑动Mosaic模式,在25 km×25 km范围内实现距离向及方位向均为1.8 m分辨率的成像[6]。作为TECSAR上成功实现的模式[7, 8],滑动Mosaic可以在大范围内实现高分辨率连续成像[9],是该文研究的重点。
自从以色列科学家在2004年的EUSAR会议中提出了Mosaic模式,并成功地在2008年发射的TECSAR卫星上实现该模式,该模式的一些问题引起了许多研究者的注意。问题主要分为4个方面:系统设计、成像算法、扇贝效应校正及缺失数据处理。由于Mosaic模式的基本工作原理是基于天线的复杂扫描方式,系统设计是该模式的关键。以色列科学家在文献[6, 7]中对TECSAR的系统设计进行了综述。一些中国科学工作者也对系统性能进行了评估。在扇贝效应校正的问题上,R. K. Haskins和P. W. Vachon在文献[10]中分析了3种扇贝效应校正的方法,其中的天线方向图逆加权方法去除扇贝效应的效果最好。为了解决空缺数据成像问题,Ury Naftaly和Ronit Levy-Nathansohn在文献[6, 7]中介绍了Mosaic模式的工作原理,并提出了连续成像的条件。现有的滑动Mosaic成像算法通常将每个Burst作为具有不同斜视角的滑动聚束数据单独处理[11]。较高的方位向分辨率需要较长的积累时间及方位向的大范围扫描,导致边缘Burst展现出明显的斜视特性[12]。扩展的两步式算法可以去除由斜视造成的方位向频谱混叠,即斜视造成的多普勒频率的倾斜,从而对边缘Burst进行聚焦成像[13-15]。为了合成连续的图像,单Burst成像的后处理操作需要对图像进行方位向拼接及配准,但拼接处目标的回波数据是相邻Burst数据的结合,导致不同Burst间出现多普勒相位跳变,从而破坏了如点目标分析的插值等操作[16]。为了避免图像后处理操作,采用类似于ScanSAR中的全孔径成像算法,将Burst间的空缺数据补零,作为单视滑动聚束数据进行处理。
然而,相干处理会导致目标响应出现交叉调制,这使图像变得杂乱。尽管对于幅度图像来说,交叉调制可以用低通滤波器进行滤除,但残余信息仍会影响图像进一步处理。另外,滑动Mosaic模式作为Burst模式的一种,其固有的扇贝效应与ScanSAR不同。天线方位向扫描导致多普勒中心的变化,改变了方位向的等效天线方向图,传统的扇贝效应校正方法的参数并不准确,故不能很好地去除扇贝效应。
本文分析了滑动Mosaic模式中,方位向扫描对等效方位向天线方向图的影响,并提出了针对滑动Mosaic模式的扇贝效应校方法。经过方位向去斜处理后,消除了方位向天线转动的影响,此时,通过双程天线方向图反加权,即可补偿扇贝辐射变化。基于方位向辐射均匀的数据,我们将现代谱估计理论引入到滑动Mosaic模式中,在距离压缩及距离徙动校正(RCMC)处理之后,通过线性预测模型(LPM)外推补全Mosaic模式Burst之间缺失的数据。这种方法不仅能成功地抑制杂乱图像中的“矛刺”,也可以增强图像的信噪比。通过本文所述的方法,改进的全孔径算法可以将不连续的滑动Mosaic数据聚焦为无杂乱的连续图像。
本文组织结构如下。第2节,简要介绍了滑动Mosaic模式。第3节,介绍了扇贝效应校正和全孔径处理的相关工作。第4节分析了等效天线方向图,并介绍了扇贝效应校正方法。第5节分析了“矛刺”的来源,并进行了孔径外推来抑制“矛刺”。第6节通过实际数据验证了本文提出的算法。最后,第7节对本文进行了总结。
2 滑动Mosaic模式Mosaic模式是一种有效的高分宽测成像方法。在方位向,雷达天线围绕远离场景的虚拟旋转中心扫描,地面足印连续滑动,以获取比ScanSAR更高的方位向分辨率。在距离向,雷达天线周期性地在几个不同的扫描角之间切换,可以覆盖不同的测绘带,实现ScanSAR一样的宽测绘带成像功能。相对于滑动聚束模式,滑动Mosaic模式牺牲了方位向分辨率来获取更大的距离向覆盖区域。方位向的图像质量是由子测绘带个数和距离向扫描角切换频率共同决定的。距离向扫描角的切换越频繁,方位向分辨率的变化越小,但整体图像分辨率是由子测绘带数量决定的。
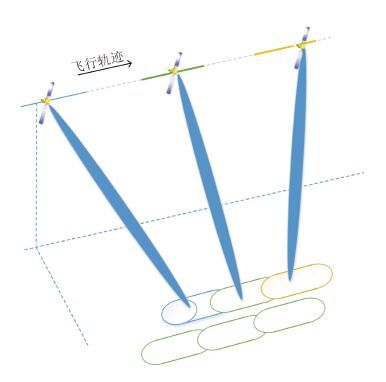
在滑动Mosaic模式数据处理中,像ScanSAR模式一样,我们通常将不同距离向扫描角的回波信号单独处理。在某个确切的扫描角度,以近距扫描为例,如图 1所示,相邻Burst的聚焦图像必须重叠,以进行图像拼接,形成连续图像。沿飞行轨迹的虚线表示雷达天线正在照射其余测绘带。在成像区域,沿航迹天线波束中心是间断的,但沿航迹波束照射区域的重叠确保了成像区域的重叠,是Mosaic模式连续成像的基础。单一子测绘带的回波数据可以看作是方位向周期性缺失数据的滑动聚束模式,也称作是间断SAR。文献[6, 17, 18]表明,由于不同方位向位置被天线方向图加权的系数不同,间断SAR的扇贝效应是不可避免的。
|
图 1 滑动Mosaic的成像 Fig.1 Imaging geometry of the sliding Mosaic mode |
本节介绍了扇贝效应和全孔径处理的基本概念,并详细分析了已有算法在处理Mosaic模式数据时的局限性,是本文的基础。
3.1 辐射扇贝效应扇贝效应是为了定量描述方位向辐射调制而提出的模型[10, 19, 20],通常出现在Burst模式SAR中,特别是ScanSAR和Mosaic模式。在Burst模式中,周期性的方位时间缺失,导致整个方位向多普勒频谱出现周期性的凹口,即扇贝效应,由固定的方位调制造成。
在Mosaic模式中,我们通常认为每个Burst的持续时间相同,且雷达天线距离向扫描角切换时丢失的数十余脉冲,相对于整个数据缺失长度是可以容忍的。在满足此种假设的条件下,扇贝随Burst周期性出现而重复。文献[10]指出,Mosaic图像中的扇贝调制主要由Burst随方位向波束移动时的波束错位和波束采样时间的变化共同影响。简而言之,可以用方位向反加权来均衡Burst中的能量变化。权重方程可表示如下:
| ${W_{\rm L}}(t) = \frac{1}{{{G^2}(t)}}$ | (1) |
WL(t)是权重系数,G2(t)是时域双程天线方向图。
在常规的SAR成像模式中,如ScanSAR,此权重模型经过实验检验有效。但是,此模型假设成像区域中的不同点的回波信号,被固定方位扫描角的双程天线方向图加权。Mosaic模式中,为了获得方位向高分辨率,雷达天线的方位向扫描增加了场景目标照射时间,从而拉伸了接收信号的加权模型,然而天线方向图保持不变。
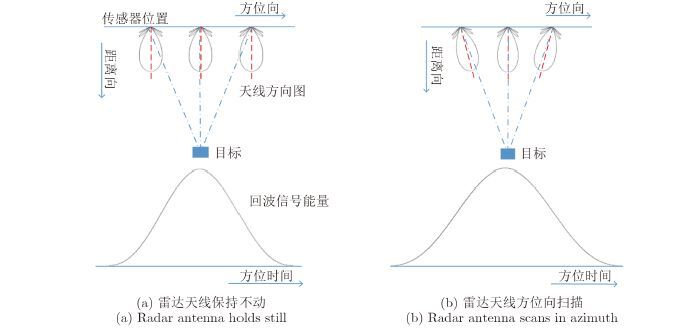
如图 2所示,单个点的加权模型随雷达天线方位向扫描发生变化。因此,之前的权重模型并不适合Mosaic模式扇贝效应校正,Burst中的能量不能被均衡。
|
图 2 不同方位向扫描模式中单点目标的加权模型 Fig.2 Different weighting models of individual point target for different azimuth scanning mode |
传统的全孔径成像算法,在处理周期性缺失的数据时,如ScanSAR,将丢失的数据补零[21, 22]。只有保持了正确的Burst间隔,单个目标分布在不同Burst之间的回波数据才能被相关处理。如此,不仅能保持相位信息,而且聚焦图像的地理信息和频谱特性也与相对应的连续成像模式相同。但是,由于对全孔径数据进行相关处理,图像中会出现交叉调制,也被称作“矛刺”。“矛刺”来源于Burst模式数据的周期性缺失。周期性缺失数据可以看作完整数据与周期性缺失的脉冲序列相乘。脉冲序列可以看作是冲击序列和矩形窗的卷积,导致了“矛刺”。
尽管图像中的“矛刺”可以通过低通滤波器抑制,但残余“矛刺”也会导致图像杂乱。为了更好地抑制其影响,文献[23]中提出基于ScanSAR的全孔径成像算法,通过线性预测模型外推的数据来补全ScanSAR数据Burst之间的间隙。由于ScanSAR数据并不符合线性预测模型,故需要先进行预处理,将其转换成符合线性预测模型的数据形式。实验证明,此方法对由周期性的ScanSAR数据间隙导致的矛刺抑制作用明显。
然而,由于天线方位向扫描,该方法并不能直接用于Mosaic模式数据处理。天线的方位向扫描导致多普勒带宽的增加,而脉冲重复频率(PRF)由单个点的多普勒带宽决定,并不会提升,从而造成频谱的混叠[24]。Mosaic模式中,多普勒中心会随天线方位向扫描线性的改变。因此,不同方位向位置目标的多普勒中心不同,与适用于线性预测的聚束模式数据形式类此。
4 扇贝效应校正不同于条带SAR和ScanSAR模式,滑动Mosaic的天线在方位向绕虚焦点旋转,以获得方位向高分辨率。权重角q,即波束中心线与天线相位中心到目标的连线的夹角,不仅随SAR平台变化,也随着方位向天线的旋转变化。方位向天线的旋转改变了点目标回波信号加权模型。假设单程天线方向图近似为sinc方程,可得加权模型为:
| $\begin{align} & G(\eta )\approx {{G}_{0}}\text{sin}{{\text{c}}^{2}}\left( \frac{0.886}{{{\beta }_{\text{bw}}}}\left( \theta -{{\theta }_{\text{rot}}} \right) \right) \\ & \approx {{G}_{0}}\sin {{\text{c}}^{2}}\left( \frac{0.886}{{{\beta }_{\text{bw}}}}\left( \frac{{{V}_{\text{r}}}\eta }{{{R}_{0}}}-{{K}_{\text{w}}}\eta \right) \right) \\ \end{align}$ | (2) |
其中,G0为天线增益,h为方位向时间,bbw为方位波束带宽,q为斜平面的权重角,qrot为波束转动角,Kw为天线转动角速度,Vr为等效速度,R0为最近斜距。
方位向天线方向图的旋转,导致现有的扇贝效应校正方法失效。通常,我们选用方位向天线方向图的Doppler模型进行进一步分析,表示如下:
| $G={{G}_{\text{a}}}\left( {{f}_{\eta }}-{{f}_{\text{dc}}} \right)$ | (3) |
其中,G为等效天线方向图,Ga为天线方向图,fh为多普勒频率,fdc为多普勒中心的变化。当考虑到波束转动及斜视情况:
| ${f_{{\rm{dc}}}} = {f_{{\rm{sq}}}} + {f_{{\rm{rot}}}}$ | (4) |
其中,fsq为斜视多普勒中心,frot为由于方位向天线扫描导致的多普勒中心变化量。frot随时间线性变化,而fsq是定值。一种去除扇贝的方法是计算出等效方位向天线方向图,这种方法不仅复杂,而且不准确。另一种方法是通过方位去斜去除frot的影响。文献[25]表明,方位多普勒中心的变化可以通过去斜方程去除,即
| ${{H}_{1}}=\exp \left[ -\text{j}\pi {{k}_{\text{rot}}}{{\left( t-{{t}_{\text{mid}}} \right)}^{2}} \right]$ | (5) |
其中,krot为瞬时多普勒中心变化率,tmid为Burst中心时间,t为方位时间。逆去斜方程表示如下:
| ${{H}_{2}}=\exp \left[ \text{j}\pi {{k}_{\text{rot}}}{{\left( t-{{t}_{\text{mid}}} \right)}^{2}} \right]$ | (6) |
去斜操作后的权重方程表示如下:
| $W({f_\eta }) = \frac{1}{{G_{\rm{a}}^2({f_\eta })}}$ | (7) |
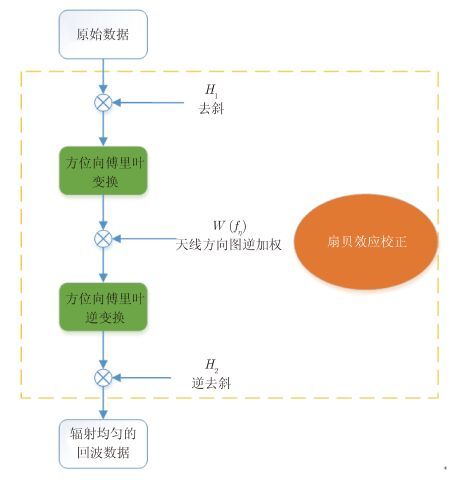
扇贝效应校正的流程图如图 3所示。
|
图 3 扇贝效应校正流程图 Fig.3 The flow-chart of scalloping correction |
如上文所述,滑动Mosaic模式中会出现方位向频谱混叠。为了消除多普勒频谱的混叠,在去斜及去除扇贝效应之后,需要通过在多普勒域补零来升采样,如图 3所示。之后进行逆去斜,去方位向频谱混叠及能量均衡的输出数据可以用常规的条带成像算法聚焦[26, 27]。文献[28, 29]指出,不同子测绘带的相位误差可通过全孔径聚焦方法同时去除,从而获得更好的聚焦效果。
5 全孔径数据处理针对周期性缺失数据的传统全孔径成像算法,仅仅将缺失部分补零,这将导致最终的成像结果中出现了“矛刺”等图像杂乱现象。为了更好地去除矛刺,我们选用了孔径外推的方法来补全缺失数据,而不是简单的用低通滤波器去滤除矛刺。基于逆SAR和聚束SAR中使用的现代谱估计理论,我们通常利用线性预测模型来外推预测Burst之间的空缺数据。但是,在滑动Mosaic模式的全孔径成像算法中,在距离徙动校正之后,利用方位向的频域匹配滤波来聚焦数据,会导致散射点的相位并不符合孔径外推理论中的线性预测模型。因此,我们引入了预处理步骤,采用时域的匹配滤波方法保留散射点相位与方位时间的线性关系,满足线性预测模型。
在滑动Mosaic模式中,单个Burst是斜视的滑动聚束数据,由文献[24, 30]可知,经距离压缩、RCMC及时域匹配滤波后的方位向第n个采样点的回波信号表示为:
| $S[n]={{A}_{n}}\exp \left( \frac{\text{j}2\pi f{{R}_{n}}}{\text{c}} \right)$ | (8) |
其中,
| $S[n]=\left\{ \begin{array}{*{35}{l}} -\sum\limits_{i=1}^{p}{a[i]S[n-i]}\text{ } 前向预测 \\ -\sum\limits_{i=1}^{p}{{{a}^{*}}[i]S[n+i]} 后向预测 \\ \end{array} \right.$ | (9) |
其中,a[i]为预测模型系数,p为预测模型的阶数(在SAR中表示散射中心的个数)。关于预测模型系数的计算,文献[17, 18]中指出,在图像恢复的孔径外推处理中,Burg算法的表现优于改进的Burg算法,Forward-Backward (FB)算法,及Tufts-Kumaresan (TK)算法等其他算法。因此,我们选用Burg算法作为基于线性预测模型的孔径外推算法。在特殊情况下,多个目标的集合中,某些目标的回波相位相反后累加,则会出现正弦形式的数据。此时,S[n]的相位与n并不成线性关系,但Burg算法仍然可以胜任,将正弦形式的回波近似为多个目标点的回波之和。这种近似会降低外推数据的质量,外推长度越长,准确度越低,然而,这种现象并不常见,也不会对图像分析造成影响[18]。
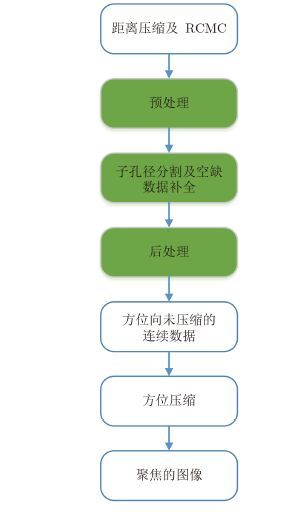
图 4给出了结合线性预测模型的滑动Mosaic数据方位向处理方法。相比传统的线性预测操作,我们引入了预处理和后处理步骤到滑动Mosaic数据处理中。
|
图 4 抑制矛刺”的方位处理流程 Fig.4 Block diagram of azimuth processing to suppress the spikes |
在预处理步骤中,利用回波信号与方位线性调频信号的共轭相乘进行脉冲压缩。只有通过这种方法,脉冲压缩后的信号形式才类似于逆SAR或聚束SAR,适用于基于线性预测模型的孔径外推方法。后处理操作通过逆去斜获得了连续的滑动Mosaic数据。
5.2 子孔径分割及数据外推为了便于孔径外推处理,带间隙的全孔径数据可以由两个Burst和一个邻近数据空缺的多个子孔径。相邻的子孔径有一个Burst的重叠。可得,单个点目标的回波数据形式如下:
| $\left. \begin{array}{l} {S_{\rm{L}}}[n] = \left\{ \begin{array}{l} {A_0}\left( {f,n\Delta t} \right)\exp \left( {\frac{{{\rm{j}}2{{π}} fR\left( {n\Delta t} \right)}}{{\rm{c}}}} \right),\quad n = 1,2,\cdots ,B - 1{\rm{ }}\\ 0,\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \ {否则} \end{array} \right.\\ {S_{\rm{H}}}[n] = \left\{ \begin{array}{l} {A_0}\left( {f,n\Delta t} \right)\exp \left( {\frac{{{\rm{j}}2{{π}} fR\left( {n\Delta t} \right)}}{{\rm{c}}}} \right),\quad n = E,E + 1,\cdots ,N{\rm{ }}\\ 0,\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \ {否则} \end{array} \right. \end{array} \right\}$ | (10) |
其中,
子孔径分块中的每个Burst通过以下方程,向中间的空缺数据内推:
| $ \left. \begin{aligned} {S_{\rm{L}}}\left[n \right] = & - \mathop \sum \limits_{i = 1}^{{N_{\rm{L}}}} {a_{\rm{L}}}\left[i \right]{S_{\rm{L}}}\left[{n - i} \right],\\ & n = B,B + 1,\cdots ,E\\ {S_{\rm{H}}}\left[n \right] = & - \mathop \sum \limits_{i = 1}^{{N_{\rm{H}}}} a_{\rm{H}}^{\rm{*}}\left[i \right]{S_{\rm{H}}}\left[{n + i} \right],\\ & n = E,E - 1,\cdots ,B \end{aligned} \right\}$ | (11) |
其中,aL和aH分别为Burg算法前向估计和后向估计系数,NL和NH分别为Burg模型前向孔径外推和后向孔径外推的阶数。子孔径空缺部分预测数据可以通过外推数据SL[n]和SH[n]的加权和得到。
综合孔径内推后的数据,滑动Mosaic模式中空缺数据被基于线性预测模型的相邻Burst数据外推填充。逆去斜操作后,获得了连续的方位向未压缩数据,可以用常规的频率匹配滤波算法将其聚焦。
6 结果分析如上文所述,滑动Mosaic模式的单个子测绘带,可以通过周期性的丢弃滑动聚束模式的方位向数据来进行模拟,故大多数SAR系统并没有专门设计滑动Mosaic模式。因此,对全孔径算法的性能分析,是基于方位向大范围扫描的滑动聚束数据。本实验的数据来自中国科学院电子学研究所的实验机载合成孔径雷达系统。系统的关键参数如下:载频为C波段(5.4 GHz),带宽200 MHz,飞机平均速度为133 m/s,方位向扫描角从+11.7°到-11.7°,脉冲重复频率(PRF)为2133 Hz。
在本次实验中,从原始滑动聚束数据中,周期性地每隔一个Burst丢弃N-1个Burst数据,即可获得单个子测绘带的滑动Mosaic数据。其中,N表示距离向的子测绘带个数。全孔径数据的多普勒中心频率等于中心Burst的多普勒频率或者中间两个Burst的多普勒中心频率均值。线性预测模型的阶数通常取作单个Burst长度的三分之一,这是Burg算法在保证精确预测的前提下,所能估算最多的系数[18]。之后的实验结果可以证明,包含3个Burst的子测绘带足以用来分析、评估提出的算法。文中所有的滑动Mosaic图像都在方位向进行了10倍多视操作,以降低相干斑噪声,并使2维分辨率相匹配。实验模拟了距离向4个子测绘带的情况,不仅可以避免单视数的情况出现,而且可以清晰地展示图像的扇贝效应及矛刺。
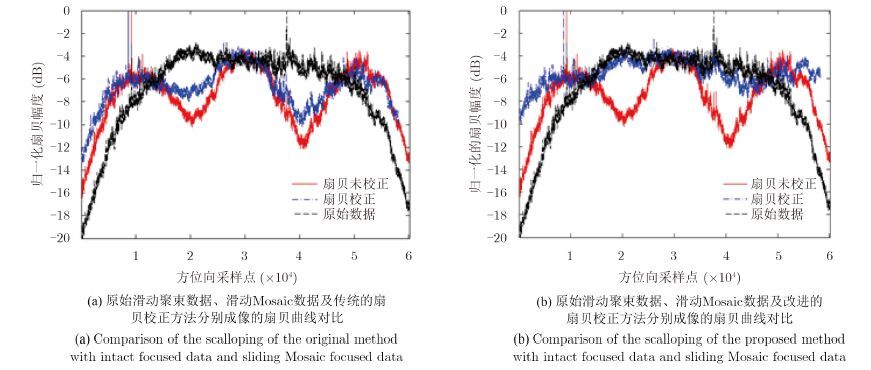
6.1 扇贝效应校正性能评估通常,假设图像聚焦良好,且场景中的目标均匀分布时,扇贝效应可以通过距离向像素幅度的累加来评估[10]。本次实验中,我们计算了4幅不同聚焦图像的扇贝效应,以验证改进的扇贝效应校正方法的有效性。其中,选取原始的滑动聚束数据及原始的滑动Mosaic数据的聚焦图像作为参考,其余两幅分别是利用传统扇贝效应校正方法及本文提出的改进的扇贝效应校正方法处理后的图像。由于边缘非完全成像区域的影响,图像的扇贝曲线在两端降低,属正常现象,因此,在评估实验结果时被忽略。滑动Mosaic图像的扇贝曲线中出现的驼峰,来源于数据的缺失,是本次实验校正的对象。均匀场景中的部分强点目标,导致标准的扇贝曲线出现3.5 dB的浮动,而周期性的数据缺失导致9 dB的浮动。传统的单视天线方向图逆加权处理后,如图 5(a)所示,扇贝曲线的凹口稍稍上升,扇贝效应略有改善,但仍然明显低于原始滑动聚束扇贝曲线,曲线的浮动仍高达5.5 dB,图像上仍会出现明暗相间的条纹。图 5(b)展示了原始图像和改进的扇贝效应校正处理后的扇贝曲线,可见,凹口处的扇贝曲线基本与原始数据相同,浮动低于3.5 dB。
|
图 5 扇贝效应结果,通过距离向像素幅度累加评估 Fig.5 The scalloping correction result by integrating pixel across range direction |
相比实验数据的成像结果,图像方位向的明暗变化更加明显。图 6展示了未进行扇贝效应校正的全孔径滑动Mosaic图像,图像大小为2048×6011像素,约1.5 km×12 km。从视觉效果可分辨出,图 6中方位向明暗相间的条纹,与图 5中扇贝曲线的变化相匹配,暗条纹出现的位置即扇贝曲线中的凹口位置。对图 6的数据进行改进的扇贝效应校正操作,即得图 7,方位向的亮暗变化相对较少,暗条纹消失。对扇贝曲线的分析也验证了此结论。

|
图 6 孔径内推未经扇贝效应校正的C波段雷达图像 Fig.6 C-Band radar image processed with aperture interpolation, without scalloping correction |

|
图 7 孔径内推及扇贝效应校正后的C波段雷达图像 Fig.7 C-Band radar image processed with de-scalloping and aperture interpolation |
通过扇贝曲线及图像视觉对比,扇贝现象明显地被抑制,即改进的扇贝效应校正方法适合处理滑动Mosaic数据。由于此方法中的方位向天线方向图是固定的,取决于雷达天线的参数,故扇贝效应校正的结果与场景无关。扇贝效应校正结果的精确度依赖于算法利用的多普勒中心的准确度,然而,多普勒中心估计的结果依赖于回波数据。由于单视加权模型的副作用,当低信噪比部分的信号被放大到高信噪比的幅度,噪声同样被放大,进而影响了整体图像的信噪比[10]。
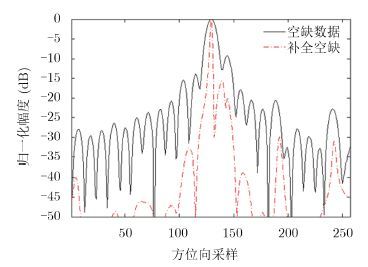
6.2 “矛刺”抑制效果为了验证改进的全孔径算法针对不同场景的效果,我们从图 7中选取了包含建筑、农田、河流、道路的区域,即红框标记的区域A和区域B。数据空缺率(每个周期内,数据空缺时间占总时间的比率)高达80%。原始数据及去除“矛刺”数据的聚焦图像局部区域放大部分分别为图 8的左右部分。如图 8(a)及图 8(b)所示,区域A包含了一些人造建筑的强散射点、一条河流、道路及周围的植被覆盖。为了更清晰地展示图 8(a)及图 8(b)的区别,对图 8(a)中标出的区域D进行放大,分别得到图 8(c)及图 8(d)。对比发现,图 8(d)中建筑屋顶的强散射点的方位向拖长的旁瓣被抑制,消除了对周围区域成像的干扰,图 8(b)中的道路变得更加清晰,河流的边缘更容易分辨,图像中的模糊被去除。如图 8(e)及图 8(f)所示,区域B主要是农田部分,包括稻田及部分强散射点,相比图 8(e),图 8(f)整体的分辨率及信噪比明显提升,农田区域更加清晰,旁边的强散射点区域旁瓣被压制,强弱目标的对比更加明显。针对不同的场景,如图 8(e)及图 8(f)所示,均匀场景区域的图像质量虽然有所提升,但并不如图 8(c)及图 8(d)中强散射点的效果明显。为了更详细地分析成像结果,我们取出了图 8(a)中红圈标出的孤立强点的方位向剖面图。图 9展示了空缺数据及孔径内推补全数据聚焦图像的方位向剖面图,点目标的3 dB宽度明显变小,旁瓣被抑制。需要指出的是,根据孔径外推算法的原理,线性预测模型的阶数(即等效散射中心)有限,平坦区域中,少数弱目标的贡献会被忽略,因此,虽然弱散射点的图像分辨率会有所提升,但效果并不如图 9中强点目标那么明显。

|
图 8 不同场景的SAR图像 Fig.8 SAR image of different landscape |
|
图 9 空缺数据及孔径内推数据的滑动Mosaic图像点目标剖面图 Fig.9 Azimuth profile of point target in the gapped and interpolated sliding Mosaic image |
为了研究全孔径成像算法对图像信噪比的影响,需要从图像中提取出噪声能量和信号能量,如图 7中黄框所示。由于平静的河流区域中大部分为镜面反射,可近似认为河流区域的回波为噪声信号,故选取图 7中的区域0作为噪声参考区域。为了更好地评估图像信噪比的变化,选取了图像中均匀场景,如农田区域1及河流旁的草地区域2-区域4等,不同场景的信噪比对比如表 1所示,对比发现,该方法可以改善图像的信噪比。总而言之,改进的全孔径算法成功地利用线性预测模型去除了“矛刺”,并提升了图像信噪比。
| 表 1 矛刺”抑制前后图像信噪比变化的对比 Tab.1 Signal-Noise Ratio (SNR) difference between the gapped and interpolated sliding Mosaic image |
在本文中,我们证明了抑制滑动Mosaic模式数据扇贝效应的可行性。通过对单个Burst进行去斜处理,并乘以天线方向图反加权模型,即可消除图像中明暗相间的条纹。改进的全孔径成像处理算法可以去除滑动Mosaic模式中相干处理引起的“矛刺”。利用Burg算法进行孔径内推操作,可以抑制图像中强点的旁瓣,并提高信噪比。滑动Mosaic数据处理实验验证了以上所述方法。可以认为,此方法提供了一种更精确的处理滑动Mosaic数据的方法,避免了Burst单独处理及图像拼接。
| [1] |
Carrara W G, Goodman R S, and Majewski R M.
Spotlight Synthetic Aperture Radar: Signal processing algorithms[M]. Boston: London, Artech House, 1995 : 1 -3.
( 0) 0)
|
| [2] |
邓云凯, 赵凤军, 王宇. 星载SAR技术的发展趋势及应用浅析[J].
雷达学报 , 2012, 1 (1) : 1-10 Deng Yun-kai, Zhao Feng-jun, and Wang Yu. Brief analysis on the development and application of spaceborne SAR[J].
Journal of Radars , 2012, 1 (1) : 1-10 ( 0) 0)
|
| [3] |
Belcher D P and Baker C J. High resolution processing of hybrid strip-map/spotlight mode SAR[J].
IEE Proceedings-Radar, Sonar and Navigation , 1996, 143 (6) : 366-374 ( 0) 0)
|
| [4] |
Mittermayer J, Lord R, and Borner E. Sliding spotlight SAR processing for TerraSAR-X using a new formulation of the extended chirp scaling algorithm[C]. 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 2003, 3: 1462-1464.
( 0) 0)
|
| [5] |
Levy-Nathansohn R and Naftaly U. Overview of the TECSAR satellite modes of operation[C]. EUSAR 2006-6th European Conference on Synthetic Aperture Radar, Dresden, Germany, 2006: 1-4.
( 0) 0)
|
| [6] |
Naftaly U and Levy-Nathansohn R. Overview of the TECSAR satellite hardware and mosaic mode[J].
IEEE Geoscience and Remote Sensing Letters , 2008, 5 (3) : 423-426 ( 0) 0)
|
| [7] |
Naftaly U. TecSAR-performance, design and status[C]. 5th European Conference on Synthetic Aperture Radar, Ulm, Germany, 2004: 27-30.
( 0) 0)
|
| [8] |
Sharay Y and Naftaly U. TECSAR: Design considerations and programme status[J].
IEE Proceedings-Radar, Sonar and Navigation , 2006, 153 (2) : 117-121 ( 0) 0)
|
| [9] |
Freeman A, Johnson W, Huneycutt B, et al. The "myth" of the minimum SAR antenna area constraint[J].
IEEE Transactions on Geoscience and Remote Sensing , 2000, 38 (1) : 320-324 ( 0) 0)
|
| [10] |
Hawkins R K and Vachon P W. Modelling SAR scalloping in burst mode products from RADARSAT-1 and ENVISAT[C]. Proceedings of CEOS Working Group on Calibration/Validation SAR Workshop, London, UK, 2002.
( 0) 0)
|
| [11] |
Han X, Li S, Yu W, et al. On the Mosaic mode spaceborne SAR[C]. 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 2012: 3983-3986.
( 0) 0)
|
| [12] |
Davidson G W and Cumming I. Signal properties of spaceborne squint-mode SAR[J].
IEEE Transactions on Geoscience and Remote Sensing , 1997, 35 (3) : 611-617 ( 0) 0)
|
| [13] |
Lanari R, Tesauro M, Sansosti E, et al. Spotlight SAR data focusing based on a two-step processing approach[J].
IEEE Transactions on Geoscience and Remote Sensing , 2001, 39 (9) : 1993-2004 ( 0) 0)
|
| [14] |
An D, Huang X, Jin T, et al. Extended two-step focusing approach for squinted spotlight SAR imaging[J].
IEEE Transactions on Geoscience and Remote Sensing , 2012, 50 (7) : 2889-2900 ( 0) 0)
|
| [15] |
Wang Y, Zhang Z, and Deng Y. Squint spotlight SAR raw signal simulation in the frequency domain using optical principles[J].
IEEE Transactions on Geoscience and Remote Sensing , 2008, 46 (8) : 2208-2215 ( 0) 0)
|
| [16] |
Cumming I G and Wong F H.
Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation[M]. Artech House, 2005 .
( 0) 0)
|
| [17] |
Salzman J, Akamine D, Lefevre R, et al. Interrupted synthetic aperture radar (SAR)[J].
IEEE Aerospace and Electronic Systems Magazine , 2002, 17 (5) : 33-39 ( 0) 0)
|
| [18] |
Moore T G, Zuerndorfer B W, and Burt E C. Enhanced imagery using spectral-estimation-based techniques[J].
Lincoln Laboratory Journal , 1997, 10 (2) : 171-186 ( 0) 0)
|
| [19] |
Bamler R. Optimum look weighting for burst-mode and ScanSAR processing[J].
IEEE Transactions on Geoscience and Remote Sensing , 1995, 33 (3) : 722-725 ( 0) 0)
|
| [20] |
Moore R K, Claassen J P, and Lin Y H. Scanning spaceborne synthetic aperture radar with integrated radiometer[J].
IEEE Transactions on Aerospace and Electronic Systems , 1981, 17 (3) : 410-421 ( 0) 0)
|
| [21] |
Bamler R. Adapting precision standard SAR processors to ScanSAR[C]. 1995 International IEEE Geoscience and Remote Sensing Symposium, IGARSS’95, Quantitative Remote Sensing for Science and Applications, Firenze, Italia, 1995, 3: 2051-2053.
( 0) 0)
|
| [22] |
Bamler R, Geudtner D, Schattler B, et al. RADARSAT ScanSAR interferometry[C]. IEEE 1999 International Geoscience and Remote Sensing Symposium, IGARSS’90 Proceedings, Alaska, USA, 1999, 3: 1517-1521.
( 0) 0)
|
| [23] |
Li N, Wang R, Deng Y, et al. Improved full-aperture ScanSAR imaging algorithm based on aperture interpolation[J].
IEEE Geoscience and Remote Sensing Letters , 2015, 12 (5) : 1101-1105 ( 0) 0)
|
| [24] |
Lanari R, Zoffoli S, Sansosti E, et al. New approach for hybrid strip-map/spotlight SAR data focusing[J].
IEE Proceedings-Radar, Sonar and Navigation , 2001, 148 (6) : 363-372 ( 0) 0)
|
| [25] |
Xu W, Huang P, Wang R, et al. TOPS-mode raw data processing using chirp scaling algorithm[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2014, 7 (1) : 235-246 ( 0) 0)
|
| [26] |
Raney R K, Runge H, Bamler R, et al. Precision SAR processing using chirp scaling[J].
IEEE Transactions on Geoscience and Remote Sensing , 1994, 32 (4) : 786-799 ( 0) 0)
|
| [27] |
Moreira A, Mittermayer J, and Scheiber R. Extended chirp scaling algorithm for air-and spaceborne SAR data processing in stripmap and ScanSAR imaging modes[J].
IEEE Transactions on Geoscience and Remote Sensing , 1996, 34 (5) : 1123-1136 ( 0) 0)
|
| [28] |
Li N, Wang R, Deng Y, et al. MOCO for High-resolution ScanSAR via full-aperture processing[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing , 2015, 8 (4) : 1721-1726 ( 0) 0)
|
| [29] |
Li N, Wang R, Deng Y, et al. Extension and evaluation of PGA in ScanSAR mode using full-aperture approach[J].
IEEE Geoscience and Remote Sensing Letters , 2015, 12 (4) : 870-874 ( 0) 0)
|
| [30] |
Mehrdad S.
Synthetic Aperture Radar Signal Processing with MATLAB Algorithms[M]. Canada, John Wiley &: Sons, Inc, 1999 : 220 -252.
( 0) 0)
|




