②(中国科学院 北京 100864)
③(中国科学院国家天文台月球与深空探测重点实验室 北京 100012)
②(Chinese Academy of Sciences, Beijing 100864, China)
③(Key Laboratory of Lunar and Deep Space Exploration, National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China)
极化合成孔径雷达通过发射和接收不同极化方式的电磁波测量地物目标的极化散射特性,获得目标极化散射矩阵[1]。由于电磁波的极化对目标的表面粗糙度、介电常数、几何形状和取向等物理特性比较敏感,因而极化散射矩阵蕴含着丰富的目标信息。极化测量获得的目标散射矩阵可用于提取目标极化特征参数,在农业大面积地物分类[2, 3]、森林物种识别[4]、地质结构描述[5, 6]、土壤湿度估计[7]、海冰监测[8]、海洋学[9, 10]和军事目标检测与识别[11]等领域有着广泛的应用。
极化合成孔径雷达极化层次和系统工作方式是极化合成孔径雷达系统总体设计的关键技术之一。随着极化合成孔径雷达系统及其应用技术的快速发展,极化层次和系统工作方式得到了深入发展。本文讨论了极化合成孔径雷达的极化层次,含单极化、双极化、全极化和简缩极化合成孔径雷达,较深入地分析了极化合成孔径雷达系统的工作方式,包括极化时间分割、极化频率分割、极化编码分割和方位向极化空间分割等方式。
2 极化合成孔径雷达的极化层次按照获取极化散射矩阵的极化层次不同,极化合成孔径雷达可以分为单极化、双极化、全极化和简缩极化,表 1给出极化合成孔径雷达的极化层次对比。
| 表 1 极化合成孔径雷达的极化层次 Tab. 1 Polarization hierarchies of PolSAR |
单极化合成孔径雷达是成像雷达最基本的形式。具有单一极化天线,单一发射通道和相同极化的单一接收通道,产生HH或VV单幅实图像。国外早期的星载合成孔径雷达,如Seasat、ERS-1、JERS-1、Radarsat-1等[12, 13]都是单极化合成孔径雷达。
双极化合成孔径雷达具有水平(H)和垂直(V)双极化天线,单路H或V极化正交发射。如果单路接收,可以得到HH和VV的两幅实图像,典型的双极化系统例子为Envisat-ASAR[14, 15];如果双通道接收,可以得到HH/HV或VV/VH的2×2矩阵的两幅实图像,SIR-C[16, 17]、RadarSat-2[18]、ALOS-PALSAR[19]都具有双极化条带模式。
全极化合成孔径雷达为标准的极化合成孔径雷达,它由H和V双极化天线正交发射、双通道接收组成。发射极化与接收极化必须是正交的极化对。全极化SAR固有的数据产品是场景每一分辨单元4×4散射矩阵。如果满足互易性、对称性假设,可能产生3×3矩阵,如被压缩的Stokes矩阵,或被压缩的Sinclair散射矩阵,这种形式通常被称为四极化(Quad-Polarization)合成孔径雷达。国外已有的星载合成孔径雷达任务中,RadarSat-2与ALOS-PALSAR都具有四极化条带模式[18, 19],TerraSAR-X将四极化作为试验模式[20, 21]。
全极化合成孔径雷达的优点是系统完善,能得到全面反映目标极化散射矩阵的全极化信息。目前全极化系统通常采用极化时分的工作方式,脉冲重复频率(PRF)是单极化或双极化合成孔径雷达的两倍。主要缺点是:系统复杂,成本高;成像带宽度是单极化或双极化合成孔径雷达的一半;数据率为单极化雷达的4倍,平均数据率与双极化雷达可比;平均功率大于单极化雷达的两倍;大视角交叉极化距离模糊恶化[18, 19]。为克服上述缺点,降低系统复杂性,权衡成像带宽度、数据率、脉冲重复频率、模糊比等指标与参数,必须寻求极化合成孔径雷达新的结构体系。简缩极化(Compact Polarimetry,CP)就是为降低全极化系统复杂性而提出的新技术。
简缩极化雷达仅发射一种极化,接收两种正交极化及其相对相位。简缩极化雷达产生的原始数据是后向散射场的协方差矩阵,并可转换为Stokes矢量。Stokes矢量的4个要素可以由两路接收极化的强度及相关相位的实部和虚部来估计。简缩极化主要是争取获得与全极化系统可比的后向散射定量分类,而避免全极化系统相关的缺点。
按照发射和接收的极化序列,简缩极化结构主要的模式有p/4模式、双圆极化模式(DCP)和圆极化发射线极化接收模式(CTLR)等[22]。近些年,已发射或正在研制中的星载极化SAR多采用简缩极化方式实现。印度Chandraayan-1月球探测器的Mini-SAR[23]、美国月球勘察轨道器的Mini-RF[24]以及印度的RISAT-1[25]都选择了双圆极化简缩极化模式,日本ALOS-2卫星上搭载的PALSAR-2亦将简缩极化作为试验模式,加拿大Radarsat-2后续的雷达卫星星座(RadarSat Constellation Mission,RCM)[26]计划也采用双圆极化的简缩极化模式是实现全极化。目前,简缩极化是在不增加系统复杂度、不降低分辨率和成像带宽度的前提下获得全极化数据的优选方案。
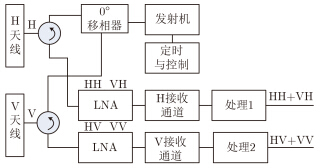
2.1 p/4简缩极化模式[22, 27, 28]图 1给出了p/4简缩极化模式的工作原理图。系统由H和V双极化天线、单路发射、单路移相器、H极化和V极化两路相干接收通道、两路极化处理器组成。
|
图 1 p/4简缩极化模式的工作原理图 Fig.1 Principle diagram of p/4 compact polarization radar |
p/4极化信号的产生过程为:发射信号经0°移相后,同时激励水平极化天线和垂直极化天线,在空间形成相对于水平向和垂直向成45°倾斜的p/4极化发射信号。由地物反射的p/4极化信号,经水平极化天线和垂直极化天线分别进入H极化和V极化两路正交极化接收机,再经处理器处理,得到2×2平均协方差矩阵。
p/4模式中,极化分解主要在水平向和垂直向对场景中的散射体分布进行。处理器进行聚焦和多视处理:聚焦级输出单视复图像数据;多视级输出2×2平均协方差矩阵,它可转换为4单元Stokes矢量。经处理重建全极化数据。
目标散射矢量为:
| ${{k}_{\pi /4}}={{\left[ {{S}_{\text{HH}}}+{{S}_{\text{HV}}}\quad {{S}_{\text{HV}}}+{{S}_{\text{VV}}} \right]}^{\text{T}}}/\sqrt{2}$ | (1) |
对应的目标协方差矩阵为:
| ${{J_{\pi /4}}}=\left\langle {{k}_{\pi /4}}k_{\pi /4}^{\text{H}} \right\rangle =\frac{1}{2}\left[ \begin{matrix} \left\langle {{\left| {{S}_{\text{HH}}} \right|}^{2}} \right\rangle \quad & \quad \left\langle {{S}_{\text{HH}}}\cdot S_{\text{VV}}^{\text{*}} \right\rangle \\ \left\langle {{S}_{\text{VV}}}\cdot S_{\text{HH}}^{\text{*}} \right\rangle \quad & \quad \left\langle {{\left| {{S}_{\text{VV}}} \right|}^{2}} \right\rangle \\ \end{matrix} \right]\\ \qquad +\frac{1}{2}\left[ \begin{matrix} \left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle \quad & \quad \left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle \\ \left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle \quad & \quad \left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle \\ \end{matrix} \right]\\ \qquad +\frac{1}{2}\left[ \begin{matrix} 2\text{Re}(\left\langle {{S}_{\text{HH}}}\cdot S_{\text{HV}}^{\text{*}} \right\rangle )\quad & \quad \left\langle {{S}_{\text{HH}}}\cdot S_{\text{HV}}^{\text{*}}+S_{\text{VV}}^{\text{*}}\cdot {{S}_{\text{HV}}} \right\rangle \\ \left\langle S_{\text{HH}}^{\text{*}}\cdot {{S}_{\text{HV}}}+{{S}_{\text{VV}}}\cdot S_{\text{HV}}^{\text{*}} \right\rangle \quad & \quad 2\text{Re}(\left\langle {{S}_{\text{VV}}}\cdot S_{\text{HV}}^{\text{*}} \right\rangle ) \\ \end{matrix} \right]$ | (2) |
重建的伪全极化目标协方差矩阵为:
| ${{\left[ {{C}_{\pi /4}} \right]}_{\text{pseudo }\text{quad}}}=\left[ \begin{matrix} {{J}_{11}}-{{\left| {{S}_{\text{HV}}} \right|}^{2}}\quad & \quad \text{0}\quad & \quad {{J}_{12}}-{{\left| {{S}_{\text{HV}}} \right|}^{2}} \\ 0\quad & \quad 2{{\left| {{S}_{\text{HV}}} \right|}^{2}}\quad & \quad 0 \\ {{\left( {{J}_{12}}-{{\left| {{S}_{\text{HV}}} \right|}^{2}} \right)}^{*}}\quad & \quad 0\quad & \quad {{J}_{22}}-{{\left| {{S}_{\text{HV}}} \right|}^{2}} \\ \end{matrix} \right]$ | (3) |
| ${J_{11}} = \left\langle {{{\left| {{S_{{\rm{HH}}}}} \right|}^2}} \right\rangle + \left\langle {{{\left| {{S_{{\rm{HV}}}}} \right|}^2}} \right\rangle $ |
| $\quad {J_{12}} = \left\langle {{S_{{\rm{HH}}}} \cdot S_{{\rm{VV}}}^{\rm{*}}} \right\rangle + \left\langle {{{\left| {{S_{{\rm{HV}}}}} \right|}^2}} \right\rangle $ |
| ${J_{22}} = \left\langle {{{\left| {{S_{{\rm{VV}}}}} \right|}^2}} \right\rangle + \left\langle {{{\left| {{S_{{\rm{HV}}}}} \right|}^2}} \right\rangle $ |
p/4简缩极化模式在脉冲重复频率选择、成像带宽度、两接收通路的辐射平衡、功率消耗、下传数据率、极化分解和定标处理方法等方面有优势。与全极化方式不同,p/4模式不能区分点目标(单次反射、偶次反射、偶极子)散射点相对雷达视角的方位。但对分布目标,如作物、森林等,p/4模式具有与全极化模式一致的区分能力。
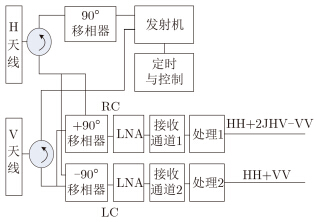
2.2 双圆极化发射接收(DCP)简缩极化模式[22, 29, 30]双圆极化模式简缩极化由H和V双极化天线左旋或右旋圆极化发射,左旋和右旋双极化相干接收组成。旋转不变性要求发射的极化必须是圆极化。标准的方法是发射圆极化,接收相干的双圆极化。双圆极化发射接收简缩极化模式由H和V双极化天线、单路发射机和单路发射移相器、双路接收移相器、H和V两路双极化相干接收和双极化处理器组成。图 2给出了双圆极化模式的工作原理图。
|
图 2 双圆极化模式的工作原理图 Fig.2 Principle diagram of DCP compact polarization radar |
圆极化发射信号的产生过程为:发射信号经发射+90°(或–90°)移相后,同时激励水平极化和垂直极化天线,在空间形成右旋圆极化(或左旋圆极化) 的发射信号。由地物反射的右旋(或左旋)圆极化信号,进入水平极化和垂直极化天线。H极化天线信号经过接收移相器1进行+90°移相,产生右旋圆极化波,进入右旋圆极化接收机;V极化天线信号经过接收移相器2进行–90°移相,产生左旋圆极化波,进入左旋圆极化正交极化接收机,分别经两路处理器处理,获得的2×2协方差矩阵,经处理重建3×3四极化协方差矩阵。
目标散射矢量为(以发射右旋极化为例):
| ${{k}_{\text{DCP}}}={{[{{S}_{\text{RR}}}\quad {{S}_{\text{RL}}}]}^{\text{T}}}=\left[ \left( {{S}_{\text{HH}}}-{{S}_{\text{VV}}}+i2{{S}_{\text{HV}}} \right) \right.\quad {{\left. i({{S}_{\text{HH}}}+{{S}_{\text{VV}}}) \right]}^{\text{T}}}/2$ | (4) |
| ${{J}_{\text{DCP}}}=\left\langle {{k}_{\text{DCP}}}k_{\text{DCP}}^{\text{H}} \right\rangle\\ =\frac{1}{4}\left[ \begin{matrix} \left\langle {{\left| \left( {{S}_{\text{HH}}}-{{S}_{\text{VV}}} \right) \right|}^{2}} \right\rangle \ & \ -i\left\langle \left( {{S}_{\text{HH}}}-{{S}_{\text{VV}}} \right)\cdot {{\left( {{S}_{\text{HH}}}+{{S}_{\text{VV}}} \right)}^{*}} \right\rangle \\ i\left\langle \left( {{S}_{\text{HH}}}+{{S}_{\text{VV}}} \right)\cdot {{\left( {{S}_{\text{HH}}}-{{S}_{\text{VV}}} \right)}^{*}} \right\rangle \ & \ \left\langle {{\left| {{S}_{\text{HH}}}+{{S}_{\text{VV}}} \right|}^{2}} \right\rangle \\ \end{matrix} \right]\\+\frac{1}{4}\left[ \begin{matrix} 4\left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle & 0 \\ 0 & 0 \\ \end{matrix} \right]+\frac{1}{4}\left[ \begin{matrix} 4\text{Im}\left( \left\langle \left( {{S}_{\text{HH}}}-{{S}_{\text{VV}}} \right)\cdot S_{\text{HV}}^{*} \right\rangle \right) & 2\left\langle {{\left( {{S}_{\text{HH}}}+{{S}_{\text{VV}}} \right)}^{*}}\cdot {{S}_{\text{HV}}} \right\rangle \\ 2\left\langle \left( {{S}_{\text{HH}}}+{{S}_{\text{VV}}} \right)\cdot S_{\text{HV}}^{*} \right\rangle & 0 \\ \end{matrix} \right]$ | (5) |
重建的伪全极化目标协方差矩阵为:
| \[\begin{array}{*{35}{l}} {{\left[ {{C}_{\text{DCP}}} \right]}_{\text{pseudo }\text{quad}}} \\ \ \ \ \ \\=\left[ \begin{matrix} \frac{{{J}_{11}}+{{J}_{22}}-4\left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle }{4}-\frac{1}{2}\text{Im}({{J}_{12}})\ & \ \text{0} & \frac{{{J}_{22}}-{{J}_{11}}+4\left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle }{4}+i\frac{\text{Re}({{J}_{12}})}{2} \\ 0\ & \ 2{{\left| {{S}_{\text{HV}}} \right|}^{2}}\ & \ 0 \\ \frac{{{J}_{22}}-{{J}_{11}}}{2}-i\frac{\text{Re}({{J}_{12}})}{2}\ & \ 0\ & \ \frac{{{J}_{11}}+{{J}_{22}}-4\left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle }{4}+\frac{1}{2}\text{Im}({{J}_{12}}) \\ \end{matrix} \right] \\ \end{array}\] | (6) |
| $\,{J_{11}} = \left\langle {{{\left| {\left( {{S_{{\rm{HH}}}} - {S_{{\rm{VV}}}}} \right)} \right|}^2}} \right\rangle + 4\left\langle {{{\left| {{S_{{\rm{HV}}}}} \right|}^2}} \right\rangle $ |
| $\quad{J_{12}} = - i\left\langle {\left( {{S_{{\rm{HH}}}} - {S_{{\rm{VV}}}}} \right) \cdot {{\left( {{S_{{\rm{HH}}}} + {S_{{\rm{VV}}}}} \right)}^{\rm{*}}}} \right\rangle $ |
| ${J_{22}} = \left\langle {{{\left| {{S_{{\rm{HH}}}} + {S_{{\rm{VV}}}}} \right|}^2}} \right\rangle \quad \quad \quad \quad \quad \quad $ |
这种方法在基于Stocks矩阵参数的后向散射体分析方面已获得了很好的结果。后向散射场的Stocks参数主要是:极化度、圆极化比和后向散射场对两种线性电场矢量的相对相位等。圆极化基接收的Stokes参数公式与常规情况相对应。
双圆极化模式在Stokes参数计算、两接收通道接收信号不平衡、极化模式串扰、定标、分解策略等方面都具有优势。需要特别考虑的内容包括:圆极化比的测量、可区分不同散射体类型的最大电压、对二面角散射体分布状态的随机取向的鲁棒性等。
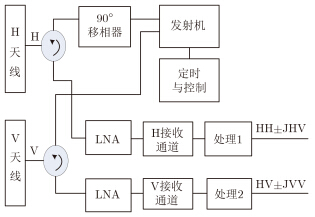
2.2 圆极化发射线极化接收(CTLR)简缩极化模式[22, 29, 30]圆极化发射线极化接收模式由H和V双极化天线左旋或右旋圆极化发射,H和V双线极化相干接收组成。发射圆极化,接收正交线极化。如果同时馈给H和V天线相位差90°的信号,双线极化天线将辐射圆极化电磁波。回波由H和V双线极化天线接收后,经H、V接收通道到达处理器。处理器进行聚焦和多视处理:聚焦级输出单视复图像数据,多视级输出2×2平均协方差矩阵,它可转换为4单元Stokes矢量。图 3给出了圆极化发射线极化接收简缩极化模式的工作原理图。
|
图 3 圆极化发射线极化接收简缩极化模式的工作原理图 Fig.3 Principle diagram of CTLR compact polarization radar |
圆极化信号的产生过程为:发射信号经发射+90°(或–90°)移相后,同时激励水平极化和垂直极化天线,在空间形成右旋圆极化(或左旋圆极化)的发射信号。由地物反射的信号,经水平极化和垂直极化天线分别进入H极化和V极化两路正交极化接收机,再经处理器处理,得到2×2平均的协方差矩阵,并可转换为4单元Stokes矢量。经处理重建全极化数据。目标散射矢量为(以发射右旋极化为例):
| ${{k}_{\text{CTLR}}}=\left[ {{S}_{\text{HH}}}-i{{S}_{\text{HV}}} \right.\ {{\left. -i{{S}_{\text{VV}}}+{{S}_{\text{HV}}} \right]}^{\text{T}}}/\sqrt{2}$ | (7) |
对应的目标协方差矩阵为:
| ${{J}_{\text{CTLR}}}=\left\langle {{k}_{\text{CTLR}}}k_{\text{CTLR}}^{\text{H}} \right\rangle =\frac{1}{2}\left[ \begin{matrix} \left\langle {{\left| {{S}_{\text{HH}}} \right|}^{2}} \right\rangle & i\left\langle {{S}_{\text{HH}}}\cdot S_{\text{VV}}^{\text{*}} \right\rangle \\ -i\left\langle {{S}_{\text{VV}}}\cdot S_{\text{HH}}^{\text{*}} \right\rangle & \left\langle {{\left| {{S}_{\text{VV}}} \right|}^{2}} \right\rangle \\ \end{matrix} \right]\\ \qquad \ +\frac{1}{2}\left[ \begin{matrix} \left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle & -i\left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle \\ i\left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle & \left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle \\ \end{matrix} \right]\\ \qquad \ +\frac{1}{2}\left[ \begin{matrix} -2\text{Im}\left( \left\langle {{S}_{\text{HH}}}\cdot S_{\text{HV}}^{*} \right\rangle \right)\quad & \quad \left\langle {{S}_{\text{HH}}}\cdot S_{\text{VV}}^{\text{*}} \right\rangle +\left\langle S_{\text{VV}}^{\text{*}}\cdot {{S}_{\text{HV}}} \right\rangle \\ \left\langle S_{\text{HH}}^{*}\cdot {{S}_{\text{HV}}} \right\rangle +\left\langle {{S}_{\text{VV}}}\cdot S_{\text{HV}}^{*} \right\rangle & 2\text{Im}\left( \left\langle {{S}_{\text{VV}}}\cdot S_{\text{HV}}^{*} \right\rangle \right) \\ \end{matrix} \right]$ | (8) |
重建的伪全极化目标协方差矩阵为:
| ${{\left[ {{C}_{\text{CTLR}}} \right]}_{\text{pseudo }\text{quad}}}=\left[ \begin{matrix} {{J}_{11}}-\left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle \quad & \quad \text{0}\quad & \quad \left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle -i{{J}_{12}} \\ 0\quad & \quad 2\left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle \quad & \quad 0 \\ {{\left( \left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle -i{{J}_{12}} \right)}^{*}}\quad & \quad 0\quad & \quad {{J}_{22}}-\left\langle {{\left| {{S}_{\text{HV}}} \right|}^{2}} \right\rangle \\ \end{matrix} \right]$ | (9) |
| ${J_{11}} = \left\langle {{{\left| {{S_{{\rm{HH}}}}} \right|}^2}} \right\rangle + \left\langle {{{\left| {{S_{{\rm{HV}}}}} \right|}^2}} \right\rangle $ |
| $\quad\quad {J_{12}} = i\left\langle {{S_{{\rm{HH}}}} \cdot S_{{\rm{VV}}}^{\rm{*}}} \right\rangle - i\left\langle {{{\left| {{S_{{\rm{HV}}}}} \right|}^2}} \right\rangle $ |
| ${J_{22}} = \left\langle {{{\left| {{S_{{\rm{VV}}}}} \right|}^2}} \right\rangle + \left\langle {{{\left| {{S_{{\rm{HV}}}}} \right|}^2}} \right\rangle $ |
圆极化发射线极化接收模式可简化系统体系结构,需要较少的射频硬件、重量轻、功耗低,系统在Stokes参数产生、通道信号平衡、对相对误差、串扰的鲁棒性等方面有优势。这种模式优化了相对相位定标和幅度定标,数据通过2×2矩阵完全表征,更适合于改进分解策略,是月球及行星探测器优选的极化雷达结构,同时也是探地雷达的一种可选的、具有吸引力的技术。
3 极化合成孔径雷达系统的工作方式为获得地物目标的全极化散射矩阵,要求多极化合成孔径雷达系统具有获得HH、VH、HV、VV 4种极化回波的能力;要同时获得上面4种极化,必须采用2个并行的发射通道和4个并行的接收通道,但这会大大增加设备的复杂性。对实际多极化系统而言,通常采用双极化天线单通道发射、单或双通道接收,利用发射和接收通道的组合,获得准同时的4种极化回波。极化合成孔径雷达通常采用极化时间分割、极化频率分割、极化编码分割、方位向极化空间分割等方式实现全极化功能。
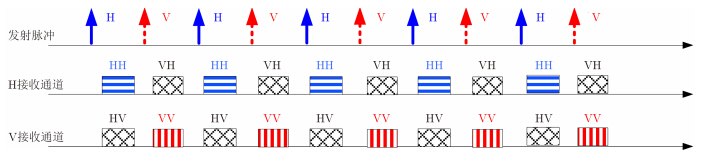
3.1 极化时间分割工作方式[16,17, 18,19,20,21, 31]极化时间分割方式由H与V双极化天线、一路极化开关和一路发射通道,H极化与V极化两路接收通道组成,图 4为基于极化时间分割方式的SAR原理图。图 5为极化时间分割方式收发时序关系图。雷达在脉冲重复周期(PRT)内交替发射H极化、V极化波,同时接收某一极化入射波对应的H极化与V极化散射回波。这样,按照极化时间分割方式,可以得到HH/VH/HV/VV 4路极化信息,构成目标的极化散射矩阵,实现全极化功能。

|
图 4 基于极化时间分割方式的SAR系统原理框图 Fig.4 Principle diagram of polarization time-division multiplexing pulse SAR |
|
图 5 基于极化时间分割方式的信号收发时序图 Fig.5 Timing sequence diagram of polarization time-division multiplexing pulse SAR |
极化时间分割工作方式的优点是结构简单,易于实现。缺点是:由于每一极化组合信号其方位向取样频率仅为PRF值的一半,所以为改善方位模糊需将系统PRF值提高一倍,这使平均功率增加一倍、成像带宽变窄、交叉极化图像的距离模糊恶化。
现今许多机载多极化SAR系统,如加拿大的C/X SAR、NASA-JPL的AIRSAR、日本的Pi-SAR以及德国的ESAR[32],部分星载SAR系统,如美国的SIR-C/X SAR[16, 17]、加拿大RadarSat-2[18]、德国TerraSAR[20, 21]以及日本PALSAR[19]等,均采用PRF加倍的极化时间分割方式实现全极化。
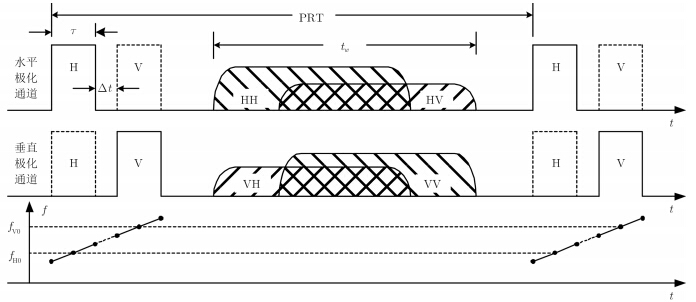
3.2 极化频率分割工作方式[31]极化频率分割工作方式分别由水平、垂直线极化天线同时发射两种不同极化、不同中心频率的脉冲信号,两接收通道同时接收回波并进行记录,然后通过滤波器对回波信号进行频率分离,从而得到目标的4种全极化信息。考虑到平台对发射信号功率的限制,水平极化与垂直极化两种脉冲信号只能成对发射,并且两个发射脉冲之间要留有一很窄的时隙以便功率转换。图 6为极化频率分割工作方式信号收发时序图。
|
图 6 基于极化频率分割方式的信号收发时序图 Fig.6 Timing sequence diagram of polarization frequency-division multiplexing pulse SAR |
极化频率分割方式所发射的H、V极化脉冲对在频域上是连续的,这样发射脉冲信号带宽将要增加一倍以上,高质量的天线系统和滤波器研制增加了系统实现的难度和复杂性。
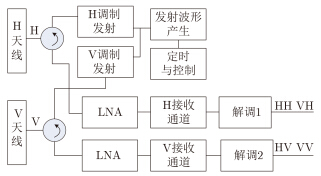
3.3 极化编码分割工作方式[19, 31]极化编码分割工作方式要求H极化和V极化两幅天线同时发射H和V线极化脉冲信号,并对发射脉冲进行正交编码,在接收通道通过正交解码来分离同极化和交叉极化信号,从而得到目标的散射矩阵。图 7给出极化编码分割方案下系统的原理示意。
|
图 7 基于极化编码分割工作方式的SAR系统原理框图 Fig.7 Principle diagram of polarization code-division multiplexing pulse SAR |
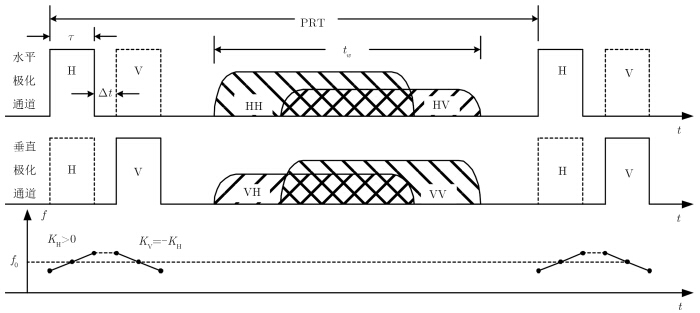
图 8给出采用具有正负调频斜率的线性调频脉冲信号的极化SAR系统收发信号时序。
|
图 8 基于极化编码分割工作方式的信号收发时序图 Fig.8 Timing sequence diagram of polarization code-division multiplexing pulse SAR |
同极化和交叉极化回波信号分别经过与正负调频斜率发射信号相对应的匹配滤波器后,能够很好地分离开来,同时保持了较好的压缩效果。理想情况下,极化编码分割工作方式的方位模糊和距离模糊与极化频率分割工作方式相同,但这种方案不需要转换开关,有利于提高系统的寿命和可靠性。
3.4 方位向极化空间分割工作方式[14, 15, 33, 34]方位向极化空间分割工作方式,是在一个合成孔径时间内,将方位向空间分割为若干子孔径,在极化开关控制下H和V天线交替辐射成对极化脉冲串(Twin-burst),H和V天线同时接收,得到全极化数据。
方位向极化空间分割成对脉冲串获得全极化的方式,采用与ScanSAR类似的方法,以牺牲方位分辨率为代价获得全极化。将方位向合成孔径时间Ts分成多个驻留时间段。与ScanSAR不同的是,雷达在多个驻留时间段之间不切换波位,而是在同一波位内切换发射信号的极化方式,即在相邻两段驻留时间内交替发射水平极化和垂直极化脉冲串(burst),并接收脉冲串的回波。这种工作方式简化了全极化合成孔径雷达结构,减少数传数据率,降低成本。在已发射的星载合成孔径雷达中,欧空局的Envisat-ASAR[14, 15]与意大利的Cosmo-Skymed[33, 34]都采用这种方式实现多极化,德国的TerraSAR[20, 21]亦将这种极化方式作为试验模式。
方位向极化空间分割方式有双通道接收和单通道接收两种模式。
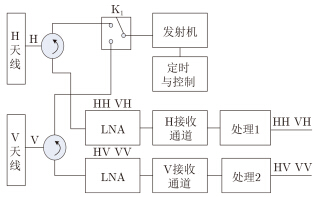
3.4.1 双接收通道方位向极化空间分割方式双接收通道方位向极化空间分割方式由H极化和V极化天线、1路发射机、1个发射极化开关、两路正交极化接收机和两路数据处理器组成,系统工作原理如图 9所示。发射机由发射极化开关K1控制,交替切至H极化天线和V极化天线发射成对脉冲串,地物散射回波同时经H极化和V极化天线进入H和V极化接收通道,顺序得到HH/HV、VH/VV极化数据。经数据处理,最终得到成像区域的HH/HV/VH/VV全极化数据。
|
图 9 双接收通道方位向极化空间分割方式工作原理图 Fig.9 Principle diagram of polarization space-division in Azimuth of dual-receiver radar |
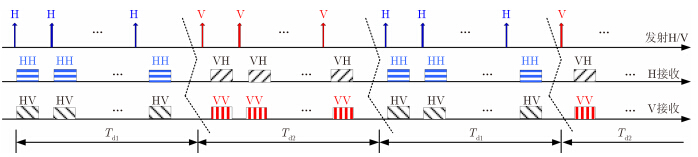
图 10给出双接收通道方位向极化空间分割方式发射与接收极化状态示意。该工作方式下,需要将方位向合成孔径时间Ts等分成3段,每段驻留时间为Ts/3。雷达在相邻波束驻留时间Td1与Td2内交替发射H极化脉冲串和V极化脉冲串,H极化与V极化双通道同时接收。
|
图 10 双接收通道方位向极化空间分割方式收发极化状态示意图 Fig.10 Tx/Rx polarization of polarization space-division in azimuth of dual-receiver rada |
图 11(a)给出驻留时间Td1内H极化发射、H与V双极化接收的方位向成像区域示意,可见在多个驻留时间Td1内可获得方位向连续拼接的HH与HV极化图像;图 11(b)给出驻留时间Td2内V极化发射、H与V双极化接收的方位向成像区域示意,可见在多个驻留时间Td2内可获得方位向连续拼接的VH与VV极化图像。

|
图 11 双接收通道方位向极化空间分割方式方位向成像区域示意图 Fig.11 Imaging area in Azimuth of Polarization Space-division dual-receiver SAR |
由分析可知:雷达通过波束在相邻驻留时间内交替发射H极化脉冲串和V极化脉冲串、H极化与V极化双通道同时接收的方式,可准同时获得方位向同一区域的HH/HV/VH/VV全极化雷达图像。该种工作方式下的全极化雷达图像的方位单视分辨率较常规双极化雷达图像恶化3倍。
3.4.2 单接收通道方位向极化空间分割方式单接收通道方位向极化空间分割方式由H极化和V极化天线、1路发射机、1个发射极化开关K1、1个接收极化开关K2、1路接收机和数据处理器组成。单接收通道方位向极化空间分割方式工作原理如图 12所示。发射机通过发射极化开关K1控制,交替切至H极化天线和V极化天线发射成对脉冲串,地物反射的回波经H极化和V极化天线接收,经接收极化开关K2控制,分别将H极化天线接收到的HH或VH极化数据、V极化天线接收到的HV或VV极化数据送入单路相干接收机。经数据处理得到HH/HV/VH/VV全极化数据。

|
图 12 单接收通道方位向极化空间分割方式工作原理 Fig.12 Principle diagram of polarization space-division in azimuth of single-receiver radar |
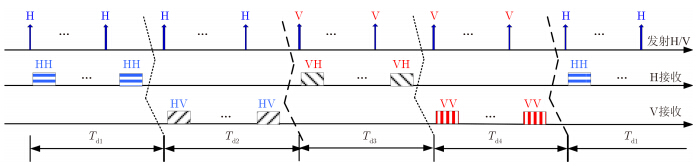
图 13给出单接收通道方位向极化空间分割方式发射与接收极化状态示意。该工作方式下,需要将方位向合成孔径时间Ts等分成5段,每段驻留时间为Ts/5。雷达在波束驻留时间Td1+Td2与Td3+ Td4内交替发射H极化脉冲串和V极化脉冲串;Td1驻留时间内H极化发射、H极化接收,Td2驻留时间内H极化发射、V极化接收,Td3驻留时间内V极化发射、H极化接收,Td4驻留时间内V极化发射、V极化接收。
|
图 13 单接收通道方位向极化空间分割方式收发极化状态示意图 Fig.13 Tx/Rx polarization of polarization space-division in azimuth of single-receiver radar |
雷达在相邻驻留时间内交替发射H极化脉冲串和V极化脉冲串,每种极化脉冲串的回波分别采用H极化和V极化轮流接收,可准同时获得方位向同一区域的HH/HV/VH/VV全极化雷达图像。该种工作方式下的全极化雷达图像方位单视分辨率较常规单极化雷达图像恶化5倍。
方位向发射成对极化脉冲串获得多极化的方式比较灵活,可根据极化和分辨率需求灵活设置驻留时间和发射接收极化方式。
4 结束语在极化合成孔径雷达系统技术研究中,雷达的极化结构和工作方式是首要考虑的关键问题。早期研制的单极化和双极化SAR系统已逐渐不能满足极化合成孔径雷达应用发展的需要。为获得反映目标极化散射矩阵的全极化信息,极化SAR系统通常采用极化天线、发射通道与接收通道在时间和空间不同的组合获得准同时的四极化回波。
(1) 极化时间分割。结构简单,易于实现;缺点是脉冲重复频率提高一倍,平均功率增大一倍、成像带宽变窄、交叉极化图像的距离模糊恶化。
(2) 极化频率分割或极化编码分割。均可以在一定程度上抑制极化SAR的距离模糊。极化频率分割的信号带宽将增加一倍,高质量的带通滤波器增加实现的难度;极化编码分割工作方式能较好地抑制距离模糊,不增加信号带宽,下传数据率降低一倍。在MIMO-SAR系统中有进一步的发展前景。
(3) 方位向极化空间分割。是以牺牲方位分辨率为代价获得全极化。这种工作方式雷达结构简化,数据率低,受到普遍重视。
简缩极化合成孔径雷达仅发射单一的极化而接收两路正交极化及其相对的相位,测量2×2协方差矩阵,再作为4单元Stokes矢量重建全极化数据。简缩极化SAR虽不像全极化系统那样完美,然而在很多应用中,简缩极化雷达的结果可近似等效于全极化雷达,且简缩极化雷达的结果远优于单极化合成孔径雷达,并总是优于常规双极化雷达[35,36,37,38]。按照发射和接收的极化方式,简缩极化主要工作模式归纳如下:
(1) p/4简缩极化模式。在脉冲重复频率选择、成像带宽度、两接收通路的幅相平衡、功率消耗、下传数据率、极化分解和定标处理方法等方面有优势。
(2) 双圆极化模式。系统硬件复杂,但在Stokes参数计算、两接收通道接收信号不平衡、极化模式串扰、定标、分解策略等方面都具有优势。
(3) 圆极化发射线极化接收模式。结构简化,射频硬件设备量少、重量轻、功耗低,系统在Stokes参数产生、通道信号平衡、对相对误差、串扰的敏感性降低等方面有优势。这种模式优化了相对相位定标和幅度定标,数据通过2×2矩阵完全表征,更适合于改进分解策略,可作为极化雷达的首选结构。
| [1] | Kostinski A B and Boerner W M. On foundation of radar polarimetry[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(12): 1395-1403.( 1) 1) |
| [2] | Cloude S R and Pottier E. An entropy based classification scheme for land application of polarimetric SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(1): 68-78.( 1) 1) |
| [3] | Dong Y, Milne A K, and Forster B C. Segmentation and classification of vegetated areas using polarimetric SAR image data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(2): 321-329.( 1) 1) |
| [4] | Freeman A. Fitting a two-component scattering model to polarimetric SAR data from forests[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(8): 2583-2592.( 1) 1) |
| [5] | Mattia F, Floury N, and Moreira A. Foreword to the special issue on retrieval of bio-and geophysical parameters from SAR data for land applications[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(2): 379-380. DOI: 10.1109/TGRS.2009.2012837.( 1) 1) |
| [6] | Ulaby F T and Elachi Charles. Radar Polarimetry for Geoscience Applications[M]. Artech House Inc, Boston, London, 1990: 281-295.( 1) 1) |
| [7] | Oh Y, Sarabandi K, and Ulaby F T. An inversion algorithm for retrieving soil moisture and surface roughness from polarimetric radar observation[C]. IEEE Geoscience and Remote Sensing Symposium, Pasadena, 1994, 3: 1582-1584. DOI: 10.1109/IGARSS.1994.399504.( 1) 1) |
| [8] | Dierking W and Wesche C. C-band radar polarimetry— useful for detection of icebergs in sea ice?[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(1): 25-37.( 1) 1) |
| [9] | He Yijun, Perrie W, and Xie Tao, et al.. Ocean wave spectra from a linear polarimetric SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(11): 2623-2631.( 1) 1) |
| [10] | Zhang B, Perrie W, and Vachon P W, et al.. Ocean vector winds retrieval from C-band fully polarimetric SAR measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(11): 4252-4261.( 1) 1) |
| [11] | Novak L M, Sechtin M B, and Cardullo M J. Studies of target detection algorithms that use polarimetric radar data[J]. IEEE Transactions on Aerospace and Electronic Systems, 1989, 25(2): 150-165.( 1) 1) |
| [12] | Monaldo F. SEASAT sees the winds with SAR[C]. IEEE International Geoscience and Remote Sensing Symposium, 2003, 1: 38-40. DOI: 10.1109/IGARSS.2003.1293671.( 1) 1) |
| [13] | Monaldo F M, Jackson C R, and Pichel W G. Seasat to RADARSAT-2: research to operations[J]. Oceanography, 2013, 26(2): 34-45.( 1) 1) |
| [14] | Desnos Y L, Buck C, Guijarro J, et al.. The envisat advance synthetic aperture radar system[C]. IEEE International Geoscience and Remote Sensing Symposium, 2000, 3: 1171-1173. DOI: 10.1109/IGARSS.2000.858057.( 3) 3) |
| [15] | Hawkins R K, Touzi R, Wolfe J, et al.. ASAR AP mode performance and applications potential[C]. IEEE International Geoscience and Remote Sensing Symposium, 2003, 2: 1115-1117. DOI: 10.1109/IGARSS.2003.1294029.( 3) 3) |
| [16] | Freeman A, Alves M, Chapman B, et al.. SIR-C data quality and calibration results[J]. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(4): 848-857. DOI: 10.1109/36.406671.( 3) 3) |
| [17] | Jordan R L, Huneycutt B L, and Werner M. The SIR-C\X-SAR synthentic aperture radar system[J]. IEEE Transactions on Geoscience and Remote Sensing, 1995, 33(4): 829-839. DOI: 10.1109/3.4066696( 2) 2) |
| [18] | Fox Peter A, Luscombe Anthony P, and Thompson Alan A. Radarsat-2 SAR modes development and utilization[J]. Canadian Journal of Remote Sensing, 2004, 30(3): 258-264.( 4) 4) |
| [19] | Fujimra T and Kimura T. Compact polarimetric observation using phased array antenna and its case study for PALSAR[C]. EUSAR, 2008: 1-4.( 5) 5) |
| [20] | Mittermayer J and Runge H. Conceptual studies for exploiting the TerraSAR-X dual receive antenna[C]. IEEE International Geoscience and Remote Sensing Symposium, 2003, 3: 2140-2142.DOI: 10.1109/IGARSS.2003.1294365.( 3) 3) |
| [21] | Stangl M, Werninghaus R, and Zahn R. The TerraSAR-X active phased array antenna[C]. IEEE International Symposium on Phased Array Systems and Technology, 2003: 70-75. DOI: 10.1109/PAST.2003.1256959.( 4) 4) |
| [22] | ME Nord, Ainsworth T L, Lee J S, et al.. Comparison of compact polarimetric synthetic aperture radar modes[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(1): 174-188.( 4) 4) |
| [23] | Spudis P, Nozette S, Bussey B, et al.. Mini-SAR: an imaging radar experiment for the Chandrayaan-1 mission to the Moon[J]. Current Science, 2009, 96(4): 533-539.( 1) 1) |
| [24] | Raney R K, Spudis P D, Bussey B, et al.. The lunar mini-RF radars: hybrid polarimetric architecture and initial results[J]. Proceedings of the IEEE, 2010, 99(5): 808-823.( 1) 1) |
| [25] | Misra Tapan, Rana S S, Bora V H, et al.. SAR Payload of Radar Imaging Satellite (RISAT) of ISRO[C]. EUSAR, 2006: 1-4.( 1) 1) |
| [26] | Geldsetzer T, Arkett M, and Zagon T. All season assessment of RADARSAT constellation mission compact polarimetry modes for canadian ICE service operational implementation[C]. 2014 IEEE International Geoscience and Remote Sensing Symposium, Quebec City, 2014: 1560-1563. DOI: 10.1109/IGARSS.2014.6946737.( 1) 1) |
| [27] | Souyris J C and Mingot S. Polarimetry based on one transmitting and two receiving polarizations: the π/4 mode[C]. IEEE International Geoscience and Remote Sensing Symposium, 2002, 1: 629-631. DOI: 10.1109/IGARSS.2002.1025127.( 1) 1) |
| [28] | Souyris J C, Imbo P, Fjortoft R, et al.. Compact polarimetry based onsymmetry properties of geophysical media: the π/4 mode[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(3): 634-646. DOI: 10.1109/TGRS.2004.842486.( 1) 1) |
| [29] | Raney R K. Hybrid-polarity SAR architecture[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3397-3404. DOI: 10.1109/TGRS.2007.895883.( 2) 2) |
| [30] | Raney R K. Hybrid-quad-pol SAR[C]. IEEE Geoscience and Remote Sensing Symposium, 2008, 4: 491-493. DOI: 10.1109/IGARSS.2008.4779765.( 2) 2) |
| [31] | 戴博伟. 多极化合成孔径雷达系统与极化信息处理研究[D]. [博士论文], 中国科学院电子研究所, 2000. Dai Bowei. The research of polarimetric SAR system and polarimetric information processing[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2000.( 3) 3) |
| [32] | Raney R K. Dual-polarized SAR and Stokes parameters[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(3): 317-319.( 1) 1) |
| [33] | COSMO-SkyMed System Description & User Guide[R]. 4 May, 2007.( 2) 2) |
| [34] | COSMO-SkyMed System HandBook[R]. 30 April, 2007.( 2) 2) |
| [35] | Shirvany R, Chabert M, and Tourneret J Y. Comarision of ship detection on performance based on the degree of polarization in hybrid/compact and linear dual-pol SAR imagery[C]. IEEE International Geoscience and Remote Sensing Symposium, Vancouver, 2011: 3550-3553. DOI: 10.1109/IGARSS.2011.6049988.( 1) 1) |
| [36] | Lardeux C, Niamen D, Routier J B, et al.. Use of PALSAR polarimetric data for tropical forest stratification and comparison of simulated dual and compact polarimetric modes[C]. IEEE International Geoscience and Remote Sensing Symposium, Honolulu, 2010: 1855-1858. DOI: 10.1109/IGARSS.2010.5650441.( 1) 1) |
| [37] | Singh G, Yamaguchi Y, Park Sang-Eun, et al.. Categorization of the glaciated terrain of indian himalaya using CP and FP mode SAR[J]. IEEE Journal of Earth Observations and Remote Sensing, 2014, 7(3): 872-880. DOI: 10.1109/JSTARS.2013.2266354.( 1) 1) |
| [38] | Yin Junjun, Yang Jian, Zhou Zheng-Shu, et al.. The extended bragg scattering model-based method for ship and oil-spill observation using compact polarimetric SAR[J]. IEEE Journal of Earth Observations and Remote Sensing, 2015, 8(8): 3760-3772. DOI: 10.1109/JSTARS.2014.2359141.( 1) 1) |


