1 引言

随着空间资源开发日益增加，废弃的卫星碎片等垃圾在太空堆积，这给未来空间资源的利用带来安全隐患。如果在轨运行的飞船与碎片发生碰撞，即便尺寸小于1 cm的碎片，都能对飞船造成致命伤害。现有的雷达或者光学仪器能够实现对尺寸大于30 cm的目标监控，采用保护罩能够保护飞船免受尺寸小于1 cm的碎片伤害，因此开展对1～30 cm 尺寸的空间碎片检测、成像与识别有广阔的应用前景和战略意义^{[1, 2, 3]}。

空间碎片因为轨迹、惯性的筛选通常以群聚的形式出现，同时，碎片存在高速自旋运动，且各自的运动状态因质量、密度等因素存在明显差异。各个碎片的转动速度不同，导致各目标回波去相干时间不一致，无法对回波数据进行统一处理，为了得到清晰的各碎片ISAR像，有必要对各个目标的数据进行抽取。文献^[4]利用各目标平动带来的多普勒调频率的差异，实现各目标回波的抽取及成像；文献^[5]通过对粗成像的结果进行图像分割，抽取出属于各个目标的回波，再进行精确成像。然而上述方法均没有考虑高速自旋目标引起的距离徙动问题，且各目标的转速不同导致徙动量存在差异，在宽带雷达系统中，包络补偿难以实现，同时，对于小尺寸远距离的微弱目标，采用宽带雷达体制很难发现目标，有必要限制系统的带宽从而提高对微弱小目标的敏感性。此处采用窄带雷达系统，能够提高对于小目标的检测概率，同时，窄带系统的距离分辨率通常在几十米数量级，碎片自旋所引起的徙动问题可以忽略。由于空间碎片绕着其主轴做高速自旋运动，单距离多普勒干涉(Single Range Doppler Interferometry,SRDI)方法^[6]能够对尺寸小于发射信号波长的目标进行成像，SRDI利用时频分析方法将目标所在距离单元的方位向回波数据转换到时频域，尽管线性时频方法不受交叉项的影响，但存在时间与频率分辨率的折衷，无法得到聚焦良好的图像。相干单距离多普勒干涉(Coherent Single Range Doppler Interferometry,CSRDI)方法^[7]能够联合利用时频域的相位与幅度信息，在低信噪比条件下仍能够得到较好的性能，然而，CSRDI方法需要沿着不同的曲线进行积分，运算复杂度非常高。文献^{[8, 9]}提出了单距离匹配滤波方法及其修正算法(Single Range Matched-Filter,SRMF method and its modified version,SRMF-CLEAN)。SRMF根据不同的旋转半径构建匹配滤波器，并通过FFT估计各半径下的散射中心，然而，该方法存在明显的旁瓣，微弱目标很容易淹没在强信号的杂波中，不利于微弱目标的检测，同时，该方法没有考虑目标旋转引起的阴影现象，因此匹配滤波器无法匹配目标的回波信号，导致成像性能显著下降。上述方法分辨率主要取决于多普勒带宽，短波长引入更大的多普勒带宽，而在多任务情况下，ISAR成像系统倾向于发射低重复频率信号，此时，存在多普勒模糊现象，算法性能均会显著下降。由于空间碎片尺寸通常较小，在成像场景中表现出非常强的稀疏特性，可以利用该特性得到更好的性能。文献^[10]提出了一种基于稀疏重构的空间碎片成像方法，该方法通过建立观测矩阵，解决了目标自旋情况下出现的遮挡效应，同时，抽取的数据提升了系统的等效采样率，解决了低重复频率系统的模糊问题。CS理论已经证明，在少量观测样本下，能够以高概率重构出稀疏信号^[11]。然而，若字典构建不完备，信号能量渗透到其他的原子上，会导致恢复的信号出现错误。该方法在处理多目标成像问题时，效果显著下降。

针对窄带、低重复频率系统下的空间平台空间群目标成像问题，本文结合回波的自相关函数与转速扫描，获取观测范围内多目标的转速信息，从而构建完备的字典，并根据所获取的目标转速信息，对不同的目标设计不同的观测矩阵，提取各目标的有效信息，得到多周期观测下的目标有效数据，并结合SL0^[12]方法进行稀疏恢复。由于该方法的抽取操作针对各个目标都是彼此独立的，因此可以进行并行操作，同时得到各个目标的成像结果。

2 窄带系统下的高速自旋目标回波模型

ISAR成像雷达通常发射大带宽信号获取高的距离向分辨率，然而，针对空间平台，雷达功率较小，无法有效检测到远距离的微弱目标，此时，有必要采用窄带系统，提高发现目标的概率。同时，窄带系统下距离分辨率通常在几十米到上百米量级，因此在成像时间内，高速自旋目标的旋转引起的跨距离徙动现象可以忽略，利于实现包络补偿。然而，窄带系统下，单个距离门内会存在多个目标。此时，考虑单个距离门的目标方位回波，第k个目标的第i个散射点回波信号如下：

\[{s _{ki}}\left( {{t_m}} \right) = {\sigma _{ki}}\exp \left( {{\rm{j}}2\pi f{_{\rm{c}}}\left( {{t_m} - {\tau _{mki}}} \right)} \right)\]

(1)

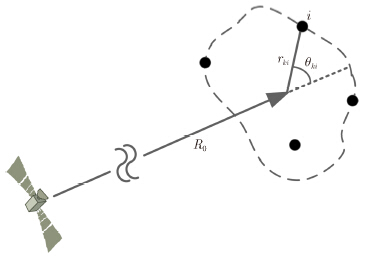
其中σ_ki表示第k个目标内第i个散射点的散射强度，f_c代表发射信号的载频，t_m表示方位慢时间，m表示脉冲数。t_mki=2R_ki(t_m)/c,R_ki(t_m)是目标在成像时间内与雷达的斜距。假定已经实现了回波的包络对齐与相位补偿^{[13, 14]}，此时，目标的转台模型如图 1所示。

第k个目标的第i个散射点与雷达之间的斜距R_ki(t_m)表示为：

${R_{ki}}\left( {{t_m}} \right) = {R_0} + {r_{ki}}\cos \left( {{\varphi _{ki}} + \left( {{\omega _k} + {\omega _{\rm r}}} \right){t_m}} \right)$

(2)

其中R₀是雷达到目标群中心的初始距离，r_ki和φ_ki分别是第k个目标第i个散射点的自旋半径与初始转角。包络补偿过后，雷达视线LOS(Line Of Sight)相对于目标存在一个转动量ω_r，同时，目标的高速自旋也存在一个转动分量ω_k。由于成像时间内目标转角较小，相比于自旋分量，可以忽略转动量ω_r带来的影响。此时式(2)简化为：

\[{R_{ki}}\left( {{t_m}} \right) = {R_0} + {r_{ki}}\cos \left( {{\varphi _{ki}} + {\omega _k}{t_m}} \right)\]

(3)

将式(3)代入式(1)，回波形式如下：

\[\begin{array}{l} {s_{ki}}\left( {{t_m}} \right) = {\sigma _{ki}}\exp \left( {{\rm{j}}2\pi {f_{\rm{c}}}} \right.\\ \quad \quad \quad \quad \left. { \cdot \left( {{t_m} - 2\frac{{{R_0} + {r_{ki}}\cos \left( {{\varphi _{ki}} + {\omega _k}{t_m}} \right)}}{{\rm{c}}}} \right)} \right) \end{array}\]

(4)

式(4)的信号利用载频进行下变频，可以得到：

\[{s_{ki}}\left( {{t_m}} \right) = {\sigma _{ki}}\exp \left( {{\rm{j}}4\pi \frac{{{R_0} + {r_{ki}}\cos \left( {{\varphi _{ki}} + {\omega _k}{t_m}} \right)}}{\lambda }} \right)\]

(5)

其中l表示雷达发射信号的波长。忽略掉常数相位，式(5)简化为：

\[{s_{ki}}\left( {{t_m}} \right) = {\sigma _{ki}}\exp \left( {{\rm{j}}4\pi \frac{{{r_{ki}}\cos \left( {{\varphi _{ki}} + {\omega _k}{t_m}} \right)}}{\lambda }} \right)\]

(6)

根据几何衍射(Geometrical Theory of Diffraction,GTD)理论^[15]，在高频系统下的高分辨率图像，其目标的回波响应可以近似为多个散射点的响应之和，因此，该距离单元的方位基带回波可以表示为：

\[s\left( {{t_m}} \right) = \sum\limits_k^K {\sum\limits_i^{{I_k}} {{\sigma _{ki}}\exp \left( {{\rm{j}}4\pi \frac{{{r_{ki}}\cos \left( {{\varphi _{ki}} + {\omega _k}{t_m}} \right)}}{\lambda }} \right)} } \]

(7)

其中K代表碎片个数，I_k表示第k个碎片的散射点数目。只看式(7)中的相位部分，如式(8)所示：

\[{\phi _{ki}}\left( {{t_m}} \right) = \frac{{4\pi }}{\lambda }{r_{ki}}\cos \left( {{\varphi _{ki}} + {\omega _k}{t_m}} \right)\]

(8)

对式(8)做微分，可以得到瞬时多普勒为：

\[\begin{array}{l} {f_{{\rm{d}}ki}}\left( {{t_m}} \right) = \frac{1}{{2\pi }}\frac{{d{\phi _{ki}}\left( {{t_m}} \right)}}{{d{t_m}}} = \\ \quad \quad \quad \quad - \frac{2}{\lambda }{\omega _k}{r_{ki}}\sin \left( {{\omega _k}{t_m} + {\varphi _{ki}}} \right) \end{array}\]

(9)

当观测目标超过1个周期时，可以得到第k个目标的第i个散射点的多普勒带宽为：

\[{B_{ki}} = \frac{4}{\lambda }{\omega _k}{r_{ki}}\]

(10)

式(10)表明信号的多普勒带宽与碎片的转速、半径、发射信号波长有关系，信号波长越短，目标转速越快，其多普勒带宽就越大，可得到更高的2维分辨率^{[8, 9]}。然而，更大的多普勒带宽在低重频系统下也会引起多普勒模糊问题，若要实现对碎片目标的2维成像，需要解决多普勒带宽的模糊问题，或者提高采样率。

3 基于稀疏重采样的空间碎片群目标成像方法 3.1 空间碎片的转速估计

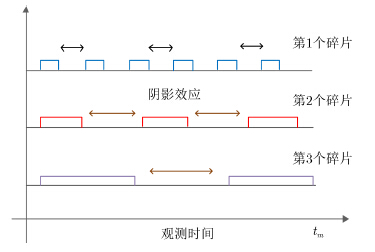
由于空间碎片在成像时间内通常做高速自旋运动，其回波在观测时间内会表现出明显的周期性质。假定有3个碎片目标，每个碎片目标的转速分别为ω₁=8.20 rad/s,ω₂=5.25 rad/s,ω₃=2.15 rad/s。回波的接收数据窗形式如图 2所示。考虑空间碎片高速自旋时出现的阴影效应，假定所能观测到的成像角度区间为180°。由图 2可知，3个碎片的接收数据存在明显的周期性。

在观测时间内，若对回波数据进行自相关处理，在各个目标所在的周期及其整数倍的时刻会出现明显的自项峰值。定义自相关函数为：

\[R\left( {{\tau _m}} \right) = \int {s\left( {{t_m}} \right){s^*}\left( {{t_m} - {\tau _m}} \right)} {\rm{d}}{t_m}\]

(11)

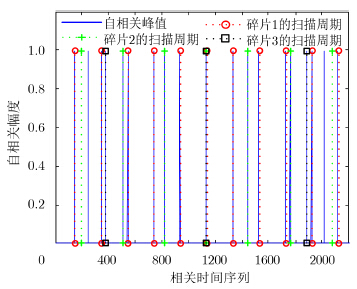
根据信号处理可知，自相关函数的时域表示可以通过信号的傅里叶变换与其共轭相乘的逆傅里叶变换得到。对3个目标回波的自相关函数进行峰值提取，并利用转速对峰值进行扫描，可以得到各个目标的转速信息。图 3给出了信噪比为10 dB时的自相关峰值与转速匹配结果，其中圆圈、十字与方块3个线条分别代表了3个碎片的周期扫描线。从图 3 可知，在目标个数已知的前提下，3个转速能够匹配所有的自相关峰值。

3.2 空间碎片群目标成像方法

图 2给出了碎片接收的回波数据形式，由于目标的转动，需要考虑目标的遮挡效应，如文献^[16]所述，散射点的阴影效应表现为：在一段持续的时间内，后向散射系数比较大，在其它的位置后向散射系数接近零。即雷达在观测自旋目标时，会有一个加窗效应。假定此处的有效观测角度为150°，其它角度范围内的散射系数为零。对于第k个碎片而言，其等效的回波形式如下：

\[{s_{k{\rm{e}}}}\left( {{t_m}} \right) = {W_k}\left( {{t_m}} \right)s\left( {{t_m}} \right)\]

(12)

其中窗函数形式为：

\[{W_k}({t_m}) = \left\{ {\begin{array}{*{20}{l}} {{\rm{ }}1,\quad 0\;\; \le \;\;{\omega _k}{t_m}\;\; \le \;\;2\pi /3}\\ {{\rm{ }}0,\quad 2\pi {\rm{/}}3\;{\rm{ \lt }}\;{\omega _k}{t_m}\;\; \le \;\;2\pi } \end{array}} \right.\]

(13)

为了抽取出属于第k个碎片的回波数据，可以结合压缩感知理论，利用测量矩阵对观测数据进行抽取，从而提高对空间碎片的成像质量。

假设第k个碎片目标在观测时间内旋转L个周期，将方位慢时间用离散时间表示，可得

\[{t_m} = m{T_{\rm{a}}},\quad m = 1,2,3, \cdots ,M\]

(14)

其中T_a表示脉冲重复间隔，M表示观测的离散时间长度。式(12)可以表示为如下的离散形式：

\[{S_{k{\rm{e}}}} = {H_k}{E_k} = {H_k}{F_k}{a_k} + \varepsilon \]

(15)

其中α_k(PQ×1)对应第k个碎片的散射中心强度，F_k矩阵(M×PQ)是根据第k个碎片的回波模型设计的字典，其具体形式如下：

\[\begin{array}{l} {F_k} = \left[ {{F_{11}}, \cdots ,{F_{1{P_k}}},{F_{21}}, \cdots ,{F_{2{P_k}}}, \cdots ,} \right.\\ \quad \quad \left. {{F_{{Q_k}1}}, \cdots ,{F_{{Q_k}{P_k}}}} \right] \end{array}\]

(16)

其中

\[\begin{array}{*{20}{l}} {{F_{{q_k}{p_k}}} = }&{\left[ {\exp \left( {\frac{{{\rm{j}}4\pi }}{\lambda }\left( {{r_{{p_k}}}\cos \left( {{\varphi _{{q_k}}} + {T_{\rm{a}}}{\omega _k}} \right)} \right)} \right),} \right.}\\ {}&{\exp \left( {\frac{{{\rm{j}}4\pi }}{\lambda }\left( {{r_{{p_k}}}\cos \left( {{\varphi _{{q_k}}} + 2{T_{\rm{a}}}{\omega _k}} \right)} \right)} \right), \cdots }\\ {}&{{{\left. {\exp \left( {\frac{{{\rm{j}}4\pi }}{\lambda }\left( {{r_{{p_k}}}\cos \left( {{\varphi _{{q_k}}} + M{T_{\rm{a}}}{\omega _k}} \right)} \right)} \right)} \right]}^{\rm{T}}}} \end{array}\]

(17)

P_k和Q_k分别表示第k个目标在距离和方位分辨单元总数。H_k是根据窗效应及旋转周期建立的观测矩阵，其形式由碎片目标的转速ω_k与自转周期决定。矩阵形式为：

\[{H_k} = {\left[ {\begin{array}{*{20}{c}} {{H_{k1}}}&{}&|&{}&{}&{}&{}&{}&{}&{}\\ {}&0&|&{{H_{k2}}}&{}&{}&{}&{}&{}&{}\\ - & - & + & - & - & - & - & - & - & - \\ {}&{}&|&{}& \ddots & \ddots &{}&{}&{}&{}\\ {}&{}&|&{}&{}&{}&0&{{H_{kL - 1}}}&{}&{}\\ {}&{}&|&{}&{}&{}&{}&{}&0&{{H_{kL}}} \end{array}} \right]_{{M_k} \times M}}\]

(18)

其中$\left[ {\begin{array}{*{20}{c}} {{H_{kl}}}&{}\\ {}&0 \end{array}} \right]$与diag(W_k(t_m))一一对应，${M_k} = {\rm{floor}}\left( {M{T_{\rm{a}}}{\omega _k}/(2\pi )} \right)$。由于空间碎片目标在成像场景内表现出了明显的稀疏特性，可以结合压缩感知理论得到空间碎片的高分辨清晰图像。通过解决如下的数学优化问题，建立稀疏恢复与成像之间的关系：

\[{\rm{min}}{\left\| {{\alpha _k}} \right\|_0},{\rm{ subject \ to }}{\left\| {{S_{k{\rm{e}}}} - {H_k}{F_k}{\alpha _k}} \right\|_2} \le \eta \]

(19)

其中η约束了数据恢复过程中的噪声量级。解决如上所述的l₀范数问题是NP问题。本文结合SL0算法^[12]，通过高斯函数近似目标函数中的l₀范数，从而结合凸优化的方法求解式(19)。一旦得到了稀疏系数α_k，将稀疏矢量α_k重排成p_k×q_k维矩阵，即得到第k个目标的2维像I(p_k,q_k)。然而，回波分量是由多个碎片目标的回波组合得到的，此时，无法得到属于某个碎片的独立回波分量，在建立字典时，需要联合各个目标的字典，以确保字典的冗余性，构建如下的字典：

\[F = \left[ {{F_1},{F_2}, \cdots ,{F_K}} \right]\]

(20)

问题式(19)可以重新写为：

\[{\rm{min}}{\left\| {{\alpha _k}} \right\|_0},{\rm{ subject \ to }}{\left\| {{S_{k{\rm{e}}}} - {H_k}F\alpha } \right\|_2} \le \eta \]

(21)

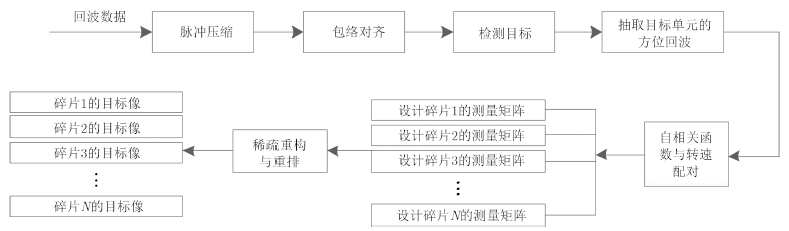
稀疏重构式(21)所述的问题，可得到对应第k个碎片目标回波的稀疏向量α，因为α对应的是观测矩阵H_k下的稀疏矢量，需要对α进行抽取，将α等间隔地分成K份，对其中的第k段进行重排，即可得到第k个目标的2维图像，此时，其他碎片目标的回波能量会落到各自字典所对应的稀疏区间，可以降低多目标问题下彼此能量渗透现象。为了同时得到多个碎片目标的2维像，可以根据自相关函数估计得到的转速设计多组观测矩阵，因为稀疏重构的过程是彼此独立的，可以同时得到多个目标的2维像。具体算法流程如图 4所示。

4 仿真实验分析 4.1 本文方法实验结果

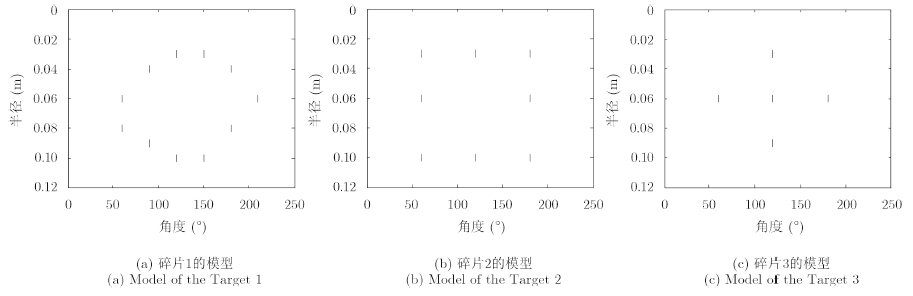
以空间平台星载雷达对空间碎片群目标成像为仿真背景，通过仿真实验验证本文方法的有效性。假定观测范围内存在3个高速自旋的碎片目标，转动角速度分别为ω₁=8.20 rad/s,ω₂=5.25 rad/s,ω₃=2.15 rad/s，各个碎片的散射模型如图 5所示，其散射幅度在观测时间内保持不变，均为1。

雷达发射信号的载频为30 GHz，脉冲重复频率200 Hz。若观测目标的半径为10 cm，针对3个目标的转速，如式(10)所述，对应的多普勒带宽分别为324.8 Hz,204.8 Hz以及86.0 Hz。当目标的转速和尺寸更大，且载频更高时，多普勒带宽会更大。由于高速自转的碎片目标会引入比较大的多普勒带宽，当带宽大于脉冲重复频率，会出现多普勒模糊。采用文献^[10]所述的方法，能够结合稀疏抽取与目标自旋特性提高等效采样率，从而克服高速自旋目标引起的多普勒模糊。

图 6(a)-图 6(c)是采用本文方法得到的3个碎片目标的2维图像，图 6(d)-图 6(f)是采用文献^[10]所述方法得到的3个碎片目标的2维图像。从图 6可以发现，采用文献^[10]的方法无法得到清晰的碎片图像，会出现一些虚假的点，或者目标的部分散射点消失，而本文方法能够得到各个碎片更清晰的图像。由于空间碎片多以群目标的形式出现，因此接收到的信号是由多个目标的回波分量组成的。文献^[10]中构建的字典是不完备的，无法包含所有目标的信息，此时，当针对某一个目标进行重构时，其余目标的能量也会泄露到该重构信号中，导致无法得到目标的清晰图像。本文先结合自相关函数及转速配对实现目标个数及其对应转速的估计，并构建群目标条件下的完备字典，结合测量矩阵获取不同目标的有效观测数据，这样其他目标的大部分能量都会渗透到属于自己所在的块字典内。由于所构建的字典并非传统的小波基或者傅里叶基，字典的RIP(Restricted Isometry Property，限制等距条件)性质会变差，导致剩余的小部分能量泄露，但是不会影响到目标的成像结果。

4.2 不同的稀疏重构方法所得目标像

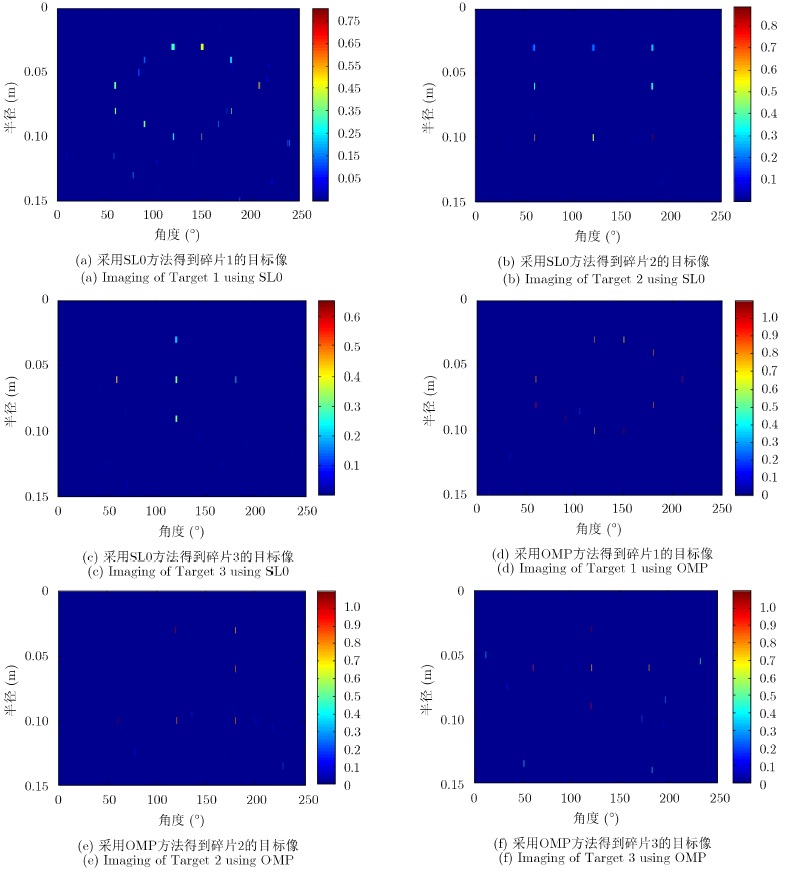
本文针对的是空间高速自旋目标成像，其回波相位如式(8)所示，字典中每个原子的时频关系满足正弦关系，并非常用的傅里叶基或者小波基等，感知矩阵的RIP性质会有所下降，不利于稀疏重构。文献^[12]所提的SL0方法通过平滑高斯函数近似l₀范数，能够将稀疏重构问题转化为凸优化问题，并且降低对字典RIP性质的要求，在本文的应用背景下，更适合求解如式(20)所述的稀疏重构问题。图 7对比了采用SL0方法和经典OMP(Orthogonal Matching Pursuit)方法得到的各个碎片的目标像。图 7(d)-图 7(f)表明，各个碎片目标也能够实现稀疏恢复，但碎片2和碎片3的散射点中存在一些非目标散射点，不利于目标的识别。因为构建的感知矩阵RIP性质不如典型的傅里叶基或者小波基，匹配追踪过程会出现信号能量的交错现象^[11]。然而，SL0算法降低了对RIP性质的要求，本文采用SL0方法能够得到比较清晰的目标像。

5 结论

针对空间平台雷达在低重频、窄带条件下的空间碎片群目标成像问题，本文结合群目标的高速自旋特性，提出了一种稀疏重采样的碎片群目标成像方法。在目标个数已知的前提下，该方法对回波进行自相关处理，通过转速配对获取观测范围内与碎片对应的转速，并结合不同的转速构建联合字典，利用观测矩阵抽取不同碎片目标的回波数据，在克服遮挡效应的同时，实现了空间的等效插值，从而避免了低重频系统下的多普勒模糊问题。仿真实验结果证明了本文方法针对碎片群目标成像的有效性。然而，本文方法在信噪比低于10 dB、回波中存在强弱目标的情况下，无法准确估计碎片目标的转速，不利于设计冗余字典，严重影响目标的成像质量。另外，如何设计观测字典，在抽取数据的同时得到更优RIP性质的感知矩阵，是下一步需要进行的工作。