② (微波成像技术重点实验室 北京 100190)
③ (中国科学院大学 北京 100049)
② (National Key Laboratory of Microwave Imaging Technology, Beijing 100190, China)
③ (University of Chinese Academy of Science, Beijing 100049, China)
圆迹SAR(Circular Synthetic Aperture Radar,CSAR)作为近年新发展起来的全方位高分辨3维成像模式,具有独特的优势[1]。与SAR的其他成像模式相比,圆迹SAR主要具有以下三大优势:首先,360°观测使圆迹SAR具有全方位观测的优势;其次,通过拓展波数域有效带宽,使得圆迹SAR具有高平面分辨率;最后,场景中不同位置的两个目标具有不同的距离徙动曲线,可实现目标的3维重建。正因圆迹SAR具有这些独特的优势,所以其一经提出,便受到广泛的关注。国内的一些研究机构如中国科学院电子学研究所、清华大学、中国民航学院、北京航空航天大学、西安电子科技大学、中国科学院空间中心、国防科学技术大学等都开展了圆迹SAR相关方面的研究[2-5]。
但是圆迹SAR的3维重建能力依赖于目标的散射方向一致性。圆迹SAR对于强方向性目标,只具有方位向和斜距向的分辨能力,在垂直于数据采集平面的分辨能力非常弱。尤其是对于单轨迹圆迹SAR而言,它对于强方向性目标的高程向的提取能力非常弱。国外的一些研究机构也注意到这一问题并开展了相关研究,德宇航(DLR)和俄亥俄大学(Ohio State University)[6, 7]开展了多基线圆迹SAR 3维成像方法研究,具有一定的高程向分辨能力,然后再利用压缩感知方法进行了高度向的超分辨,由于需要进行多次飞行,对轨迹基线的控制要求较高。本文采用一种新的干涉圆迹SAR 3维重建方法来解决这一问题以实现目标的3维重建。
本文以单轨迹圆迹SAR为数据获取方式,以典型目标为研究对象,通过干涉圆迹SAR成像方法,对高度向进行均匀分层,对于每一高度层,获取得到的两个通道数据首先在同一3维直角坐标系中分别进行圆迹SAR成像,然后对两个通道图像进行干涉处理,确定其相干性和干涉相位,通过对干涉相位设定阈值的方法,只保留属于这一高度平面的目标,以增强单轨迹圆迹SAR对强方向性目标的3维重建能力。该文针对典型目标开展3维圆迹SAR干涉方法研究,开展了基于暗室实验的原理性验证,首次给出了实际坦克金属模型的干涉圆迹SAR的3维重建结果,验证了该方法的有效性,同时展示了3维重建与全方位观测相结合在目标精细特征描述方面具有的重要应用潜力。
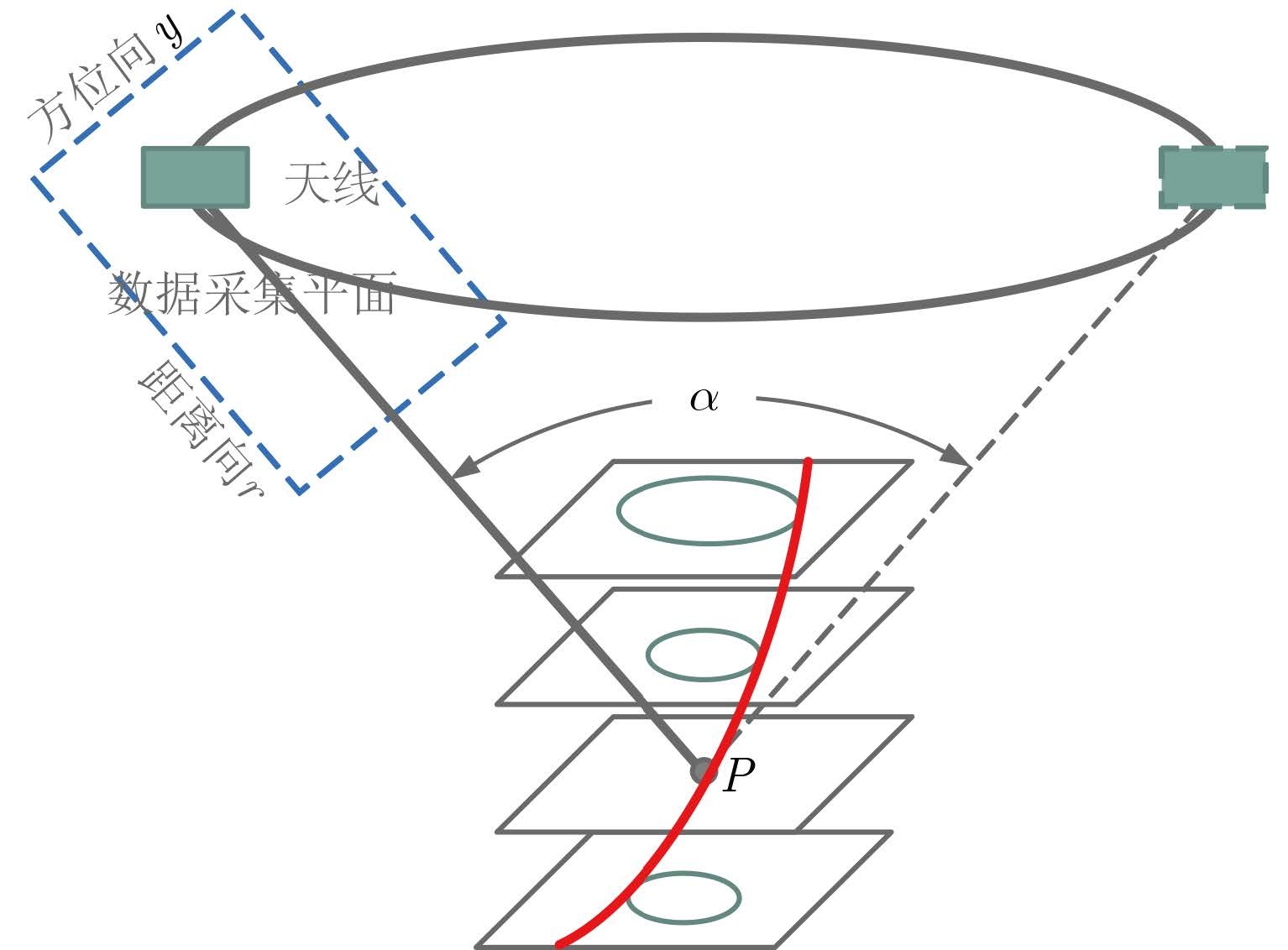
2 单孔径圆迹SAR聚焦成像的局限性我们认为目标的散射特性在散射相干角范围内保持一致,一旦超出这个范围,散射特性就会发生变化。图 1为不同散射相干角的聚焦成像示意图,从中可以看到,当散射体的散射相干角较大时,当聚焦面为它的真实高度平面时,目标可以很好地聚焦为一个亮点,在其他高度平面,会形成一个圆弧,圆环半径与散射体真实高度和成像平面之间的高度差成正比,因此我们依然可以通过图像判断散射体的3维位置。然而,根据经验研究发现,大多数目标的散射相干角都不超过20°[8],意味着大多数目标都是强方向性目标。对于散射相干角较大的散射体,我们可以通过圆环半径与散射体真实高度与聚焦平面之间的高度差来判断散射体的真实高度。然而对于强方向性目标,它只具有方位向和斜距向的分辨能力,在垂直于数据采集平面的分辨能力非常弱。
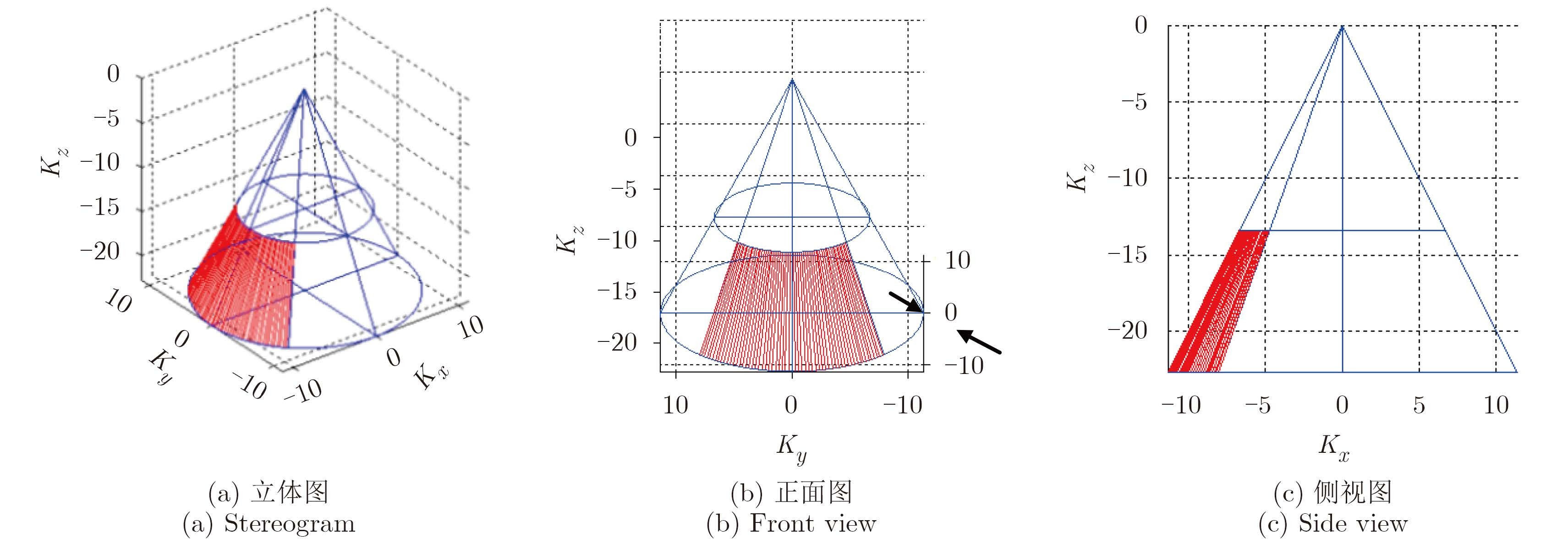
对于各向同性目标,圆迹SAR的360°观测可以实现波长量级的水平分辨率,同时还具备3维分辨能力。但是,对于强方向性目标,它只具有方位向和斜距向的分辨能力,在垂直于数据采集平面的分辨能力非常弱。图 2从频谱的角度分析了强方向性目标在圆迹SAR模式下的3维分辨率:数据采集平面(如图 1蓝色框所示平面)上沿斜距方向的距离分辨率Dr,沿雷达平台运动轨迹方向的方位分辨率Dy,垂直于数据采集平面方向的垂直分辨率Dz,且这3个方向分辨率的表达式如下所示:
| ${{D}_{r}}=\frac{\pi }{{{K}_{\max }}-{{K}_{\min }}}$ | (1) |
| ${{D}_{y}}=\frac{\pi }{2{{K}_{\text{c}}}\cos \alpha \sin (\varphi )}$ | (2) |
| ${{D}_{z}}=\frac{\pi }{{{K}_{\text{c}}}\sin \beta }$ | (3) |
其中,$\beta = \left( {\pi /2} \right) - \alpha - {\rm{arctan}}[{\rm{cot}}\alpha {\rm{cos}}\varphi]$,α为雷达天线波束俯仰角,φ为散射相干角,${K_{\rm{c}}} = \left( {2\pi {f_{\rm c}}/{\rm{c}}} \right)$为中心波数,fc为中心频率,c为光速,Kx,Ky,Kz为沿x,y,z方向的瞬时波数。
|
图 1 不同散射相干角的聚焦成像示意图 Fig.1 Schematic diagram of different scattering angle |
从式(1)–式(3)可以看出,对于强方向性目标,其距离分辨率仅与发射信号带宽有关,方位向分辨率和垂直向分辨率主要与中心频率和目标自身的相干散射角的大小相关。当相干散射角较小时,如图 2(c)所示目标的3维频谱近似为平面,此时垂直于斜距平面的方向上分辨能力较弱,CSAR将不能实现3维分辨。
|
图 2 强方向性目标的频谱支撑域 Fig.2 Spectral domain support of highly directive scatters |
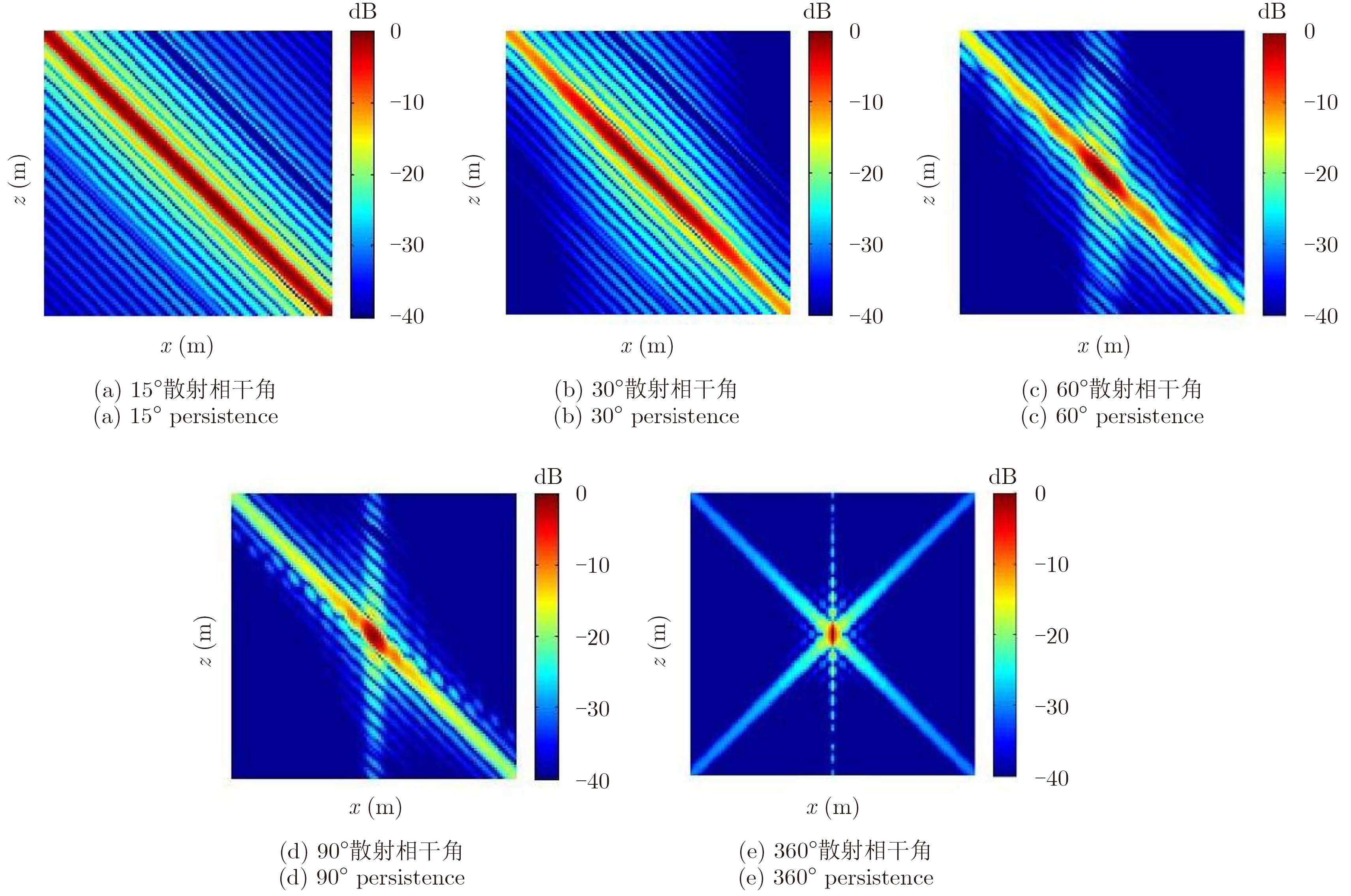
图 3所示为对不同散射相干角下的情况以点目标为例进行仿真的实验结果,依次分别是15°,30°,60°,90°,360°散射相干角下目标在垂直于数据采集平面的投影情况,从中可以看出对于强方向性目标,它的散射特性不能在整个圆形孔径中保持一致。散射相干角是90°的情况下,才具有一定的分辨能力,在360°才能达到理论分辨率,但是在15°和30°的时候,它在3维空间中形成一条垂直于数据采集平面的直线,我们没有办法通过图像判断它的真实高度。因此圆迹SAR 3维成像对强方向性目标高度成像具有一定困难。这就是单轨迹圆迹SAR对强方向性目标高度向分辨能力的局限性,也是本文所要探讨的主要问题。
|
图 3 不同散射相干角下垂直于数据采集平面的投影 Fig.3 Projection of different scattering angle |
干涉圆迹SAR 3维重建方法采用单轨迹圆迹SAR数据获取方式,对于强方向性目标而言,圆迹SAR360°的全方位观测可以获取其准确的(x,y),但是对于高度向z的分辨能力较弱。而干涉SAR[9]利用两幅天线对同一区域进行重复观测,充分利用雷达回波信号所携带的相位信息,提取同一目标对应的两个回波信号之间的相位差。本方法的关键是对于同一场景,在相同的3维直角坐标系下成像,无需配准,对高度z方向的每一切片层,两个通道获得的全孔径数据分别进行圆迹SAR成像,再利用干涉SAR的方法获取这一切片层的干涉相位,为了获得更好的效果,我们对干涉相位在复数域做滤波处理,由于干涉相位只在目标的真实高度平面为0,所以可以通过设定阈值的方法,只保留属于这一切片层的目标。简言之,干涉圆迹SAR 3维重建方法是将圆迹SAR360°全方位观测的优势与干涉SAR测高的优势相结合,以改善单轨迹圆迹SAR对于强方向性目标高度向分辨能力弱的特点,进而提高3维重建能力。
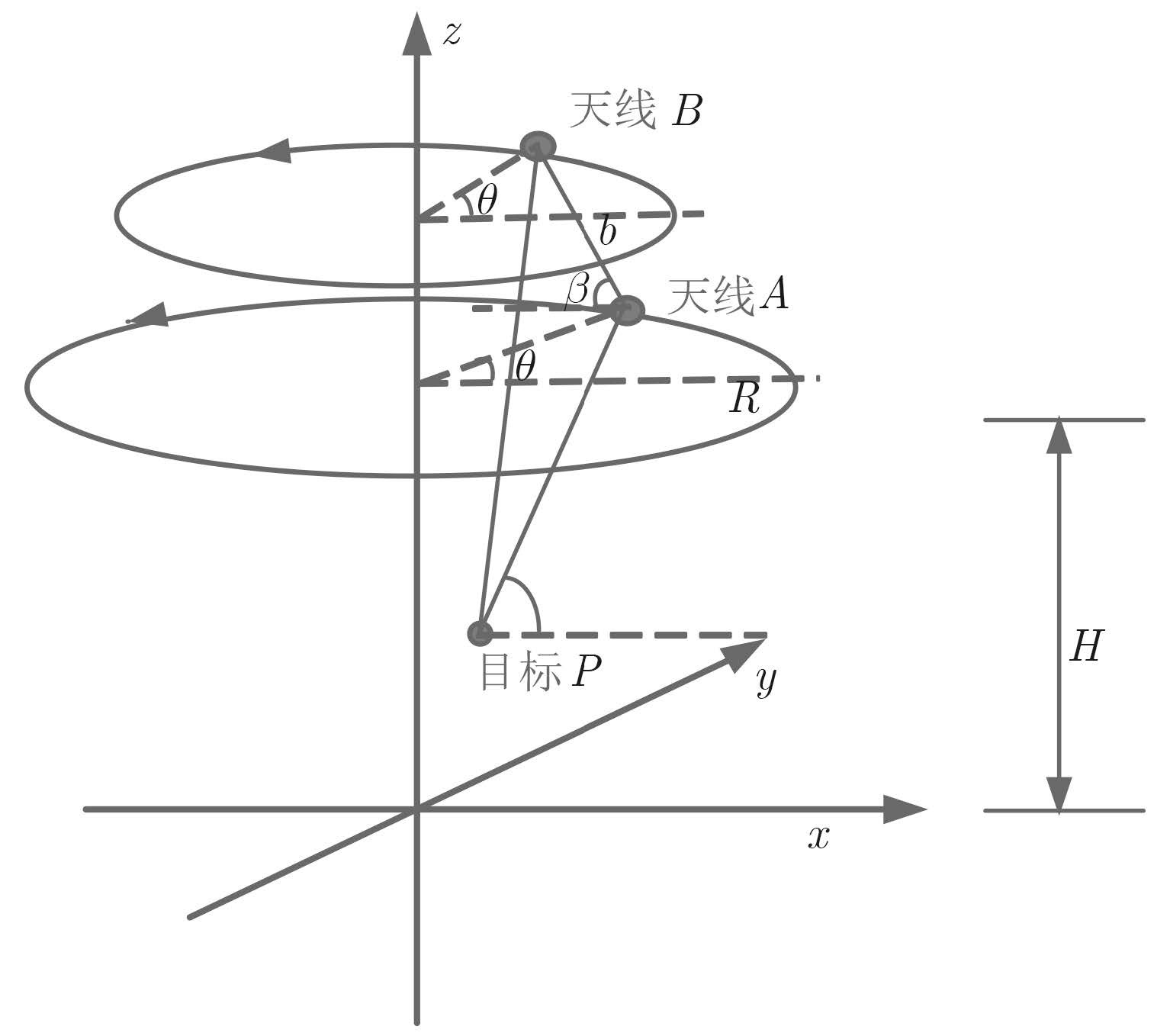
3.1 几何模型干涉圆迹SAR的几何模型如图 4所示,两个雷达天线间的基线长度为b,与水平面的夹角为β,其中天线A为主天线,天线B为副天线。雷达平台在距离地面高度H的平面作圆周运动,雷达平台在运动的过程中,其基线方向始终与速度方向保持垂直。两个天线分别形成两条独立的圆形孔径,方位角$\theta \in [0,2 \pi )$。天线A的轨迹半径为R。在本文中,假设两天线采用乒乓收发模式,即轮流自发自收,每个天线各自发射Chirp信号,中心频率为fc,带宽为Br。设场景中有一任意点目标P,其散射特性在方位角范围内$[{\theta _p} - \Delta \alpha /2,{\theta _p} + \Delta \alpha /2]$保持一致,散射系数为σp,在其他方向,散射系数为0。Δα就是散射相干角,当Δθ较小时,目标P就是我们说的强方向性目标。
|
图 4 干涉圆迹SAR几何模型 Fig.4 InCSAR geometric model |
即使散射特性随方位向变化,但在不同角度下干涉相位的差别较小,因此可以对360°全孔径的数据直接处理,本文中的实验也正是这样处理的。因此,生成2维复图像时,散射相干角设置为360°,虽然这里以强方向性目标为主要研究对象,但是本方法对其他散射相干角较大的目标也同样适用。
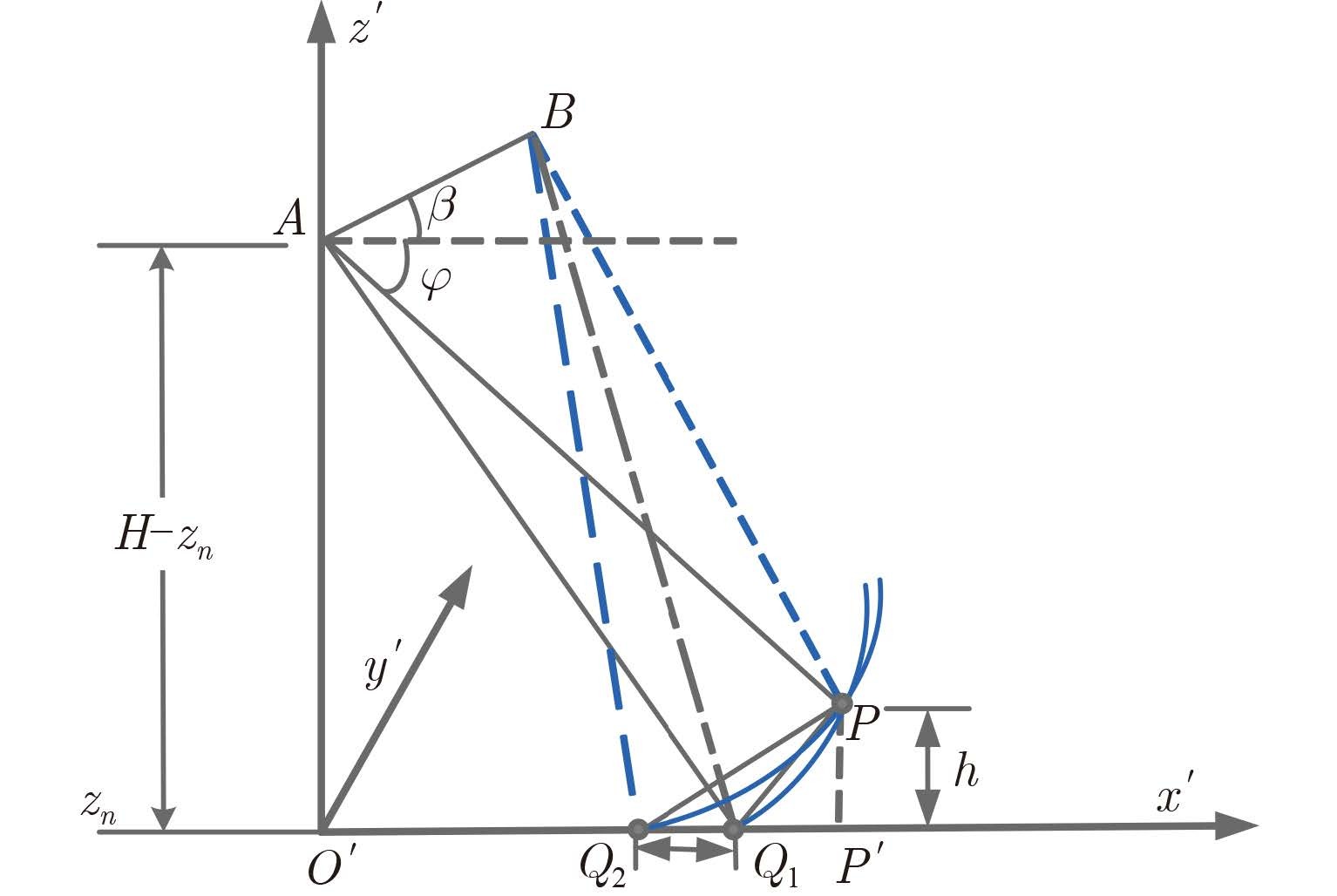
3.2 相位模型如图 5所示为干涉圆迹SAR的局部几何关系,其中,$z'$轴等同于z轴,$y'$轴指向雷达平台在零多普勒位置的飞行方向,$x'$轴由右手坐标系确定。位置A,B分别对应天线A和天线B的零多普勒位置,φ为天线A关于目标P的下视角。在3维空间中,对于天线A,目标P被重建为弧线段PQ1(远场下弧线段可近似认为是直线段),对于天线B,目标P被重建为弧线PQ2。由于两干涉天线观测视角存在差异,所以两条弧线段只在P的真实高度处相交,而在其他高度平面,其真实高度与成像参考平面之间的高度差Δh将引起图像对之间的偏移,如图 5中所示的Δl。高度差Δh引起图像偏移Δl,图像偏移Δl是斜距差Δr在地距的反应,斜距差Δh引起干涉相位,因此我们可以建立干涉相位Δ$\phi $与高度差Δh的几何关系。
|
图 5 干涉CSAR局部几何关系 Fig.5 InCSAR partial geometry |
本文的相位模型与传统的干涉测高模型的不同之处在于:干涉相位产生的方式不同。在传统的干涉测高模型中,干涉相位的产生是由于两副天线对同一点目标的斜距差产生的,需要通过配准来提取干涉相位,且它的图像是基带的;而本文的相位模型推导中,干涉相位是通过图像偏移产生的,在同一3维坐标系中进行处理,无需配准且图像是非基带的。
首先我们来推导一下干涉相位与高度差的关系:
假设目标P的高度为zp,成像采用参考高度zn进行聚焦成像,即对主副天线在高度zn获得的两幅图像进行干涉处理,目标P的干涉相位可以表示为:
| $\Delta \phi = \frac{{4\pi{f_{\rm c}}}}{\rm c}\Delta r$ | (4) |
其中,Δr为斜距差,fc为信号中心频率,c为光速。
| $\Delta r{\rm{ = }}\left| {{\rm{B}}{{\rm{Q}}_2}} \right| - \left| {{\rm{B}}{{\rm{Q}}_1}} \right| = \left| {{\rm{BP}}} \right| - \left| {{\rm{B}}{{\rm{Q}}_1}} \right|$ | (5) |
在给定高度zn,点目标P在主图像中的重建位置为Q1,在副图像中的重建位置为Q2。假设Q1的坐标为(xq,yq,zn),则Q2的坐标为(xq–Δl,yq,zn)。
在三角形ABP中,使用余弦定理可得$\left| {{\rm{BP}}} \right|$与φ的表达式:
| ${\left| {{\rm{BP}}} \right|^2} = {b^2} + {\left| {{\rm{AP}}} \right|^2} - 2b\left| {{\rm{AP}}} \right|\cos (\beta + \varphi )$ | (6) |
| $\left| {{\rm{B}}{{\rm{Q}}_1}} \right| = \sqrt {{{({x_q} - b\cos \beta )}^2} + {{(b\sin \beta + H - {z_n})}^2}} $ | (7) |
高度差Δh=zp–zn与φ的表达式为:
| $\Delta h = H - {z_n} - \left| {{\rm{AP}}} \right|{\rm{sin}}\varphi $ | (8) |
斜距差Δr与高度差Δh的关系主要为线性关系,可通过Δr对Δh求导得到:
| $\frac{{{\rm{d}}(\Delta {{r}})}}{{{\rm{d}}(\Delta {{h}})}} = \frac{{{\rm{d}}(\Delta {{r}})}}{{{\rm{d}}\varphi }}\Big /\frac{{{\rm{d}}(\Delta {{h}})}}{{{\rm{d}}\varphi }}$ | (9) |
式(5)两边分别对φ求导,得到:
| $\frac{{{\rm{d}}(\Delta {{r}})}}{{{\rm{d}}\varphi }} \!=\! \frac{{{\rm{d}}(\left| {{\rm{BP}}} \right|)}}{{{\rm{d}}\varphi }} \!-\! \frac{{{\rm{d}}(\left| {{\rm{B}}{{\rm{Q}}_1}} \right|)}}{{{\rm{d}}\varphi }} \!=\! \frac{{{{b}}\left| {{\rm{AP}}} \right|{\rm{sin}}(\beta \!+\! \varphi )}}{{\left| {{\rm{BP}}} \right|}}$ | (10) |
式(8)两边分别对φ求导,得到:
| $\frac{{{\rm{d}}(\Delta {{h}})}}{{{\rm{d}}\varphi }} = - \left| {{\rm{AP}}} \right|{\rm{cos}}\varphi $ | (11) |
把式(10),式(11)代入式(9)可得:
| $\frac{{{\rm{d}}(\Delta r)}}{{{\rm{d}}(\Delta h)}} = - {\rm{ }}\frac{{b\:{\rm{sin}}(\beta + \varphi )\left| {{\rm{BP}}} \right|{\rm{cos}}\varphi }}{{\left| {{\rm{BP}}} \right|{\rm{cos}}\varphi }}$ | (12) |
因为Δh=0时,Δr=0,所以可以得到Δr与Δh的关系式:
| $\Delta r = - \frac{{b \,{\rm{sin}}(\beta + \varphi )}}{{\left| {{\rm{BP}}} \right|{\rm{cos}}\varphi }}\Delta h$ | (13) |
在三角形ABP中,根据正弦定理得:
| $b\;{\rm{sin}}(\beta + \varphi ) = \left| {{\rm{BP}}} \right|{\rm{sin}}(\Delta \theta )$ | (14) |
其中Δθ=∠APB为干涉角。把式(13),式(14)代入式(4),可得到Δ$\phi$与Δh的关系式:
| $\begin{aligned} \Delta \phi = & - \frac{{4 \pi {f_{\rm c}}}}{\rm c}\frac{{b \,{\rm{sin}}(\beta + \varphi )}}{{\left| {{\rm{BP}}} \right|{\rm{cos}}\varphi }}\Delta h\\ = & - \frac{{4 \pi {f_{\rm c}}}}{\rm c}\frac{{{\rm{sin}}(\Delta \theta )}}{{{\rm{cos}}\varphi}}\Delta h \end{aligned}$ | (15) |
类似的求解方法,我们也可以得到图像偏移Δl与高度差Δh的关系式:
| $\Delta l = \frac{{b \,{\rm{sin}}(\beta + \varphi )}}{{\sqrt {{{\left| {{\rm{BP}}} \right|}^2} - {{(b \,{\rm{sin}}\beta + H - {z_n})}^2}} {\rm{cos}}\varphi }}\Delta h$ | (16) |
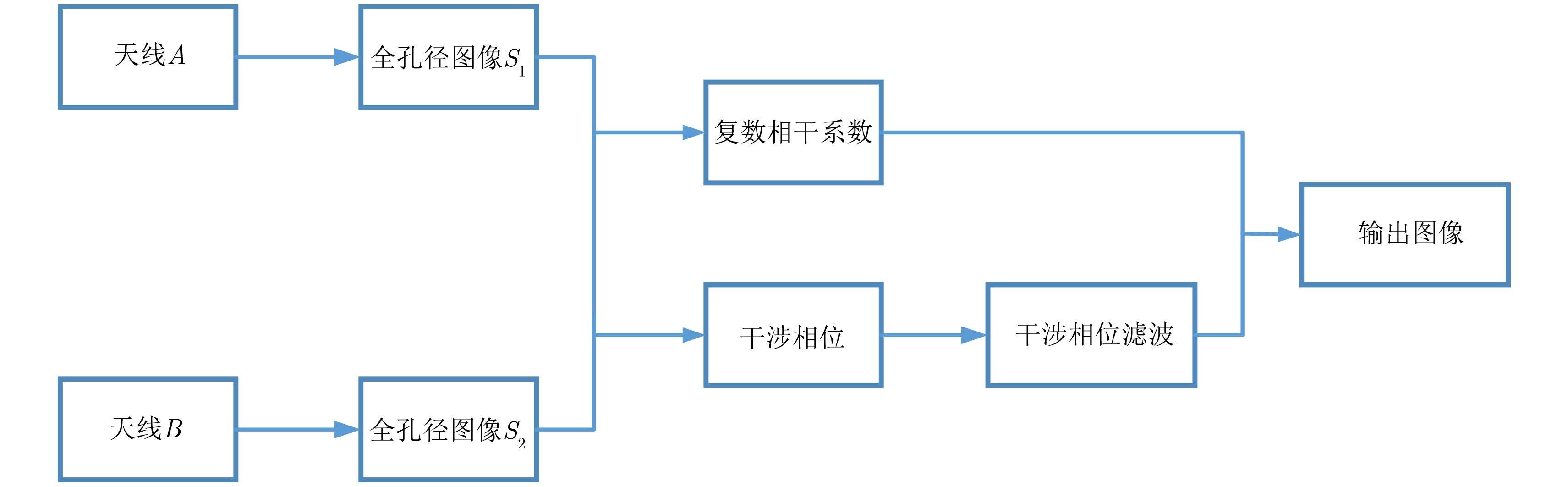
干涉圆迹SAR 3维重建方法对每一高度切片的处理流程图如图 6所示。
|
图 6 处理流程图 Fig.6 Process flow chart |
干涉圆迹SAR 3维重建方法对每一高度切片的具体的操作步骤如下所示:
步骤 1 对两个干涉天线采集的全孔径数据分别在同一3维直角坐标系中聚焦成像,获得图像S1(x,y,zn)和S2(x,y,zn),其中zn=nΔz,Δz为重建平面高度向的采样间隔。
步骤 2 计算主图像S1与副图像S2之间的复数相关系数图r(x,y,zn),两个图像像素的相关系数定义为[10]:
| $r(x,y,{z_n}) = \frac{{\left | {{\rm E}[{S_1}{S^*_2}]} \right|}}{{\sqrt {{\rm E}\big[{{\left| {{S_1}} \right|}^2}\big]} \sqrt {{\rm E}\big[{{\left| {{S_2}} \right|}^2}\big]} }}$ | (17) |
其中,E$\left[{*} \right]$表示计算数学期望,在实际估计相关系数时,数学期望以空间平均的形式进行,即以估计点为中心,计算大小固定的窗内的图像的相关性。
步骤 3 对主副图像生成干涉图,即求得S1(x,y,zn)和S2(x,y,zn)的共轭乘积。再由此生成干涉相位图,即:
| ${\phi _1}(x,y,{z_n}) = {\rm{arg}}({S_1}(x,y,{z_n}){S^*_2}(x,y,{z_n}))$ | (18) |
步骤 4 在复数域对干涉相位图进行滤波,针对干涉相位图的滤波方法较多,如自适应迭代滤波[11]及矢量滤波法[12],针对本次实验的典型目标,综合考虑计算复杂度及滤波效果,因此选择矢量滤波方法,其对干涉相位的实部和虚部分别进行滤波,公式表示为:
| ${\phi _1}(m,n) = {\rm{arctan}}\left[ {{{\sum {{\rm{sin}}{\phi _1}(i,j)} } \over {\sum {{\rm{cos}}{\phi _1}(i,j)} }}} \right]{\rm{ }}$ | (19) |
与计算相关系数类似,实际计算时,滤波以空间平均的形式进行。
步骤 5 当两幅图像的相关系数小于阈值ξ或干涉相位超过阈值δ时,将相应的像素置为零。即:
| ${\rm{Gout}}(x,y,{z_n}) = {S_1} \cdot [(r(x,y,{z_n}) > \xi ) \cdot (\left| {{\phi _1}} \right| < \delta )]$ | (20) |
对于n=1,2,···的每个高度切片zn,重复以上各步骤,就能够去除聚焦于非真实高度平面的目标,从而保留真实高度平面的目标,获得增强了的场景区的3维图像。
4 暗室实验 4.1 关键参数设计及分析本次实验采用的参数如表 1所示。
| 表 1 实验参数 Tab.1 Experiment parameters |
(1) 相关系数ξ的选择
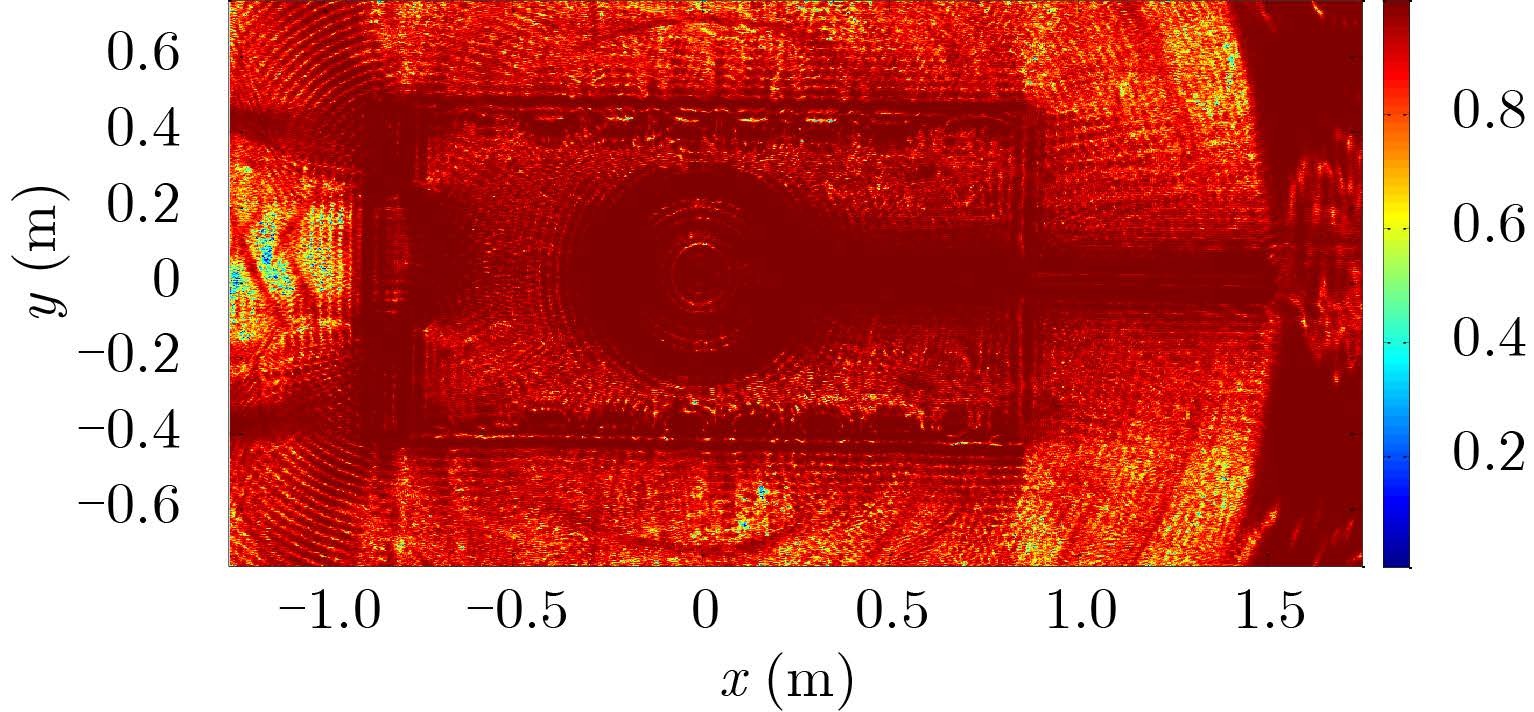
只有当图像偏移小于一个分辨单元时,干涉相位才满足式(15),否则由于图像对的不相关,干涉相位将类似于噪声,不能用于判断。当图像对的相关性小于设定的阈值ξ时,将相应目标去除。阈值ξ的选择可以参照差分干涉中PS点的选取[13],也可以根据实际情况进行设计。本次实验中根据式(16),可计算得图像最大偏移量为0.0036 m,地距分辨率为0.025 m,因此图像对之间都是相干的,这一点从图 7所示的相干图中也可以看出,因此在本次实验中跳过这一步,不再计算图像的相干系数。
|
图 7 z=0平面的相干图 Fig.7 Coherence map of z=0 |
本文中的干涉圆迹SAR方法是在同一3维坐标系中进行处理的,无需对图像进行配准。本文中因为图像对之间的相干性比较高,所以没有加入相干系数阈值。如果图像对的偏移比较大,相干系数比 较低,则需要加入相干系数阈值,那么我们认为小于阈值的部分图像已去相干,不进行干涉处理,只对大于阈值的相干性比较高的部分图像进行处理。如果在实验数据处理中将相干系数阈值设为0.8,处理结果证明对于本次实验中的情况,加入相干系数阈值,对重构结果几乎没有影响。
(2) 切片高度间隔设计及干涉相位阈值δ选择
干涉相位阈值δ的下限主要由高度间隔Δz和相位均方误差${\sigma _\phi }$决定,因为场景中的目标可能并不刚好出现在高度向采样间隔处,考虑式(15),阈值δ需满足:
| $\delta > \max \Big(\frac{{4 \pi {f_{\rm c}}\;{\rm{sin}}(\Delta \theta )}}{{{\rm c}\;{\rm{cos}}\varphi }}\frac{{\Delta z}}{2},{\sigma _\phi }\Big)$ | (21) |
由于受到相位均方误差${\sigma _\phi }$的制约,所以不管高度间隔划分的如何精细,要想保证最后得到的目标的完整性,干涉相位阈值都必须满足式(21)的条件,而且如果高度间隔划分的很小,会增加计算开销,因此,综合考虑计算效率和精度,Δz的设计可以使式(21)中的两项相等,即:
| $\Delta z{\rm{ = }}\frac{{{\sigma _\phi }{\rm c}\;{\rm{cos}}\varphi }}{{2 \pi {f\!_{\rm c}}\;{\rm{sin}}(\Delta \theta )}}$ | (22) |
干涉相位图的滤波窗口大小选择为11×11,经滤波后,平均噪声水平${\sigma _\phi }$约为0.02 rad,具体计算方法参照文献[14],本次实验中Δθ=0.2°,φ=8°,因此由式(22)计算得到Δz约为0.01 m。
因图像的噪声水平并不恒定,为保证3维重建后所有目标的完整性,结合多次试验的结果,因此我们综合选择δ=0.08 rad,此时3维重建效果、效率及精度较优。
因Δz是${\sigma _\phi }$的函数,切片高度间隔Δz确定之后,干涉相位阈值δ与Δz相关,如果δ选择较小,则属于该层的目标没有全部得到重建;如果δ选择较大,则最后重建的结果中会包含不属于该层的目标。
(3) 相对高程提取精度分析
结合式(4)及式(15),可以得到相对高程提取精度为:
| ${\rm d}z = \frac{{{\rm c} \,{\rm{cos}}\varphi }}{{4 \pi {f\!_{\rm c}}\;{\rm{sin}}(\Delta \theta )}} \cdot {\rm d}\phi = \frac{{{\rm c} \,{\rm{cos}}\varphi }}{{4 \pi {f\!_{\rm c}}\;{\rm{sin}}(\Delta \theta )}} \cdot \delta $ | (23) |
本次暗室实验中Δθ=0.2°,φ=8°,δ=0.08 rad,fc=15 GHz,可以计算得到,相对高程提取精度的理论值为0.0361 m。关于实际的相对高程精度分析将在后续工作中进一步分析及验证。
(4) 不模糊高度分析
根据式(15)可以计算得到不模糊高度满足如下关系:
| ${h_{{\rm{max}}}} \le \frac{{{\rm c} \,{\rm{cos}}\varphi }}{{2{f_{\rm c}}\;{\rm{sin}}(\Delta \theta )}}$ | (24) |
本次实验中Δθ=0.2°,hmax为2.8369,且坦克目标高度小于1 m,所以对于本次实验中的典型目标及相应参数,暂不涉及相位解缠绕问题[13],这一问题将在后续研究中开展。
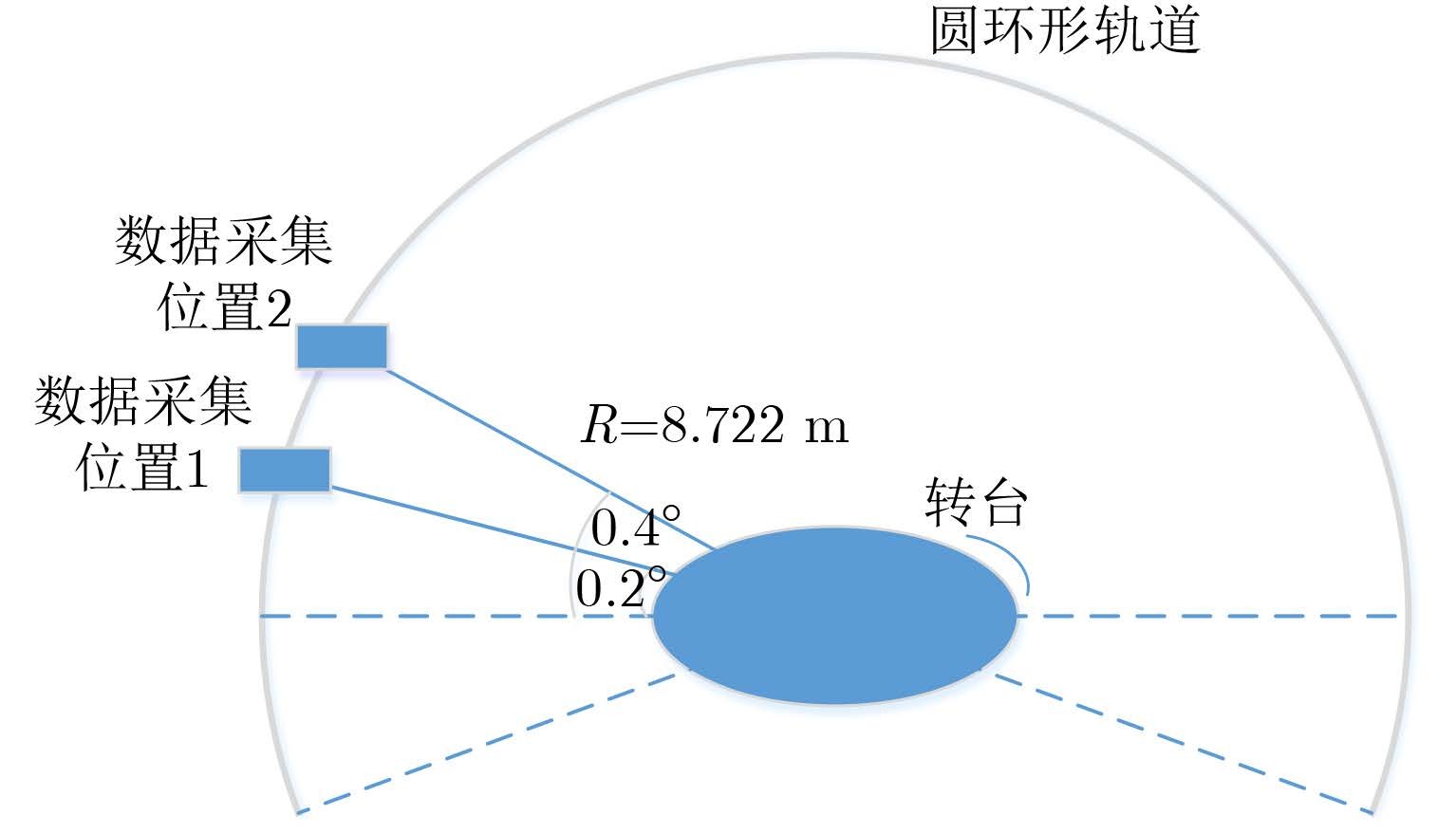
4.2 实际模型暗室实验成像几何如图 8所示,转台匀速转动,目标放置在转台中心,图 9为在实验现场拍摄的实验场景照片,其中目标的模型如图 10所示。
|
图 8 实验成像几何 Fig.8 Experiment imaging geometry |

|
图 9 实验现场 Fig.9 Experiment site |
|
图 10 实验目标 Fig.10 Experiment target |
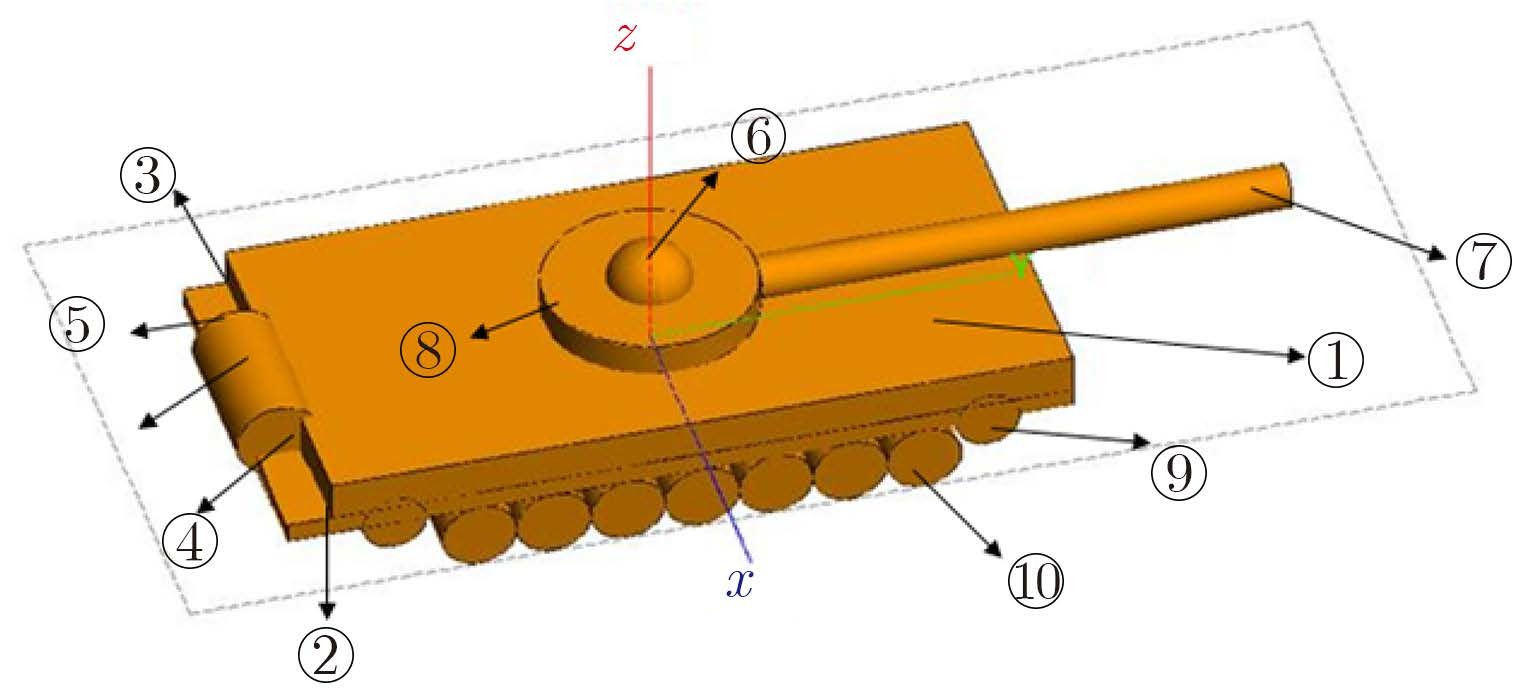
本次实验的目标为如图 10所示的坦克,坦克材质为金属,其中坦克由长方体、圆柱体、半球、二面角、三面角等组成,各个部分的组合形式如图 10所示,其中各个部分的尺寸大小如表 2所示。
| 表 2 实验目标尺寸 Tab.2 Target size |
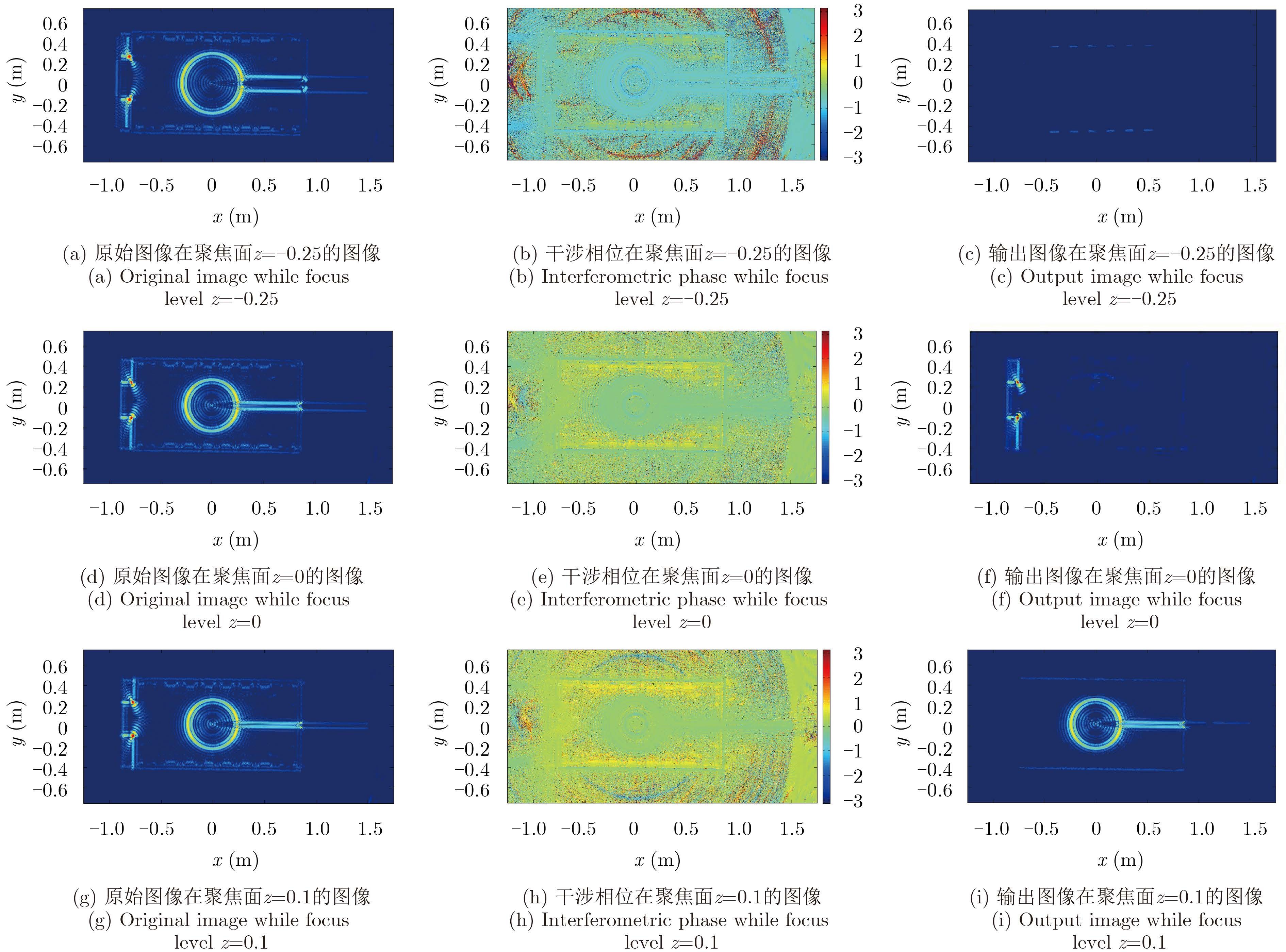
从图 10的坦克模型示意图中可以看出,该目标为强方向性目标,本文选择了散射性较强的几个部分进行分析:分别是圆柱⑦与长方体①相交处,圆柱⑧与长方体①相交处,②③④⑤所示的三面角、二面角部分以及⑩所示的6个轮子部分。图 11为处理前后的图像在不同聚焦面的结果及其干涉相位图。原始图像指未使用本方法前圆迹SAR的成像结果。输出图像为使用本方法后的成像结果。本方法主要是利用给干涉相位设定阈值的方法只保留属于这一平面的目标。从原始图像图 11(a)、图 11(d)和图 11(g)中可以看到,炮管聚焦情况的变化最为明显,当聚焦面z=–0.25,z=0时,可以看到炮管为两根,说明这两个成像平面不是炮管的聚焦平面,当聚焦面为z=0.1时,炮管得到了很好的聚焦。也就是说,原始图像不但包含属于该平面的目标,还包括不属于该平面的目标,经过本方法处理后,如输出图像图 11(b)、图 11(d)和图 11(f)中所示,只保留了聚焦于这一平面的目标,而去除了不属于这一平面的目标。
|
图 11 处理前后的图像不同聚焦面的结果对比 Fig.11 Original image and Output image at different focus levels |
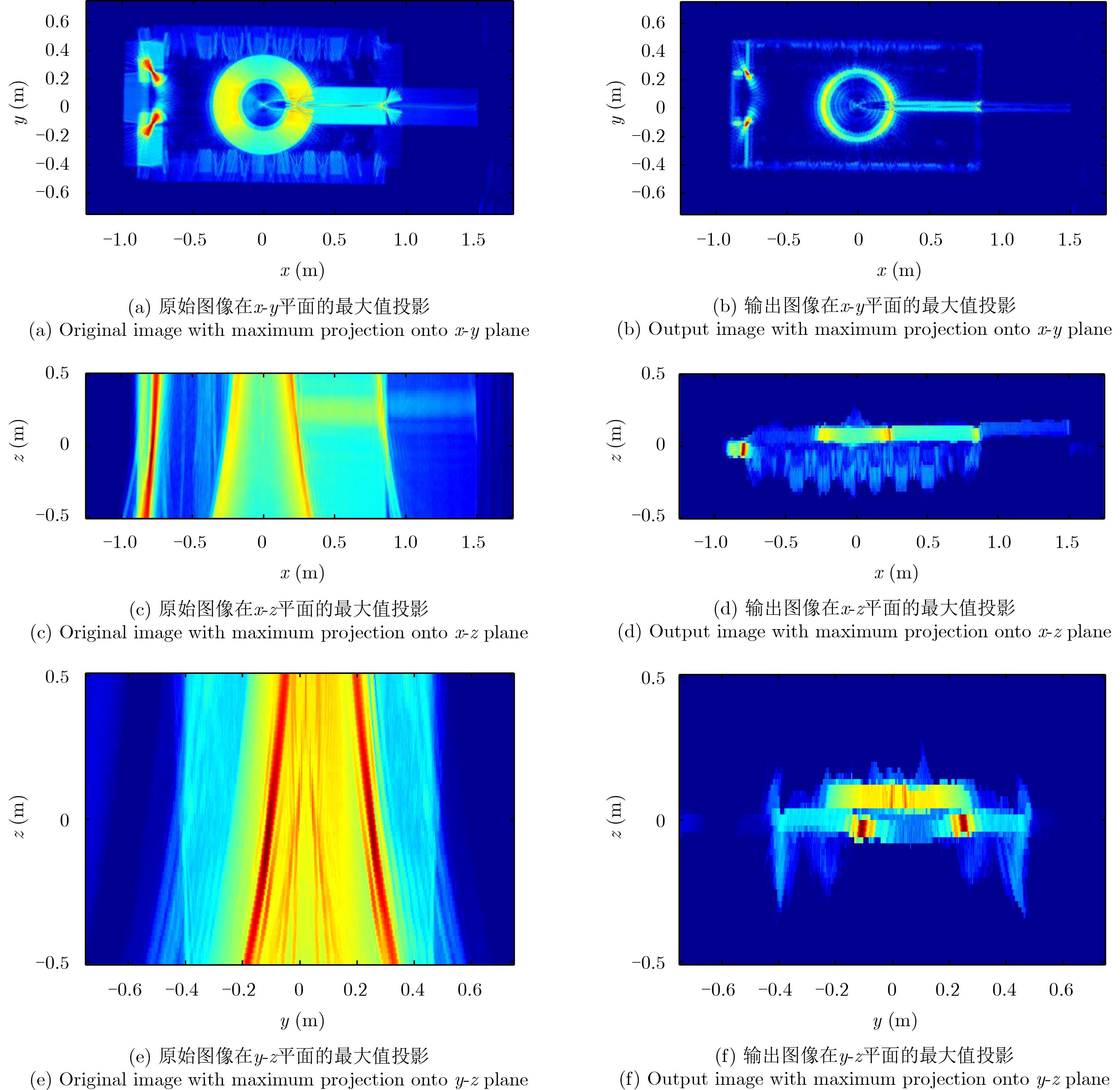
图 12为采用最大值投影法对处理前后的图像进行比较。从原始图像图 12(a)、图 12(c)和图 12(e)中可以看到,由于圆迹SAR对强方向性目标在垂直于数据采集平面的方向上几乎没有分辨能力,因此这类目标在重建图像中表现为直线段或弧线段,无法从图像中判断其真实高度。通过本方法处理后,如输出图像图 12(b)、图 12(d)和图 12(f)中可以看到的,几乎所有的目标都聚焦到了其正确的位置上。从图 12(d)中可以清晰地看到坦克的6个轮子、炮管以及最顶端的半球状。从图 12(f)中可以看到圆柱形炮台及两个特别强的三面角部分。
|
图 12 采用最大值投影法对处理前后图像进行对比 Fig.12 Original image and Output image after maximum projection |
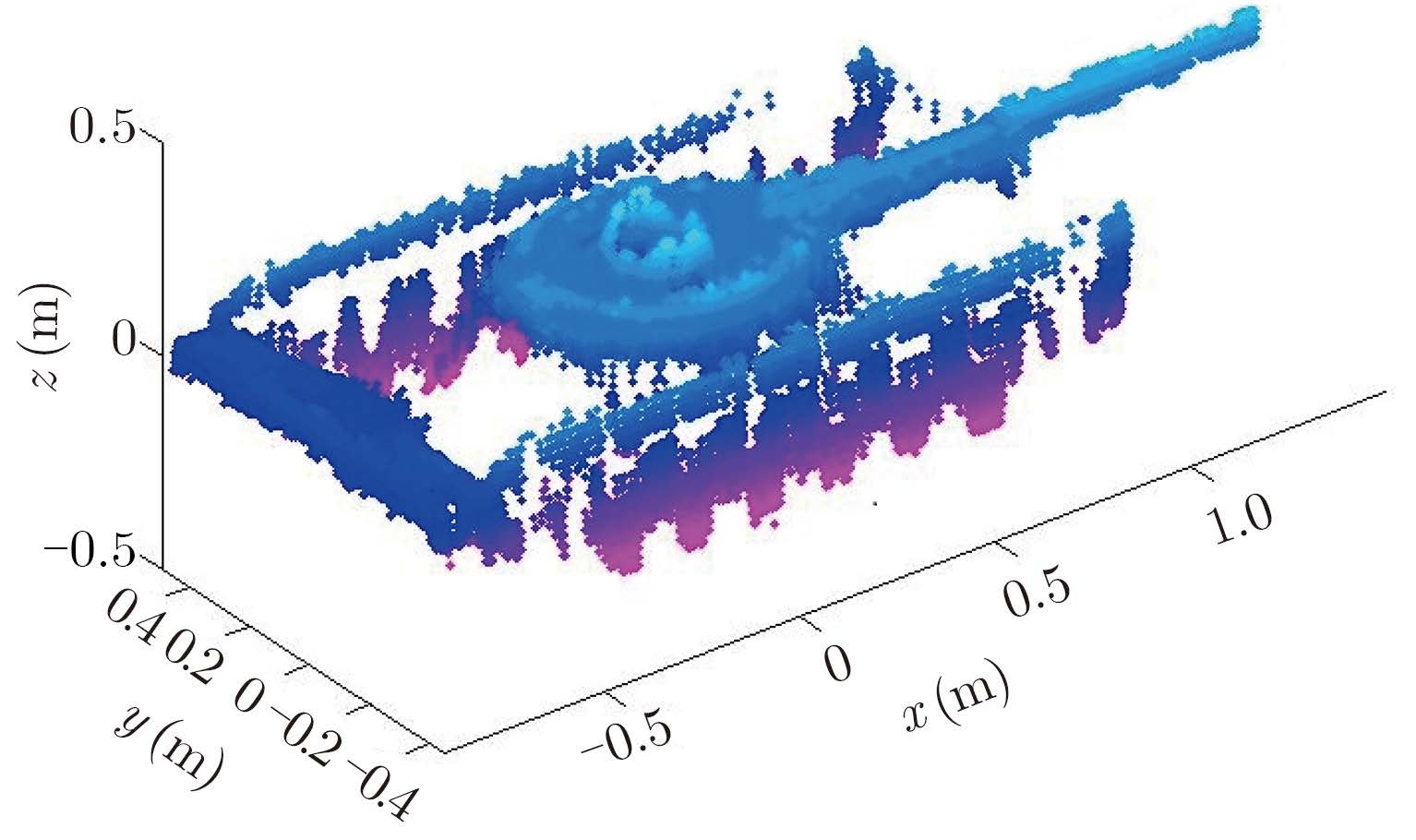
图 13为采用干涉圆迹SAR 3维重建方法得到的3维效果图,从图中可以看到坦克的大致轮廓,6个轮子清晰可见,炮管、炮台等也比较清楚。
|
图 13 3维效果图 Fig.13 Target’s 3d image |
对于本文中的典型目标,由于选择的基线较短,所以没有出现模糊,但是也限制了成像的精度。在后续的研究中,我们将选择长一些的基线以提高成像精度,可能会出现高度模糊,涉及到相位缠绕的问题将在后续研究中进行探讨。本方法是实际数据的原理性验证,对于实际的机载干涉圆迹SAR模式,还需分析运动误差对干涉相位误差的影响,但如果采用双天线单航过干涉模式,不同通道间的运动误差近似相同,并不会对干涉相位产生较大的影响,不过仍需进一步开展机载飞行实验进行验证。
5 结束语圆迹SAR的360°的全方位观测可以获取目标准确的(x,y),但是对于高度向z的分辨能力较弱。本文针对典型目标开展3维圆迹SAR干涉方法研究,开展了基于暗室实验的原理性验证,首次给出了实际坦克金属模型的干涉圆迹SAR的3维重建结果,验证了该方法的有效性,同时展示了3维重建与全方位观测相结合在目标精细特征描述方面具有的重要应用潜力。本文的目的是新体制的暗室实验的原理性验证,针对本次实验中特定的目标及实验条件,目标不会出现模糊问题,所以不涉及相位缠绕问题。此外,本次实验采用双天线模式,运动误差对于双天线而言,对干涉相位的影响较小,因此没有考虑运动补偿问题。这一问题将在后续开展的机载飞行实验中进行研究。
| [1] |
洪文. 圆迹SAR成像技术研究进展[J].
雷达学报 , 2012, 1 (2) : 124-135 Hong Wen. Progress in circular SAR imaging technique[J].
Journal of Radars , 2012, 1 (2) : 124-135 ( 0) 0)
|
| [2] |
林赟. 圆迹合成孔径雷达成像算法研究[D]. [博士论文], 中国科学院电子学研究所, 2011, 第1章: 2-5.
Lin Yun. Study on algorithms for circular synthetic aperture radar imaging[D]. [Ph.D. dissertation], Institute of Electronics, Chinese Academy of Sciences, 2011, Chapter 1: 2-5.
( 0) 0)
|
| [3] |
吴越. 圆周轨迹SAR三维成像算法研究与仿真[D]. [硕士论文], 电子科技大学, 2013, 第1章: 4-6.
Wu Yue. Study on circular SAR 3-D imaging algorithm and simulation[D]. [Master dissertation], School of Electronic Engineering, 2013, Chapter 1: 4-6.
( 0) 0)
|
| [4] |
张子善. 曲线合成孔径雷达三维成像相关技术研究[D]. [硕士论文], 国防科学技术大学, 2009, 第1章: 3-4.
Zhang Zi-shan. Research on the 3-D imaging technology of curvilinear SAR[D]. [Master dissertation], National University of Defense Technology, 2009, Chapter 1: 3-4.
( 0) 0)
|
| [5] |
廖轶, 邢孟道, 保铮. 调频连续波圆迹环扫SAR成像方法[J].
系统工程与电子技术 , 2015, 37 (9) : 1994-1997 Liao Yi, Xing Meng-dao, Bao Zheng. Imaging method for circular scanning SAR based on FMCW technology[J].
Systems Engineering and Electronics , 2015, 37 (9) : 1994-1997 ( 0) 0)
|
| [6] |
Ponce O, Prats P, Scheiber R, et al.. Analysis and optimization of multi-circular SAR for fully polarimetric holographic tomography over forested areas[C]. Proceedings of IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 2013: 2365-2368.
( 0) 0)
|
| [7] |
Ertin E, Moses R, Potter L. Interferometric methods for three-dimensional target reconstruction with multipass circular SAR[J].
IET Rader, Sonar & Navigation , 2010, 4 (3) : 464-473 ( 0) 0)
|
| [8] |
Mosesa R L, Pottera L C, and Cetinb M. Wide angle SAR imaging[C]. Proceedings of SPIE, San Jose, California, 2005: 164-175.
( 0) 0)
|
| [9] |
毛永飞, 汪小洁, 向茂生. 机载干涉SAR区域网三维定位算法[J].
雷达学报 , 2013, 2 (1) : 60-67 Mao Yong-fei, Wang Xiao-jie, Xiang Mao-sheng. Joint three-dimensional location algorithm for airborne interferometric SAR system[J].
Journal of Radars , 2013, 2 (1) : 60-67 ( 0) 0)
|
| [10] |
廖明生, 林珲.
雷达干涉测量-原理与信号处理基础. 北京: 测绘出版社[M]. 2003 : 52 -54.
Liao Ming-sheng and Lin Hui.
Synthetic Aperture Radar Interferometry-Principle and Signal Processing. Beijing: Surveying and Mapping Press[M]. 2003 : 52 -54.
( 0) 0)
|
| [11] |
林雪, 李曾玺, 李芳芳, 等. 一种自适应迭代的非局部干涉相位滤波方法[J].
雷达学报 , 2014, 3 (2) : 166-175 Lin Xue, Li Zeng-xi, Li Fang-fang, et al. An adaptive iterated nonlocal interferometry filtering method[J].
Journal of Radars , 2014, 3 (2) : 166-175 ( 0) 0)
|
| [12] |
靳国旺, 徐青, 张红敏.
合成孔径雷达干涉测量. 北京: 国防工业出版社[M]. 2014 : 48 -52.
Jin Guo-wang, Xu Qing, Zhang Hong-min.
Synthetic Aperture Radar Interferometry. Beijing: National Defense Industry Press[M]. 2014 : 48 -52.
( 0) 0)
|
| [13] |
Mora O, Mallorqui J, Broquetas A. Linear and nonlinear terrain deformation maps from a reduced set of interferometric SAR images[J].
IEEE Transactions on Geoscience and Remote Sensing , 2003, 41 (10) : 2243-2253 ( 0) 0)
|
| [14] |
Bamler R and Eineder M. Accuracy of differential shift estimation by correlation and split-bandwidth interferometry for wideband and delta-k SAR systems[J].
IEEE Geoscience and Remote Sensing Letters , 2005, 2 (2) : 152-155 ( 0) 0)
|




