②(中国科学院大学 北京 100049)
③(中国资源卫星应用中心 北京 100094)
②(University of Chinese Academy of Sciences, Beijing 100049, China)
③(China Center for Resources Satellite Data and Application, Beijing 100094, China)
SAR层析(SAR Tomography,TomoSAR)成像是传统单基线InSAR的扩展,其通过多基线数据集在高度向形成合成孔径来获得目标的3维空间信息。TomoSAR成像在经历实验室研究[1]、机载TomoSAR成像[2]和星载TomoSAR成像[3, 4, 5, 6, 7, 8]的发展同时,国内外学者提出了多种不同的成像方法。最初的TomoSAR成像方法是利用傅里叶变换聚焦法[1, 2, 3],该方法不仅需要高度孔径上的基线均匀分布,而且还需要大的高度孔径长度,以获得较高的高度向分辨率;然而在实际应用中,可用到的观测基线数少且多为非均匀分布,因此高度向分辨率很低。为了解决这个矛盾,文献[4, 5, 6, 7, 8, 9]采用了APES,Capon,MUSIC等具有超分辨能力的空间谱估计法,但是该方法需要进行目标信号源数目的估计,当估计的信号源数目与真实的信号源数目不一致时会产生严重的重构误差,大大增加虚假目标的出现概率。随着稀疏信号处理理论在微波成像中的应用[10],针对上述问题文献[11]提出将压缩感知技术(Compressive Sensing,CS)[12]应用于TomoSAR实验并进行了系统性的论证分析,研究表明该方法具有独特的超分辨率优势,能在基线数量少和非均匀稀疏分布的情况下实现高度向的高分辨率聚焦;然而该方法对目标聚集在少数区域内而并非出现在任意位置的结构信号进行重构时,无法保证目标的准确重构率[13, 14, 15, 16, 17]。
本文在压缩感知方法的基础上,基于稀疏信号非零元素具有的块结构特性,将目标的稀疏特性和其本身具有的结构特性一起考虑,提出采用块压缩感知(Block Compressive Sensing,BCS)[18, 19, 20, 21]方法对目标进行TomoSAR成像反演,通过模拟仿真数据对压缩感知与块压缩感知进行比较分析,结果表明本文所采用的方法能更好地实现结构特性稀疏信号的恢复。
2 TomoSAR成像原理TomoSAR成像的典型观测几何如图 1所示,同一目标区的M+1景航过SAR单视复图像数据集中选择一幅作为主图像,除主图像外第m航过影像中每个分辨率单元的复数值gm可看作是相同方位同一斜距下N个散射目标信号在层析向s上的叠加,其表达式为:
| \[\begin{array}{*{20}{l}} {{g_m} = \sum\limits_{n = 1}^N {{\gamma _n}\exp \left( { - {\rm{j}}2\pi {\xi _m}{s_n}} \right) + {e_m}} ,}\\ {\quad \quad {\xi _m} = \frac{{2{B_{ \bot m}}}}{{\lambda R}},m = 1,\cdots ,M,n = 1,\cdots ,N} \end{array}\] | (1) |
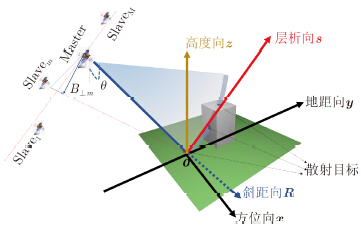 | 图 1 图 1 TomoSAR 3维成像的观测几何模型Fig.1 Model of TomoSAR imaging geometry |
在对多航过SAR序列数据集进行单视复图像(Single Look Complex,SLC)序列配准、去斜(Deramping)、相位补偿以及基线估计等预处理步骤后,TomoSAR要解决的问题是根据m航过影像中每个像元的复数值gm,通过各种方法反演每个层析向采样间隔sn上的散射点能量,进而确定该像素内主导散射点的数量及每个散射点的层析向位置或高度向位置,从而实现TomoSAR 3维成像。
3 基于CS和BCS的TomoSAR成像方法 3.1 基于CS的TomoSAR成像方法(CS-TomoSAR)经过预处理后的多航过SAR序列数据,在同一方位向-斜距向分辨单元中TomoSAR信号的观测向量可表示为G=[g1 g2 ··· gm]T,若令γ=[γ1 γ2 ··· γN]T和e=[e1 e2 ··· eM]T,则可将式(1)写成矩阵形式为:
| \[G = \Phi \cdot \gamma + e\] | (2) |
| \[\Phi = \left[{\begin{array}{*{20}{c}} {\exp \left( { - {\rm{j}}2\pi {\xi _1}{s_1}} \right)}&{\exp \left( { - {\rm{j}}2\pi {\xi _1}{s_2}} \right)}& \cdots &{\exp \left( { - {\rm{j}}2\pi {\xi _1}{s_N}} \right)}\\ {\exp \left( { - {\rm{j}}2\pi {\xi _2}{s_1}} \right)}&{\exp \left( { - {\rm{j}}2\pi {\xi _2}{s_2}} \right)}& \cdots &{\exp \left( { - {\rm{j}}2\pi {\xi _2}{s_N}} \right)}\\ \vdots & \vdots & \ddots & \vdots \\ {\exp ( - {\rm{j}}2\pi {\xi _M}{s_1})}&{\exp \left( { - {\rm{j}}2\pi {\xi _M}{s_1}} \right)}& \cdots &{\exp \left( { - {\rm{j}}2\pi {\xi _M}{s_N}} \right)} \end{array}} \right] = \left[{{\varphi _1}\;\;{\varphi _2}\;\; \cdots \;\;{\varphi _N}} \right]\] | (3) |
根据CS稀疏重构理论[12, 22, 23],利用观测向量G来重构目标信号γ必须满足目标信号γ的稀疏表示和观测矩阵Φ的限制等距特性(Restricted Isometry Property,RIP)。对于高分辨星载TomoSAR,目标位于层析向上一个较小的空间范围内,如图 1所示,同一方位向-斜距向分辨单元中只包含了少数几个的层析向散射目标,每一个层析向散射目标可看作为一个非零元素,那么同一方位向-斜距向分辨单元信号中只包含少数几个非零信号,满足信号的稀疏性。因此,对于高分辨星载TomoSAR,目标散射点在层析向上的空间分布是稀疏的,即目标信号γ可以稀疏表示的(设非零元个数即稀疏度为K);对于观测矩阵Φ的限制等距特性,由式(3)知F为离散傅里叶变换矩阵,又由于多航过SAR的垂直基线为随机分布,故F也为随机离散傅里叶变换矩阵,文献[22, 23]已证明其满足RIP特性。因此,K稀疏信号γ可以通过l1范数最小化求解准确地重构出来:
| \[\mathop {\min }\limits_\gamma {\left\| \gamma \right\|_1},\begin{array}{*{20}{c}} {}&{{\rm{s}}.{\rm{t}}.}&{} \end{array}G = \Phi \cdot \gamma + e\] | (4) |
BCS方法是在CS稀疏理论的基础上进一步刻画了目标信号的块稀疏结构特性——非零系数成块出现,即目标信号中的非零元素聚集在少数的块内而不是任意的杂乱无章地分布着[18, 19, 20, 21, 24]。为此,目标信号γ的k块稀疏(非零元块数)可定义为:
| \[\left. {\begin{array}{*{20}{l}} {\gamma = {{[\underbrace {{\gamma _1} \cdots {\gamma _b}}_{{\gamma ^{\rm{T}}}[1]}\underbrace {{\gamma _{b + 1}} \cdots {\gamma _{2b}}}_{{\gamma ^{\rm{T}}}[2]} \cdots \underbrace {{\gamma _{M - b + 1}} \cdots {\gamma _N}}_{{\gamma ^{\rm{T}}}[L]}]}^{\rm{T}}}}\\ {N = L \times b} \end{array}} \right\}\] | (5) |
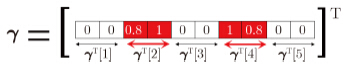 | 图 2 块稀疏信号示意图Fig.2 Diagram of block sparse signal |
按照与目标信号γ相似的分块,可将观测矩阵Φ分块定义为:
| \[\Phi = [\underbrace {{\varphi _1} \cdots {\varphi _b}}_{\Phi [1]}\underbrace {{\varphi _{b + 1}} \cdots {\varphi _{2b}}}_{\Phi [2]} \cdots \underbrace {{\varphi _{N - b + 1}} \cdots {\varphi _N}}_{\Phi [L]}]\] | (6) |
故依据上述块稀疏信号的描述,块稀疏信号的压缩观测模型为:
| \[G = \sum\limits_{l = 1}^{l = L} {\Phi \left[l \right] \cdot \gamma \left[l \right] + e} \] | (7) |
由于k块稀疏信号可看成稀疏度为K=k×b的随机稀疏信号,其观测矩阵Φ也符合K=k×b稀疏下的RIP条件的约束[25, 26],故k块稀疏信号γ可以通过混合l1/l2范数最小化求解准确地重构出来:
| \[\mathop {\min }\limits_\gamma {\left\| \gamma \right\|_{2,1}}\begin{array}{*{20}{c}} {}&{{\rm{s}}.{\rm{t}}.}&{} \end{array}G = \Phi \cdot \gamma + e\] | (8) |
对于高分辨星载TomoSAR,若层析向采样间隔δs较小,则同一方位向-斜距向分辨单元中每个层析向上的散射目标将采样多个散射点,即层析向上的一个散射目标由多个散射点组成,尽管这一散射目标中的多个散射点在反射量上各不相同,但它们在空间上呈现聚集块的结构形式,满足信号的块稀疏性。因此,利用目标的这种隐含结构特性采用BCS方法可进行TomoSAR成像反演,其稀疏子块的长度b与雷达视角θ、以及斜距向分辨采样间隔ΔR存在以下关系:
| \[b = {\rm{round}}(\frac{{\Delta s}}{{{\delta _s}}})\] | (9) |
由上式可知,同一散射目标中或同一块稀疏数下,随着层析向采样间隔减小,块稀疏子块长度增加,获得的散射目标中更多的散射点信息可以全面刻画散射目标的整体结构;层析向采样间隔变大,块稀疏子块长度减小,获得的散射目标中较少的散射点信息只能突出散射目标的主要结构特性。若层析向间隔δs增大到以Δs采样,则b=1,此时块稀疏退化为式(4)所示的普通意义上的稀疏性。
4 仿真试验及分析为了对块压缩感知的性能进行验证,下面将给出仿真数据和实测数据的处理结果。实测数据处理中使用了Radarsat-2自2012年9月至2014年5月期间获得的19轨超精细波束数据,目标选定为位于安徽省淮南市的淮南联合大学教学楼。图 3为目标的光学图像,图 4为目标的SAR图像。
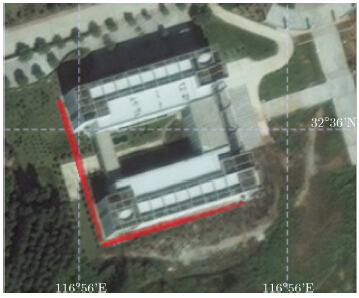 | 图 3 目标的光学图像Fig.3 Optical image of the object |
 | 图 4 目标的SAR图像Fig.4 Corresponding SAR image of the object |
为了更加合理地说明BCS-TomoSAR方法的优越性和有效性,仿真所需的参数,采用Radarsat-2超精细波束数据的实际参数(主图为2013年8月2日时的垂直基线分布,如图 5所示);仿真的散射目标,假设为不受各种误差影响的理想散射目标;仿真的结果,主要从分辨率性能、虚假散射目标的出现概率和散射目标中散射点位置的准确重构概率3方面进行评价。
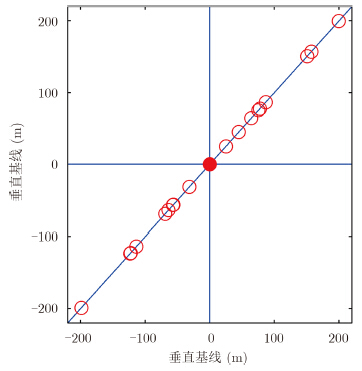 | 图 5 垂直基线分布图Fig.5 Perpendicular baseline distribution |
由Radarsat-2主图数据的中心视角θc=34.11°,主图的中心斜距Rc=937456.59 m,垂直基线的总长度B⊥=398.61 m,可知层析向瑞利分辨率[2]${\rho _s} = \frac{{\lambda {R_c}}}{{2{B_ \bot }\sin {\theta _c}}} \approx$ 116.39 m非常低。超精细波束数据的斜距向分辨率采样间隔ΔR=2.66 m,相应层析向上的距离间隔Δs≈3.92 m,为了分析BCS方法和CS方法在层析向超分辨率性能及两者的对比情况,层析向采样间隔以δs=1.0 m远小于层析向瑞利分辨率ρs≈116.39 m进行采样,即同一方位向-斜距向分辨单元中每个层析向上的散射目标将有4个1 m间隔的的散射点,相应层析向上每个块稀疏的子块长度b为4,并假定同一块稀疏数中散射点的反射能量相同,γ1=1.0,γ2=0.2,γ3=0.6。
图 6、图 7、图 8选取的是块稀疏数k=1,2,3和b=4时两方法重构的散射目标中散射点位置图。从图中可以看出,在块稀疏数k=1,2,3时,BCS方法和CS方法都能清晰分辨出不同散射目标中4个1 m间隔的散射点,这充分展现了两种方法具有相同的超分辨性能,但两种方法在虚假散射目标的出现概率和散射目标中散射点位置的准确重构概率方面表现出较大差别。在块稀疏数k=1,2时,BCS方法和CS方法都没有虚假散射目标,但CS方法在每个散射目标的周边多出1~2错误散射点,而BCS方法完整地恢复原始信号;在块稀疏数k=3时,BCS方法和CS算法都有虚假散射目标出现并没有完整地恢复原始信号,但CS方法虚假散射目标出现数明显远大于BCS方法且每个散射目标的周边都有增多的错误散射点。
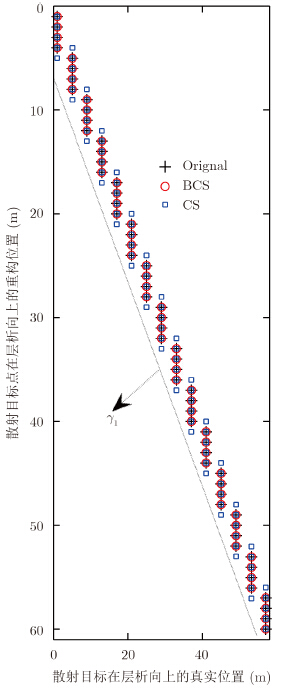 | 图 6 k=1、b=4时散射点的重构位置Fig.6 Reconstruction position of scattering point using k=1、b=4 |
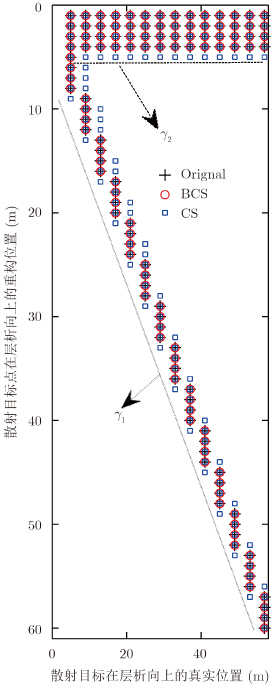 | 图 7 k=2、b=4时散射点的重构位置Fig.7 Reconstruction position of scattering point using k=2、b=4 |
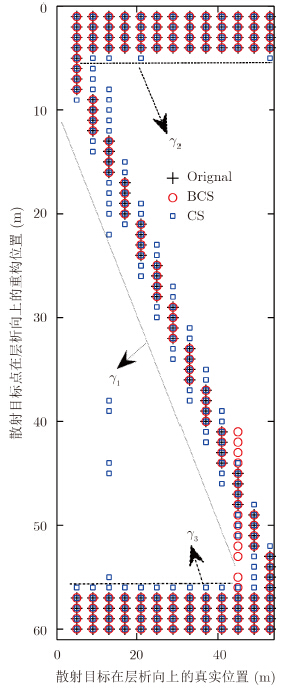 | 图 8 k=3、b=4时散射点的重构位置Fig.8 Reconstruction position of scattering point using k=3、b=4 |
保持4.1节仿真参数不变,层析向采样间隔δs以3.0 m,2.0 m,1.5 m,1.0 m,0.5 m,0.25 m进行采样对应子块长度b=1,2,3,4,8,16,分析块稀疏数k=1,2,3不同情况下不同子块长度时虚假散射目标的出现概率和散射目标中散射点位置的准确重构概率。结果如图 9和图 10所示。从图中可以看出,随着块稀疏数的增加,两种方法的虚假散射目标的出现概率都相应增加且散射点位置的准确重构率减小,但CS方法在子块长度b大于3时开始出现虚假散射目标且准确重构率已小于0.5、b大于8时虚假散射目标出现概率已大于0.1且准确重构率已衰减到0,而BCS方法在子块长度b大于4开始出现虚假散射目标且最大虚假散射目标出现概率不大于0.1、准确重构率也开始衰减但其最小值仍大于0.5。这一结果表明,BCS方法的性能明显优于CS方法。
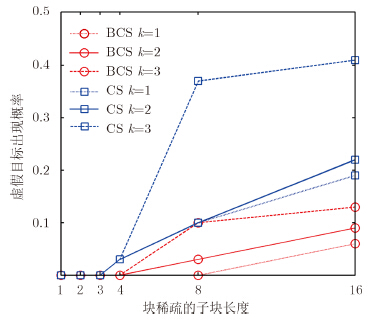 | 图 9 不同k, b时虚假散射目标出现概率Fig.9 Probability of false scattering target using different k and b |
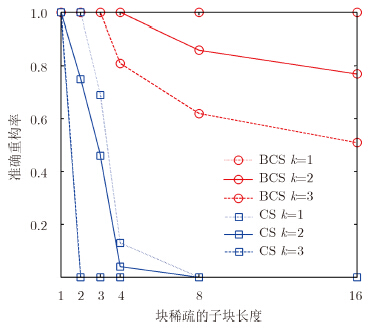 | 图 10 不同k, b时散射点准确重构率Fig.10 Reconstruction accurate of scattering point using different k and b |
保持4.1节仿真参数不变,块稀疏数k=2,其散射点的反射能量一块为γ1=1.0,另一块取γ2=0.2γ1,γ2=0.4γ1,γ2=0.6γ1,γ2=0.8γ1,γ2=1.0γ1 5组。对比不同反射能量情况下不同子块长度时虚假散射目标的出现概率和散射目标中散射点位置的准确重构概率。结果如图 11和图 12所示。从图中可以看出,随着反射能量的增加,BCS方法和CS方法在不同子块长度下的虚假散射目标的出现概率都有所增加且散射点位置的准确重构率也有减小,然而CS方法虚假散射目标出现概率明显高于BCS方法 ,且CS方法的散射点准确重构率远远小于BCS方法。
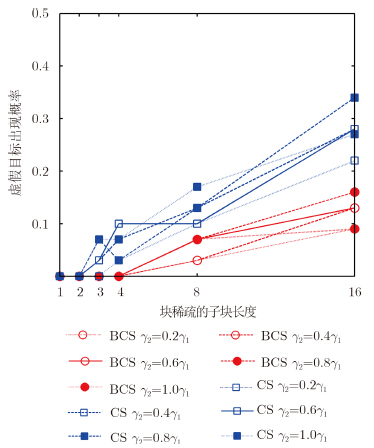 | 图 11 不同γ时虚假散射目标出现概率Fig.11 Probability of false scattering target using different γ |
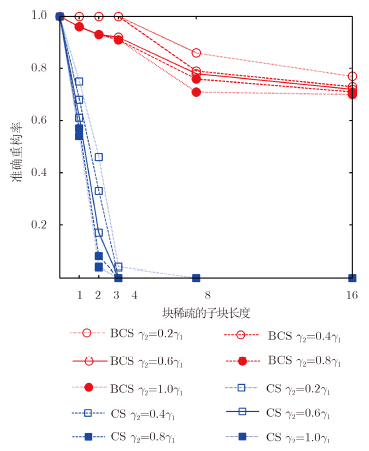 | 图 12 不同γ时散射点准确重构率Fig.12 Reconstruction accurate of scattering point using different γ |
以上仿真数据已充分说明了本文采用BCS算法的优越性,下面将利用实测数据验证算法的可行性。依据4.1节的分析,目标建筑物的BCS-TomoSAR成像处理中块稀疏的子块长度选择为b=4,此时虚假散射目标的出现概率小于0.1、散射目标中散射点位置的准确重构概率大于0.85,可以保证反演的准确度。在BCS-TomoSAR成像处理完成后,将层析向距离已根据雷达入射角转换为高度向上垂直于地面的绝对高度,对目标建筑物外立面散射体的点云信息进行3维重建,可获得目标建筑物的3维模型,图 13给出了雷达视线方向的教学楼外立面散射点高程分布图,虽然受到环境及噪声等因素的影响,但信号重建结果仍然比较理想,参照图 14建筑物外立面的照片,从图 13外立面散射点高程分布图可以清晰看出目标建筑物的整体轮廓以及窗户、过道等细节特征;再结合试验区的幅度影像图像进行分析,选取位于建筑物顶部的多个散射点,剔除粗大误差后估算得到建筑高度为19.3 m,该估计值与建筑物总体高度20 m非常接近。
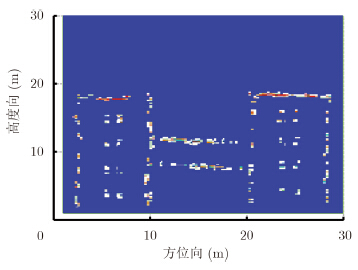 | 图 13 雷达视线方向的建筑物外立面散射点高程分布图Fig.13 Elevation distribution of scattering point for building facade in the LOS direction |
 | 图 14 建筑物外立面的照片Fig.14 Corresponding photo of building facade |
针对基于压缩感知的TomoSAR成像方法,对具有结构特性的散射目标重构时无法保证准确重构率的不足,本文从散射目标信号的稀疏性和结构特性出发,提出了采用块压缩感知的TomoSAR成像方法。在利用实测数据系统参数进行的仿真实验中,通过块稀疏设置和反射能量的变化对两种方法的性能进行了详细对比分析,结果表明相比压缩感知方法,本文所采用的块压缩感知方法不仅可以降低虚假目标出现概率,而且大大提高散射点准确重构概率。在利用Radarsat-2实测数据对淮南联合大学教学楼的TomoSAR成像中,本文方法得到了较好的结果,获得了建筑物的整体结构和细节特征,实现了高度向精度的准确估计。
| [1] | Knaell K and Cardillo G P. Radar tomography for the generation of three-dimensional images[J]. IEEE Proceedings-Radar, Sonar and Navigation, 1995, 142(2): 54-60.( 2) 2) |
| [2] | Reigber A and Moreira A. First demonstration of airborne SAR Tomography using multibaseline L-band data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(9): 2142-2152.( 3) 3) |
| [3] | She Z, Gray D A, Bogner R E, et al. Three-dimensional space-borne Synthetic Aperture Radar (SAR) imaging with multiple pass processing[J]. International Journal of Remote Sensing, 2002, 23(20): 4357-4382.( 2) 2) |
| [4] | Gini F and Lombardini F. Multilook APES for multibaseline SAR interferometry[J]. IEEE Transactions on Signal Processing, 2002, 50(7): 1800-1803.( 2) 2) |
| [5] | Lombardini F and Reigber A. Adaptive spectral estimation for multibaseline SAR Tomography with airborne L-band data[C]. 2003 IEEE International Geoscience and Remote Sensing Symposium IGARSS'03, Toulouse, France, 2003, 3: 2014-2016.( 2) 2) |
| [6] | Fornaro G, Serafino F, and Soldovieri F. Three dimensional focusing with multipass SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(4): 507-517.( 2) 2) |
| [7] | Fornaro G, Lombardini F, and Serafino F. Three-dimensional focusing multipass SAR focusing: experiments with long-term spaceborne data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4) : 702-714.( 2) 2) |
| [8] | Frey O and Meier E. 3-D time-domain SAR imaging of a forest using airborne multibaseline data at L- and P-Bands[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3660-3664.( 2) 2) |
| [9] | 任笑真, 杨汝良. 利用FB-MAPES算法估计Tomography SAR高度维信号源数[J]. 电子与信息学报, 2009, 31(7): 1669-1673. Ren Xiao-zhen and Yang Ru-liang. On detection of number of Tomogaphy SAR signals in the elevation direction using the FB-MAPES method[J]. Journal of Electronics & Information Technology, 2009, 31(7): 1669-1673.( 1) 1) |
| [10] | 吴一戎, 洪文, 张冰尘, 等. 稀疏微波成像研究进展[J]. 雷达学报, 2014, 3(4): 384-395. Wu Yi-rong, Hong Wen, Zhang Bing-chen, et al. Current development of sparse microwave imaging[J]. Journal of Radars, 2014, 3(4): 384-395.( 1) 1) |
| [11] | Zhu X X and Bamler R. Tomographic SAR inversion by L1-Norm regularization—The compressive sensing approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3839-3846.( 1) 1) |
| [12] | Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.( 2) 2) |
| [13] | Zhu X X and Bamler R. Super-resolution power and robustness of compressive sensing for spectral estimation with application to spaceborne Tomographic SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 247-258.( 1) 1) |
| [14] | Zhu X X and Bamler R. Superresolving SAR Tomography for multidimensional imaging of urban areas: compressive sensing-based TomoSAR inversion[J]. IEEE Signal Processing Magazine, 2014, 31(4): 51-58.( 1) 1) |
| [15] | 李烈辰, 李道京. 基于压缩感知的连续场景稀疏阵列SAR三维成像[J]. 电子与信息学报, 2014, 36(9): 2166-2172. Li Lie-chen and Li Dao-jing. Sparse array 3D imaging for continuous scene based on compressed sensing[J]. Journal of Electronics & Information Technology, 2014, 36(9): 2166-2172. DOI: 10.3724/SP.J.1146.2013.01645.( 1) 1) |
| [16] | 张冰尘, 王万影, 毕辉, 等. 基于压缩多信号分类算法的森林区域极化SAR层析成像[J]. 电子与信息学报, 2015, 37(3): 625-630. Zhang Bing-chen, Wang Wan-ying, Bi Hui, et al. Polarimetric SAR tomography for forested areas based on compressive multiple signal classification[J]. Journal of Electronics & Information Technology, 2015, 37(3): 625-630.( 1) 1) |
| [17] | 廖明生, 魏恋欢, 汪紫芸, 等. 压缩感知在城区高分辨率SAR层析成像中的应用[J]. 雷达学报, 2015, 4(2): 124-129. Liao Ming-sheng, Wei Lian-huan, Wang Zi-yun, et al. Compressive sensing in high-resolution 3D SAR Tomography of urban scenarios[J]. Journal of Radars, 2015, 4(2): 124-129.( 1) 1) |
| [18] | Baraniuk R G, Gevher V, Duarte M F, et al. Model-based compressive sensing[J]. IEEE Transactions on Information Theory, 2010, 56(4): 1982-2001.( 2) 2) |
| [19] | 孙洪, 张智林, 余磊. 从稀疏到结构化稀疏: 贝叶斯方法[J]. 信号处理, 2012, 28(6): 759-773. Sun Hong, Zhang Zhi-lin, and Yu Lei. From sparsity to structured sparsity: bayesian perspective[J]. Signal Processing, 2012, 28(6): 759-773.( 2) 2) |
| [20] | 李廉林, 周小阳, 崔铁军. 结构化信号处理理论和方法的研究进展[J]. 雷达学报, 2015, 4(5): 491-502. Li Lian-lin, Zhou Xiao-yang, and Cui Tie-jun. Perspectives on theories and methods of structural signal processing[J]. Journal of Radars, 2015, 4(5): 491-502.( 2) 2) |
| [21] | Shervashidze N and Bach F. Learning the structure for structured sparsity[J]. IEEE Transactions on Signal Processing, 2015, 63(18): 4894-4902.( 2) 2) |
| [22] | Candès E, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.( 2) 2) |
| [23] | Candès E, Romberg J, and Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communication on Pure and Applied Mathematics, 2006, 59(8): 1207-1223.( 2) 2) |
| [24] | Eldar Y C and Mishali M. Robust recovery of signals from a structured union of subspaces[J]. IEEE Transactions on Information Theory, 2009, 55(11): 5302-5316.( 1) 1) |
| [25] | Eldar Y C, Kuppinger P, and Bolcskei H. Block-sparse signals: uncertainty relations and efficient recovery[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 3042-3054.( 1) 1) |
| [26] | Fu Y, Li H, Zhang Q, et al. Block-sparse recovery via redundant block OMP[J]. Signal Processing, 2014, 97(7): 162-171.( 1) 1) |


