由于受到星下点回波和发射脉冲遮挡的制约关系,星载SAR系统往往需要在方位模糊能量和距离向观测幅宽之间寻找平衡。经典SAR方位分辨理论指出:若期望提高方位向空间分辨力,则需扩大方位向获取信号的带宽;而奈奎斯特采样定律则限制了无模糊采样的最小间隔,该时间间隔直接关系到SAR系统的占空比、间接决定了距离向的观测幅宽。受到加工能力的限制,雷达天线系统无法生成理想矩形的方向图。因此,方位向多普勒信号实际上是带宽无限的,方位模糊存在于一切的SAR系统中。对于星载SAR系统,由于波位设计冗余较小,只能保证波束主瓣内的能量不发生混叠,而其余部分的能量则会形成“鬼影”在真实目标两侧成对出现,造成图像质量明显下降。
针对以上问题,现有文献从系统和处理两个方面提出解决方案。系统方面,可以通过增大脉冲重复频率(PRF)[1]或采用多接收相位中心技术[2],提高方位采样率、压低模糊能量。但这两种方法前者损失观测幅宽且抑制效果有限,后者需要对硬件系统进行大幅改变,因此多数文献中还是更加倾向在处理上抑制方位模糊。针对理想点目标,Moreira在文献[3]中使用理想滤波器抑制模糊能量,Wang等人提出通过精确计算方位模糊出现的位置和能量,在图像中直接去除模糊能量[4],但以上方法无法处理真实场景和复杂目标,且需要极为精确的雷达参数进行演算;Guarnieri和Martino在文献[5, 6]中利用方位模糊信号在多普勒频谱上的非均匀性,通过筛选模糊地图和构建选择滤波器的方法抑制模糊能量,由于进行了谱加权,受到处理的区域会损失分辨率、图像一致性也受到破坏,所以该类方法依然只适用于背景简单的海面场景;Chen等人在寻找模糊地图的基础上,提出综合使用小波反演和图像修补算法(Inpainting)替代选择滤波器对模糊区域进行处理[7],虽然该方法获得的图像一致性较好,但无法反映大片受模糊掩盖目标的真实情况,因此一样无法用于复杂场景下的模糊抑制。
近年来所提出的压缩感知方法[6, 7]对以上问题的解决提供了一种全新的思路。该方法将最优化方程替代传统匹配滤波作为雷达信号核心处理手段,充分利用场景的先验信息,使用更少的数据获得更好的处理结果[8, 9, 10, 11, 12]。利用压缩感知恢复算法的优势,本文提出一种针对SAR图像的方位模糊抑制方法:通过对复图像多普勒频率的截断,分离真实目标能量和方位模糊能量,而后利用压缩感知恢复算法从低维的谱数据中反演高维度的高分辨率图像。该方法只针对SAR复数图像进行处理,无需精确的成像参数作为参考,且无论对简单场景还是复杂场景均有显著效果。
文中第2节将简要介绍方位模糊现象的成因和多普勒谱特性,第3节提出方位模糊抑制方法,第4节给出实验结果。经过仿真和真实数据验证,该方法可以将方位模糊能量压低8 dB以上,并保证图像分辨率没有明显损失。
2 方位模糊的成因及其谱特性 2.1 方位模糊的成因当不受到加权影响时,天线单程方向图可以近似视为一个与角度θ相关的sinc函数
| \[G\left( \theta \right) = \sin {\rm{c}}\left( {\frac{{{L_a}}}{\lambda }\theta } \right)\] | (1) |
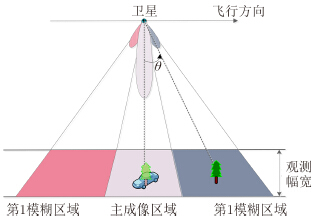 | 图 1 方位向天线方向图 Fig.1 Antenna pattern along azimuth |
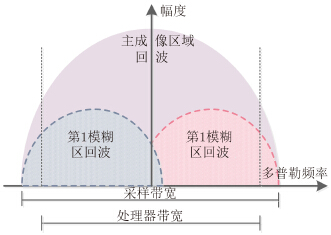 | 图 2 多普勒频谱卷绕示意图 Fig.2 Doppler spectrum winding |
在SAR系统中,经常使用方位模糊度(Azimuth Ambiguity-to-Signal Ratio,AASR)来衡量某一特定参数下的方位模糊情况[1]
| \[{\rm{AASR}} \approx \frac{{\sum\limits_{\begin{array}{*{20}{c}} {m = - \infty }\\ {m \ne 0} \end{array}}^\infty {\int_{ - B/2}^{B/2} {{G^2}\left( {f + m{B_a}} \right){\rm{d}}f} } }}{{\int_{ - B/2}^{B/2} {{G^2}\left( f \right){\rm{d}}f} }}\] | (2) |
受到回波时延的影响,经过1维距离脉冲压缩后的回波信号,其距离徙动呈现出抛物线特性。经过距离徙动矫正后,主区徙动线被完全拉直,而卷绕进主区的模糊区徙动线则是倾斜的,倾斜的徙动线会导致成像结果出现距离向弥散和方位向散焦(如图 3所示)。当载波波长较小时,其合成孔径时间内较短,模糊区徙动线与主区徙动线相似度高、聚焦效果好,因此X波段图像中的模糊现象要强于C波段或L波段。
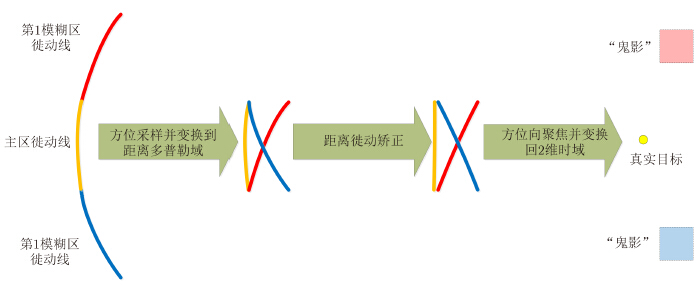 | 图 3 方位模糊聚焦示意图 Fig.3 Azimuth ambiguities focus processing |
以此为基础,分析SAR成像结果在距离多普勒域中的特性。由于主区目标的徙动线得到了矫正,一个距离向分辨单元内的目标能量均集中在一个距离门中,该1维信号的自相关性极强;而模糊目标的谱线是倾斜的,跨越了数个距离门,因此在某一距离门上模糊信号自相关性较弱(如图 4)。
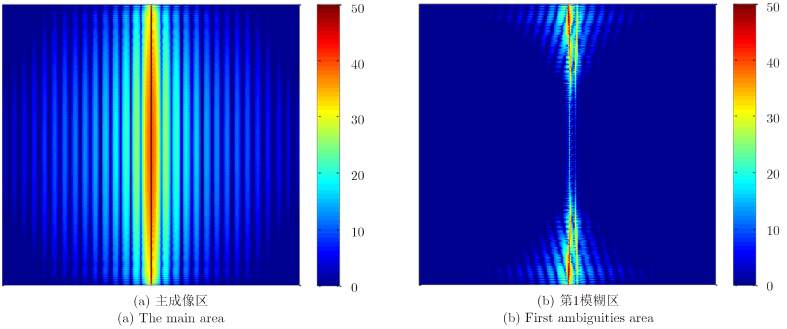 | 图 4 理想点目标距离多普勒域能量分布示意图(dB) Fig.4 Energy distribution of point target in Range Doppler domain (dB) |
由于模糊能量往往集中分布在多普勒频谱的两端,利用模糊谱相关性低的特点,可以通过简单的谱加权来压低方位模糊能量,或通过谱加权前后图像的能量分布差异筛选出模糊能量较大的区域[5]。但该种方法同时也改变了主区目标的谱形状,会干扰到真实目标的成像结果,最直接的影响就是被模糊覆盖的区域分辨率大幅下降。
3 基于压缩感知算法的抑制方法 3.1 压缩感知框架压缩感知恢复算法是一种基于矩阵模型下的最优化估计方法。其充分利用恢复目标的先验信息,从较低维观测结果中恢复出高维的信号信息。可使用矩阵方程将其描述为:
| \[\begin{array}{l} {y_{M \times 1}} = {\Phi _{M \times N}}{\psi _{N \times N}}{x_{N \times 1}} + {n_{M \times 1}}\\ \quad \quad = {A_{M \times N}}{x_{N \times 1}} + {n_{M \times 1}} \end{array}\] | (3) |
| \[\hat x = \min \left\| {y - Ax} \right\|_2^2 + \beta \left\| x \right\|_a^a\] | (4) |
式(4)不具备显式解,可以使用Newton迭代法获得近似解[13]
| \[{\hat x_{n + 1}} = {\left[{{A^{\rm{H}}}A + \beta {\rm{diag}}\left( {{{\left| {{{\hat x}_n}} \right|}^{2 - a}}} \right)} \right]^{ - 1}}{A^{\rm{H}}}y\] | (5) |
| \[\frac{{\left\| {{{\hat x}_{n + 1}} - {{\hat x}_n}} \right\|_2^2}}{{\left\| {{{\hat x}_n}} \right\|_2^2}} \le \varepsilon \] | (6) |
若将某一距离门上复图像时域信号视作x,用矩阵Ψ实现傅里叶变换,Φ作为截断矩阵,则y就是截断后的多普勒频谱。由第2节的结论可知,通过对多普勒频谱的截断可以有效抑制方位模糊能量,但同时需要付出分辨率恶化的代价。由于主区、模糊区信号的相关性不同,若由低维度的截断谱信号y恢复高维度、高分辨率的图像${\hat {x}}$,则恢复结果中将包含大量主区信息而模糊区能量则较低。从而在不损失分辨率的条件下实现主区能量和模糊区能量的分离(如图 5)。
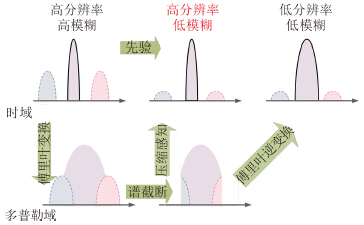 | 图 5 压缩感知方位模糊抑制方法流程图 Fig.5 The azimuth ambiguity suppression process flow chart based on CS |
与超分辨理论所不同的是:由于我们已经获取掺杂了模糊能量的高分辨率图像作为先验信息${\hat {x}}_0$,在该条件下从截断谱中恢复高分辨率的图像,恢复向量的自由度变得更低,恢复过程更加稳健、快速,图像质量可以得到保证。
4 实验结果 4.1 1维仿真实验结果本文中使用如表 1所示的参数进行方位向1维回波信号的仿真与处理,在成像中心区域布置一理想点目标,在远离成像主区处布置一产生模糊的点目标,其“鬼影”出现在成像中心区域附近,调整两个目标的强度,使得模糊峰值能量与真实目标峰值能量相当。在处理过程中,选择在多普勒谱±30 Hz处截断带宽,保留低频部分。根据式(5)得到的处理结果如图 6所示,经过评估真实目标处没有明显分辨率损失,而方位模糊峰值处的能量被抑制了13 dB。
| 表 1 1维仿真参数 Tab. 1 One-dimensional simulation parameters |
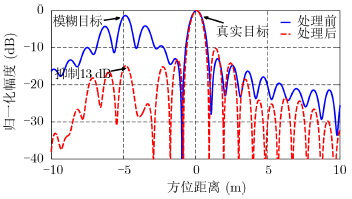 | 图 6 1维信号处理结果 Fig.6 One-dimensional result |
文中使用模糊能量比和图像相关系数作为评价标准,前者反映模糊能量抑制能力,后者反映非模糊目标保持能力,两个指标分别定义为:
| \[S = \frac{{\overline {\hat I} }}{{\bar I\;}}\] | (7) |
| \[r = \frac{{\sum\limits_m {\sum\limits_n {\left( {{I_{mn}} - \bar I} \right)\left( {{{\hat I}_{mn}} - \overline {\hat I} } \right)} } }}{{\sqrt {\sum\limits_m {\sum\limits_n {{{\left( {{I_{mn}} - \bar I} \right)}^2}} \sum\limits_m {\sum\limits_n {{{\left( {{{\hat I}_{mn}} - \overline {\hat I} } \right)}^2}} } } } }}\] | (8) |
本文首先采用TerraSAR-X条带模式数据进行验证,其具体成像参数如表 2所示,该地区为上海市长江入海口附近。
| 表 2 TerraSAR-X条带模式数据相关参数 Tab. 2 Stripmap mode parameters of TerraSAR-X |
从图 7(a)可见,河道中出现了极为严重的方位模糊现象,干扰到对河道中轮船的识别。其中图 7(d)所示模糊地图为使用选择滤波器[5]所筛选出来的强模糊区域位置,通过修改图层的方法将其标红,可见模糊区与有效主区图像出现部分重叠。使用本文方法对该数据进行处理,可以得到非常“干净”的图像。对处理前后图像中的模糊能量进行评估,发现模糊较强的区域能量下降了约16 dB,较弱的区域也抑制了13 dB;选择没有受到模糊影响的轮船目标进行相关性计算,处理前后该目标相关系数达到0.99。
 | 图 7 TerraSAR-X条带模式数据验证 Fig.7 Experiments based on stripmap mode data of TerraSAR-X |
选择TerraSAR-X滑动聚束模式的图像进行第2组实验,其具体成像参数如表 3所示,该照射区域为天津市水上公园附近处,处理结果如图 8所示。
| 表 3 TerraSAR-X滑动聚束模式数据相关参数 Tab. 3 Spotlight mode parameters of TerraSAR-X |
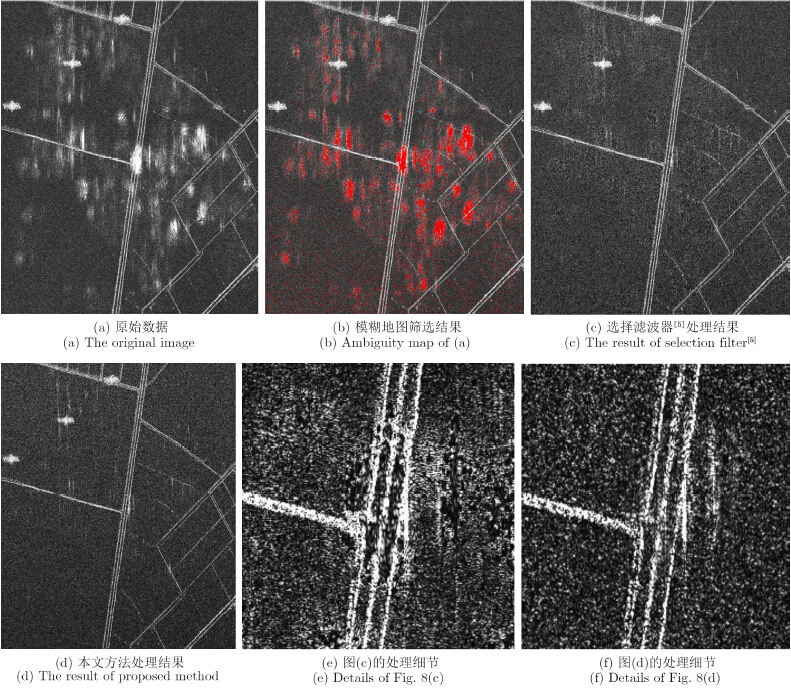 | 图 8 TerraSAR-X滑动聚束模式处理结果 Fig.8 Experiments based on spotlight mode data of TerraSAR-X |
相较于第1幅图像该区域背景更为复杂,模糊区域与主区出现大量重叠,且由于使用滑动聚束模式进行观测,生成该模糊能量的场景并未出现在图像中。使用选择滤波器依然可以搜索到强模糊出现的区域,但是由于受到背景的干扰,该地图的筛选并不完全正确。对比不同处理方法结果中被模糊能量覆盖的道路,选择滤波器使得路的边缘变得模糊不清,而本文的方法依然可以得到较为清晰的图像。比较处理前后的结果,较强模糊区域能量减弱20 dB,较弱模糊区域能量减弱8.5 dB;没有受到模糊干扰的强目标相关系数为0.96。
两次实验结果统计如表 4所示。从处理结果中可见,经过本文方法处理过的图像方位模糊得到了非常好的抑制、主区目标没有明显改变,且图像一致性比文献[5]中所用方法更好。
| 表 4 TerraSAR-X数据实验结果 Tab. 4 Comparison results based on TerraSAR-X |
本文介绍了一种基于压缩感知恢复算法的方位模糊抑制方法,通过对频谱的截断实现了主区与模糊区目标能量分离,使用最优化方法恢复低模糊、高分辨率的图像。经过1维仿真和真实数据验证,证明该方法可以在有效保持主区目标分辨率的前提下,有效抑制方位模糊能量,具有较好的稳定性和适用性。
频谱的截断位置与处理效果有很重要的关系,谱截断过少模糊能量抑制效果不好,截断过大则恢复过程变得不稳定;对于非对称模糊(左右模糊不同时出现),截断的中心位置也需要调整才能获得更好的结果。本文中我们只能根据谱形状初步估计谱截断的位置,并逐步尝试不同参数下的处理效果,这种方法效率较低且并不是最优策略。我们下一步的工作方向,一是分析如何根据雷达系统参数和预估的AASR设计谱截断策略,二是探讨能否使用更优的恢复算法对场景进行重建。
| [1] | Curlander J C and Mcdonough R N著. 韩传钊, 等译. 合成孔径雷达: 系统与信号处理[M]. 北京: 电子工业出版社, 2006: 205-214.Curlander J C, Mcdonough R N, Han C Z, et al. Synthetic Aperture Radar: Systems and Signal Processing[M]. Beijing: Electronic Industry Press, 2006: 205-214.( 2) 2) |
| [2] | Runge H, Laux C, Gabele M, et al. Performance analysis of virtual multi-channel modes for TerraSAR-X[C]. EUSAR, 2006: 1-4.( 1) 1) |
| [3] | Moreira A. Suppressing the azimuth ambiguities in synthetic aperture radar images[J]. IEEE Transactions on Geoscience and Remote Sensing, 1993, 31(4): 885-895.( 1) 1) |
| [4] | Wang K, Chen J, Yang W, et al. Suppression of azimuth ambiguities in spaceborne stripmap SAR using accurate restoration modeling[C]. 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2015), Milan Italy, 2015: 2429-2432.( 1) 1) |
| [5] | Guarnieri A M. Adaptive removal of azimuth ambiguities in SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(3): 625-633.( 4) 4) |
| [6] | Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.( 2) 2) |
| [7] | Candè E J and Wakin M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30.( 2) 2) |
| [8] | Di Martino G, Iodice A, Riccio D, et al. Filtering of azimuth ambiguity in stripmap synthetic aperture radar images[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(9): 3967-3978.( 1) 1) |
| [9] | Chen J, Iqbal M, Yang W, et al. Mitigation of azimuth ambiguities in spaceborne stripmap SAR images using selective restoration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(7): 4038-4045.( 1) 1) |
| [10] | 吴一戎, 洪文, 张冰尘, 等. 稀疏微波成像研究进展(科普类)[J]. 雷达学报, 2014, 3(4): 383-395.Wu Yirong, Hong Wen, Zhang Bingchen, et al. Current developments of sparse microwave imaging[J]. Journal of Radars, 2014, 3(4): 383-395.( 1) 1) |
| [11] | Zhang B C, Hong W, and Wu Y R. Sparse microwave imaging: principles and applications[J]. SCIENCE CHINA Information Sciences, 2012, 55(8): 1722-1754.( 1) 1) |
| [12] | Ender J H G. On compressive sensing applied to radar[J]. Signal Processing, 2010, 90(5): 1402-1414.( 1) 1) |
| [13] | Cetin M. Feature-enhanced synthetic aperture radar imaging[D]. [博士论文], University of Salford, Manchester, 2001.( 1) 1) |


