1 引言

极化合成孔径雷达(Polarimetric Synthetic Aperture Radar,PolSAR)具备合成孔径雷达的全天时全天候工作能力，并且它发射的极化电磁波与观测目标相互作用后返回，回波中包含了发射与接收极化状态的各种组合。这些极化组合信息是目标极化散射机制的一种表现形式。极化散射机制包含丰富的内容，能够反映目标的几何结构、分布方向、介电特性等；但它本身非常复杂，于是人们运用各种方法从极化组合信息中提取极化特征，试图描述和解释目标的极化散射机制。具体到极化SAR数据分类应用时，地物类型不同，极化散射机制也不同，极化特征就会有差异；运用极化特征的差异，可实现不同地物的分类。

根据极化特征的使用方式不同，将极化SAR数据分类的方法划为两大类。第1类是直接将极化特征对应地物类别，即运用极化特征描述地物的极化散射机制，同时赋予类别。主要采用模型归纳或者经验阈值划分，最早由van Zyl^[1]提出，将地物归纳为奇次散射类、偶次散射类、漫散射类及不确定类共4种模型与地物类别。后来，Cloude和Pottier^[2]提出了采用矩阵特征值分解的极化特征提取方法，进而将极化特征H,α构成的特征平面用经验阈值划分为8个区域，并为每个区域赋予地物类别。由于H-α平面的区域阈值是硬性划定的，Lee等人^[3]采用Wishart统计特性对H-α分类结果进行优化。随后，Pottier和Lee^[4]引入了极化特征A将该方法的类别数增加至16类。相似的思路下，Lee等人^[5]发展了基于Freeman-Durden分解的Wishart距离合并算法，将3种极化分解模型及其地物类别与Wishart统计优化相结合。第2类是将极化特征作为机器学习的输入。在机器学习中，将输入的、用于分类的测量值称为特征。对已知类别标记的样本提取极化特征的数值，输入分类器中进行学习，得到相应的分类规则，再将规则应用于未分类的样本即可预测类别，得到分类结果。经典的机器学习方法^[6]包括，神经网络及模糊神经网络，支持向量机，AdaBoost，随机森林，马尔可夫随机场及条件随机场等。

第1类方法能够为地物提供极化散射机制的解释，利于我们得到关于地物更深刻的物理层面的认识；然而由于类别的赋予受经验阈值及固定模型的影响，仅在散射机制差异很大的几类典型地物分类时精度较好。第2类方法在各种地物分类时都获得了较好的分类精度；但在经典的机器学习方法中，极化特征只是作为数值输入，失去了物理意义，甚至在得到的分类规则中已经找不到极化特征的痕迹，更无法描述分类结果的极化散射机制。决策树^[7]属于机器学习的范畴，但它得到的分类规则是嵌入了特征的树形分级结构，能够在分类规则中保留输入特征，简单、可读且便于解释；并且它在赋予类别时，通过学习和归纳已知类别标记的样本，灵活地采用模型、适应性地调节阈值。因此，采用决策树分类极化SAR数据，既能描述分类结果的极化散射机制，又能在非典型地物的分类应用中也获得较好的分类精度^[8]。然而，现有决策树方法在节点上使用的是单个特征，当地物的极化散射机制非常相似时(例如多种植被)，分类精度显出了不足。

本文分析了决策树模型和“纯度”的概念，介绍了可以用于决策树的极化特征，并将由2个极化特征组成的2维特征矢量引入决策树节点，建立了适用于2维特征矢量的决策树分支准则和分支停止准则，从而解决了节点采用单个极化特征导致相似地物分类精度不足的问题。利用AIRSAR-Flevoland数据实验，验证了在特征集相同时，本方法的分类精度优于经典决策树，提高了相似地物的分类精度；并且利用分类结果的混淆矩阵定位了导致分类误差的节点，对指定地物的分类精度进行了反馈调整；在对实验结果的分析过程中，利用极化特征描述了Flevoland地区多种植被的极化散射机制。

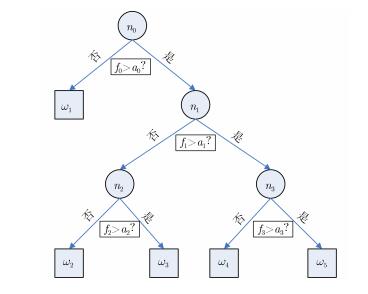
2 算法原理 2.1 决策树模型

决策树^[7]是描述对象属性与对象值之间映射关系的一种树形预测模型，具有可读性，有助于人工分析和解释；分为名称型和数字型两类，数据分类属于数字型。如图 1所示，n_i是节点，表示一种属性，数字型决策树的节点必须具备的要素是特征f_i和阈值a_i，从而继续分支得到新的节点(或属性) n_i+1; w_i 是叶子，表示一个类，不再继续分支。全部节点特征f_i(i=1,2,···,m)构成特征集F={f₁ ,f₂ ,···,f_m}。

对某个样本进行决策树分类时，从根节点n₀开始，对样本的f₀特征进行测试，根据测试结果f₀>a₀，将样本分配到其子节点n₁，依次递归进行测试和分配，直到叶子。而在决策树的训练和建树分支操作中，有一个重要的概念是“纯度”，其含义为，若节点所包含的全部样本均为同种类别标记，则称该节点是“纯”的，决策树的分支操作也就结束了，节点变为叶子；“纯度”的度量方法有很多，例如采用熵、方差、分类错误概率等形式^[7]。现有的决策树建树算法包括ID3、C4.5与CART等^[7]，采用的思想是一致的，也就是使分支操作所带来的“纯度”增益最大；而它们的节点采用的都是单个特征。具体来说，分支操作前，节点n_i的单个特征f_i及其相应阈值a_i均未知。此时需要一一考察特征集F中的每一个特征f_k(k=1,2,···,m)；测量当前节点所包含的全部样本的f_k特征值，遍历所有相邻两数值的中间值，作为f_k的候选阈值待定；而单个特征f_i及其相应阈值a_i的最终确定遵从的是“纯度”增益最大原则。f_i和a_i的确定，标志着节点n_i分支操作的完成。对于整棵树来说，需要设置“纯度”增益门限来停止分支，以及采用多数规则来判断叶子的最终所属类别。因此，这些算法的分支停止需要依赖门限值，并且会出现过拟合，需要剪枝算法^[7]来提升推广性。

2.2 用于决策树的极化特征

所有数值形式的、能够反映不同地物之间差异的极化特征都可以用于上述决策树模型。极化SAR数据分类时，对接收到的极化组合信息进行参数化、模型化等处理，可以提取出数值形式的信息，也就是极化特征^[9]；通常它们能够反映同类地物的共性和不同地物之间的差异，因此可以引入决策树作为节点的特征。在全极化观测模式下，常用水平(H)-垂直(V)极化收发方式，此时，包含观测目标影响的散射过程表示为：

$ {\boldsymbol{E}_{\rm{S}}} = \frac{{{{\rm{e}}^{ - {\rm{j}}kr}}}}{r}\left[{\begin{array}{*{20}{c}} {{S_{{\rm{HH}}}}}&{{S_{{\rm{HV}}}}}\\ {{S_{{\rm{VH}}}}}&{{S_{{\rm{VV}}}}} \end{array}} \right]{\boldsymbol{E}_{\rm{I}}} $

(1)

其中，E_I和E_S分别是入射电磁波和散射电磁波的琼斯矢量，r是散射体与接收天线之间的距离，k是波数。于是得到了Sinclair极化后向散射矩阵S,S_HH和S_VV称为同极化散射系数，S_HV和S_VH称为交叉极化散射系数；由于互易性理论，S_HV=S_VH，散射矩阵简化为：

$ S = \left[{\begin{array}{*{20}{c}} {{\boldsymbol{S}_{{\rm{HH}}}}}&{{S_{{\rm{HV}}}}}\\ {{S_{{\rm{HV}}}}}&{{S_{{\rm{VV}}}}} \end{array}} \right] $

(2)

对散射矩阵进行圆极化基变换就得到了圆极化分量，即右-右圆极化(RR)、左-左圆极化(LL)以及右-左圆极化(RL)分量，通常变换到其他极化基之后会得到更多样化的信息。

$ \begin{array}{l} \left. \begin{array}{l} {S_{{\rm{RR}}}} = \left( {{S_{{\rm{HH}}}} - {S_{{\rm{VV}}}} + i2{S_{{\rm{HV}}}}} \right)/2\\ {S_{{\rm{LL}}}} = \left( {{S_{{\rm{VV}}}} - {S_{{\rm{HH}}}} + i2{S_{{\rm{HV}}}}} \right)/2\\ {S_{{\rm{RL}}}} = i\left( {{S_{{\rm{HH}}}} + {S_{{\rm{VV}}}}} \right)/2 \end{array} \right\} \end{array} $

(3)

自然地物属于分布式目标，具有随机性，常用2阶统计量来分析描述。极化协方差矩阵C₃与极化相干矩阵T₃都是散射矩阵S的2阶统计量形式。

$ {\boldsymbol{C}_3} = \left[{\begin{array}{*{20}{c}} {\langle |{S_{{\rm{HH}}}}{|^2}\rangle }&{\sqrt 2 \langle {S_{{\rm{HH}}}}S_{{\rm{HV}}}^*\rangle }&{\langle {S_{{\rm{HH}}}}S_{{\rm{VV}}}^*\rangle }\\ {\sqrt 2 \langle {S_{{\rm{HV}}}}S_{{\rm{HH}}}^*\rangle }&{2\langle |{S_{{\rm{HV}}}}{|^2}\rangle }&{\sqrt 2 \langle {S_{{\rm{HV}}}}S_{{\rm{VV}}}^*\rangle }\\ {\langle {S_{{\rm{VV}}}}S_{{\rm{HH}}}^*\rangle }&{\sqrt 2 \langle {S_{{\rm{VV}}}}S_{{\rm{HV}}}^*\rangle }&{\langle |{S_{{\rm{VV}}}}{|^2}\rangle } \end{array}} \right] $

(4)

$ \begin{array}{l} {{\bf{T}}_3} = \\ \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {\langle |{S_{{\rm{HH}}}} + {S_{{\rm{VV}}}}{|^2}\rangle }&{\langle ({S_{{\rm{HH}}}} + {S_{{\rm{VV}}}}){{({S_{{\rm{HH}}}} - {S_{{\rm{VV}}}})}^*}\rangle }&{2\langle ({S_{{\rm{HH}}}} + {S_{{\rm{VV}}}})S_{{\rm{HV}}}^*\rangle }\\ {\langle ({S_{{\rm{HH}}}} - {S_{{\rm{VV}}}}){{({S_{{\rm{HH}}}} + {S_{{\rm{VV}}}})}^*}\rangle }&{\langle |{S_{{\rm{HH}}}} - {S_{{\rm{VV}}}}{|^2}\rangle }&{2\langle ({S_{{\rm{HH}}}} - {S_{{\rm{VV}}}})S_{{\rm{HV}}}^*\rangle }\\ {2\langle {S_{{\rm{HV}}}}{{({S_{{\rm{HH}}}} + {S_{{\rm{VV}}}})}^*}\rangle }&{2\langle {S_{{\rm{HV}}}}{{({S_{{\rm{HH}}}} - {S_{{\rm{VV}}}})}^*}\rangle }&{4\langle |{S_{{\rm{HV}}}}{|^2}\rangle } \end{array}} \right] \end{array} $

(5)

散射总功率SPAN来自2阶统计量矩阵C₃或T₃的对角元素之和，是反映回波功率的信息，与图像的灰度相联系，是空间信息的重要表征，可用于图像的边缘提取、纹理分析、保留细致结构等。

$ \begin{array}{l} {\rm{SPAN}} = {\rm{Tr}}\left\{ {{\boldsymbol{C}_3}} \right\} = {\rm{Tr}}\left\{ {{\boldsymbol{T}_3}} \right\}\\ \;\;\;\;\;\;\;\;\;\; = \langle |{S_{{\rm{HH}}}}{|^2}\rangle + 2\langle |{S_{{\rm{HV}}}}{|^2}\rangle + \langle |{S_{{\rm{VV}}}}{|^2}\rangle \end{array} $

(6)

Freeman-Durden(F-D) 3分量分解参数是极化协方差矩阵C₃的导出参数，基于3种模型进行极化分解。由于自然地物满足反射对称性假设，C₃矩阵的同极化项与交叉极化项的相关系数为零；f_S代表表面散射模型，f_D代表二面角散射模型，f_V代表体散射模型，a和b是分解参数，运用数值算法可以确定这5个参数。其中，3种模型参数f_S,f_D和f_V是极化分类中的常用特征。

$ \begin{array}{l} {{\bf{C}}_3} = \left[ {\begin{array}{*{20}{c}} {\langle |{S_{{\rm{HH}}}}{|^2}\rangle }&{0}&{\langle {S_{{\rm{HH}}}}S_{{\rm{VV}}}^*\rangle }\\ 0&{\langle 2|{S_{{\rm{HV}}}}{|^2}\rangle }&{0}\\ {\langle {S_{{\rm{VV}}}}S_{{\rm{HH}}}^*\rangle }&{0}&{\langle |{S_{{\rm{VV}}}}{|^2}\rangle } \end{array}} \right]\\ = \left[ {\begin{array}{*{20}{c}} {{f_{\rm{S}}}{{\left| \beta \right|}^2} + {f_{\rm{D}}}{{\left| \alpha \right|}^2} + \frac{{3{f_{\rm{V}}}}}{8}}&{0}&{{f_{\rm{S}}}\beta + {f_{\rm{D}}}\alpha + \frac{{{f_{\rm{V}}}}}{8}}\\ 0&{\frac{{2{f_{\rm{V}}}}}{8}}&{0}\\ {{f_{\rm{S}}}{\beta ^*} + {f_{\rm{D}}}{\alpha ^*} + \frac{{{f_{\rm{V}}}}}{8}}&{0}&{{f_{\rm{S}}} + {f_{\rm{D}}} + \frac{{3{f_{\rm{V}}}}}{8}} \end{array}} \right] \end{array} $

(7)

极化相干矩阵T₃的对角元素可以与圆极化比联系起来。圆极化比CPR定义为右-右圆极化(或左-左圆极化)分量与右-左圆极化分量的比值，即同圆极化与交叉圆极化功率的比值，用来衡量不同通道之间的功率关系，也可以看作是T₃对角元素的组合之比。

$ {\rm{CPR}} = \frac{{\langle |{S_{{\rm{RR}}}}{|^2}\rangle }}{{\langle |{S_{{\rm{RL}}}}{|^2}\rangle }} = \frac{{\langle |{S_{{\rm{HH}}}} - {S_{{\rm{VV}}}}{|^2}\rangle + 4\langle |{S_{{\rm{HV}}}}{|^2}\rangle }}{{\langle |{S_{{\rm{HH}}}} + {S_{{\rm{VV}}}}{|^2}\rangle }} $

(8)

散射角α、极化熵H与极化各向异性度A都是极化相干矩阵T₃的导出参数。矩阵T₃具有特殊的性质，其共轭转置矩阵等于自身，在数学上称为埃尔米特矩阵，这种矩阵进行特征值分解之后所得的特征值为实数。即$ {\boldsymbol{T}_3} = \sum\nolimits_{i = 1}^3 {{\lambda _i}{\boldsymbol{u}_i} \cdot \boldsymbol{u}_i^{{\rm{T}}*}} $，其中实数λ_i(i=1,2,3)表示T₃的特征值；u₁,u₂和u₃分别对应3个正交的单位特征矢量，可以看作是3个互不相关的目标，在散射过程中出现的概率为$ {P_k} = {\lambda _k}/\sum\nolimits_{k = 1}^3 {\lambda _k} $ (k=1,2,3)；将特征矢量参数化，$ {\boldsymbol{u}_i} = [{\rm{cos}}{\alpha _i}{{\rm{e}}^{{\rm{j}}{\phi _i}}}{\left. {{\rm{sin}}{\alpha _i}{\rm{cos}}{\beta _i}{{\rm{e}}^{{\rm{j}}\left( {{\delta _i} + {\phi _i}} \right)}}\quad {\rm{sin}}{\alpha _i}{\rm{sin}}{\beta _i}{{\rm{e}}^{{\rm{j}}\left( {{\gamma _i} + {\phi _i}} \right)}}} \right]^{\rm{T}}} $，联立求解可以提取出3个正交单位特征矢量的参数α₁,α₂,α₃，结合出现概率得到平均散射角参数：

$\alpha = \bar \alpha = \sum\limits_{k = 1}^3 {{P_k}{\alpha _k}} $

(9)

散射角α与平均物理散射机制直接相关，对应于物理散射机制的连续变化，即从表面散射(α=0°)，偶极子散射(α=45°)到二面角散射(α=90°)；由于其旋转不变性，是极化分类中的常用特征。同样旋转不变的还有极化熵H与极化各向异性度A，其中H用来衡量散射过程的随机性，A用来描述第2个和第3个特征值的相对大小：

$ H = - \sum\limits_{k = 1}^N {{P_k}{{\log }_N}\left( {{P_k}} \right)} $

(10)

$ A = \begin{array}{*{20}{c}} {\frac{{{\lambda _2} - {\lambda _3}}}{{{\lambda _2} + {\lambda _3}}},}&{{\lambda _1} > {\lambda _2} > {\lambda _3}} \end{array} $

(11)

决策树灵活采用上述模型参数等极化特征作为节点的特征，然后通过调节阈值来分配不同的地物^[8]，在分类的同时，也能够结合极化特征对地物的极化散射机制加以描述。

2.3 2维极化特征与线性可分

分类时可以采用单个特征，也可以采用由l个特征f_i(i=1,2,···,l)组成的 l 维特征矢量v=[f₁ f₂ ··· f_l]。以特征f_i(i=1,2,···,l)为坐标轴构建 l 维特征空间，将样本描绘在坐标系中，再将这个特征空间分割成不同的类空间，使其中分布的样本归属正确的类，这是对分类的另一种直观描述^[10]。

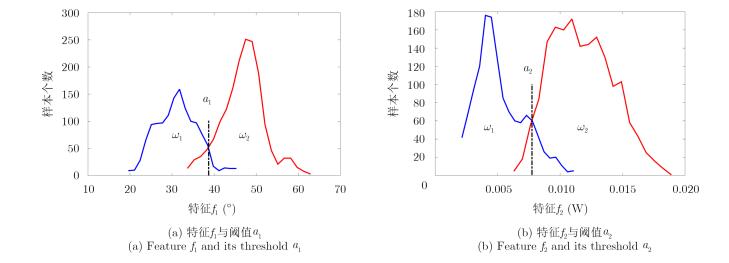
当采用单个极化特征f_i(i=1,2,···,l)时，样本的分布情况是通过直方图来描述的。选取AIRSAR-Flevoland数据中的两类样本，分别用蓝色与红色表示，图 2(a)统计了它们的散射角f₁的取值分布，图 2(b)统计了它们的HH通道后向散射功率f₂的取值分布。在直方图中采用阈值a_i(i=1,2)，可以将样本划分为w₁和w₂两类，即w₁:f_i≤a_i,w₂:f_i>a_i(i=1,2)。然而，由于两类样本的散射机制相似、极化特征值的分布出现混叠，无论怎样调节阈值都无法避免分类错误。

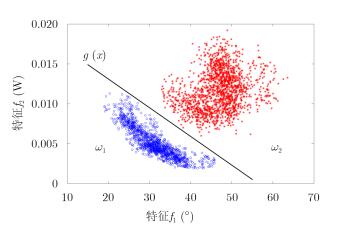
当采用由f₁和f₂组成的2维特征矢量v=[f₁ f₂]时，样本的分布情况是通过2维平面散点图来描述的。图 3使用了与图 2相同的数据、样本以及极化特征(f₁和f₂)，绘成2维平面散点图之后，发现原本混叠的两类样本完全分离了。这里要用到线性可分^[10]的概念，它的定义是，存在某个超平面g(x)= w^Tv+w₀=0，能够将两类样本完全正确地分开；而这个超平面就是2维“阈值”，即边界。

$ \left. {\begin{array}{*{20}{l}} {{\omega _{\rm{1}}}:{w^{\rm{T}}}v + {w_0}{\rm{ < }}0}\\ {{\omega _2}:{w^{\rm{T}}}v + {w_0} > 0} \end{array}} \right\} $

(12)

3 基于2维特征的决策分类方法

由2.3节可知，使用单个极化特征，在划分散射机制相似的两类地物时，无论怎样调节阈值都无法避免分类错误；而采用由两个极化特征组成的2维特征矢量，则可以明显地提高分类正确率。本节将2维特征与决策树模型相结合，重点介绍了基于2维特征的决策分类步骤，为此引入Fisher线性判别作为线性可分度量，引入超平面算法作为边界算法，并采用混淆矩阵计算“纯度”，制定了新的分支准则和分支停止准则，最后讨论了分类结果的反馈调整。

3.1 线性可分度量与超平面边界算法

实际应用里的线性可分不是定义中的理想情况，它容许奇异点的存在，不要求所有样本都完全正确的分类。本文采用Fisher线性判别^[11]来度量线性可分，它的原理是借助准则函数值J(w)最大化来确定最佳投影方向，使得投影后的两类样本最大程度的分开，

$ \begin{array}{*{20}{l}} {\boldsymbol{y} = {\boldsymbol{w}^{\rm{T}}}\boldsymbol{x},{\mkern 1mu} {\mkern 1mu} J\left( \boldsymbol{w} \right) = \frac{{{{\left| {{m_1} - {m_2}} \right|}^2}}}{{s_1^2 + s_2^2}}} \end{array} $

(13)

其中，x表示样本矢量(1维特征)或样本矩阵(l维特征，l>1)，由x₁和x₂两类样本构成。w为投影方向，y为样本的投影，m代表投影样本的均值，s²代表投影样本的类内散布即方差。一般来说J(w)值越大，x₁与x₂两类样本的线性可分性越好。因此，J(w)值可以用来度量x₁与x₂两类样本的线性可分性。

若x₁与x₂线性可分，可以采用超平面算法^[12]计算2维“阈值”，即边界，

$ g\left( {{\boldsymbol{x}}} \right) = {{{\boldsymbol{w}}}^{\rm{T}}}{{\boldsymbol{x}}} + {w_0} = 0$ $

(14)

其中，由l维特征矢量展开的特征空间中，w=[w₁ w₂ ··· w_l]^T是超平面的权向量，w₀是常量。

超平面边界算法不需要概率分布和先验知识，而是通过数值计算的方法对权向量进行调整来确定最合适的超平面，使得x₁与x₂获得较理想的分类正确率。

3.2 “纯度”度量

x₁与x₂由超平面划分边界之后，统计各个样本点的类别归属与其正确的类别标记是否一致，进而计算混淆矩阵C：

${{\boldsymbol{C}}} = \left[{\begin{array}{*{20}{c}} {{c_{11}}} & {{c_{12}}}\\ {{c_{21}}} & {{c_{22}}} \end{array}} \right]$

(15)

其中，c_ij表示x_i被划分为x_j的样本数，则第i行元素之和等于第i类的样本总数。于是，对角元素代表正确分类的样本数，非对角元素代表错误分类的样本数。为了得到“纯度”度量值，对行进行归一化，使得每一行的元素之和为1：

$\tilde C = \left[{\begin{array}{*{20}{c}} {\frac{{{c_{11}}}}{{{c_{11}} + {c_{12}}}}}&{\frac{{{c_{12}}}}{{{c_{11}} + {c_{12}}}}}\\ {\frac{{{c_{21}}}}{{{c_{21}} + {c_{22}}}}}&{\frac{{{c_{22}}}}{{{c_{21}} + {c_{22}}}}} \end{array}} \right]$

(16)

采用混淆矩阵$ \tilde C $的行列式作为“纯度”度量值p，即p=|$ \tilde C $|(–1≤p≤1)。p的值越大，则“纯度”越高。这种度量方式同时考虑了x₁和x₂两类的分类正确率，确保x₁被错分为x₂的样本比率和x₂被错分为x₁的样本比率都尽可能地小。

3.3 分支准则与分支停止准则

决策树建树的核心思想是通过对原始样本集的连续分割，创建与各个类相对应的区域^[7]；因此，不断地分割和更新样本集是决策树建树过程中的一个显著特点。经典决策树方法是通过遍历样本值来确定阈值从而实现样本集的分割，然而这种计算单点数值的算法仅适用于单个特征的情况。在2维特征矢量所对应的2维平面散点图中，区域的分割与样本聚类的整体分布形状有关，单个样本点的计算无意义。因此，本文将样本子集所形成的聚类作为研究对象，用于分支准则与分支停止准则。

步骤1 选取特征集

选取若干极化特征，构成特征集F={f₁ ,f₂,···,f_m}，m为极化特征的个数。类别标记已知的k类训练样本组成样本集U={u₁,u₂,···,u_k}；其中，拥有同类标记的样本子集u_i(i=1,2,3,···,k)，称为类单元。

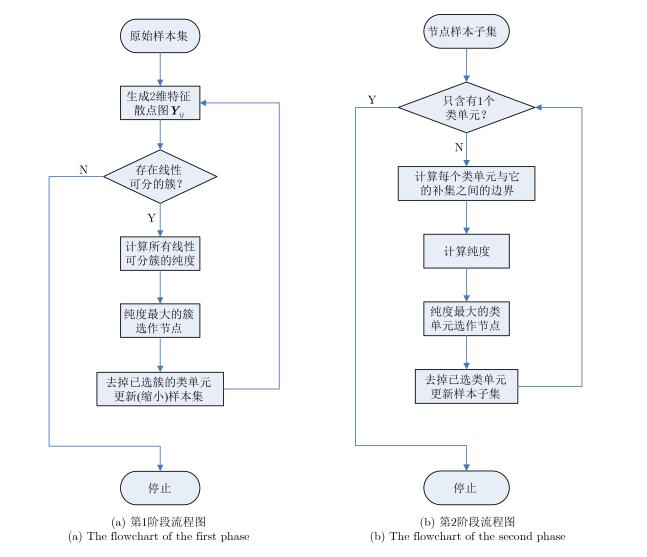
经典决策树由单个特征和阈值来完成节点的分支，本文方法则采用2维特征矢量和边界算法来完成节点的分支。分支过程分为两个阶段，第1阶段寻找线性可分的聚类集团，按照线性可分性将样本集分割成若干子集，每个子集设为一个节点，详述见步骤2；第2阶段对各个节点、亦即线性不可分的各个样本子集做进一步的细分，直至所包含的类单元唯一，分支停止，详述见步骤3，两阶段流程见图 4。

步骤2 决策树分支的第1阶段

将m个极化特征两两组合，生成以f_i和f_j(i=1,2,···m; j=1,2,···,m; i≠j)为坐标轴的2维平面散点图Y_ij，简称特征图。特别地，类单元因为是由同一类样本组成，在特征图中往往聚集在一起。若干个类单元u_i进一步组成样本子集U_j，称为簇；令集合I_j表示簇U_j中所包含类单元的类别标记，I_j$ \subset ${i=1,2,3,···k}，

${{{U}}_j} = \bigcup\limits_{i \in {{{I}}_j}} {\left\{ {{{{u}}_i}} \right\}} $

((17))

此时，U_j的补集${{{{\overline {{U}}}}}_j} $也是一个簇，U_j${{{{\overline {{U}}}}}_j}$=U；令U_j为x₁,${{{{\overline {{U}}}}}_j}$为x₂。依据Fisher线性判别计算x₁与x₂的准则函数值J(w)，认为J(w)值大于J_th的x₁与x₂线性可分(门限值J_th可调)。对于线性可分的x₁与x₂，采用超平面算法计算它们的边界，进而计算划定边界之后的混淆矩阵和“纯度”。最后，U_j和${{{{\overline {{U}}}}}_j}$二者里，所包含类单元较少的那个簇，作为候选节点，并将计算所得“纯度”赋予该候选节点。从m(m–1)/2个特征图中找出所有的候选节点，其中“纯度”最大的确定为节点N₁。下一步，从样本集里去掉已选簇中所包含的类单元，更新样本集，进而生成新的特征图，用同样的方法确定节点N₂···重复操作，直至生成的新特征图中不再有线性可分的簇，停止。于是确定了N₁,N₂,···,N_h共h个节点，并将最后剩余的线性不可分的簇设置为节点N_h+1。此时，节点N_q对应的样本子集为U_q (q=1,2,···,h,h+1),U₁U₂···U_h+1=U且两两互斥，从而按照线性可分性将样本集分割成了若干子集。各个节点的分支顺序按照下标由小到大依次进行。

步骤3 决策树分支的第2阶段

各个节点是否要继续分支，判断准则为样本子集所包含的类单元的个数。如果类单元个数大于1，继续分支；如果等于1，分支停止。节点N_q继续分支之前，假设样本子集U_q里含有r个类单元，则样本子集U_q可以表示为：

${{{\boldsymbol{U}}}_q} = \bigcup\limits_{j \in {{{\boldsymbol{I}}}_q}} {\left\{ {{{{\boldsymbol{u}}}_j}} \right\}} $

(18)

其中，I_q代表类别标记的集合，共有r个元素。

对每一个类单元u_j，将其视作簇V_j={u_j}，则它的补集${{{\overline {V}}_j}} $也是一个簇，V_j${{{\overline {V}}_j}} $=U_q。采用与第1阶段相同的算法来计算V_j与${{{\overline {V}}_j}} $之间的边界和“纯度”。选出“纯度”最大的类单元u_j作为继续分支的第1个子节点。下一步，去掉该类单元，更新样本子集，重复上述操作，直至新的样本子集中只剩一个类单元，分支停止。于是，整棵树建造完成，可以对未分类的样本进行预测和分类。将拥有同类标记的样本子集作为类单元，制定分支和分支停止准则，保证了每个叶子的最终所属类别在节点分支时就已经确定，不同叶子的最终所属类别不会出现雷同，避免了过拟合。

3.4 混淆矩阵与反馈调整

两个分支阶段完成，得到了整棵决策树，用它预测测试样本的类别，就得到了测试样本的分类结果。为了评估分类结果，首先，计算总体分类精度，即分类正确的测试样本数占总测试样本数的百分比；其次，计算分类结果的混淆矩阵，与“纯度”计算中使用的混淆矩阵类似，设总类别数为n，

$C = \left[{\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}& \cdots &{{c_{1n}}}\\ {{c_{21}}}&{{c_{22}}}& \cdots &{{c_{2n}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{c_{n1}}}&{{c_{n2}}}& \cdots &{{c_{nn}}} \end{array}} \right] $

(19)

其中，c_ij表示第i类被划分成第j类的测试样本数，于是第i行元素之和等于第i类的测试样本总数。对角元素代表分类正确的样本数，非对角元素代表分类错误的样本数。为了分析误差率，对行做归一化，使得每一行的元素之和为1。

依据分类结果的混淆矩阵，可以定位每一类地物的错分样本来自哪些节点，从而进行反馈调整，进一步提高分类精度。可以采用的反馈调整手段包括：适当调整节点顺序，以及修改极化特征等。

4 实验与结果分析

实验选用了AIRSAR荷兰Flevoland地区L波段全极化4视复数据，STK文件格式，含有11类真值(ground-truth)标记数据，分别为茎豆、森林、马铃薯、紫花苜蓿、小麦、裸地、甜菜、油菜籽、豌豆、草地和水，其中9类属于植被，散射机制相似。全图像素尺寸750×1024，标记样本所占比例为5.34%。在标记样本的坐标范围之内以四边形框选择训练样本，其余的标记样本作为测试样本，具体的样本数量见表 1(a)。另外，为减少相干斑影响，保证极化特征参数的准确性，对数据采用了7×7 Lee滤波的预处理。

选取8种极化特征参数组成特征集F={f₁,f₂,···,f₈}，详见表 1(b)。选取的参数均为适用于自然地物的2阶统计量参数，范围涵盖了常用的两大类，即，直接来自2阶统计量矩阵的后向散射系数，以及对2阶统计量矩阵进行变换之后导出的极化分解参数。其中，后向散射系数的选取同时考虑了同极化分量、同极化分量之间的相关系数、圆极化基变换下的同极化分量与交叉极化分量的比值，以及各通道分量的总和；极化分解参数的选取主要考虑旋转不变性，另外加入了描述冠层与植被散射特点的体散射功率参数。

f₁是HH后向散射系数$\left\langle {{{\left| {{S_{{\rm{HH}}}}} \right|}^2}} \right\rangle $，为同极化通道HH的后向散射功率。f₂是VV后向散射系数$\left\langle {{{\left| {{S_{{\rm{VV}}}}} \right|}^2}} \right\rangle $，为同极化通道VV的后向散射功率。f₃是HH-VV相关项的幅度$\left| {\Big\langle {{S_{{\rm{HH}}}} \cdot S_{{\rm{VV}}}^*} \Big\rangle } \right|$。f₄是散射总功率SPAN，见式(6)。f₅是F-D分解的体散射功率P_V，见式(7),P_V=f_V，模型来自森林冠层散射。f₆是极化散射角α，见式(9)。f₇是圆极化比CPR，见式(8)。f₈是极化熵与各向异性度组合H(1–A)，见式(10),式(11)，表征高熵、低各向异性度的随机散射过程，可描述植被。

4.1 分类结果与分析

决策树分支的第1阶段，需要注意的是，由于裸地和水的回波功率非常接近于零，信噪比太低会导致极化分解参数不准确，有可能干扰各个节点分支的准确性，因此在实际操作中特别规定，回波功率接近于零的地物最先分支。具体做法是，回波功率SPAN分别与另外7个特征依次组合得到7个特征图，计算每个特征图中，由裸地和水组成的簇的边界和“纯度”，“纯度”最大的簇设为第1个节点A。

接下来按照分支第1阶段所述的方法，寻找线性可分的簇(实验中门限值J_th设为0.005)，依次得到了节点B,C,D和E如表 2所示。其中，门限值J_th并没有统一的设置标准，它的作用是为线性可分的判定提供一个大致的范围。实际操作时，在特征图中人工选择若干个线性可分的簇，分别计算它们的J值，取其中的最小值设置为门限值J_th。一般来说，建议将门限值J_th设置得略低一些，从而尽可能多地保留可分性较好的簇(即候选节点)。

决策树分支的第2阶段，对各个节点继续分支，直至样本子集中的类单元唯一时，停止分支。

(1) 节点A：裸地+水

由特征矢量[f₆ f₈]继续分支，将裸地、水分离。

(2) 节点B：紫花苜蓿+草地

由特征矢量[f₃ f₄]继续分支，将紫花苜蓿、草地分离。

(3) 节点C：茎豆+森林+马铃薯

由特征矢量[f₅ f₇]继续分支，分出茎豆；

由特征矢量[f₄ f₇]继续分支，将森林、马铃薯分离。

(4) 节点D：油菜籽

(5) 节点E：小麦+甜菜+豌豆

由特征矢量[f₄ f₇]继续分支，分出豌豆；

由特征矢量[f₂ f₄]继续分支，将小麦、甜菜分离。

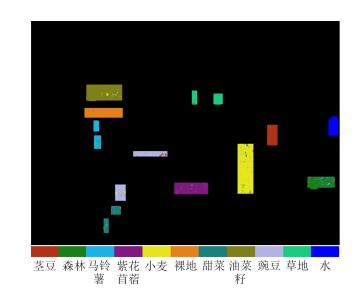
利用训练样本建树之后，对测试样本进行测试，得到了测试结果的混淆矩阵如表 3所示；而全体标记样本的分类结果图如图 5所示，其他未标记样本为黑色显示。

该方法的总体分类精度为95.75%，其中，紫花苜蓿、茎豆、油菜籽、水和裸地5类地物的分类精度都在98%以上，草地的精度也达到了97.47%，马铃薯、豌豆、小麦和甜菜4类地物的精度都在92.17%～94.75%之间。需要注意的是，森林的分类精度只有86.81%，且森林和马铃薯互相错分的比例较大(达到8.02%和5.70%)，猜测与森林中的物种构成有关，可能含有灌木或者大小不同的树种，使其与马铃薯在散射特点上出现相似和混淆。

另外，表 4对比了若干组采用其他分支顺序的分类结果的总精度。其中，第1栏代表的是本文采用的分支顺序ABCDE，第2栏的分支顺序为ACDBE，第3栏的分支顺序为ACEBD，第4栏的分支顺序为ADCEB，第5栏的分支顺序为ABECD。对比发现，本文的总体分类精度优于其他4种顺序，说明采用本文的分支准则可以得到最优的分支顺序。

在特征集相同时，采用经典决策树也得到了一组分类结果，与本文分类结果的对比见表 5。可以看出，在区分散射机制相似的植被时，本文方法的总体分类精度比经典决策树提高了6.21%。其中茎豆、马铃薯、甜菜的分类精度提高20%～60%；紫花苜蓿、小麦、裸地、草地的分类精度也有1.71%～6.19%的不同程度的提高；油菜籽的分类精度下降0.41%，豌豆的分类精度下降2.18%，总地来说分类精度有了显著的提高。需要注意的是，经典决策树对森林的分类精度高达91.98%，但具体分析结果之后发现，91.98%的森林被分为森林的同时，超过60%的马铃薯也被错分为森林，从而导致了马铃薯的分类精度只有30.61%；换句话说，森林的高分类精度并不能说明经典决策树有能力将散射特点相似的森林和马铃薯分开，反而是本文的分类结果中，森林和马铃薯互相错分的比例更小、提高了相似地物的分类精度。

获得分类结果的同时，也分析了11类地物的极化散射特点：裸地和水以表面散射为主，回波功率小，明显区别于其他地物；两者的差异在于，水受风浪影响表面粗糙度更高，散射角较大。森林、马铃薯和茎豆三者较为相似，属于偶极子散射，回波功率大，明显区别于其他地物；但马铃薯和森林都具有森林冠层散射的特点，与茎豆有差异。油菜籽近似于表面散射，而回波功率大，明显区别于其他地物。紫花苜蓿和草地较为相似，近似于偶极子散射，明显区别于其他地物；两者的差异在于，紫花苜蓿更接近森林冠层散射。豌豆、小麦和甜菜三者较为相似，豌豆近似于表面散射，但回波功率较大，可以区别于小麦和甜菜；小麦和甜菜介于表面散射和偶极子散射之间，两者的回波功率相似，但与极化波的相互作用不同，可以运用同极化通道HH和VV通道的功率差异来区分。综上，“明显区别于其他地物”描述的就是决策分支第1阶段里的线性可分簇，从相似中寻找“差异”描述的就是决策分支第2阶段里的将各个线性不可分的簇进一步细分。先易后难，先粗后细，对目标进行层次分类，是本文方法的主要思想；分析极化特征，描述了Flevoland地区多种植被的极化散射机制的特点，可以为其他植被的散射机制研究提供参考。

极化SAR数据分类中常用的随机性参数H和Freeman-Durden 3种模型的分类体系对植被数据的分类并不理想，这是因为植被的随机性都比较高，且适用于植被的F-D模型只有体散射模型。本方法的特征集选用了极化散射角和多种回波功率，包括总功率SPAN、散射角α、HH后向散射系数、VV后向散射系数和圆极化比CPR等，实验证明它们对植被的分类效果良好。

4.2 分类结果的反馈调整

由于样本的复杂性，各个节点很难达到100% 的分类精度，误差不可避免；而树状结构带来了误差的累积效应^[7]，即：节点的顺序越靠后，受前面各节点累积误差的影响越明显，甚至有可能超过自身分支的误差。在植被监测的很多实际应用中，通常只关注一种或者几种目标地物的情况，对其他无关地物的分类精度则没有要求。此时，对节点的顺序进行适当的调整，虽然降低了总体分类精度(参见表 4的分析)，却可以将目标地物受到的累积误差的影响尽可能降低。

例如表 5提到的，比经典决策树分类精度下降了2.18%的豌豆，分析表 3混淆矩阵可知，豌豆的分类正确率为92.61%，分类错误的主要原因之一来自之前的C节点。测试样本在经由C节点分支后，3.09%的豌豆被错分成了茎豆，0.05%的豌豆被错分成了森林，0.17%的豌豆被错分成了马铃薯；也就是总计3.31%的豌豆被错分到了C节点所包含的样本子集中。因此，我们尝试将包含豌豆的E节点调整到C节点之前，即表 4中第5栏的分支顺序ABECD，得到的分类结果中豌豆的分类精度为94.99%，提高了2.38%，实现了对指定地物分类精度的进一步调整。

如果不存在目标地物与无关地物的概念、所有地物同等重要的情况下，依然可以对分类结果进行改善。仍以豌豆为例，为了减少C节点错分的豌豆数量，关键在于找到更准确区分豌豆与非豌豆的特征。一方面，可以参考2.3节，由单个特征扩展为2维特征矢量时可以将原本有混叠的类分开，于是，可以进一步地由2维扩展为3维甚至更高维的特征矢量；另一方面，可以考虑引入新的极化特征，更新特征集。

综上，决策树能够通过分类结果的混淆矩阵准确定位并找到产生分类误差的原因，而定位之后，无论节点顺序的调整，还是节点特征的分析与修改都成为了可能，从而进一步调整和优化分类结果。另外补充说明一点，分类与反馈调整是两个相互独立的阶段，当分类精度已经满足了当前应用需求，或者标记样本太少的时候，反馈调整的意义不大，可以只完成分类阶段。

4.3 问题与展望

决策树分支的第1阶段包含大量循环，计算复杂度明显高于经典决策树算法。这一阶段的主要目的是寻找线性可分的簇，而为了使用Fisher线性判别分析，必须遍历若干个类单元的排列组合，这也是导致大量循环的原因。如果能够找到更加简单的方法快速定位线性可分的簇，例如引入人机交互参与线性可分簇的筛选等，有望大规模提高运算速度。

4.2节中提到，节点采用3维或者更高维特征矢量可以进一步改善分类结果，然而，计算的复杂度也变得更高。因此，本文在分类精度与计算复杂度之间作了折中，选取了2维特征矢量作为研究对象，得到了较理想的分类结果(总体分类精度95.8%，与支持向量机SVM的总体分类精度96.6%基本相当)。未来的实验中，如何更加快速有效地找到线性可分的簇、降低计算复杂度，是3维以及更高维特征矢量得以应用的关键。

采用2维或多维特征矢量的决策树，可以将边界算法直接融入节点的分支操作中。如3.1节中所述，本文采用了超平面边界算法，得到的分类结果较为理想。而实际上，采用不同的边界算法会得到不同的分类精度，进一步提高边界算法的精度也是未来实验中可以继续探讨的问题。

5 结束语

基于2维极化特征的决策分类提出了在节点使用2维特征矢量代替单个特征的决策树分类方法，对Flevoland地区的若干种极化散射机制相似的地物进行分类。得到了更理想分类精度的同时，也获得了若干种植被的极化散射机制的一些特点，以及极化特征选取的有用结论。从而为类似植被的散射机制研究与分类特征选择提供了参考。另外，分析分类结果的混淆矩阵，可以定位导致分类误差的节点；通过节点顺序的调整或者节点特征的修改，可以实现对分类结果的反馈调整和进一步优化。