②(中国科学院电子学研究所 北京 100190)
②(The Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)
合成孔径雷达具有全天候、全天时的对地观测能力,已成为资源勘探、环境监测和灾害评估的重要手段。差分干涉合成孔径雷达技术利用不同时间获得的同一成像区域的微波影像,通过统计分析,查找不受时间、空间基线去相关和大气变化影响的点目标来获取地表形变信息,监测建筑、冰川和斜坡的形变等[1, 2]。然而差分干涉合成孔径雷达假定成像区域同一个方位-距离分辨单元中只有一个主散射体,只能获得地表变化的一个平均信息。对于存在高密度散射体的区域,例如城市地区,大量的建筑,围墙,人造目标等表现为复杂的纵向结构,层叠效应严重,此时一个像素接收的信号可能来自于多个散射体响应的叠加,若采用单一散射体假设将导致某些散射体不能被监测,限制了差分干涉合成孔径雷达对复杂构造区域的监测能力。
合成孔径雷达4维成像技术是在差分干涉合成孔径雷达基础上发展起来的一种新型微波成像技术,通过雷达平台在不同时间和不同高度位置上对同一成像区域的多次平行观测,获取目标沿高度向和时间向的多次采样信息,构造对目标观测的高度向和时间向等效孔径,从而能够估计同一方位-距离分辨单元中不同散射体的高度和相应的形变速率,具有方位-距离-高度-形变速率4维成像能力[3, 4]。与采用单一散射体假设的差分干涉合成孔径雷达相比,能够最大限度地追踪目标数量,估计层叠散射体的相对形变,提高了对复杂散射体的监测能力,可为高度-形变速率应用领域的需求提供整体解决方案。
当前技术条件下,合成孔径雷达4维成像技术通过平台在不同时间对同一区域的多次成像来实现,不可避免地存在基线-时间数量少且分布不均匀的问题。传统频谱估计方法受高度和时间基线影响,分辨率不高[5, 6, 7, 8]。随着压缩感知理论的提出,稀疏信号处理在雷达成像领域受到了高度关注[9, 10]。合成孔径雷达4维成像所需要获取的信息相对于整个观测空间的信息来讲,可看作是一个稀疏性较强的信号表示,满足信号可压缩性。因此基于压缩感知的成像方法成为合成孔径雷达4维成像领域的研究热点。文献[11]在层析合成孔径雷达模型的基础上,在相位信息中引入形变因子,将压缩感知技术引入合成孔径雷达4维成像,文献[12]提出了一种基于贝叶斯压缩感知的合成孔径雷达4维成像方法。然而标准的压缩感知成像方法是针对实数据进行处理,合成孔径雷达4维成像所处理的数据为复数据。因此本文提出了一种基于幅度和相位迭代重建的合成孔径雷达4维成像方法,通过在成像过程中引入相位信息来改善成像质量。仿真结果验证了该算法的有效性。
2 4维合成孔径雷达成像原理4维合成孔径雷达成像几何配置如图 1所示,x轴表示距离向,y轴表示方位向,r轴为斜距向。y和r构成成像平面,s轴是与成像平面垂直方向。设载机在同一时间对同一成像区域航过M次,得到M幅合成孔径雷达图像,之后在不同时间对该成像区域共进行N次上述操作,则共获得MN幅合成孔径雷达图像。MN幅合成孔径雷达图像进行精确配准后,相同位置的像素点就对应成像区域中同一点,构成一个长度为MN的序列。将成像区域中任意一像素所对应的序列按照获得时的基线和时间进行排列,得到一个M×N基线-时间分布矩阵,用H表示,其中hm,n表示第n个时间时第m次航过所获得的2维合成孔径雷达图像数据。假设在成像区域(y',x')处有一散射源,沿s向分布,以平均速率v沿视线向运动,N次时间间隔内目标运动不会超出它所在的分辨单元,则像素点(y',r')所对应的2维合成孔径雷达图像数据可表示为[8]:
| $\begin{aligned} {h_{m,n}} = & \iint {{\rm d}y{\rm d}rf(y' - y,r' - r)} \\ & \cdot \iint {\rm d}s{\rm d}v\gamma (y,r,s,v) \\ & \cdot \exp \left[{ - {\rm j}\frac{{4\pi }}{\lambda }{R_{m,n}}(r,s,v)} \right] \end{aligned}$ | (1) |
| $\begin{aligned} {R_{m,n}}(r,s,v) \! = & \! \sqrt {{{\left(r \! - \! {b_{/\!\!/(m,n)}}\right)}^2} + {{\left(s \! - \! {b_{ \bot (m,n)}}\right)}^2}} \! + \! v{t_n} \\ \approx & r \! - \! {b_{/\!\!/(m,n)}} \! + \! \frac{{{{\left(s \! - \! {b_{ \bot (m,n)}}\right)}^2}}}{{2\left(r \! - \! {b_{/\!\!/(m,n)}}\right)}} \! + \! v{t_n} \\ \end{aligned} $ | (2) |
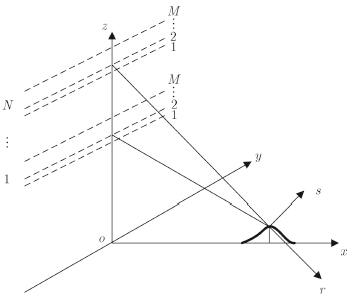 | 图 1 4维合成孔径雷达几何配置示意图 Fig.1 The system geometry of 4D SAR |
由式(1)看出4维合成孔径雷达的方位-斜距向成像与常规的合成孔径雷达成像没有区别,是成像场景在方位-斜距平面的2维映射。高度-速率维信息包含在式(1)的相位因子里。因此为简化分析,本文假定每次航行合成孔径雷达都能实现理想的方位-斜距向2维聚焦,聚焦点扩展函数f(y,r)为2维狄拉克函数,将f(y,r)=d(y)d(r)代入式(1)可将4维合成孔径雷达方位-斜距-高度-速率4维成像问题转化为高度-速率2维成像问题。因此对于成像场景中任意一像素(y',r'),雷达在第n个时间时第m次航过时所获得的图像数据可表示为:
| $\begin{aligned} {h_{m,n}} \! = & \! \int\nolimits_{ - {v_{\text{o}}}}^{{v_{\text{o}}}} \! \int\nolimits_{ - {s_{\text{o}}}}^{{s_{\text{o}}}} \gamma (s,v) \\ & \cdot \exp \! \left[{ - {\rm j}\frac{{4\pi }}{\lambda }{R_{m,n}}(s,v)} \right] \! {\rm d}s{\rm d}v \end{aligned}$ | (3) |
由式(2)知hm,n的指数项存在2次相位误差,将式(2)进行去斜操作后,方位-斜距分辨单元(y',r')所对应的2维合成孔径雷达图像数据可表示为:
| ${y_{m,n}} = \int\nolimits_{ - {v_o}}^{{v_o}} {\int\nolimits_{ - {s_o}}^{{s_o}} {\gamma (s,v){g_{m,n}}(s,v)} } {\rm d}s{\rm d}v$ | (4) |
| $\begin{aligned}{g_{m,n}}(s,v) = & \exp \left[{j2\pi \left( {\frac{{2s}}{{\lambda r}}{b_{ \bot m}} + \frac{{2v}}{\lambda }{t_n}} \right)} \right],\\ & m \! = \! 1,\;2,\cdots,M; \quad n \! = \! 1,\;2,\cdots,N \end{aligned}$ | (5) |
由式(3)可知对于成像场景中任意一个固定的方位-斜距分辨单元,4维合成孔径雷达获得的M×N接收数据矩阵Y表示雷达散射强度在高度和速率方向的2维联合谱,在基线和时间均匀采样条件下,用2维傅里叶变换就可获得满意的结果。然而实际条件下,基线和时间数目都较少且采样不均匀,导致傅里叶变换的效果严重恶化,旁瓣很高,应选取合适的成像算法克服基线时间不均匀的影响。
3 基于幅度和相位迭代重建的4维合成孔径雷达成像算法由上面的分析知4维合成孔径雷达成像可分为两步。首先获得所有航过的方位-斜距图像,之后再对高度-速率维成像。由于方位-斜距成像与传统的合成孔径雷达成像一样,因此本文仅对高度-速率维成像进行分析。
3.1 4维合成孔径雷达高度-速率维的信号模型为简化分析,4维合成孔径雷达高度-速率维的连续成像模型式(4)可离散化为:
| \[Y = BRT\] | (6) |
| $\quad\quad\quad\quad {B_{m,p}} = \exp \left( {{\rm j}\frac{{4\pi p{\Delta _s}}}{{\lambda r}}{b_{ \bot m}}} \right)$ | (7) |
| $\quad\quad\quad\quad {T_{q,n}} = \exp \left( {{\rm j}\frac{{4\pi q{\Delta _v}}}{\lambda }{t_n}} \right)$ | (8) |
由上面的分析可发现,4维合成孔径雷达高度-速率维成像处理就是要重建反射率系数$\gamma $(pDs,qDv)。从式(6)可看出反射率系数$\gamma $(pDs,qDv)包含在矩阵R中,很难由式(6)直接获得R的值,因此将式(6)重记为:
| $\begin{aligned} {\rm vec}\left({Y} \,\right) = & {\rm vec}({BRT} \,) \\ = & \left( {{{T}^{\rm T}} \otimes {B}} \right){\rm vec}({R}) \\ \end{aligned} $ | (9) |
现实条件下,4维合成孔径雷达系统每次只能获得一条或有限的几条基线。假设每次获得的真实基线数是M',此时可将真实接收的数据${Y'_{M' \times N}}$看做是从MN个总接收数据YM×N中萃取M'N个数据出来。因此,真实接收数据可表示为:
| $\begin{aligned} {\rm vec}({{{Y}'}_{\!\!\!\! M' \times N}}) = & {{\Phi} _{M'N \times MN}}{\rm vec}({{Y}_{M \times N}}) \\ = & {{\Phi} _{M'N \times MN}}\left( {{{T}^{\rm T}} \otimes {B}} \right){\rm vec}({R}) \\ \end{aligned} $ | (10) |
| ${{\Phi} _{M'N \times MN}} = \left[{\begin{array}{*{20}{c}} {{{\bar {\Phi} }_1}}& \mathbf{0}& \cdots & \mathbf{0} \\ \mathbf{0} & {{{\bar {\Phi} }_2}}& \cdots & \mathbf{0} \\ \vdots & \vdots & \ddots & \vdots \\ \mathbf{0}& \mathbf{0}& \cdots & {{{\bar {\Phi} }_N}} \end{array}} \right]$ | (11) |
令y表示vec(${Y'_{M' \times N}}$),$\gamma $表示vec(R),$\Lambda $表示TT$\otimes$B,则式(10)可重记为:
| \[y = \Phi \Lambda \gamma {\rm{ + }}n = \Theta \gamma {\rm{ + }}n\] | (12) |
由式(12)可看出4维合成孔径雷达高度-速率维成像就是重建目标的复散射系数$\gamma $。由于4维合成孔径雷达成像所需要获取的目标信息相对于整个观测空间的信息来讲,可看作是一个稀疏性较强的信号,因此可利用稀疏重构算法来获取目标像。
3.2 4维合成孔径雷达成像算法标准的压缩感知成像方法是针对实数据进行处理,由式(12)可看出4维合成孔径雷达高度-速率维成像所处理的数据为复数据。若直接采用标准压缩感知算法进行处理,则忽略了目标的相位信息。因此,这里我们将复散射系数向量$\gamma $记为[13, 14]:
| \[\gamma = {\rm{diag}}\left\{ {\exp \left( {{\rm{j}}{\varphi _l}} \right)} \right\} \cdot \left| \gamma \right| = \Phi \delta \] | (13) |
其中$\delta = |\gamma |$表示复散射系数向量$\gamma $的幅度,$\Psi $=diag{exp($j{\varphi _l}$)}是一个对角阵,其中${\varphi _l}$表示复散射系数向量$\gamma $的第l个相位。因此,式(12)可重记为:
| \[y = \Theta \gamma {\rm{ + }}n = \Theta \Psi \delta + n\] | (14) |
如果复散射系数向量$\gamma $的相位已知,则矩阵$\Psi $确定,我们可采用${\lambda _1}$范数最优化来获得观测场景高度和速率的幅度图像[9]
| \[\hat \delta = \min {\left\| \delta \right\|_1},\quad {\rm{s}}.{\rm{t}}.{\rm{ }}{\left\| {\Theta \Psi \delta - y} \right\|_2} \le \varepsilon \] | (15) |
然而,实际上相位矩阵$\Psi $未知,我们必须在估计幅度图像之前获得相位值。为解决这个问题,我们将复散射系数向量$\gamma $重记为:
| \[\gamma = {\rm{diag}}\left\{ {\left| {{\gamma _i}} \right|} \right\} \cdot \exp \left( {{\rm{j}}\varphi } \right) = TP\] | (16) |
| \[y = \Theta \gamma {\rm{ + }}n = \Theta TP + n\] | (17) |
| \[J(P) = \left\| {y - \Theta TP} \right\|_2^2 + {\lambda _1}\sum\limits_{i = 1}^{PQ} {{{\left( {{{\left| {{{(P)}_i}} \right|}^q} - 1} \right)}^2}} \] | (18) |
| \[\begin{array}{*{20}{l}} {\hat P = {\rm{arg min}}\;J(P)}\\ {\quad = \arg \min [\left\| {y - \Theta TP} \right\|_2^2}\\ {\quad + {\lambda _1}\sum\limits_{i = 1}^{PQ} {{{\left( {{{\left| {{{(P)}_i}} \right|}^q} - 1} \right)}^2}} ]} \end{array}\] | (19) |
求解上述最优化问题可重新得到相位向量P的估计,将新获得的相位值代入$\Psi $=diag{(P)i}可对相位矩阵进行更新,然后将更新后的$\Psi $代入式(15)可对复散射系数向量$\gamma $的幅度值进行更新。因此本文所提出的4维合成孔径雷达成像算法可描述为:
步骤1 利用传统压缩感知成像方法获得复散射系数向量$\gamma $的初始估计,获得矩阵T=diag{|$\gamma $i|};
步骤2 将矩阵T代入式(19),获得相位向量P,更新相位矩阵$\Psi $=diag{(P)i};
步骤3 将更新的相位矩阵$\Psi $代入式(15)获得复散射系数向量$\gamma $的幅度值,更新矩阵T=diag{|$\gamma $i|};
步骤4 返回步骤2,重复步骤2-步骤4直到$\left\| {{{\hat \gamma }^{(n + 1)}} - {{\hat \gamma }^{(n)}}} \right\|_2^2{\rm{ \lt }}\zeta $,其中$\zeta $为一个小的正数。
3.3 幅度和相位重建方法为从式(19)获得相位向量P的解,用一个处处可微的函数对lq范数进行近似
| \[\left\| P \right\|_q^q \approx \sum\limits_{i = 1}^{PQ} {{{\left( {{{\left| {{{(P)}_i}} \right|}^2} + \varepsilon } \right)}^{q/2}}} \] | (20) |
此时代价函数式(18)可重记为:
| \[\begin{array}{*{20}{l}} {J(P) = \left\| {y - \Theta TP} \right\|_2^2}\\ {\quad \quad \quad + {\lambda _1}\sum\limits_{i = 1}^{PQ} {{{\left( {{{\left| {{{(P)}_i}} \right|}^2} + \varepsilon } \right)}^q}} }\\ {\quad \quad \quad - 2{\lambda _1}\sum\limits_{i = 1}^{PQ} {{{\left( {{{\left| {{{(P)}_i}} \right|}^2} + \varepsilon } \right)}^{q/2}}} } \end{array}\] | (21) |
对J(P)求偏微分得
| \[\nabla J(P) = \tilde H(P)P - 2{\left( {\Theta T} \right)^{\rm{H}}}y\] | (22) |
| \[\begin{array}{*{20}{l}} {\tilde H(P) = 2{{\left( {\Theta T} \right)}^{\rm{H}}}\left( {\Theta T} \right) + 2{\lambda _1}q{\Lambda _1}(P)}\\ {\quad \quad \quad - 2{\lambda _1}q{\Lambda _2}(P)} \end{array}\] | (23) |
| \[{\Lambda _1}(P) = {\rm{diag}}\left\{ {{{\left( {{{\left| {{{(P)}_i}} \right|}^2} + \varepsilon } \right)}^{q - 1}}} \right\}\] | (24) |
| \[{\Lambda _2}(P) = {\rm{diag}}\left\{ {{{\left( {{{\left| {{{(P)}_i}} \right|}^2} + \varepsilon } \right)}^{q/2 - 1}}} \right\}\] | (25) |
根据拟牛顿算法[13],相位向量P的迭代解可表示为:
| \[{\hat P^{(n + 1)}} = 2{\tilde H^{ - 1}}({\hat P^{(n)}}){\left( {\Theta T} \right)^{\rm{H}}}y\] | (26) |
另一方面,为从式(15)求得复散射系数向量g的幅度值d,将式(15)的有约束优化问题转化为如下的无约束优化问题:
| \[\begin{array}{*{20}{l}} {\hat \delta = \min J(\delta )}\\ {\quad = \min \left( {{{\left\| {\Theta \Psi \delta - y} \right\|}_2} + {\lambda _2}{{\left\| \delta \right\|}_1}} \right)}\\ {\quad \approx \min \left( {{{\left\| {\Theta \Psi \delta - y} \right\|}_2} + {\lambda _2}\sum\limits_{i = 1}^{PQ} {{{\left( {{{\left| {{{(\delta )}_i}} \right|}^2} + \varepsilon } \right)}^{1/2}}} } \right)} \end{array}\] | (27) |
对J($\delta $)求偏微分得
| \[\nabla J(\delta ) = \tilde H(\delta )\delta - 2{\left( {\Theta \Psi } \right)^{\rm{H}}}y\] | (28) |
| \[\tilde H(\delta ) = 2{\left( {\Theta \Psi } \right)^{\rm{H}}}\left( {\Theta \Psi } \right) + {\lambda _2}{\Lambda _3}(\delta )\] | (29) |
| \[{\Lambda _3}(\delta ) = {\rm{diag}}\left\{ {{{\left( {{{\left| {{{(\delta )}_i}} \right|}^2} + \varepsilon } \right)}^{ - 1/2}}} \right\}\] | (30) |
根据拟牛顿算法[13],幅度向量d的迭代解可表示为:
| \[{\hat \delta ^{(n + 1)}} = 2{\tilde H^{ - 1}}\left( {{{\hat \delta }^{(n)}}} \right){\left( {\Theta \Psi } \right)^{\rm{H}}}y\] | (31) |
为了验证利用本文提出算法反演4维合成孔径雷达高度-速率2维像的性能,本文进行了数字仿真实验。以机载平台合成孔径雷达参数为例,设雷达工作在L波段,载频1.3 GHz,载机飞行高度5000m,载机与成像场景中心之间的地距为5000m,基线长度500 m,成像场景目标高度最大不模糊范围为40 m,目标速率最大不模糊范围为0.288 m/a,沿s方向有两个散射点,分别位于-2m和2 m处,相应的变化速率分别为0.02 m/a和-0.02 m/a,信噪比分别为10 dB。
假定载机每个固定时间对成像场景航过一次,得到一幅SAR图像,不同时间共进行25次实验。成像场景高度范围为20 m,目标速率范围为0.2 m/a。适当选择各次载机航行的基线长度,使其能够尽可能分散填充基线-时间2维平面。不同时间获得的基线分布如图 2所示。从图 2可看出4维合成孔径雷达系统获取的数据集是在基线-时间两维空间稀疏分布,若直接对观测数据进行傅里叶变换来恢复目标函数,则因强副瓣存在,成像效果不佳。
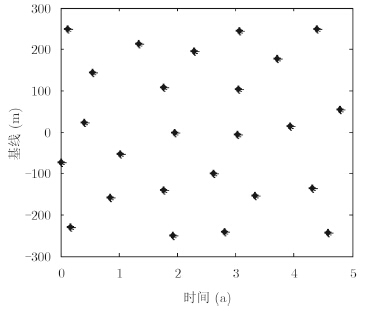 | 图 2 载机在基线-时间平面的位置分布 Fig.2 The position distributions of 4D SAR in the baseline-time plane |
为分析提出算法的性能,将传统正交匹配追踪算法和本文算法的重建结果进行了对比。信噪比10dB下利用传统正交匹配追踪算法获得的高度-速率维重建结果如图 3(a)所示,信噪比10 dB下利用本文算法获得的高度-速率维重建结果如图 3(b)所示,信噪比0 dB下利用传统正交匹配追踪算法获得的高度-速率维重建结果如图 3(c)所示,信噪比0dB下利用本文算法获得的高度-速率维重建结果如图 3(d)所示。
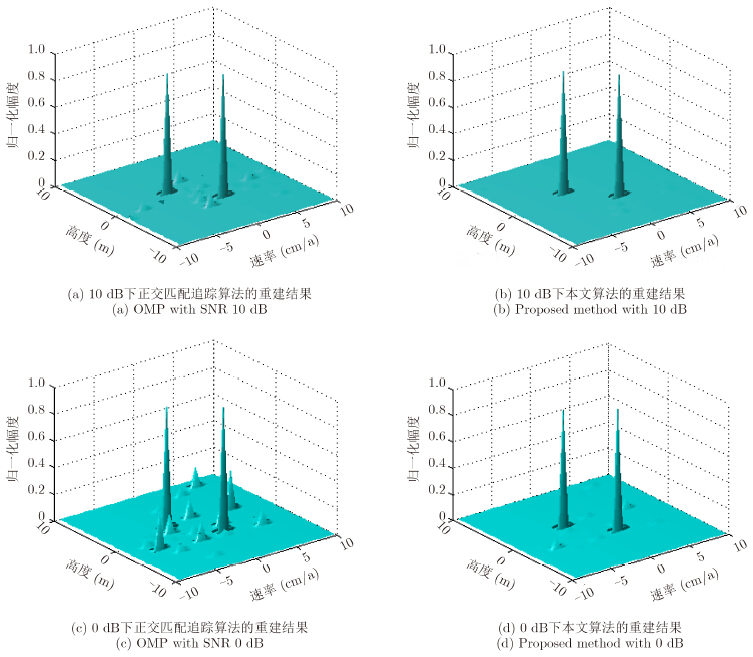 | 图 3 4维合成孔径雷达高度-速率重建结果比较 Fig.3 Comparison of the height-velocity reconstruction results of 4D SAR |
仿真实验结果表明,传统正交匹配追踪算法和本文算法在高信噪比下均可获得良好的目标高度-速率维重建结果,两个目标的高度和速率信息均能很好地反映在图像上。尤其是本文算法对旁瓣的抑制效果要好于传统正交匹配追踪算法。当信噪比降为0 dB时,传统正交匹配追踪算法获得的重建结果中出现很多虚假目标,干扰了对真实目标的判断,而本文算法在低信噪比下能有效抑制虚假目标影响,准确估计真实目标的高度和速率信息。
为验证本文算法对不同散射系数目标的成像性能。我们进行了仿真实验。假设某一方位-斜距分辨单元有3个散射点,散射系数分别为3,2和1,分别位于高度位置2 m,-2 m和2 m处,相应的变化速率分别为-0.02 m/a,0.02 m/a和0.02 m/a。并在接收数据中添加了方差为1的加性高斯白噪声。传统正交匹配追踪算法获得的高度-速率维重建结果如图 4(a)所示,本文提出算法获得的高度-速率维重建结果如图 4(b)所示。从图 4可以看出,传统正交匹配追踪算法获得的成像结果中弱目标几乎被噪声所掩盖,很难从噪声中正确识别散射系数最小的目标,但是本文算法对不同散射系数的目标仍然能够正确重建。
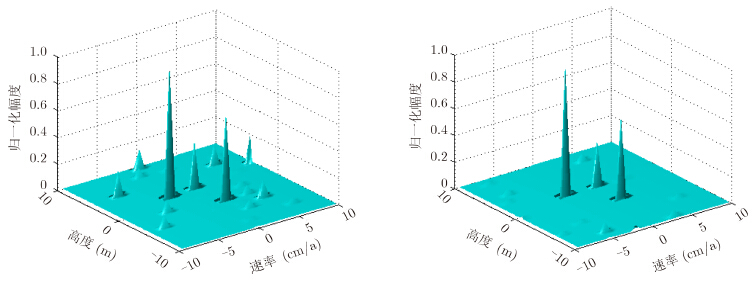 | 图 4 不同散射系数目标高度-速率重建结果比较 Fig.4 Comparison of the height-velocity reconstruction results of different scattering factors targets |
本文算法需要进行迭代来获得最终的重建结果。为定量分析算法的收敛性能,我们给出了不同迭代次数下重建图像与真实图像之间的重建误差${{\|\hat x - }x\|_2} / \|x\|_2$来进行定量分析。其中$\hat x$表示重建图像,x表示真实图像。图 5给出了不同迭代次数下的重建误差曲线。从图 5可看出经过很少的迭代次数后就可获得满意的重建效果。
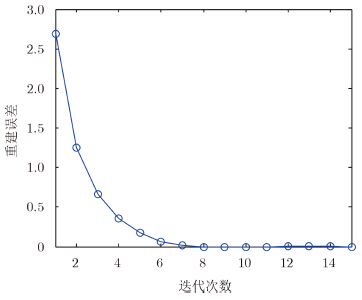 | 图 5 不同迭代次数下的重建误差曲线 Fig.5 Reconstruction error with varying iterations |
合成孔径雷达4维成像技术是传统微波成像技术的扩展,与采用单一散射体假设的差分干涉合成孔径雷达相比,能够最大限度地追踪目标数量,估计层叠散射体的相对形变,提高了对复杂散射体的监测能力。在未来城市规划、地表沉降、冰川和地下掩埋物探测等领域具有重要的应用价值和巨大的应用潜力。本文将4维合成孔径雷达高度-速率成像问题转化为目标复散射系数的幅度和相位联合重建问题,提出了一种基于幅度和相位迭代重建的4维合成孔径雷达成像方法,通过在成像过程中引入相位信息来提高重建质量。仿真分析表明,该方法在低信噪比下能有效抑制虚假目标影响,改善成像质量。
| [1] | Morrison K, Bennett J C, and Nolan M. Using DInSAR to separate surface and subsurface features[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(6): 3424-3430.( 1) 1) |
| [2] | Fornaro G, D’Agostino N, Giuliani R, et al.. Assimilation of GPS-derived atmospheric propagation delay in DInSAR data processing[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(2): 784-799.( 1) 1) |
| [3] | Fornaro G, Reale D, and Serafino F. Four-dimensional SAR imaging for height estimation and monitoring of signal and double scatterers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(1): 224-237.( 1) 1) |
| [4] | Lombardini F. Differential tomography: a new framework for SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(1): 37-44.( 1) 1) |
| [5] | Reigber A, Lombardini F, Viviani F, et al.. Three-dimensional and higher-order imaging with tomographic SAR: techniques, applications, issues[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 2015: 2915-2918.( 1) 1) |
| [6] | Serafino F, Soldovieri F, Lombardini F, et al.. Singular value decomposition applied to 4D SAR imaging[C]. IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Seoul, Korea, 2005: 2701-2704.( 1) 1) |
| [7] | 孙希龙, 余安喜, 董臻, 等. 一种差分SAR层析高分辨成像方法[J]. 电子与信息学报, 2012, 34(2): 273-278. Sun Xi-long, Yu An-xi, Dong Zhen, et al.. A high resolution method for differential SAR tomography[J]. Journal of Electronics & Information Technology, 2012, 34(2): 273-278.( 1) 1) |
| [8] | 任笑真, 杨汝良. 一种基于逆问题的差分干涉SAR层析成像方法[J]. 电子与信息学报, 2010, 32(3): 582-586. Ren Xiao-zhen and Yang Ru-liang. An inverse problem based approach for differential SAR tomography imaging[J]. Journal of Electronics & Information Technology, 2010, 32(3): 582-586.( 2) 2) |
| [9] | Candes E J, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.( 2) 2) |
| [10] | Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.( 1) 1) |
| [11] | Zhu X X and Bamler R. Sparse reconstruction techniques for SAR tomography[C]. 17th International Coference on Digital Signal Processing, Corfu, Greece, 2011: 1-8.( 1) 1) |
| [12] | Ren Xiao-zhen and Chen Li-na. Four-dimensional SAR imaging algorithm using Bayesian compressive sensing[J]. Journal of Electromagnetic Waves and Applications, 2014, 28(13): 1661-1676.( 1) 1) |
| [13] | Cetin M and Karl W C. Feature enhanced synthetic aperture radar image formation based on non-quadratic regularization[J]. IEEE Transactions on Image Processing, 2001, 10(4): 623-631.( 3) 3) |
| [14] | Samadi S, Cetin M, and Masnadi-Shirazi M A. Sparse representation-based synthetic aperture radar imaging[J]. IET Radar, Sonar & Navigation, 2011, 5(2): 182-193.( 1) 1) |


