1 引言

UHF波段雷达作为国家防御体系中的重要环节，肩负预警和目标探测等重要任务。随着人类电磁活动日益频繁，电磁波频率互调交调等造成频谱间相互串扰现象严重，使得UHF波段雷达所面临的电磁环境日益复杂，特别是随着无线通信业务的广泛推广，UHF波段雷达不可避免地受到来自同频段GSM(Global System for Mobile Communication)移动基站通信信号的干扰，从而会影响到雷达对目标的正常探测和跟踪^[1]。GSM基站信号虽然在时频域上具有特定的调制编码形式，然而由于承载大量业务信息，无法预先为雷达装订，因此就雷达而言该类信号类似于噪声干扰，仅从时频域角度往往难以从该类信号中分离出雷达目标回波。

除时频域信息外，对电磁波极化信息的获取与处理为改善雷达信息获取能力提供新的思路。文献[2]提出了对通信基站信号采用极化滤波抑制方法，对主波束内基站干扰信号能够有效抑制。对于极化度较高的电磁波信号而言，一般可以基于传统确定性极化表征方法予以分析和处理，主要包括极化椭圆、Jones矢量、极化比和Stokes矢量等。然而在当雷达实际工作环境周围存在多个基站时，接收到的信号极化度会严重下降，且极化状态起伏更加剧烈，仍采用确定性极化描述方法表述时会存在较大误差，近年来关于电磁波极化统计特性的研究受到广泛的关注。

早期对电磁波极化统计特性的研究工作，集中在波的幅度、相位、极化椭圆几何描述子以及Stokes矢量等极化参量上：Ecker等人给出了左右旋圆极化基下的电磁波幅度比统计特性^[3]；文献[4]在线极化假设下给出了两极化信号相位差的统计特性；Barakat基于部分极化光的统计特性，分析了高斯假设下Stokes矢量的概率密度函数^{[5, 6]}。Touzi等人通过分析极化SAR图像Stokes矢量的统计特性，验证了概率密度函数模型的正确性^[7]。无论是极化比、极化椭圆或是Stokes矢量一方面均需要至少对两个或两个以上参数分别做统计分析，才能完整描述极化特性，另一方面因为会受到极化基的选取的影响而不具有极化不变性，造成难以在同一量化标准下开展对比性分析。相比而言极化度作为描述电磁波极化纯度的一个重要参量，常作为极化滤波器性能的关键指标^[8]，在极化滤波抗干扰领域中具有重要的作用。此外，由于其良好的鲁棒性且具有不受极化基变换影响等优势，近年来逐渐成为雷达极化学的一个研究热点^{[9, 10, 11, 12, 13]}，极化度属性方面，文献[9, 10, 11]给出了极化度同极化反射率、线性去极化率、交叉极化相关系数等极化参量间的对应关系，验证了极化度在鲁棒性方面的优势；极化度统计特性方面Rio^[12]和Medkou^[13]等人则分别推导了复高斯假设下极化度的概率密度函数模型。目前对于极化度的研究多停留在基础理论层面，相关的实验分析则鲜有报道。

本文首先建立了具有正交双极化同时接收能力的雷达接收信号极化模型，在Stokes矢量极化表征基础上，基于随机矢量正态分布假设推导了极化比和极化度的概率密度函数，进而设计并开展了针对单个基站和多个基站情形的UHF雷达接收基站信号的外场实验，通过极化处理方法分析了通信基站信号的极化特性，统计极化幅度比、相位差以及极化度的分布直方图，并分别同理论推导的概率密度函数进行拟合，最后给出了单基站和多基站情形下雷达接收信号极化的差异性分析。

2 双极化雷达接收电磁波的极化表征模型 2.1 极化状态表征

极化表示电磁波矢量端点的运动轨迹，由于电磁波矢量位于垂直于传播方向的平面内，其运动轨迹可用椭圆表述，椭圆的形状和倾角定义了波的极化状态。考虑极化雷达系统具有水平和垂直正交双极化接收能力，且水平、垂直通道能够在各自极化基下同时采集到达天线的电磁波信号。当电磁波沿固定方向传播时，两极化基下接收到的电磁波瞬时时域信号分别表示为S_h(t)和S_v(t)，则在该组极化基下可定义“瞬时Jones矢量”如下式所示：

$S(t)=\left[\begin{array}{*{35}{l}} {{S}_{\text{h}}}(t) \\ {{S}_{\text{v}}}(t) \\ \end{array} \right]=\left[\begin{array}{*{35}{l}} \ \ {{A}_{\text{h}}}(t) \\ {{A}_{\text{v}}}(t){{\text{e}}^{\text{j}\delta (t)}} \\ \end{array} \right]\cdot S(t)$

(1)

式中，A_h(t)和A_v(t)分别表示水平和垂直极化基下的瞬时幅度，δ(t)为极化相位差，S(t)表示电磁波的相干波形。当电磁波为完全极化波时极化幅度比和相位差不会随时间而变化，即满足

$\frac{{{A_{\text{v}}}(t)}}{{{A_{\text{h}}}(t)}} = {\text{constant}},\delta (t) = {\text{constant}}$

(2)

不难看出，当电磁波在完全极化状态下Jones 矢量能够给出基本的极化表征。而当电磁波为部分极化波时，通常利用该矢量成分的2阶统计特性也可用于描述接收电磁波的极化，也就是通常定义的Stokes矢量^[6]

${J} = \left[{\begin{array}{*{20}{l}} {{g_0}} \\ {{g_1}} \\ {{g_2}} \\ {{g_3}} \end{array}} \right] = \left[{\begin{array}{*{20}{l}} {\left\langle {{{\left| {{S_{\text{h}}}} \right|}^2}} \right\rangle + \left\langle {{{\left| {{S_{\text{v}}}} \right|}^2}} \right\rangle } \\ {\left\langle {{{\left| {{S_{\text{h}}}} \right|}^2}} \right\rangle - \left\langle {{{\left| {{S_{\text{v}}}} \right|}^2}} \right\rangle } \\ {\quad \;\;{\mkern 1mu} 2{\text{Re}}\left\langle {{S_{\text{h}}}S_{\text{v}}^*} \right\rangle } \\ {\quad - 2{\text{Im}}\left\langle {{S_{\text{h}}}S_{\text{v}}^*} \right\rangle } \end{array}} \right]$

(3)

其中，$\left\langle \cdot \right\rangle $代表期望值，Re 代表复数实部，Im 代表虚部。根据Stokes矢量，部分极化波可以被分解为一个完全极化波${J_{{\rm{cp}}}} = {[{g_p}{\mkern 1mu} {g_1}{\mkern 1mu} {g_2}{\mkern 1mu} {\mkern 1mu} {g_3}]^{\rm{T}}}$和一个完全未极化波${J_{\rm{u}}} = {\left[{\left( {{g_0} - {g_p}} \right)0\;0\;0} \right]^{\rm{T}}}$的和，这里$g_{\text{p}}^2 = g_1^2 + g_2^2 + g_3^2$。电磁波的极化度是表示部分极化波中完全极化成分的功率与波的总功率的比值，即可定义为P=${g_{\rm p}}/{g_0}$，当P=0时代表完全未极化波，P=1时表示完全极化波。

2.2 极化比统计模型

通过实际观测发现，雷达接收电磁波信号的极化特性会随时间呈起伏变化，因此极化雷达研究工作者利用统计学理论开展了相关的电磁波极化特性研究，通常将电磁波视为一个具有各态历经性的平稳随机过程，并假设Jones矢量$S$服从零均值2维复高斯随机分布，其协方差矩阵为Hermit矩阵，用${\bf{\Sigma }} = {\text{ }}\left\langle {{\bf{S}}{\rm{ }}{{\bf{S}}^H}} \right\rangle = \left[{\begin{array}{*{20}{l}} {\sigma _{{\text{hh}}}^2\;\;{\sigma _{{\text{hv}}}}} \\ {{\sigma _{{\text{vh}}}}\;\;\sigma _{{\text{vv}}}^2} \end{array}} \right]$表示，根据Hermit矩阵的性质，有${\sigma _{{\rm{hv}}}} = \sigma _{{\rm{vh}}}^*$，则根据文献[4]可知，接收信号极化矢量满足如下概率密度函数：

$f\left( {\bf{S}} \right) = \frac{{\rm{1}}}{{{{\rm{\pi }}^2}\left| {\bf{\Sigma }} \right|}} \cdot \exp \{ - \frac{{\sigma _{{\text{vv }}}^2{{\left| {{S_{\text{h}}}} \right|}^2} + \sigma _{{\text{hh }}}^2{{\left| {{S_{\text{v}}}} \right|}^2} - 2{\text{Re}}({\sigma _{{\text{hv }}}}S_{\text{h}}^*{S_{\text{v}}})}}{{\left| {\bf{\Sigma }} \right|}}\} {\text{ }}$

(4)

令${S_{\text{h}}}\; = \;{a_{\text{h}}}{{\text{e}}^{{\text{j}}{\varphi _{\text{h}}}}},{S_{\text{v}}}\; = \;{a_{\text{v}}}{{\text{e}}^{{\text{j}}{\varphi _{\text{v}}}}}$以及${\bf{delta}} = \;{\varphi _{\text{h}}} - {\varphi _{\text{h}}} + \arg ({\sigma _{{\text{hv}}}})$，这里$\arg \left( \cdot \right)$代表求复角，将其代入式(4)可以得到水平垂直极化基下的极化幅度和相位差的联合概率密度函数为：

$\begin{gathered} f({a_{\text{h}}},{a_{\text{v}}},\delta ) = \frac{{2{a_{\text{h}}}{a_{\text{v}}}}}{{{\rm{\pi }} \left( {\sigma _{{\text{hh}}}^2\sigma _{{\text{vv}}}^2 - {{\left| {{\sigma _{{\text{hv}}}}} \right|}^2}} \right)}} \hfill \\ \cdot \exp - \left\{ {\frac{{\sigma _{{\text{vv}}}^2a_{\text{h}}^2 + \sigma _{{\text{hh}}}^2a_{\text{v}}^2 - 2\left| {{\sigma _{{\text{hv}}}}} \right|{a_{\text{h}}}{a_{\text{v}}}\cos (\delta )}}{{\left( {\sigma _{{\text{hh}}}^2\sigma _{{\text{vv}}}^2 - {{\left| {{\sigma _{{\text{hv}}}}} \right|}^2}} \right)}}} \right\} \hfill \\ \end{gathered} $

(5)

用$\rho = \frac{{{a_{\rm{v}}}}}{{{a_{\rm{h}}}}}$表示极化幅度比，代入式(5)后得到$(\rho ,{a_{\text{h}}},\delta )$的联合密度函数：

$\begin{align} & f(\rho ,{{a}_{\text{h}}},\delta )=\frac{2\rho a_{\text{h}}^{3}}{{\rm{\pi }} \left( \sigma _{\text{hh}}^{2}\sigma _{\text{vv}}^{2}-{{\left| {{\sigma }_{\text{hv}}} \right|}^{2}} \right)} \\ & \cdot \exp \left\{ -\frac{\sigma _{\text{vv}}^{2}+\sigma _{\text{hh}}^{2}{{\rho }^{2}}-2\left| {{\sigma }_{\text{hv}}} \right|\rho \cos (\delta )}{\sigma _{\text{hh}}^{2}\sigma _{\text{vv}}^{2}-{{\left| {{\sigma }_{\text{hv}}} \right|}^{2}}}a_{\text{h}}^{2} \right\} \\ \end{align}$

(6)

对式(6)中a_h从0～＋$\infty $积分可以得到幅度比和相位差的联合分布函数：

$\begin{align} & f(\rho ,\delta )=\int_{0}^{\infty }{f(\rho ,{{a}_{\text{h}}},{\bf{\Sigma }} )}\text{d}{{a}_{\text{h}}} \\ & =\frac{\rho \left( \sigma _{\text{hh}}^{2}\sigma _{\text{vv}}^{2}-{{\left| {{\sigma }_{\text{hv}}} \right|}^{2}} \right)}{{\rm{\pi }} {{\left[\sigma _{\text{vv}}^{2}+\sigma _{\text{hh}}^{2}{{\rho }^{2}}-2\rho \left| {{\sigma }_{\text{hv}}} \right|\cos (\delta ) \right]}^{2}}} \\ \end{align}$

(7)

再对相位差δ(积分限[0,2π])积分，即可得到极化幅度比的概率密度函数：

$f(\rho )=\frac{2\rho \left| {\bf{\Sigma }} \right|\left( \sigma _{\text{vv}}^{2}+\sigma _{\text{hh}}^{2}{{\rho }^{2}} \right)}{{{\left[{{\left( \sigma _{\text{vv}}^{2}+\sigma _{\text{hh}}^{2}{{\rho }^{2}} \right)}^{2}}-4{{\rho }^{2}}{{\left| {{\sigma }_{\text{hv}}} \right|}^{2}} \right]}^{3/2}}}$

(8)

另一方面重新对式(5)中的a_h和a_v分别从0～＋$\infty $作连续积分，可以得到极化相位差的概率密度函数：

$\begin{align} & f(\delta )=\frac{\left| {\bf{\Sigma }} \right|}{2{\rm{\pi }}\ \left( \sigma _{\text{hh}}^{2}\sigma _{\text{vv}}^{2}-{{\left| {{\sigma }_{\text{hv}}} \right|}^{2}}{{\cos }^{2}}(\delta ) \right)}\cdot \\ & \left[1+\frac{\gamma }{\sqrt{1-{{\gamma }^{2}}}}\left( \frac{\pi }{2}\text{+arctan}\frac{\gamma }{\sqrt{1-{{\gamma }^{2}}}} \right) \right] \\ \end{align}$

(9)

式中，$\gamma = \frac{{\left| {{\rm{ }}{\sigma _{{\rm{hv}}}}{\rm{ }}} \right|}}{{{\sigma _{{\rm{hh}}}}{\rm{ }}{\sigma _{{\rm{vv}}}}}}\cos (\delta )$，根据式(8)和式(9)得到了极化比全部参量的理论分布函数。

2.3 极化度估计量统计模型

根据上节内容可知，若要完整描述电磁波极化的统计特性，极化比表征至少需要两个参数，而Stokes表征则至少需要4个，由于各个参数都具有不同的分布特性，因此较难在统一的尺度下表征极化特性，相比而言极化度作为描述电磁波极化特性的重要参量具有良好的鲁棒性，并且不会随极化基的选取而变化等优势。在实际应用中，极化度已被许多研究人员广泛应用于雷达探测、地理信息遥感以及光学等领域。特别是在雷达探测方面，极化SAR通过测量极化度可以用于各类地形地貌的信息识别，例如城市、农田、海洋等^[14]。此外，极化度还被用做检验统计量来检测均匀杂波环境中的人造金属目标(包括高压电线塔、舰船、浮标以及油井等等)^[15]。

实际工程中待测信号的真实极化度难以预先掌握，因此我们需要通过对电磁波信号时间采样序列的相关处理对其进行估计并推导其统计分布模型。雷达接收信号的瞬时Jones矢量仍然如式(1)所示，其服从复高斯分布，首先利用采集的Jones矢量样本由式(3)能够得到的Stokes矢量的估计值，定义为$\hat J = {[{\hat g_0}{\mkern 1mu} {\hat g_1}{\mkern 1mu} {\hat g_2}{\mkern 1mu} {\hat g_3}]^{\text{T}}}$，则其在复高斯分布下的K个样本的联合分布函数可从文献[12]的结论中得到：

$\begin{gathered} f(\hat J) = \frac{{4{K^{2K}}}}{{{\rm{\pi }} \Gamma (K)\Gamma (K - 1)}}\frac{{{{(\hat g_0^2 - \hat g_1^2 - \hat g_2^2 - \hat g_3^2)}^{K - 2}}}}{{{{(g_0^2 - g_1^2 - g_2^2 - g_3^2)}^K}}} \hfill \\ \cdot \exp \left[{ - 2K\frac{{{g_0}{{\hat g}_0} - {g_1}{{\hat g}_1} - {g_2}{{\hat g}_2} - {g_3}{{\hat g}_3}}}{{g_0^2 - g_1^2 - g_2^2 - g_3^2}}} \right] \hfill \\ \end{gathered} $

(10)

式中G$\left( \cdot \right)$代表Gamma函数，根据极化度同Stokes矢量的关系，极化度估计量可表示为$\hat p = {\hat g_{\rm p}}/{\hat g_0}$，其中 $\hat g_{\rm p}^2 = \hat g_1^2 + \hat g_2^2 + \hat g_3^2$，定义

$g_{\rm e}^2 = g_0^2 - g_{\rm p}^2 = g_0^2 - g_1^2 - g_2^2 - g_3^2$

(11)

则极化度还可表示为：

$P = \frac{{{g_{\rm p}}}}{{{g_0}}} = \frac{{\sqrt {g_0^2 - g_{\rm e}^2} }}{{{g_0}}}$

(12)

作如下变量替换

$\left\{ {\begin{array}{*{20}{l}} {A = \hat g_0^2 - \hat g_1^2 - \hat g_2^2 - \hat g_3^2} \\ {B = \hat g_0^2} \\ {C = \sqrt {\hat g_2^2 + \hat g_3^2} } \\ {\phi = {\text{atan}}\frac{{{{\hat g}_3}}}{{{{\hat g}_2}}}} \end{array}} \right.$

(13)

可以给出其反函数

$\!\left\{\!\!\! \begin{array}{l} {{\hat g}_0} = \sqrt B \\ {{\hat g}_1} = \sqrt {B - A - {C^2}} \\ {{\hat g}_2} = C\cos \phi \\ {{\hat g}_3} = C\sin \phi \end{array} \right. \!\!\!,\! \left\{\!\!\! \begin{array}{l} {{\hat g}_0} = \sqrt B \\ {{\hat g}_1} = - \sqrt {B - A - {C^2}} \\ {{\hat g}_2} = C\cos \phi \\ {{\hat g}_3} = C\sin \phi \end{array} \right.$

(14)

求出对应的雅克比因子$\left| {{J_1}} \right| = \left| {{J_2}} \right| = $$ \frac{C}{{4\sqrt B \sqrt {B - A - {C^2}} }}$，代入后可得：

$\begin{gathered} f(A,B,C,\phi ) = \frac{{{K^{2K}}}}{{{\rm{\pi }} \Gamma (K)\Gamma (K - 1)}}\frac{{{{(A)}^{K - 2}}}}{{{{(g_{\text{e}}^2)}^K}}}\frac{C}{{\sqrt B \sqrt {B - A - {C^2}} }} \hfill \\ \cdot \left\{ {\exp \left[{ - 2K\frac{{{g_0}\sqrt B - {g_1}\sqrt {B - A - {C^2}} - {g_2}C\cos \phi - {g_3}C\sin \phi }}{{g_{\text{e}}^2}}} \right]} \right. \hfill \\ \left. { + \exp \left[{ - 2K\frac{{{g_0}\sqrt B + {g_1}\sqrt {B - A - {C^2}} - {g_2}C\cos \phi - {g_3}C\sin \phi }}{{g_{\text{e}}^2}}} \right]} \right\} \hfill \\ \end{gathered} $

(15)

对φ积分可得(利用文献[16]3.338-4.6)：

$\begin{array}{l} f(A,B,C) = \int_{ - \pi }^\pi {f(A,B,C,\phi ){\rm{d}}\phi } \\ = \frac{{2{K^{2K}}}}{{\Gamma (K)\Gamma (K - 1)}}\frac{{{{(A)}^{K - 2}}}}{{{{(g_{\rm{e}}^2)}^K}}}\frac{C}{{\sqrt B \sqrt {B - A - {C^2}} }}\exp \left( { - \frac{{2K{g_0}\sqrt B }}{{g_{\rm{e}}^2}}} \right){\rm{ }}\\ {\rm{ }} \cdot \left\{ {\exp \left[ {2K\frac{{{g_1}\sqrt {B - A - {C^2}} }}{{g_{\rm{e}}^{\rm{2}}}}} \right]} \right.\left. { + \exp \left[ { - 2K\frac{{{g_1}\sqrt {B - A - {C^2}} }}{{g_{\rm{e}}^{\rm{2}}}}} \right]} \right\}{\rm{ }}\\ {\rm{ }} \cdot {I_0}\left( {\frac{{2KC\sqrt {g_2^2 + g_3^2} }}{{g_{\rm{e}}^{\rm{2}}}}} \right) \end{array}$

(16)

对C 积分(做变量替换$x = \sqrt {1 - \frac{{{C^2}}}{{B - A}}} $，并利用文献[16]6.616-5.3)可得：

$\begin{array}{l} f(A,B) = \int_0^{\sqrt {B - A} } {f(A,B,C){\rm{d}}C} \\ = \frac{{2{K^{2K - 1}}}}{{\Gamma (K)\Gamma (K - 1)}}\frac{{{{(A)}^{K - 2}}}}{{{{(g_{\rm{e}}^2)}^{K - 1}}}}\frac{1}{{{g_{\rm{p}}}}}\frac{1}{{\sqrt B }}\\ \cdot \exp \left( { - \frac{{2K{g_0}}}{{g_{\rm{e}}^2}}\sqrt B } \right)\\ \cdot \sinh \left( {\frac{{2K{g_{\rm{p}}}}}{{g_{\rm{e}}^2}}\sqrt {B - A} } \right) \end{array} $

(17)

令$\hat z = \frac{A}{B},\hat w = B$，其雅克比因子为$\hat w$，代入式(17)得：

$\begin{array}{l} f(\hat z,\hat w) = \frac{{2{K^{2K - 1}}}}{{\Gamma (K)\Gamma (K - 1)}}\frac{{{{(\hat z)}^{K - 2}}}}{{{{(g_{\rm{e}}^2)}^{K - 1}}}}\frac{1}{{{g_{\rm{p}}}}}\\ \cdot {{\hat w}^{K - 3/2}}\exp \left( { - \frac{{2K{g_0}}}{{g_{\rm{e}}^2}}\sqrt {\hat w} } \right)\\ \cdot \sinh \left( {\frac{{2K{g_{\rm{p}}}\sqrt {1 - \hat z} }}{{g_{\rm{e}}^2}}\sqrt {\hat w} } \right) \end{array} $

(18)

对$\hat w$积分得到$\hat z$的概率密度函数(令$x = \sqrt {\hat w} $利用文献[16]2.482-1和2.321-1)

$\begin{gathered} f(\hat z) = \frac{{\Gamma (2K - 1)}}{{\Gamma (K)\Gamma (K - 1)}}\frac{{{{(\hat z)}^{K - 2}}}}{{{{(g_e^2)}^{K - 1}}}}\frac{1}{{{g_p}}} \hfill \\ \cdot \left[{{{\left( {\frac{{2{g_0}}}{{g_e^2}} - \frac{{2{g_p}}}{{g_e^2}}\sqrt {1 - \hat z} } \right)}^{1 - 2K}}} \right. \hfill \\ \left. { - {{\left( {\frac{{2{g_0}}}{{g_e^2}} + \frac{{2{g_p}}}{{g_e^2}}\sqrt {1 - \hat z} } \right)}^{1 - 2K}}} \right] \hfill \\ \end{gathered} $

(19)

令$\hat p = \sqrt {1 - \hat z} $，代入式(19)，可得到极化度估计量的概率密度函数：

$\begin{gathered} f(\hat p) = \frac{{{4^{1 - K}}{{(1 - {P^2})}^K}{{(1 - \hat p)}^{K - 2}}\hat p}}{{B(K,K - 1)P}} \hfill \\ \cdot \left[{{{\left( {1 - P\hat p} \right)}^{1 - 2K}} - {{\left( {1 + P\hat p} \right)}^{1 - 2K}}} \right] \hfill \\ \end{gathered} $

(20)

3 UHF雷达干扰环境测量

为验证第2节给出的极化模型，并分析雷达面临基站干扰环境的极化特性，于2014年10月25日和2015年7月13日分两个批次开展了UHF波段极化雷达接收周围通信基站信号的外场实验。实验地点设置在湖北省武汉市花山附近，一部具有水平垂直双极化同时接受能力的UHF波段雷达系统被用于获取干扰环境数据。接收天线如图 1所示，它是由2行8列个正交双极化偶极子阵元构成，图中红色数字表示阵元序号。表 1则进一步给出了所采用的雷达试验系统的主要参数，可以看出交叉极化和极化隔离度均具有较高指标。

雷达所处工作频段主要会受到GSM基站信号的影响，GSM通信系统采用蜂窝FDMA(频分多址)+TDMA(时分多址)方式通信，移动台发射信号的链路称为上行链路(890-915 MHz)，基站发射信号的链路称为下行链路(935-960 MHz)，一个脉冲串承载一个时隙所传输的信息，称为“突发”，每个“突发”可以看成是时宽约577 μs，带宽200 kHz的窄带调制信号^[2]。

实验中分别针对单个基站情形和多基站情形，利用两正交极化通道同时采集GSM信号，再通过离线分析不同情形下电磁波极化特性。图 2给出了两种情形下的测量及数据处理流程。

具体实验过程如下：

(1) 单基站GSM信号接收

选取试验点附近某一通信基站，首先利用频谱仪接一对数周期天线测量该基站辐射电磁波信号的中心频率，结果显示该基站下行信号频率为953.2 MHz，将雷达接收机工作频率调至该频点附近，并使雷达双极化天线中心指向待测基站天线，雷达接收机开机，并接通采集卡录取基站信号数据。雷达接收机带宽约1.2 MHz，大于基站信号带宽200 kHz，采用数字滤波方式对接收信号预处理，从而获取中心频点为953.2 MHz，带宽200 kHz的较为纯净的单基站下行信号样本。

(2) 多基站GSM信号接收

雷达在实际工作当中，周围往往存在多个基站，且相邻基站间所采用的频道相隔不大，即所辐射的射频信号频谱比较接近，当接收机带宽覆盖多个基站所使用的频道时，同一时刻可能有多部基站信号进入雷达接收机，形成多基站干扰情形。对于此类情形的测量，我们设定雷达工作频率为940 MHz(经测量发现雷达所处位置周围辐射该频率信号的基站数量较多)，令雷达天线按固定转速(约10 s/转)旋转，水平垂直接收通道同时采样接收，接收机处理过程与单基站时相同，为了同时获取多个基站的混叠信号，不再像单基站信号测量时所采用的对所录取的数据做窄带滤波处理，而直接进行极化特性分析。下节将给出两种场景下雷达接收基站信号极化特性的分析。

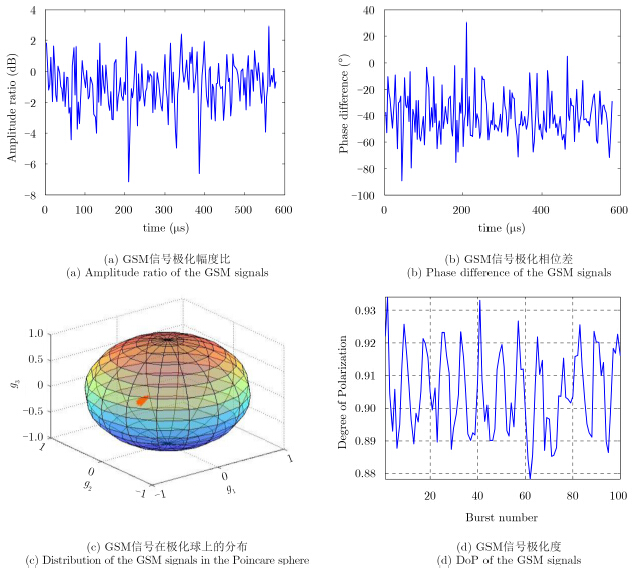
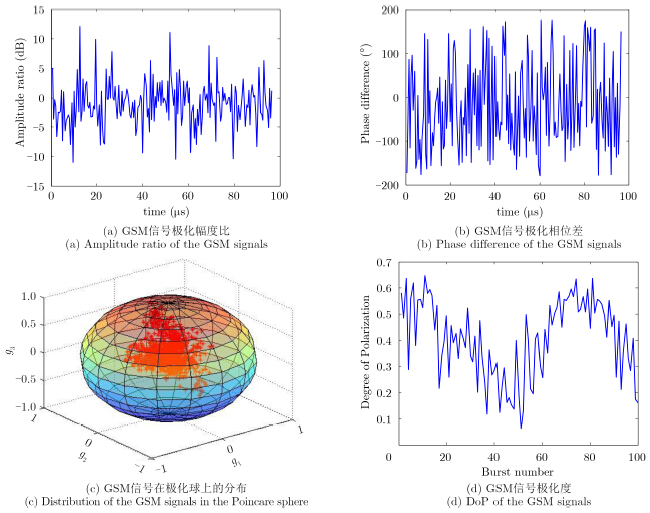
4 基站干扰信号极化特性分析 4.1 极化状态分析

利用实验采集到的数据，首先开展极化状态分析，分析内容包括信号样本的极化比与极化度，以及其Stokes矢量在Poincare球上的分布情况。极化比通过将两路极化通道每组采集样本的复数据直接求比值得到，Stokes矢量的计算方法如式(3)和式(12)所示。分别将单基站和多基站场景下每组样本的极化参量计算结果绘制在图 3和图 4中。其中图 3(a)，图 3(b)和图 4(a)，图 4(b)分别为两种场景下获得信号的极化幅度比和极化相位差，不难看出无论是哪种情形下，极化幅度比和相位差都随时间呈现出一定的起伏特性。各场景下极化参量的统计结果则被列在表 2中，其中左边两列经统计计算进一步给出了极化幅度比和相位差的样本均值和标准差，通过标准差值的对比可见单一基站信号的极化起伏程度明显小于多基站信号。

从数据样本中随机选取100个“突发”信号，利用式(3)估计电磁波信号极化Stokes矢量，并将其归一化后描绘在Poincare极化球上，单基站和多基站情形下观测到的GSM信号极化Stokes矢量分别被绘制在图 3(c)和图 4(c)上。单个基站的GSM信号Stokes矢量分布较为集中，接近右旋椭圆极化；而多基站信号则呈现散布状态，没有明显占优的极化。

极化度的估计结果可以在Stokes矢量的基础上，利用式(12)计算得到，两个场景下每个“突发”信号的极化度如图 3(d)和图 4(d)所示。由于单基站情形下，无论基站天线或是雷达天线都相对固定，从图 3(d)可以看出，该情形下信号极化度普遍较高且起伏较小，位于0.88～0.93之间；而多基站由于非相干信号的叠加，雷达接收到的合成信号极化度下降严重，如图 4(d)所示其起伏更加剧烈，在0.10～0.65之间均有分布。与极化比类似，表 2的右边一列给出了极化度均值和标准差的统计结果。综合以上分析可以说明，对于极化度较高的信号(如单基站情形)，利用传统极化表征方法，例如Stokes矢量、极化椭圆和极化比等确定性极化表征方法可以较好地予以描述，在此基础，无论采用极化增强或极化滤波手段处理该类信号，都可以达到预期的增强或抑制效果。而对于电磁波极化度较低的信号(如多基站情形)，从图 4(c)中可以看出该类信号极化散布程度严重，对于此类没有明显极化占优的情形，难以采用确定性极化表征手段加以描述，因此，拟通过统计表述的研究手段分析其极化特性。

4.2 极化统计特性分析

本节将利用极化比和极化度作为统计参量，描述不同情形下雷达接收干扰信号的极化特性，通过对比实测数据和理论概率密度函数，一方面验证极化度统计模型的正确性，另一方面寻找不同情形下雷达面临基站干扰环境的极化特性差异，并分析其原因。在上节基础利用两类场景下极化幅度比和相位差计算结果绘制统计直方图如图 5中的圆圈符号所示，图 5(a)和图 5(c)上的实线对应式(8)所表示的极化幅度比理论概率密度函数，而由式(9)描述的相位差概率密度函数则对应如图 5(b)和图 5(d)上的实线。从图中良好的拟合结果可以看出，无论是单基站或是多基站情形，利用极化比统计模型均可以予以准确描述。

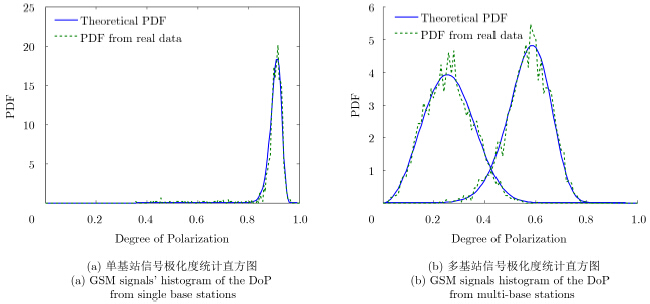
设定用于估计极化度的每组样本点数为32，以0.01为间隔统计极化度的概率密度直方图，不同情形下实测数据的极化度统计结果如图 6(a),6(b)中虚线所示，图中实线所代表的理论极化度概率密度函数曲线由式(20)获得，真实极化度参数用所有样本的平均极化度近似代替。同样可以看出理论曲线和统计结果能够很好地拟合，从而验证了本文推导的极化度统计模型的正确性和适用性。

对比图 6(a)，图 6(b)可知，单基站信号极化度较多基站极化度更高，且分布更为集中。相比于传统确定性极化描述方法对多基站信号难以准确描述而言，利用统计表征方法可以概括其分布特性。图 6(b)两条分离开的曲线分别由天线处于不同方位角时的测量数据统计得到，极化度较低的曲线代表天线主瓣方向没有功率较强的基站信号，基站信号主要从副瓣进入接收机；极化度较高的曲线代表天线主波束内存在较近距离基站，主瓣方向基站使极化度提高，但由于副瓣基站信号的非相干合成，总的极化度明显低于单基站信号极化度。

5 结论

对单基站的测量结果说明，基站信号在时频域上由于承载了编码信息，而这些信息不能为雷达所用，可被视为噪声干扰，而极化域的分析显示，该类信号具有明显的极化特征，且极化度较高。单个基站信号的极化状态呈现部分极化特性，其Stokes矢量点以Poincare球体内某点为中心，随机分布在其周围。单一基站信号的极化度呈现随机起伏特性，可以认为影响接收信号极化度的主要环境因素包括接收机噪声、多径效应、大气传输效应、通道耦合效应等因素。

多个基站的测量结果显示，接收信号功率很强，不仅在时频域上没有明显特征，极化的确定性特征同样不明显，主要表现在极化度较低，极化状态起伏剧烈。这是因为多个基站情况下，由于雷达天线转动，不可避免存在强功率基站信号从天线副瓣方向进入接收机，而实际极化雷达天线通常只对波束中心方向的极化予以校准，副瓣的信号与主瓣信号的叠加而可能造成接收信号极化度下降。另一方面，主瓣内还可能存在同频基站干扰问题，即基站信号即使从主瓣进入，若主瓣内存在两个或两个以上同频基站，由于基站间信号不相干，也会造成接收信号极化度下降。

本文以UHF波段雷达面临基站干扰信号的极化特性为例，说明了电磁波极化的确定描述方法存在一定的局限性，进而给出了极化比和极化度统计特性的表征模型，通过对实测数据的统计分析，验证了理论模型的正确性，分析了极化统计分布特性的成因，本文的研究结论有助于改善雷达在复杂电磁环境下的抗干扰及目标检测能力，后续研究将着重关注基于极化度等参量统计特性开展的干扰极化抑制滤波器和极化检测器设计。