基于外辐射源的无源定位方法,又称为无源相干定位(Passive Coherent Location,PCL)。作为一种特殊的双基地雷达,PCL系统本身不辐射电磁波,而是利用第三方的非合作辐射源来探测目标,具有结构简单,成本低,高隐蔽性,不占用频谱资源,抗电子干扰,可探测隐形目标等优点[1]。多年来,一直是国际雷达领域的研究热点。
无源定位中,对于本身可以辐射电磁波的辐射源目标,可以通过接收其信号对其定位[2]。而当目标处于无线电静默或目标本身不能辐射电磁波时,上述方法将失效。此时,可以利用第三方的外辐射源来照射目标,通过接收外辐射源的直达信号和目标回波信号,实现对目标定位[3]。外辐射源的选取需充分考虑所选信号的功率大小、瞬时带宽及位置等参数[4]。目前,可用于定位的外辐射源包括模拟电视信号[5],调频广播信号[6],数字音频广播信号[7],数字视频广播信号[7],手机基站信号[8],WIFI信号[9]等。而相比于多站系统,单站系统机动性强,不存在时间和数据同步的问题。因此,研究高精度的单站无源相干定位方法具有重要意义。
目前对于固定目标的无源定位方法主要包括基于信号到达强度(Received Signal Strength,RSS)[10]、信号到达角度(Direction Of Arrival,DOA)[11]、信号到达时差(Time Difference Of Arrival,TDOA)[12],以及联合其中两种或者3种观测信息的定位体制[13]。其中,基于RSS的定位方法受信号衰减的影响,定位精度较低。基于DOA的定位方法需要多个接收机,因而并不适用于单站无源相干定位模型。基于TDOA的定位方法通过测量外辐射源直达信号与经目标反射后的回波信号到达观测站的时差来确定目标位置。由于外辐射源位置已知,因此又称“距离和定位”(外辐射源到目标的距离与目标到观测站的距离之和)[14]。但现有的TDOA定位算法主要针对双/多站无源定位系统,此时,时差指的是信号从目标到达不同观测站的时间差。这类算法常常需要两步估计,或建立为带约束的非线性优化问题,求解算法较为复杂,包括两步加权最小二乘算法[15],约束加权最小二乘算法[16],约束总体最小二乘算法[17],以及以上一些算法的改进算法。当时差测量准确时,TDOA定位方法的精度较高。但当时差测量误差较大时,TDOA定位方法的性能并不理想。而文献[18]证明了对于多站无源定位系统,联合角度和时差信息可以获得比仅TDOA和仅DOA定位方法更高的定位精度。但由于定位模型不同,文献[18]的定位算法并不能应用于本文单站无源相干定位系统。
文献[19]针对单站无源相干定位系统,提出了一种基于约束总体最小二乘的时差定位算法。但由于仅利用了时差一种信息,因而在时差测量误差较大时,定位性能迅速下降。为此,本文针对利用外辐射源的单站无源相干定位问题,提出了一种联合角度和时差信息的加权最小二乘(Weighted Least Squares,WLS)定位算法。在将角度和时差观测方程线性化后,考虑到方程中各项系数的误差,将定位问题转化为加权最小二乘问题,并利用迭代方法求解。
2 定位场景本文考虑的3维单站PCL定位场景如图 1:假设场景中含有N个外辐射源,1个目标,1个观测站。观测站上布设两副天线,分别用来接收来自外辐射源的直达信号和经目标反射后的回波信号[20]。
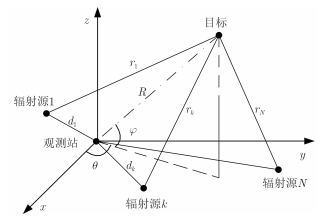
|
图 1 单站无源相干定位模型 Fig. 1 Single-observer passive coherent location model |
以观测站为原点,建立空间直角坐标系。目标位置X=[x y z]T为待估参量,外辐射源位置已知,为Xk=[xk yk zk]T (k=1,2,···,N)。目标到观测站的距离$R = \sqrt {{x^2} + {y^2} + {z^2}} $,目标到外辐射源k的距离${r_k} = \sqrt {{{(x - {x_k})}^2} + {{(y - {y_k})}^2} + {{(z - {z_k})}^2}} $,外辐射源k到观测站的距离${d_k} = \sqrt {x_k^2 + y_k^2 + z_k^2} $。假设信号传播速度为c,则外辐射源k的直达信号与其经过目标反射后的回波信号到达观测站的时差为$(R + {r_k} - {d_k})/c$,考虑观测中存在的误差,则时差的观测方程为:
| ${\tau _k} = \frac{1}{c}(R + {r_k} - {d_k}) + {v_{\tau k}}$ | (1) |
其中,${\tau _k}$为时差的观测值,${v_{\tau k}}$为时差的观测噪声。
目标到观测站的方位角为arctan (y/x),俯仰角为$\arctan (z/\sqrt {{x^2} + {y^2}} )$,则由于角度观测误差的影响,方位和俯仰角的观测方程为:
| $\left\{ \! \! \begin{array}{l} \theta = \arctan \frac{y}{x} + {v_\theta }\\ \varphi = \arctan \frac{z}{{\sqrt {{x^2} + {y^2}} }} + {v_\varphi } \end{array} \right.$ | (2) |
式中θ和φ分别为方位角和俯仰角的观测值,vθ和vφ分别为它们的观测噪声。
令观测量θ=[θ φ τ1 ··· τN]T,则本文的主要工作是通过含有噪声的观测量θ来估计目标的位置[x y z]T。
3 加权最小二乘定位首先将角度和时差的观测方程进行线性化处理。对式(2)移项整理,可将方位和俯仰角的观测方程表示为如下线性形式:
| $\quad \quad x\tan (\theta - {v_\theta }) - y = 0$ | (3) |
| $x\tan (\varphi - {v_\varphi })\sqrt {1 + {{\tan }^2}(\theta - {v_\theta })} - z = 0$ | (4) |
由于${r_k} \,=\,\sqrt {{{(x - {x_k})}^2} \,+ \,{{(y - {y_k})}^2} \,+ \,{{(z - {z_k})}^2}} $,$R = \sqrt {{x^2} + {y^2} + {z^2}} $,将R和rk的表达式平方相减,得到$(R + {r_k})(R - {r_k})$为:
| $\begin{aligned} (R + {r_k})(R - {r_k}) = & 2{x_k}x + 2{y_k}y + 2{z_k}z \\ & - x_k^2 - y_k^2 - z_k^2 \end{aligned}$ | (5) |
将式(1)移项,得到$(R + {r_k})$的表达式为:
| $R + {r_k}{\rm{ = }}c({\tau _k} - {v_{\tau k}}) + {d_k}$ | (6) |
将式(5)中的$(R + {r_k})(R - {r_k})$除以式(6)中的$(R + {r_k})$,得到 $(R - {r_k})$如下:
| $\begin{aligned} R - {r_k} & = \frac{{2{x_k}x + 2{y_k}y + 2{z_k}z - d_k^2}}{{R + {r_k}}} \\ & = \frac{{2{x_k}x + 2{y_k}y + 2{z_k}z - d_k^2}}{{c({\tau _k} - {v_{\tau k}}) + {d_k}}} \end{aligned}$ | (7) |
将式(6)和式(7)相加,得到R的表达式为:
| \[R = \frac{{{x_k}x + {y_k}y + {z_k}z}}{{c({\tau _k} - {v_{\tau k}}) + {d_k}}} + \frac{{{{\left( {c({\tau _k} - {v_{\tau k}}) + {d_k}} \right)}^2} - d_k^2}}{{2\left( {c({\tau _k} - {v_{\tau k}}) + {d_k}} \right)}}\] | (8) |
将式(3)和式(4)代入式(8),得到时差观测方程的线性形式为:
| \[\frac{{{x_k}x + {y_k}y + {z_k}z}}{{c({\tau _k} - {v_{\tau k}}) + {d_k}}} - \frac{{\sqrt {1 + {{\tan }^2}(\varphi - {v_\varphi })} }}{{\tan (\varphi - {v_\varphi })}}z{\mkern 1mu} {\kern 1pt} {\mkern 1mu} = \frac{{d_k^2 - {{\left( {c({\tau _k} - {v_{\tau k}}) + {d_k}} \right)}^2}}}{{2\left( {c({\tau _k} - {v_{\tau k}}) + {d_k}} \right)}}\] | (9) |
将式(3)、式(4)、式(9)在观测值[θ φ τk]T处泰勒展开,并忽略2阶及以上误差项,得
| \[\left\{ {\begin{array}{*{20}{l}} {x\tan \theta - y = \frac{x}{{{{\cos }^2}\theta }}{v_\theta }}\\ {x\tan \varphi \sqrt {1 + {{\tan }^2}\theta } - z = \frac{{x\tan \varphi \tan \theta }}{{{{\cos }^2}\theta \sqrt {1 + {{\tan }^2}\theta } }}{v_\theta } + \frac{{x\sqrt {1 + {{\tan }^2}\theta } }}{{{{\cos }^2}\varphi }}{v_\varphi }}\\ {\frac{{{x_k}x + {y_k}y + {z_k}z}}{{c{\tau _k} + {d_k}}} - \frac{{\sqrt {1 + {{\tan }^2}\varphi } }}{{\tan \varphi }}z = \frac{{d_k^2 - {{(c{\tau _k} + {d_k})}^2}}}{{2(c{\tau _k} + {d_k})}} + \left( {\frac{{cd_k^2}}{{2{{(c{\tau _k} + {d_k})}^2}}} + \frac{c}{2}} \right){v_{\tau k}}}\\ {\;\:\;\:\;\:\;\:\;\:\;\:\;\:\;\:\;\:\;\:\;\:\;\:\;\:\;\:\;\:{\mkern 1mu} {\kern 1pt} - \frac{{c({x_k}x + {y_k}y + {z_k}z)}}{{{{(c{\tau _k} + {d_k})}^2}}}{v_{\tau k}} + \frac{z}{{{{\sin }^2}\varphi \sqrt {1 + {{\tan }^2}\varphi } }}{v_\varphi }} \end{array}} \right.\] | (10) |
式(10)表示成矩阵形式为:
| ${{HX}} = {{b}} + {{e}}$ | (11) |
式中
| ${{H}}= \left[{\begin{array}{*{20}{c}} {\tan \theta } & { - 1} & 0\\ {\tan \varphi \sqrt {1 + {{\tan }^2}\theta } } & 0 & { - 1}\\ {\frac{{{x_1}}}{{c{\tau _1} + {d_1}}}} & {\frac{{{y_1}}}{{c{\tau _1} + {d_1}}}} & {\frac{{{z_1}}}{{c{\tau _1} + {d_1}}} - \frac{{\sqrt {1 + {{\tan }^2}\varphi } }}{{\tan \varphi }}}\\ \vdots & \vdots & \vdots \\ {\frac{{{x_N}}}{{c{\tau _N} + {d_N}}}} & {\frac{{{y_N}}}{{c{\tau _N} + {d_N}}}} & {\frac{{{z_N}}}{{c{\tau _N} + {d_N}}} - \frac{{\sqrt {1 + {{\tan }^2}\varphi } }}{{\tan \varphi }}} \end{array}} \right],{{b}} = \left[{\begin{array}{*{20}{c}} 0\\ 0\\ {\frac{{ - {{(c{\tau _1} + {d_1})}^2} + d\,_1^2}}{{2(c{\tau _1} + {d_1})}}}\\ \vdots \\ {\frac{{ - {{(c{\tau _N} + {d_N})}^2} + d\,_N^2}}{{2(c{\tau _N} + {d_N})}}} \end{array}} \right]$ | (12) |
| $\quad {{e}} = {{D}}({{X}}){{v}}$ | (13) |
其中$v = {[\begin{array}{*{20}{c}} {{v_\theta }}&{{v_\varphi }}&{{v_{\tau 1}}}& \cdots &{{v_{\tau N}}} \end{array}]^{\rm{T}}},D(X) = A(X) + B$,
\[A(X) = \left[ {\begin{array}{*{20}{c}} {\frac{x}{{{{\cos }^2}\theta }}}&0&{0_{N \times 1}^{\rm{T}}}\\ {\frac{{x\tan \varphi \tan \theta }}{{{{\cos }^2}\theta \sqrt {1 + {{\tan }^2}\theta } }}}&{\frac{{x\sqrt {1 + {{\tan }^2}\theta } }}{{{{\cos }^2}\varphi }}}&{0_{N \times 1}^{\rm{T}}}\\ {{0_{N \times 1}}}&{{\Sigma _1}}&{{\Sigma _2}} \end{array}} \right],\] \[B = \left[ {\begin{array}{*{20}{c}} {{O_{2 \times 2}}}&{{O_{2 \times N}}}\\ {{O_{N \times 2}}}&{{\Sigma _3}} \end{array}} \right],{\Sigma _1} = \left[ {\begin{array}{*{20}{c}} {\frac{z}{{{{\sin }^2}\varphi \sqrt {1 + {{\tan }^2}\varphi } }}}\\ \vdots \\ {\frac{z}{{{{\sin }^2}\varphi \sqrt {1 + {{\tan }^2}\varphi } }}} \end{array}} \right]\]
\[{\Sigma _2} = {\rm{diag}}\left\{ {\frac{{ - cX_1^{\rm{T}}X}}{{{{(c{\tau _1} + {d_1})}^2}}}, \cdots ,\frac{{ - cX_N^{\rm{T}}X}}{{{{(c{\tau _N} + {d_N})}^2}}}} \right\},\] \[{\Sigma _3} = {\rm{diag}}\left\{ {\frac{{cd{\kern 1pt} _1^2}}{{2{{(c{\tau _1} + {d_1})}^2}}} + \frac{c}{2}, \cdots ,\frac{{cd{\kern 1pt} _N^2}}{{2{{(c{\tau _N} + {d_N})}^2}}} + \frac{c}{2}} \right\}\]
当式(11)中的误差项e中各项误差方差相同且互不相关时,可用最小二乘算法对其求解:
| ${{\hat {{X}}}_{{\rm{LS}}}} = {({{{H}}^{\mathop{\rm T}\nolimits} }{{H}})^{ - 1}}{{{H}}^{\mathop{\rm T}\nolimits} }{{b}}$ | (14) |
但从式(13)可知,e中的各项误差方差不同且相关,此时最小二乘解得到的目标位置估计并不准确。而加权最小二乘算法通过对误差项进行加权,从而得到更加准确的目标位置估计。式(11)的加权最小二乘解即为满足如下目标函数极小化的变量X:
| $J({{X}}) = {({{HX}} - {{b}})^{\mathop{\rm T}\nolimits} }{{W}}({{HX}} -{{b}})$ | (15) |
其中W为加权矩阵,
| ${{W}} \!=\! {({\rm{E}}\{ {{e}}{{{e}}^{\mathop{\rm T}\nolimits} }\} )^{ - 1}} \! =\! {({{D}}{\rm{E}}\{ {{v}}{{{v}}^{\mathop{\rm T}\nolimits} }\} {{{D}}^{\mathop{\rm T}\nolimits} })^{ - 1}} \! =\! {({{DQ}}{{{D}}^{\mathop{\rm T}\nolimits} })^{ - 1}}$ | (16) |
式中Q为观测噪声的协方差矩阵。
则式(11)的加权最小二乘解为:
| $ {{{X}}_{{\rm{WLS}}}} = {({{{H}}^{\mathop{\rm T}\nolimits} }{{WH}})^{ - 1}}{{{H}}^{\mathop{\rm T}\nolimits} }{{Wb}}$ | (17) |
注意到,式中加权矩阵W的计算需要用到目标位置。而在估计过程中,目标位置是未知的。因此,在实际估计过程中,先令W=Q–1,得到目标位置的粗估计,而后将得到的目标位置估计代入式(16)中更新W,从而进一步得到更加准确的目标位置估计。
算法的具体实现过程总结如下:
(1) 初始化W=Q–1;
(2) 利用式(17)计算目标位置估计;
(3) 将目标位置估计代入式(16),更新矩阵W,返回步骤(2),得到更加准确的目标位置估计。
上述迭代过程收敛判断采用文献[2]中的收敛检验标准:若当前解的$\delta _{{X}}^{(i)} = \Big|\Big|{{X}}_{{\rm{WLS}}}^{\left( i \right)} - {{X}}_{{\rm{WLS}}}^{(i - 1)}\Big|{{\Big|}_2}$比前一次迭代的$\delta _{{X}}^{(i{\rm{ - }}1)}$大,则此过程不收敛,停止迭代,直接以上一次迭代的结果作为目标位置估计。若当前解的$\delta _{{X}}^{(i)} = \Big|\Big|{{X}}_{{\rm{WLS}}}^{(i)} - {{X}}_{{\rm{WLS}}}^{(i - 1)}\Big|{{\Big|}_2} \le \varepsilon $,则认为已收敛,否则继续迭代。实际中对于本文定位模型,仅需1至2次迭代,即可收敛,极少出现不收敛的情况。
4 性能分析 4.1 CRLB分析假设观测向量θ=[θ φ τ1 ··· τN]T的观测误差${{v}} \!=\! {[{ \!\! \!\begin{array}{*{20}{c}} {{v_\theta }} \! & \! {{v_\varphi }} \! & \! {{v_{\tau 1}}} \! & \! \cdots \! & \! {{v_{\tau N}}} \!\!\! \end{array}}]^{\mathop{\rm T}\nolimits} }$服从零均值的高斯分布,其协方差矩阵为${{Q}}\!=\! {\rm{diag}}\{ \sigma _\theta ^2,\sigma _\varphi ^2,\sigma _{\tau 1}^2,\cdots ,\sigma _{\tau N}^2\} $,则给定目标位置X的条件下,观测向量θ的概率密度函数为:
| $\begin{aligned} p({{θ}} ,{{X}}) = & \frac{1}{{{{(2{{π}} )}^{\frac{{N + 2}}{2}}}{{\left| {{Q}} \right|}^{\frac{1}{2}}}}}\\ & \cdot \exp \left( { \!\!-\! \frac{1}{2}{{[{{θ}} \!-\! {{h}}( \! {{X}})]}^{\rm{T}}}{{{Q}}^{ - 1}}[{{θ}} \!-\! {{h}}(\!{{X}})]} \! \right) \end{aligned}$ | (18) |
其中,
| ${{h}}({{X}}) = \left[{\begin{array}{*{20}{c}} {\arctan (y/x)}\\ {\arctan (z/\sqrt {{x^2} + {y^2}} )}\\ {(R + {r_1} - {d_1})/c}\\ \vdots \\ {(R + {r_N} - {d_N})/c} \end{array}} \right]$ | (19) |
CRLB等于Fisher信息矩阵(Fisher Information Matrix,FIM)的逆。根据FIM的定义,对式(18)中的概率密度函数取对数,并关于X中元素求偏导,得:
| $\frac{{\partial \ln p({{θ}} ,{{X}})}}{{\partial {{{X}}_i}}} = {\left( {\frac{{\partial {{h}}({{X}})}}{{\partial {{{X}}_i}}}} \right)^{\rm{T}}}{{{Q}}^{ - 1}}[{{θ}} - {{h}}({{X}})]$ | (20) |
式中${{{X}}_i}(i = 1,2,3)$表示向量X中的第i个变量。根据式(19)中h(X)的表达式,得到h(X)的一阶偏导为:
| $\frac{{\partial {{h}}({{X}})}}{{\partial {{X}}}} = \left[{\begin{array}{*{20}{c}} {\frac{{ - y}}{{{x^2} + {y^2}}}} & {\frac{x}{{{x^2} + {y^2}}}} & 0\\ { - \frac{{xz}}{{{R^2}\sqrt {{x^2} + {y^2}} }}} & { - \frac{{yz}}{{{R^2}\sqrt {{x^2} + {y^2}} }}} & {\frac{{\sqrt {{x^2} + {y^2}} }}{{{R^2}}}}\\ {\frac{1}{c}\left( {\frac{x}{R} + \frac{{x - {x_1}}}{{{r_1}}}} \right)} & {\frac{1}{c}\left( {\frac{y}{R} + \frac{{y - {y_1}}}{{{r_1}}}} \right)} & {\frac{1}{c}\left( {\frac{z}{R} + \frac{{z - {z_1}}}{{{r_1}}}} \right)}\\ \vdots & \vdots & \vdots \\ {\frac{1}{c}\left( {\frac{x}{R} + \frac{{x - {x_N}}}{{{r_N}}}} \right)} & {\frac{1}{c}\left( {\frac{y}{R} + \frac{{y - {y_N}}}{{{r_N}}}} \right)} & {\frac{1}{c}\left( {\frac{z}{R} + \frac{{z - {z_N}}}{{{r_N}}}} \right)} \end{array}} \right]$ | (21) |
进而得到FIM矩阵中的元素为:
| $\begin{aligned} {{J}}({{X}}) & = {{E}}\left[{\frac{{\partial \ln p({{θ}} ,{{X}})}}{{\partial {{X}}}}{{\left( {\frac{{\partial \ln p({{θ}} ,{{X}})}}{{\partial {{X}}}}} \right)}^{\rm{T}}}} \right] \\ & = {\left( {\frac{{\partial {{h}}({{X}})}}{{\partial {{X}}}}} \right)^{\rm{T}}}{({{{Q}}^{ - 1}})^{\rm{T}}}\left( {\frac{{\partial {{h}}({{X}})}}{{\partial {{X}}}}} \right) \end{aligned}$ | (22) |
CRLB是算法估计方差的下限。则算法估计误差的均方误差(Mean Square Error,MSE)满足下列不等式:
| ${\mathop{\rm E}\nolimits} \left[{\Big|\Big|{\hat {{X}}} - {{X}}\Big|{\Big|}_2^2} \right] \ge {\rm{tr(}}{{{J}}^{ - 1}})$ | (23) |
式中${\hat {{X}}}$表示向量X的估计值,${\rm{tr}}( \bullet )$表示矩阵的迹。
4.2 理论误差设算法的估计误差为$\Delta{{X}} = {{{X}}_{{\rm{WLS}}}} -{{X}}$。则目标位置的加权最小二乘解${{{X}}_{{\rm{WLS}}}}$应能满足目标函数偏导为零。
| $\begin{aligned} {\left. {\frac{{\partial J({{X}})}}{{\partial {{X}}}}} \right|_{{{X}} = {{{X}}_{{\rm{WLS}}}}}} = & 2{{{H}}^{\mathop{\rm T}\nolimits} }{{W}}({{H}}{{{X}}_{{\rm{WLS}}}} - {{b}}) \\ & + 2{({{H}}{{{X}}_{{\rm{WLS}}}} - {{b}})^{\mathop{\rm T}\nolimits} } \\ & \cdot \frac{{\partial {{W}}}}{{\partial {{X}}}}({{H}}{{{X}}_{{\rm{WLS}}}} - {{b}}) = {{0}} \end{aligned}$ | (24) |
将${{{X}}_{{\rm{WLS}}}} = {{X}} + \Delta {{X}}$,${{HX}} - {{b}} = {{Dv}}$代入式(24),得:
| $\begin{array}{l} {{{H}}^{\mathop{\rm T}\nolimits} }{{W}}({{H}}\Delta {{X}} + {{Dv}}) \\ +{({{H}}\Delta {{X}} + {{Dv}})^{\mathop{\rm T}\nolimits} }\frac{{\partial {{W}}}}{{\partial {{X}}}}({{H}}\Delta {{X}} + {{Dv}}) = 0 \end{array}$ | (25) |
忽略式(25)中的2阶及以上误差项,得:
| ${{{H}}^{\mathop{\rm T}\nolimits} }{{W}}({{H}}\Delta {{X}} + {{Dv}}) = 0$ | (26) |
从式(26)可以解得:
| $\Delta {{X}} = - {({{{H}}^{\mathop{\rm T}\nolimits} }{{WH}})^{ - 1}}{{{H}}^{\mathop{\rm T}\nolimits} }{{WDv}}$ | (27) |
将$\Delta {{X}}$乘以其转置并求期望,得到算法的误差协方差矩阵为:
| $\begin{aligned} {\mathop{\rm E}\nolimits} (\Delta {{X}}\Delta {{{X}}^{\mathop{\rm T}\nolimits} }) = & {({{{H}}^{\mathop{\rm T}\nolimits} }{{WH}})^{ - 1}}{{{H}}^{\mathop{\rm T}\nolimits} }{{WD}}{\rm{E}} \\ & \cdot ({{v}}{{{v}}^{\mathop{\rm T}\nolimits} }){{{D}}^{\mathop{\rm T}\nolimits} }{{{W}}^{\mathop{\rm T}\nolimits} }{{H}}{({{{H}}^{\mathop{\rm T}\nolimits} }{{WH}})^{ - {\mathop{\rm T}\nolimits} }} \\ = & {({{{H}}^{\mathop{\rm T}\nolimits} }{{WH}})^{ - 1}} \end{aligned}$ | (28) |
本节通过仿真实验评估本文算法的估计性能,并分析影响算法估计性能的因素。仿真场景设置如下:场景中有1个固定目标,4个外辐射源,其位置如表 1所示。角度和时差的测量误差设置为服从零均值的高斯分布。根据文献[21, 22],将角度测量误差标准差${\sigma _\theta }$设置为0.1°~10°,时差测量误差标准差${\sigma _\tau }$设置为10~105 ns。
| 表 1 外辐射源位置 Tab. 1 Positions of the illuminators |
算法的定位误差为5000次蒙特卡洛仿真的均方根误差。其定义如下:
| ${\mathop{\rm RMSE}\nolimits} ({{X}}) = \sqrt {\frac{1}{{5000}}\sum\limits_{n = 1}^{5000} {\Big|\Big|{{{\hat {{X}}}}^{(n)}} - {{X}}\Big|{\Big|}_2^2} } $ | (29) |
式中${{\hat {{X}}}^{(n)}}$为向量X在第n次蒙特卡洛仿真中的估计值。
仿真1 联合DOA和TDOA定位方法与仅TDOA 定位方法定位精度比较
分别计算角度测量误差为0.1°,1°和10°时,联合DOA和TDOA定位方法的CRLB,并与TDOA定位方法的CRLB对比。目标位置设置为[10000 10000 10000]T m,仿真结果如图 2所示。
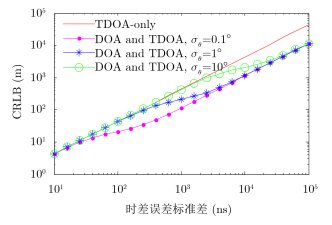
|
图 2 联合DOA和TDOA定位方法与仅TDOA定位方法的CRLB Fig. 2 CRLB of the jointing DOA and TDOA method and the TDOA-only method |
图 2描述了不同测量误差条件下,联合DOA和TDOA定位方法与TDOA定位方法的定位精度比较情况。从图中可以看出,在相同的时差测量误差条件下,联合DOA和TDOA定位方法的精度高于TDOA定位方法。在时差测量误差较小时,两种定位方法的CRLB非常接近,但随着时差测量误差增大,联合DOA和TDOA定位方法的CRLB开始低于并偏离TDOA定位方法,且角度测量误差越小,偏离越快。
仿真2 迭代次数对算法定位精度的影响
本文算法需通过一定次数的迭代来得到目标位置的精确估计。而算法迭代收敛至全局最优解所需的迭代次数将是衡量算法性能的重要指标。为此,统计不同迭代次数时算法估计的均方根误差。外辐射源和目标位置设置同仿真1,角度测量误差设置为1°,时差测量误差设置为100 ns,仿真结果如图 3所示。
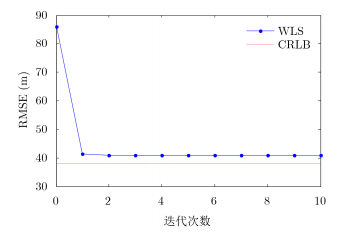
|
图 3 迭代次数对定位误差的影响 Fig. 3 Localization errors versus iteration numbers |
图 3描述了不同迭代次数对应的定位误差。可以看出,算法仅需1次迭代,定位误差即可收敛至逼近CRLB。再增加迭代次数,定位精度不再提高。因此,在后续仿真中,迭代次数设置为2。
仿真3 不同测量误差条件下算法的定位误差
为了评估本文算法的估计性能,在不同时差和角度测量误差条件下,利用本文算法进行仿真定位实验,统计算法估计的均方根误差,并将其与LS算法、CRLB及文献[19]中TDOA定位方法对比。定位系统几何分布如图 4所示。目标位置设置为近场和远场两种情况,近场目标设置在4个外辐射源所围成的区域内,位置为[1000 1000 1000]T m。远场目标位置设置在4个外辐射源所围成的区域外,位置为[100000 100000 10000]T m。仿真结果如图 5和图 6所示。
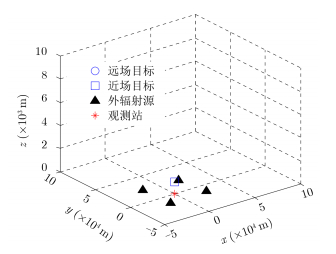
|
图 4 定位系统几何分布 Fig. 4 Localization geometry for simulations |

|
图 5 不同测量误差条件下算法对近场目标的定位精度 Fig. 5 Localization errors versus measurement errors for near-field target |
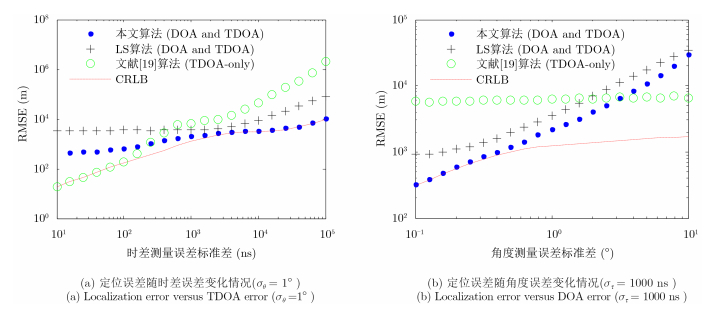
|
图 6 不同测量误差条件下算法对远场目标的定位精度 Fig. 6 Localization errors versus measurement errors for far-field target |
图 5(a)给出了角度测量误差为1°,时差测量误差10~105 ns时,算法对近场目标的均方根误差情况。从图中可以看出,LS算法达不到CRLB。在时差测量误差小于100 ns时,本文算法的定位误差稍微偏离CRLB,定位精度低于文献[19]中TDOA定位方法;但当时差测量达到100 ns时,文献[19]中TDOA定位方法的定位误差随着时差测量误差迅速增大并超过本文算法,而本文算法的定位误差则逼近CRLB。图 5(b)给出了角度测量误差为0.1°~10°,时差测量误差1000 ns时,算法对近场目标的均方根误差情况。从中可以看出,本文算法的定位误差低于LS算法和TDOA定位方法,在角度测量误差较小时,算法定位误差逼近CRLB,在测量误差增加至4°时,算法定位误差开始偏离CRLB。
综合来看,当${\sigma _\theta }{\rm{/}}{\sigma _\tau }$较大时,算法估计误差偏离CRLB,定位精度与TDOA定位方法相近,而${\sigma _\theta }{\rm{/}}{\sigma _\tau }$较小时,算法估计误差逼近CRLB,定位精度高于TDOA定位方法。
图 6给出了算法对远场目标定位的均方根误差情况。在${\sigma _\theta }{\rm{/}}{\sigma _\tau }$较小时,算法同样表现出了较高的估计精度。不同的是,相比于近场目标,算法在${\sigma _\theta }{\rm{/}}{\sigma _\tau }$较大时,偏离CRLB的程度更大,定位精度也略低于仅TDOA定位。原因角度测量误差随着目标距离的增大对定位的影响会增加。换言之,即同样的角度测量误差,对远场目标定位造成的误差会大于近场目标。
仿真4 外辐射源数量对定位精度影响
为分析外辐射源数量对算法定位误差的影响,分别计算不同数量的外辐射源进行定位时的CRLB,并与仅TDOA定位方法对比。目标位置设置为[10000 10000 10000]T m,角度测量误差设置为1°,时差测量误差设置为1000 ns,仿真结果如图 7所示。
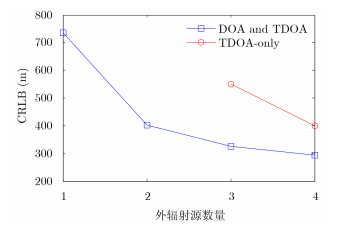
|
图 7 外辐射源数量对定位精度的影响 Fig. 7 Localization errors versus numbers of illuminators |
图 7给出了算法定位误差随外辐射源数量变化的情况。总体上,随着外辐射源数量的增加,联合DOA和TDOA定位方法和仅TDOA定位方法的定位误差均不断减小。但是联合DOA和TDOA定位方法仅需一个外辐射源即可对目标定位,而TDOA定位方法则至少需要3个外辐射源。原因在于TDOA定位方法至少需要3个外辐射源,以构建3个外辐射源的直达信号与对应反射信号到达观测站的时差方程,从而解得目标的3维坐标估计。而本文联合DOA和TDOA的定位方法仅需1个外辐射源,即可构建出时差、方位角、俯仰角3个方程,从而解得目标3维坐标。
仿真5 GDOP图
系统几何精度因子(Geometric Dilution Of Precision,GDOP)也是衡量系统定位性能的重要指标,其定义为:
| ${\mathop{\rm GDOP}\nolimits} = \sqrt {\sigma _x^2 + \sigma _y^2 + \sigma _z^2} $ | (30) |
式中$\sigma _x^2,\sigma _y^2,\sigma _z^2$分别为目标位置估计在$x,y,z$方向上的误差方差。根据式(28)中估计误差$\Delta {{X}}$的协方差矩阵,有:
| ${{P}}({{X}}) = {\rm{E}} (\Delta {{X}}\Delta {{{X}}^{\mathop{\rm T}\nolimits} }) = {({{{H}}^{\mathop{\rm T}\nolimits} }{{WH}})^{ - 1}}$ | (31) |
P(X)的主对角线元素分别对应$\sigma _x^2,\sigma _y^2,\sigma _z^2$,那么
| ${\rm{GDOP(}}{{X}}{\rm{)}} \!=\! \sqrt {{\rm{tr}}\left( {{{P}}({{X}})} \right)} \!=\! \sqrt {{\rm{tr}}\left( {{{({{{H}}^{\mathop{\rm T}\nolimits} }{{WH}})}^{ - 1}}} \! \right)} $ | (32) |
为分析目标位置对系统估计精度的影响,需要画出不同目标位置上的GDOP等高线图。但目标位置有3个坐标变量,而GDOP等高线图是2维的,为此,分别展示目标高度为1000 m和10000 m时,系统的GDOP等高线图。DOA测量误差设置为1°,4个外辐射源对应的时差测量误差分别设置为0.1 ns,1 ns,10 ns,100 ns。仿真结果如图 8所示。

|
图 8 GDOP图 Fig. 8 GDOP figure |
图 8给出了目标高度分别为1000 m和10000 m的GDOP图。从中看出,在x,y坐标相同时,目标高度越高,定位误差越小。当目标位于外辐射源和观测站所在的中央区域上方时,定位精度最高,随着目标远离该中心区域,定位误差增大,且在观测站和外辐射源连线方向,定位误差增加相对较快。而虽然不同外辐射源对应的TDOA测量误差不同,但对于整个系统而言,不同外辐射源TDOA测量误差的不同对目标定位精度分布的影响并不显著。
6 结论本文研究了利用外辐射源的单站无源相干定位问题,提出了一种联合角度和时差的加权最小二乘定位方法。本文算法具有如下优势:
(1) 联合角度和时差的定位方法相比于仅利用时差的定位方法,具有更高的定位精度,在时差测量误差较大时,这一优势尤其明显。
(2) 加权最小二乘算法考虑了定位方程中各项系数的误差,定位精度优于最小二乘算法。
(3) 联合角度和时差定位方法仅需一个外辐射源即可对目标定位,而仅时差定位方法则至少需要3个外辐射源。因而在远海、高海拔等可用外辐射源稀少地区,这一优势非常明显。而对于沿海、内陆等可用外辐射源数量较多地区,联合角度和时差定位方法的定位精度和稳定性也同样优于仅时差定位方法。
(4) 对系统GDOP图的分析表明,目标相对于外辐射源和观测站的位置对定位精度有显著影响。目标距离外辐射源和观测站所在的中央区域上方,且高度较高时,定位效果最好。
| [1] | Liu Jun, Li Hong-bin, and Himed B. On the performance of the cross-correlation detector for passive radar applications[J]. Signal Processing, 2015, 113: 32-37.( 1) 1) |
| [2] | 曲付勇, 孟祥伟. 基于约束总体最小二乘方法的到达时差到达频差无源定位算法[J]. 电子与信息学报, 2014, 36(5): 1075-1081. Qu Fu-yong and Meng Xiang-wei. Source localization using TDOA and FDOA measurements based on constrained total least squares algorithm[J]. Journal of Electronics & Information Technology, 2014, 36(5): 1075-1081.(  2) 2) |
| [3] | Subedi S, Zhang Y D, Amin M G, et al.. Motion parameter estimation of multiple ground moving targets in multi-static passive radar systems[J]. EURASIP Journal on Advances in Signal Processing, 2014, 2014: 157.( 1) 1) |
| [4] | Palmer J, Palumbo S, Summers A, et al.. An overview of an illuminator of opportunity passive radar research project and its signal processing research directions[J]. Digital Signal Processing, 2011, 21(5): 593-599.( 1) 1) |
| [5] | Ansari F and Taban M R. Clutter and direct signal cancellation in analog TV-based passive radar[J]. Journal of Radar, 2014, 1(2): 1-14.( 1) 1) |
| [6] | You Jun, Wan Xian-rong, Fu Yan, et al.. Experimental study of polarisation technique on multi-FM-based passive radar[J]. IET Radar, Sonar & Navigation, 2015, 9(7): 763-771.( 1) 1) |
| [7] | Michael E, Alexander S, and Folker M. Design and performance evaluation of a mature FM/DAB/DVB-T multi-illuminator passive radar system[J]. IET Radar, Sonar & Navigation, 2014, 8(2): 114-122.( 1) 1) |
| [8] | Zemmari R, Broetje M, Battistello G, et al.. GSM passive coherent location system: performance prediction and measurement evaluation[J]. IET Radar, Sonar & Navigation, 2014, 8(2): 94-105.( 1) 1) |
| [9] | Falcone P, Colone F, Macera A, et al.. Two-dimensional location of moving targets within local areas using WiFi-based multistatic passive radar[J]. IET Radar, Sonar & Navigation, 2014, 8(2): 123-131.( 1) 1) |
| [10] | Weiss A J. On the accuracy of a cellular location system based on RSS measurement[J]. IEEE Transactions on Vehicular Technology, 2003, 52(6): 1508-1518.( 1) 1) |
| [11] | Zhong Yu, Wu Xiao-yan, and Huang Cai-shu. Geometric dilution of precision for bearing-only passive location in three-dimensional space[J]. Electronics Letters, 2015, 51(6): 518-519.( 1) 1) |
| [12] | Wu Pan-long, Li Xing-xiu, Zhang Lian-zheng, et al.. Passive location using TDOA measurements from compass satellite illuminators[J]. Asian Journal of Control, 2015, 17(2): 722-728.( 1) 1) |
| [13] | Gaber A and Omar A. A study of wireless indoor positioning based on joint TDOA and DOA estimation using 2-D matrix pencil algorithms and IEEE 802.11ac[J]. IEEE Transactions on Wireless Communications, 2015, 14(5): 2440-2454.( 1) 1) |
| [14] | 李红伟. 外辐射源雷达目标定位与跟踪方法研究[D]. [博士论文], 西安电子科技大学, 2012: 15-39. Li Hong-wei. Studies on target localization and tracking in passive coherent location radar[D]. [Ph.D. dissertation], Xidian University, 2012: 15-39.(  1) 1) |
| [15] | Ho K C, Lu Xiao-ning, and Kovavisaruch L. Source localization using TDOA and FDOA measurements in the presence of receiver location errors: analysis and solution[J]. IEEE Transactions on Signal Processing, 2007, 55(2): 684-696.( 1) 1) |
| [16] | Lin Lanxin, So H C, Chan F K W, et al.. A new constrained weighted least squares algorithm for TDOA-based localization[J]. Signal Processing, 2013, 93(11): 2872-2878.( 1) 1) |
| [17] | Yang Kai, An Jian-ping, Bu Xiang-yuan, et al.. Constrained total least-squares location algorithm using time-difference-of-arrival measurements[J]. IEEE Transactions on Vehicular Technology, 2010, 59(3): 1558-1562.( 1) 1) |
| [18] | Norouzi Y and Derakhshani M. Joint time difference of arrival/angle of arrival position finding in passive radar[J]. IET Radar, Sonar & Navigation, 2009, 3(2): 167-176.( 1) 1) |
| [19] | Li Wan-chun, Wei Ping, and Xiao Xian-ci. A robust TDOA-based location method and its performance analysis[J]. Science in China Series F: Information Sciences, 2009, 52(5): 876-882.( 3) 3) |
| [20] | He You, Zhang Cai-sheng, Tang Xiao-ming, et al.. Coherent integration loss due to pulses loss and phase modulation in passive bistatic radar[J]. Digital Signal Processing, 2013, 23(4): 1265-1276.( 1) 1) |
| [21] | 梁浩, 崔琛, 代林, 等. 基于ESPRIT算法的L型阵列MIMO雷达降维DOA估计[J]. 电子与信息学报, 2015, 37(8): 1828-1835. Liang Hao, Cui Chen, Dai Lin, et al.. Reduced-dimensional DOA estimation based on ESPRIT algorithm in MIMO radar with L-shaped array[J]. Journal of Electronics & Information Technology, 2015, 37(8): 1828-1835.(  1) 1) |
| [22] | Li Jing, Zhao Yong-jun, and Li Dong-hai. Passive multipath time delay estimation using MCMC methods[J]. Circuits, System, and Signal Processing, 2015, 34(12): 3897-3913.( 1) 1) |


