② (内蒙古工业大学雷达技术研究所 呼和浩特 010051)
③ (上海卫星工程研究所 上海 200240)
② (Radar Research Institute, Inner Mongolia University of Technology, Hohhot 010051, China)
③ (Shanghai Institute of Satellite Engineering, Shanghai 200240, China)
合成孔径雷达(Synthetic Aperture Radar, SAR)是一种先进的微波成像系统[1],主动发射电磁波并接收目标的散射回波实现对目标的探测,具有全天时、全天候和高分辨率成像的遥感对地观测能力。SAR图像分类是SAR图像解译的重要研究内容,在地质勘探、地形制图、植被生长状况评估、城市规划以及海洋监测等方面得到广泛应用[2]。与单极化SAR图像相比,极化SAR (Polarimetric SAR, PolSAR)系统能得到多个极化通道数据,能更完整地表征地物散射特性。利用PolSAR数据的分类已成为SAR图像处理的主要研究方向之一。
典型的分类器,如K最近邻分类器(K-Nearest Neighbor, KNN)、神经网络、支持向量机(Support Vector Machine, SVM)[3, 4],随机森林(Random Forest, RF)[5]已经成功地应用到PolSAR图像分类[6, 7]中。极化SAR图像的复杂性使得分类任务变得艰巨,单个分类器往往不能满足高分类精度以及高泛化能力的要求。因此,人们提出利用多个分类器来构建一个强分类器,这个多分类器系统也称为集成学习系统,在人工智能和机器学习领域得到了广泛的关注[8]。文献[9]提出一种基于集成学习的PolSAR图像分类方法,它将多个基于bagging和boosting的分类器结合形成一个强泛化能力的分类器。文献[10]提出了一种基于光谱、纹理和极化特征融合和多分类器集成的多源遥感图像分类方法。文献[11]将集成学习算法与极化特征相结合进行SAR图像分类,而文献[12]又提出了对极化特征进行选择的方法。
本文针对PolSAR图像中的分类难点,提出了一种利用多特征融合和集成学习的极化SAR图像分类方法。该方法首先提取了PolSAR图像解译中常用到的5组特征,然后在特征空间上进行采样并得到基本的SVM分类器。最后将所有基本分类器的预测概率输入到随机森林模块,将多棵决策树学习到规则进行集成给出最终结果。
2 极化特征描述在PolSAR图像的分析过程中常用极化散射矩阵S来描述地物的极化散射特性,通过变换又可得到极化协方差矩阵C和极化相干矩阵T的表现形式。
| $ \ \, {S} = \left[{\begin{array}{*{20}{c}} {{S_{{\rm{hh}}}}}& {{S_{{\rm{hv}}}}}\\ {{S_{{\rm{vh}}}}}& {{S_{{\rm{vv}}}}} \end{array}} \right] $ | (1) |
| $ \begin{aligned} {C} = & \left[{\begin{array}{*{20}{c}} {\langle {{\left| {{S_{{\rm{hh}}}}} \right|}^2}\rangle } & {\sqrt 2 \langle {S_{{\rm{hh}}}}S_{{\rm{hv}}}^*\rangle } & {\langle {S_{{\rm{hh}}}}S_{{\rm{vv}}}^*\rangle }\\ {\sqrt 2 \langle {S_{{\rm{hv}}}}S_{{\rm{hh}}}^*\rangle } & {2\langle {{\left| {{S_{{\rm{hv}}}}} \right|}^2}\rangle } & {\sqrt 2 \langle {S_{{\rm{hv}}}}S_{{\rm{vv}}}^*\rangle }\\ {\langle {S_{{\rm{vv}}}}S_{{\rm{hh}}}^*\rangle } & {\sqrt 2 \langle {S_{{\rm{vv}}}}S_{{\rm{hv}}}^*\rangle } & {\langle {{\left| {{S_{{\rm{vv}}}}} \right|}^2}\rangle } \end{array}} \right]\:\\ = & \left[{\begin{array}{*{20}{c}} {{C_{{\rm{hhhh}}}}} & {{C_{{\rm{hhhv}}}}} & {{C_{{\rm{hhvv}}}}}\\ {{C_{{\rm{hvhh}}}}} & {{C_{{\rm{hvhv}}}}} & {{C_{{\rm{hvvv}}}}}\\ {{C_{{\rm{vvhh}}}}} & {{C_{{\rm{vvhv}}}}} & {{C_{{\rm{vvvv}}}}} \end{array}} \right] \end{aligned} $ | (2) |
为了提取与地物类别相关性更强的特征,提高特征集本身区分地物的能力,本文选取了5种有代表性的极化特征:基于散射测量数据的组合特征[13],基于kennaugh矩阵的Huynen分解特征[14],基于C矩阵的Hoekman分解特征[15],基于特征值分解的H/alpha/A分解特征[16]和基于模型的扩展四分量分解特征[17, 18]。
(1) EPFS (Extended Polarimetric Feature Space)特征
Doulgeris等人提出一组简单有效的特征描述子EPFS[13],是基于散射数据S矩阵及其简单变换的特征。EPFS特征一共有6维以邻域窗为基础提取,如表 1所示。
| 表 1 EPFS 6维特征 Tab.1 EPFS 6-dimension features |
(2) Huynen分解特征
根据Huynen分解理论[14],Huynen分解是针对T矩阵的特征分解,相干矩阵具有以下形式:
| $ {T} = \left[{\begin{array}{*{20}{c}} {2{A_0}}& {C-jD}& {H + jG}\\ {C + jD}& {{B_0} + B}& {E + jF}\\ {H-jG}& {E-jF}& {{B_0} - B} \end{array}} \right] $ | (3) |
| 表 2 Huynen参数 Tab.2 Huynen parameters |
(3) Hoekman九分量分解特征
Hoekman是一种基于协方差矩阵C的方法[15],该方法将极化目标的属性用协方差矩阵的后向散射强度来描述。使得传统的方法能应用到极化SAR图像的分类上,并得到简单通用的分类器。9个强度分量
| $ \left[{\begin{array}{*{20}{c}} {{S_{{\rm{hh}}}}S_{{\rm{hh}}}^*}\\ {{S_{{\rm{vv}}}}S_{{\rm{vv}}}^*}\\ {{S_{{\rm{hv}}}}S_{{\rm{hv}}}^*}\\ {{\mathop{\rm Re}\nolimits} \left( {{S_{{\rm{hh}}}}S_{{\rm{hh}}}^*} \right)}\\ {{\rm{Im}}\left( {{S_{{\rm{hh}}}}S_{{\rm{hh}}}^*} \right)}\\ {{\mathop{\rm Re}\nolimits} \left( {{S_{{\rm{vv}}}}S_{{\rm{vv}}}^*} \right)}\\ {{\rm{Im}}\left( {{S_{{\rm{vv}}}}S_{{\rm{vv}}}^*} \right)}\\ {{\mathop{\rm Re}\nolimits} \left( {{S_{{\rm{hv}}}}S_{{\rm{hv}}}^*} \right)}\\ {{\rm{Im}}\left( {{S_{{\rm{hv}}}}S_{{\rm{hv}}}^*} \right)} \end{array}} \right]{\rm{ = }}\frac{1}{{4{{π}} }}\left[{\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} 1 && 0 & 0\\ 0 & 1 & 0\\ {-\frac{1}{4}} & {-\frac{1}{4}} & {\frac{1}{4}} \end{array}} & {\begin{array}{*{20}{c}} 0 & 0 & 0\\ 0 & 0 & 0\\ {\frac{1}{4}} & {\frac{1}{4}} & {\frac{1}{4}} \end{array}} & {\begin{array}{*{20}{c}} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array}}\\ {\begin{array}{*{20}{c}} 0 & 0 & {\frac{1}{2}}\\ {\frac{1}{4}} & {\frac{1}{4}} & {\frac{3}{4}}\\ {-\frac{3}{8}} & {\frac{1}{8}} & { - \frac{1}{8}} \end{array}} & {\begin{array}{*{20}{c}} {\frac{1}{2}} & { - \frac{1}{2}} & { - \frac{1}{2}}\\ { - \frac{1}{4}} & {\frac{3}{4}} & { - \frac{1}{4}}\\ { - \frac{1}{8}} & { - \frac{1}{8}} & { - \frac{1}{8}} \end{array}} & {\begin{array}{*{20}{c}} 0 & 0 & 0\\ 0 & 0 & { - 2}\\ 1 & 0 & 0 \end{array}}\\ {\begin{array}{*{20}{c}} {\frac{3}{8}} & { - \frac{1}{8}} & {\frac{1}{8}}\\ {\frac{3}{8}} & { - \frac{1}{8}} & {\frac{5}{8}}\\ { - \frac{3}{8}} & {\frac{1}{8}} & { - \frac{1}{8}} \end{array}}& {\begin{array}{*{20}{c}} {\frac{1}{8}}& {\frac{1}{8}}& {\frac{1}{8}}\\ { - \frac{3}{8}} & {\frac{1}{8}}& {\frac{1}{8}}\\ { - \frac{1}{8}} & { - \frac{5}{8}}& {\frac{3}{8}} \end{array}} & {\begin{array}{*{20}{c}} 0 & { - 1} & 0\\ { - 1} & 0 & 0\\ 0 & 1 & 0 \end{array}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {\sigma _{{\rm{hh}}}^0}\\ {\sigma _{{\rm{vv}}}^0}\\ {\sigma _{ + + 45}^0}\\ {\sigma _{--45}^0}\\ {\sigma _{{\rm{ll}}}^0}\\ {\sigma _{{\rm{rr}}}^0}\\ {\sigma _{{\rm{h}} + 45}^0}\\ {\sigma _{{\rm{hl}}}^0}\\ {\sigma _{ + 45{\rm{l}}}^0} \end{array}} \right] $ | (4) |
(4) H/alpha/A分解特征
H/alpha/A分解方法是基于极化相干矩阵T的特征值以及特征向量的分解方法[16],所得到的特征如表 3所示。
| 表 3 H/alpha/A分解特征 Tab.3 H/alpha/A decomposition features |
该方法通过极化散射矩阵变换得到极化相干矩阵,利用单位相似变换对角化相干矩阵并将其分解为3个相干矩阵的加权和,每个矩阵表示一种散射过程。
| $ T = {U_3}\Lambda U_3^H = \sum\limits_{n = 1}^3 {{\lambda _n}{T_n} = {\lambda _1}\left( {{e_1} \cdot {e_1}} \right)} \\ + {\lambda _2}\left( {{e_2} \cdot {e_2}} \right) + {\lambda _3}\left( {{e_3} \cdot {e_3}} \right) $ | (5) |
| $ \quad \ \ \, H = - \mathop \sum \limits_{i = 1}^3 {P_i}{\log _3}{P_i}, \quad {P_i} = {\lambda _i} {\LARGE{/}} \sum\limits_{j = 1}^3 {{\lambda _j}} $ | (6) |
| $ \quad\quad \overline {α} = \mathop \sum \limits_{i = 1}^3 {P_i}{{a} _i} $ | (7) |
| $ \quad\quad \overline {β} = \mathop \sum \limits_{i = 1}^3 {P_i}{{b} _i} $ | (8) |
极化各向异性量A的定义如下:
| $ A = \frac{{{\lambda _2} - {\lambda _3}}}{{{\lambda _2} + {\lambda _3}}} $ | (9) |
当H很高时,A提供信息几乎为0。当H很低时,λ2和λ3接近0。当H值较低或中等时,H无法提供附加信息。此时,A提供附加信息。
(5)扩展的四分量分解特征
原始的Yamaguchi四分量分解将极化相干矩阵T分解为4种散射成分,除了面散射、二次散射和体散射分量外,还加上螺旋散射分量。然而,建筑区和植被有相同的体散射机制,很难将植被和倾斜的建筑区分开。为了解决这个问题,文献[17]提出将相干矩阵先去方位角,再进行如下分解。
| $ \begin{array}{l} \left\langle {\left| {T'} \right|} \right\rangle = {f_{\rm{s}}}{\left\langle {\left| {T} \right|} \right\rangle _{{\rm{surface}}}} + {f_{\rm{d}}}{\left\langle {\left| {T} \right|} \right\rangle _{{\rm{double}}}}\\ \quad \quad \quad \;\; + {f_{\rm{v}}}{\left\langle {\left| {T} \right|} \right\rangle _{{\rm{vol}}}} + {f_{\rm{c}}}{\left\langle {\left| {T} \right|} \right\rangle _{{\rm{helix}}}} \end{array} $ | (10) |
扩展的体散射模型[18]主要是为单次或二次散射提供合适的体散射模型。单次散射物体(如植被)和二次散射物体(如倾斜的建筑区)有相同的体散射分量,很难区分开这两种目标,扩展的体散射模型可以很好地区分开这两种目标。基于扩展的体散射模型的四分量分解可表示为:
| $ \begin{aligned} \left| {\langle T'\rangle } \right| = & {f_{\rm{s}}}{\left| {\langle T\rangle } \right|_{{\rm{surface}}}} + {f_{\rm{d}}}{\left| {\langle T\rangle } \right|_{{\rm{double}}}}\\ & + {f_{\rm{c}}}{\left| {\langle T\rangle } \right|_{{\rm{helix}}}} + \left\{ \!\! {\begin{array}{*{20}{c}} \!\!\! {{f_{\rm{v}}}\left| {\langle T\rangle } \right|_{{\rm{vol}}}^{{\rm{dipole}}}}\\ {{f_{{\rm{vd}}}}\left| {\langle T\rangle } \right|_{{\rm{vol}}}^{{\rm{dihedral}}}} \end{array}} \right. \end{aligned} $ | (11) |
| $ {\rm{Span}} = {\left| {{S_{{\rm{hh}}}}} \right|^2} + 2{\left| {{S_{{\rm{hv}}}}} \right|^2} + {\left| {{S_{{\rm{vv}}}}} \right|^2} \\ \quad \quad \ \! \; = {P_{\rm{S}}} + {P_{\rm{D}}} + {P_{\rm{C}}} + {P_{\rm{V}}} $ | (12) |
本文所提出的集成学习算法流程如图 1所示。
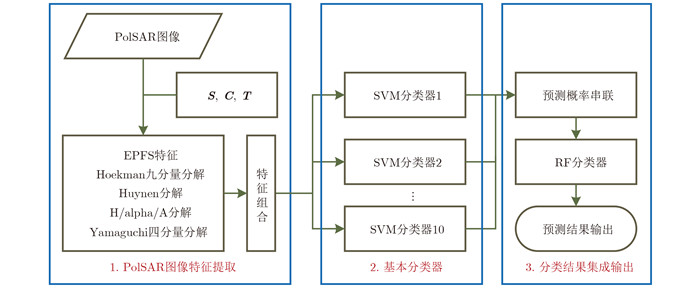
|
图 1 本文算法流程 Fig.1 The flowchart of our method |
支持向量机是一种二分类模型,是一种有监督的统计学习方法。它的学习策略就是最小化经验误差和最大化几何边缘,使得特征空间上的间隔最大化,可形式化为一个求解二次规划(convex quadratic programming)。式(13)中w表示权重系数,ξi是松弛变量,C表示惩罚参数。
| $ \left. {\begin{array}{*{20}{l}} {{{\min }_{w, b, \xi }}\frac{1}{2}\parallel w{\parallel ^2} + C\sum\limits_{i = 1}^N {{\xi _i}} }\\ {{\rm{s}}.{\rm{t}}{\rm{.}} \ \ {y_i}\left( {w \cdot {x_i} + b} \right) \ge 1 - {\xi _i}, }\\ i = 1, 2, \cdots, N, \ \ \ \ \ {{\xi _i} \ge 0} \end{array}} \right\} $ | (13) |
当输入空间为欧式空间或离散集合、特征空间为希尔伯特空间时,核函数(kernel function)表示将输入从输入空间映射到高维空间得到的特征向量之间的内积。通过使用核函数可以学习非线性支持向量机,等价于隐式的在高维的特征空间中学习线性支持向量机。支持向量是训练SVM过程中获得的在分类超平面上的点,SVM的决策函数是由少数几个支持向量来决定的,它的计算复杂度取决于支持向量的数目,而不是样本空间的维数,避免了维数灾难。同时,这样还可以抓住关键样本,“剔除”大量冗余样本,使得该方法不但运算简单,而且具有较好的鲁棒性。
随机森林是一种采用决策树作为基本分类器的集成学习方法,通过bootstrap重采样技术,从总数量为N的原始训练样本集中有放回的重复随机采样N个样本,由此得到一个训练数据集。这样使得每一棵树的输入样本都不是全部的样本,使其不至于产生局部最优解。对于决策树的每个节点,从所有特征中随机无放回的采样得到选取m维特征(训练样本的总特征数目为M,

|
图 2 RF分类器分类流程 Fig.2 The classification flowchart of random forest |
针对传统分类框架中将所有特征串联进行分类的方法会引起过拟合以及降低泛化能力的问题,本文提出了一种应用于极化SAR图像的集成学习监督分类框架。该框架的思路是在进行分类的时候,把若干基本分类器进行集成,通过将多个基本分类器的预测结果进行某种组合来决定最终的分类[19, 20],以取得比单个分类器更好的性能。本文通过特征空间上的随机采样得到特征子集并用支持向量机构建基本的分类器。然后,随机森林分类器将所有基本分类器的结果整合给出最终的预测结果,具体由以下3个步骤构成:
步骤1 提取极化SAR图像的EPFS特征,Hoekman分解特征,Huynen分解特征,H/alpha/A分解特征以及扩展四分量分解特征。通过这5组不同类型的特征,获得地物特性较为完备的描述。为避免相干斑噪声的影响,实验数据经过Lee滤波处理。
步骤2 为保证基本分类器的准确性和差异性,实验在特征空间进行了采样。具体地,我们从5组特征集中任选两组特征进行串联融合,训练出10个差异性SVM分类器。这里取两组特征进行融合是考虑到单组特征不能很好地反映地物特性会导致基本分类器的性能较差,而3组或3组以上的特征融合所产生的特征子集中存在较多的重复会导致基本分类器间的差异性较小。这是因为两种特征组合的方式中有1/3的概率不重复,2/3的概率重复50%。而在3种特征组合方式中有1/3的概率重复33.3%,2/3的概率重复66.7%,在4种特征组合方式中以1的概率重复75%。重复性越高差异性越小,故选取两种特征组合的方式。
步骤3 将所有SVM分类器的预测概率输出串联,作为新的特征输入到随机森林分类器得到最终的分类结果。集成学习系统中最后一步是将基本分类器的预测结果相结合。本文采用Stacking的思想,将所有差异性SVM分类器的预测概率串联作为RF分类器的输入。利用众多决策树的集成,有效地对差异性分类器的结果进行整合。
4 实验结果与分析本节选取的实验数据集为:来自德国航空航天中心FSAR机载系统X波段数据以及美国JPL的AIRSAR系统获取的荷兰Flevoland地区L波段数据。具体区域如图 3(a)和图 3(b)所示。本文在FSAR数据上进行的是基于区域的分类实验,在Flevoland数据上进行的是基于像素的分类实验。选取的特征有5组:扩展的极化特征(6维),Hoekman分解特征(9维),Huynen分解特征(9维),H/alpha/A分解(3维)和改进的Yamaguchi四分量分解(4维)。选取的对比实验为:利用统计分布的Wishart分类方法,将所有特征作为输入的SVM和RF分类方法,以及本文所提出的基于集成学习的分类方法。为研究选取特征子集方式对结果的影响,对比了取每组特征单独构造基本分类器和任取两组特征串联融合的方式,分别记作OM (Our Method)1和OM2。实验中SVM均采用的是RBF核的LIBSVM[21],并通过交叉验证得到最佳参数C和γ。分类性能综合评估指标为总体分类精度(Overall Accuracy, OA)和Kappa系数。

|
图 3 原始数据 Fig.3 Original data |
选取图像大小为2000×700的FSAR数据进行测试,将大图分为20×20不重叠的小图像块,共3400块。每个图像块的标号为块中最多像素点的标号,基于块的Ground Truth如图 4(a)。本数据集共4类,分别是森林,作物1,作物2和作物3。每类选取100个样本作为训练样本集,其它的作为测试样本。
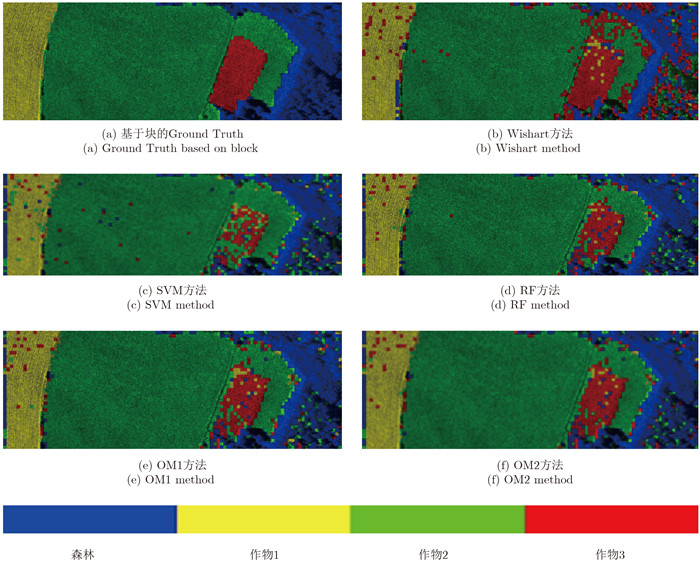
|
图 4 FSAR数据监督分类结果图 Fig.4 The supervised classification results of FSAR data |
分类结果如图 4所示,图 4中OM1和OM2方法的整体效果优于Wishart和SVM方法,作物2和森林区域的分类效果较好。在Wishart结果中作物3区域的分类效果最好,然而更多的其它区域也被误检为作物3,在森林区域的分类效果较差。SVM结果中作物3区域的分类效果最差,多被误检为作物2。为了进一步对各个方法的分类性能进行比较,本文计算了各个方法中每类地物分类的准确率,并用OA和Kappa系数进行综合评估,如表 4所示。结果表明,OM2方法有最高的分类精度0.905和kappa系数0.836,在森林和作物2上有最佳的分类精度,与目视分析一致。
| 表 4 FSAR数据分类结果 Tab.4 The classification results of FSAR data |
选取图像大小为300×300的Flevoland地区的PolSAR数据进行测试,本数据集有6类地物,小麦,草地,甜菜,土豆,豌豆和苜蓿。在所有标记样本中随机选取10%的样本做训练样本,其它的作为测试样本。实验结果如图 5所示。
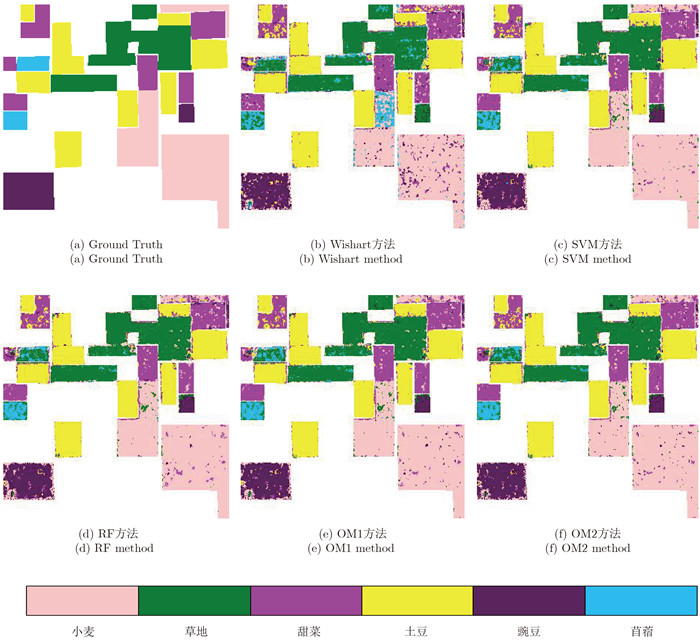
|
图 5 Flevoland数据监督分类结果图 Fig.5 The supervised classification results of Flevoland data |
表 5给出了定量评估数据,从表中可以看到,OM2方法取得了最佳的整体分类精度0.894和Kappa系数0.864,并且在土豆,苜蓿,小麦,甜菜和豌豆区域上的分类精度均为最高。并且,同样采取本文所提集成构架的OM1的结果也优于Wishart, SVM和RF分类器,该基于像素的分类实验进一步表明了本文所提算法的有效性。
| 表 5 Flevoland数据分类结果 Tab.5 The classification results of Flevoland data |
两个数据的分类结果中,OM方法的分类效果均优于基于统计分布的Wishart方法以及将所有特征进行串联的SVM和RF方法,有更高的OA和Kappa值,该结果表明了本文所提集成学习算法的有效性。另一方面,OM2和OM1方法的结果对比表明随机选取两组特征进行基本分类器构造的方式优于只取一组特征的方式。通过两组特征的融合在兼顾分类器差异性的同时,提升了其准确性,从而取得了更佳的效果。
5 结论极化SAR图像数据复杂性使得单一的特征很难描述自身丰富的散射特性,单一的分类器也很难取得很好的分类效果。针对此问题,本文分析了极化SAR图像的特征参数并选取了5组不同类型的特征进行描述,在此基础上提出了一种基于集成学习的极化SAR图像监督分类算法。通过特征空间的采样得到特征子集,并使用SVM作为基本分类器,最后利用随机森林算法给出最终分类结果。通过两组极化SAR图像分类实验表明了本文所提出方法的有效性。
| [1] |
李春升, 杨威, 王鹏波. 星载SAR成像处理算法综述[J].
雷达学报, 2013, 2 (1) : 111-122 Li Chun-sheng, Yang Wei, Wang Peng-bo. A review of spaceborne SAR algorithm for image formation[J].
Journal of Radars, 2013, 2 (1) : 111-122 DOI:10.3724/SP.J.1300.2013.20071 ( 0) 0)
|
| [2] |
田维, 徐旭, 卞小林, 等. 环境一号C卫星SAR图像典型环境遥感应用初探[J].
雷达学报, 2014, 3 (3) : 339-351 Tian Wei, Xu Xu, Bian Xiao-lin, et al. Applications of environmental remote sensing by HJ-1C SAR imagery[J].
Journal of Radars, 2014, 3 (3) : 339-351 ( 0) 0)
|
| [3] |
Yang Wen, Yin Xiao-shuang, Song Hui, et al. Extraction of built-up areas from fully polarimetric SAR imagery via PU learning[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7 (4) : 1207-1216 DOI:10.1109/JSTARS.4609443 ( 0) 0)
|
| [4] |
Banerjee B, Bhattacharya A, Buddhiraju K M. A generic land-cover classification framework for polarimetric SAR images using the optimum Touzi decomposition parameter subset-An insight on mutual information-based feature selection techniques[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7 (4) : 1167-1176 DOI:10.1109/JSTARS.4609443 ( 0) 0)
|
| [5] |
Hariharan S, Tirodkar S, De S, et al..Variable importance and random forest classification using RADARSAT-2 PolSAR data[C].IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec, 2014:1210-1213.
( 0) 0)
|
| [6] |
滑文强, 王爽, 侯彪. 基于半监督学习的SVM-Wishart极化SAR图像分类方法[J].
雷达学报, 2015, 4 (1) : 93-98 Hua Wen-qiang, Wang Shuang, Hou Biao. Semi-supervised Learning for classification of polarimetric SAR images based on SVM-Wishart[J].
Journal of Radars, 2015, 4 (1) : 93-98 ( 0) 0)
|
| [7] |
Yang Wen, Yin Xiao-shuang, Xia Gui-song. Learning high-level features for satellite image classification with limited training samples[J].
IEEE Transactions on Geoscience and Remote Sensing, 2015, 53 (8) : 4472-4482 DOI:10.1109/TGRS.2015.2400449 ( 0) 0)
|
| [8] |
Yuan Han-ning, Fang Meng, Zhu Xing-quan. Hierarchical sampling for multi-instance ensemble learning[J].
Knowledge and Data Engineering, 2013, 25 (12) : 2900-2905 DOI:10.1109/TKDE.2012.245 ( 0) 0)
|
| [9] |
Zhang La-mei, Wang Xiao, Li Meng, et al..Classification of fully polarimetric SAR images based on ensemble learning and feature integration[C].IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec, 2014:2758-2761.
( 0) 0)
|
| [10] |
刘培, 杜培军, 谭琨. 一种基于集成学习和特征融合的遥感影像分类新方法[J].
红外与毫米波学报, 2014, 33 (3) : 311-317 Liu Pei, Du Pei-jun, Tan Kun. A novel remotely sensed image classification based on ensemble learning and feature integration[J].
Journal of Infrared and Millimeter Waves, 2014, 33 (3) : 311-317 ( 0) 0)
|
| [11] |
Samat A, Du P, Baig M H A, et al. Ensemble learning with multiple classifiers and polarimetric features for polarized SAR image classification[J].
Photogrammetric Engineering & Remote Sensing, 2014, 80 (3) : 239-251 ( 0) 0)
|
| [12] |
Wang Y, Zhang Y, Zhuo T, et al..Ensemble learning based on multi-features fusion and selection for polarimetric SAR image classification[C].International Conference on Signal Processing (ICSP), Hangzhou, 2014:734-737.
( 0) 0)
|
| [13] |
Doulgeris A P.A simple and extendable segmentation method for multi-polarisation SAR images[C].6th International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry, 2013.
( 0) 0)
|
| [14] |
Yang J, Peng Y N, Yamaguchi Y, et al. On Huynen's decomposition of a Kennaugh matrix[J].
IEEE Geoscience and Remote Sensing Letters, 2006, 3 (3) : 369-370 DOI:10.1109/LGRS.2006.873229 ( 0) 0)
|
| [15] |
Hoekman D H, Vissers M A M. A new polarimetric classification approach evaluated for agricultural crops[J].
IEEE Transactions on Geoscience and Remote Sensing, 2003, 41 (12) : 2881-2889 DOI:10.1109/TGRS.2003.817795 ( 0) 0)
|
| [16] |
Cloude S R, Pottier E. An entropy based classification scheme for land applications of polarimetric SAR[J].
IEEE Transactions on Geoscience and Remote Sensing, 1997, 35 (1) : 68-78 DOI:10.1109/36.551935 ( 0) 0)
|
| [17] |
Yamaguchi Y, Sato A, Boerner W, et al. Four-component scattering power decomposition with rotation of coherency matrix[J].
IEEE Transactions on Geoscience and Remote Sensing, 2011, 49 (6) : 2251-2258 DOI:10.1109/TGRS.2010.2099124 ( 0) 0)
|
| [18] |
Sato A, Yamaguchi Y, Singh G, et al. Four-component scattering power decomposition with extended volume scattering model[J].
IEEE Geoscience and Remote Sensing Letters, 2012, 9 (2) : 166-170 DOI:10.1109/LGRS.2011.2162935 ( 0) 0)
|
| [19] |
Zhang Cha, Ma Yun-qian.
Ensemble Machine Learning[M]. 2012 : 1 -34.
( 0) 0)
|
| [20] |
陈博, 王爽, 焦李成, 等. 利用0-1矩阵分解集成的极化SAR图像分类[J].
电子与信息学报, 2015, 37 (6) : 1495-1501 Chen Bo, Wang Shuang, Jiao Li-cheng, et al. Polarimetric SAR image classification via weighted ensemble based on 0-1 matrix decomposition[J].
Journal of Electronics & Information Technology, 2015, 37 (6) : 1495-1501 ( 0) 0)
|
| [21] |
Chang Chih-Chung, Lin Chih-Jen. Libsvm:A library for support vector machines[J].
ACM Transactions on Intelligent Systems and Technology, 2011, 2 (3) : 27 ( 0) 0)
|




