压缩感知(Compressed Sensing,CS)^{[1, 2, 3]}是一种新的信号获取与处理的理论框架，其基本思想是利用信号的稀疏性或者可压缩性，在信号采样的同时进行压缩，能以远低于奈奎斯特采样定理所需的测量值精确重建原始信号，广泛应用于雷达、通信、核磁成像等领域^{[4, 5, 6]}。

压缩感知理论包括3个方面：信号的稀疏表征、测量矩阵的设计以及重构算法。假设信号$x \in {\Re ^n}$在某个基下能稀疏表征，即x=Ys，其中$\Psi \in {\Re ^{n \times n}}$是稀疏表征矩阵，s中只有k个非零元素，且k<<n。设计测量矩阵对信号x进行线性测量，得到y=Φx，其中${\Phi } \in {\Re ^{m \times n}}$(m<n) 为测量矩阵。由于m<n，由y重建x是病态问题。利用信号x的稀疏性，可以通过求解l₀范数最小化问题来恢复原始信号，即$\hat x = \arg \mathop {\min }\limits_{x \in {\Re ^n}} {\left\| {{\Psi ^{ - 1}}x} \right\|_0},\;{\rm{s}}.{\rm{t}}.\;y = \Phi x = \Phi \Psi s$，其中l₀范数${\left\| \cdot \right\|_0}$表示向量中的非零元素的个数，矩阵$\Theta = \Phi \Psi $称为感知矩阵。对于重构算法，主要有基于凸优化的l₁范数最小化算法(比如基追踪算法(Basis Pursuit,BP)^[7])和贪婪类算法(比如正交匹配追踪算法(Orthogonal Matching Pursuit, OMP)^[8])等。

信号能够稀疏表征是应用压缩感知的前提，而测量矩阵的设计对信号采样和重构环节有重要影响。测量矩阵把信号从高维空间投影到低维空间，必须保证降维后的低维信号不丢失原始信号的信息才能准确重建原始信号。这就要求设计的测量矩阵$\Psi $和稀疏矩阵$\Psi $不相干。文献^[9]中证明了当测量矩阵是高斯随机矩阵时，能够满足与大多数稀疏矩阵不相关，因而随机测量矩阵常被用在压缩感知中。近年来很多文献^{[10, 11, 12, 13]}指出，对随机测量矩阵进行优化可使其与稀疏矩阵之间的相关性进一步减小，从而提高信号的重建性能。它们的基本思想是优化测量矩阵使得感知矩阵$\Theta = \Phi \Psi $的不同列(也称为原子)间的相关性变得更小，即减小感知矩阵的Gram矩阵$G = {\Theta ^{\rm{T}}}\Theta $的非对角元素。这些测量矩阵优化方法主要是在稀疏矩阵$\Psi $确定的情况下来优化设计测量矩阵$\Psi $，并未结合重构算法的特点来设计测量矩阵。

在压缩感知重构算法中，贪婪类算法由于计算复杂度低而受到广泛关注，其主要思想是通过迭代寻找稀疏信号非零分量相对应的原子，然后根据这些原子重构出原始信号。OMP是经典的贪婪算法，其重构性能与感知矩阵的相关系数有关，感知矩阵的相关性越低，越能准确识别正确的原子^[8]。因此，文献^[14]提出一种改进的OMP算法，本文称之为双字典正交匹配追踪算法(Two Dictionaries OMP,TDOMP)，该算法通过引入一个新矩阵D(称为匹配矩阵)来识别原子，并且匹配矩阵和感知矩阵之间具有更低的相关性，从而提高原子识别的准确性。本文主要针对TDOMP算法的特点，提出了一种适用于TDOMP算法的测量矩阵优化方法，其主要思想是通过交替投影来优化测量矩阵，使得构造的匹配矩阵与感知矩阵具有更小的相关性，从而进一步提高重构性能。1维稀疏信号和2维图像重构实验验证了所提方法的性能，仿真结果显示使用优化测量矩阵的TDOMP算法的性能将明显提高。

TDOMP算法^[14]是一种改进的OMP算法，它从降低感知矩阵$\Theta $的相关性的思想出发，通过构造与感知矩阵互相关性低的匹配矩阵D来辨识正确的感知矩阵的原子。该算法用到两个字典$\Theta $和D，因此称为双字典正交匹配追踪算法。TDOMP算法和OMP算法的区别在于感知原子阶段，OMP算法使用感知矩阵$\Theta $对原子进行识别，而TDOMP算法使用匹配矩阵D对原子进行辨识。令感知矩阵$\Theta $的每个原子满足$\parallel $q_i$\parallel $=1,i=1,2,···,n，匹配矩阵D=[d₁,d₂,···,d_n]，且满足|<d_i,q_i>|=1,i=1,2,···,n，表 1 给出了TDOMP算法的流程^[15]。

表 1(Tab. 1)

表 1 TDOMP算法 Tab. 1 TDOMP algorithm 输入：感知矩阵Θ，匹配矩阵D，测量信号y，迭代终止门限tol， 稀疏度K 初始化：r0=y(初始化残差)，Λ0=∅(估计支撑集)，T0={1, 2,···,n} (可用集)，k=1(迭代计数器) 循环：   (1) 感知原子：     ${i_k} = \arg \max \left| {\left\langle {{d_j},{r_{k - 1}}} \right\rangle } \right|$   (2) 更新估计支撑集和可用集     ${\Lambda _k} = {\Lambda _{k - 1}} \cup \left\{ {{i_k}} \right\},{T_k} = {T_{k - 1}}\backslash \left\{ {{i_k}} \right\}$(防止已经选中 的原子被再次选中)   (3) 重构信号并更新残差：     $\begin{array}{*{20}{l}} {{{\hat x}_k} = \left\{ {\begin{array}{*{20}{l}} {{{\left( {\Theta _{{\Lambda _k}}^{\rm{T}}{\Theta _{{\Lambda _k}}}} \right)}^{ - 1}}\Theta _{{\Lambda _k}}^{\rm{T}}y,\;0,} \end{array}} \right.}&{在支撑集{\Lambda _k}上}\\ {{r_k} = y - \Theta {{\hat x}_k}}&其他 \end{array}$   (4) 如果${\left\| {{r_k}} \right\|_2}{\rm{ \lt tol}}$或者k>K，迭代中止，否则k=k+1，返回第(1)步。 输出：重构的支撑集Λk和重构的稀疏信号${\hat x_k}$

表 1 TDOMP算法 Tab. 1 TDOMP algorithm

在TDOMP算法中，为了构造与感知矩阵$\Theta $相关性低的匹配矩阵D，其基本思想是使伪Gram矩阵G=D^T$\Theta $在Frobenius范数意义下与理想的Gram 矩阵充分接近，即

表 2(Tab. 2)

表 2 构造低相关性的匹配矩阵 Tab. 2 Construction of matching matrix with low cross-coherence 输入：感知矩阵$\Theta \in {\Re ^{m \times n}}$，最大迭代次数iter   (1) 初始化：$G = {\Theta ^{\rm{T}}}\Theta ,\;{\mu _{\min }} = \sqrt {\left( {n - m} \right)/\left[ {\left( {n - 1} \right)m} \right]} $   (2) 进行循环操作，直到达到最大迭代次数iter：    (a) 求$H = \mathop {\arg\min }\limits_{H'} {\left\| {H' - G} \right\|_F},H' \in H$，其解为： $\quad \quad \quad H = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {{h_{ii}} = 1,}&{}&{}\\ {{h_{ij}} = {g_{ij}},}&{{\mkern 1mu} \left| {{g_{ij}}} \right| \le {\mu _{\min }}}&{(2)}\\ {{h_{ij}} = {\rm{sign}}\left( {{g_{ij}}} \right){\mu _{\min }},}&{\left| {{g_{ij}}} \right| > {\mu _{\min }}}&{} \end{array}} \end{array}} \right.$    (b) 求$D = \mathop {{\rm{argmin}}}\limits_{\tilde D} {\left\| {{{\tilde D}^{\rm{T}}}\Theta - H} \right\|_F},{\tilde D^{\rm{T}}}\Theta \in \Gamma $，其解为： $\quad \quad \quad \quad \quad D = (H\Theta $†${)^{\rm{T}}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \;(3)$    (c) 计算$G = {D^{\rm{T}}}\Theta = H\Theta $†$\Theta $ 输出：匹配矩阵$D \in {\Re ^{m \times n}}$

表 2 构造低相关性的匹配矩阵 Tab. 2 Construction of matching matrix with low cross-coherence

根据上述方法，给定感知矩阵$\Theta $就可以得到和$\Theta $相关性低的矩阵D。已有研究表明，OMP算法识别原子的能力依赖于感知矩阵自身的相关系数，而TDOMP感知原子的能力依赖于感知矩阵和匹配矩阵两者的相关系数。当D和$\Theta $的相关系数低于$\Theta $自身的相关系数时，TDOMP算法的重构性能将好于OMP算法^[15]。

本节主要研究测量矩阵的优化来进一步提高TDOMP算法的性能，其基本思想是设计测量矩阵使得伪Gram矩阵G=D^T$\Theta $=D^T$\Phi \Psi $在Frobenius范数意义下与理想的Gram矩阵充分接近。与式(1)不同的是，感知矩阵$\Theta $在优化过程中可以变化，从而可以优化设计测量矩阵。仍采用交替投影的方法来求得优化的测量矩阵$\Psi $以及与$\Theta $相关性低的匹配矩阵D，所提算法具体如表 3所示。

表 3(Tab. 3)

表 3 基于交替投影的测量矩阵优化算法 Tab. 3 Measurement matrix optimization method based on alternative projection 输入：测量矩阵$\Phi \in {\Re ^{m \times n}}$，稀疏矩阵$\Psi \in {\Re ^{n \times n}},\;i = 1$，迭代终止门限ε   (1) 初始化：$\Theta = \Phi \Psi ,\;G = {\Theta ^{\rm{T}}}\Theta ,\;$ $\quad \quad \quad \quad \quad \quad {\mu _{\min }} = \sqrt {\left( {n - m} \right)/\left[ {\left( {n - 1} \right)m} \right]} $   (2) 进行循环操作：    (a) 求$H = \mathop {{\mathop{\rm argmin}\nolimits} }\limits_{H'} {\left\| {H' - G} \right\|_F},\;H' \in H$，其解如式(2)所示。    (b) 求$D = \mathop {{\rm{argmin}}}\limits_{D'} {\left\| {{{D'}^T}\Theta - H} \right\|_F}$，其解为： $\quad \quad \quad \quad \quad \quad D = (H\Theta $†${)^{\rm{T}}}\quad \quad \quad \quad \quad \quad \quad \quad (4)$    (c) 求$\Theta = \mathop {{\rm{argmin}}}\limits_{\tilde \Theta } {\left\| {{D^{\rm{T}}}\tilde \Theta {\rm{ - }}H} \right\|_F}$，其解为 $\quad \quad \quad \quad \quad \quad \Theta = ({H^{\rm{T}}}D$†${)^{\rm{T}}}\quad \quad \quad \quad \quad \quad \quad \; (5)$    (d) 计算$G = {D^{\rm{T}}}\Theta ,\;{r_i} = {\left\| {H - G} \right\|_F}$    (e) 如果$i \ge 2$且$\left| {{r_i} - {r_{i - 1}}} \right| \le \varepsilon $，退出；否则到(a)且$i = i + 1$   (3) 最后根据$\Phi = \mathop {{\rm{argmin}}}\limits_{\Phi '} {\left\| {\Phi '\Psi - \Theta } \right\|_F}$，求得 $\quad \quad \quad \quad \quad \quad \Phi = \Theta \Psi $†$\quad \quad \quad \quad \quad \quad \quad \quad \quad \;\;{\mkern 1mu} (6)$ 输出：测量矩阵$\Phi \in {\Re ^{m \times n}}$和匹配矩阵$D \in {\Re ^{m \times n}}$

表 3 基于交替投影的测量矩阵优化算法 Tab. 3 Measurement matrix optimization method based on alternative projection

因此，当测量矩阵可以设计时，首先基于表 3 的交替投影法构造出测量矩阵$\Psi $_opt和匹配矩阵D，此时观测方程为y_opt=$\Phi $_opt$\Psi $s，然后由$\Theta =\Phi $_opt$\Psi $和D，利用TDOMP算法重构稀疏信号。

本节对所提的针对TDOMP重构算法的测量矩阵优化方法进行仿真，分析测量矩阵优化前后对重构性能的影响。

假设稀疏信号x=$\Psi $s，稀疏矩阵$\Psi $为高斯随机矩阵或者离散余弦变换(Discrete Cosine Transform, DCT)矩阵；稀疏系数s为高斯稀疏信号或者0-1稀疏信号。对信号x采用不同的测量矩阵进行观测，然后采用OMP算法和TDOMP算法来重构稀疏系数。下面主要从准确重构概率和重构误差来比较测量矩阵优化前后的重构性能。若重构的稀疏系数满足$\mathop {\max }\limits_{i = 1,2,\cdots ,n} \left( {\left| {{s_i} - {{\hat s}_i}} \right|} \right){\rm{ \lt }}{10^{ - 3}}$，则认为准确重构，准确重构概率为准确重构次数与总重构次数的比值。重构误差采用均方根误差，其定义为${\rm{RMSE}} = \sqrt {\left\| {\hat s - {s^2}} \right\|/n} $。

仿真中主要比较4种情况：采用Gaussian随机阵的OMP算法(用--*表示)、采用Gaussian随机阵的TDOMP算法(用--o表示)、采用优化测量矩阵的OMP算法(其中优化算法为Duarte^[10]所提，用--表示)、采用所提优化测量矩阵的TDOMP算法(称为Optimized TDOMP，用--☆表示)，如表 4所示。

表 4(Tab. 4)

表 4 仿真说明 Tab. 4 Simulation description 重构算法 测量矩阵 表示方式 OMP 高斯矩阵 --* TDOMP 高斯矩阵 --o OMP Duarte优化矩阵 --- TDOMP 所提优化测量矩阵 --☆

表 4 仿真说明 Tab. 4 Simulation description

仿真实验1：稀疏信号长度n=128，稀疏基$\Psi $为128×128，测量矩阵$\Phi $为64×128。给定测量数m=64的情况下，观察不同测量矩阵下的准确重构概率和重构误差随信号稀疏度k变化的情况。每个稀疏度下，独立重复500次仿真实验。

稀疏基为高斯随机矩阵，稀疏系数为高斯稀疏信号和0-1稀疏信号的结果如图 1和图 2所示。可以看出，在测量数m固定不变的情况下，随着稀疏度k的增加，信号的准确重构概率降低，重构误差增大。采用所提优化的测量矩阵的TDOMP算法的重构效果最好，但优化测量矩阵对TDOMP算法重构性能的提高程度不如优化测量矩阵对OMP算法重构性能的提高程度。

图 1(Fig.1)

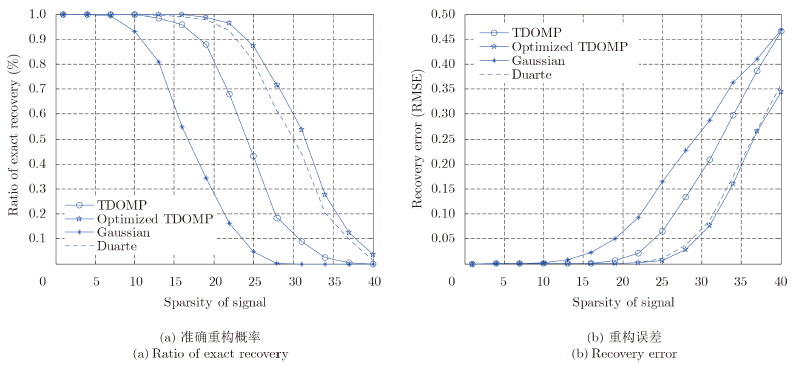图 1 高斯稀疏基下OMP和TDOMP算法重构高斯稀疏系数的性能比较 Fig.1 The performance comparison of recovering Gaussian sparse coefficients by using OMP and TDOMP with Gaussian sparse basis

图 2(Fig.2)

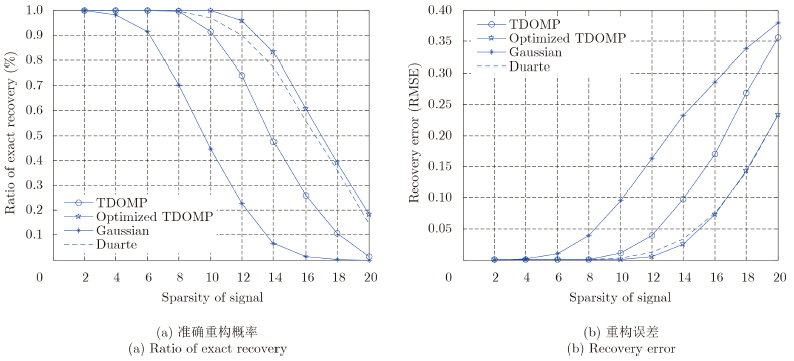图 2 高斯稀疏基下OMP和TDOMP算法重构0-1稀疏系数的性能比较 Fig.2 The performance comparison of recovering 0-1 sparse coefficients by using OMP and TDOMP with Gaussian sparse basis

稀疏基采用DCT矩阵，稀疏系数为高斯稀疏信号和0-1稀疏信号的结果如图 3和图 4所示。可以看出，采用优化测量矩阵的TDOMP算法的重构效果最好。与稀疏系数为0-1稀疏信号的情况相比，优化后的测量矩阵对高斯稀疏系数的重构效果提高得更为显著。

图 3(Fig.3)

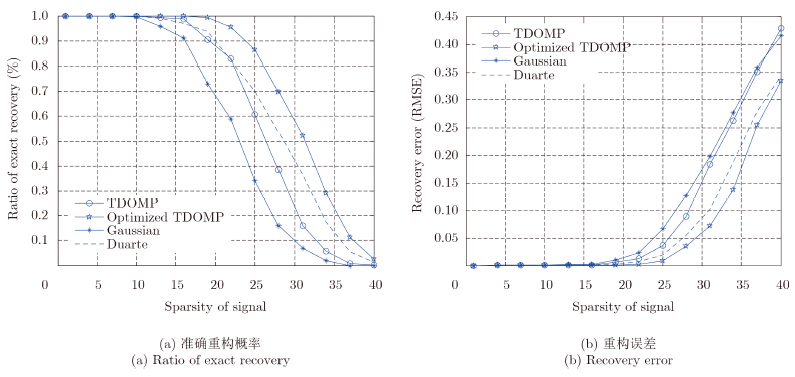图 3 DCT稀疏基下OMP和TDOMP算法重构高斯稀疏系数的性能比较 Fig.3 The performance comparison of recovering Gaussian sparse coefficients by using OMP and TDOMP with DCT sparse basis

图 4(Fig.4)

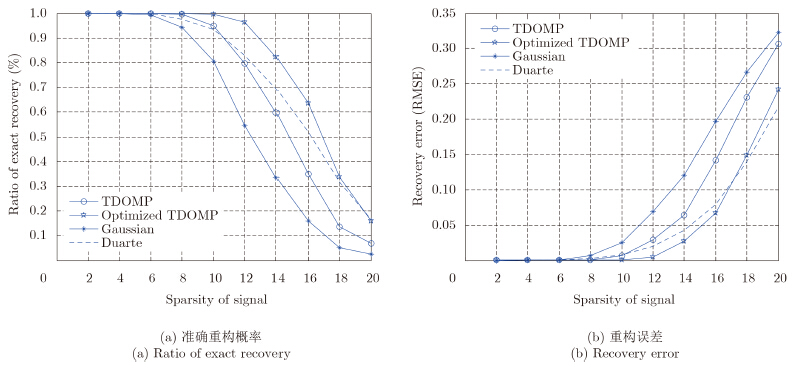图 4 DCT稀疏基下OMP和TDOMP算法重构0-1稀疏系数的性能比较 Fig.4 The performance comparison of recovering 0-1 sparse coefficients by using OMP and TDOMP with DCT sparse basis

仿真实验2：稀疏信号长度n=128，稀疏基$\Psi $为128×128，采用高斯随机矩阵和DCT矩阵，稀疏系数为高斯稀疏信号和0-1稀疏信号。给定稀疏度k，观察不同测量矩阵下的准确重构概率和重构误差随信号测量数m变化的情况。测量数m从64到96以步长4变化，每个测量数下，独立重复500次仿真实验。固定稀疏度k，当稀疏系数是高斯时，k=30；当稀疏系数为0-1信号时，k=19。

稀疏矩阵采用高斯随机矩阵，稀疏系数为高斯稀疏信号和0-1稀疏信号的结果如图 5和图 6所示。稀疏矩阵采用DCT矩阵，稀疏系数为高斯稀疏信号和0-1稀疏信号的结果如图 7和图 8所示。可以看出，在稀疏度k固定不变时，随着测量数m的增加，信号的准确重构概率增加，重构误差下降。实验结果表明，采用优化的测量矩阵的TDOMP算法的重构效果最好。

图 5(Fig.5)

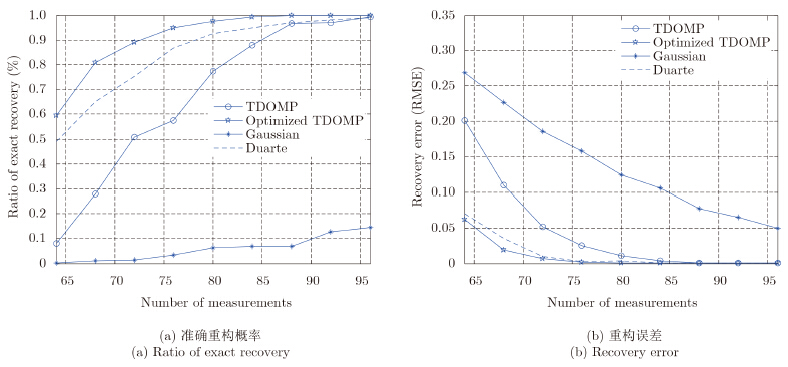图 5 高斯稀疏基下OMP和TDOMP算法重构高斯稀疏系数的性能比较 Fig.5 The performance comparison of recovering Gaussian sparse coefficients by using OMP and TDOMP with Gaussian sparse basis

图 6(Fig.6)

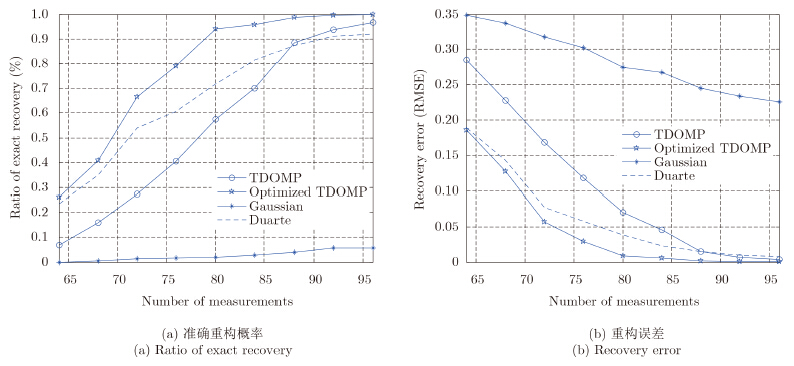图 6 高斯稀疏基下OMP和TDOMP算法重构0-1稀疏系数的性能比较 Fig.6 The performance comparison of recovering 0-1 sparse coefficients by using OMP and TDOMP with Gaussian sparse basis

图 7(Fig.7)

图 7 DCT稀疏基下OMP和TDOMP算法重构高斯稀疏系数的性能比较 Fig.7 The performance comparison of recovering Gaussian sparse coefficients by using OMP and TDOMP with DCT sparse basis

图 8(Fig.8)

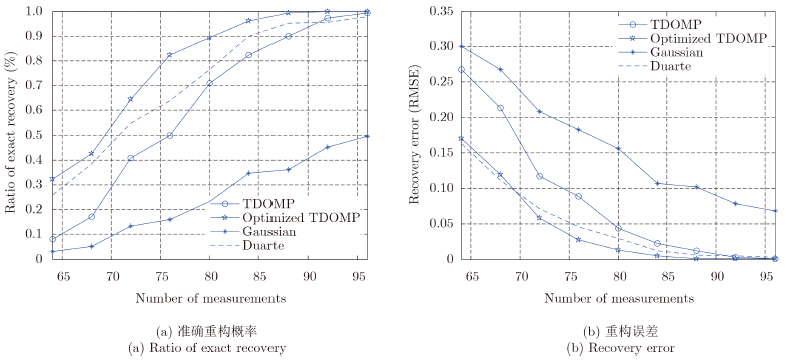图 8 DCT稀疏基下OMP和TDOMP算法重构0-1稀疏系数的性能比较 Fig.8 The performance comparison of recovering 0-1 sparse coefficients by using OMP and TDOMP with DCT sparse basis

为了进一步验证测量矩阵优化算法的性能，本节将对2维图像信号进行重构实验。源图像采用256×256的Lena图像，如图 9所示。稀疏基采用DCT基。重构效果采用PSNR (Power Signal-to-Noise Ration)值来进行评价，其计算公式为：${\rm{PSNR}} = 20{\rm{lg}}\left( {\frac{{255}}{{\sqrt {{\rm{MSE}}} }}} \right)$，其中${\rm{MSE}} = \frac{1}{{P \times Q}} \cdot \sum\nolimits_{p = 1}^P {\sum\nolimits_{q = 1}^Q {{{\left( {\mathop {\hat x}\limits^\: \left( {p,q} \right) - x\left( {p,q} \right)} \right)}^2}} } $。当测量值为140 (即压缩比m/n=0.55)时，给出4种情况下的仿真结果，如图 10所示。

图 9(Fig.9)

图 9 原始图像 Fig.9 Original image

图 10中，图 10(a)为采用高斯随机测量矩阵下OMP的仿真结果，图 10(b)为采用高斯随机测量矩阵下TDOMP的仿真结果，图 10(c)为采用Duarte^[10] 所提优化测量矩阵下OMP的仿真结果，图 10(d)为采用本文所提优化测量矩阵下TDOMP的仿真结果，测量矩阵优化情况下的TDOMP称为Optimized TDOMP。从图 10可以看出，TDOMP算法对图像的重构效果好于OMP算法的重构能力，而对于TDOMP算法，测量矩阵优化后对图像的重构效果好于没有优化的测量矩阵的重构效果。但优化测量矩阵对TDOMP算法重构性能的提高程度不如优化测量矩阵对OMP算法重构性能的提高程度。

图 10(Fig.10)

图 10 在不同测量矩阵下OMP和TDOMP算法的重建图像 Fig.10 Reconstructed images by using OMP and TDOMP with different measurement matrix

本文研究了针对特定重构算法TDOMP的测量矩阵优化方法。TDOMP算法通过构造与感知矩阵相关性低的匹配矩阵来提高原子识别的准确性。所提测量矩阵优化方法首先利用交替投影法构造相关性低的感知矩阵和匹配矩阵，然后基于其中的新感知矩阵利用最小二乘实现测量矩阵的优化。最后，通过对1维稀疏信号和2维图像的仿真实验，验证了该优化测量矩阵显著提高了TDOMP算法的重构性能。