②(特拉华大学电子与计算机工程系 纽瓦克 DE 19716)
②(Department of Electical & Computer Engineering, University of Delaware, Newark DE 19716, USA)
稀疏信号处理是信号处理领域近年来最活跃的分支之一,主要研究如何从低维采样数据中实现高维稀疏信号的准确恢复。对信号稀疏性的关注可以追溯到上世纪50年代,当时人们研究“回归子集选择”问题时,考虑了对信号加入稀疏性约束。90年代LASSO(Least Absolute Shrinkage and Selectionator Operator)方法[1]将稀疏性约束与L1范数最小化联系到一起。2006年以来,Donoho在文献[2]中提出了压缩感知的概念,进一步阐述了稀疏性与L1凸优化之间的关系。Candes和Tao在文献[3, 4]中从理论上证明了在观测矩阵满足一定条件即限制等容条件(Restricted Isometric Property,RIP) 时,稀疏信号恢复问题与L1凸优化问题具有等价性;他们还证明了在原始信号并非完全稀疏或受到噪声干扰的情况下,利用L1优化逼近信号的误差能够得到控制。基于这些优秀学者的工作,稀疏信号处理近年来得到了长足的发展,其基础理论不断完善,应用领域也越来越广泛,目前在医学、地震学、声学、雷达、通信等领域得到了广泛应用[5]。值得注意的是,在RIP性质不满足或不易验证的情况下,稀疏信号处理在诸多领域也取得了令人欣喜的处理结果。
稀疏信号处理已经在雷达探测中得到应用。Baraniuk首次将稀疏信号处理引入雷达成像[6],Potter研究了雷达成像处理中采用的稀疏重建算法以及随机采样策略[7],Ender分析了稀疏信号处理在典型雷达应用中的潜力[8]。国内中国科学院电子学研究所、北京航空航天大学、西安电子科技大学、清华大学、国防科技大学、电子科技大学等单位也开展了相关的研究工作。在国家重点基础研究计划(973 计划)支持下,中国科学院电子学研究所联合国内优势单位组织全面开展了稀疏微波成像的研究,在理论、体制、算法等方面取得了原创性成果,并完成了基于航空和地面平台的稀疏雷达成像实验验证[9, 10, 11]。
在稀疏信号处理的框架下,雷达对目标的探测过程被建模为一个线性(或准线性)系统,用字典矩阵给予描述,对目标的探测问题则被转化成稀疏约束优化问题。在传统稀疏信号处理中,字典矩阵是预先设定的,且在稀疏求解过程中保持不变。然而,雷达目标探测过程中往往存在目标运动、雷达轨迹误差等未知因素,这导致预先设计的字典矩阵无法实现雷达信号的最优稀疏表征,甚至导致雷达探测信息错误。字典学习是解决字典矩阵偏差条件下稀疏重建问题的有效工具,与传统稀疏信号处理单纯求解稀疏解不同,字典学习的目标是字典矩阵和稀疏信号的联合优化求解。本文介绍字典学习的一个分支——参数化稀疏表征,该方法通过构建参数化的字典矩阵,能够实现对雷达探测过程中未知参数的动态学习和雷达信号的最优稀疏表征。针对逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)成像、合成孔径雷达(Synthetic Aperture Radar,SAR)自聚焦、基于微多普勒的目标识别等雷达探测应用问题,本文将给出参数化稀疏表征在若干实际雷达数据实验中的处理结果。
本文组织结构如下。第2节简要回顾经典稀疏信号恢复问题。第3节介绍参数化稀疏表征模型及其在若干雷达应用中的物理意义。第4节给出参数化稀疏表征在若干实际雷达数据实验中的处理结果。第5节总结全文并对未来发展做出展望。
2 经典稀疏信号恢复问题假设观测数据${y} \in {\mathbb{C}^P}$和稀疏信号${x} \in {\mathbb{C}^Q}$之间的关系如下:
| \[y = \Phi x + n\] | (1) |
理论上,式(1)中的稀疏信号求解可以如下实现:
| \[\hat x = \arg \min {\left\| x \right\|_0},\;\;{\rm{s}}.{\rm{t}}.\;\;\left\| {y - \Phi x} \right\|_2^2 \le \varepsilon \] | (2) |
| \[\hat x = \arg \min {\left\| x \right\|_1},\;\;{\rm{s}}.{\rm{t}}.\;\;\left\| {y - \Phi x} \right\|_2^2 \le \varepsilon \] | (3) |
| \[\hat x = \mathop {\arg \min }\limits_x \left\{ {{{\left\| x \right\|}_1} + \lambda \left\| {y - \Phi x} \right\|_2^2} \right\}\] | (4) |
在雷达探测应用中,字典矩阵$ \Phi$是对雷达探测过程的线性近似。由于雷达探测过程中往往存在目标运动、雷达平台轨迹误差等未知因素,这导致预先设计的字典矩阵无法正确描述雷达探测过程,因此无法实现雷达信号的最优稀疏表征,甚至导致基于稀疏恢复的雷达处理无法获取目标的正确信息。为了解决此类问题,我们提出了下面的参数化稀疏表征模型。
假设雷达探测过程中的未知因素可以用参数w来描述,并构造与w有关的字典矩阵$\Phi \left( \omega \right)$。期望在$\Phi \left( \omega \right)$的表征下,能够对观测数据y进行稀疏表征,即
| \[y = \Phi (\omega )x + n\] | (5) |
| \[\{ \hat \omega ,\hat x\} = \mathop {\arg \min }\limits_{\{ \omega ,x\} } \left\{ {{{\left\| x \right\|}_1} + \lambda \left\| {y - \Phi (\omega )x} \right\|_2^2} \right\}\] | (6) |
最直观的参数化稀疏表征求解方法是搜索法。给定一个参数w的候选值,产生相应的字典矩阵$\Phi \left( \omega \right)$,然后按照经典稀疏信号恢复算法利用观测数据y和字典矩阵$\Phi \left( \omega \right)$求解x。当w发生变化时,显然输出的稀疏解x也随之发生变化,因此x也可视为w的函数,记为$x\left( \omega \right)$。在诸多参数候选值$\{ {\omega _1},{\omega _2},{\omega _3},\cdots \} $对应的求解结果$\{ {{x}}({\omega _1}),{{x}}({\omega _2}),$${{x}}({\omega _3}),\cdots \} $中依照某种寻优准则找到最优解:
| \[\left\{ {\begin{array}{*{20}{l}} {\hat \omega = \arg \min C\left( {x\left( {{\omega _i}} \right)} \right),\quad i = 1,2,3, \cdots }\\ {\hat x = x(\hat \omega )} \end{array}} \right.\] | (7) |
参数化稀疏表征求解还可以借鉴信号处理领域常用的交替迭代更新思路来实现。假设经过i步迭代之后,未知参数估计值为${\hat \omega ^{(i)}}$,则第(i+1)步的迭代过程包括如下两个操作。
(1) 更新稀疏解:
| \[{\hat x^{(i)}} = \mathop {\arg \min }\limits_x \left\{ {{{\left\| x \right\|}_1} + \lambda \left\| {y - \Phi ({{\hat \omega }^{(i)}})x} \right\|_2^2} \right\}\] | (8) |
(2) 更新参数估计值:
| \[{\hat \omega ^{(i + 1)}} = \mathop {\arg \min }\limits_\omega \left\{ {{{\left\| {y - \Phi (\omega ){{\hat x}^{(i)}}} \right\|}_2}} \right\}\] | (9) |
| \[\Phi (\omega ) \approx \Phi \left( {{\omega ^{(i)}}} \right){\rm{ + }}{\left. {\frac{{\partial \Phi (\omega )}}{{\partial \omega }}} \right|_{\omega = {\omega ^{(i)}}}} \cdot \Delta \omega \] | (10) |
| \[\Delta {\omega ^{(i)}} = \mathop {\arg \min }\limits_{\Delta \omega } \left\{ {\left\| {y - \left( {\Phi \left( {{\omega ^{(i)}}} \right){\rm{ + }}{{\left. {\frac{{\partial \Phi (\omega )}}{{\partial \omega }}} \right|}_{\omega = {\omega ^{(i)}}}} \cdot \Delta \omega } \right)\hat x_2^{(i)}} \right\|} \right\}\] | (11) |
| \[{\hat \omega ^{(i + 1)}} = {\hat \omega ^{(i)}} + \Delta {\omega ^{(i)}}\] | (12) |
参数化稀疏表征在诸多雷达应用中均可发挥作用,下面介绍这一方法在不同雷达应用中的物理意义。限于篇幅,这里仅阐述在不同应用场合下参数化稀疏表征模型中各变量的具体物理含义,详细公式表达请查阅相关参考文献。
ISAR成像能获得飞机、舰船等运动目标的高分辨2维图像。进行平动补偿之后,目标相对于雷达的运动可以等效为转台模型,假设在较短的观测时间内目标相对于雷达以恒定角速度做匀速转动。将观测场景沿距离维、方位维均匀划分为多个单元,则可认为ISAR回波数据是由每个单元的回波数据加和得到的。此时在参数化稀疏表征的信号模型式(5)中,y代表ISAR回波数据,$\omega $代表目标的转动速度,x代表离散化的观测场景散射强度分布,$\Phi \left( \omega \right)$的各列代表场景中各离散单元的单位强度回波数据。
(2) 在SAR自聚焦中的应用[20]
SAR成像过程中,雷达平台运动测量偏差将导致成像散焦,需要通过自聚焦予以校正。这里考虑一种简单情况,散焦由雷达平台速度的误差导致。将观测场景沿距离维、方位维均匀划分为多个单元,则可认为SAR回波数据是由每个单元的回波数据加和得到的。此时在参数化稀疏表征的信号模型式(5)中,y代表SAR回波数据,$\omega $代表载机平台的速度误差,x代表观测场景中强散射点的强度分布,$\Phi \left( \omega \right)$的各列代表场景中各离散单元的单位强度回波数据。尽管SAR对地观测应用中,观测场景散射强度的稀疏性并不明显,但文献[23]曾阐述,当不存在雷达平台运动测量误差的时候,稀疏信号处理在非稀疏场景SAR成像中也能获得令人满意的图像。在下一节的实验中我们将展示,当雷达平台运动测量误差存在的时候,利用参数化稀疏表征能够获取非稀疏场景SAR自聚焦良好的处理结果。
(3) 在基于微多普勒的雷达目标识别中的应用[21, 22, 24]
目标的振动/转动将给雷达回波带来附加的幅度和相位调制,这被称为微多普勒效应。将目标振动/转动的初相、幅度空间均匀划分为多个单元,则可认为雷达回波数据是由具有相同振动/转动频率、不同的初相和幅度的振动/转动分量回波加和组成。此时在参数化稀疏表征的信号模型式(5)中,y代表雷达回波数据,$\omega $代表目标的振动/转动频率,$\Phi \left( \omega \right)$的各列代表具有相同振动/转动频率、不同的初相和幅度的振动/转动分量单位回波,x代表目标上散射点强度分布。各振动/转动分量的初相差异能够描述目标结构,振动/转动幅度正比于散射点和振动/转动中心的距离,再结合振动/转动频率信息,能够实现基于微多普勒的目标识别。
3.3 参数化稀疏表征与字典学习的关系信号的稀疏表征是进行稀疏恢复的前提,只有选择了合适的字典矩阵(基信号)才能保证观测数据映射后的稀疏性,从而保证信号稀疏恢复的准确性。傅里叶变换,小波变换、离散余弦变换等常见的变换作为字典矩阵,在发掘信号稀疏性方面发挥了重要作用。然而这些固定的基信号并不能准确表示所有的实际信号,因为实际的信号往往都伴随着特定的结构及相应的参数。为了突破固定字典矩阵的局限性,字典学习理论获得了越来越多的关注,即对字典矩阵和稀疏解进行联合优化:
| \[\{ \hat \Phi ,\hat x\} = \arg \mathop {\min }\limits_{\{ F,x\} } \left\{ {{{\left\| x \right\|}_1} + \lambda \left\| {y - \Phi x} \right\|_2^2} \right\}\] | (13) |
针对ISAR成像、SAR自聚焦、雷达目标识别等应用,本节给出参数化稀疏表征的若干真实雷达数据实验结果。
(1) ISAR成像实验[17]
地基ISAR载频5.52 GHz,发射信号带宽400 MHz,脉冲宽度25.6 μs,脉冲重复频率200 Hz。采用参数化稀疏表征的交替迭代更新方法,对不同的输入数据块,经不超过10次迭代,最终估计得到目标转动速度稳定在约0.01 rad/s。图 1给出了傅里叶分析方法、Capon谱估计方法和参数化稀疏表征方法的成像结果,可以明显看到参数化稀疏表征提升了ISAR成像质量。
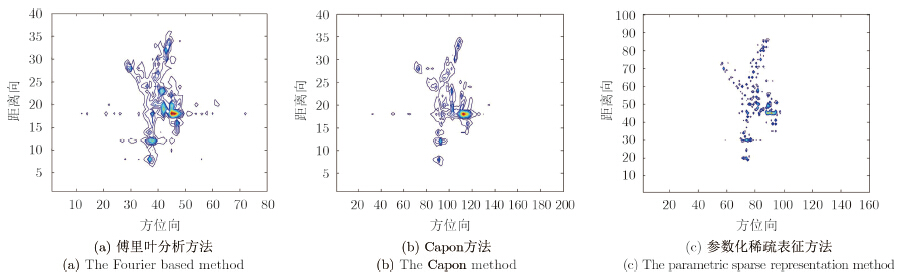 | 图 1 ISAR成像结果 Fig.1 ISAR imaging results |
(2) SAR自聚焦处理实验[20]
机载SAR载频9.68 GHz,发射信号带宽200 MHz,脉冲宽度15 μs,脉冲重复频率1 kHz。采用参数化稀疏表征的交替迭代更新方法,对不同的输入数据块,经10余次左右迭代,能够准确估计得到雷达载机平台速度。图 2给出了相位差(Phase Difference,PD)方法[31]、相位梯度自聚焦(Phase Gradient Autofocusing,PGA)方法[32]和参数化稀疏表征方法的SAR自聚焦处理结果,图 3给出了图 2中所标注的强散射目标成像结果的方位向剖面图。从图 2和图 3中可以看到:PD方法的成像质量有一定损失,这主要来自于方位向信号相位对消时多个线性调频分量的互相干扰;PGA方法聚焦效果很好,但其性能受聚焦参考点选择、窗长设置等因素的影响较大;参数化稀疏表征方法SAR成像质量可以和PGA方法相比拟,同时避免了参考点、窗长等因素的复杂影响,实际可操作性更强。
 | 图 2 SAR自聚焦结果 Fig.2 SAR autofucusing results |
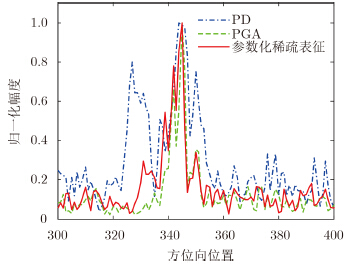 | 图 3 强散射点成像结果的方位向剖面图 Fig.3 Azimuth profile of the dominant target |
(3) 基于微多普勒的雷达目标识别实验[21, 22, 24]
地载调频连续波雷达载频24 GHz,采样频率22 kHz。某直升机的3种旋翼转动状态被记为3类目标,记为目标A,B和C,对应着旋翼转动速度分别为6.72 rps,9.12 rps和12.42 rps。雷达观测直升机的几何关系如图 4所示,从与旋翼平面呈0°、30°和60°的观测角进行3组观测,参数化稀疏表征方法的识别正确率如表 1所示。在观测角为0°时,雷达和直升机连线基本处于旋翼旋转平面内,此时直升机旋翼的RCS(Radar Cross Section)太小,因此识别正确率不高。在观测角为30°和60°时,旋翼RCS较强,参数化稀疏表征方法对3类直升机目标的识别正确率均在80%以上,对目标A和目标B的识别正确率达到100%。可见当雷达探测以直升机旋翼为代表的转动目标的相关应用中,参数化稀疏表征能够获得良好的目标识别性能。
 | 图 4 直升机目标识别实验场景 Fig.4 Experimental setup for helicopter classification |
| 表 1 基于参数化稀疏表征的直升机识别正确率(%) Tab. 1 Successful rates of helicopter classification based on parametric sparse representation (%) |
本文介绍了参数化稀疏表征及其在雷达探测中的应用。作为字典学习的一个分支,参数化稀疏表征把稀疏信号和字典矩阵同时作为优化求解目标,其中对字典矩阵的更新是通过更新字典内部的特定参数来实现的。实际雷达数据实验验证了参数化稀疏表征在若干雷达探测应用中的有效性。未来的研究包括:(1)字典矩阵设计及内部的参数(矢量或标量)选择;(2)参数化稀疏表征求解的理论分析和稳健算法;(3)尝试应用于其他领域。
致谢 美国雪城大学的Pramod K. Varshney教授,英国思克莱德大学的John J. Soraghan教授、Carmine Clemente博士及指导的研究生,清华大学的王希勤教授、饶玮博士,空军工程大学的张群教授、陈一畅博士都在参数化稀疏表征的研究过程中做出了贡献,在此向他们表示感谢。本文部分研究内容是在973 计划项目“稀疏微波成像的理论、体制和方法研究”(2010CB731900)资助下完成的,在项目进行过程中,我们的研究得到了以首席科学家吴一戎院士为代表的诸多专家的指导,也得到了中国科学院电子学研究所、北京航空航天大学、西安电子科技大学、上海交通大学、西安交通大学、北京理工大学、中国科学技术大学、中国航天科工集团二院207 所等项目参研单位的宝贵建议,在此也一并表示感谢。| [1] | Tibshirani R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society, Series B (Methodological), 1996: 267-288.( 1) 1) |
| [2] | Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.( 1) 1) |
| [3] | Candès E J, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.( 1) 1) |
| [4] | Candes E J and Tao T. Near-optimal signal recovery from random projections: universal encoding strategies[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425.( 1) 1) |
| [5] | Eldar Y and Kutyniok G. Compressed Sensing: Theory and Applications[M]. Cambridge University Press, 2012.( 1) 1) |
| [6] | Baraniuk R and Steeghs P. Compressive radar imaging[C]. 2007 IEEE Radar Conference, 2007: 128-133.( 1) 1) |
| [7] | Potter L C, Ertin E, Parker J T, et al. Sparsity and compressed sensing in radar imaging[J]. Proceedings of the IEEE, 2010, 98(6): 1006-1020.( 1) 1) |
| [8] | Ender J H G. On compressive sensing applied to radar[J]. Signal Processing, 2010, 90(5): 1402-1414.( 1) 1) |
| [9] | Zhang B, Hong W, and Wu Y. Sparse microwave imaging: principles and applications[J]. SCIENCE CHINA Information Sciences, 2012, 55(8): 1722-1754.( 1) 1) |
| [10] | 吴一戎, 洪文, 张冰尘, 等. 稀疏微波成像研究进展[J]. 雷达学报, 2014, 3(4): 383-395.Wu Yi-rong, Hong Wen, Zhang Bing-chen, et al. Current developments of sparse microwave imaging[J]. Journal of Radars, 2014, 3(4): 383-395.( 1) 1) |
| [11] | Hong W, Zhang B, Zhang Z, et al. Radar imaging with sparse constraint: principle and initial experiment[C]. Proceedings of 10th European Conference on Synthetic Aperture Radar, EUSAR 2014, Berlin, Germany, 2014: 1-4.( 1) 1) |
| [12] | CVX: matlab software for disciplined convex programming[OL]. http://cvxr.com/cvx, 2015.( 1) 1) |
| [13] | Tropp J A and Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666.( 1) 1) |
| [14] | Dai W and Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Transactions on Information Theory, 2009, 55(5): 2230-2249.( 1) 1) |
| [15] | Needell D and Tropp J A. CoSaMP: iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3): 301-321.( 1) 1) |
| [16] | Li G, Zhang H, Wang X, et al. ISAR 2-D imaging of uniformly rotating targets via matching pursuit[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1838-1846.( 2) 2) |
| [17] | Rao W, Li G, Wang X, et al. Adaptive sparse recovery by parametric weighted L1 minimization for ISAR imaging of uniformly rotating targets[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(2): 942-952.( 3) 3) |
| [18] | Rao W, Li G, Wang X, et al. Comparison of parametric sparse recovery methods for ISAR image formation[J]. SCIENCE CHINA Information Sciences, 2014, 57(2). doi: 10.1007/s11432-013-4859-9.( 2) 2) |
| [19] | Rao W, Li G, Wang X, et al. Parametric sparse representation method for ISAR imaging of rotating targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 910-919.( 1) 1) |
| [20] | Chen Y, Li G, Zhang Q, et al. Parametric sparse representation method for air-borne SAR autofocusing. submitted to IEEE Transactions on Geoscience and Remote Sensing.( 3) 3) |
| [21] | Li G and Varshney P K. Micro-Doppler parameter estimation via parametric sparse representation and pruned orthogonal matching pursuit[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(12): 4937-4948.( 3) 3) |
| [22] | Gaglione D, Clemente C, Coutts F, et al. Model-based sparse recovery method for automatic classification of helicopters[C]. 2015 IEEE Radar Conference, Arlington, 2015: 1161-1165.( 3) 3) |
| [23] | Alonso M T, Lopez-Dekker P, and Mallorqui J J. A novel strategy for radar imaging based on compressive sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4285-4295.( 1) 1) |
| [24] | Coutts F K, Gaglione D, Clemente C, et al. Label consistent K-SVD for sparse micro-Doppler classification[C]. 2015 IEEE International Conference on Digital Signal Processing, Singapore, 2015: 90-94.( 2) 2) |
| [25] | Peyre G. Best basis compressed sensing[J]. IEEE Transactions on Signal Processing, 2010, 58(5): 2613-2622.( 1) 1) |
| [26] | Zhu H, Leus G, and Giannakis G B. Sparsity-cognizant total least-squares for perturbed compressive sampling[J]. IEEE Transactions on Signal Processing, 2011, 59(5): 2002-2016.( 1) 1) |
| [27] | Olshausen B A and Field D J. Sparse coding with an overcomplete basis set: a strategy employed by V1?[J]. Vision Research, 1997, 37(23): 3311-3325.( 1) 1) |
| [28] | Kreutz-Delgado K, Murray J F, Rao B D, et al. Dictionary learning algorithms for sparse representation[J]. Neural Computation, 2003, 15(2): 349-396.( 1) 1) |
| [29] | Bryta O and Elad M. Compression of facial images using the K-SVD algorithm[J]. Journal of Visual Communication and Image Representation, 2008, 19(4): 270-282.( 1) 1) |
| [30] | Tosic I and Frossard P. Dictionary learning[J]. IEEE Signal Processing Magazine, 2011, 28(2): 27-38.( 1) 1) |
| [31] | Donohoe G W. Subaperture autofocus for synthetic aperture radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(2): 617-621.( 1) 1) |
| [32] | Wahl D E, Eichel P H, Ghiglia D C, et al. Phase gradient autofocus—a robust tool for high resolution SAR phase correction[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(3): 827-835.( 1) 1) |


