天波超视距雷达(Over-The-Horizon Radar,OTHR)利用电离层对高频电磁波的反射特性探测视距外的目标,具有重要的军事意义。OTHR通常选址在电磁干扰较弱的地区,并且通过实时选频以避开外界短波干扰[1]。尽管如此,由于高频波段上用户众多,远处的短波干扰有时仍会通过电离层反射进入接收机,影响了雷达的探测性能。短波干扰具有明显的方向性,因此可以采用自适应波束形成(Adaptive Digital BeamForming,ADBF)加以抑制。但是,由于电离层是运动的反射媒介,经它反射的短波干扰通常是空间非平稳的,从而增加了ADBF处理的难度。
近年来,学者们对天波雷达的ADBF抗干扰问题进行了大量的研究。文献[2-4]对干扰源和干扰特性进行了分析,指出电离层运动使干扰经常呈现空间非平稳性。文献[5-7]研究了在相干处理间隔(Coherent Processing Interval,CPI)上进行分段自适应的ADBF方法,权矢量是时变的,以适应干扰的非平稳性,同时还要保持杂波的相干性。文献[8]提出了基于递归最小二乘的天波雷达ADBF方法,能兼顾干扰抑制和杂波相干性保持。这些ADBF方法都是在距离-脉冲域上实现的,处理都比较复杂,而且在获取自适应训练样本时需要预先滤除杂波。
本文推导了短波干扰在距离-多普勒域上的解析表达式,分析了电离层运动导致的短波干扰空间非平稳性,在此基础上提出了天波超视距雷达后多普勒自适应波束形成方法,首先将各阵元接收信号分别变换到距离-多普勒域上,然后在各个频点上分别进行自适应处理,以抑制短波干扰。在天波雷达对空探测中,目标与杂波在多普勒域上是分开的,ADBF处理只需在非杂波区进行,因此干扰样本可以从非杂波区获取,从而避免了杂波的影响。
2 雷达信号模型与短波干扰特性 2.1 雷达信号模型设OTHR的接收阵为N元均匀线阵,阵元间距为d,阵列导向矢量为:
| $a\left( \theta \right)=\left[ 1\exp \left( j2\pi /\lambda d\sin \left( \theta \right) \right)\cdots \exp \left( j2\pi /\lambda \left( N-1 \right)d\sin \left( \theta \right) \right) \right]$ |
其中θ为波达方向,λ为波长。OTHR阵列接收信号表示为:
| $x(m,t)=s(m,t)+c(m,t)+z(m,t)+n(m,t),m=1,\cdots ,M$ | (1) |
式中:s(m,t)为目标回波信号;c(m,t)为杂波;z(m,t)为经电离层反射到达接收阵的短波干扰;n(m,t)为接收机噪声;m为脉冲序号,M为相干脉冲数。
目标信号s(m,t)来自于波束指向θ0,表示为s(m,t)=s0(m,t)a(θ0),s0(m,t)是目标信号复包络,a(θ0)为目标导向矢量。杂波c(m,t)是全向的,只是在波束指向方向上增益更高,主要包括1阶Bragg分量以及一些较弱的高阶分量。s(m,t)和c(m,t)都是相干脉冲序列,利用脉冲压缩和相干积累处理在距离和多普勒域上分辨两者,同时提高目标信噪比。短波干扰z(m,t)位于波束副瓣上,受电离层运动影响呈现空间非平稳性。噪声n(m,t)是空间白噪声,且与式(1)中的其它3个分量不相关。
2.2 短波干扰的距离-多普勒谱天波雷达通过脉冲压缩和相干积累处理分辨目标信号和杂波,并提高目标信噪比,此时伴随目标信号和杂波一同进入接收机的短波干扰会受到同样的处理,因此有必要分析短波干扰的距离-多普勒谱特征。
OTHR发射线性调频连续波信号,表示为:
| $u(t)=\text{rect}\left( t/{{T}_{\text{r}}} \right)\exp (\text{j}\pi K{{t}^{2}})\ $ | (2) |
式中:Tr为脉宽(也是脉冲重复周期),K=B/Tr为调频斜率,B为带宽。
为方便起见,假设在第m个重复周期上雷达接收到的短波干扰为[9]:
| ${{v}_{m}}(t)=\text{rect}\left( \frac{t-m{{T}_{\text{r}}}}{{{T}_{\text{r}}}} \right)\exp (\text{j2}\pi {{f}_{1}}t),-B/2<{{f}_{1}}<B/2$ | (3) |
当BT$\gg $1时,匹配滤波器的近似频率响应为[10]:
| $G(f)=\text{rect}\left( \frac{f}{B} \right)\exp \left( \text{j}\pi \frac{{{f}^{2}}}{K} \right)\ $ | (4) |
该滤波器的群延迟为:
| ${{t}_{\text{d}}}(f)=-\frac{f}{K}$ | (5) |
因此短波干扰通过匹配滤波器后的输出为:
| $\begin{align} & {{y}_{m}}(t)={{v}_{m}}[t-{{t}_{\text{d}}}({{f}_{1}})]=\text{rect}\left( \frac{t+{{f}_{1}}/K-m{{T}_{\text{r}}}}{{{T}_{\text{r}}}} \right) \\ & \cdot \exp [\text{j2}\pi {{f}_{1}}(t+{{f}_{1}}/K)] \\ \end{align}$ | (6) |
令t'=t - mTr,则式(6)变为:
| $\begin{align} & {{y}_{m}}({t}')=\text{rect}\left( \frac{{t}'+{{f}_{1}}/K}{{{T}_{\text{r}}}} \right) \\ & \cdot \exp [\text{j2}\pi {{f}_{1}}({t}'+{{f}_{1}}/K+m{{T}_{\text{r}}})] \\ \end{align}$ | (7) |
式(7)表明短波干扰可以无失真地通过匹配滤波器,分布于全程距离上。
在对各重复周期上的接收信号进行脉冲压缩处理后,OTHR还要对各距离单元上的接收信号进行相干积累处理。由式(7)可见,短波干扰也会同样实现相干积累,若有M个连续的相干脉冲,则可以得到:
| $\begin{align} & Y({t}',{{f}_{\text{d}}})=M\cdot \exp [\text{j2}\pi {{f}_{1}}({t}'+{{f}_{1}}/K)+\text{j}\pi ({{f}_{1}}-{{f}_{\text{d}}}) \\ & \cdot (M-1){{T}_{\text{r}}}]\cdot \text{sinc}\pi ({{f}_{1}}-{{f}_{\text{d}}})M{{T}_{\text{r}}}] \\ \end{align}$ | (8) |
式(7)和(8)表明,短波干扰在距离−多普勒谱图上表现为平行于距离轴的恒幅谱脊,其位置为${f_{{\rm{d1}}}}=\bmod ({f_1},\;{f_{\rm{r}}}),{f_{\rm{r}}}=1/{T_{\rm{r}}}$为脉冲重复频率。前面为了推导的方便假设短波干扰是单频的,实际短波干扰总有一定的带宽,会造成谱脊位置抖动和基底抬高,但是基本特征不会改变。
2.3 短波干扰的空间非平稳性当短波干扰通过电离层反射进入OTHR接收机时,由于电离层是运动的反射媒介,经它反射的短波干扰通常是空间非平稳的,即干扰的角度随时间变化。
在脉冲压缩后,第n个阵元、第m个脉冲、第k个距离门上的干扰表示为:
| $\begin{align} & z(n,m,k)=\exp \left[ \text{j}\frac{2\pi }{\lambda }nd\sin ({{\theta }_{m}}) \right] \\ & \cdot {{y}_{m}}(\text{ }t_{k}^{\prime }),\ n=0,1,\cdots ,N-1 \\ \end{align}$ | (9) |
式中θm为干扰的方位角,这里假设它是慢时变的,即在脉冲重复周期之间变化,而在1个脉冲重复周期内不变化。
设短波干扰的初始方位角为θ,有θm=θ+δθm,若δθm较小,则式(9)可近似表示为:
| $\begin{align} & z(n,m,k)\approx \exp \left[ \text{j}\frac{2\pi }{\lambda }nd\sin (\bar{\theta }) \right] \\ & \cdot \exp \left[ \text{j}\frac{2\pi }{\pi }nd\cos (\bar{\theta })\cdot \delta {{\theta }_{m}} \right]\cdot {{y}_{m}}(\text{ }t_{k}^{\prime }) \\ \end{align}$ | (10) |
式(10)右边的第2项刻画了干扰的空间非平稳性,与阵元n和角度变化量δθm有关。
将式(10)变换到多普勒域上得到:
| $\begin{align} & Z(n,{{f}_{\text{d}}},k)\approx \exp \left[ \text{j}\frac{2\pi }{\lambda }nd\sin (\overline{\theta }) \right] \\ & \cdot \left[ \Gamma (n,{{f}_{\text{d}}})\otimes Y(\text{ }t_{k}^{\prime },{{f}_{\text{d}}}) \right] \\ \end{align}$ | (11) |
式中:Γ(n,fd)是式(10)右边第2项的频谱,Y(t'k,fd)是第3项的频谱,⊗表示卷积运算。
忽略式(8)中辛格函数的副瓣,式(11)中的卷积运算将辛格函数的主瓣搬移到多个多普勒频点上,幅度按Γ(n,fd)分布。对于不同的阵元,频谱Γ(n,fd)是变化的,但是对于单个阵元,它在所有距离单元上都相同。当在各个频点上分别进行ADBF处理时,变化的Γ(n,fd)等效于阵元之间的幅相误差,对ADBF性能的影响可以忽略[11],因此短波干扰能够被有效地抑制。
3 自适应波束形成器上一节的分析表明,在距离-多普勒域上,短波干扰沿距离维是平稳的,电离层运动转化为阵元之间的幅相误差,对ADBF性能的影响并不大,另外,在天波雷达的对空探测中,目标信号通常位于非杂波区,因此本文提出在距离-多普勒域上进行自适应处理,即后多普勒自适应波束形成,以抑制非杂波区中的短波干扰。
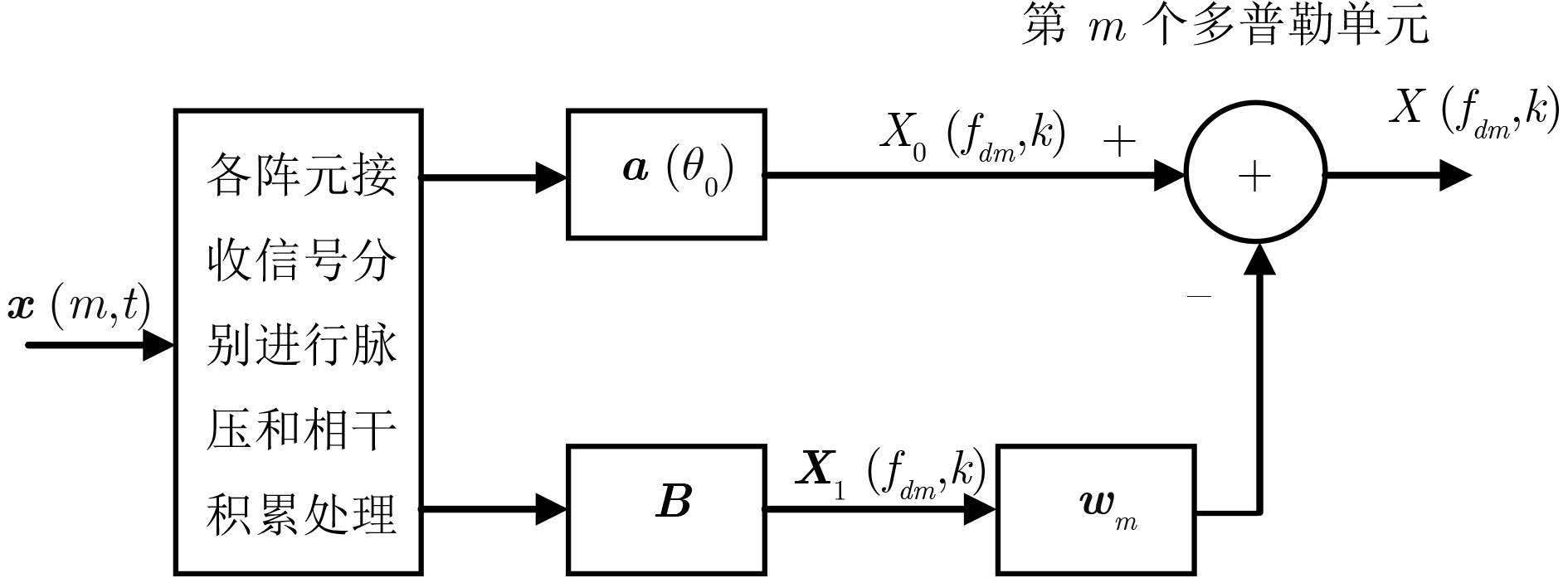
OTHR接收阵规模庞大,为了降低自适应处理的复杂度,ADBF采用广义副瓣对消结构[8],如图 1所示,首先将各阵元接收信号分别变换到距离-多普勒域上,然后执行副瓣对消自适应处理,其中上支路实现常规波束形成,下支路计算ADBF权矢量用来对消上支路中的短波干扰,虚线框中给出了第m个多普勒单元上的自适应波束形成。B为阻塞矩阵,满足条件BHa(θ0)=0,从而阻塞了目标信号进入下支路。为了降维,B的列数只要略大于干扰数即可,式(12)是一个N ×(N -1)维的两阵元差波束系数矩阵,从中随机选择若干列构成矩阵B。
|
图 1 广义副瓣对消器 Fig.1 Generalized sidelobe canceller |
| ${{B}_{0}}=\left[ \begin{matrix} 1 & 0 & \cdots & 0 & 0 \\ b & 1 & \cdots & \vdots & 0 \\ 0 & b & \ddots & 0 & \vdots \\ \vdots & 0 & \ddots & 1 & 0 \\ 0 & \vdots & \cdots & b & 1 \\ 0 & 0 & \cdots & 0 & b \\ \end{matrix} \right]$ | (12) |
式中b=-exp[j2π/λdsin(θ0)]。
在距离-多普勒域的非杂波区中,ADBF处理按多普勒单元进行,训练样本沿距离维取得。对于第m个单元,设上支路输入信号为X0(fdm,k),下支路输入信号为X1(fdm,k),则副瓣对消器输出为:
| $X({{f}_{\text{d}m}},k)={{X}_{0}}({{f}_{\text{d}m}},k)-\omega _{m}^{\text{H}}{{X}_{1}}({{f}_{\text{d}m}},k)$ | (13) |
式中
| ${{w}_{m}}=R_{m}^{-1}{{r}_{m}}$ | (14) |
| ${{R}_{m}}=\sum\limits_{k}{{{X}_{1}}({{f}_{\text{d}m}},k)X_{1}^{\text{H}}({{f}_{\text{d}m}},k)}$ | (15) |
| ${{r}_{m}}=\sum\limits_{k}{{{X}_{1}}({{f}_{\text{d}m}},k)\text{ }X_{0}^{*}({{f}_{\text{d}m}},k)}$ | (16) |
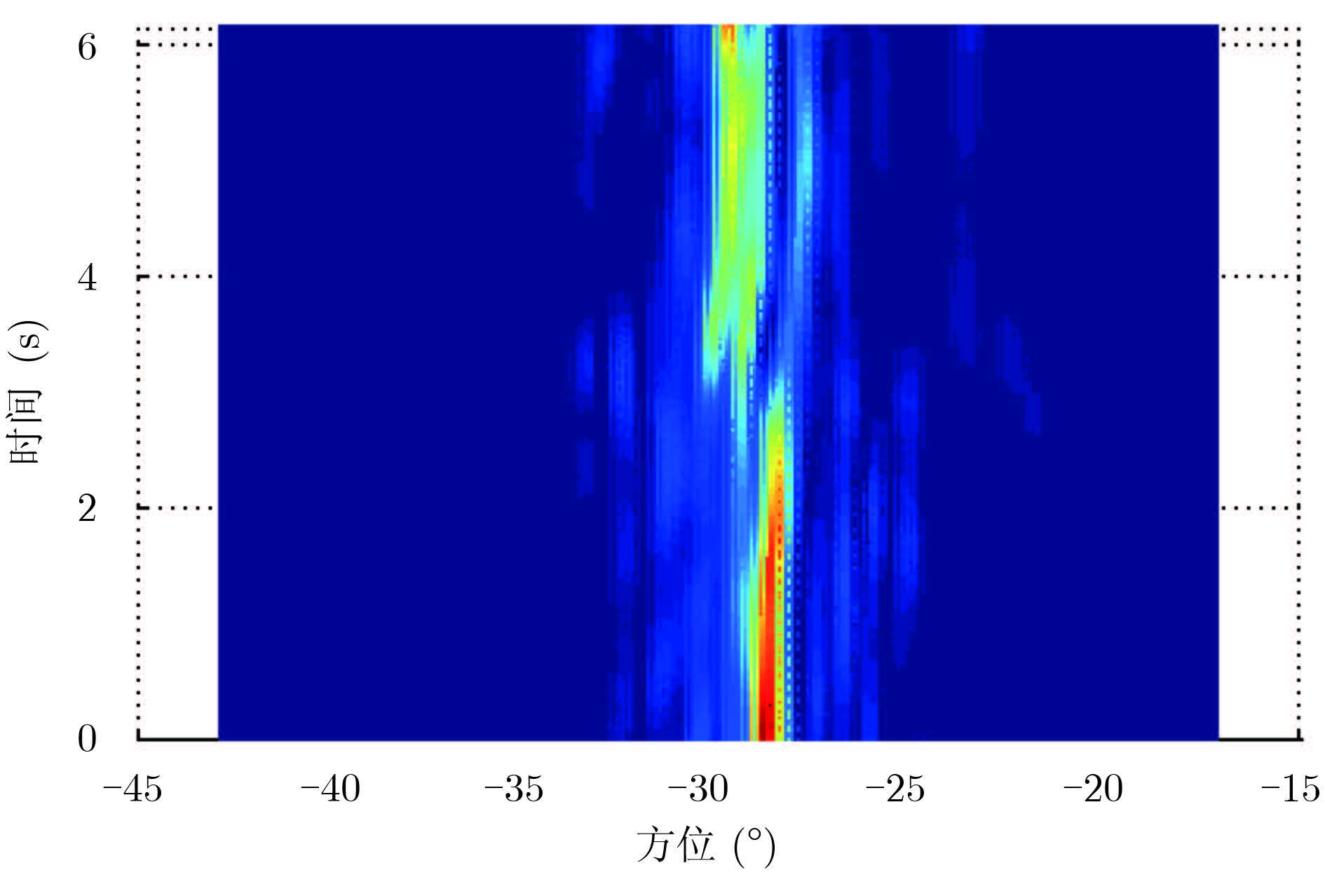
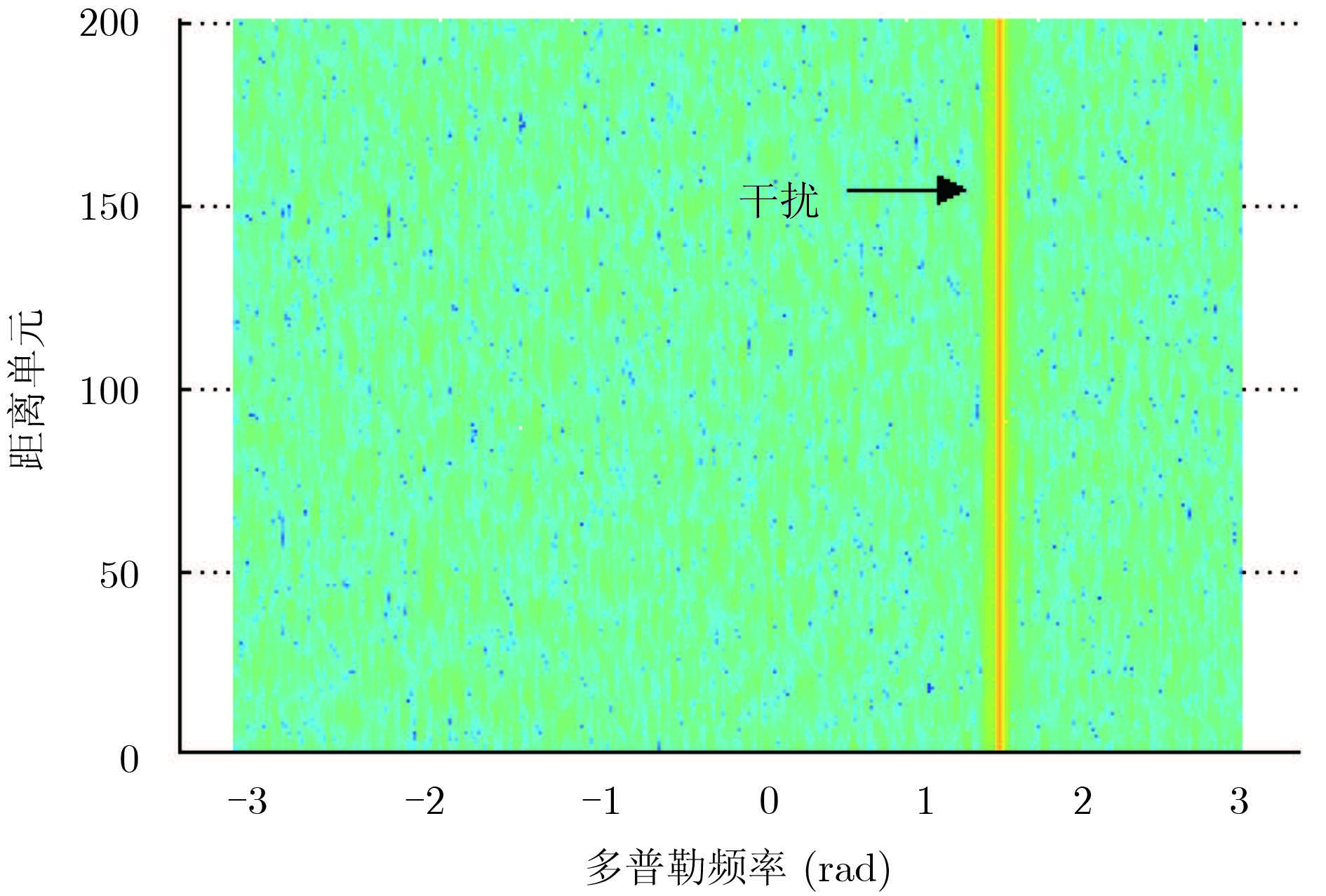
实验中干扰信号采用正弦波,频偏为1.63 rad,方位角为-30.6°,距接收站1000 km,该干扰信号经电离层反射到达接收机。图 2是采用前后向平滑MUSIC技术估计的干扰空间谱,可见在CPI内干扰信号呈现明显的空间非平稳性,主要表现为多径传播、传播路径的随机漂移和起伏等。对接收数据进行常规数字波束形成(Digital BeamForming,DBF),波束指向为0°,其距离-多普勒谱如图 3所示,表现为一条平行于距离轴的恒幅谱脊。
|
图 2 干扰的MUSIC谱 Fig.2 MUSIC spectrum of interference |
|
图 3 干扰的距离-多普勒谱 Fig.3 Range-Doppler spectrum of interference |
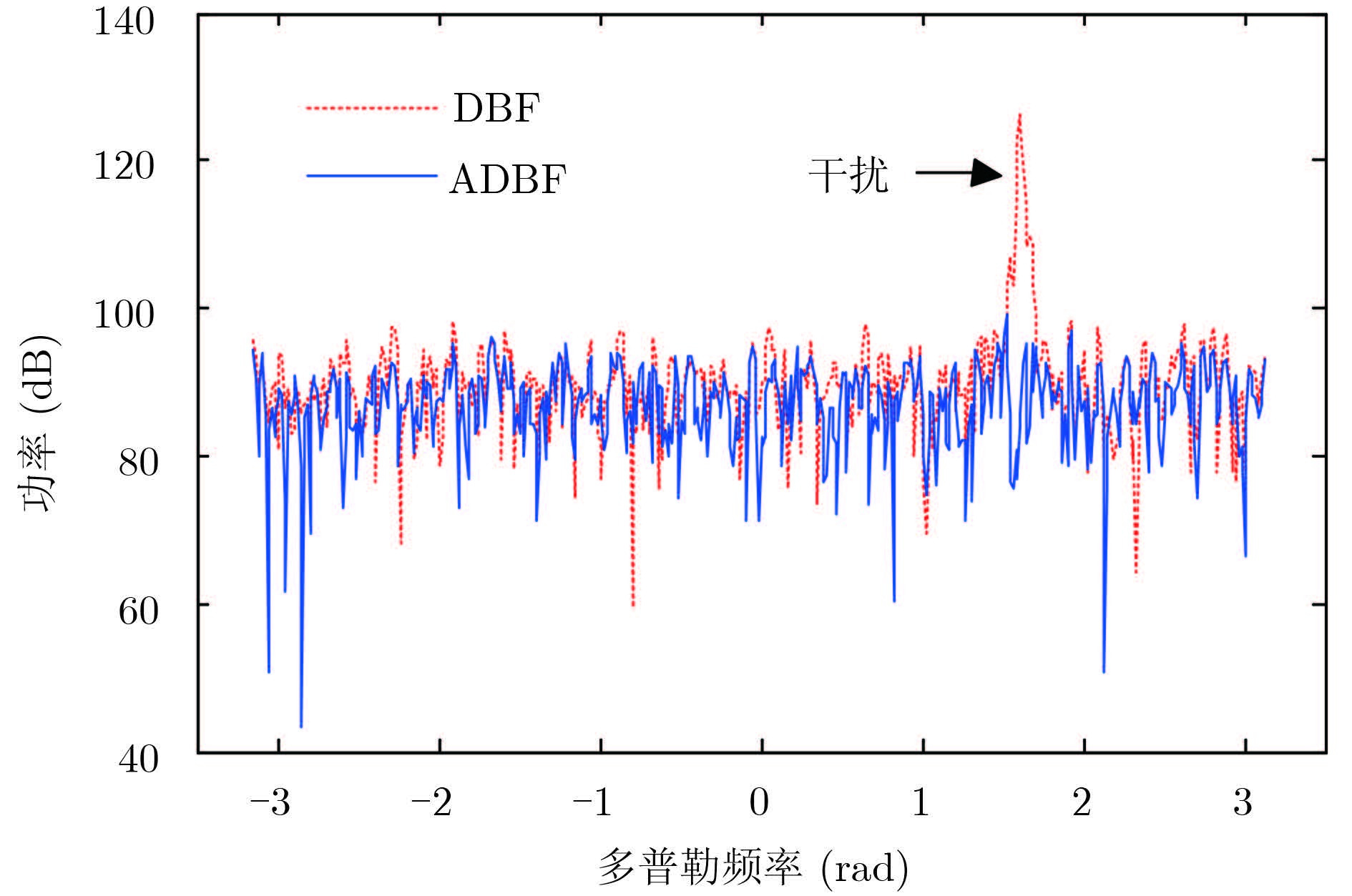
从矩阵B0中随机选择4列构成阻塞矩阵B,按照图 1的流程进行自适应波束形成,结果也示于图 4中,可见干扰被有效地抑制,作为比较,图中还给出了常规波束形成的处理结果。
|
图 4 DBF与ADBF的比较 Fig.4 Comparison of DBF and ADBF |
ADBF实验中,雷达发射线性调频连续波信号,一个CPI(约6 s)内包含若干个重复周期。在雷达正常工作的同时,开启干扰机,干扰机的位置和采用的信号形式同4.1节。实验中,另外一个很强的正弦波干扰也进入了接收机,该干扰来源不明,方位约8.6°,频偏为0.49 rad。图 5和图 6分别示出了两个干扰的MUSIC谱,两者都是空间非平稳的。
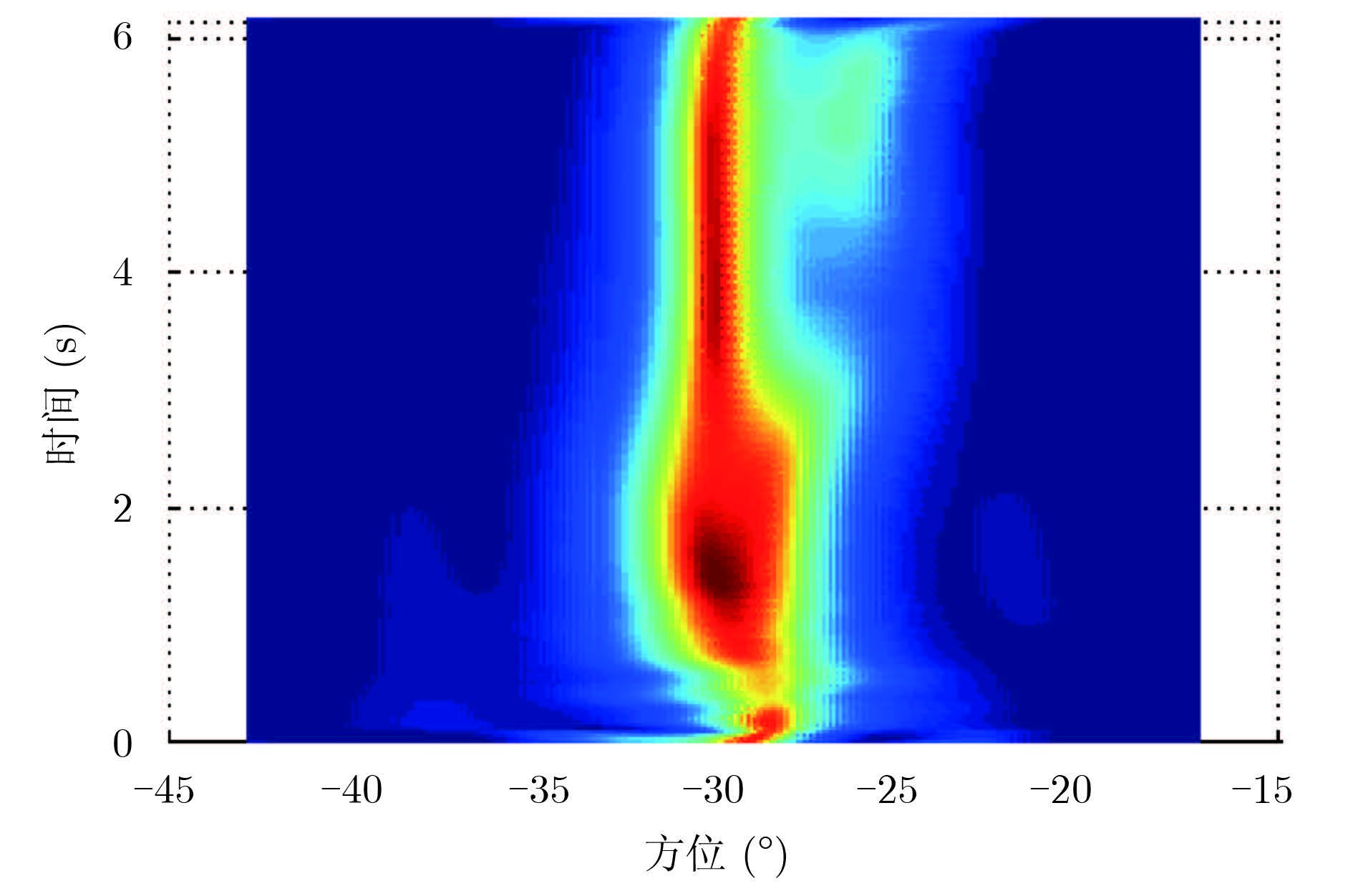
|
图 5 干扰1的MUSIC谱 Fig.5 MUSIC spectrum of interference 1 |
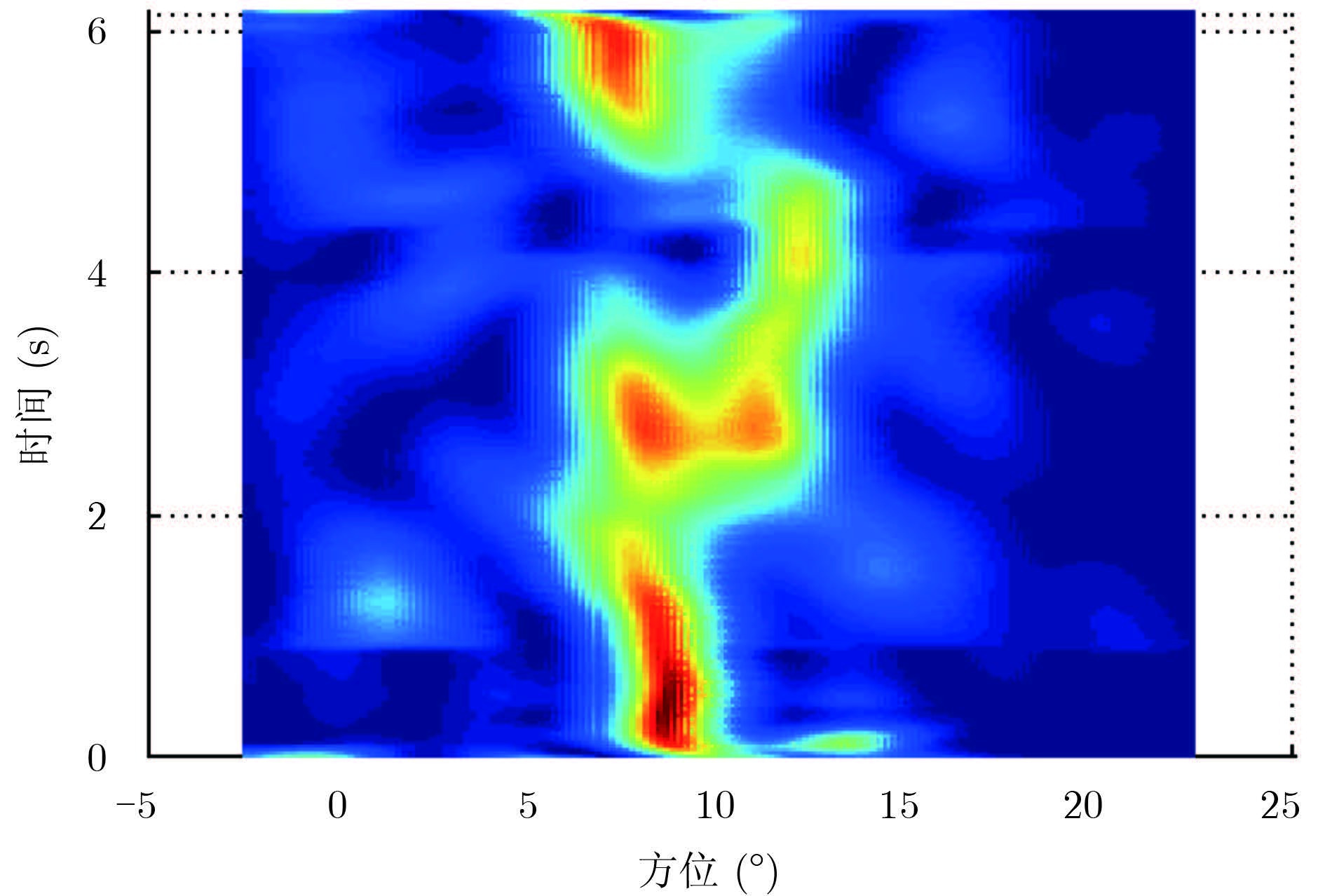
|
图 6 干扰2的MUSIC谱 Fig.6 MUSIC spectrum of interference 2 |
对雷达接收信号进行常规数字波束形成、脉冲压缩、相干积累,某一距离单元上的处理结果如图 7所示,-1.26 rad处的尖峰为目标,0.49 rad和1.63 rad处的两个尖峰为干扰。从矩阵B0中随机选择4列构成阻塞矩阵B,按照图 1的流程进行自适应波束形成,结果也示于图 7中,可见两个单频干扰被有效地抑制,同时目标信噪比基本保持不变。
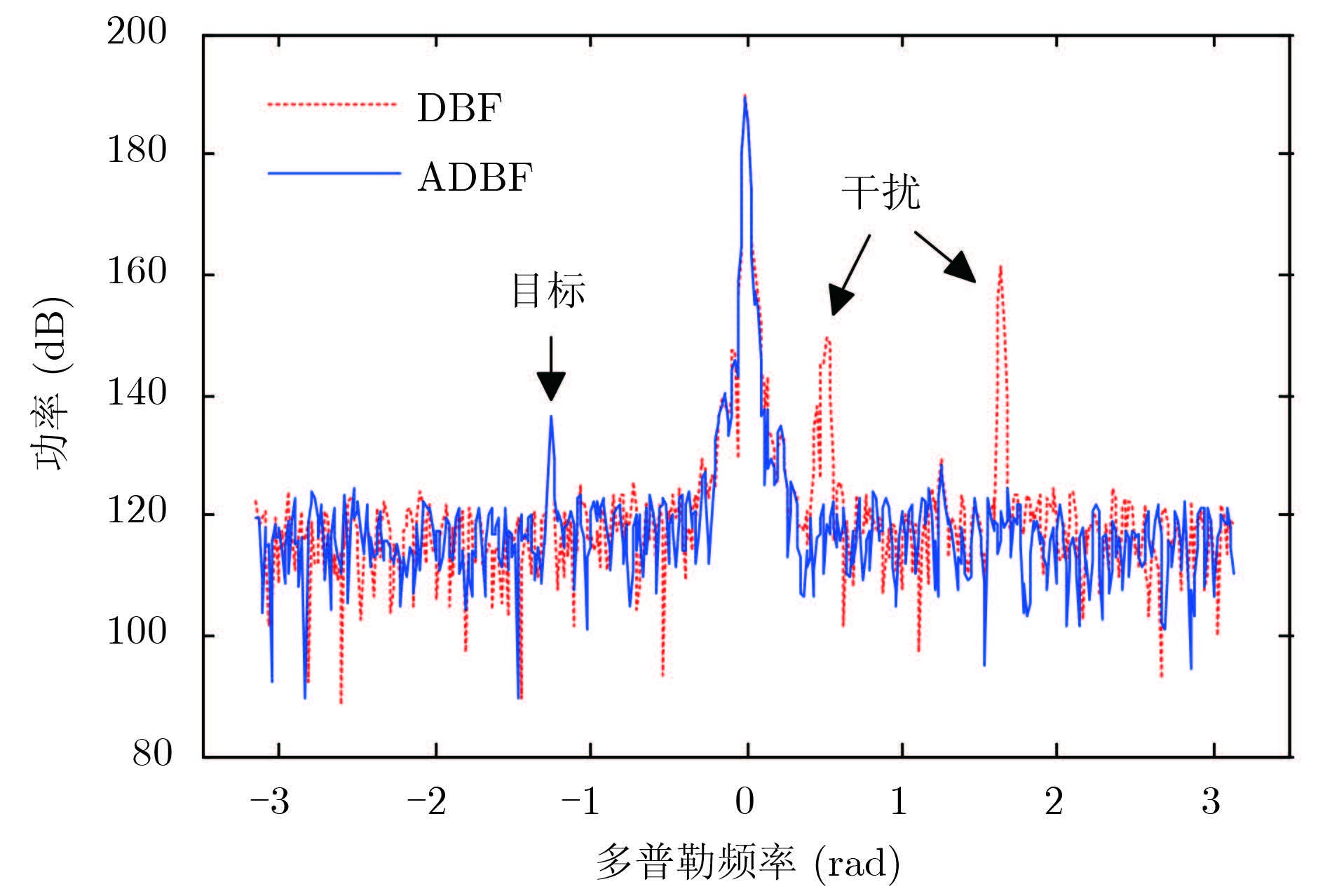
|
图 7 DBF与ADBF的比较 Fig.7 Comparison of DBF and ADBF |
天波雷达需要采用ADBF技术抑制同频段上的众多短波干扰,但是,远处的短波干扰经电离层反射后呈现空间非平稳性,增加了ADBF处理的难度。由于脉冲压缩和相干积累是天波雷达中必要的信号处理步骤,短波干扰也会受到同样的处理,因此该文推导了短波干扰在距离−多普勒域上的解析表达式,表现为平行于距离轴的恒幅谱脊,并分析了电离层运动导致的短波干扰空间非平稳性,其等效为各阵元上相同多普勒频点之间的幅相误差。在此基础上提出了天波雷达后多普勒自适应波束形成方法,即首先将各阵元接收信号分别变换到距离−多普勒域上,然后在各个频点上分别进行自适应处理,以抑制短波干扰。大量实测数据处理表明该方法的抗干扰性能良好,由于采用的都是常规处理,因此该方法的稳健性也较强。
| [1] |
周文瑜, 焦培南.
超视距雷达技术[M]. 北京: 电子工业出版社, 2008 : 235 -243.
Zhou Wen-yu, Jiao Pei-nan.
Over-The-Horizon Radar Technique[M]. Beijing: Publishing House of Electronics Industry, 2008 : 235 -243.
( 0) 0)
|
| [2] |
Fabrizio G A, Abramovich Y I, Anderson S J. Adaptive cancellation of nonstationary interference in HF antenna array[J].
IEE Proceedings-Radar, Sonar and Navigation,1998, 145 (1) : 19 –24.
( 0) 0)
|
| [3] |
唐晓东, 周文瑜. 短波雷达干扰与抗干扰技术[J].
现代雷达,2003, 25 (2) : 21 –25.
Tang Xiao-dong, Zhou Wen-yu. Interference and anti-interference techniques of HF radar[J].
Modern Radar,2003, 25 (2) : 21 –25.
( 0) 0)
|
| [4] |
沈石坚, 黄银和, 朱炳元. 高频雷达干扰特性研究[J].
现代雷达,2008, 30 (11) : 30 –33.
Shen Shi-jian, Huang Yin-he, Zhu Bing-yuan. A study on interference characteristics in high frequency radar[J].
Modern Radar,2008, 30 (11) : 30 –33.
( 0) 0)
|
| [5] |
Fabrizio G A, Gershman A B, Turley M D. Robust adaptive beamforming for HF surface wave radar[J].
IEEE Transactions on Aerospace and Electronic Systems,2004, 40 (2) : 510 –524.
( 0) 0)
|
| [6] |
李高鹏, 李雷, 许荣庆. 基于海杂波保持的高频地波雷达干扰抑制方法研究[J].
电波科学学报,2005, 20 (3) : 358 –362.
Li Gao-peng, Li Lei, Xu Rong-qing. RF interference suppression method based on sea-clutter-wave maintaining for HF ground-wave radar[J].
Chinese Journal of Radio Science,2005, 20 (3) : 358 –362.
( 0) 0)
|
| [7] |
Su H T, Liu H, Shui P, et al. Adaptive HF interference cancellation for sky wave over-the-horizon radar[J].
Electronics Letters,2011, 47 (1) : 50 –52.
( 0) 0)
|
| [8] |
陈希信, 韩彦明, 于景兰. 高频雷达自适应波束形成抗干扰研究[J].
电波科学学报,2010, 25 (6) : 1169 –1174.
Chen Xi-xin, Han Yan-ming, Yu Jing-lan. Research for interference suppression in HF radar based on ADBF[J].
Chinese Journal of Radio Science,2010, 25 (6) : 1169 –1174.
( 0) 0)
|
| [9] |
周浩, 文必洋, 吴世才, 等. 应用时频分析进行高频雷达射频干扰抑制[J].
电子学报,2004, 32 (9) : 1546 –1548.
Zhou Hao, Wen Bi-yang, Wu Shi-cai, et al. HF radar radio frequency interference suppression based on time-frequency analysis[J].
Acta Electronica Sinica,2004, 32 (9) : 1546 –1548.
( 0) 0)
|
| [10] |
林茂庸, 柯有安.
雷达信号理论[M]. 北京: 国防工业出版社, 1984 : 133 -134.
Lin Mao-yong and Ke You-an, Ke You-an, Ke You-an.
Radar Signal Theory[M]. Beijing: National Defense Industry Press, 1984 : 133 -134.
( 0) 0)
|
| [11] |
王永良, 丁前军, 李荣峰.
自适应阵列处理[M]. 北京: 清华大学出版社, 2009 : 276 -282.
Wang Yong-liang, Ding Qian-jun, Li Rong-feng.
Adaptive Array Processing[M]. Beijing: Tsinghua University Press, 2009 : 276 -282.
( 0) 0)
|


