雷达发射电磁波，电磁波遇到运动目标后可能会产生多普勒效应，而在目标主体运动的同时，目标上的某些部件也可能相对目标质心做机械振动、旋转或摆动等运动，这些运动也会对雷达发射的电磁波产生幅度、相位和频率等方面的调制。分析信号在多普勒域的调制情况，这些目标部件的运动会在目标主体运动相应的多普勒频率附近附加多普勒谱调制，即产生微多普勒效应^[1]。文献^[2]综述了当前国内外微多普勒效应研究的发展和应用现状；文献^{[3, 4]}利用微动信息对地面目标的分类进行了研究；文献^{[5, 6]}基于微多普勒效应深入分析了空间锥体目标微动特性与识别方法。上述文献表明利用微动特征对目标进行分类和识别是可行且有效的。

飞机上存在周期性旋转的旋转部件，如旋翼、涡扇发动机风扇等。在一定的飞行姿态下，雷达探测飞机目标时，飞机的旋转部件对雷达回波会产生周期性的调制，这种调制被称为雷达回波的喷气引擎调制(Jet Engine Modulation,JEM)^[7]。在多普勒域，JEM效应的表现就是产生围绕由飞机机身运动引起的中心频率的边带频率。飞机旋转部件的转动速度、部件结构等不同，会对雷达回波产生不同的调制即不同类型的飞机具有不同的JEM特性，因此，直升机、螺旋桨飞机和喷气式飞机不同的JEM特征可以作为有效的目标特征，用于实现3类飞机目标的分类。文献^[8]采用复自回归(AR)双谱技术分析了常规雷达回波中的JEM特征，从信号的双谱切片中提取了具有相对不变性的JEM周期特征，并基于JEM周期特征实现了直升机和螺旋桨飞机的分类。对于信号周期的估计，现有方法主要通过估计雷达时域信号的周期或多普勒谱调制谱线的谱线间隔来实现3类飞机目标的分类^[9]，进而将提取出的时域回波调制周期作为特征，实现3类飞机的分类；但使用多普勒谱的谱线间隔进行周期估计的方法对雷达驻留时间、脉冲重频的要求较高，为了准确地估计调制周期，不仅需要较高的脉冲重频保证多普勒域不发生混叠，还需要保证较长的驻留时间以提高多普勒谱的分辨率。实际情况中，用于3类飞机目标分类的低分辨雷达常常无法同时保证较高的脉冲重频和较长的驻留时间，并且实现3类飞机目标的分类，也不需要我们精确地估计飞机时域回波的周期，只需要特征能够反映3类飞机的时域回波差异即可。因此，利用时域信号的周期特性差异，我们提出了时域相关性特征实现3类飞机目标的分类。

本文以微多普勒效应为基础，提出了一种基于时域回波相关性特征的飞机目标分类方法。时域相关性特征不直接提取飞机旋翼具体的时域调制周期，而是间接地反映时域回波的调制周期的大小。由于3类飞机的时域回波有较大的差异，直升机调制周期大，螺旋桨次之，喷气式飞机调制周期小，通过提取时域相关性特征，反映3类飞机的周期性差异，可以实现3类飞机目标的分类。基于仿真数据和实测数据的实验结果表明，在脉冲重频较低，多普勒谱发生混叠，多普勒域特征可分性下降的情况下，本文提出的2维时域相关特征对3类飞机目标仍达到较好的分类效果。

根据文献^[10]可知，在旋翼旋转过程中，当旋翼的桨叶与雷达视线垂直时，旋翼回波将产生一次闪烁，且旋翼回波闪烁的周期与旋翼转速和桨叶数有关。

下面以拥有4片桨叶的旋翼为例来分析拥有偶数片桨叶旋翼的回波闪烁周期与旋翼转速和桨叶数的关系。如图 1所示，比如，在雷达视线不变的情况下，当桨叶1转动到A位置与雷达视线垂直时，3号桨叶刚好处于B位置也与雷达视线垂直，两片桨叶的回波将同时产生1次闪烁；当桨叶2转动到A位置与雷达视线垂直时，4号桨叶刚好处于B位置也与雷达视线垂直，两片桨叶的回波也将同时产生1次闪烁，因此一个拥有4片桨叶的旋翼，在旋转一周时间内，旋翼回波产生4次闪烁，如图 2。

图 1(Fig.1)

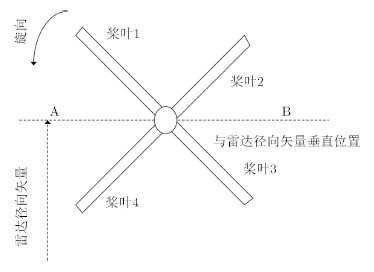图 1 偶数片桨叶旋转示意图Fig.1 Rotation diagram for the case of even blades

图 2(Fig.2)

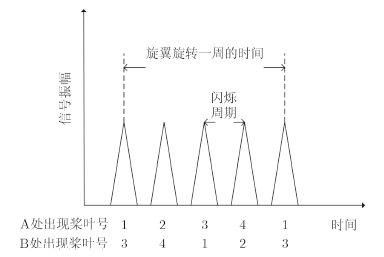图 2 偶数叶片旋翼时域回波示意图Fig.2 Time-domain echo diagram from a rotor with even blades

根据以上拥有4片桨叶的旋翼的雷达回波分析可得：假设旋翼的转速为${\omega _0}$，那么拥有N(N为偶数)片桨叶的旋翼，旋翼回波的闪烁周期$\tau $为：$\tau = 2\pi /N{\omega _0}$。

拥有奇数片桨叶的旋翼雷达回波与拥有偶数片桨叶的旋翼雷达回波的情况有所区别，下面以拥有5片桨叶的旋翼为例来分析拥有奇数片桨叶旋翼的回波闪烁周期与旋翼转速和桨叶数的关系。如图 3所示，比如，在雷达视线不变的情况下，当桨叶1位于A位置时，桨叶与雷达视线垂直，旋翼回波产生1次闪烁，而当桨叶2转动到A位置与雷达视线垂直这段时间内，桨叶4在某一时刻转动到位置B处与雷达视线垂直，旋翼回波也将产生1次闪烁，只是桨叶4与雷达做相离运动，因此一个拥有5片桨叶的旋翼，在旋转一周时间内，旋翼回波产生10次闪烁，如图 4。

图 3(Fig.3)

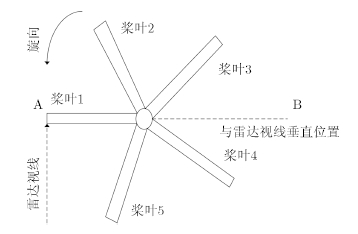图 3 奇数片桨叶旋转示意图Fig.3 Rotation diagram for the case of odd blades

图 4(Fig.4)

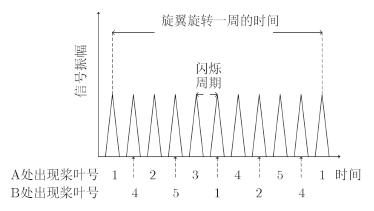图 4 奇数叶片旋翼时域回波示意图Fig.4 Time-domain echo diagram from a rotor with odd blades

根据以上拥有5片桨叶的旋翼的雷达回波分析可得：假设旋翼的转速为${\omega _0}$，那么拥有N(N为奇数)片桨叶的旋翼，旋翼回波的闪烁周期$\tau $为：$\tau = 2\pi /2N{\omega _0}$。

由以上分析可得：旋翼回波的闪烁周期与旋翼转速和桨叶数的乘积成反比，即旋翼时域回波的周期与旋翼转速和桨叶数的乘积成反比。

根据3类飞机实际旋转部件的几何尺寸和旋翼转速：直升机旋翼转速最小，桨叶数最少；螺旋桨飞机旋翼转速居中，桨叶数居中；喷气式飞机旋翼转速最大，桨叶数最多，理论上可得：直升机时域回波的周期最大，螺旋桨飞机居中，喷气式最小。

图 5(a)，图 5(b)和图 5(c)分别给出了在合作环境条件下采集到的直升机、螺旋桨飞机和喷气式飞机实测数据的时域波形。其中，本文所用的实测数据是在飞机接近飞机跑道时采集到的，飞机的俯仰角较小，雷达与飞机之间的距离比较近。由于飞机目标的实测数据是在合作环境条件下，实验条件较好，实测数据的信噪比较大，大约为15～18 dB 。从图 5可以看出，3类飞机实测数据的时域调制周期同上述的理论分析相吻合，即3类飞机时域回波的调制周期有明显的差异，即直升机时域回波的调制周期最大，喷气式飞机时域回波的调制周期最小，螺旋桨飞机时域回波的调制周期介于直升机与喷气式飞机之间。

图 5(Fig.5)

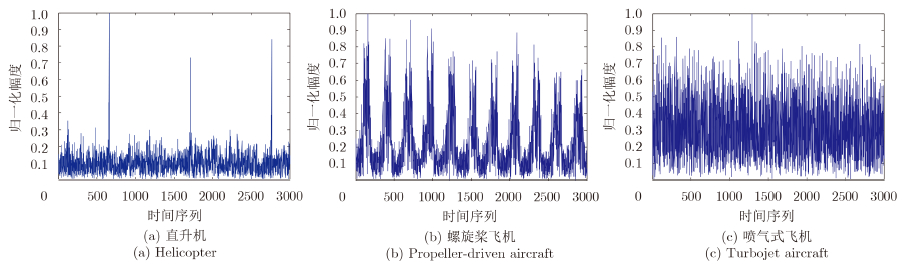图 5 3类飞机实测数据的时域回波Fig.5 Time-domain echoes of measured data from three kinds of aircrafts

时域相关性特征的核心思想是利用循环自相关函数与循环平均幅度差函数相结合的方法来判定回波时域周期的大小。循环自相关函数与循环平均幅度差函数的定义如下^{[9, 11]}：

设进行杂波抑制后雷达接收的飞机目标时域回波信号为u(n)，其中，n表示时域信号的第n个时域点，n=0,1,2,···,M,M为时域回波信号点数；对接收到的雷达回波进行能量归一化处理，得到能量归一化后的雷达时域回波信号$\bar u\left( n \right) $，求取雷达回波$ \bar u\left( n \right)$的幅值为$ x\left( n \right) = \left| {u(n)} \right|$，其中符号$\left| \bullet \right|$为取模运算。

定义归一化后的雷达时域回波幅值x(n)的循环自相关函数$\phi \left( l \right)$为：

定义归一化后的雷达时域回波幅值x(n)的循环平均幅度差函数$\varphi \left( l \right)$为：

将式(1)和式(2)相结合，构造幅值相关函数，即：

循环自相关函数$\phi \left( l \right)$和循环平均幅度差函数$\varphi \left( l \right)$分别在时域回波的周期的整数倍处取得极大值与极小值，因此，循环自相关函数$\phi \left( l \right)$和循环平均幅度差函数$\varphi \left( l \right)$均反映了时域回波的周期，但两种方法相结合后得到的幅度相关函数$f\left( l \right)$在时域回波周期整数倍处的峰值点变得更为突出，可以更好地反映时域回波的周期。

由于幅值相关函数f(l)的峰值点也一定是函数f(l)的极值点，因此，函数f(l)的极值点在一定程度上能够反映出时域回波幅值x(n)的周期，求取函数f(l)的极大值点，记为样本的峰值函数peak(l)。当雷达回波的幅值相关函数满足f(l)>f(l–1)且f(l)>f(l+1)的条件时，雷达回波的峰值函数peak(l)=f(l)，否则，峰值函数peak(l)=0；其中，l 表示时域平移变量，l=1,2,···,fix(M/2),M为时域回波信号点数，其中fix表示朝零取整操作。

图 6(a)，图 6(b)和图 6(c)分别给出了在雷达载频为1.3 GHz (L波段)、雷达驻留时间200 ms和脉冲重频4 kHz的条件下，直升飞机、螺旋桨飞机和喷气式飞机3类飞机仿真数据的峰值函数peak(l)，其中第1行子图为飞机时域信号回波，第2行子图为时域回波对应的峰值函数peak(l)的图。

图 6(Fig.6)

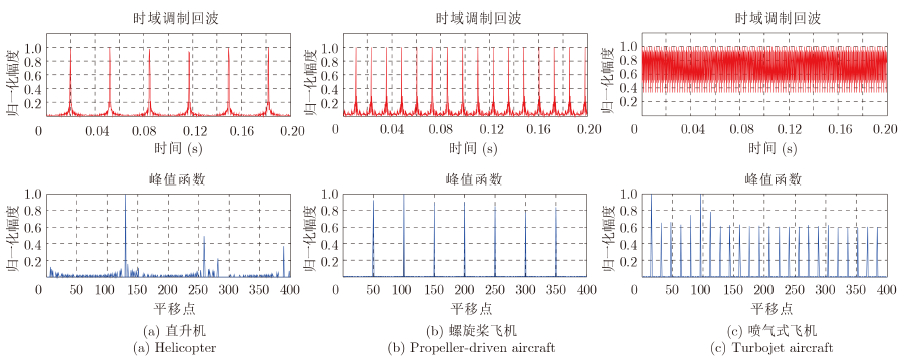图 6 脉冲重频4 kHz时，3类飞机的时域回波和对应的峰值函数Fig.6 Time-domain echoes and corresponding peak functions, when Pulse Repetition Frequency (PRF) being 4 kHz

如图 6，在雷达驻留时间较长、脉冲重频较高的情况下，可得3类飞机的峰值函数有明显的差异，即直升机较高的峰值间的间隔相对较大；螺旋桨飞机的峰值间的间隔居中；喷气式飞机的峰值间的间隔最小，因此，峰值函数peak(l)在一定程度上反映出了3类飞机时域回波调制周期的差异。

图 7(a)，图 7(b)和图 7(c)分别给出了在雷达载频为1.3 GHz (L波段)、雷达驻留时间200 ms和脉冲重频2 kHz的条件下，直升飞机、螺旋桨飞机和喷气式飞机3类飞机目标仿真数据的峰值函数peak(l)，其中第1行子图为时域信号回波，第2行子图为时域回波对应的峰值函数peak(l)的图。

图 7(Fig.7)

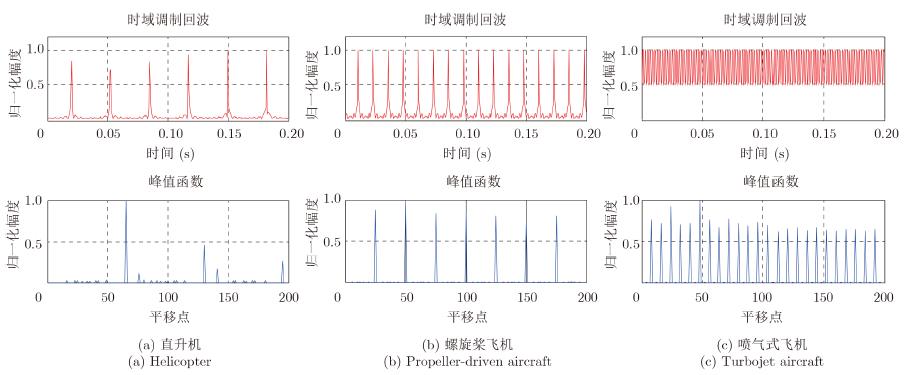图 7 脉冲重频2 kHz时，3类飞机的时域回波和对应的峰值函数Fig.7 Time-domain echoes and corresponding peak functions, when Pulse Repetition Frequency (PRF) being 2 kHz

图 7中，脉冲重频降低至2 kHz时，多普勒谱已经发生明显的混叠，但从实验结果可以看出，3类飞机的峰值函数仍然有较明显的差异，即直升机较高的峰值间的间隔相对较大；螺旋桨飞机的峰值间的间隔居中；喷气式飞机的峰值间的间隔最小。因此，在脉冲重频较低的情况下，峰值函数peak(l)在一定程度上仍能反映3类飞机时域回波调制周期的差异。

根据上述分析，峰值函数在一定程度上反映出3类飞机时域回波调制周期的差异，因此，可以提取出反映3类飞机雷达回波样本峰值函数peak(l)差异的时域相关性特征，用于对3类飞机目标进行分类。

本文提出了2维时域相关特性：

特征1 雷达回波峰值函数peak(l)的方差：

特征2 雷达回波峰值函数的熵：

本文使用仿真数据训练，利用SVM分类器对仿真数据和实测数据进行测试的模式来验证所提飞机目标分类方法对3类飞机目标的分类性能。

仿真数据按照文献^{[8, 9, 11]}仿真产生典型场景下22架飞机的旋转部件回波，具体飞机参数如表 1，场景参数如表 2。

表 1(Tab. 1)

表 1 5架喷气式飞机(T), 8架螺旋桨飞机(P), 9架直升机(H)仿真参数Tab. 1 Simulation parameters of five helicopters, eight propeller-driven aircrafts and nine turbojet aircrafts 飞机编号 转速(r/min) L1(m) L2(m) 叶片数 飞机编号 转速(r/min) L1(m) L2(m) 叶片数 T-1 3520.0 0.38 1.100 38 P-7 2180.0 0.17 0.915 2 T-2 8615.0 0.18 0.510 27 P-8 1690.0 0.23 1.180 3 T-3 3000.0 0.30 1.000 30 H-1 394.0 0 5.640 2 T-4 5000.0 0.20 0.600 33 H-2 265.0 0 7.800 4 T-5 4000.0 0.24 0.800 42 H-3 394.0 0 5.345 3 P-1 950.0 0.28 1.905 6 H-4 265.5 0 8.150 4 P-2 1650.0 0.12 1.150 5 H-5 185.0 0 10.650 5 P-3 1150.0 0.23 1.675 4 H-6 324.0 0 7.315 2 P-4 1800.0 0.10 1.065 5 H-7 205.0 0 9.450 6 P-5 800.0 0.49 2.350 4 H-8 383.0 0 5.500 4 P-6 1380.0 0.28 1.905 6 H-9 400.0 0 4.875 3

表 1 5架喷气式飞机(T), 8架螺旋桨飞机(P), 9架直升机(H)仿真参数Tab. 1 Simulation parameters of five helicopters, eight propeller-driven aircrafts and nine turbojet aircrafts

表 2(Tab. 2)

表 2 实验场景参数(U(a, b)指(a, b)上的均匀分布)Tab. 2 Experiment scene parameters (U(a, b) denotes uniform distribution on (a, b)) 参数 喷气式飞机 螺旋桨飞机 直升机 距离(m) U(30000, 40000) U(30000, 40000) U(30000, 40000) 高度(m) U(15000, 25000) U(4000, 12000) U(500, 10000) 速度(m/s) U(150, 200) U(100, 150) U(50, 100)

表 2 实验场景参数(U(a, b)指(a, b)上的均匀分布)Tab. 2 Experiment scene parameters (U(a, b) denotes uniform distribution on (a, b))

实验1 雷达载频为1.3 GHz (L波段)，仿真数据中加入20 dB的高斯白噪声；仿真过程中，训练样本和测试样本对应的飞机型号不同，且按照Swerlling起伏模型加入了机身分量，对于喷气式飞机和螺旋桨飞机考虑双发旋翼；利用3类飞机目标特征训练高斯核的SVM分类器时，分类器的核参数是利用交叉验证方法选取的。对比分析在不同的脉冲重频和驻留时间条件下，利用时域相关特征和多普勒域特征进行分类的效果。输入到SVM分类器中的具体特征包括^[12]：(1)时域相关特征：峰值函数的熵、峰值函数的方差；(2)多普勒域特征：多普勒域2阶中心矩、多普勒域4阶中心距、多普勒域熵。

图 8给出了不同脉冲重复频率下，驻留时间对3类飞机分类正确率的影响。值得说明的，图 8纵轴的分类正确率是指多次回波提取的特征对3类飞机目标分类的平均识别率。

图 8(Fig.8)

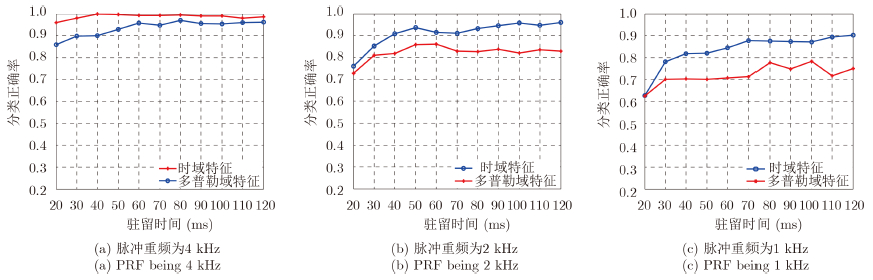图 8 不同PRF下，驻留时间与平均分类正确率之间的关系Fig.8 Variation curves of average classification rates with the dwell time under different Pulse Repetition Frequency (PRF) conditions

从图 8(a)，图 8(b)和图 8(c)中可得，在脉冲重复频率一定的条件下，对于时域相关特征，当驻留时间T=60 ms时，再继续增加驻留时间对分类性能的改善有限。因为大多数直升机的调制周期都在60 ms以上，当T=60 ms时，计算得到的3类飞机的峰值函数在形状上具有一定的差异，因此，所提取的时域相关特征可以用于3类飞机的分类；若驻留时间继续减小，由于直升机的调制周期较大，驻留时间太短时，可能无法采集到主旋闪烁，这样的3类飞机的峰值函数形状上的差异也会逐步减小，其中直升机将容易被误判，分类性能下降。但如图 8(b)和图 8(c)在脉冲重频较低条件下，时域相关特征对3类飞机的分类性能要明显优于多普勒域特征对3类目标的分类性能，因为在本次实验的仿真条件下，当脉冲重频小于2 kHz时，多普勒谱发生混叠，严重影响了多普勒域特征对3类飞机目标的分类性能。

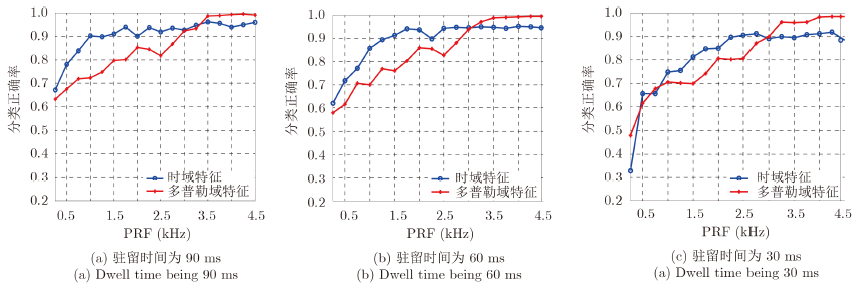
图 9给出了不同驻留时间下，脉冲重频对3类飞机分类正确率的影响。值得说明的，图 9纵轴的分类正确率是指多次回波提取的特征对3类飞机目标分类的平均识别率。

图 9(Fig.9)

图 9 不同驻留时间下，脉冲重频与平均分类正确率之间的关系Fig.9 Variation curves of average classification rates with Pulse Repetition Frequency (PRF) under different dwell time conditions

从图 9(a)，图 9(b)和图 9(c)中可得，当驻留时间一定时，随着脉冲重复频率的增加，对于时域相关特征，在一定的范围内，分类正确率会随着脉冲重频的增加而增大，当脉冲重频大于一定频率时，分类正确率趋于稳定；驻留时间固定为90 ms和60 ms时，识别率趋于稳定时所能达到的值基本一致，驻留时间固定为30 ms时，分类正确率趋于稳定时所能达到的值略低于前两种情况。分析原因，时域相关特征主要利用的是时域信号的幅度信息，反映时域信号的周期性，如果脉冲重复频率太低，相当于对时域信号的采样率低，对于雷达回波我们可能没有采到时域回波信号的峰值，在很大程度上，时域信号幅值的周期性会体现的不好，但是相对于多普勒域特征而言，在脉冲重频较低情况下时域相关特征有较好的分类性能。分析原因，计算观测所有仿真飞机回波的双边谱宽，在本次实验的仿真条件下，脉冲重频大于3.5 kHz时才能保证绝大部分飞机回波的多普勒谱不混叠，所以多普勒域不混叠是保证所提取的多普勒域特征有较好分类性能的一个重要条件。

因此从实验1的实验结果可得：脉冲重频较低时，时域相关特征对3类飞机目标的分类性能要明显优于多普勒域特征对飞机目标的分类性能。

实验2 实测场景中，雷达目标包括多种类型的3类飞机，雷达载频为37.5 GHz (Ka波段)。训练数据全部采用仿真数据，3类飞机各450个样本；测试数据全部选用实测数据，3类飞机各150个样本。实测数据是在飞机接近飞机跑道时测得的，飞机的俯仰角较小；雷达与飞机之间的距离比较近；实测数据在合作环境条件下获取，实验条件较好，实测数据的信噪比较大，大约为15～18 dB。对比分析在不同的脉冲重频条件下，时域相关特征以及多普勒域特征的分类效果。分类器选用高斯核的SVM分类器，核参数是利用交叉验证方法选取的。

图 10分别给出了脉冲重频固定为16.67 kHz和8.33 kHz时，3类飞机的平均分类正确率随驻留时间的变化曲线结果。

图 10(Fig.10)

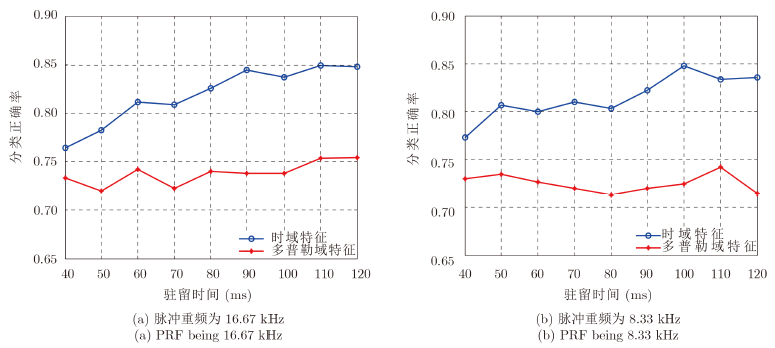图 10 脉冲重频为16.67 kHz和8.33 kHz时，实测3类飞机平均分类正确率随驻留时间的变化Fig.10 Variation curves of average classification rates with dwell time of measured data of three kinds of aircraft, when the Pulse Repetition Frequency (PRF) being 16.67 kHz and 8.33 kHz respectively

从图 10可得，在Ka波段，脉冲重频为16.67 kHz和8.33 kHz时，多普勒谱均发生混叠，随着驻留时间的增大，多普勒域特征的分类正确率变化不大，基本失效；但时域相关特征的分类正确率随着驻留时间的增大逐渐增大，当驻留时间达到一定时分类正确率较好，能达到80%以上。

因此，从实验2的实验结果可得：当脉冲重频较低，多普勒谱混叠时，时域相关特征对3类飞机的分类性能要明显优于多普勒域特征对3类飞机目标的分类性能。

实验3 实测数据的雷达载频为5.52 GHz (C波段)，脉冲重频为1.43 kHz，驻留时间为30.5 ms；由于测试条件有限，实测数据只包含喷气式飞机的回波；实验中，仿真产生3类飞机的训练数据，只测试实测数据即喷气式飞机的分类正确率。实测数据的测量条件和实验2类似，信噪比大约为15～18dB。分类器选用高斯核的SVM分类器，核参数是利用交叉验证方法选取的。

喷气式飞机的分类正确率如表 3所示。

表 3(Tab. 3)

表 3 两种特征提取方法下，实测数据平均分类正确率Tab. 3 Average classification rates of measured data, based on two kinds of feature extraction methods 特征 PRF 分类正确率 时域特征 1.43 kHz 90.72% 多普勒域特征 1.43 kHz 85.87%

表 3 两种特征提取方法下，实测数据平均分类正确率Tab. 3 Average classification rates of measured data, based on two kinds of feature extraction methods

从表 3的结果上看，利用时域相关特征进行分类，喷气式飞机的分类正确率明显优于利用多普勒域特征进行分类的实验结果，这在一定程度上说明时域相关特征在较低重频下仍能表现出较好的优势。

进一步考虑信噪比对两种特征分类正确率的影响，多普勒域特征首先需要利用傅里叶变换将时域信号变换到多普勒域，对于白噪声傅里叶变换的累加作用有一定的噪声抑制效果；而时域特征首先利用循环自相关法求取信号的峰值函数，循环自相关法对信号也具有类似于傅里叶变换的累积作用，因此，时域特征和多普勒域特征都具有一定的噪声稳健性，且性能应该比较接近。

在多普勒域提取的特征主要反映3类飞机谱宽以及谱线数目的差异，但脉冲重频较低时，多普勒域混叠，多普勒域特征对3类飞机目标的可分性明显下降，本文提出了基于时域相关特性的3类飞机目标分类方法，该方法通过提取反映时域信号的周期性差异的时域相关特征来实现3类飞机目标的分类。实验证明了本文中特征提取方法在脉冲重复频率较低的条件下具有较好的分类性能。