1 引言

太赫兹(Terahertz,THz)波广义上是指频率范围在0.1～10 THz(波长为3 mm～30 μm)范围内的电磁波。太赫兹波在频谱上处于微波和红外光之间，是宏观电子学向微观电子学过渡的区域，被称为电磁波谱的“太赫兹空隙(THz Gap)”。太赫兹波具有许多独特的优越性，与可见光和红外光相比，太赫兹波能够轻松穿透诸如塑料、衣物、木板等非极性材料的遮蔽物；与低频段的微波和毫米波相比，太赫兹波成像可以获得更高的图像分辨率；与X射线相比，太赫兹波光子能量低，只有毫电子伏特，对人体是无害的。由于具备上述众多优点，近些年来，太赫兹技术在安全检查、无损检测等领域得到了广泛的应用^{[1, 2, 3]}。

目前已经研制出的太赫兹成像系统大都采用聚焦波束成像方法体制^{[4, 5]}。相比于聚焦波束成像体制，太赫兹全息成像体制可对任意距离的目标进行聚焦成像，更利于在安检等领域的应用。在设计太赫兹全息实时成像系统时，不仅要求太赫兹成像雷达能够对大场景范围的目标进行实时的高分辨率成像，同时雷达系统的复杂度和图像处理的计算复杂度要尽可能的低。根据雷达成像理论，不论是线性调频连续波体制雷达还是步进频连续波雷达，发射信号带宽决定了距离向分辨率，频率采样间隔决定了最大不混叠距离。当提高成像场景景深或者为了得到更高的距离分辨率而提高发射信号带宽时，太赫兹雷达的采样频点数会大幅增加。这不仅要求雷达系统具有更高的采样率，而且雷达回波信号的采样时间和数据量也随之增加，这会对雷达实时成像系统的储存深度和处理能力有更高的要求。为了减少全息成像对数据量的要求，需要一种有效的数据获取方式和与之相对应重建算法。

由于太赫兹波的无法穿透人体皮肤的特性，人体目标在太赫兹3维全息图像中的距离向呈现稀疏特性。因此满足奈奎斯特采样定理的3维回波数据具有冗余性。这启发我们可以通过稀疏频点数据进行高分辨率成像。近几年来，压缩感知理论广泛应用于雷达成像方法中，其主要原理是信号在满足一定的稀疏特性下，可通过远低于奈奎斯特采样率的数据精确重建原始信号。然而目前压缩感知原理中的常用的重建算法，比如正交匹配追踪法^[6]和迭代收缩法^[7]，都需要复杂的处理流程和多次迭代，不利于低成本的实时太赫兹全息成像系统中。

本文利用稀疏随机频点采样能有效消除距离向模糊的原理，提出了一种适用于人体安检3维稀疏太赫兹快速成像体制和相应的算法。该成像体制能有效降低对距离向采样频点数的要求，降低系统复杂度；同时，本文提出一种快速而有效的重建算法，实现了在去除距离模糊的同时保留目标的完整信息。数值仿真和实验结果验证了文中提出的成像体制和成像算法的有效性，对设计用于人体安检领域的低成本的3维太赫兹全息成像系统提供了一种有效的解决方案。

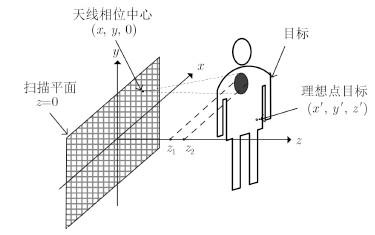
2 3维太赫兹成像几何及回波信号模型

图 1为用于人体安检的太赫兹全息成像系统示意图。雷达天线在2维口面上发射太赫兹高斯波束照射目标，目标的回波信号在接收端通过相干接收，通过IQ解调得到幅度和相位信息。设平面扫描孔径的中心为坐标原点，图中x方向和y方向为雷达天线移动方向，统称为方位向；z方向为雷达照射方向，称为距离向。雷达天线沿方位向进行机械扫描形成平面扫描孔径。假设人体目标的反射模型由一系列的位于(x',y',z')理想点目标组成，理想点目标的反射系数为σ(x',y',z')。雷达天线相位中心位于(x,y,0)，其在扫描平面z = 0上发射束腰半径大小为w₀的太赫兹高斯波束。假设发射的高斯波束的中心频率为f_c，带宽为B。则雷达天线接收到的人体目标的回波为^[8]：

$\begin{align} & s\left( x,y,0,k \right)=\iiint{-\sigma \left( {x}',{y}',{z}' \right){{\left[\frac{{{w}_{0}}}{w\left( {z}',k \right)} \right]}^{2}}} \\ & \cdot \exp \left[-\frac{2{{\rho }^{2}}\left( {x}',{y}' \right)}{{{w}^{2}}\left( {z}',k \right)} \right] \\ & \cdot \exp \left[-\text{j}\varphi \left( {x}',{y}',{z}',k \right) \right]\text{d}{x}'\text{d}{y}'\text{d}{z}' \\ \end{align}$

\[ \cdot \] (1)

式中k = 2πf/c为高斯波束在真空中的波数大小；${\rho ^2}\left( {x',y'} \right) = {\left( {x - x} \right)^2} + {\left( {y - y'} \right)^2}$；f 和c分别为电磁波的频率和在真空中的传播速度；$w\left( {z}',k \right)={{w}_{0}}{{\left[1+{{\left( 2{z}'/kw_{0}^{2} \right)}^{2}} \right]}^{0.5}}$为高斯波束传播到z = z'平面的束腰半径。在式(1)中，当目标与扫描平面的距离远大于波长时，空间相移项$\varphi \left( {x',y',z',k} \right)$可表示为：

$\varphi \left( {x}',{y}',{z}',k \right)=2kR\left( {x}',{y}',{z}',k \right)$

(2)

式中$R\left( {x}',{y}',{z}',k \right)={z}'+\frac{2{z}'{{\rho }^{2}}\left( {x}',{y}' \right)}{4{{{{z}'}}^{2}}+{{k}^{2}}w_{0}^{4}}$为高斯波束照射下理想点目标(x',y',z')到雷达天线相位中心的等效距离。回波信号s(x,y,0,k)关于波数k的带宽为：

${{B}_{k}}=\frac{1}{\pi }\Delta R$

(3)

式中ΔR = max[R(x',y',z',k)] - min[R(x',y',z',k)]为人体目标在高斯波束照射范围内的等效距离分布范围。通过式(3)可以得到，回波信号的带宽跟照射范围内的等效距离分布范围成正比关系。

3 基于频谱搬移的3维稀疏重建算法 3.1 3维稀疏重建算法

对于大部分的雷达成像系统来说，目标有可能分布在整个雷达系统的最大不混叠范围R_max内。根据奈奎斯特采样定理，在距离向上，雷达系统的采样频点数M需满足：

$M \ge 2B{R_{\max }}{\rm{/}}c$

(4)

而对于用于人体安检的3维太赫兹全息成像系统来说，虽然人体目标可能分布在最大不混叠范围R_max的任意位置，而利用太赫兹波不能有效穿透人体的皮肤的特性，能够发现人体目标在高斯波束照射范围内的等效距离分布范围是很小的。如图 1所示，当雷达天线运动到某一位置时，被高斯波束照射的人体目标在距离向的分布范围为[z₁,z₂]，其占据的空间范围$\Delta R = {z_2} - {z_1} \ll {R_{\max }}$。这意味着人体目标在距离向上呈现出稀疏特性，根据式(3)、式(4)可得，雷达成像系统的回波信号带宽变小，对应的对距离向采样频点数的要求大大降低。

设雷达系统发射的高斯波束的频率点数为N(N < M)，发射的高斯波束信号频率向量为在带宽B范围内随机均匀分布的频率：

$F_{{\rm{sparse}}}^{\rm{T}} = \left( {{{f'}_1},{{f'}_2}, \cdots ,{{f'}_N}} \right)$

(5)

相对应的回波信号向量表达式为：

$\begin{align} & S_{1}^{\text{T}}\left( x,y,F_{\text{sparse}}^{\text{T}} \right)=[s\left( x,y,0,{{{{k}'}}_{1}} \right),s\left( x,y,0,{{{{k}'}}_{2}} \right),\cdots ,\\ & s\left( x,y,0,{{{{k}'}}_{N}} \right)] \\ \end{align}$

(6)

式中${k'_i} = 2\pi {f'_i}{\rm{ /}}c,i = 1,2, \cdots N$。由于发射信号频率向量${F}_{{\text{sparse}}}^{\text{T}}$在带宽B范围内是随机分布的，因此采样点数减少而造成的距离向模糊则可有效地消除^[9]。这意味着稀疏采样的回波信号向量包含目标关于M个采样频点的完整回波信息。由于回波信号向量${S}_1^{\text{T}}\left( {x,y,{F}_{{\text{sparse}}}^{\text{T}}} \right)$在频谱中是个带通信号，N个采样频点数据不能直接恢复出M个采样频点的完整回波信息，需通过设计带通滤波器将其频谱搬移至基带，以满足奈奎斯特采样定理的要求。

设回波参考信号向量${S}_2^{\text{T}}\left( {x,y,{F}_{{\text{sparse}}}^{\text{T}},{R_j}} \right)$的表达式为：

$\begin{align} & S_{2}^{\text{T}}\left( x,y,F_{\text{sparse}}^{\text{T}},{{R}_{j}} \right)=[\exp \left( -2\text{j}{{{{k}'}}_{1}}{{R}_{j}} \right),\exp \left( -2\text{j}{{{{k}'}}_{2}}{{R}_{j}} \right),\\ & \cdots ,\exp \left( -2\text{j}{{{{k}'}}_{N}}{{R}_{j}} \right)] \\ \end{align}$

(7)

式中成像区域中的距离向单元格为R_j=jc/(2B),j = 0,1,2,$ \cdots $,M - 1。通过回波信号向量$ {S}_1^{\text{T}}$(x,y,${F}_{{\text{sparse}}}^{\text{T}}$)与回波参考信号向量${S}_2^{\text{T}}$(x,y,${F}_{{\text{sparse}}}^{\text{T}}$,R_j)的互相关：

$\begin{align} & \text{Corr}\left( x,y,{{R}_{j}} \right)=S_{\text{1}}^{\text{T}}\left( x,y,{{F}^{\text{T}}} \right)S_{2}^{*}\left( x,y,F_{\text{sparse}}^{\text{T}},{{R}_{j}} \right) \\ & =\sum\limits_{n=1}^{N}{\exp \left( -2\text{j}{{{{k}'}}_{n}}R \right)} \\ \end{align}$

(8)

式中δR = R(x',y',z',k) - R_j，得到了目标在距离向的粗分辨结果。其中距离向的主瓣最大处位于${R_j} = {R'_{\!\!\! \max }}\left( {x,y} \right)$，既是雷达天线到目标的距离估计也是回波信号向量${S}_1^{\text{T}}\left( {x,y,{F}_{{\text{sparse}}}^{\text{T}}} \right)$的中心频率估计。则设计带通滤波器的表达式为：

$\begin{array}{l} S_{\rm{3}}^{\rm{T}}\left( {x,y,F_{{\rm{sparse}}}^{\rm{T}}} \right) = \{ \exp \left[ {2{\rm{j}}{{k'}_1}{{R'}_{\max }}\left( {x,y} \right)} \right],\\ \exp \left[ {2{\rm{j}}{{k'}_2}{{R'}_{\max }}\left( {x,y} \right)} \right], \cdots ,\\ \exp \left. {\left[ {2{\rm{j}}{{k'}_N}{{R'}_{\max }}\left( {x,y} \right)} \right]} \right\} \end{array}$

(9)

回波信号向量${S}_1^{\text{T}}\left( {x,y,{F}_{{\text{sparse}}}^{\text{T}}} \right)$通过设计带通滤波器后变为基带信号，满足奈奎斯特采样定理，可通过插值恢复出M个采样频点的完整回波信息。具体插值方法采用非均匀快速傅里叶变换(NUFFT)进行插值操作，随机采样数据通过NUFFT得到其频谱，然后通过补零和逆傅里叶变换得到密集均匀采样数据。

$\begin{align} & S_{\text{5}}^{\text{T}}\left( x,y,{{F}^{\text{T}}} \right)=\text{inter}{{\text{p}}_{k}}\left[S_{\text{4}}^{\text{T}}\left( x,y,F_{\text{sparse}}^{\text{T}} \right) \right] \\ & \text{=}\text{inter}{{\text{p}}_{k}}\left[S_{\text{1}}^{\text{T}}\left( x,y,F_{\text{sparse}}^{\text{T}} \right) \right.\left. {}\circ S_{\text{3}}^{\text{T}}\left( x,y,F_{\text{sparse}}^{\text{T}} \right) \right] \\ \end{align}$

(10)

式中F^T = (f₁,f₂,$ \cdots $,f_M)，“$ \circ $”表示矩阵哈达玛积(Hadamard product)。最后将M个采样频点的完整回波信号的基带形式${S}_{\text{5}}^{\text{T}}\left( {x,y,{{F}^{\text{T}}}} \right)$搬移至其实际所在频率上：

${S}_{\text{7}}^{\text{T}}\left( {x,y,{{F}^{\text{T}}}} \right) = {S}_{\text{5}}^{\text{T}}\left( {x,y,{{F}^{\text{T}}}} \right) \circ {S}_{\text{6}}^{\text{T}}\left( {x,y,{{F}^{\text{T}}}} \right)$

(11)

式中：

$\begin{align} & S_{\text{6}}^{\text{T}}\left( x,y,{{F}^{\text{T}}} \right)=\{\exp \left[-2\text{j}{{k}_{1}}{{{{R}'}}_{\max }}\left( x,y \right) \right],\\ & \exp \left[-2\text{j}{{k}_{2}}{{{{R}'}}_{\max }}\left( x,y \right) \right],\cdots ,\\ & \exp \left[-2\text{j}{{k}_{M}}{{{{R}'}}_{\max }}\left( x,y \right) \right]\} \\ \end{align}$

(12)

由式(11)可得，计算得到的回波信号${S}_{\text{7}}^{\text{T}}\left( {x,y,{{F}^{\text{T}}}} \right)$包含目标的完整信息，并且频点数为M，满足最大不混叠距离R_max的要求，可利用增强相位偏移算法^[10]快速重建目标信息。

3.2 频点数N的选择

在互相关步骤中，寻找距离向的主瓣最大处位置${R'_{\!\!\! \max }}\left( {x,y} \right)$对整个算法流程是至关重要的。通过3.1节可知，目标在距离向的分布为：

$\text{Corr}\left( x,y,{{R}_{j}} \right)=\sum\limits_{n=1}^{N}{\exp \left( -2\text{j}{{{{k}'}}_{n}}\delta R \right)}$

(13)

由于回波信号频点是随机均匀分布的，相位项$- 2{k'_n}\delta R$是一个随机变化量，因此距离向的旁瓣水平也是随机波动的，这也是距离模糊现象可以被有效地消除的根本原因。通过3.1节对算法流程的讨论可知，目标距离估计关键在于能否正确找到主瓣最大处位置，但是随机波动的旁瓣会对算法中的目标距离估计这步产生不利影响，为此定义参数最大旁瓣与主瓣的功率比g。在阵列天线设计中由Q个随机均匀分布的天线单元组成的阵列天线的方向图f(u)能够表示为^[11]：

$f \! \left(u \right) = \sum\limits_{q = 1}^Q {\exp \left( {{\rm j}k{x_q}u} \right)}$

(14)

式中f (u)为随机相位项kx_qu的累加。对比式(13)、式(14)可得，两式都是对随机相位项的累加结果。定义最大旁瓣与主瓣的功率比不超过g的置信水平为b，则需满足：

$\gamma = \left( {\ln M - \ln \left( {1 - \beta } \right) + 1 + \frac{2}{{\ln M - \ln \left( {1 - \beta } \right)}}} \right)/N$

(15)

于是，根据式(4)、式(15)可得，频点数N需满足：

$\begin{array}{*{35}{l}} N\ge \max \{[\ln M-\ln \left( 1-\beta \right)+1 \\ \quad \quad +\frac{2}{\ln M-\ln \left( 1-\beta \right)}]/\gamma ,2B\Delta R/c\} \\ \end{array}$

(16)

3.3 3维稀疏太赫兹快速成像算法流程

根据上文所述，3维稀疏太赫兹快速成像算法可以概括为以下几个步骤：

(1) 根据雷达系统参数和成像场景范围，确定采样频点数N；

(2) 将采集的稀疏回波信号通过频谱搬移原理和插值得到频点数为M的回波数据；

(3) 利用增强相位偏移算法得到目标的3维重建结果。

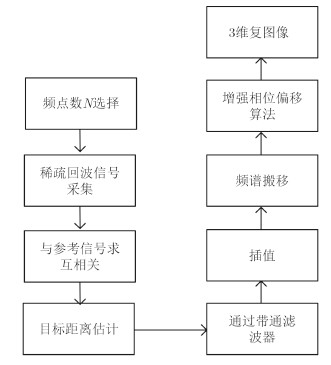
算法的流程可以概括为图 2所示的处理过程。

4 仿真及实验数据验证

为了验证成像算法的有效性，对理想点目标进行仿真成像。仿真时高斯波束的束腰大小为2.7 mm，雷达的中心频率设为0.2 THz，发射信号为步进频连续波，带宽为20 GHz，成像距离为0.6 m，原始满采样频点数为200。根据式(4)，对应的最大不混叠距离为1.5 m。根据先验知识，高斯波束照射范围内的等效距离分布范围设为0.1 m，设最大旁瓣与主瓣的功率比不超过-5 dB的置信水平为95%。由式(16)可得，稀疏频点数设为20。图 3(a)所示选取的20个随机频点的距离估计结果，可以看到目标位置位于中心为0.6 m，跨度为0.1 m的范围内，最大旁瓣与主瓣的功率比不超过-5 dB，目标距离位置的估计满足算法成像的要求。由20个稀疏随机频点恢复数据结果的相位信息与原始200个满采样频点数据相位的对比如图 3(b)所示，相位分布完全吻合，验证了算法重建结果满足进行太赫兹3维全息成像要求。

为了进一步验证算法的正确性和有效性，基于实验室已开发的0.2 THz成像原型机获取的实验数据，分别对金属条目标和携带金属枪的人体模特进行3维全息重建。原型机天线发射的高斯波束的束腰大小为2.7 mm，发射信号为步进频连续波，带宽为30 GHz，原始满采样频点数为200，同理根据式(4)，对应的最大不混叠距离为1 m。根据先验知识，高斯波束照射范围内的等效距离分布范围设为0.1 m。为了避免噪声对成像结果的影响，设最大旁瓣与主瓣的功率比不超过-5 dB的置信水平为95%。由式(16)可得，稀疏频点数设为20。金属条目标的重建结果如图 4所示。对比图 4(b)和图 4(c)，20随机频点稀疏数据重建结果的方位向分辨率与200满频点数据基本吻合，本文提出的算法的聚焦效果并没有因为频点数的减少而出现恶化；由图 4(d)可知，10随机频点数据聚焦结果变差，这是因为算法过程中距离估计偏差造成的结果，证明了式(16)中对频点数的要求。

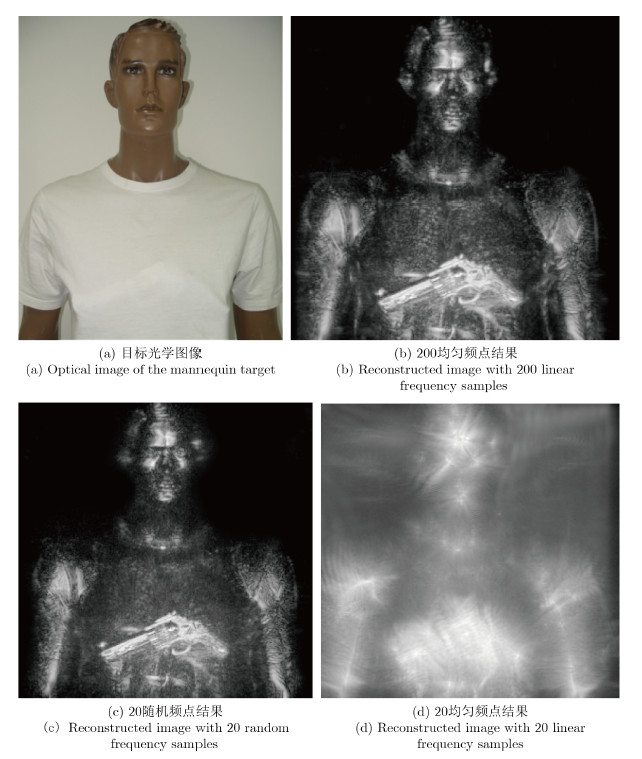
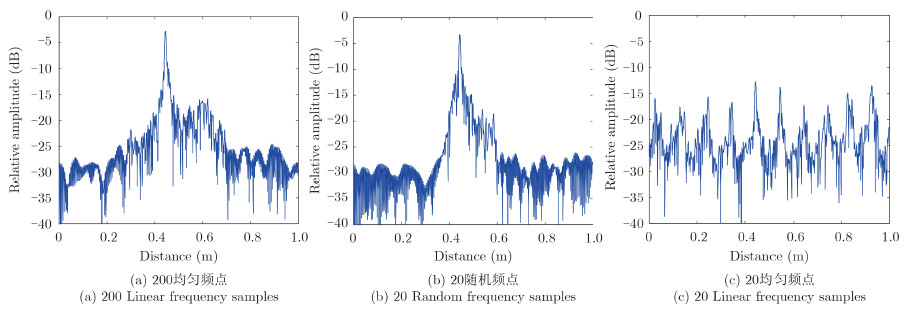
图 5显示了携带金属枪的人体模特目标的重建结果。对比图 5(b)和图 5(c)，20频点稀疏数据重建结果的同200满频点数据重建效果基本保持一致，能够对隐匿危险物品进行探测。由图 5(d)可知，20均匀频点数据聚焦结果变差，这是由于采样频点是均匀稀疏采样而带来的距离模糊现象造成的。图 6显示了3种频点选择的距离向重建结果，进一步说明了本文提出的算法的聚焦效果并没有因为频点数的减少而出现恶化。

5 结束语

本文提出了一种基于随机稀疏频点的3维稀疏太赫兹快速成像体制和成像算法，能够有效消除频点稀疏造成的距离混叠现象。仿真和实验结果验证了算法在人体安检快速成像中的有效性，重建结果包含人体目标完整信息的3维数据。