为了探测隐藏在树林中的目标,雷达通常工作在树叶对电磁波吸收较弱的低波段(如VHF/UHF波段)。工作在低波段的叶簇穿透合成孔径雷达(FOliage PENetration Synthetic Aperture Radar, FOPEN SAR)能够获得树林中隐蔽目标的雷达图像,提高对隐蔽目标探测能力[1]。尽管叶簇对电磁波的反射较弱,但是粗大的树干对电磁波的反射很强,在FOPEN SAR图像上形成很多亮点,称为树干杂波。强烈的树干杂波几乎会淹没目标,导致目标与所在区域的叶簇、树干背景对比度降低,使目标的检测难度增大。与此同时,FOPEN SAR工作波长较长,大多数散射体处在瑞利区,目标的回波主要由大的散射体回波构成,接收回波仅仅反映目标总体轮廓,略去了目标大部分精细结构信息,很难通过雷达图像的几何形状特征区分感兴趣目标和树干杂波。
目前SAR目标检测/识别普遍采用美国林肯实验室提出的分级处理流程[2],首先对成像得到的大面积SAR图像进行预筛选,提取若干感兴趣区域(Region Of Interest,ROI),每个ROI包含一个疑似目标;接着进行目标鉴别,剔除大部分自然杂波;最后进行目标识别。分级处理流程3个阶段待处理数据量依次降低,但采用的算法复杂性依次增加,在保证检测/识别性能的同时提高处理效率。然而,该处理流程最初是针对高波段SAR设计的,没有考虑到工作在低波段的FOPEN SAR在回波数据量和目标特性上与高波段SAR的区别,因此直接套用这种分级处理框架对于FOPEN SAR并不合适。
目标散射函数不仅与空间位置有关,还与频率、观测角度和极化等有关[3]。FOPEN SAR 为了获得与高波段SAR 相当的方位分辨率,需要更大的积累角,于是获得相同场景需要处理的回波数据量也相应增加。为了提高处理效率,Kaplan等人[4]提出了修剪四分树算法,它是将预筛选结合到四分树形式的快速后向投影成像算法中,在分辨率由粗到精不断提高的过程中对各个阶段的图像都进行预筛选处理,确定可能包含目标的局部区域,然后只对这些局部区域进一步提高分辨率。通过各个阶段的预筛选不断剔除一些不可能包含目标的区域,减小了成像的运算量。但是在修剪四分树算法中,预筛选仍然采用基于图像幅度特征的恒虚警率技术,由于粗分辨率图像目标信噪比不高,使得目标区域的确定十分困难。
实际中,FOPEN SAR感兴趣对象主要为树林中隐藏的车辆等目标。上述目标与地面构成了比较明显的二面角结构。因此,可以利用二面角散射随方位变化特性提高FOPEN SAR目标探测性能。子孔径处理[5, 6, 7, 8, 9]是提取目标散射方位角特征常用的方法,可以结合成像算法或是针对图像切片进行,但是子孔径在获得方位角特征的同时牺牲了方位分辨率。Chaney等人[10]提出了方位相关成像算法,在成像处理中利用目标散射函数随方位角的变化特性增强目标信噪比,提高预筛选性能。虽然方位相关成像算法在成像过程中自适应调整成像孔径的长度和位置,但它需要在方位角特征提取精度和方位分辨率之间取折衷,不利于后续鉴别和识别处理。
树干杂波作为FOPEN SAR目标探测面临的主要干扰,可以等效为圆柱体,其散射具有方位不变特性;而二面角目标的散射随方位变化较大,当雷达视线与二面角轴线垂直时,二面角散射最强,称为正侧散射。本文提出一种利用二面角正侧散射的增强成像方法,该方法通过提高车辆类目标图像的信杂比,在相同检测概率的情况下减少预筛选输出的ROI数量,避免鉴别处理饱和,保证整体信息处理流程效率。与子孔径处理牺牲方位分辨率不同,提出的方法在利用二面角正侧散射的同时,仍能提供与传统成像方法相当的高方位分辨率图像,不会减少后续鉴别和识别阶段的信息量。
2 FOPEN SAR回波模型在正侧视条带工作方式下,天线波束指向始终与雷达速度方向垂直(不考虑载机运动误差),其成像几何如图 1所示,其中x,y,z和r分别称为地距,方位,高度和斜距。x和y确定的平面x-y称为地距平面(ground-plane),r和y确定的平面r-y为斜距平面(slant-plane)。由于SAR只具有2维成像能力,因此SAR图像是实际场景在斜距平面的投影,因此斜距平面也称为成像平面。图 1(a)中阴影部分表示被雷达天线波束扫过的区域,称为测绘带;图 1(b)中阴影部分是图 1(a)中阴影部分在成像平面上的投影。
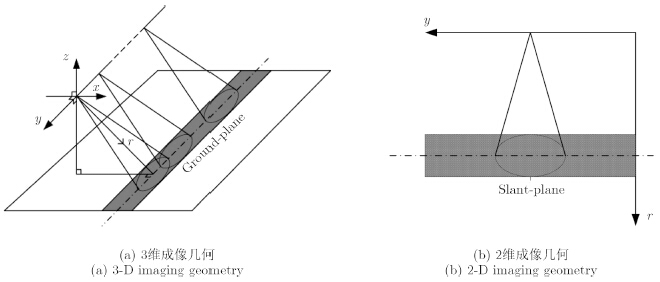 | 图 1 正侧视条带工作方式成像几何示意图 Fig. 1 Imaging geometry of broadside trip-map operation mode |
雷达平台距地面高度
| ${\theta }=\arctan \left(\frac{u-y}{r} \right)$ | (1) |
雷达接收回波s(t,u)为快时间t和方位孔径位置(又称为慢时间)u的2维函数:
| \[\begin{array}{*{20}{c}} {s(t,u) = \int {\int {\frac{1}{{{{(u - y)}^2} + {r^2}}}{\cal F}_{f \to t}^{\; - 1}\left[ {{g_{\rm{A}}}(f,\theta ){{\rm{g}}_{\rm{T}}}\left( {r,y,f,\theta } \right)} \right]} } }\\ {{ \otimes _t}\;p\left( {t - \frac{{\rm{2}}}{{\rm{c}}}\sqrt {{{\left( {u - y} \right)}^{\rm{2}}}{\rm{ + }}{r^{\rm{2}}}} } \right){\rm{drdy}}} \end{array}\] | (2) |
式中c为光速,
设成像区域中有一位于$({{r}_{n}},{{y}_{n}})$处的点目标,其散射特性随频率和方位角变化特性表示为
| $s(t,u)=\mathcal{F}_{f\to t}^{\ -1}[{{g}_{_ \rm{\Large A}}}(f,{\theta }){{A}_{_ \rm{\Large T}}}(f,{\theta })] \\ \quad\quad\quad \quad {{\otimes }_{t}} \ p \left(t-\frac{2}{\rm{c}}\sqrt{{{(u-{{y}_{n}})}^{2}}+r_{n}^{2}} \right)$ | (3) |
为了表达式简单,球面波衰减因子${[{({u_n} - y)^2} + r_n^2]^{ - 1}}$结合到天线特性中。
对回波沿快时间t进行1维Fourier变换,并将f用快时间波数$k=2 {\pi } f/{\rm{c}}$替换:
| $S(k,u)=P(k){{g}_{_ \rm{\Large A}}}(k,{\theta }){{A}_{_ \rm{\Large T}}}(k,{\theta }) \\ \quad\quad\quad\quad \cdot \exp \left[{ - {\rm{j}}2k\sqrt {r_n^2 + {{({u_n} - y)}^2}} } \right]$ | (4) |
式中$P(k)$为发射信号频谱。
对$S(k,u)$沿方位孔径u进行1维Fourier变换,利用驻定相位定理可得:
| \[\begin{array}{*{20}{l}} {S'(k,{k_u}) \approx }&{\frac{{\exp ( - {\rm{j}}\pi /4)}}{{\sqrt {4{k^2} - k_u^2} }}P(k){g_{\rm{A}}}\left( {k,\frac{{ - {k_u}}}{{\sqrt {{\rm{4}}{k^{\rm{2}}} - k_u^{\rm{2}}} }}} \right)}\\ {}&{ \cdot {{\rm{A}}_{\rm{T}}}\left( {k,\frac{{ - {k_u}}}{{\sqrt {{\rm{4}}{k^{\rm{2}}} - k_u^{\rm{2}}} }}} \right)}\\ {}&{ \cdot \exp \left( { - {\rm{j}}{r_n}\sqrt {{\rm{4}}{k^{\rm{2}}} - k_u^{\rm{2}}} - {\rm{j}}{y_n}{k_u}} \right)} \end{array}\] | (5) |
FOPEN SAR 2维回波时域和频域(波数域)模型分别如式(3)和式(5)所示,定量表示了回波中目标散射随频率和方位角变化的信息。
3 增强成像机理与实现 3.1 成像模型FOPEN SAR为了获得与高波段SAR相当的方位分辨率,需要更大的积累角,距离向和方位向存在强耦合。距离迁移(RM)算法针对该特性,利用Stolt变换在2维回波波数域对距离向和方位向解耦。Stolt变换定义为:
| $\left\{ \!\!\! \begin{array}{l} k = \frac{1}{2}\sqrt {k_r^2 + k_y^2} \\ {k_u} = {k_y} \end{array} \right.$ | (6) |
式中
首先对回波进行匹配滤波,实现脉冲压缩,然后利用Stolt变换对脉冲压缩之后的回波2维频谱进行变量代换可得:
| \[\begin{array}{*{20}{c}} {\tilde S({k_r},{k_y}) = \frac{{\exp ( - {\rm{j}}\pi /4)}}{{{k_r}}}\left| {{J_{{\rm{ST}}}}} \right|{{\left| {P(k)} \right|}^2}{g_{\rm{A}}}\left( {k,\frac{{ - {k_y}}}{{{k_r}}}} \right)}\\ { \cdot {{\rm{A}}_{\rm{T}}}\left( {k,\frac{{ - {k_y}}}{{{k_r}}}} \right)\exp \left( { - {\rm{j}}{r_n}{k_r} - {\rm{j}}{y_n}{k_y}} \right)} \end{array}\] | (7) |
式中
| ${J_{{\rm{ST}}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial k}}{{\partial {k_r}}}}&{\frac{{\partial k}}{{\partial {k_y}}}}\\ {\frac{{\partial {k_u}}}{{\partial {k_r}}}}&{\frac{{\partial {k_u}}}{{\partial {k_y}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\frac{{{k_r}}}{{2\sqrt {k_r^2 + k_y^2} }}}&{\frac{{{k_y}}}{{2\sqrt {k_r^2 + k_y^2} }}}\\ 0&1 \end{array}} \right]$ | (8) |
由式(8)可知
| $\left| {{J_{{\rm{ST}}}}} \right| = \frac{{{k_r}}}{{2\sqrt {k_r^2 + k_y^2} }}$ | (9) |
将式(9)代入式(7)中得,并校正畸变项$\frac{\exp (-{\rm{j}}{\pi } /4)}{2\sqrt{k_{r}^{2}+k_{y}^{2}}}$可得:
| $\begin{array}{l} \tilde S({k_r},{k_y})\\ = {\left| {P\left( {\frac{1}{2}\sqrt {k_r^2 + k_y^2} } \right)} \right|^2}{{g}_{_\rm{\Large A}}}\left( {\frac{1}{2}\sqrt {k_r^2 + k_y^2} ,\frac{{ - {k_y}}}{{{k_r}}}} \right)\\ \quad \cdot {{A}_{_ \rm{\Large T}}} \left( \! {\frac{1}{2}\sqrt {k_r^2 \! + \! k_y^2} ,\frac{{ - {k_y}}}{{{k_r}}}} \right)\exp ( \! - \! {\rm{j}}{r_n}{k_r} \! - \! {\rm{j}}{y_n}{k_y}) \end{array}$ | (10) |
RM算法成像结果$f(r,y)$是$\tilde{S}({{k}_{r}},{{k}_{y}})$的2维逆Fourier变换,还可以表示为:
| $f(r,y)={{f}_{\text{psf}}}(r,y){{\otimes }_{r,y}}{{\tilde{g}}_{_ \rm{\Large T}}}(r,y)$ | (11) |
式中${{f}_{\text{psf}}}(r,y)$为由系统参数决定的点扩展函数,${{\tilde{g}}_{_ \rm{\Large T}}}(r,y)$为目标散射函数估计
| $\begin{array}{l} \!\! {f_{{\rm{psf}}}}(r,y) = {\cal F}_{{k_r},{k_y} \to r,y}^{ \ - 1}\left[{{{\left| {P\left( {\frac{1}{2}\sqrt {k_r^2 + k_y^2} } \right)} \right|}^2}} \right.\\ \quad\quad\quad\quad\quad \cdot \left. {{{g}_{_\rm{\Large A}}}\left( {\frac{1}{2}\sqrt {k_r^2 + k_y^2} ,\frac{{ - {k_y}}}{{{k_r}}}} \right)} \right] \end{array}$ | (12) |
| $\begin{array}{l} {{\tilde g}_{_ \rm{\Large T}}}(r,y) = {\cal F}_{{k_r},{k_y} \to r,y}^{ \ - 1}\left[{{{A}_{_ \rm{\Large T}}} \left( {\frac{1}{2}\sqrt {k_r^2 + k_y^2} ,\frac{{ - {k_y}}}{{{k_r}}}} \right)} \right] \hspace{8pt}\\ \quad\quad\quad\quad\quad { \otimes _{r,y}}[\delta (r - {r_n})\delta (y - {y_n})] \hspace{8pt} \end{array}$ | (13) |
式(13)表明目标散射特性随频率和方位角变化的特性通过2维逆Fourier变换耦合到图像空间域,其中利用了由Stolt变换得到的回波域变量
| $\left\{ {\begin{array}{*{20}{l}} {{k_r} = 2k\cos \theta }\\ {}\\ {{k_y} = 2k\sin \theta } \end{array}} \right.$ | (14) |
考虑到地面,车辆目标可以近似为二面角结构,树干可以近似为顶帽结构,其参数化散射模型分别为[11]:
| $\begin{array}{*{20}{l}} {{A_{{\rm{dih}}}}(k,{\theta }) = \frac{{{\rm{j}}2k{L_{{\rm{dih}}}}{H_{{\rm{dih}}}}}}{{\sqrt {\pi } }}{\rm{sinc}}\left[{k{L_{{\rm{dih}}}}\sin ({\theta } - {α} )} \right.} {\left.{\left. {\cos {\phi } } \right)} \right] \left \{\!\!\! \begin{array}{l} \sin {\phi },\ \ {\phi } \in \left[{0,{\pi } /4} \right]\\ \cos {\phi },\ \ {\phi } \in \left[{{\pi } /4,{\pi } /2} \right] \end{array} \right.} \end{array}$ | (15) |
| $\quad\quad\quad\quad\quad\ \begin{array}{l} {A_{{\rm{top}}}}(k,{\theta }) = {H_{{\rm{top}}}}\sqrt {{{{\rm{j}}8k{r_{{\rm{top}}}}} \mathord{\left/ {\vphantom {{{\rm{j}}8k{r_{{\rm{top}}}}} {\sqrt 2 }}} \right.} {\sqrt 2 }}} \left\{ \!\!\! \begin{array}{l} \sin {\phi },\ \ {\rm{ }}{\phi } \in \left[{0,{\pi } /4} \right]\\ \cos {\phi },\ \ {\rm{ }}{\phi } \in \left[{{\pi } /4,{\pi } /2} \right]{\rm{ }} \end{array} \right. \end{array}$ | (16) |
式中,$\phi $为俯仰角,$\alpha $为二面角姿态角,${{L}_{\text{dih}}}$和${{H}_{\text{dih}}}$分别为二面角的轴长和边宽,${{H}_{\text{top}}}$和${{r}_{\text{top}}}$分别为顶帽的高和其圆柱部分半径。当雷达视线与二面角轴线垂直时,即$\theta {\rm{ = }}\alpha $,二面角散射最强;而顶帽散射强度不随方位角变化。
根据前面推导的成像模型可知,二面角散射强度随着方位角偏离其轴线垂直方向逐渐减弱;而雷达图像为积累角范围内不同方位角目标散射的叠加。由于FOPEN SAR地面杂波和叶簇杂波能量在积累角范围近似均匀分布,虽然增大积累角能够提高方位分辨率,但会一定程度降低二面角目标的图像信杂比;而树干杂波散射基本不随方位角变化,增大积累角对其图像信杂比影响不大。
为了增强车辆目标的图像信杂比,一个途径是获得方位角等于车辆姿态角对应的雷达图像。因此根据成像模型,可以借鉴时频分析的思想,在波数域数据对雷达回波进行增强成像处理。Wigner-Ville分布(WVD)是双线性时频分析方法的基础和核心[12],它最早由Wigner在1932年提出并将其应用在量子力学上,后来由Ville引入信号的时频分析领域中。可以获得信号的2次时频联合分布,基于WVD的增强成像公式可以表示为:
| $\begin{array}{l} {f_{{\rm{WVD}}}}(r,y;{\theta }) = \int\!\!\!\!\int {{{\tilde S}^*}({k_r},{k_r}\tan {\theta } - {{k'}\!\!_y}/2)} \\ \quad\quad\quad\quad\quad\quad \ \cdot \tilde S({k_r},{k_r}\tan {\theta } + {{k'}\!\!_y}/2)\\ \quad\quad\quad\quad\quad\quad \ \cdot \exp ({\rm{j}}{k_r}r + {\rm{j}}{{k'}\!\!_y}y){\rm{d}}{k_r}{\rm{d}}{{k'}\!\!_y} \end{array}$ | (17) |
WVD作为最基本的双线性时频表示方法,其主要缺点是存在交叉项的干扰,为了克服这个问题,需要对WVD进行改进,对交叉项进行抑制。Choi-Williams分布(CWD)具有好的交叉项抑制能力,与WVD相比它只需在运算中添加一个核函数[13]。基于CWD的增强成像公式可以表示为
| $\begin{array}{l} {f_{{\rm{CWD}}}}(r,y;{\theta }) = \int\!\int\!\int \Gamma \left( {k\!_y^{'},k\!_y^{'''}} \right)\tilde S\left( {{k_r},{{k''}\!\!\!_y} + \frac{{{{k'}\!\!_y}}}{2}} \right)\\ \quad\quad\quad\quad\quad\quad \ \cdot {{\tilde S}^*}\left( {{k_r},{{k''}\!\!\!_y} - \frac{{{{k'}\!\!_y}}}{2}} \right)\\ \quad\quad\quad\quad\quad\quad \ \cdot \exp \left[{{\rm{j}}{{k'''}\!\!\!\!_y}\left( {{k_r}\tan \theta - {{k''}\!\!\!_y}} \right)} \right]\\ \quad\quad\quad\quad\quad\quad \ \cdot \exp \left( {{\rm{j}}{k_r}r + {\rm{j}}k_y^{'}y} \right){\rm{d}}{k_r}{\rm{d}}{{k'}\!\!_y}{\rm{d}}{{k''}\!\!\!_y}{\rm{d}}{{k'''}\!\!\!\!_y} \end{array}$ | (18) |
而波数域抑制交叉项的核函数$\Gamma ({{{k}'}\!\!_{y}},{{{k}'''}\!\!\!\!_{y}} \ )$为:
| $\Gamma \left( {{{k'}\!\!_y}{{k'''}\!\!\!\!_y}} \ \right)=\exp \left[{ - {\beta _{{k_y}}}{{\left( {{{k'}\!\!_y}{{k'''}\!\!\!\!_y}} \ \right)}^2}} \right]$ | (19) |
其中ky方向的平滑参数${{β} _{{k_y}}}$非负,用于控制交叉项抑制程度。
当${f_{{\rm{CWD}}}}(r,y;\theta )$中,$\theta {\rm{ = }}\alpha $即为增强成像结果。实际中,车辆姿态角可以通过先验知识获得,也可以基于不同$\theta $对应的增强成像结果对车辆姿态角进行估计。
4 实测数据验证采用机载FOPEN SAR实测数据对提出的增强成像方法进行验证。该机载FOPEN SAR发射线性调频信号,工作在VHF/UHF波段。成像区域为在茂密的树林中隐藏着4辆卡车。传统成像和基于CWD的增强成像结果如图 2所示,图像动态范围30 dB。传统成像结果中,目标淹没在杂波背景中,为了保证高检测概率,预筛选会出现大量虚警;而增强成像结果中,叶簇散射得到大幅度抑制,仅剩余了若干较强的树干散射,而卡车目标散射并没有减弱,因此目标信杂比大幅度增加,有利于提高预筛选性能。
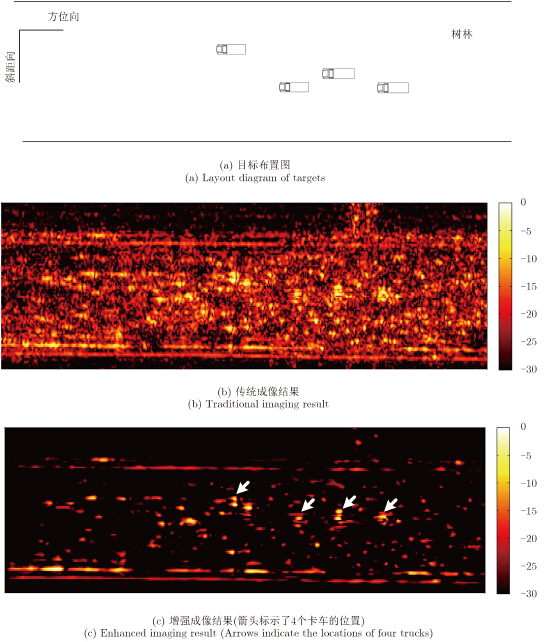 | 图 2 FOPEN SAR成像结果 Fig. 2 FOPEN SAR imaging results |
本文提出了一种FOPEN SAR增强成像方法,能够有效提高树林中车辆类目标图像的信杂噪比,从而提高预筛选性能,大幅度减少包含虚警杂波的ROI数目,从而提高信息处理流程的整体效率。在增强成像处理的基础上,可以结合圆周孔径和极化信息[14],一方面提供更丰富的角度信息,另一方面提供3维成像能力,区分植被区的冠层和树干,从而进一步提高FOPEN SAR隐蔽目标图像信杂比。
| [1] | Davis M E. Foliage Penetration Radar: Detection and Characterization of Objects under Trees[M]. SciTech Publishing, Inc, 2011: 60-92.( 1) 1) |
| [2] | Novak L M, Halversen S D, Owirka G J, et al. Effects of polarization and resolution on SAR ATR[J]. IEEE Transactions on Aerospace and Electronic Systems, 1997, 33(1): 102-116.( 1) 1) |
| [3] | 吴一戎. 多维度合成孔径雷达成像概念[J]. 雷达学报, 2013, 2(2): 135-142. Wu Yi-rong. Concept on multidimensional space joint-observation SAR[J]. Journal of Radars, 2013, 2(2): 135-142.(  1) 1) |
| [4] | Kaplan L M, McClellan J H, and Seung-Mok Oh. Prescreening during image formation for ultrawideband radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(1): 74-88.( 1) 1) |
| [5] | Carin L, Ybarra G, Bharadwaj P, et al. Physics-based classification of targets in SAR imagery using subaperture sequences[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, Phoenix, AZ, USA, 1999: 3341-3344.( 1) 1) |
| [6] | Runkle P, Nguyen L H, McClellan J H, et al. Multi-aspect target detection for SAR imagery using hidden Markov models[J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 46-55.( 1) 1) |
| [7] | Soumekh M, Gunther G, Linderman M, et al. Digitally-spotlighted subaperture SAR image formation using high performance computing[C]. Proceedings of SPIE, 2000, 4053: 260-271.( 1) 1) |
| [8] | Wong D and Carin L. Analysis and processing of ultra wide-band SAR imagery for buried landmine detection[J]. IEEE Transactions on Antennas and Propagation, 1998, 46(11): 1747-1748.( 1) 1) |
| [9] | 杨威, 陈杰, 李春升. 面向目标特性精细提取的SAR数据融合成像处理方法[J]. 雷达学报, 2015, 4(1): 29-37. Yang Wei, Chen Jie, and Li Chun-sheng. SAR data fusion imaging method oriented to target feature extraction[J]. Journal of Radars, 2015, 4(1): 29-37.(  1) 1) |
| [10] | Chaney R D, Willsky A S, and Novak L M. Coherent aspect-dependent SAR image formation[C]. Proceedings of SPIE, 1994, 2230: 256-274.( 1) 1) |
| [11] | Jackson J A, Rigling B D, and Moses R L. Canonical scattering feature models for 3D and bistatic SAR[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(2): 525-541.( 1) 1) |
| [12] | Martin W and Flandrin P. Wigner-Ville spectral analysis of nonstationary processes[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1985, 33(6): 1461-1470.( 1) 1) |
| [13] | Choi H-I and Williams W J. Improved time-frequency representation of multicomponent signals using exponential kernels[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(6): 862-871.( 1) 1) |
| [14] | 洪文. 圆迹SAR成像技术研究进展[J]. 雷达学报, 2012, 1(2): 124-135. Hong Wen. Progress in circular SAR imaging technique[J]. Journal of Radars, 2012, 1(2): 124-135.(  1) 1) |
 0, Vol. 0
0, Vol. 0
