②(东南大学毫米波国家重点实验室 南京 210096)
②(State Key Laboratory of Millimeter Waves, Southeast University, Nanjing 210096, China)
1 引言
结构化(包括稀疏)信号处理是过去10多年间信息领域发展最为迅猛的一个研究分支,它革新了人们对信息领域众多理论方法的认知,极大推动了通信、医疗、电子学、雷达、应用数学、物理等学科的发展。结构化信号处理是“实验—理论—计算—数据挖掘”这种科学发展模式的必然产物,是信息论、数值计算、概率与统计等多学科融合发展的结果(图 1)。结构化信号处理研究结构化信号的获取、表征、复原及应用等问题,具体包含4方面的研究内容[1, 2, 3]:(1)研究结构化信号表征与测度的模型和理论;(2)研究结构化信号的复原模型、理论及算法实现;(3)研究信号获取的新体制;(4)研究结构化信号处理的应用。
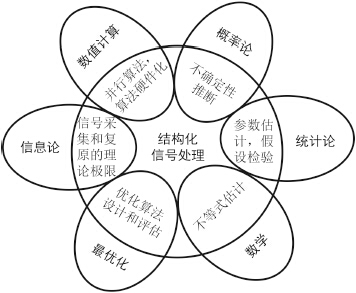 | 图 1 结构化信号处理与信息论等学科之间的关系 Fig. 1 The relation of structural signal processing to other disciplines |
经典信号处理根植于20世纪初由Kotelnikov,Nyquist,Shannon及Whittaker等人建立的连续信号采样理论(Nyquist-Shannon信号采样理论):为保证信号的无失真处理,信号的采样频率必须不低于该信号最大频率的2倍。从线性代数的角度,经典信号处理体系处理完备或超完备线性方程组y=Ax,其中dim(y)≥dim(x),其核心是测量数据y
| 表 1 经典信号处理和结构化信号处理两种体系的差异 Tab. 1 Comparisons between classical signal processing and structural signal processing |
信号结构性的一个代表性例子就是信号的稀疏性(Sparsity)。例如,如果图像的像素之间具有相关性,那么该图像在离散余弦或某种小波变换域是稀疏的。目前流行的各种图像或视频压缩技术正是利用了这种结构性。对信息领域的多数科研工作者而言,稀疏这个术语并不陌生,这里对稀疏信号的发展历史作个回顾。1795年,Prony提出了噪声干扰情况下从稀疏复指数函数的线性组合中估计复指数参数的方法(Prony方法)[18]。1809年,Laplace提出Laplace分布以及l1测度的概念,Gauss对该工作评价是“Laplace made use of another principle for the solution of linear equations,the number of which is greater than the number of unknown quantities,
结构化信号处理的研究在国外迅速开展的同时,国内在该领域的研究也开始起步。2007年,中国科学院电子学研究电磁场理论与应用研究室的李芳课题组在国内率先开展了稀疏信号处理方面的研究,向寅的博士论文首次将稀疏信号处理引入聚束合成孔径雷达成像领域,将稀疏信号处理引入电磁逆散射问题,发展了若干分辨率增强的新型电磁逆散射算法[40]。张文吉的博士论文将稀疏信号处理引入穿墙雷达成像,研究了稀疏信号处理在降低穿墙雷达数据量和提高成像质量方面的作用[41]。刘艳丽的博士论文将稀疏成像引入电离层层析成像,降低了电离层层析成像的病态性,提高了成像效果[42]。2009年,由中科院电子所牵头的稀疏微波成像项目列入了我国973计划资助[4],随后国家自然科学基金委也陆续资助了其它多项关于稀疏信号处理研究的重大和重点项目。在这些项目资助下,中科院电子所、中科院数学与系统应用研究所、西安电子科技大学、北京理工大学、北京航空航天大学、西安交通大学、国防科技大学、清华大学等单位在结构化信号处理领域(主要是应用领域)开展了广泛的研究,例如,西安电子科技大学保铮课题组在稀疏雷达(ISAR,InSAR)成像方面的研究[43, 44]、西安电子科技大学石光明课题组在图像处理方面的研究[45]、西安交通大学徐宗本课题组在稀疏信号复原算法方面的研究[46]、国防科技大学金添课题组在稀疏穿墙雷达成像应用方面的研究[47]、等等,使我国在稀疏信号处理领域的研究得到了长足发展。我国在稀疏信号处理领域发表论文数方面超欧美国家的论文数(是美国的2倍,德国的8倍左右),但从具有原创性和高影响力的论文方面来看,我国在结构化信号处理方面的研究还具有较大差距(见图 2)。
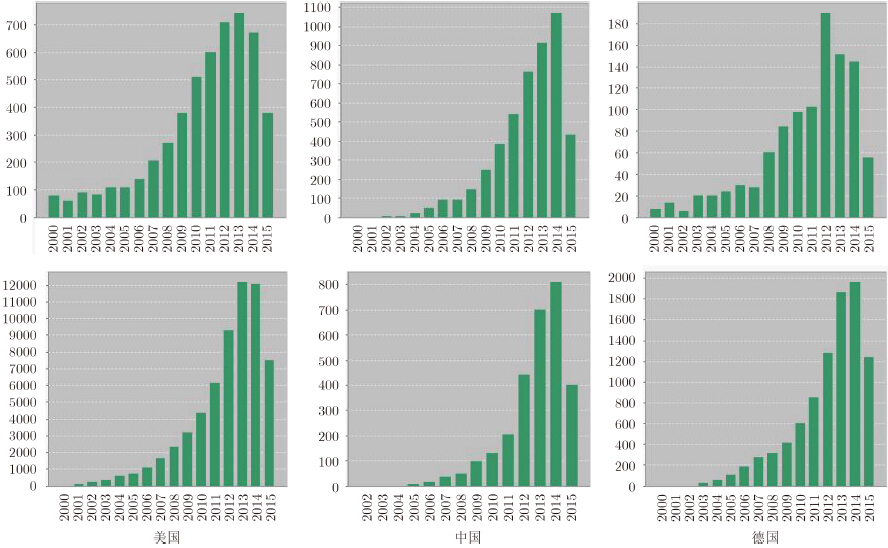 | 图 2 自2000年以来WEB-OF-SCIENCE统计的美国、中国及德国等的关于稀疏信号处理的论文发表(第1行)和论文引用(第2行)情况 Fig. 2 The Web-of-Science statistical results on published paper (the first row) and citation (the second row) of structural signal processing since 2000 for USA (first column),China (second column),and Germany (third column) |
目前虽然稀疏信号处理理论和方法都获得了长足发展,但是人们对信号结构性的挖掘和利用仍不够充分,尚在起步阶段,亟待建立更有效的信号结构性模型和测度,建立以此为基础的有效信号获取及高效复原算法体系,以及推动这些研究成果在相关应用领域的发展。
2 结构化信号感知问题的数学描述不失一般性,观测数据${y} \in \mathbb {R} {^M}$和目标信号${x} \in \mathbb {R} {^N}$两者之间满足如下关系:
| ${y} = {A}({x}) + {n}$ | (1) |
| ${\rm{Pr}}(x|y) = \frac{{{\rm{Pr}}(y|x){\rm{Pr}}(x)}}{{{\rm{Pr}}(y)}}$ | (2) |
| ${\rm{Pr}}(x) = \prod {P({x_i})} \;或 -\log {\rm{Pr}}(x) = \sum {\varphi ({x_i})} $ |
尽管上面的独立同分布的稀疏性及lp(0≤p≤1)范数等稀疏测度能很好地描述信号的结构性,并且在众多应用领域得到了广泛的应用,但是大多数实际问题中信号具有除了信号元素稀疏性之外更丰富的结构,这种结构性信息的利用将有助于提升信号获取和处理的性能。例如,很多微波遥感图像具有分区连续特性(Region-based smooth或Block-based smooth);大多数雷达监测信号具有准周期特性,其时频谱具有良好的聚类现象;小波系数的树状结构等。针对此类结构性信号的研究也相对成熟,目前已发展了系统的理论、算法和应用体系,例如,基于模式的压缩感知理论(Model-CS理论)[59],基于l1/lp(0 ≤p ≤∞)混合范数的稀疏分组测度[60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72],基于非局部梯度的Non-local TV信号模型和信号复原算法[73],Group-LASSO算法和Group稀疏Bayesian信号复原算法[60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72]。
(3) 相互交叠稀疏组上述信号结构化模型属于浅层结构,它仅考虑了统计独立稀疏组的简单特性,没有考虑稀疏分组之间的依赖关系(如图 3,图 4,图 5从不同角度演示了不同的信号结构性)。考虑不同组之间的相关性属于深度学习的内容,目前发展了一些简单的方法,相关研究属于起步阶段。2009年Jacob等人[64]和2012年Obozinski和Bach等人[74]提出了含隐藏变量的互相交叠组的稀疏测度:
| \[g = \sum {_{A' \subseteq A, \cup A' \in A = {\rm{supp}}(x)}f(A')} \] | (3) |
| \[g = \sum {_{A' \subseteq A, \cup A' \in A = {\rm{supp}}(x)}{{\left\| {{w_{A'}}} \right\|}_2}\sqrt {f(A')} } \] |
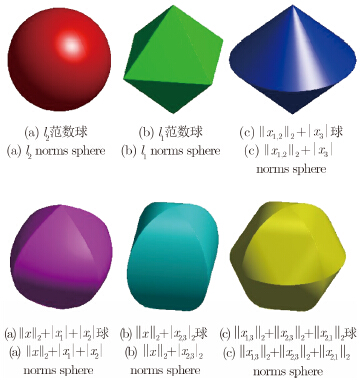 | 图 3 范数诱导的稀疏表征方法的3维示意图。||x1,2||2+|x3|球表示无交叠的混合范数,第2排的3个图表示有交叠的混合范数球 Fig. 3 Illustration of norm-inducing sparse measures in three-dimensional case |
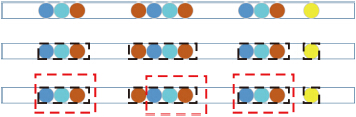 | 图 4 信号的多层结构性描述。第1行表示向量是稀疏的,第2行用黑色方框标出了该向量是具有分组稀疏性,第3行用红色方框进一步表示该向量具有“天蓝色-浅蓝色-深红色”特定模式的深层结构性 Fig. 4 Hierarchal structural illustration. The first row corresponds to the i.i.d. sparse vector,and the second row for grouped sparse vector in red rectangle,and the third line for group mode with some certain structure |
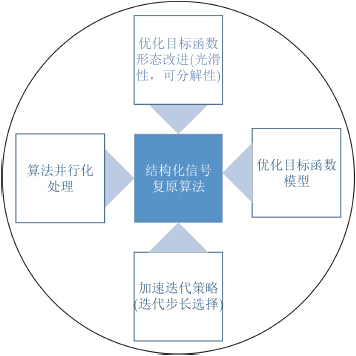 | 图 5 结构化信号复原算法的研究体系,它主要包括针对具体应用建立合适的优化目标函数模型,充分利用数据和先验两种信息源。根据实际应用对精度和效率的需求,调整价格函数的数学形态(包括可分解性、光滑性、凸性等)等4个方面 Fig. 5 The basic requirements on the efficient reconstruction algorithm of very-large-scale structural signals |
(4) 基于机器学习的信号结构建模
值得说明的是上述前3类信号结构性测度需已知信号的结构性模型,例如,信号的稀疏变换域,或者稀疏组的结构(Probabilistic or deterministic graphic model),因此如何构造信号的结构性模型成为一个公开的挑战性研究课题。目前常用的策略包括3类:(1)使用多个经典的变换域构造超完备字典,(2)基于大量样本采用确定性或者统计性训练的方法构造元素独立[58, 59]或具有结构[65, 77, 78]的超完备字典,(3)将区域分割或者聚类等方法引入算法复原过程,该方法无需训练样本,在信号重构过程中自适应引入信号结构型的度量。
除了上述4类模型外,我们要强调的是在许多实际应用中还有一类重要的问题需引起研究者的关注。在这类问题中目标信号本身不具备结构性,但它在某种非线性变换的情况下却具有良好的结构性。例如,森林的微波遥感图像类似于零均值的随机数,它本身没有结构性,但是通过方差或者其它度量变换下图像会变成典型的分段连续,呈现良好的结构性[1]。相信这类问题将会引起结构化信号领域的研究者的高度关注。
下面重点介绍式(2)的最大后验估计或者是模式分析:
| $\hat x = {\rm{arg}}\mathop {{\rm{max}}}\limits_x {\rm{Pr}}(x|y)$ | (4a) |
| $\hat x = \arg \mathop {{\rm{max}}}\limits_x \left[ {\frac{1}{2}\parallel y - A(x)\parallel _2^2 + \gamma {\rm{logPr}}(x)} \right]$ | (4b) |
定义(广义RIP)设测量矩阵${Φ} \in \mathbb {R} {^{m \times n}}$ (m < n)和稀疏字典${D} \in \mathbb {R} {^{p \times n}}\;(p \ge n)$,如果存在dk$ \in $(0,1)使得如下不等式成立:
| $\begin{array}{*{20}{l}} {\left( {1 - \delta _k^D} \right)\parallel Dx_k^D\parallel _2^2 \le \parallel \Phi x_k^D\parallel _2^2}\\ \quad\quad\quad\quad\quad\quad\quad\quad\;{ \le \left( {1 + \delta _k^D} \right)\parallel Dx_k^D\parallel } \end{array}$ | (5) |
广义RIP是Candes-Romberg-Tao定理中RIP概念的推广,它能够任意稀疏字典${D} \in \mathbb {R}{^{p \times n}}$和测量矩阵之间${Φ} \in {\mathbb {R}^{m \times n}}$之间的相互关系。当${D} \in {\mathbb {R}^{ \times n}}$是某个基或紧框架时,DTD=I,此时广义RIP定义退化为标准RIP。广义RIP概念有利于统一研究稀疏分析(Sparse analysis)和稀疏综合(Sparse synthetic)这对对偶问题。稀疏信号问题式(4b)更一般的表示形式为如下约束优化问题:
| ${\hat {x}} = \arg {\min_{{z}}}{\left\| {{Dz}} \right\|_1},\ {\rm{s.t.}} \ \ {z} \in {\cal B}\left( {y} \right)$ | (6) |
定理(稀疏问题的唯一性)设${h} = {\hat {x}} - {x}$ $ \left( {{\hat {x}},{x} \! \in \! \mathbb {R}{^N}} \right)\!$,且$\; \delta _{2k}^D \!<\! \sqrt 2 \!-\! 1\!$。如果$\; {\left\| {{{D}\hat {x}}} \right\|_1}\! \le \! {\left\| {{Dx}} \right\|_1}\!$,那么如下结论成立:
| \[\parallel Dh{\parallel _2} \le {C_0}\frac{{{\sigma _k}\left( x \right)}}{{\sqrt k }} + {C_1}\frac{{\left| {\left\langle {\Phi h_\Lambda ^D,\Phi h} \right\rangle } \right|}}{{\parallel Dh_\Lambda ^D{\parallel _2}}}\] | (7) |
上述定理是Candes-Romberg-Tao定理的推广,它适应于任意稀疏字典${D} \in \mathbb {R}{^{p \times n}}$和测量矩阵${Φ} \in \mathbb {R}{^{m \times n}}$。在这里我们要强调的是,尽管RIP在压缩感知和其它结构化信号感知中扮演着重要的角色,但判定某种测量方式是否满足RIP或其它类似特性却是一个公开的难题。除特殊情况外(例如,过于保守的相关性分析Coherence-based analysis[1, 2],高斯随机矩阵等特殊的测量方法等),目前可行的方式是采用蒙特卡洛方法计算Donoho-Tanner相转换曲线 (Phase-transition method[13, 81])。压缩感知理论自诞生以来,经过多年的发展其内涵和外延均得到了极大的发展。例如,2006年Raraniuk等人提出了基于模式的压缩感知方法(Model-based CS)[59],2010年Candes等人提出了低秩矩阵填充(Low-rank matrix completion)理论及算法[82],2011年Duarte和Elad提出了结构化压缩感知理论和方法[3]等。近年来结构化信号的非线性感知成为信号处理领域的一个重要研究分支,例如,压缩相位复原(Compressive Phase Retrieval)问题[83, 84]、1-bit压缩感知(one-bit compressive sensing,也称指数测量(Single-index measurement)[85, 86])问题[85, 86, 87, 88, 89, 90]等。尤其是对压缩相位复原问题的研究较为深入,建立了与经典压缩感知理论相对应的系统理论和算法体系。2015年Thrampoulidis等人对非线性稀疏感知问题作了一个突破性的工作,理论上证明了非线性测量yi=gi(<ai,x>)(i=1,2,$ \cdots $,M)的结构化信号感知问题与某个线性测量yi=μ<ai,x>+szi(其中m和s是与非线性函数gi有关的已知参数)的鲁棒性广义LASSO问题minx[‖y-Ax‖2+γf(x)]的解在统计平均意义上是等价的,该工作为研究结构化信号的非线性感知开辟了一条新思路[83]。最近,Brunton,Proctor以及Kutz等人采用通过结构化信号处理复原数据的非线性物理方程[91]。
3 大尺度结构化信号感知问题的信号复原算法信号复原算法是稀疏信号处理体系的核心组成部分,它是直接影响稀疏信号处理体系能否实用的关键。稀疏信号复原算法的设计主要从以下4个方面入手考虑[92, 93, 94, 95, 96]:(1)针对具体应用建立合适的优化目标函数模型,充分利用数据和先验两种信息源;(2)根据实际应用对精度和效率的需求,调整价格函数的数学形态(包括可分解性、光滑性、凸性等);(3)结合价格函数具体的数学形态设计迭代策略,建立实现超线性收敛速度的算法;(4)针对具体应用实现算法的并行化。对应这4个组成部分,信号复原算法的评价体系包含4个方面:即目标函数模型是否充分挖掘了数据和先验两种信息源、目标函数的数学形态是否具有低复杂性、优化迭代策略是否超收敛以及算法是否可以并行化处理。
下面介绍两种信号复原的算法模型:最大后验估计(Maximum A Posteriori)和最大均值对数后验估计(Maximum Mean log Posteriori),它们的定义分别如下:
| $\begin{array}{*{20}{l}} {\hat x = {\rm{arg}}\mathop {\max }\limits_x P(x|y) = {\rm{arg}}\mathop {\max }\limits_x [{\rm{log}}P(x|y)]}\\ {\;\;\; = {\rm{arg}}\mathop {\min }\limits_x [{\rm{log}}P(y|x) + {\rm{log}}P(x)]} \end{array}$ | (8) |
| $\hat x = {\rm{arg}}\mathop {\max }\limits_x \int {P(y){\rm{log}}P(x|y){\rm{d}}y} $ | (9) |
下面以高斯观测模型为例展开讨论:
| $\begin{array}{*{20}{r}} {P(y|x) = \mathbb{N} (A(x),{\sigma ^2}I) = {{\left( {\frac{1}{{\sqrt {2\pi } \sigma }}} \right)}^M}}\\ { \cdot {\rm{exp}}\left( { - \frac{1}{{2{\sigma ^2}}}\left\| {y - A(x)} \right\|_2^2} \right)} \end{array}$ | (10) |
| $\hat x = {\rm{arg}}\mathop {\min }\limits_x \left[ {\frac{1}{{{\sigma ^2}}}\sum\limits_{t = 1}^M {{L_t}({y_t},x) - {\rm{log}}P(x)} } \right]$ | (11) |
| $\hat x = {\rm{argmi}}{{\rm{n}}_x}\left[ {\frac{1}{{{\sigma ^2}}}\sum\limits_{t = 1}^M {\int {{L_t}({y_t},x)P({y_t}){\rm{d}}{y_t}} } - {\rm{log}}P(x)} \right]$ | (12) |
式(11)和式(12)的区别是前者不需要数据y的概率模型,而后者需要已知数据的概率模型,称之为统计优化问题(Stochastic Optimization)。特别地,如果数据y是统计均匀分布,那么式(11)和式(12)是等价的;从这个角度,式(11)是式(12)的一种特例。除非特殊情况(例如,A(x)=Ax且先验P(x)是高斯分布),式(11)和式(12)没有解析解,需采用迭代算法求解。如上所述,目前发展了大量信号复原算法求解问题式(11),例如匹配追踪算法、概率匹配追踪算法、压缩采样匹配追踪算法(CoSaMP)、迭代硬门限算法、迭代软门限算法、迭代加权算法、梯度投影算法、基追踪算法、Nesterov算法(或NESTA算法)、Split-Bregman迭代算法、亚梯度迭代算法方法等。这些方法均具有坚实优化理论作基础(例如,算法的收敛性、计算复杂性、精度等),但这些优化算法的每一步迭代需要遍历所有观测数据,同时又需要处理信号的所有维度,这导致了处理海量数据大尺度优化问题的主要技术瓶颈。由于被观测对象的结构性和观测数据的海量性和冗余性,大多数海量数据大尺度稀疏优化问题的数据在统计上是独立同分布的,海量数据存在严重的冗余,少部分数据甚至极少部分数据就足以反映数据集的统计规律。利用这个特性,在线学习的优化方法成为处理海量数据大尺度优化问题的一个重要工具,它的迭代策略是[97, 98]:
| ${x_{t + 1}} = {x_t} - {\mu _t}\left[ {\frac{1}{{{\sigma ^2}}}{L_t}'({y_t},x) - \frac{1}{M}{\rm{lo}}{{\rm{g}}^\prime }P(x)} \right]$ | (13) |
为进一步提高算法性能,使其有效处理海量数据的大尺度稀疏优化问题,目前已经发展了一些非常有用的辅助技术。针对l1范数正则化的稀疏优化问题,可以采用价格函数的1阶泰勒级数展开结合软门限方法进行解析求解[50, 93, 94, 95, 98, 99, 100, 101, 102, 103, 104, 105, 106],或采用Split技术结合软门限方法处理(例,交替迭代乘子法,ADMM[107])。改善优化价格函数的强凸性也可有效加快算法的收敛速度,例如,增强拉格朗尔方法(Augmented Lagrangian Method),Bregman距离辅助方法。为增强价格函数的强凸性,在凸优化框架下考虑式(11)和式(12):
| ${\hat x_{t + 1}} = {\rm{arg}}\mathop {\min }\limits_x \left[ {\frac{1}{{2{\sigma ^2}}}{L_t}({y_t},x) - \frac{1}{M}\log P(x) + {D_\psi }(x,{{\hat x}_t})} \right]$ | (14) |
| ${D_\psi }(x,{\hat x_t}) = \psi (x) - \psi ({\hat x_t}) - \left\langle {\nabla \psi ({{\hat x}_t}),x - {{\hat x}_t}} \right\rangle $ | (15) |
在线学习优化和随机坐标优化这两种方法在求解高维大样本问题时简单、高效,各有特点和优势。在线学习优化方法主要利用大规模数据独立同分布的统计规律;而坐标优化主要利用目标信号结构化的特性,有复杂性较低的计算目标函数及其梯度的技巧。在线优化和坐标优化方法充分地利用了大尺度优化问题自身的特点,很好地满足了大尺度结构化信号感知问题的实际需求。
| [1] | 李廉林, 李芳. 稀疏信号处理讲义[M]. 北京大学内部讲义, 2015. Li Lian-lin and Li Fang. Lecture on Sparse Signal Processing (Preprint)[M]. Peking University, 2015.( 6) 6) |
| [2] | Elad M.Sparse and redundant representation modeling—what next?[J]. IEEE Signal Processing Letters, 2012, 19(12): 922-928.( 2) 2) |
| [3] | Duarte M F and Eldar Y C. Structured compressed sensing: from theory to applications[J]. IEEE Transactions on Signal Processing, 2011, 59(9): 4053-4085.( 2) 2) |
| [4] | 吴一戎. 稀疏微波成像理论、体制和方法研究, 国家973项目 申请书(项目首席科学家: 吴一戎, 中国科学院电子学研究所), 2010. Wu Yi-rong. Sparse microwave imaging: theories, methods, and systems, The proposal submitted to the National Basic Research Program of China, Leading Scientist: Wu Yirong, Institute of Electronics, Chinese Academy of Sciences, 2010.( 2) 2) |
| [5] | Candes E J and Tao T. Near-optimal signal recovery from random projections: universal encoding strategies?[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425.( 2) 2) |
| [6] | Donoho D L. Neighborly polytopes and sparse solutions of underdetermined linear equations[J]. Preprint, 2005.( 2) 2) |
| [7] | Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.( 2) 2) |
| [8] | Donoho D L. For most large underdetermined systems of linear equations the minimal l1-norm solution is also the sparsest solution[J]. Communications on Pure and Applied Mathematics, 2006, 59(7): 797-829.( 2) 2) |
| [9] | Donoho D L and Elad M. Optimally sparse representation in general (nonorthogonal) dictionaries via l1 minimization[J]. Proceedings of the National Academy of Sciences, 2003, 100(5): 2197-2202.( 2) 2) |
| [10] | Donoho D L and Elad M. On the stability of the basis pursuit in the presence of noise[J]. Signal Processing, 2006, 86(3): 511-532.( 2) 2) |
| [11] | Donoho D L, Elad M, and Temlyakov V N. Stable recovery of sparse overcomplete respresentations in the presence of noise[J]. IEEE Transactions on Information Theory, 2006, 52(1): 6-18.( 2) 2) |
| [12] | Donoho D L and Jared T. Sparse nonnegative solution of underdetermined linear equations by linear programming[J]. Proceedings of the National Academy of Sciences, 2005, 102(27): 9446-9451.( 2) 2) |
| [13] | Donoho D L and Tanner J. Precise undersampling theorems[J]. Proceedings of the IEEE, 2010, 98(6): 913-924.( 3) 3) |
| [14] | Donoho D L and Tsaig Y. Fast solution of l1-norm minimization problems when the solution may be sparse[J]. IEEE Transactions on Information Theory, 2008, 54(11): 4789-4812.( 2) 2) |
| [15] | Candes E J, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.( 2) 2) |
| [16] | Candès E J, Romberg J K, and Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207-1223.( 4) 4) |
| [17] | Candès E J and Tao T.Decoding by linear programming[J]. IEEE Transactions on Information Theory, 2005, 51(12): 4203-4215.( 2) 2) |
| [18] | Prony R. Essai experimental et analytique sur les lois de la Dilatabilit_e des uideselastiques et sur celles de la Force expansive de la vapeur de l'eau et de la vapeur de l'alkool, a dierentes temperatures. J. de l' Ecole Polytechnique, Floreal et Prairial III, 1795, 1(2): 24-76.( 1) 1) |
| [19] | Tarantola A. Inverse Problem Theory and Method for Model Parameter Estimation[M]. SIAM Press.( 1) 1) |
| [20] | Jaynes E. Probability Theory: The Logic of Science[M]. Cambridge University Press, 2003.( 1) 1) |
| [21] | Carathéodory C. Über den Variabilitätsbereich der Koeffizienten von Potenzreihen, die gegebene Werte nicht annehmen[J]. Mathematische Annalen, 1907, 64(1): 95-115.( 1) 1) |
| [22] | Carathéodory C. Über den variabilitätsbereich der fourier'schen konstanten von positiven harmonischen funktionen[J]. Rendiconti Del Circolo Matematico Di Palermo, 1911, 32(1): 193-217.( 1) 1) |
| [23] | Beurling A. Sur les integrales de Fourier absolument convergentes et leur application a une transformation fonctionelle[C]. In Proc. Scandinavian Math. Congress, Helsinki, Finland, 1938.( 1) 1) |
| [24] | Claerbout J F and Muir F. Robust modeling of erratic data[J]. Geophysics, 1973, 38(5): 826-844.( 1) 1) |
| [25] | Taylor H, Banks S, and McCoy J. Deconvolution with the l1 norm[J]. Geophysics, 1979, 44(1): 39-52.( 1) 1) |
| [26] | Santosa F and Symes W W. Linear inversion of bandlimited reflection seismograms[J]. SIAM Journal on Scientific and Statistical Computing, 1986, 7(4): 1307-1330.( 1) 1) |
| [27] | Santosa F and Symes W. Inversion of impedance profile from band-limited data[C]. International Geoscience and Remote Sensing Symposium, 1983.( 1) 1) |
| [28] | Tibshirani R. Regression shrinkage and selection via the Lasso[J]. Journal of the Royal Statistical Society, Series B, 1996, 58(1): 267-288.( 1) 1) |
| [29] | Chen S,Donoho D,and Saunders M.Atomic decomposition by basis pursuit[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 33-61.( 1) 1) |
| [30] | Samadi S, Cetin M, and Masnadi-Shirazi M. Sparse representation-based synthetic aperture radar imaging[J]. IET Radar, Sonar & Navigation, 2011, 5(2): 182-193.( 1) 1) |
| [31] | Soldovieri F, Solimene R, and Ahmad F. Sparse tomographic inverse scattering approach for through-the wall radar imaging[J].IEEE Transactions on Instrumentation & Measurement, 2012, 61(12): 3340-3350.( 1) 1) |
| [32] | Oliveri G, Rocca P, and Massa A. A bayesian-compressivesampling- based inversion for imaging sparse scatterers[J]. IEEE Transactions on Geoscience & Remote Sensing, 2011, 49(10): 3993-4006.( 1) 1) |
| [33] | Desmal A and Bagci H. Shrinkage-thresholding enhanced Born iterative method for solving 2D inverse electromagnetic scattering problem[J]. IEEE Transactions on Antennas & Propagation, 2014, 62(7): 3878-3884.( 1) 1) |
| [34] | Solimene R, Ahmad F, and Soldovieri F. A novel CSTSVD strategy to perform data reduction in linear inverse scattering problems[J]. IEEE Geoscience & Remote Sensing Letters, 2012, 9(5): 881-885.( 1) 1) |
| [35] | Winters D W, Van Veen B D, and Hagness S C. A sparsity regularization approach to the electromagnetic inverse scattering problem.[J]. IEEE Transactions on Antennas & Propagation, 2010, 58(1): 145-154.( 1) 1) |
| [36] | Huang Q, Qu L, Wu B, et al. UWB through-wall imaging based on compressive sensing[J]. IEEE Transactions on Geoscience & Remote Sensing, 2010, 48(3): 1408-1415.( 1) 1) |
| [37] | Yoon Y S and Amin M G. Through-the-wall radar imaging using compressive sensing along temporal frequency domain[C]. 2010 IEEE International Conference on Acoustics, Speech, and Signal Processing, 2010: 2806-2809.( 1) 1) |
| [38] | Leigsnering M, Ahmad F, Amin M G, et al. Compressive sensing based specular multipath exploitation for throughthe- wall radar imaging[C]. 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2013: 6004-6008.( 1) 1) |
| [39] | Zhu X X and Bamler R. Super resolving SAR tomography for multidimensional imaging of urban areas: compressive sensing-based TomoSAR inversion[J]. IEEE Signal Processing Magazine, 2014, 31(4): 51-58.( 1) 1) |
| [40] | 向寅. 压缩采样、稀疏约束成像及等效辐射源无相位逆散射[D]. [博士论文] , 中国科学院研究生院, 2010. Xiang Yin. Study of compressed sampling, sparse imaging its applications in phaseless inverse scattering[D]. [Ph.D. dissertation] , University of Chinese Academy of Sciences, 2010.( 1) 1) |
| [41] | 张文吉. 电磁逆散射成像方法及压缩感知理论在成像中的应用[D]. [博士论文] , 中国科学院研究生院, 2009. Wenji Zhang, Study of fast methods of electromagnetic inverse scattering and compressive electromagnetic imaging[D]. [Ph.D. dissertation] , University of Chinese Academy of Sciences, 2009.( 1) 1) |
| [42] | 刘艳丽. 基于抛物线方程的电波传播问题及电离层成像研究[D]. [博士论文] , 中国科学院研究生院, 2009. Yanli Liu, Study of parabolic equations based radio wave propagation and its applications in ionosphere tomography[D]. [Ph.D. dissertation] , University of Chinese Academy of Sciences, 2009.( 1) 1) |
| [43] | Xu G, Xing M D, Xia X G, et al. Sparse regularization of interferometric phase and amplitude for InSAR image formation based on bayesian representation[J]. IEEE Transactions on Geoscience & Remote Sensing, 2015, 53(4): 2123-2136.( 1) 1) |
| [44] | Zhang L, Qiao Z J, Xing M, et al. High-resolution ISAR imaging with sparse stepped-frequency waveforms[J]. IEEE Transactions on Geoscience & Remote Sensing, 2011, 49(11): 4630-4651.( 1) 1) |
| [45] | 石光明, 刘丹华, 高大化, 等. 压缩感知理论及其研究进展[J]. 电子学报, 2009, 37(5): 1070-1078. Guangming Shi, Danhua Liu, Dahua Gao, et al. Theory of compressive sensing and its recent progress, Recent progress on theory and compressive sensing[J]. Chinese Journal of Electronics, 2009, 37(5): 1070-1078.( 1) 1) |
| [46] | Xu Z, Chang X, Xu F, et al. L1/2 regularization: a thresholding representation theory and a fast solver[J]. IEEE Transactions on Neural Networks & Learning Systems, 2012, 23(7): 1013-1027.( 1) 1) |
| [47] | 黄晓涛, 杨俊刚, 金添. 压缩感知雷达成像[M]. 北京: 科学出 版社, 2014. Huang Xiao-tao, Yang Jun-gang, and Jin Tian. Compressed Radar Imaging[M]. Science Press, 2014.( 1) 1) |
| [48] | Mallat S and Zhang Z. Matching pursuit in a timefrequency dictionary[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415.( 2) 2) |
| [49] | Needell D and Tropp J A. CoSaMP: iterative signal recovery from incomplete and inaccurate samples[J]. Applied & Computational Harmonic Analysis, 2008, 26(12): 93-100.( 2) 2) |
| [50] | Nesterov Y.Introductory Lectures on Convex Optimization: A Basic Course[M]. Kluwer Academic Publishers, 2004.( 4) 4) |
| [51] | Wainwright M J. Structured regularizers for highdimensional problems: statistical and computational issues[J]. Social Science Electronic Publishing, 2014, 1(1): 233-253.( 2) 2) |
| [52] | Donoho D and Tsaig Y. Fast solution of l1 norm minimization problems when thesolution may be sparse[J]. IEEE Transactions on Information Theory, 2008, 54(11): 4789-4812.( 2) 2) |
| [53] | Chen S S, Donoho D L, and Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM Review, 2001, 43(1): 129-159.( 2) 2) |
| [54] | Koh K, Kim S J, and Boyd S. An interior-point method for large-scale l1 -regularized logistic regression[J]. Journal of Machine Learning Research, 2007, 8(3): 1519-1555.( 2) 2) |
| [55] | Shevade S K and Keerthi S S. A simple and efficient algorithm for gene selection using sparse logistic regression[J]. Bioinformatics, 2003, 19(17): 2246-2253.( 2) 2) |
| [56] | Hui Z and Trevor H. Regularization and variable selection via the elastic net[J]. Journal of the Royal Statistical Society, 2005, 67(2): 301-320.( 2) 2) |
| [57] | Candès E J, Wakin M B, and Boyd S P. Enhancing sparsity by reweighted l1 minimization[J]. Journal of Fourier Analysis & Applications, 2008, 14: 877-905.( 2) 2) |
| [58] | Tosic I and Froccard P. Dictionary learning[J]. Signal Processing Magazine, 2011: 27-38.( 2) 2) |
| [59] | Aharon M, Elad M, and Bruckstein A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322.( 3) 3) |
| [60] | Van den Berg E, Schmidt M, Friedlander M P, et al. Group sparsity via linear-time projections[R]. Technical Report, University of British Columbia, 2008, Technical Report Number TR-2008, 2008.( 2) 2) |
| [61] | Friedman J, Hastie T, and Tibshirani R. A note on the group lasso and a sparse group lasso[J]. Preprint arXiv:1001:0736v1, 2010.( 2) 2) |
| [62] | Huang J and Zhang T. The benefit of group sparsity[J]. Annals of Statistics, 2009, 38(4): 1978-2004.( 2) 2) |
| [63] | Huang J, Zhang T, and Metaxas D. Learning with structured sparsity[J]. Journal of Machine Learning Research, 2011, 12(7): 3371-3412.( 2) 2) |
| [64] | Jacob L and Obozinski G. Group lasso with overlaps and graph lasso[C]. Proceedings of the 26th International Conference on Machine Learning, 2009.( 3) 3) |
| [65] | Jenatton R, Audibert J Y, and Bach F. Structured variable selection with sparsity-inducing norms[J]. Journal of Machine Learning Research, 2011, 12(10): 2777-2824.( 3) 3) |
| [66] | Baraniuk R G, Cevher V, Duarte M F, et al. Model-based compressive sensing[J]. IEEE Transactions on Information Theory, 2010, 56(4): 1982-2001.( 2) 2) |
| [67] | He L and Carin L. Exploiting structure in wavelet-based bayesian compressive sensing[J]. IEEE Transactions on Signal Processing, 2009, 57(9): 3488-3497.( 2) 2) |
| [68] | He L, Chen H, and Carin L. Tree-structured compressive sensing with variational bayesian analysis[J]. IEEE Signal Processing Letters, 2010, 17(3): 233-236.( 2) 2) |
| [69] | Eldar Y C, Kuppinger P, and Bölcskei H. Block-sparse signals: uncertainty relations and efficient recovery[J]. IEEE Transactions on Signal Processing, 2010, 58(6): 3042-3054.( 2) 2) |
| [70] | Yuan M and Lin Y. Model selection and estimation in regression with grouped variables[J]. Journal of the Royal Statistical Society, 2006, 68(1): 49-67.( 2) 2) |
| [71] | Robert T, Michael S, Saharon R, et al. Sparsity and smoothness via the fused lasso[J]. Journal of the Royal Statistical Society, 2005, 67(1): 91-108.( 2) 2) |
| [72] | Amit Y, Fink M, Srebro N, et al. Uncovering shared structures in multiclass classification[C]. Twenty-fourth International Conference on Machine Learning, 2007: 17-24.( 2) 2) |
| [73] | Gilboa G and Osher S. Nonlocal operators with applications to image processing[J]. SIAM Journal on Multiscale Modeling & Simulation, 2008, 7(3): 1005-1028.( 1) 1) |
| [74] | Bach F and Obozinski G. Structured sparsity through convex optimization[J]. Statistical Science, 2011, 27(4): 450-468.( 2) 2) |
| [75] | Peleg T, Eldar Y C, and Elad M. Exploiting statistical dependencies in sparse representations for signal recovery[J]. IEEE Transactions on Signal Processing, 2012, 60(5): 2286-2303.( 1) 1) |
| [76] | Dremeau A, Herzet C, and Daudet L. Boltzmann machine and mean-field approximation for structured sparse decompositions[J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3425-3438.( 1) 1) |
| [77] | Marlin B M and Murphy K P. Sparse Gaussian graphical models with unknown block structure[C]. ICML'09 Proceedings of the 26th International Conference on Machine Learning, 2009: 705-712.( 1) 1) |
| [78] | Marlin B M, Schmidt M, and Murphy K P. Group sparse priors for covariance estimation[C]. Appears in Proceedings of the Twenty-Fifth Conference on Uncertainty in Artificial Intelligence, 2012: 383-392.( 1) 1) |
| [79] | Li L. Note on RIP-based co-sparse analysis[OL]. http://arxiv.org/abs/1202.2037.( 2) 2) |
| [80] | Pournaghi R and Wu X. Coded acquisition of high frame rate video[J]. IEEE Transactions on Image Processing, 2013, 23(12): 5670-5682.( 2) 2) |
| [81] | Donoho D and Tanner J. Observed universality of phase transitions in high-dimensional geometry, with implications for modern data analysis and signal processing[J]. Philosophical Transactions A: Mathematical, Physical and Engineering Sciences, 2009, 367(1906): 4273-4293.( 1) 1) |
| [82] | Candès E J and Recht B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2008, 9(6): 717-772.( 1) 1) |
| [83] | Thrampoulidis C, Abbasi E, and Hassibi B. The LASSO with non-linear measurements is equivalent to one with linear measurements[OL]. http://arxiv.org/abs/1506.02181.( 2) 2) |
| [84] | Candes E J and Plan Y. Matrix completion with noise[J]. Proceedings of the IEEE, 2009, 98(6): 925-936.( 1) 1) |
| [85] | Hardle W, Hall P, and Ichimura H. Optimal smoothing in single-index models[J]. The Annals of Statistics, 1993, 21(1): 157-178.( 2) 2) |
| [86] | Hristache M and Spokoiny V. Direct estimation of the index coefficient in a single-index model[J]. The Annals of Statistics, 2001, 29(3): 595-623.( 2) 2) |
| [87] | Gopi S, Netrapalli P, Jain P, et al. One-bit compressed sensing: provable support and vector recovery[C]. In International Conference on Machine Learning, 2013.( 1) 1) |
| [88] | Jacques L, Laska J, Boufounos P, et al. Robust 1-bit compressive sensing via binary stable embeddings of sparse vectors[J]. arXiv:1104.3160, 2011.( 1) 1) |
| [89] | Plan Y and Vershynin R. One-bit compressed sensing by linear programming[J]. Communications on Pure & Applied Mathematics, 2013, 66(8): 1275-1297.( 1) 1) |
| [90] | Plan Y and Vershynin R. Robust 1-bit compressed sensing and sparse logistic regression: a convex programming approach[J]. IEEE Transactions on Information Theory, 2013, 59(1): 482-494.( 1) 1) |
| [91] | Bahmani S and Romberg J. Efficient compressive phase retrieval with constrained sensing vectors. arXiv: 1507. 08254v1, 2015.( 1) 1) |
| [92] | Cevher V, Becker S, and Schmidt M. Convex optimization for big data: Scalable, randomized, and Parallel algorithms for big data analytics[J]. IEEE Signal Processing Magazine, 2014, 31(5): 32-43.( 1) 1) |
| [93] | Slavakis K, Giannakis G B, and Mateos G. Modeling and Optimization for Big Data Analytics: (Statistical) learning tools for our era of data deluge[J]. IEEE Signal Processing Magazine, 2014, 31(5): 18-31.( 3) 3) |
| [94] | Yuan G X, Chang K W, Hsieh C J, et al. A comparison of optimization methods and software for large-scale L1- regularized linear classification[J]. Journal of Machine Learning Research, 2010, 11(2): 3183-3234.( 3) 3) |
| [95] | Fercoq O, Qu Z, Richtarik P, et al. Fast distributed coordinate descent for non-strongly convex losses[OL]. http://arxiv.org/abs/1405.5300.( 3) 3) |
| [96] | Bertsekas D P and Tsitsiklis J N. Parallel and Distributed Computation: Numerical Methods[M]. Prentice Hall, 1989.( 1) 1) |
| [97] | Nemirovski A, Juditsky A, Lan G, et al. Robust stochastic approximation approach to stochastic programming[J]. SIAM Journal on Optimization, 2009, 19(4): 1574-1609.( 1) 1) |
| [98] | Kushner H and Yin G. Stochastic Approximation Algorithms and Applications[M]. New York: Springer, 1997.( 3) 3) |
| [99] | Nesterov Y. Efficiency of coordinate descent methods on huge-scale optimization problems[J]. SIAM Journal on Optimization, 2012, 22(2): 341-362.( 3) 3) |
| [100] | Richtárik P and Taká M. Iteration complexity of randomized block-coordinate descent methods for minimizing a composite function[J]. Mathematical Programming, 2014, 144(1): 1-38.( 3) 3) |
| [101] | Nesterov Y. Gradient methods for minimizing composite objective function[OL]. http://eonpapers.repec.org/paper/ corlouvco/2007076.htm.( 2) 2) |
| [102] | Fercoq O and Richtarik P. Accelerated, parallel and proximal coordinate descent[OL]. http://arXiv:1312.5799.( 2) 2) |
| [103] | Hazan E, Levy K, and Shalev-Shwartz S. Beyond convexity: stochastic quasi convex optimization[OL]. http://arxiv.org/abs/1507.02030.( 3) 3) |
| [104] | Qu Z, Richtarik P, and Zhang T. Randomized dual coordinate ascent with arbitrary sampling[OL]. http://arxiv.org/abs/1411.5873.( 2) 2) |
| [105] | Hardt M, Recht B, and Singer Y. Train faster, generalize better: stability of stochastic gradient descent[OL]. http://arxiv.org/abs/1509.01240.( 2) 2) |
| [106] | Johnson R and Zhang T. Accelerating stochastic gradient descent using predictive variance reduction[C]. Advances in Neural Information Processing Systems, 2013, 26: 315-323.( 2) 2) |
| [107] | Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning, 2011, 3(1): 1-122.( 2) 2) |
| [108] | Su W, Boyd S, and Candes E J. A differential equation for modeling nesterov's accelerated gradient method: theory and insights[OL]. http://arxiv.org/abs/1503.01243.( 1) 1) |


