外辐射源雷达因具有隐蔽性好、不占用频谱等优点而受到雷达界广泛研究[1]。目前,外辐射源雷达所利用的辐射源主要集中于广播、电视等信号,而基于IEEE无线局域网标准(802.11)的WiFi信号已覆盖世界各大城市,且具有带宽大,副峰抑制后的信号模糊函数为图钉状等优点,非常有利于用作无源探测[1, 2]。利用WiFi信号进行无源探测是一个新领域,国内外研究还不多,目前国外主要有英国的UCL和意大利Rome大学等[3, 4, 5, 6, 7, 8],国内主要有武汉大学等在该方向进行了一些初步研究[9],并开展了相关实验。
利用外辐射源雷达进行目标探测过程中,其参考信号质量对于实现探测功能及性能都有很大的影响[10]。通常参考信号获取有空时域滤波等方法,但在WiFi外辐射源雷达中,尤其是在穿墙探测应用中,作为辐射源的WiFi路由器方位并不能完全预先确定,所以天线不能完全直接对准发射源。同时,室内环境给信号传输带来的多径效应、墙体回波及多普勒扩展等[11]使得采用空域滤波[12]和时域自适应滤波[13]等方法的效果都受到极大影响而无法正常应用。
因此,在WiFi外辐射源雷达参考信号获取方面,Rome大学通过网线直接连接路由器获得参考信号[6, 7],该方法回避了参考信号传输过程中可能带来的问题,但只能用于实验,实用性差;UCL最初的研究采用空域滤波方法,将天线直接对准路由器获取参考信号[8],但由于效果较差,故在最新的实验研究中与Rome大学一样,也采用了网线直接连接路由器获取参考信号的方法[3]。
和空时域滤波等方法相比,重构是WiFi外辐射源雷达参考信号获取的一个很好的选择,即对接收到的发射信号进行解调和再调制,从而使参考信号与发射信号一致。但与广播、电视等信号不同,WiFi不仅具有CDMA和OFDM等不同的信道接入方式,也随信道条件不同而具有QAM、PSK等不同调制方式,而且其协议还变得更复杂,这使得WiFi信号的重构一直是一个具有挑战性的问题。同时,WiFi信号是计算机网络信号,采用分组传输,则在探测过程中雷达会接收到来自路由器和与其关联的移动端信号,即会收到多站同频照射源的信号,而且传输协议相同,则在探测中会出现虚假目标的“重影”,且无法通过空域及时域自适应滤波方法进行抑制。但在参考信号重构过程中可根据信号结构进行有用信号识别而仅保留来自路由器的信号,从而消除“重影”,这对WiFi参考信号重构具有重要意义,也是区别于其它外辐射源雷达信号重构的不同之处,该方法目前尚未见到公开报道。
本文从WiFi外辐射源探测应用出发对WiFi信号形式进行分析,并针对典型OFDM的WiFi信号建立了发射信号的重构流程及多站同频信号识别与修正方法。基于仿真数据研究了重构过程中直达波信噪比等因素对重构及探测性能的影响,并用实测数据验证了重构算法的有效性。
本文第2节介绍了典型的WiFi信号结构,第3节研究了典型WiFi信号的重构流程及信号识别方法,第4节和第5节进行了重构信号质量及其对探测性能的影响分析,最后对全文进行了总结。
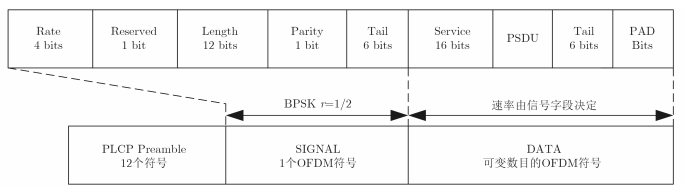
2 典型WiFi信号模型IEEE 802.11标准包括a/b/g/n等一系列协议,其中802.11g以其高速率与后向兼容性成为第3代WLAN标准,IEEE工作组为这一标准定义了DSSS/CCK(Complementary Code Keying)和OFDM等4种物理层。本文将以典型的OFDM模式进行分析,该模式下信号带宽可达20 MHz,具有较好的距离分辨率,其物理层帧结构如图 1所示。
|
图 1 OFDM模式物理层帧结构 Fig. 1 Physical layer frame structure of OFDM mode |
由于信道的突发性,每帧信号长度具有时变特性,由图 1可知,信号结构主要由前导符号、信号、数据3部分组成。前导符号由短训练序列和长训练序列组成。信号部分包含数据部分的调制信息,单独形成一个OFDM符号,以鲁棒性较强的BPSK调制和1/2编码率发送。数据部分以Rate字段中指示的数据速率发送,并且可能组成多个OFDM符号。
OFDM模式下,基带复信号s(t)可以表示为:
| $S(t)\! = {S_{\rm{preamble}}}(t) \!+ \!{S_{\rm{signal}}}(t \!-\! {T_{\rm{pre}}})\! + \!{S_{\rm{data}}}(t \!- \!{T_\rm{d}})$ | (1) |
其中,Spreamble(t)为前导符号部分,Ssignal(t-Tpre)为信号部分,Sdata(t-Td)为数据部分。Tpre=16 μs,为前导符号持续时间,Td=20 μs,为前导符号和信号部分持续时间。
3 参考信号获取方法 3.1 参考通道信号模型与其它无源雷达信号模型一致,参考通道接收天线获得的信号除了含有直达波外,还包括多径分量、杂波和噪声等,故信号模型可表示为:
| ${y_{\rm{ref}}}(t) = {A_{\rm{ref}}}s(t) + \sum\limits_{k = 1}^N {{\lambda _k}} s(t - {\tau _k}) + {n_{\rm{ref}}}(t) $ | (2) |
其中,第1项为参考通道所接收到的直达波信号,Aref表示直达波信号的幅度;第2项为多径信号,N表示路径条数,$\lambda _k$与$\tau _k$分别表示各路径信号的幅度与时延;第3项表示参考通道中的高斯噪声。
3.2 基于同步信号的自适应滤波提纯算法自适应滤波提纯直达波的核心思想是通过滤波器滤除所接收信号中的多径干扰来得到较为纯净的参考样本。为得到s(t),需构造滤波器,滤波器输入为x(t),输出是s(t)的估计值$\hat s(t)$,如式(3)。
| $\hat s(t) = \sum\limits_{k = 0}^{M - 1} {{w_k}} x(n - k)$ | (3) |
其中,用离散序号n代替了连续时间t,wk是滤波器抽头系数,M为滤波器阶数。
每一帧WiFi信号都具有2个已知的完全相同的长训练序列符号。利用这个训练序列可实时捕获信道的变化,求取滤波器的抽头系数wk,构造滤波器。将该滤波器应用于WiFi信号的数据符号部分,如式(3),即可滤除参考信号中的多径干扰。同步信号求取滤波器系数需采用自适应算法,本文选取递归最小二乘方(RLS,Recursive Least Square)算法[13]进行时域参考信号提纯,并与重构方法进行比较。
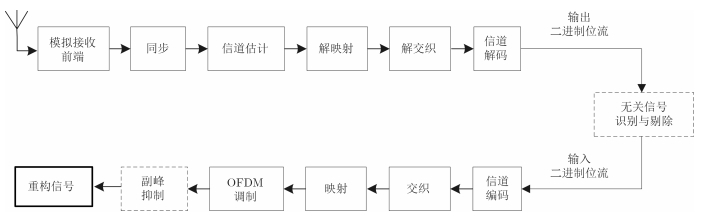
3.3 基于WiFi发射信号的重构算法OFDM技术有很强的抗多径衰落和窄带噪声的能力,参考信号提取应该充分利用信号结构本身的优势,为此,在深究WiFi信号形成机制的基础上,我们提出了适用于WiFi无源探测的参考信号重构方法,其流程如图 2所示。
|
图 2 WiFi信号重构流程框图 Fig. 2 Block diagram of WiFi signal reconstruction |
参考天线接收信号后,经放大、滤波和下变频等处理并得到数字化的基带信号后,依次进行同步、信道估计、均衡、解交织和解码[16],再经纠错之后得到原始二进制位流,对于该位流数据,需要进行协议解包以根据上层协议进行无关信号识别与剔除,仅保留来自路由器的数据,再按照发射端信号的形成步骤进行再调制,并对重构后的物理层数据进行副峰抑制,最后得到经修正后的参考信号。
由图 2可以看出,在整个信号重构过程中,同步和信道估计算法是关键,直接影响参考信号的质量。同步的主要任务是获取信号的帧起点,估计出混频过程中出现的频率偏差和采样过程中引进的采样误差,并对其进行补偿。频率偏差和采样误差会影响同步结果,增大信道解码的误比特率,降低重构信号的准确性。信道估计主要被用于信道均衡,以抵消信道对发射信号带来的畸变。
3.3.1 同步算法根据WiFi信号结构,OFDM的前导符号由10个完全相同的短训练序列和2个长训练序列组成,利用延时和自相关算法[17]可以获取同步信号的位置,其中帧同步利用802.11g标准中10个短训练序列符号。若第n个接收信号为rn,则
| $\quad \ \; {C_n} = \sum\limits_{k = 0}^{L - 1} {{r_{n + k}}} {{{\Large { \cdot } }}} \mathop r\nolimits_{n + k + D}^* $ | (4) |
| ${P_n} = \sum\limits_{k = 0}^{L - 1} {{r_{n + k + D}}} {{{\Large { \cdot } }}} \mathop r\nolimits_{n + k + D}^* = \sum\limits_{k = 0}^{L - 1} {{{\left| {{r_{n + k + D}}} \right|}^2}} $ | (5) |
| $\quad \ {M_n} = \sum\limits_{k = 0}^{L - 1} {{{\left| {{C_n}} \right|}^2}} /\mathop P\nolimits_n^2 $ | (6) |
其中,延迟单位D=16,即一个短训练序列符号的长度,Cn是接收信号和接收信号延时的互相关,Pn表示了相应接收信号的能量,用于做判决统计的归一化,当Mn跳变为最大值,表明数据帧信号已经到达。
对于符号定时,我们采用长训练序列的相关矢量来确定符号的起始点,利用接收的信号和本地已知的长训练序列互相关,然后归一化,如式(7)。
| $\begin{array}{*{20}{l}} {{\rm{Local}}\_{\rm{corr}}(n)}\\ { = \frac{{{{\left| {\sum\limits_{k = 0}^{L - 1} {r\left( {n + k} \right) \cdot {\rm{Local\_long}}*\left( k \right)} } \right|}^2}}}{{\sum\limits_{k = 0}^{L - 1} {{{\left| {r\left( {n + k} \right)} \right|}^2} \cdot \sum\limits_{k = 0}^{L - 1} {{{\left| {{\rm{Local\_long}}\left( k \right)} \right|}^2}} } }}} \end{array}$ | (7) |
由于多普勒效应或者接收机本地载波和发射机载波频偏不匹配,会产生收发端之间的载频偏差。从而影响OFDM信号子载波之间的正交性,导致解调错误。根据信号结构,在符号同步后,再利用前导序列之间的相关关系来实现载波同步,即
| $\quad \quad \quad \quad \quad \ \ \,R = \sum\limits_{k = 0}^{L - 1} {{r_n}} {{{\Large { \cdot } }}} \mathop r\nolimits_{n + D}^* $ | (8) |
| $\Delta f = - \angle R/2{{π}} D{T_\rm{{sym}}}$ | (9) |
其中,D为两个连续重复符号之间的延时,R为周期重复的接收信号的延时相关和,Tsym=4 μs,为符号间隔。
因此,先用短训练序列进行粗频偏估计和纠正;经符号定时后,再利用长训练序列得到精频偏估计Df,对相应采样点n乘以${{\rm{e}}^{ - {\rm{j}}2{{π}} n\Delta fT}}$进行精频偏纠正,从而实现同步。
3.3.2 信道估计和均衡多径信道会造成传输数据的频率选择性衰落,体现为一些载波点上数据功率的衰落。在传输数据进入接收端判决电路之前,需对接收到的数据进行1次复数乘法运算,以消除多径信道对数据所造成的影响,弥补信道的乘性干扰。同时,同步过程中的频偏估计并不是一个完备的过程,会存在剩余的频率误差,需要对残余的频率偏差造成的相位旋转进行跟踪补偿。因此,我们利用已知长训练序列做信道估计和均衡,并采用最小平方(Least Square,LS)算法,在导频位置为+7,+21,-7,-21处,得到由残余载波频偏影响产生的相位旋转量${\Phi _{m,k}}$为:
| ${\Phi _{m,k}} = \arg \left[ {\sum\limits_{k = 1}^{{k_p}} {{R_{n,k}}{{({{\hat H}_{n,k}} \cdot {P_{n,k}})}^*}} } \right] = 2\pi n\Delta f{T_{sym}}$ | (10) |
其中,${{R_{n,k}}}$表示接收到的第n个OFDM符号的第k个导频,${\hat H_{n,k}}$表示频域信道响应估计值,${{P_{n,k}}}$为+1或-1,${{k_p}}$=4,$\Delta f$为经载波频偏校正后的频率误差。${T_{sym}}$=4 μs,为符号间隔。
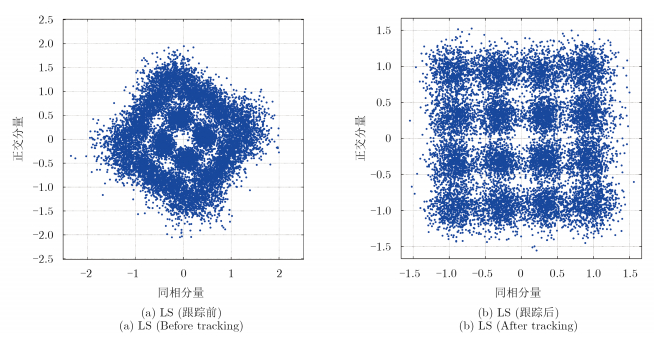
为了验证信道估计和均衡的性能,我们进行了仿真,其设置为:信噪比SNR=30 dB,瑞利信道,5条多径(各径延时系数为delay=[1, 2, 3, 4, 5];各径衰落系数为decay=[0.15,0.12,0.11,0.20,0.05]),其结果如图 3所示。
|
图 3 基于LS信道估计均衡图 Fig. 3 Channel estimation equalization based on LS |
由图 3可以看出,未实施相位跟踪前,还存在少量残余的频率偏差,造成了星座图上复数点的相位旋转,在经过信道估计与均衡后,消除了多径、多普勒等导致的符号间干扰ISI和载波间干扰ICI,能够得到较好的星座图,但是传输过程中存在的噪声还是会产生一定的误比特率,这可进一步通过信道解码进行纠错。
参考通道接收信号经过同步、信道估计、均衡、相位跟踪、译码纠错之后可得到原始的发送比特流,为了构造出无源雷达探测中相对纯净的参考信号,需要对此干净比特流进行再编码,经过交织、映射等过程生成参考信号。
3.3.3 参考信号修正重构不仅可获得纯净的参考信号,而且在重构过程中,还可对参考信号进行修正以克服WiFi信号本身缺陷对探测的影响。WiFi外辐射源雷达主要利用路由器发射信号进行探测,但网络所采用的共享信道方式使得雷达接收机还会收到同一局域网内其它设备的信号,这些信号的频率、格式等都与路由器信号相同,会形成目标“重影”,对于探测来说可以认为是干扰信号,但与其它干扰信号不同,无法采用常用的方法进行抑制,即在物理层无法对不同来源的数据包进行区分。
对物理层帧PSDU域,即MAC层帧进行分析发现不同来源的数据在MAC层帧头的地址域不同,可用于区分不同的数据来源,MAC帧结构如图 4所示。

|
图 4 MAC帧结构 Fig. 4 MAC frame structure |
对于MAC数据帧,由于Address 2总是发送该帧数据的STA(STAtion)的MAC地址,故可通过该域进行数据来源识别。在重构过程中,对接收信号解调后即可对数据包来源进行识别,当地址Address 2与所用来探测的AP地址一致时,则保留该帧数据并继续进行再调制恢复生成路由器的原始发送信号,否则,将该帧数据置零,从而使得重构后参考信号只保留来自路由器的数据,而滤掉其他来源的信号。
另外,由图 1可知,OFDM格式的WiFi信号中前导符号和循环前缀会产生模糊函数副峰,在重构过程中将该部分置零即可实现副峰抑制。
因此,信号重构可实现直达波提纯,还可在再调制过程中对解调后信号进行修正,实现无关信号剔除及副峰抑制,从而得到适用于无源探测的参考信号。
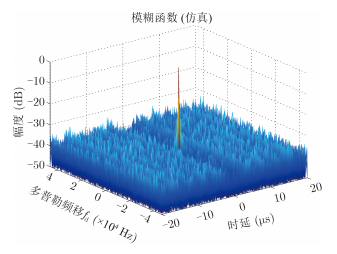
4 参考信号获取算法分析与比较 4.1 重构质量与误比特率关系分析为了考察重构效果,将重构信号与原始发射信号做互相关,仿真结果如图 5所示,可以看到,重构的参考信号与原始信号具有良好的互相关性。并且随着参考信号解调时误比特率(Bit Error Rate,BER)的降低,其互相关函数的噪声基底也在不断下降,表明重构的效果越好,其对应关系如图 6所示。
|
图 5 重构信号与发送信号互相关函数图 Fig. 5 Mutual correlation function of the reconstructed signal and the transmitted signal |
|
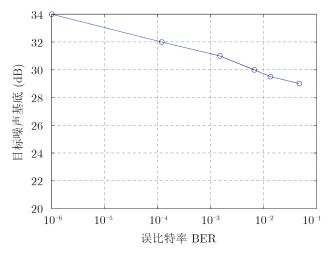
图 6 误比特率与互相关函数噪声基底之间的关系图 Fig. 6 The relationship between the bit error rate and the cross correlation function noise base |
为了比较重构与时域自适应滤波两种参考信号获取方法的提纯性能,我们定义波形失真度指标,如式(11)所示。
| $\eta = \frac{{\sum\limits_{i = 1}^N {{{\left| {s\left( i \right) - {s_{\rm{o}}}\left( i \right)} \right|}^2}} }}{{\sum\limits_{i = 1}^N {{{\left| {{s_{\rm{o}}}\left( i \right)} \right|}^2}} }} \times 100\%$ | (11) |
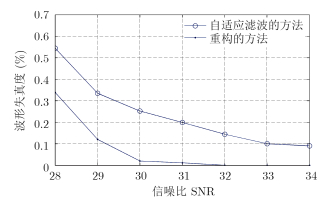
其中,${s\left( i \right)}$为直达波提纯后的信号,so(i)为纯净的直达波信号。波形失真度表征了提纯后的直达波信号与纯净的直达波信号的相似程度。在相同接收信号条件下,两种方法所获得的参考信号波形失真度仿真结果如图 7所示。
|
图 7 不同直达波提取方法的波形失真度 Fig. 7 Waveform distortion of different direct wave extraction methods |
由图 7可以看出,自适应滤波以后的信号与纯净直达波信号之间的失真度比重构信号与纯净直达波信号之间的失真度要大。通过分析式(2)也可得知,参考通道天线所接收到的直达波信号幅度Aref不仅会受多径的影响,还会受空间传输衰减和噪声的影响,而自适应滤波只对多径有一定的抑制作用,对于直达波传输所带来的幅度衰减则完全没有补偿作用,且RLS算法对信号中的噪声也未作过多处理,因此,自适应滤波以后的信号与纯净直达波信号之间存在着比较大的差异,当然,增加滤波器的阶数可以进一步提高滤波性能,但会增加信号延时和降低算法效率。而重构的方法则基本上不受多径的影响,只要多径延时在循环前缀长度内,没有引起符号间干扰,就可恢复出原始发送信号。而且重构的方法还能将Aref重生至1。因此,重构信号的波形失真度很小。这说明重构方法的提纯性能较自适应滤波方法更好。
5 重构质量对探测性能的影响分析重构的参考信号在目标探测中所起的作用主要表现在两个方面:(1)作为参考信号用于目标通道的直达波及多径杂波抑制;(2)用作匹配滤波,与直达波抑制后的目标信号相关以检测目标。因此,重构参考信号质量会影响杂波抑制效果,并影响目标探测性能,故可从相关检测中影响目标回波信息的信噪比角度,研究不同重构信号质量对目标探测的影响。
5.1 参考信号质量对时域杂波抑制方法的影响直达波和多径杂波的抑制是无源雷达系统中信号处理的关键步骤,参考信号作为杂波抑制算法的输入,其质量将直接影响杂波抑制性能,从而影响与监测通道信号进行互相关的噪声基底。由于参考通道接收到的信号具有一定信噪比,故重构信号将具有一定的误比特率,该误比特率将影响抑制算法性能。我们采用无源探测中常用的扩展相消算法(Extensive Cancellation Algorithm-Block,ECA-B)来探讨重构信号质量对杂波抑制效果的影响。
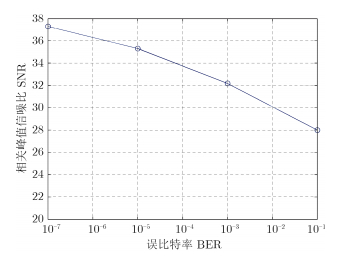
在瑞利信道环境下进行仿真,调制方式为典型的16QAM,监测通道接收到1个目标和5条多径信号(各径延时系数为delay=[1, 2, 3, 4, 5];各径衰落系数为decay=[0.15,0.12,0.11,0.20,0.05]),且多径信号比目标信号强45 dB。积累时间为3个突发脉冲,大约为8.212 ms。在重构参考信号的BER分别为10-1,10-3,10-5,10-7时,匹配滤波后相关峰值信噪比的变化如图 8所示。
|
图 8 参考信号重构时不同误码率的相关峰值信噪比 Fig. 8 Correlation peak signal to noise ratio of different bit error rate when the reference signal is reconstructed |
由图 8可以看到,随着重构的参考信号误比特率降低,互相关函数的噪声基底也在不断下降,也即目标信号的信噪比SNR在不断地增大。因此,参考信号重构质量越高,对监测信号进行杂波抑制的效果越好,从而使得匹配滤波后目标信号信噪比提高,进而改善了探测性能。
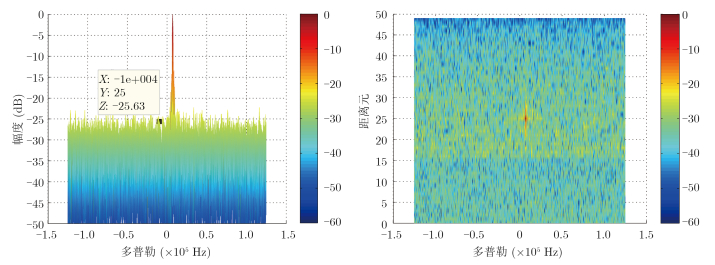
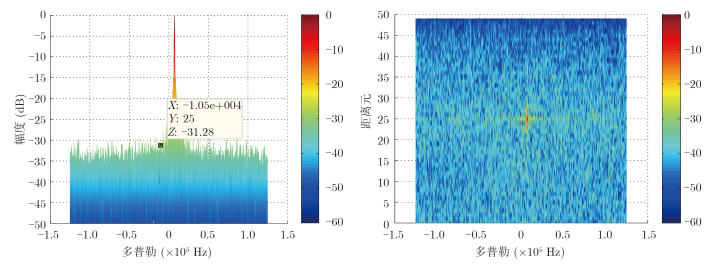
5.2 实测信号处理武汉大学利用自行设计的多通道外辐射源雷达系统分别于2013年3月和2015年6月开展了WiFi探测实验,下面结合实测数据处理分析参考信号纯度对探测性能的影响。因实际误比特率无法获得,故分两种情况考虑:(1)参考信号直接用参考通道天线所接收的信号;(2)参考信号用重构以后的信号。比较两种情况下得到的目标信噪比即可定性判断参考信号纯度对探测性能的改善作用,将第1种情况下得到的参考信号与经过直达波抑制后的目标信号互相关,距离多普勒谱如图 9所示,在图上可以发现目标,该目标的信噪比约为25.63 dB,第2种情况下,重构的参考信号与经过直达波抑制后的目标信号互相关,距离多普勒谱如图 10所示,此时,目标的信噪比约为31.28 dB,相对于直接从接收天线得到的参考信号,目标的信噪比提高了约5.6 dB,实测处理结果与5.1节的仿真结论一致,即提高重构参考信号纯度能有效改善目标探测性能,对于弱目标检测来说,这种即使很小的信噪比改善也是非常有意义的。
|
图 9 原始发送信号的目标相关图,时延-幅度(左),时延-多普勒(右) Fig. 9 The original transmission signal of the target correlation graph, delay-amplitude (left), delay-Doppler (right) |
|
图 10 重构信号的目标相关图,时延-幅度(左),时延-多普勒(右) Fig. 10 Target correlation figure of the reconstructed signal, delay-amplitude (left), delay-Doppler (right) |
本文从典型WiFi信号结构出发,分析了WiFi外辐射源雷达参考信号重构流程,并对重构过程中最关键的同步、信道估计与均衡等算法进行理论与仿真分析。针对在所获取参考信号中可能来自多个数据源的情况下,提出了基于MAC数据帧地址域进行识别及去除的方法。同时,论文还从时域直达波抑制的角度,研究了参考信号重构对目标探测性能的影响。其结果表明,参考信号重构纯度越高,即误比特率越低,与目标探测信号互相关的噪声基底越低,因此,参考信号的重构对提高目标的信噪比、改善弱目标探测性能具有积极的作用。
| [1] | Griffiths H D. New direction in bistatic radar[C]. IEEE RADAR Conference, Rome, 2008: 1-6.( 1) 1) |
| [2] | 万显荣, 易建新, 程丰, 等. 单频网分布式外辐射源雷达技术[J]. 雷达学报, 2014, 3(6): 623-631. Wan Xian-rong, Yi Jian-xin, Cheng Feng, et al.. Single frequency network based distributed passive radar technology[J]. Journal of Radars, 2014, 3(6): 623-631.(  3) 3) |
| [3] | Chen Q, Tan B, Woodbridge K, et al.. Indoor target tracking using high Doppler resolution passive Wi-Fi radar[C]. 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), South Brisbane, QLD, 2015: 5565-5569.( 4) 4) |
| [4] | Falcone P, Colone F, Macera A, et al.. Two-dimensional location of moving targets within local areas using WiFi-based multistatic passive radar[J]. IET, Radar, Sonar & Navigation, 2014, 8(2): 123-131.( 3) 3) |
| [5] | Colone F, Pastina D, Falcone P, et al.. WiFi-based passive ISAR for high-resolution cross-range profiling of moving targets[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3486-3501.( 3) 3) |
| [6] | Falcone P, Bongioanni C, and Lombardo P. WiFi-based passive bistatic radar: data processing schemes and experimental results[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1061-1079.( 2) 2) |
| [7] | Colone F, Woodbridge K, Guo H, et al.. Ambiguity function analysis of wireless lan transmissions for passive radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 240-264.( 2) 2) |
| [8] | Chetty K, Smith G E, and Woodbridge K. Through-The-Wall sensing of personnel using passive bistatic WiFi radar at standoff distances[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(4): 1218-1226.( 2) 2) |
| [9] | 饶云华, 朱逢园, 张修志, 等. WiFi 外辐射源雷达信号模糊函数及副峰抑制分析[J]. 雷达学报, 2012, 1(3): 225-231. Rao Yun-hua, Zhu Feng-yuan, Zhang Xiu-zhi, et al.. Ambiguity function analysis and side peaks suppression of passive radar[J]. Journal of Radars, 2012, 1(3): 225-231.(  1) 1) |
| [10] | 万显荣, 唐慧, 王俊芳, 等. DTMB外辐射源雷达参考信号纯度对探测性能的影响分析[J]. 系统工程与电子技术, 2013, 35(4): 725-729. WAN Xian-rong, Tang Hui, Wang Jun-fang, et al.. Influence of reference signal purity on target detection performance in DTMB-based passive radar[J]. Systems Engineering and Electronics, 2013, 35(4): 725-729.(  1) 1) |
| [11] | Mazhar H and Hassan S A. Analysis of target multipaths in WiFi-based passive radars[J]. IET, Radar, Sonar & Navigation, 2016, 10(1): 140-145.( 1) 1) |
| [12] | 吴海洲, 陶然, 单涛. 数字电视辐射源雷达基于空域滤波的直达波获取[J]. 兵工学报, 2009, 30(2): 226-230. Wu Hai-zhou, Tao Ran, and Shan Tao. Direct-path signal obtaining to digital video broadcasting transmitter radar based on the spatial filtering[J]. Acta Armamentarii, 2009, 30(2): 226-230.(  1) 1) |
| [13] | 万显荣, 岑博, 易建新, 等. 中国移动多媒体广播外辐射源雷达参考信号获取方法研究[J]. 电子与信息学报, 2012, 34(2): 338-343. Wan Xian-rong, Cen Bo, Yi Jian-xin, et al.. Reference signal extraction methods for CMMB-based passive bistatic radar[J]. Journal of Electronics & Information Technology, 2012, 34(2): 338-343.(  2) 2) |
| [14] | Harms H A, Davis L M, and Palmer J. Understanding the signal structure in DVB-T signals for passive radar detection[C]. IEEE Radar Conference, Washington, 2010: 532-537. |
| [15] | Chetty K, Smith G, Guo H, et al.. Target detection in high clutter using passive bistatic WiFi radar[C]. IEEE Radar Conference, Pasadena, 2009: 1-5. |
| [16] | IEEE std 802.11g-2003. Telecommunications and information exchange between systems local and metropolitan area networks specific requirements Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) specifications-Amendment 4: Further Higher-Speed Physical Layer Extension in the 2.4 GHz Band[S]. New York: Institue of Electrical and Electronics Engineers, Inc., 2003.( 1) 1) |
| [17] | Nasraoui L, Atallah L N, and Siala M. An efficient reduced-complexity two-stage differential sliding correlation approach for OFDM synchronization in the multipath channel[C]. 2012 IEEE Wireless Communications and Networking Conference (WCNC), 2012: 2059-2063.( 1) 1) |


