1 引言

信息安全在军事通信及雷达传输领域至关重要，为解决无线通信领域中存在的窃听，电子干扰及信道混叠等问题，非合作跳频通信被广泛应用于其中。非合作跳频通信系统发射端与接收端的载波频率在既定集合内同步发生跳变，具有良好的抗截获、抗干扰及组网能力^[1]。在非合作跳频通信系统中，由于发射机与接收机之间具有非匹配性，使得在接收端接收到的跳频信号往往只包含有限信息，信号结构信息及相关调制参数均未知。而且，系统中同时含有其他干扰信号，如宽频带噪声、多频带噪声等。因此，如何在缺少先验信息，并且存在其他干扰条件下实现对信号的参数估计，已经成为非合作通讯侦查领域一个重要研究课题。

目前，跳频信号参数估计的主流方法是时频分析法，1997年，Barbarossa等人^[2]首次提出运用Wigner-Ville分布(Wigner-Ville Distribution, WVD)，在时域分析跳频信号参数特性，这种方法计算简单，但是由于存在交叉干扰，在一定程度上影响了实验结果，降低了估计精度。为解决这一问题，文献[3, 4]提出基于平滑伪Wigner-Ville分布(Smoothed Pseudo Wigner-Ville Distribution, SPWVD)和基于重排列平滑伪Wigner-Ville分布(Rearrangement Smoothed Pseudo Wigner-Ville Distribution, RSPWVD)的跳频信号参数估计方法，这两种方法利用信号分量能量重新分布实现参数估计，由于算法具有时频不变性及能量守恒的特点，因此能够改善频谱重叠现象，增强时频聚合性。为解决时频分析法中信噪比阀值的约束性，文献[5]利用多物种粒子群实现参数估计，这种方法通过搜索过完备字典，得到跳频分量最优匹配原子，再利用粒子群参数求解估计出相应跳变参数。但其对粒子距离测度阀值有严格要求，过大或过小都会影响估计精度。文献[6]引入压缩感知(Compressive Sensingm, CS)参数估计算法，利用少量不相干观测值实现跳频信号高速采样及参数估计，这种算法有效地降低了采样频率，但是在构造观测矩阵的过程中仍然需要部分先验信息，因此并不能为非合作跳频通信系统中信号的解调与破译提供足够的支持。文献[7]引入局部特征尺度分解算法，实现跳变参数盲估计，有效克服了时频不确定性及交叉干扰等影响，但是在实现过程中其他参数估计结果依赖于跳速估计值，当跳速估计错误时，会产生较大的误差。

近几年来，跳频信号的频率范围有逐渐增大的趋势，同时考虑到非合作通信系统中信号先验信息少，并且存在其他干扰信号，本文提出基于盲压缩感知(Blind Compressed Sensing, BCS)理论参数估计法，首先利用OBD-BCS算法实现非合作跳频信号重构，然后通过对重构结果进行频域分析，估计出相应跳变参数。理论分析及仿真实验表明，该方法能够在信噪比低，先验信息未知的条件下准确估计出信号的跳变频率及跳变周期。

2 盲压缩感知理论

压缩感知理论是一种基于稀疏表示^{[8, 9, 10]}，不相干观测及最优逼近理论提出的采样及重构方法，目前已被广泛应用于雷达信号的参数估计等领域^[11]。对于信号$x \in {R^{N \times 1}}$，根据其稀疏特性，构造一个N×N的正交变换基Ψ, Ψ=[Ψ₁, Ψ₂, $ \cdots $, Ψ_N]，则信号$x \in {R^{N \times 1}}$可表示为$x \in$Ψa, a是x的加权系数。另构造一个与正交基Ψ不相干的平稳测量矩阵Φ$ \in $R^M×N，即可得到压缩后观测向量y=Φx=Φ·Ψa=Θa。利用l₀范数的最优化求解，可以得到信号$x \in {R^{N \times 1}}$逼近信号$\hat {x}$，即

$\hat x = \arg \min {\left\| x \right\|_0}, \quad {\rm{s}}.{\rm{t}}.\quad \Phi x = y$

(1)

CS理论在构造矩阵Y时，信号的先验信息是至关重要的，但在实际应用过程中，信号信息往往不能被事先获知，如本文涉及的非合作跳频信号。为解决这一问题，BCS理论被提出^[12]，它将CS理论和字典学习(Dictionary Learning, DL)结合起来^[13]，一方面满足CS理论可以从少量数据中重构出高维信号的特性。另一方面，与字典学习过程一样，不需要获取信号稀疏基的先验信息。BCS理论省略了信号稀疏表示的过程，在采样和重构的过程中避免了对信号先验信息的需求，这使得BCS理论适用于非合作通信系统中信号的处理。

对于信号X∈R^m×N而言，BCS理论首先根据采样公式B=AX得到信号的测量值B∈R^n×N，其中A∈R^n×m为观测矩阵，并且有A=[A₁, A₂, $ \cdots $, A_L], A_i∈R^n×n为独立同分布正交高斯矩阵。

然后利用稀疏编码与正交基变换的不断交替迭代，直到满足

$\begin{array}{*{20}{l}} {\mathop {\min }\limits_{P, S} \parallel B - APS\parallel _F^2, \begin{array}{*{20}{c}} {}&{{\rm{s}}.{\rm{t}}.} \end{array}\;S\;{\rm{is}}\;K{\rm{ - sparse}}, }\\ {\quad \quad P\;{\rm{is}}\;{\rm{orthonormal}}} \end{array}$

(2)

的解最小，此时可得到稀疏矩阵${\hat {S}}\in {{{R}}^{m\times N}}$及正交基$\hat{P}\in {{{R}}^{m\times m}}$，进而求得重构信号$\hat{X}\text{=}\hat{P}\hat{S}$。

由于省略了稀疏表示的过程，信号观测值的维度较高，这使得BCS理论的解具有不确定性，为了确保解的唯一性，正交基P需要满足以下限制条件之一^{[14, 15]}：

(1) P是某个有限已知基字典Λ的正交子集。

(2) P可以被基字典Λ稀疏表示。

(3) P是一个块正交对角矩阵。

条件(1)可以被理解为CS理论重构过程，条件(2)可以被视作字典学习过程，考虑到跳频通信系统的跳变特性，本文主要是在正交基P满足条件(3)的前提下实现信号的重构，即有：

$\hat P = \left[{\begin{array}{*{20}{c}} {{{\hat P}_1}}&{}&{}\\ {}& \ddots &{}\\ {}&{}&{{{\hat P}_L}} \end{array}} \right]$

(3)

根据BCS理论特性可知，${{\hat {P}}\!_i} \in {{{R}}^{n \times n}}$为正交矩阵，并有信号压缩比L=m/n。

相对于条件(1)和条件(2)，当P满足条件(3)时，在对P进行变换过程中，可以对每一块单独变换而不需要改变整体序列。此时，${{S}} \in {{{R}}^{m \times N}}$中含有K项非零列，${{{A}}_i} \in {{{R}}^{n \times n}}$为正交观测矩阵，并有$\sigma ({{AP}}) = n + 1$。

3 信号模型及重构过程 3.1 跳频信号模型

跳频信号(Frequency Hopping, FH)载波频率按照一定变化规律迅速发生跳变，其间隔通常为数据调制带宽，因此，信号对于随机性，结构一致性以及调制带宽有严格要求。其信号模型为：

$\begin{array}{*{20}{l}} {x(t) = \sqrt {2S} \sum\limits_{i = 0}^{K - 1} {{\rm{rec}}{{\rm{t}}_{{T_{\rm{h}}}}}(t - i{T_{\rm{h}}} - {T_0})} }\\ {\quad \quad \quad \cdot {{\rm{e}}^{{\rm{j}}2\pi {f_i}(t - i{T_{\rm{h}}} - {T_0})}} + n(t)} \end{array}$

(4)

式中，S表示信号功率，K表示总的跳变次数，T_h表示每次跳变持续时间，T₀表示起跳时刻，f_i表示第i次的跳变频率，所对应时刻为T₀+(i+1)T_h, n(t)表示系统中所含有的高斯白噪声，窗函数${\rm{rec}}{{\rm{t}}_{{T_{\rm{h}}}}} = \left\{ {\begin{array}{*{20}{c}} {1, }&{t \in [0, {T_{\rm{h}}}]}\\ {0, }&{{\rm{others}}} \end{array}} \right.$。

为了减少相邻两次跳变之间的干扰，需满足频率间隔$\Delta f=1/{{T}_{\text{h}}}$，此时，满足各频率分量相互正交。

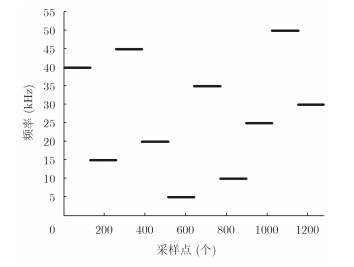
图 1给出了根据定义式(4)仿真得到的FH信号时频曲线图，从图中可以观察出跳变频率与跳变周期的对应关系。

3.2 跳频信号重构

跳频信号具有稀疏特性，这满足BCS理论前提条件。对于跳频信号而言，每一次跳变都可以表示为一段持续时间为T_h的正弦信号，在全部采样周期内，信号可以看成是K个正弦信号的线性组合。根据跳频信号这一特点，可以将其表示成X=[x₁, x₂, $ \cdots $, x_K]^T, X∈R^m×1。由于在BCS理论中，正交基$ \hat {P} $满足式(3)，因此可以推断出信号X_i在P_i下分别满足稀疏特性。

BCS理论是根据字典学习过程进一步推导得出的，字典学习的目的是利用基字典D求解：

$\begin{array}{*{20}{l}} {\mathop {\min }\limits_{D, S} \left\| {B - DS} \right\|_F^2, \begin{array}{*{20}{c}} {}&{{\rm{s}}.{\rm{t}}.}&{S\;{\rm{is}}\;K{\rm{ - sparse}}, } \end{array}}\\ {\quad D\;{\rm{is}}\;{\rm{a}}\;{\rm{union}}\;{\rm{of}}\;{\rm{orthonormal}}\;{\rm{bases}}} \end{array}$

(5)

在BCS理论中，P为正交块对角矩阵，A∈R^n×m为正交基的集合，因此，可以得到等价基字典D=AP。由于A_i及P_i均满足正交特性，因此基字典D同样具有正交性。假设测量矩阵A∈R^n×m已知，则需要找到一个正交块对角矩阵P∈R^m×m及稀疏矩阵S∈R^m×1使得B=APS，由此可得式(2)。

为了得到正交块对角矩阵P∈R^m×m及稀疏矩阵S∈R^m×1，需要进行两部分交替迭代，第1部分为稀疏编码，即首先令矩阵P固定不变，然后利用OMP算法重构出$ \hat {S} $∈R^m×1。第2部分主要是更新正交基P，我们可以将稀疏矩阵S∈R^m×1表示成S=[S₁, S₂, $ \cdots $, S_L]^T，则信号可表示为Xⁱ=PⁱSⁱ，并且可以得到

$\mathop {\min }\limits_{{{{P}}^1}, \cdot \cdot \cdot, {{{P}}^N}} \left\| {{{B}} - \sum\limits_{j = 1}^N {{{{A}}^j}{{{P}}^j}{{{S}}^j}} } \right\|_F^2, \\ \begin{array}{*{20}{c}} {{\text{s}}{\text{.t}}{\text{.}}}& {{{{P}}^1}, \cdots, {{{P}}^N}} \end{array} \text{ are orthonormal}$

(6)

为了使式(6)达到最小，我们对正交基P进行按列迭代。

具体的重构方法为：

步骤1构造独立同分布正交高斯矩阵A∈R^n×m，并利用B=AX求得信号的观测值B∈R^n×1。

步骤2对矩阵P∈R^m×m进行单位化，正交化处理。

步骤3利用D=AP构造一个基字典D∈R^n×m，并对其进行归一化，对角化处理，由于A∈R^n×m及P∈R^m×m均为正交矩阵，因此D∈R^n×m为一个正交基字典。

步骤4固定正交基P，根据B=DS，再利用OMP算法对S进行重构，可以得到稀疏矩阵$ \hat {S} $∈R^m×1。

步骤5利用重构出的$ \hat {S} $，对P^j, j=1, 2, $ \cdots $, m, j ≠ i逐一按列迭代，得到

$\mathop {{B}}\nolimits^i = {{B}} - \sum\limits_{j \ne i} {\mathop {{A}}\nolimits^j } \mathop {{P}}\nolimits^j \mathop {\widehat {{S}}}\nolimits^j $

(7)

步骤6由于P∈R^m×m是正交的，A∈R^n×m为正交子集，因此可以得出P^TA^TAP=I，进而可得：

$\begin{align} & \ \underset{P}{\mathop{\max }}\,\left\{ \text{Tr}\left[ {{B}^{\text{T}}}APS \right] \right\}, \\ & \begin{matrix} \text{s}\text{.t}\text{.}\ \ P\ \text{is}\ \text{orthonormal} \\ \end{matrix} \\ \end{align}$

(8)

其中，${\rm{Tr}}\left[\cdot \right]$表示矩阵的求迹运算，式(8)表示矩阵B^TAPS主对角线各元素之和最大，根据奇异值分解理论(Singular Value Decomposition, SVD)，可得：

${\text{Tr}}\left[{{{{B}}^{\text{T}}}{{APS}}} \right] \! = \! {\text{Tr}}\left[{{{S}}{{{B}}^{\text{T}}}{{AP}}} \right] \! = \! {\text{Tr}}\left[{{{S}}{{{V}}^{\text{T}}}{{PU}}} \right]$

(9)

步骤7构造矩阵$ \hat {P}^{i} $=VU^T。

步骤8重复步骤4-步骤8，直到满足式(2)。

步骤9得到重构信号$ \hat {X} = \hat {P} \hat {S}$。

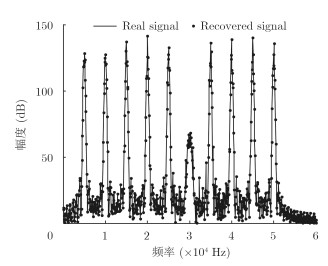
我们将信号变换到频域范围内，可以得到如图 2所示的信号原始结构和重构结果对比图，从图中可以观察出，原始信号和重构信号基本重合，且重构误差接近10^-9，因此BCS理论能够实现非合作跳频信号重构。

4 跳变参数估计 4.1 跳变频率估计

跳频信号的自相关函数及功率谱具有瞬时变化的特点，其全部能量包含在一定跳变周期内的窄带宽中，这类非平稳信号难以在时域环境下分析其特性，因此我们可以利用傅里叶变换，将信号变换到频域，以获得其全部频域信息，进而实现跳变频率估计。具体实现方法为：首先对重构跳频信号$ \hat {X} $进行快速傅里叶变换(Fast Fourier Transform, FFT)，可以得到如图 2所示的频谱图；然后对频谱图进行谱峰搜索，找到峰值所对应频率点，即为估计频率。由于信号中存在噪声，为提高估计精度，我们取信号峰值附近相邻M个点的频率平均值作为估计结果，即有

${\hat f_i} = \frac{1}{M}\sum\limits_{a = 1}^M {{{\hat f}_i}(a)}$

(10)

而峰值个数即为跳变次数，即k=K。

4.2 跳变周期估计

假设，实验中跳频信号是同步获得，则基于BCS理论可知：只有当信号长度w等于采样点个数m时，信号才能实现精确重构，式(2)的解才具有唯一性，则信号$ \; \hat {X} \; $可表示为$\hat{X}=\hat{P}\hat{S}=\left[{{{\hat{P}}}_{1}}{{{\hat{S}}}_{1}}, \cdots, \right.\left. {{{\hat{P}}}_{L}}{{{\hat{S}}}_{L}} \right]$，其中，$ \hat {S} $∈R^m×1为K阶稀疏矩阵，此时满足：

$Q = \arg \max \left( {\sum\limits_{i = 1}^m {{{\hat S}_i}} } \right)$

(11)

的值达到最大。

因此，以式(11)的计算结果作为判定条件，当Q值达到最大时，利用跳变次数k及采样点个数m求得信号的跳变周期$ \hat T_{\rm h} $=m/k。

4.3 参数估计流程

假设实验中所用到的非合作跳频信号含有高斯白噪声，则具体参数估计步骤可表述为：

步骤1计算信号$\hat {{X}}$的FFT变换，得到$\hat{X}({{\text{e}}^{\text{j}\omega }})$。

步骤2观察其频域分布图，并对$\hat{X}({{\text{e}}^{\text{j}\omega }})$进行谱峰搜索。

步骤3按照式(10)，计算得到信号的全部跳变频率$ \hat f_i $, i=1, 2, $ \cdots $, K。

步骤4观测峰值个数k。

步骤5利用观测到的峰值个数k，及实验获得的采样点个数m，根据$ \hat T_{\rm h} $=m/k可以计算出信号的跳变周期$ \hat T_{\rm h} $。

5 仿真结果及性能分析

为验证非合作跳频通信系统中，基于BCS理论的重构及跳变参数估计的有效性，现根据定义式(4)仿真得到一段含有高斯白噪声的跳频信号，信号包含1280个采样点，共发生10次跳变，跳变频率f_K={40, 15, 45, 20, 5, 35, 10, 25, 50, 30} kHz，采样频率f_s=100 kHz，跳变周期T_h=1.28 ms，起跳时刻T₀=0时刻。实验所采用的评价指标为：

${\rm{ERR}} = \frac{{{{\left\| {\hat X - X} \right\|}_2}}}{{{{\left\| X \right\|}_2}}}$

(12)

${\rm{NMSE = }}\frac{{\rm{1}}}{{{N_{{\rm{obs}}}}}}\sum\limits_{i = 1}^{{N_{{\rm{obs}}}}} {{{\left( {\frac{{{{\hat \theta }_i} - {\theta _i}}}{{{\theta _i}}}} \right)}^2}} $

(13)

其中，式(12)为信号的重构误差，式(13)为归一化平均误差(Normalized Mean Square Error, NMSE), ${\hat \theta _i}$为第i次的参数估计值，${\theta _i}$为第i次的实际参数值，N_obs为总的估计次数。

5.1 信号重构实验

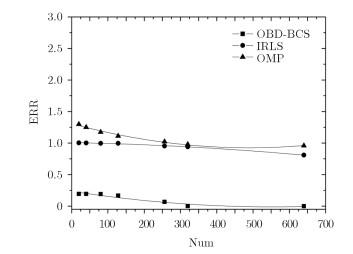
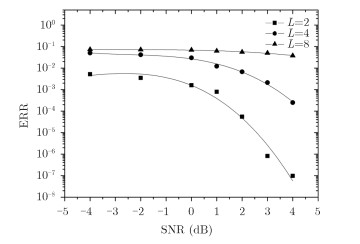
实验中，我们对比了取不同观测值时OBD-BCS, IRLS及OMP算法的重构精度，并针对OBD-BCS算法取信噪比(Signal Noise Ratio, SNR)为-5~5 dB，压缩比为L=2, L=4及L=8 3种情况进行具体分析，根据式(12)可以得到如图 3，图 4所示非合作跳频信号重构误差拟合曲线。

通过图 3中拟合曲线可以观察出，对于传统CS理论而言，由于在非合作通信系统中未知信号先验信息，导致正交基的选取存在一定偏差，因此IRLS及OMP算法的重构误差较大，而BCS理论避免了对信号先验信息的需求，因此对于非合作信号而言，BCS理论重构精度优于传统CS理论。

分析图 4中的拟合曲线可知，OBD-BCS算法的重构精度与压缩比及SNR有关。当SNR相同时，信号压缩比降低的同时，采样点数增多，重构精度逐渐增强；压缩比一定时，SNR减小会导致噪声干扰增强，重构误差增大。

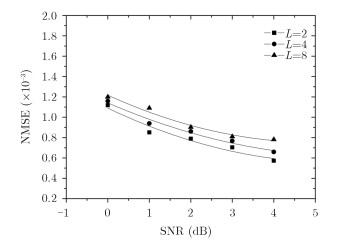
5.2 跳变频率估计实验

实验中，SNR取0~5 dB，在不同SNR下，我们针对压缩比为L=2, L=4及L=8 3种情况分别进行多次仿真实验。为了减小估计误差，我们以Au_f-Au_i≤10 dB为判定条件，其中，Au_f为峰值幅度，Au_i为第i个点的幅值。选取峰值附近M个点的频率平均值作为估计结果，并得到频率估计归一化平均误差曲线如图 5所示。

实验结果表明，SNR降低或压缩比增大，均会导致信号频率估计误差增大。由于我们求取了平均值作为频率估计值，因此在不同SNR及压缩比条件下，信号频率估计误差较为接近。

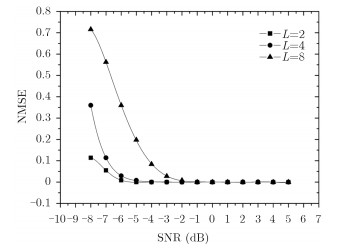
5.3 跳变周期估计实验

为了验证周期估计方法的有效性，我们比较了不同压缩比及SNR条件下的实验结果，在实验中，当连续多个采样点的幅值达到Au≥70 dB时，则视为一个峰值，即发生一次跳变；如果有不连续的采样点的幅值达到70 dB，则可视为是噪声干扰。图 6给出了压缩比为L=2, L=4及L=8, SNR为-8~5 dB时的拟合曲线。

实验数据表明，当L=2时，跳变周期估计误差在SNR=-5 dB时出现转折，当SNR≥-5 dB时，误差开始接近为0；同理当L=4及L=8时，周期估计误差分别在SNR=-4 dB及SNR=-2 dB时出现转折。通过分析实验过程及数据，可以发现这是由于跳变周期估计值受峰值个数影响所导致，当SNR较低时，受噪声干扰，信号的峰值较为杂乱，不能精准地确定峰值个数，因此会影响跳变周期的估计结果。随着信噪比增大，噪声干扰减弱，可以精确搜索出峰值个数，因此重构误差接近为0。仿真实验结果证明了盲压缩感知理论用于参数估计的可行性及有效性，适用于非合作通信系统中信号的处理。

6 结论

本文提出利用BCS理论对非合作跳频信号进行参数估计，BCS理论兼具CS理论及DL理论特性，能够有效克服稀疏表示过程中缺少信号先验信息的问题，因此能够被应用于收发双方不具备匹配协议的非合作跳频通信系统中。为了确保非合作跳频信号处理过程中BCS理论解的唯一性，通过正交基更新过程构造正交块对角矩阵，使其满足BCS理论的限制条件，并通过OBD-BCS算法实现非合作环境中信号的精确重构及参数估计。通过理论分析及仿真实验表明，BCS理论能够有效克服系统中存在的干扰，从少量的采样值中重构出原始信号结构，且不需要获得信号的先验信息。实验结果显示，随着非合作跳频信号压缩比减小及SNR的增大，噪声干扰逐渐减弱，重构及估计误差逐渐减小。