②(空军预警学院黄陂士官学校 武汉 430019)
②(Huangpi NCO School of Air Force Early Warning Academy, Wuhan 430019, China)
空时自适应处理[1, 2, 3](Space-Time Adaptive Processing,STAP)是机载相控阵雷达杂波抑制的有效技术,以空时联合为框架实现目标检测的自适应处理称为空时自适应检测处理 (Space-Time Adaptive Detection,STAD)[4],STAD同时进行杂波抑制与目标检测,通常具有恒虚警(Constant False Alarm Rate,CFAR)特性。其中广义似然比检测器(Generalized Likelihood Ratio,GLRT)[5]、自适应匹配滤波器(Adaptive Matched Filter, AMF)[6, 7]和自适应相干估计器(Adaptive Coherence Estimation,ACE)[8]是3种著名的多通道STAD检测器,可实现对匀速运动目标的有效检测。然而,随着航空技术的发展,空中目标的机动性越来越好,即目标通常具有加速度[9],使得常规STAD检测器不能直接用于机动目标检测。近年来,机动目标的检测在军事和民用领域受到了广泛关注[10, 11, 12, 13],尤其在军事领域,来袭目标往往通过机动飞行进行军事打击,对国防体系构成严重威胁,如何及时有效地实现对机动目标的检测和预警是未来雷达监视系统的一大挑战[11, 12]。因此,研究STAD检测器对机动目标的有效检测具有重要的意义。
本文考虑AMF对机动目标的检测问题。对于具有径向加速度的机动目标,其回波信号具有多普勒走动[9],则常规AMF检测器对机动目标检测时,需要进行包括多普勒1次项和多普勒2次项的匹配搜索,运算复杂度高。与此同时,AMF的检测性能与用于估计杂波协方差矩阵的独立同分布(Independent and Identically Distributed,IID)训练样本数有关[7]。文献[14]指出,为使信杂噪比损失(Signal to Clutter plus Noise Ratio Loss,SCNR Loss)[3]小于3 dB,IID训练样本数L应大于两倍的系统维数N,即$L \ge 2N$。然而现代相控阵雷达常具有成百上千的接收阵元[15],系统维数通常比较高;且机载雷达所面临的实际环境比较复杂,杂波往往具有非均匀特性[16];尤其在机载非正侧视阵雷达中,杂波具有距离依赖性[17],足够多的IID训练样本很难满足,导致检测性能不佳。因此,常规AMF检测器直接用于机动目标检测时存在运算量高以及检测性能不佳的问题,难于实际应用。
针对上述问题,本文提出一种基于修正AMF的机动目标检测方法,该方法首先采用对角加载(Diagonal Loading,DL)技术[18, 19]减少样本空间的自由度个数(Number of Degrees of Freedom, NDoF)[20],降低检测器对IID训练样本数的需求;为了减少运算量,文中通过3次相位变换(Cubic Phase Transform,CPT)[21]对机动目标加速度分离估计,以加速度估计值补偿机动目标回波的多普勒走动项之后进行积累检测,即降低了匹配搜索的维度。最后,仿真结果验证了该方法的有效性。
2 问题描述考虑阵元数为${N_{\rm{a}}}$的均匀线阵,阵元间距d = 0.5λ,λ为工作波长,1个相干处理间隔(Coherent Processing Interval,CPI)内的相干脉冲数为${N_{\rm{p}}}$;待检测单元数据x为${N_{\rm{a}}}{N_{\rm{p}}} \times 1$空时快拍矢量,则x可表示为:
| $\begin{aligned} {x} = [{x_{11}} ,& {x_{12}} ,\cdots ,{x_{1{N_{\rm{a}}}}},{x_{21}},{x_{22}},\cdots ,{x_{2{N_{\rm{a}}}}},\cdots ,\\ & {x_{{N_{\rm{p}}}1}},{x_{{N_{\rm{p}}}2}},\cdots ,{x_{{N_{\rm{p}}}{N_{\rm{a}}}}}{]^{\rm{T}}} \end{aligned}$ | (1) |
其中${[\cdot]^{\rm{T}}}$表示转置运算。对于待测单元有无目标的检测可用如下2元检测来描述[22]:
| $\left\{ {\begin{array}{*{20}{l}} {{H_0}:x = c + n}\\ {{H_1}:x = \alpha s({\varpi _m},{\vartheta _n}){\rm{ + }}c + n} \end{array}} \right.$ | (2) |
式中,假设${H_0}$表示无目标,${H_1}$表示有目标;其中c+n服从均值为0,协方差为R的复高斯分布,c和n分别表示杂波和噪声项;$\alpha = \left| \alpha \right|{{\rm e^{j\varphi }}}$为目标信号复幅度,其相位$\varphi $服从$\left[{0,2{π} } \right]$间的均匀分布;目标归一化的空时导向矢量${s}{\rm{(}} {\varpi _m},{\vartheta _n}{\rm{)}}$[3]为:
| ${s}{\rm{(}} {\varpi _m},{\vartheta _n}{\rm{)}} = {b}{\rm{(}} {\varpi _m}{\rm{)}} \otimes {a}{\rm{(}}{\vartheta _n}{\rm{)}}$ | (3) |
式中,
常规AMF检验统计量${T_{{\rm{AM}}{{\rm{F}}_{mn}}}}$为[6, 7]:
| \[{T_{{\rm{AM}}{{\rm{F}}_{mn}}}} = \frac{{{{\left| {{s^{\rm{H}}}({\varpi _m},{\rm{ }}{\vartheta _n}){{\hat R}^{ - 1}}x} \right|}^2}}}{{{s^{\rm{H}}}({\varpi _m},{\rm{ }}{\vartheta _n}){{\hat R}^{ - 1}}s({\varpi _m},{\rm{ }}{\vartheta _n})}}\mathop \gtrless \limits_{{H_0}}^{{H_1}} {\eta _{mn}}\] | (4) |
式中,x表示待测单元数据,
| ${f_{\rm{d}}} = \frac{{2v}}{\lambda } + \frac{{2ak}}{{\lambda {f_{\rm{r}}}}},\ k = 1,2,\cdots ,{N_{\rm{p}}}$ | (5) |
由式(5)可知,机动目标的多普勒频率是时变的,包括初速度引起的多普勒1次项和加速度引起的多普勒2次项,即存在多普勒走动;则机动目标时域导向矢量${b}({\varpi _m})$可表示为:
| \[\begin{array}{l} b({\varpi _m}) = \left[ {1\;\;{{\rm{e}}^{{\rm{j}}\left( {2\pi \frac{{2v}}{{\lambda {f_{\rm{r}}}}} + \pi \frac{{2a}}{{\lambda f_{\rm{r}}^2}}} \right)\;\;\; \cdots }}} \right.\\ \quad \quad \quad \quad {\left. {{{\rm{e}}^{{\rm{j}}\left( {2\pi (K - 1)\frac{{2v}}{{\lambda {f_{\rm{r}}}}} + \pi {{(K - 1)}^2}\frac{{2a}}{{\lambda f_{\rm{r}}^2}}} \right)}}} \right]^{\rm{T}}} \end{array}\] | (6) |
那么,常规AMF做机动目标检测时,需进行包括多普勒1次项以及多普勒2次项的匹配搜索,运算复杂度高。
与此同时,AMF的目标检测包括杂波抑制过程,其检测性能与用于估计杂波协方差矩阵R的IID训练样本数有关[7];为使SCNR Loss小于3 dB,训练样本数L应大于两倍的系统维数[14],此时协方差矩阵估计值$\hat {R}$为:
| $\hat R{\rm{ = }}\frac{{\rm{1}}}{L}\sum\limits_{l = 1}^L {{x_l}x_l^{\rm{H}}} $ | (7) |
式中,$ {{x}_l}$为训练样本数据,${[\cdot]^{\rm{H}}}$表示共轭转置运算。而实际中足够多的IID训练样本很难满足,即协方差矩阵估计值$ \hat {R}$存在估计误差[23, 24],致使AMF的检测性能降低。
综上所述,常规AMF用于机动目标检测时需进行联合匹配搜索,运算量高;同时,实际中足够多的训练样本很难满足,导致AMF检测性能不佳。本文考虑AMF对机动目标的检测问题,分别从降低运算量以及实现小样本下机动目标检测两个方面讨论。
3 本文算法针对常规AMF用于机动目标检测存在运算量大以及检测性能不佳的问题,本文采用分离估计机动目标加速,降低匹配搜索维度的方法减少运算量;通过对角加载技术减少样本空间自由度个数,降低检测器对训练样本数的需求,进而实现AMF在小样本下的机动目标检测。以下分别从多普勒走动补偿和对角加载AMF检测(DL-AMF)两个方面展开论述。
3.1 多普勒走动补偿本文通过CPT[21]分离估计机动目标加速度,然后以加速度估计值补偿多普勒走动项。设机动目标基带回波信号为s(k),不考虑角度信息,则可表示为:
| \[s(k) = \alpha {{\rm{e}}^{{\rm{j}}2\pi \left[ {(k - 1) \cdot \frac{{2v}}{{\lambda {f_{\rm{r}}}}} + {{(k - 1)}^2} \cdot \frac{a}{{\lambda f_{\rm{r}}^2}}} \right]}},\;k = 1,2, \cdots ,{N_{\rm{p}}}\] | (8) |
其中$\alpha $为幅度,Np表示一个CPI内的脉冲个数。对s(k)在固定点k0处做如下双线性变换[21]:
| \[\begin{array}{*{20}{l}} {g({k_0},l) = s({k_0} + l)s({k_0} - l)}\\ {\quad \quad \quad = {\alpha ^2} \cdot {{\rm{e}}^{{\rm{j}}2\pi \left[ {({k_0} - 1)\frac{{4v}}{{\lambda {f_{\rm{r}}}}} + {{({k_0} - 1)}^2}\frac{{2a}}{{\lambda f_{\rm{r}}^2}}} \right]}} \cdot {{\rm{e}}^{{\rm{j}}\frac{{4\pi a}}{{\lambda f_{\rm{r}}^2}}{l^2}}}}\\ {\quad \quad \quad = \tilde \alpha {{\rm{e}}^{{\rm{j}}\frac{{4\pi a}}{{\lambda f_{\rm{r}}^2}}{l^2}}}}\\ {\quad \quad \quad = \tilde \alpha {{\rm{e}}^{{\rm{j}}{\omega _0}{l^2}}}} \end{array}\] | (9) |
式中,$\tilde \alpha = {\alpha ^2}{{\rm{e}}^{{\rm{j}}2\pi }}[({k_0} - 1)4v/\lambda {f_{\rm{r}}} + {({k_0} - 1)^2}(2a/\lambda f_{\rm{r}}^2)]$,且在固定点${k_0}$处为常数;相位的二次项系数 ${\omega _0}$为:
| ${\omega _0} = \frac{{4{π} a}}{{\lambda {f_{\rm{r}}^2}}}$ | (10) |
式(9)表明:经双线性变换后,$g({k_0},l)$在固定点${k_0}$处的相位是关于变量l的函数,且只有2次项系数${\omega _0}$,同时${\omega _0}$与加速度a存在确定的线性关系;即通过估计${\omega _0}$,便可实现加速度a的估计。为实现${\omega _0}$的估计,可通过如下3次相位变换函数${\rm{C}}{{\rm{P}}_{\rm{s}}}{\rm{(}}{k_0},\omega )$实现[21]:
| $\begin{aligned} {\rm{C}}{{\rm{P}}_{\rm{s}}}{\rm{(}}{k_0},\omega ) & = \sum\limits_{l = 0}^{{{{N_{\rm{p}}}} \mathord{\left/ {\vphantom {{{N_{\rm{p}}}} 2}} \right. } 2} - 1} {s({k_0} + l)s({k_0} - l){{\rm e}^{ - {\rm j}\omega {l^2}}}} \\ & = \sum\limits_{l = 0}^{{{{N_{\rm{p}}}} \mathord{\left/ {\vphantom {{{N_{\rm{p}}}} 2}} \right. } 2} - 1} {\tilde \alpha {{\rm e}^{{\rm j}{\omega _0}{l^2}}}{{\rm e}^{ - {\rm j}\omega {l^2}}}} \\ & = \tilde \alpha \sum\limits_{l = 0}^{{{{N_{\rm{p}}}} \mathord{\left/ {\vphantom {{{N_{\rm{p}}}} 2}} \right. } 2} - 1} {{{\rm e}^{{\rm j}({\omega _0} - \omega ){l^2}}}} \end{aligned}$ | (11) |
其中,
| ${\hat \omega _0} = \arg \mathop {\max }\limits_\omega \left| {{\rm{C}}{{\rm{P}}_{\rm{s}}}({k_0},\omega )} \right|$ | (12) |
那么,由式(10)的线性关系,机动目标加速度的估计值
| $\hat a = \frac{{\lambda {f_{\rm{r}}^2}{{\hat \omega }_0}}}{{4{π} }}$ | (13) |
用该加速度估计值
| \[\begin{array}{*{20}{l}} {{s_{\rm{c}}}(k) = s(k){{\rm{e}}^{ - {\rm{j}}2\pi \left[ {{{(k - 1)}^2} \cdot \frac{{\hat a}}{{\lambda f_{\rm{r}}^2}}} \right]}}}\\ {\quad \quad \; = \alpha {{\rm{e}}^{{\rm{j}}2\pi \left[ {(k - 1) \cdot \frac{{2v}}{{\lambda {f_{\rm{r}}}}} + {{(k - 1)}^2} \cdot \frac{{a - \hat a}}{{\lambda f_{\rm{r}}^2}}} \right]}},}\\ {\quad \quad \quad \;k = 1,2, \cdots ,{N_{\rm{p}}}} \end{array}\] | (14) |
式中,${s_{\rm{c}}}(k)$表示补偿后的回波信号。那么,当
可以看出,多普勒走动项补偿的有效与否,直接影响AMF相干积累检测性能,为了便于分析多普勒走动项补偿的有效性,现定义如下相干积累增益(Coherent Accumulated Gain,CAG):
| ${\rm{CAG}} = \frac{1}{{{N_{\rm{p}}}}}\left| {\sum\limits_{n = 0}^{{N_{\rm{p}}} - 1} {{{\rm{e}}^{{\rm{j}}2\pi n\frac{{{a_{\rm{e}}}}}{{\lambda f_{\rm{r}}^{\rm{2}}}}}}} } \right|$ | (15) |
式中,$\left| { \cdot } \right|$表示取模运算,${N_{\rm{p}}}$表示相干积累脉冲个数,${a_{\rm{e}}} = a - \hat a$表示加速度估计误差。CAG可定性分析误差
对角加载技术作为一种简单且可有效解决训练样本不足的方法,便于工程实现。因此,本文采用对角加载技术[18, 19]减少样本空间NDoF,从而降低检测器对IID训练样本数的需求。为说明该问题,现对$N \times N$维的协方差矩阵R做如下特征分解
| $R = U\Lambda {U^{\rm{H}}} = \sum\limits_{n = 1}^N {{\lambda _n}{u_n}u_n^{\rm{H}}} $ | (16) |
其中,$\Lambda = {\rm{diag(}}{\lambda _1}{\rm{,}}{\lambda _2}{\rm{,}} \cdots ,{\lambda _N}{\rm{)}}$为$N \times N$的对角矩阵,其对角元素${\left. {{\lambda _i}} \right|_{i = 1,2,\cdots ,N}}$为R的特征值;特征向量矩阵为${U} = [{{u}_1} \ {{u}_2} \ \cdots \ {{u}_N}]$,其列向量${\left. {{{u}_i}} \right|_{i = 1,2,\cdots ,N}}$为特征向量。那么,最优权矢量${{w}_{{\rm{opt}}}}$可表示为[25]:
| \[\begin{array}{*{20}{l}} {{w_{{\rm{opt}}}} = \kappa {R^{ - 1}}s}\\ {\quad \quad = \tilde \kappa \left[ {s - \sum\limits_{n = 1}^N {\left( {\frac{{{\lambda _n} - {\lambda _{\min }}}}{{{\lambda _n}}}} \right)\left( {u_n^{\rm{H}}s} \right){u_n}} } \right]} \end{array}\] | (17) |
式中,$\tilde \kappa = \kappa /{\lambda _{\min }}$为归一化系数,${\lambda _{\min }}$为最小特征值,s为导向矢量。对R的特征值由大到小排列,则
| $\mathop \lambda \nolimits_1 \ge \mathop \lambda \nolimits_2 \ge \cdots \mathop \lambda \nolimits_p \gg \mathop \lambda \nolimits_{p + 1} = \cdots \mathop \lambda \nolimits_N = \mathop \sigma \nolimits^2 $ | (18) |
其中,$p$表示大特征值个数,${{\sigma
}^{2}}$表示热噪声方差。理论情况下,样本空间NDoF为$p$[20];然而当IID样本不足时,由于存在估计误差,使得估计值
DL[18, 19]可有效改善
| ${{\hat{{R}}}_{\text{d}}}=\hat{{R}}+{{\delta }^{2}}{{{I}}_{N}}$ | (19) |
其中${{{I}}_{N}}$为$N\times N$的单位矩阵。此时${{\hat{{R}}}_{\text{d}}}$的特征值为$\text{ }\!\!\{\!\!\text{ }{{\hat{\lambda }}_{1}}\text{+}{{\delta }^{2}}\text{,}{{\hat{\lambda }}_{2}}\text{+}{{\delta }^{2}}\text{,}\cdots ,{{\hat{\lambda }}_{N}}\text{+}{{\delta }^{2}}\text{ }\!\!\}\!\!\text{ }$,由于加载量${{\delta }^{2}}$远小于杂波特征值而大于热噪声功率[18],即在保持有效NDoF的同时将小特征值“压缩”到${{\delta }^{2}}$水平,从而减少了NDoF,进而降低了对训练样本的需求[27]。这里需指出的是,雷达工作在微波阶段时,其热噪声主要来自于接收机系统的内部噪声[28],而该内部噪声功率可以事先测量[29];不失一般性,本文假设热噪声功率已知。
经上述对角加载后,DL-AMF的检验统计量${{T}_{\text{DL-AM}{{\text{F}}_{mn}}}}$为:
| \[{T_{{\rm{DL - AM}}{{\rm{F}}_{mn}}}} = \frac{{{{\left| {{s^{\rm{H}}}({\varpi _m},\;{\vartheta _n})\hat R_{\rm{d}}^{ - 1}x} \right|}^2}}}{{{s^{\rm{H}}}({\varpi _m},\;{\vartheta _n})\hat R_{\rm{d}}^{ - 1}s({\varpi _m},\;{\vartheta _n})}}\] | (20) |
DL-AMF的精确统计分布比较复杂,得到解析解比较困难,文献[30]推导了DL-AMF的渐进统计分布,记$T_{\text{DL-AM}{{\text{F}}_{mn}}}^{\text{ a}}$为${{T}_{\text{DL-AM}{{\text{F}}_{mn}}}}$的近似表示[30],则
| \[T_{{\rm{DL - AM}}{{\rm{F}}_{mn}}}^{{\rm{ a}}} = \frac{{{{\left| {{s^{\rm{H}}}{\rm{(}}{\varpi _m},\;{\vartheta _n}{\rm{)}}Px} \right|}^2}}}{{{s^{\rm{H}}}{\rm{(}}{\varpi _m},\;{\vartheta _n}{\rm{)}}Ps{\rm{(}}{\varpi _m},\;{\vartheta _n}{\rm{)}}}}\] | (21) |
其中P为杂波子空间正交补空间的投影矩阵。此时,在${{{H}}_{0}}$假设下$T_{\text{DL-AM}{{\text{F}}_{mn}}}^{\text{ a}}$服从自由度为1的中心复卡方分布,即$T_{\text{DL-AM}{{\text{F}}_{mn}}}^{\text{ a}} \! \sim{\ } \! \! \! C\chi _{1}^{2}$;在${{{H}}_{1}}$假设下,$T_{\text{DL-AM}{{\text{F}}_{mn}}}^{\text{ a}}$服从自由度为1,非中心参数为$\rho $的复卡方分布,即$T_{\text{DL-AM}{{\text{F}}_{mn}}}^{\text{ a}} \! \sim \! \! \! {\ }C\chi _{1}^{2}(\rho )$,其中$\rho $为渐进输出SCNR。则对应虚警概率${{P}_{\text{FA}}}$的门限${{\eta }_{\text{DL-AM}{{\text{F}}_{mn}}}}$为:
| ${{\eta }_{\text{DL-AM}{{\text{F}}_{mn}}}}=-\ln ({{P}_{\text{FA}}})$ | (22) |
实际中,目标的多普勒和方位信息是未知的,即雷达需在离散的多普勒-角度通道进行检测,当所有通道的检验统计量大于门限时,检测到目标[31]。则该多普勒-角度多通道检验统计量r可表示为:
| $ \begin{aligned} r & = \mathop {\max }\limits_{m,n} \{ {T_{{\rm{DL - AM}}{{\rm{F}}_{mn}}}}\} \\ & = \mathop {\max }\limits_{m,n} \left\{ {\frac{{{{\left| {{{s}^{\rm{H}}}{\rm{(}} {\varpi _m},{\vartheta _n}{\rm{)}}\hat {R}_{\rm{d}}^{ - 1}{x}} \right|}^2}}}{{{{s}^{\rm{H}}}{\rm{(}} {\varpi _m},{\vartheta _n}{\rm{)}}\hat {R}_{\rm{d}}^{ - 1}{s}{\rm{(}} {\varpi _m},{\vartheta _n}{\rm{)}}}}} \right\}\mathop {\gtrless}\limits_{{H_0}}^{{H_1}} {\eta _{\rm{t}}} \end{aligned}$ | (23) |
其中${{\eta }_{\text{t}}}$为总门限。这里每一多普勒-角度通道相互独立,则虚警概率${{P}_{\text{FA}}}$为:
| $\begin{aligned} {P_{{\rm{FA}}}} = & \Pr \left\{ {\mathop {\max }\limits_{{\normalsize \scriptstyle1 \le m \le M} \atop \scriptstyle1 \le n \le N} {\Large (}T_{{\rm{DL - AM}}{{\rm{F}}_{mn}}}^{\rm{ \ a}} {\Large )} > {\eta _{\rm{t}}} {\Large |}{H_0}} \right\}\\ = & 1 - \Pr \Bigr\{ {T_{{\rm{DL - AM}}{{\rm{F}}_{11}}}^{\;{\rm{ \ a}}} \le {\eta _{\rm{t}}},T_{{\rm{DL - AM}}{{\rm{F}}_{12}}}^{\;{\rm{ \ a}}} \le {\eta _{\rm{t}}},} \\ & \left. { \cdots ,T_{{\rm{DL - AM}}{{\rm{F}}_{MN}}}^{\rm{\ a}} \le {\eta _{\rm{t}}} {\Large |}{H_0}} \right\}\\ = & 1 - \prod\limits_{n = 1}^N {\prod\limits_{m = 1}^M {\Pr \left\{ {T_{{\rm{DL - AM}}{{\rm{F}}_{mn}}}^{\rm{\ a}} \le {\eta _{\rm{t}}} {\Large |}{H_0}} \right\}} } \\ = & 1 - {(1 - {{\rm e}^{ - {\eta _{\rm{t}}}}})^{MN}} \end{aligned}$ | (24) |
那么,总门限${{\eta }_{\text{t}}}$为:
| ${{\eta }_{\text{t}}}=-\ln {\Large [}1-{{(1-{{P}_{\text{FA}}})}^{1/MN}}{\Large]}$ | (25) |
式中M和N分别表示多普勒和角度通道个数。
3.3 算法流程图本文所提算法流程如图 1所示,具体步骤包括:
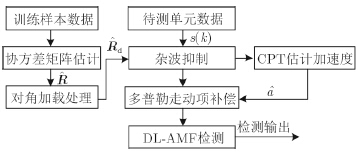 | 图 1 算法流程图 Fig. 1 Flow diagram of algorithm |
步骤1 利用参考单元样本数据估计杂波协方差矩阵$\hat{{R}}$,并对$\hat{{R}}$进行对角加载处理,得对角加载协方差矩阵${{\hat{{R}}}_{\text{d}}}$;
步骤2 对待测单元数据进行杂波抑制[3],并通过CPT分离估计机动目标加速度
步骤3 用加速度估计值
步骤4 对多普勒走动项补偿后的数据进行DL-AMF检测。
4 仿真分析为验证本文所提方法的有效性,以下分别从加速度估计、多普勒走动补偿以及目标检测几个方面进行仿真分析。
4.1 加速度估计和多普勒走动补偿仿真与分析本节仿真参数如表 1所示。
| 表 1 系统与仿真参数 Tab. 1 Parameters of system and simulation |
仿真中加速度估计的均方根误差(Root Mean Square Error,RMSE)定义为:
| $\text{RMS}{{\text{E}}_{a}}=\sqrt{\frac{1}{M}\sum\limits_{i=1}^{M}{{{(\hat{a}-a)}^{2}}}}$ | (26) |
式中
不同信噪比(Signal to Noise Ratio,SNR)下,RMSEa随样本数的变化情况如图 2所示。可以看出:RMSEa随样本数的增加而减小,当样本数大于2倍杂波大特征值个数时,RMSEa趋于稳定,说明加速度的估计相对于样本个数具有稳健性;同时,在确定样本数的情况下,当SNR增大时,RMSEa减小,说明加速度估计性能随SNR增大而得到改善,即加速度估计性能随SNR具有收敛性。
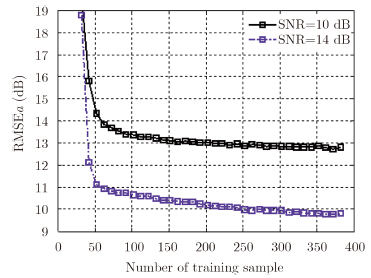 | 图 2 RMSEa随样本数变化曲线 Fig. 2 RMSEa versus number of training sample |
图 3为CAG随加速度估计误差${{a}_{\text{e}}}$的变化曲线,同时图中比较了在训练样本数为2倍杂波大特征值个数时,
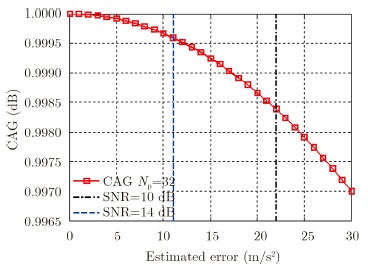 | 图 3 CAG随加速度估计误差变化曲线 Fig. 3 CAG versus estimated error of acceleration |
本部分仿真参数如表 2所示,其中系统参数与表 1一致。
| 表 2 仿真参数 Tab. 2 Parameters of simulation |
图 4中比较了样本数$L=2p$(p为杂波大特征值个数)时本文方法与样本数
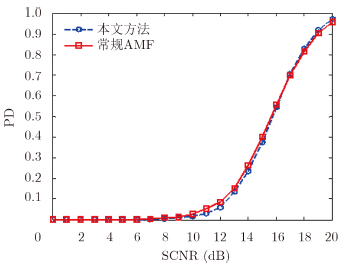 | 图 4 L=2p和L=2N时检测性能比较 Fig. 4 PD comparison when L=2p and L=2N |
为了进一步比较本文方法与常规AMF所需样本数的比较,图 5给出了SCNR Loss随样本数的变换曲线。可以看出在SCNR Loss为–3 dB时,相比于常规AMF,本文方法所需训练样本数少,这是因为本文采用了DL技术,减少了样本空间NDoF,进而降低了对训练样本数的需求。这里需指出的是,在训练样本数小于系统维数时($L<N$),协方差矩阵估计值$\hat{{R}}$为奇异矩阵,故图 5中没有给出$L<N$时常规AMF SCNR Loss变化曲线。
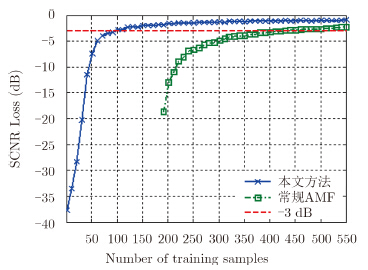 | 图 5 信杂噪比损失比较 Fig. 5 Comparison of SCNR loss |
图 6为训练样本数分别是
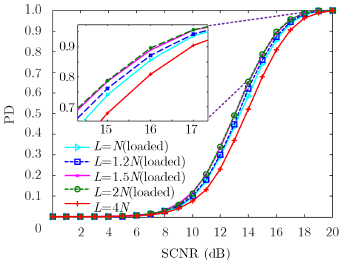 | 图 6 不同样本数时检测性能比较 Fig. 6 PD comparison under different number of training sample |
图 7为训练样本数$L=2p$时,本文方法检测门限随杂噪比(Clutter to Noise Ratio,CNR)变化曲线。图中检测门限起伏微弱,即本文方法具有CFAR特性。
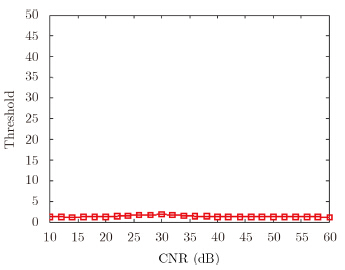 | 图 7 检测门限随CNR变化曲线 Fig. 7 Thresholds of the detector versus CNR |
本部分记1次复乘为1次运算,表 3中比较了本文方法与常规AMF方法的运算量。表中${{a}_{\text{rg}}}$和${{v}_{\text{rg}}}$分别表示加速度和速度搜索区间,
| 表 3 运算量比较 Tab. 3 Comparison of calculation |
由表 3可以看出,本文方法的运算量低于常规AMF方法的运算量。
5 结论本文提出一种基于修正自适应匹配滤波器的机动目标检测方法,该方法通过对角加载技术降低检测器对训练样本数的需求;以CPT分离估计机动目标加速度,并以估计值补偿目标信号的多普勒走动项,降低了联合匹配搜索维度;该方法加速度估计性能具有稳健性,可实现多普勒走动的有效补偿,进而可实现有效的积累检测。实验结果表明,本文方法计算量低,可实现在小样本下机动目标的有效检测,且具有CFAR特性。
| [1] | Klemm R. Principles of Space-time Adaptive Processing[M]. London: The Institution of Electrical Engineers, 2002: 87-100.( 1) 1) |
| [2] | Melvin W L. A STAP overview[J]. IEEE Aerospace and Electronic Systems Magazine, 2004, 19(1): 19-35.( 1) 1) |
| [3] | Ward J. Space-time adaptive processing for airborne radar[R]. Technical Report 1015, MIT Lincoln Laboratory, 1994: 1-79.( 4) 4) |
| [4] | 王永良, 刘维建, 谢文冲, 等. 机载雷达空时自适应检测方法研究进展[J]. 雷达学报, 2014, 3(2): 201-207. Wang Y L, Liu W J, Xie W C, et al.. Research progress of space-time adaptive detection for airborne radar[J]. Journal of Radars, 2014, 3(2): 201-207.(  1) 1) |
| [5] | Kelly E J. An adaptive detection algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 1986, 22(1): 115-127.( 1) 1) |
| [6] | Chen W S and Reed I S. A new CFAR detection test for radar[J]. Digital Signal Processing, 1991, 1(4): 198-214.( 2) 2) |
| [7] | Robey F C, Fuhrmann D R, Kelly E J, et al.. A CFAR adaptive matched filter detector[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(1): 208-216.( 4) 4) |
| [8] | Kraut S and Scharf L L. The CFAR adaptive subspace detector is a scale-invariant GLRT[J]. IEEE Transactions on Signal Processing, 1999, 47(9): 2538-2541.( 1) 1) |
| [9] | Li X L, Cui G L, Yi W, et al.. Coherent integration for maneuvering target detection based on Radon-Lv's distribution[J]. IEEE Signal Processing Letters, 2015, 22(9): 1467-1471.( 3) 3) |
| [10] | Ru J F, Jilkov V P, Li X R, et al.. Detection of target maneuver onset[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 536-554.( 1) 1) |
| [11] | Zhu S Q, Liao G S, Yang D, et al.. A new method for radar high-speed maneuvering weak target detection and imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(7): 1175-1179.( 2) 2) |
| [12] | Chen X L, Huang Y, Liu N B, et al.. Radon-fractional ambiguity function-based detection method of low-observable maneuvering target[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(2): 815-833.( 2) 2) |
| [13] | Winters D W. Target motion and high range resolution profile generation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(3): 2140-2153.( 1) 1) |
| [14] | Reed I S, Mallett J D, and Brennan L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, 10(6): 853-863.( 2) 2) |
| [15] | Güvensen G M, Candan C, Orguner U, et al.. On generalized eigenvector space for target detection in reduced dimensions[C]. Proceedings of the IEEE International Radar Conference, Arlington VA, USA, 2015: 1316-1321.( 1) 1) |
| [16] | Melvin W L. Space-time adaptive radar performance in heterogeneous clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 621-633.( 1) 1) |
| [17] | 同亚龙, 王彤, 文才, 等. 一种稳健的机载非正侧视阵雷达杂波抑制方法[J]. 电子与信息学报, 2015, 37(5): 1044-1050. Tong Y L, Wang T, Wen C, et al.. A robust clutter suppression method for airborne non-sidelooking radar[J]. Journal of Electronics & Information Technology, 2015, 37(5): 1044-1050.(  1) 1) |
| [18] | Carlson B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1988, 24(4): 397-401.( 5) 5) |
| [19] | Guerci J R and Bergin J S. Principal components, covariance matrix tapers, and the subspace leakage problem[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(1): 152-162.( 3) 3) |
| [20] | Wu Y, Tang J, and Peng Y N. On the essence of knowledge-aided clutter covariance estimate and its convergence[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(1): 569-585.( 2) 2) |
| [21] | O'shea P. A fast algorithm for estimating the parameters of a quadratic FM signal[J]. IEEE Transactions on Signal Processing, 2004, 52(2): 385-393.( 5) 5) |
| [22] | Reed I S, Gau Y L, and Truong T K. CFAR detection and estimation for STAP radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(3): 722-735.( 1) 1) |
| [23] | Mestre X. Improved estimation of eigenvalues and eigenvectors of covariance matrices using their sample estimations[J]. IEEE Transactions on Information Theory, 2008, 54(11): 5113-5129.( 1) 1) |
| [24] | Wang Y L, Liu W J, Xie W C, et al.. Reduced-rank space-time adaptive detection for airborne radar[J]. Science China Information Sciences, 2014, 57: 082310.( 1) 1) |
| [25] | Guerci J R. Space-time Adaptive Processing for Radar[M]. London: Artech House, 2003: 51-72.( 1) 1) |
| [26] | Benaych Georges F and Nadakuditi R R. The eigenvalues and eigenvectors of finite, low rank perturbations of large random matrices[J]. Advances in Mathematics, 2011, 227(1): 494-521.( 1) 1) |
| [27] | Hiemstra J D. Robust implementations of the multistage wiener filter[D]. [Ph.D. dissertation], Virginia Polytechnic Institute and State University, 2003.( 1) 1) |
| [28] | Skolnik M I. Radar Handbook[M]. New York: McGraw-Hill, 1990.( 1) 1) |
| [29] | Gerlach K and Picciolo M L. Airborne/spacebased radar STAP using a structured covariance matrix[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(1): 269-281.( 1) 1) |
| [30] | 刘维建, 谢文冲, 王永良. 基于对角加载的自适应匹配滤波器和自适应相干估计器[J]. 系统工程与电子技术, 2013, 35(3): 463-468. Liu W J, Xie W C, and Wang Y L. AMF and ACE detectors based on diagonal loading[J]. Systems Engineering and Electronics, 2013, 35(3): 463-468.(  2) 2) |
| [31] | Gau Y L. CFAR detection algorithm for STAP airborne radar[D]. [Ph.D. dissertation], University of Southern California, 1996.( 1) 1) |
 0, Vol. 0
0, Vol. 0
