②(中国科学院大学 北京 100039)
②(University of Chinese Academy of Sciences, Beijing 100039, China)
合成孔径雷达(SAR)依靠雷达平台沿固定航线的前向运动形成合成孔径,完成对静止目标的成像。经过几十年的研究,静止目标成像的技术已十分成熟[1, 2],对运动目标成像[3, 4]是合成孔径雷达的一个新发展。目标的运动导致其在常规SAR图像中是移位和散焦的,因此为获得高质量的成像结果,必须对运动目标进行正确的聚焦成像。
常用的运动目标成像方法是限制运动目标的距离徙动不超过一个分辨单元[5, 6],这将导致在对快速运动目标进行成像时,分辨率受到极大的限制;或采用额外的处理方法[7, 8]进行运动目标的距离徙动校正,然后再估计相位误差进行重新聚焦;文献[9]提出了采用Keystone变换对运动目标的线性距离徙动部分进行校正,其缺点是没有与静止场景成像结果融合。随着ISAR技术的发展,针对舰船目标出现了大量SAR与ISAR技术结合的方法[10, 11, 12, 13],其主要思想是从SAR图像中判断出舰船位置,继而提取出包含舰船数据的脉冲信号做ISAR处理。ISAR利用舰船自身运动获得方位向分辨率,而观测角度和舰船运动在秒级时间内是不断变化的,这使得ISAR图像的识别存在一定的难度[14]。而对SAR成像结果进行舰船检测的技术已经相对成熟,可见利用常规SAR方法对运动舰船进行成像是十分必要的。
本文主要针对单通道SAR回波信号,根据多普勒参数与目标运动参数的关系,提出了一套海面运动舰船成像流程。根据多普勒中心频率与舰船径向速度的关系,利用包络对齐方法得到两者精确的估计值;将自适应迭代的思想应用于最小熵方法,估计舰船的调频率值;综合多普勒参数,对舰船进行距离徙动校正和压缩,使得舰船既可以聚焦成像,又可以成像在正确的位置。本文所涉及的均为较成熟的算法,并针对特定的舰船场景对其做出了适当的改进,成像效果明显优于SAR处理结果。本文结构安排如下:第2节根据建立的几何模型,分析了运动目标回波信号;第3节详细论述了多普勒参数与运动参数的估计方法;第4节给出了运动目标成像流程,详细分析了距离徙动校正的过程;第5节给出了仿真与实测数据的成像结果及分析,验证了该方法的有效性;第6节对全文进行了总结。
2 运动目标信号分析SAR回波信号经过检波和距离压缩后,可表示为:
| \[s(t,\tau ) = \sigma \exp \left( { - {\rm{j2}}\pi {f_{\rm{0}}}\tau } \right)\] | (1) |
图 1是斜距平面内正侧视SAR的几何关系图。平台以速度va沿航迹方向飞行,在t = 0时刻,位于O点。将运动目标的速度分解为距离分量vy和方位分量vx,在t = 0时刻,运动目标位于P点,其坐标为(x0,y0)。
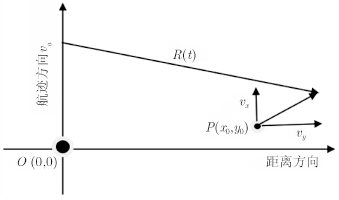 | 图 1 SAR几何模型 Fig. 1 The geometric model of SAR |
根据以上几何关系,可得在t时刻,目标到平台的距离为:
| \[R(t) = \sqrt {{{({y_0} + {v_y}t)}^2} + {{({x_0} + {v_x}t - {v_{\rm{a}}}t)}^2}} \] | (2) |
假设tc为运动目标P的波束中心照射时刻,则${t_{\rm{c}}} = \frac{{{x_0}}}{{{v_{\rm{a}}} - {v_x}}}$。而tc时刻目标的距离向位置为:yc=y0+vytc。将式(2)进行泰勒展开,忽略高次项可得:
| \[\begin{array}{*{20}{l}} {R(t - {t_{\rm{c}}}) = {y_{\rm{c}}} + {v_y}(t - {t_{\rm{c}}})}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{{{{({v_{\rm{a}}} - {v_x})}^2}}}{{2{y_{\rm{c}}}}}{{(t - {t_{\rm{c}}})}^2}} \end{array}\] | (3) |
将$\tau = \frac{{2R(t - {t_{\rm c}})}}{\rm{c}}$和式(3)代入式(1)后整理可得:
| \[\begin{array}{*{20}{l}} {s\left( {t - {t_{\rm{c}}},\tau } \right) = \sigma \exp \left\{ { - {\rm{j}}\frac{{{\rm{4}}\pi }}{\lambda }\left[{{y_{\rm{c}}} + {v_y}\left( {t - {t_{\rm{c}}}} \right)} \right.} \right.}\\ {\left. {\left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{{{{\left( {{v_{\rm{a}}} - {v_x}} \right)}^2}}}{{2{y_{\rm{c}}}}}{{\left( {t - {t_{\rm{c}}}} \right)}^2}} \right]} \right\}} \end{array}\] | (4) |
根据式(4)的相位项可得运动目标的多普勒频率为:
| \[f = - \frac{{\rm{2}}}{\lambda }\left[{{v_y} + \frac{{{{({v_{\rm{a}}} - {v_x})}^2}}}{{{y_{\rm{c}}}}}(t - {t_{\rm{c}}})} \right]\] | (5) |
由式(5)可以看出,径向速度影响运动目标的多普勒中心频率,其偏移量为:$\Delta f = - \frac{2}{\lambda }{v_y}$,这将导致运动目标的方位位置偏移,偏移量为$\Delta x = - \frac{{{v_y}{y_{\rm c}}}}{{{v_ {\rm a}}}}$。而运动目标的方位向速度影响多普勒调频率,其调频率变为:${f_{\rm tr}} = \frac{{ - 2}}{{\lambda {y_{\rm c}}}}{({v_{\rm{a}}} - {v_x})^2}$ ,多普勒调频率决定图像聚焦效果,调频率的微小误差都会使SAR图像散焦,分辨率下降,如果用静止目标的多普勒调频率对运动目标聚焦成像,必然会导致运动目标散焦。
3 多普勒参数与运动目标速度的估计根据上一节的讨论可知,运动目标的径向速度导致其多普勒中心频率发生偏移,从而影响其方位向位置,方位向速度改变了多普勒调频率,致使动目标图像散焦。若要得到高质量的运动目标成像结果,需要对影响成像效果的因素进行估计,并在成像过程中加以纠正。
3.1 多普勒中心频率与径向速度的估计多普勒中心频率的估计方法较多[15, 16],比如杂波锁定法、自相关函数法等。传统基于方位谱分析的方法只能获得多普勒中心在基带内的映射值,当多普勒中心超过PRF的一半时,便会产生多普勒模糊问题。能否正确地解多普勒模糊对于SAR成像至为关键,成像处理中的距离徙动校正以及方位聚焦要补偿的高次相位项都与绝对多普勒中心有关。因此为了得到高质量SAR图像,需要对多普勒模糊数进行求解,即寻找一个整数M,使得
| \[M = {\rm{round}}\left( {\frac{{{f_{\rm{e}}} - {{f'}_{{\rm{tc}}}}}}{{{\rm{PRF}}}}} \right)\] | (6) |
| \[{f_{{\rm{tc}}}} = {f'_{{\rm{tc}}}} + M \times {\rm{PRF}}\] | (7) |
多普勒模糊数的求取方法大多基于统计直方图,不适合运动目标。本文借鉴文献[17]估计静止场景多普勒中心的思想,提出了一种估计运动目标多普勒中心的方法。
根据式(3)可得运动目标的距离徙动量为:
| \[\Delta R(t - {t_{\rm{c}}}) = {v_y}(t - {t_{\rm{c}}}) + \frac{{{{({v_{\rm{a}}} - {v_x})}^2}}}{{2{y_{\rm{c}}}}}{(t - {t_{\rm{c}}})^2}\] | (8) |
对于每一个方位单元,距离向具有不同的偏移量。利用包络对齐方法[18, 19, 20]可得到该偏移量,将得到的数据进行曲线拟合,便可以得到运动目标径向速度的估计值。由于在海面背景中,运动目标具有高信杂比和高信噪比,因此,采取较为简单的互相关方法便可得到运动目标的偏移量。通过估计得到径向速度,求得不模糊的多普勒中心${f_{\rm e}} \approx 2{v_y}/\lambda $,代入式(6)求得多普勒模糊数,根据式(7)便可得到准确的多普勒中心频率。
3.2 多普勒调频率与方位向速度的估计运动目标的方位向速度影响信号的多普勒调频率,进而导致成像质量严重下降,并且在求取多普勒中心频率模糊数时,也需要对多普勒调频率进行估计。其估计方法也较为成熟[21, 22],主要包括图像偏移法、时频分析法、最小熵法、分数阶傅里叶变换法。本文借助文献[23]提出的思想,提出一种改进的最小熵法估计多普勒调频率。
对场景中心距离单元进行最小熵搜索,不同调频率的熵如图 2所示。由图可知,在多普勒调频率真值附近,熵的值是急剧收敛的,因此可以采用一种自适应搜索的方法代替大范围寻找,以获得较快的速度。
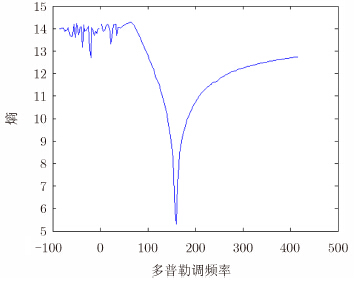 | 图 2 不同调频率对应的熵 Fig. 2 The entropy of different Doppler frequency rate |
图 3是自适应搜索方法的流程图,其中K为调频率,初始化步长D设置为32,权衡计算效率与计算精度,当步长D小于0.1时,停止迭代,输出K。如果想要达到更好的聚焦效果,可以适当减小步长最小值,以增加迭代过程,搜索到更加精确的调频率。从流程图中可以看出,该方法只能得到极小值,无法得到最小值,因此K0的选择需慎重处理,根据图 2可得,若K0选值过小,很有可能获得一个错误的极小值。根据调频率与方位向速度的关系,可得到方位速度的估计值为${v_x} = {v_{\rm{a}}} - \sqrt { - {f_{\rm tr}} \cdot \lambda \cdot {y_{\rm c}}/2} $。
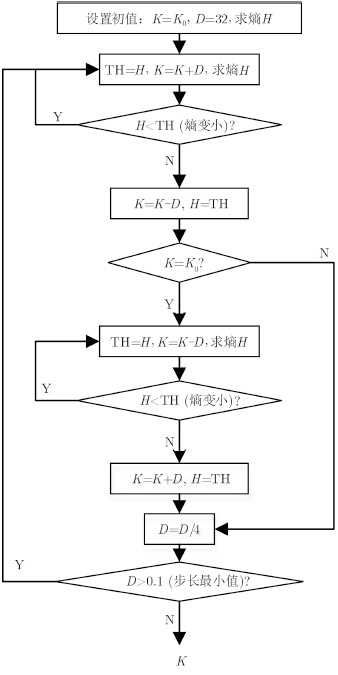 | 图 3 调频率估计流程 Fig. 3 Flow chart of Doppler frequency rate estimation |
本文采用正侧视RD算法对回波信号进行处理,主要包括3部分:距离向压缩、距离徙动校正、方位向压缩。根据第2节的分析,运动目标回波信号距离向的压缩与静止目标没有区别;方位向压缩使目标聚焦在其波束中心穿越时刻的位置,只需要与匹配滤波器相乘后变换回时域即可;下面重点介绍距离徙动部分。
距离压缩后,需进行徙动校正,此时信号在时域表现为同一距离不同方位上目标的徙动轨迹相互重叠,因此距离徙动一般在频域进行校正。图 4可以看出,在距离多普勒域,根据距离徙动曲线,便可将距离徙动校正。但目标的运动,使其距离徙动曲线发生了一定的变化。
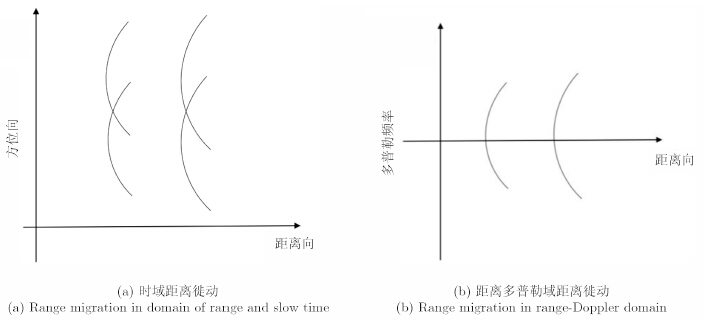 | 图 4 距离徙动 Fig. 4 Range migration |
根据方位向的时频关系$t = - \frac{{\lambda {y_{\rm{c}}}}}{{2{{({v_{\rm{a}}} - {v_x})}^2}}}{f_{\rm{a}}}$,可得运动目标的距离徙动量为:
| \[\begin{array}{*{20}{l}} {\Delta {R_t}({f_{\rm{a}}}) = \frac{{{\lambda ^2}{y_{\rm{c}}}}}{{{\rm{8}}{{({v_{\rm{a}}} - {v_x})}^2}}}f_{\rm{a}}^2 - \frac{{\lambda {y_{\rm{c}}}{v_y}}}{{{\rm{2}}{{({v_{\rm{a}}} - {v_x})}^2}}}{f_{\rm{a}}}}\\ {\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{{\lambda ^2}{y_{\rm{c}}}}}{{{\rm{8}}{{({v_{\rm{a}}} - {v_x})}^2}}}f_{\rm{a}}^2 - \frac{{\lambda {y_{\rm{c}}}{v_y}}}{{{\rm{2}}{{({v_{\rm{a}}} - {v_x})}^2}}}{f_{\rm{a}}}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \frac{{{y_{\rm{c}}}{v_y}^2}}{{2{{({v_{\rm{a}}} - {v_x})}^2}}} - \frac{{{y_{\rm{c}}}{v_y}^2}}{{2{{({v_{\rm{a}}} - {v_x})}^2}}}}\\ {\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{{\lambda ^2}{y_{\rm{c}}}}}{{8{{({v_{\rm{a}}} - {v_x})}^2}}}{{({f_{\rm{a}}} - {f_{{\rm{tc}}}})}^2} - \frac{{{y_{\rm{c}}}v_{\rm{y}}^2}}{{2{{({v_{\rm{a}}} - {v_x})}^2}}}} \end{array}\] | (9) |
其中运动目标的多普勒中心频率、径向速度和方位向速度已在第3节介绍的方法中估计得到。因此,只需对根据式(9)所示的距离徙动曲线对整个频率范围做校正。
5 仿真与实测数据成像结果及分析为验证本文提出的方法,本节给出了仿真结果,并对其进行分析。仿真参数见表 1所示。
| 表 1 仿真参数 Tab. 1 Simulation parameters |
通过点目标仿真观察成像质量,图 5为径向速度4 m/s、方位向速度9 m/s的点目标距离向和方位向的剖面图。
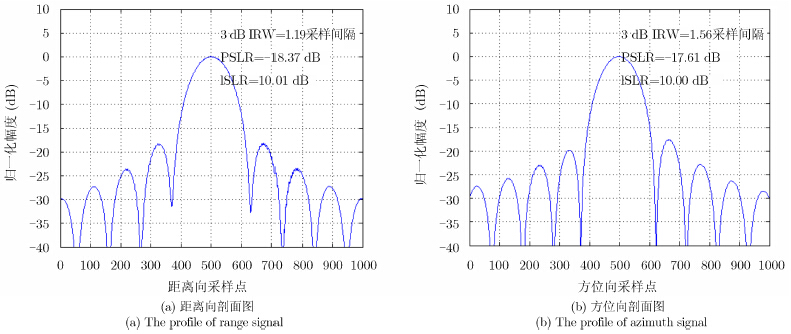 | 图 5 点目标信号质量分析 Fig. 5 Quality analysis of point target |
由于孔径加权和成像处理过程中加窗的原因,旁瓣受到抑制,3 dB IRW有所展宽,峰值旁瓣比也低于线性调频信号正常处理后的-13 dB,而积分旁瓣比影响不是很大。由此可见,该方法可以得到高质量的成像结果。
仿真场景设置为模拟的海面,场景中有一条运动的舰船。图 6(a)为参考的静止舰船,其他3幅均为以一定速度行驶的舰船。仿真时信噪比设为10 dB,信杂比设为10 dB。
 | 图 6 本文算法成像效果 Fig. 6 The results by using this article imaging algorithm |
表 2列出了成像过程中估计的运动参数及成像后舰船的位置,表中速度单位为m/s,位置单位为m,且真实位置与成像位置均为舰船质心的位置。
| 表 2 动目标的参数估计结果 Tab. 2 The estimation results of moving target parameters |
图 7为实测数据的处理结果,横向为距离向,纵向为方位向,红色方框内为传统Range Doppler Algorithm (RDA)得到的舰船成像结果,可以看到明显的徙动,处理过程中只校正了载机运动带来的徙动,忽略了目标运动的影响,使得成像结果中舰船航向发生改变,成像模糊,而且其位置没有成像在水纹交汇处。图中黄色方框内为本文提出的方法的成像结果,对比可以看出,距离徙动得到了校正,方位向得到了较好的压缩效果。可见本文提出的成像流程在运动舰船处理中明显优于传统RDA方法。
 | 图 7 实测数据处理结果 Fig. 7 The imaging of measured data |
将本文方法的成像舰船放在传统方法得到的结果图上,可见,舰船位置位于水纹交汇处。但由于舰船速度的存在,使得其成像中心时刻的位置偏离了静止的水纹交汇的位置。假设静止目标的合成孔径时间为T,运动舰船存在方位向速度,故其合成孔径时间为T+Dt,根据成像理论,目标最终的成像位置为其多普勒中心时刻位置,因此舰船的位置便偏移了△t/2时间的行程。由此可见,该偏移量的存在是必然存在的。
6 结论通过仿真与实测数据的成像结果可以看出,该方法不仅可以完成舰船的聚焦成像,还可以将其成像在其波束中心时刻的位置。本文采用的成像方法及参数估计的方法适合单个运动目标的情况,当场景中存在多个运动目标或静止目标时,需要提取出运动目标的信号单独处理。其基本思路是:利用常规SAR方法得到整个场景的成像结果,然后检测出需要单独处理舰船信号,最后根据成像算法反推其回波信号。其次,针对舰船旋转及其他运动方式的成像,将后续研究。再次,文中所用方法是基于SAR理论的,当舰船静止时,同样可以获得较好成像效果。最后,通过多组实测数据的处理,可以验证利用本文提出的运动参数估计方法,结合成像流程,可以对部分运动舰船获得较好的成像效果。
| [1] | Ausherman D A, Kozma A, Walker J L, et al. Developments in radar imaging[J]. IEEE Transactions on Aerospace and Electronic Systems, 1984, AES-20(4): 363-400.( 1) 1) |
| [2] | 张澄波. 综合孔径雷达: 原理、系统分析与应用[M]. 北京: 科学出版社, 1989. Zhang Cheng-bo. Synthetic Aperture Radar: Theory, System Analysis and Application[M]. Beijing: Science Press, 1989.( 1) 1) |
| [3] | Chen V C and Baolun L. Hybird SAR/ISAR for distributed ISAR imaging of moving targerts[C]. 2015 IEEE Radar Conference (RadarCon), Arlington, 2015: 0658-0663.( 1) 1) |
| [4] | Noviellp C, Fomaro G, and Martorella M. Focused SAR image formation of moving targets based on Doppler parameter estimation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(6): 3460-3470.( 1) 1) |
| [5] | Freeman A and Currie A. Synthetic Aperture Radar (SAR) images of moving targets[J]. GEC Journal of Research, 1987, 17(3): 629-635.( 1) 1) |
| [6] | Raney R K. Synthetic aperture imaging radar and moving targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1971, AES-7(3): 499-505.( 1) 1) |
| [7] | Barbarossa S. Detection and imaging of moving objects with synthetic aperture radar Part 1: Optimal detection and parameter estimation theory[J]. IEE Proceedings F Radar and Signal Processing, 1992, 139(1): 79-88.( 1) 1) |
| [8] | Klemm R. Application of Space-time Adaptive Processing[M]. The Institution of Electrical Engineers, 2004.( 1) 1) |
| [9] | Perry R P, DiPietro R C, and Fante R. SAR imaging of moving targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(1): 188-200.( 1) 1) |
| [10] | 师君, 马龙, 韦顺军, 等. 基于导航数据的Ka波段InSAR成像处理与分析[J]. 雷达学报, 2014, 3(1): 19-27. Shi Jun, Ma Long, Wei Shun-jun, et al. Ka-band InSAR imaging and analysis based on IMU data[J]. Journal of Radars, 2014, 3(1): 19-27.( 1) 1) |
| [11] | Martorella M, Pastina D, Berizzi F, et al. Spaceborne radar imaging of maritime moving targets with the Cosmo-SkyMed SAR system[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(7): 2797-2810.( 1) 1) |
| [12] | 汪玲, 朱岱寅, 朱兆达. 基于SAR实测数据的舰船成像研究[J]. 电子与信息学报, 2007, 29(2): 401-404. Wang Ling, Zhu Dai-yin, and Zhu Zhao-da. Research on ship imaging based on the real data of SAR[J]. Journal of Electronics & Information Technology, 2007, 29(2): 401-404.( 1) 1) |
| [13] | 邢孟道, 保铮. 外场实测数据的舰船目标ISAR成像[J]. 电子与信息学报, 2001, 23(12): 1271-1277. Xing Meng-dao and Bao Zheng. The measured data of ship ISAR imaging[J]. Journal of Electronics & Information Technology, 2001, 23(12): 1271-1277.( 1) 1) |
| [14] | Musman S, Kerr D, and Bachmann C. Automatic recognition of ISAR ship images[J]. IEEE Transactions on Aerospace & Electronic Systems, 1996, 32(4): 1392-1404.( 1) 1) |
| [15] | Bamler R. Doppler frequency estimation and the Cramer-Rao bound[J]. IEEE Transactions on Geoscience and Remote Sensing, 1991, 29(3): 385-390.( 1) 1) |
| [16] | Xue F, Chen Q, and Zhang Y. A Doppler frequency estimation algorithm based on band mismatch[C]. 2014 IEEE International Conference on Orange Technologies (ICOT), Xi’an, 2014: 77-80.( 1) 1) |
| [17] | 邢孟道, 保铮. 基于运动参数估计的SAR成像[J]. 电子学报, 2001, 29(12A): 1824-1828. Xing Meng-dao and Bao Zheng. SAR imaging motion based on parameter estimation[J]. Acta Electronica Sinica, 2001, 29(12A): 1824-1828.( 1) 1) |
| [18] | Chen C C and Candrews H. Target-Motion-Induced radar imaging[J]. IEEE Transactions on Aerospace and Electronic Systems, 1980, AES-16(1): 2-14.( 1) 1) |
| [19] | Li X, Liu G, and Ni J. Autofocusing of ISAR images based on entropy minimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(4): 1240-1252.( 1) 1) |
| [20] | Wang J and Liu X. Automatic correction of range migration in SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(2): 256-260.( 1) 1) |
| [21] | Li F K, Held D N, Curlander J C, et al. Doppler parameter estimation for spaceborne Synthetic-Aperture radars[J]. IEEE Transactions on Geoscience and Remote Sensing, 1985, 23(1): 47-56.( 1) 1) |
| [22] | Moreira J R. A new method of aircraft motion error extraction from radar raw data for real time motion compensation[J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 28(4): 620-626.( 1) 1) |
| [23] | Wang J and Liu X. SAR Minimum-Entropy autofocus using an Adaptive-Order polynomial model[J]. IEEE Geosciences and Remote Sensing Letters, 2006, 3(4): 512-516.( 1) 1) |
 2016, Vol. 5
2016, Vol. 5
