所谓的破片测量就是对弹丸爆炸后产生的大量碎片的飞行距离、速度、分布等参数进行测量。战斗部破片的初速以及初速分布是武器总体计算引战配合和杀伤概率时的必需参数[1],而得到运动状态下弹丸爆炸产生的破片参数(即动爆测量参数)更具有实战意义。战斗部破片初速主要受到炸药性能、装药与壳体质量比、装药长径比、起爆位置、壳体材料、装药约束条件等因素综合影响,十分复杂[2]。由于采用天幕靶和高速摄影机等设备完成动爆测量,存在设备架设困难等问题,因此利用雷达实现对弹丸破片的动爆测量是常用的动爆测量方法之一。
选择一种较好的信号形式对于利用雷达完成测量,实现对破片目标的分辨,是至关重要的。由于破片存在飞行前期密集后期稀疏、破片速度的变化范围较大等特点,要完成整个过程中的高速度分辨率和高距离分辨率的测量,就要求测量起始阶段距离分辨率要尽可能高,以保证在破片比较密集的情况下完成破片的区分;随着时间的推移,破片逐渐变得稀疏,数量也逐渐变少,这就要求速度分辨率尽可能高,两者是很难兼顾的。又由于破片分散的时间难以预测,因此难以采用时分信号完成测量。这就要求测量过程中,需要一个距离和速度分辨率可变的信号,或者一个具有速度多分辨和距离多分辨的信号完成测量。
目前,关于多分辨和分辨率可变的文献鲜有报道。在雷达和引信等领域,复合信号在解决各种难题方面受到广泛重视。由于伪码信号具有较好的抗干扰性能和测距性能[3, 4, 5],因此被广泛应用于复合调制信号的研究中,如:文献[6, 7, 8, 9]等充分研究了伪码信号与线性调频信号复合调制的信号形式,并分析了这种复合信号的测距、抗噪声等特性;文献[10]研究了伪码信号与正弦调频信号复合信号的参数提取问题;文献[11]研究了伪码信号与二次调频信号进行复合调制时的伪码盲估计问题等。关于复合伪码信号的研究还有很多,如:文献[12, 13, 14, 15, 16]等。这些文献的研究主要体现在复合信号的类型和特性分析上。信号的复合形式也主要集中在伪码信号的码元内或码元间复合其他信号。
本文在使用低分辨雷达实现高分辨测量的基础上,通过信号设计,提出了一种伪码族复合连续波信号,实现了雷达具有可变分辨率或多分辨率的功能,以满足靶场动爆测量的需求。在信号选择上,采用伪码与伪码复合的信号形式;在复合形式上,伪码族复合连续波信号并不是码内或码间的复合,而是基于一种载波的多种伪码调相连续波的正交组合形式。这种信号兼具伪码信号和连续波信号的优点,同时还具有多分辨率和高速度-距离2维分辨率、良好的抗干扰性能、低截获性能等特点。
2 伪码族复合连续波信号的设计伪码族复合连续波信号的整体形式如下:
| $s\left( t \right) = \sum\limits_{i = 1}^M {\sum\limits_{m = 1}^{{P_i}} {{u_i}\left( {t - m{T_i} - {h_i}{P_i}{T_i}} \right)} } \exp \left( {{\rm{j}}2\pi {f_0}t} \right)$ | (1) |
| ${{u}_{i}}\left( t-m{{T}_{i}}-{{h}_{i}}{{P}_{i}}{{T}_{i}} \right)=\left\{ \begin{array}{*{35}{l}} 1,{0 < t - m{T_i} - {h_i}{P_i}T < {T_i}} \\ 0,\text{ 其他} \\ \end{array} \right.$ | (2) |
| ${h_i} = \left[{\frac{t}{{{P_i}{T_i}}}} \right]$ | (3) |
伪码族复合连续波信号还可以表示为伪码连续波信号的组合形式,其中,Ai表示一个伪码序列。其具体形式如下所示:
| $s(t) = \sum\limits_{i = 1}^M {{s_i}\left( t \right)} = \sum\limits_{i = 1}^M {{A_i}\left( t \right)} \exp \left( {{\rm{j}}2\pi {f_0}t} \right)$ | (4) |
| ${A_i}\left( t \right) = \sum\limits_{m = 1}^{{P_i}} {{u_i}\left( {t - m{T_i} - {h_i}{P_i}{T_i}} \right)} \quad \quad \quad $ | (5) |
该信号具有如下特点:
(1) 正交性。在选择伪码序列时,要求各个序列之间正交或者准正交。
(2) 所选信号具有不同的距离分辨率$\Delta$di和多普勒分辨率$\Delta$fi(速度分辨率)。其计算过程有:$\Delta {d_i} = c{T_i}/2$和$\Delta {f_i} = {v_t}/\Delta {d_i}$。其中,vt表示相应时刻的目标速度。
3 伪码族复合连续波信号的相关特性分析为避免或降低伪码族复合连续波信号中各个子信号之间的相互干扰,本文要求所选码序列正交、准正交或相关度极弱。本节将从相关特性的角度分析伪码族复合连续波信号的干扰问题。
为了分析确定信号${x\left( t \right)}$和它时延后$x\left( {t - \tau } \right)$的相似度或差别,通常用自相关函数表示:
| ${{R}_{x}}=\int_{-\infty }^{\infty }{x\left( t \right)}x\left( t-\tau \right)\text{d}t$ | (6) |
对于本文设计的伪码族复合连续波信号,其自相关函数可以表示为:
| ${R_x} = \int_{ - \infty }^\infty {s^*\left( t \right)} s\left( {t - \tau } \right){\rm d}t$ | (7) |
将式(1)和式(4)代入式(6)中可以得到:
| $\begin{array}{*{35}{l}} {{R}_{x}} & =\int_{-\infty }^{\infty }{{{s}^{*}}\left( t \right)}s\left( t-\tau \right)\text{d}t \\ {} & =\left( \sum\limits_{i=1}^{M}{{{R}_{{{x}_{i}}{{x}_{i}}}}}+\sum\limits_{i\ne k,i=1,k=1}^{M}{{{R}_{{{x}_{i}}{{x}_{k}}}}} \right)\exp (-\text{j}2\pi {{f}_{0}}\tau ) \\ \end{array}$ | (8) |
由于码型的不同,接收、处理回波时会面临各个码型信号周期性不同的情况。考虑到更好地实现伪码族复合连续波信号各个子信号间的互相关,本文建议选取信号的长度为子信号周期的最小公倍数。接收处理时只处理一种伪码信号,因此可以任选一个码型信号,分析它与其他信号的相关情况。下面以任意两个码型的伪码序列的互相关为例进行分析,分析过程如下:
假设伪码族信号s(t)中含有M个伪码序列(A1,A2,A3,···,AM),从中任取两个信号Ai,Ak,i,k$ \in $(1,M)且i≠k。其中,Ai的码长为Pi,Ak的码长为Pk。Pi与Pk的最小公倍数为Pm。两个伪码序列的互相关用离散的形式表示,如下:
| ${R_{{A_i}{A_k}}}\left( \tau \right) = \sum\limits_{l = 0}^{{P_m} - 1} {\mathop {{A_i}}\limits^ \bullet \left( l \right)\mathop {{A_k}}\limits^ \bullet \left( {l + \tau } \right)} $ | (9) |
如果$\alpha = {{{P_m}} \mathord{\left/ {\vphantom {{{P_m}} {{P_i}}}} \right.} {{P_i}}}$,$\beta = {{{P_m}} \mathord{\left/ {\vphantom {{{P_m}} {{P_k}}}} \right.} {{P_k}}}$;则$\mathop {{A_i}}\limits^ \bullet $为$\alpha$个周期的Ai序列,$\mathop {{A_k}}\limits^ \bullet$为$\beta$个周期的Ak序列。在选取序列时,要尽量使得相关系数$\left| {{{{R_{{A_i}{A_k}}}} \mathord{\left/ {\vphantom {{{R_{{A_i}{A_k}}}} {{P_m}}}} \right.} {{P_m}}}} \right|$接近零,这样才能尽量避免相互间的干扰。
4 伪码族复合连续波信号的模糊特性分析模糊函数说明了信号的目标分辨能力、模糊度、测量精度和杂波抑制能力等问题[10, 17, 18, 19, 20]。在伪码族复合连续波信号的实际解调处理中,采用的是一种本地码与对回波信号进行解调。因此,考虑伪码族复合连续波信号的模糊特性,也就是考虑一种子信号与发射信号的互模糊特性。下面本文将对伪码族复合连续波信号的模糊函数进行分析。
假设接收通道对应的伪码序列为${A_i}(1 {≤} i {≤} M)$,其对应的子信号记为Si,那么模糊函数可用式(10)表示:
| ${\tilde X_i}\left( {\tau ,{f_{\rm{d}}}} \right) = \int_{ - \infty }^\infty {s_i^{\rm{*}}\left( t \right)s\left( {t + \tau } \right)\exp \left( {{\rm{j}}2\pi {f_{\rm{d}}}t} \right){\rm{d}}t}$ | (10) |
将式(4)代入式(10),进行展开计算,可得:
| $\begin{array}{l} {{\tilde X}_i}{\kern 1pt} \left( {\tau ,{f_{\rm{d}}}} \right)\;\: = \int_{ - \infty }^\infty {s_i^*\left( t \right)s\left( {t + \tau } \right)\exp \left( {{\rm{j}}2\pi {f_{\rm{d}}}t} \right){\rm{d}}t} = {X_{{s_i}}}\left( {\tau ,{f_{\rm{d}}}} \right)\\ + \sum\limits_{k = 1,k \ne i}^M {\int_{ - \infty }^\infty {{A_i}\left( t \right){A_k}\left( {t + \tau } \right)} } \cdot \exp \left( {{\rm{j}}2\pi {f_{\rm{d}}}t} \right)\exp \left( {{\rm{j}}2\pi {f_0}\tau } \right){\rm{d}}t \end{array}$ | (11) |
从零点位置更容易分析出信号的干扰和模糊情况:
${{f_{\rm{d}}}}$=0时,有如下结果:
| ${\tilde X_i}{\kern 1pt} {\kern 1pt} \left( {\tau ,0} \right) = {X_{{s_i}}}\left( {\tau ,0} \right) + \sum\limits_{k = 1,k \ne i}^M {R_{{x_i}{x_k}}^*\left( \tau \right)}$ | (12) |
$\tau$=0时,有:
| ${\tilde X_i}{\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {0,{f_{\rm{d}}}} \right) = {X_{{s_i}}}\left( {0,{f_{\rm{d}}}} \right) + \sum\limits_{k = 1,k \ne i}^M {\int_{ - \infty }^\infty {{A_i}\left( t \right){A_k}\left( t \right)} } \cdot \exp \left( {{\rm{j}}2\pi {f_{\rm{d}}}t} \right){\rm{d}}t$ | (13) |
$\tau$=0,${{f_{\rm{d}}}}$=0,有:
| ${\tilde X_i}{\kern 1pt} \left( {0,0} \right) = {X_{{s_i}}}\left( {0,0} \right) + \sum\limits_{k = 1,k \ne i}^M {\int_{ - \infty }^\infty {{A_i}\left( t \right){A_k}\left( t \right){\rm{d}}t} }$ | (14) |
从分析中还可以看出:子信号正交性越好,伪模糊函数越接近于其本身的模糊函数。从伪码族信号的模糊函数和伪模糊函数,以及相关性的分析结果中可以得到伪码族复合连续波信号的分辨性能、信噪比等特性,便于在实际应用中选择子信号以及分析其性能。
5 基于伪码族复合连续波信号解调的多分辨率分析伪码族复合连续波信号与通信系统中的CDMA信号类似,在发射形式上是同时发射多个正交、准正交或相干度极弱的伪码调相连续波信号,用以对目标的探测,接收到的回波信号也是这种伪码族复合连续波信号。它的多分辨率就体现在解调方式和它有多个码型的子信号上。
接收端有对应于各个伪码调相连续波信号的解调通道。解调处理时,与本地信号码型一致的回波成分将被解调,其他成分不能被解调,类似于在接收机中引入噪声和干扰。伪码族复合信号中有多少伪码调相连续波信号就要做几次解调。
由于所选码型的不同,各个伪码调相连续波信号将会具有不同的距离分辨率$\Delta {d_i}$和速度分辨率$\Delta {f_i}$。这样就使得伪码族复合连续波信号具有多分辨率的功能。对于多目标的分辨可以考虑利用各个子信号处理结果的相关程度来区分。
6 伪码族复合连续波信号多分辨率仿真分析 6.1 信号多分辨率实例分析及仿真
为了方便,本文以3种信号为例进行分析。3种伪码信号的选取如下:码钟分别为75 MHz,150 MHz,300 MHz,相应的码长为127 bit,255 bit,511 bit。3种信号对应的距离门分别为2 m,1 m,0.5 m。假设测量0时刻到t1时刻破片非常密集,破片速度的最大值为2500 m/s; t1到t2时刻破片较为密集,破片速度的最大值为2000 m/s; t2到t3时刻破片比较分散,破片速度的最大值为1500 m/s(所做假设在Ka波段,破片的最大多普勒频率约为
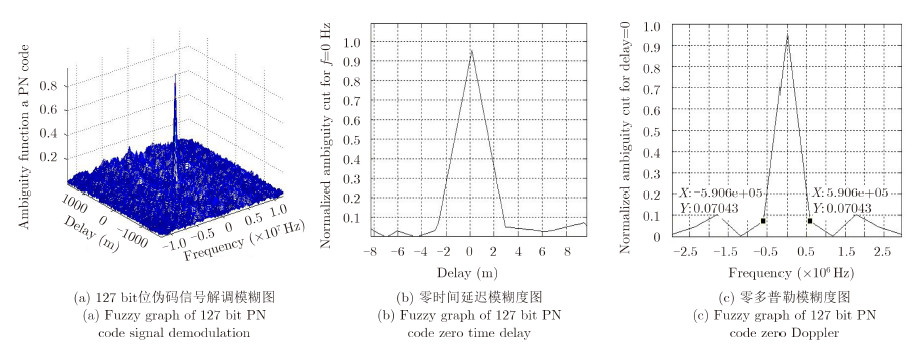
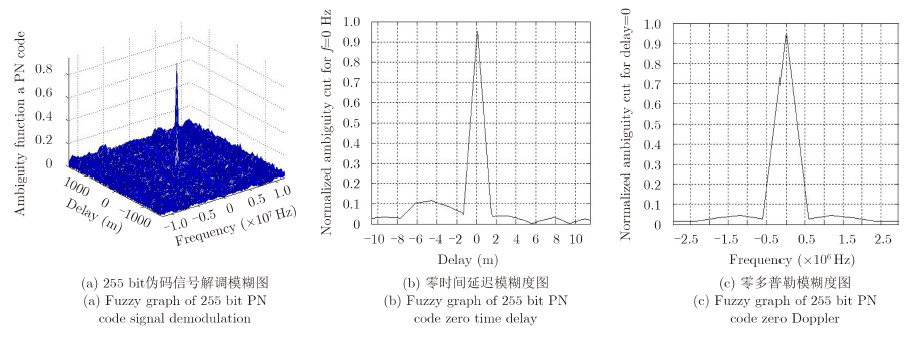
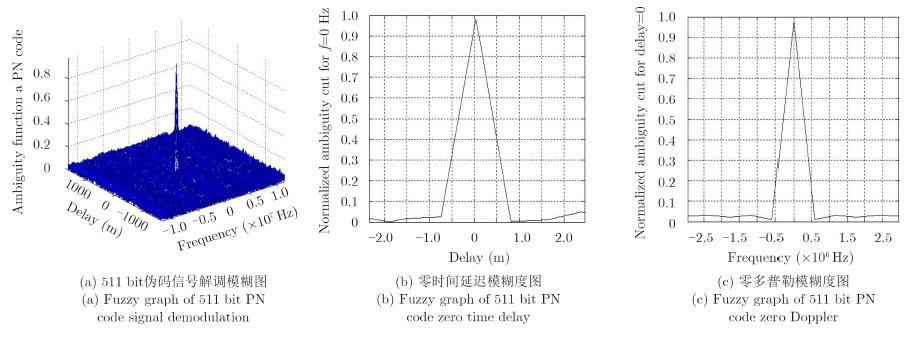
根据本文分析,在测量0时刻到t1时刻,可以采用300 MHz,511 bit码长信号的测量结果,距离分辨率为0.5 m,速度分辨率约为22 m/s; t1到t2时刻可以采用300 MHz,511 bit码长信号与150 MHz,255 bit码长信号的综合测量结果,距离分辨率约为1 m,速度分辨率约为9 m/s;在t2到t3时刻可以采用300 MHz,511 bit码长信号与75 MHz,127 bit码长信号的综合测量结果,距离分辨率约为2 m,速度分辨率约为3.3 m/s。从其模糊图看分辨特性,可见图 1,图 2,图 3。
|
图 1 127 bit伪码信号对伪码族复合连续波信号的解调分析图 Fig. 1 Analysis graph of pseudocode family signal demodulated by 127 bit PN code |
|
图 2 255 bit伪码信号对伪码族复合连续波信号的解调分析图 Fig. 2 Analysis graph of pseudocode family signal demodulated by 255 bit PN code |
|
图 3 511 bit伪码信号对伪码族复合连续波信号的解调分析图 Fig. 3 Analysis graph of pseudocode family signal demodulated by 511 bit PN code |
根据上述理论分析和仿真结果可知,伪码族复合连续波信号的模糊函数与伪码信号图钉型的模糊函数类似,因此保留了伪码信号的优点,具有良好的分辨特性。同时,采用不同的本地码信号解调,会有不同的距离和速度分辨率,能够实现多分辨的效果。3个仿真图中用的子信号周期数相同,相应的持续时间并不相同,因此截断效应的影响不同。图 1(c)中,频域旁瓣较高主要是由于仿真过程中,长周期子信号时域截断效应较大(无法做到无穷区间的仿真)造成的。总体来看,理论分析与仿真结果比较吻合。
7 总结本文针对战斗部动爆破片测量分辨难度高的问题,设计了一种伪码族复合连续波信号,该信号在具备良好的图钉型模糊函数的基础上,还具有多分辨率的特性。文中详细分析了其多分辨率特性、相关特性、模糊函数,充分说明了这种信号具有良好的距离和速度2维多分辨率的特性,能够更好地用于战斗部动爆破片测量。当然信号也有自身的一些问题:
(1) 文中关于时间节点t1,t2,t3的选择要跟据先验知识或理论分析确定初值,然后进行调整,在无法确知的情况下,适用于事后处理过程,实时处理需做进一步研究。
(2) 由于子信号间的不完全正交性会造成旁瓣或噪声功率有一定的抬高,因此本文建议选取伪码序列的数量根据实际需要确定,数目要尽量少。
(3) 本文所述的信号存在包络起伏的情况。针对这一问题,本文认为,在满足要求的情况下可以采用线性功放,也可以对伪码序列进行恒包络调制加以解决,对此不做详细介绍。
| [1] | 赵锦, 倪晋平. 光幕靶测量破片群初速的方法[J]. 测试技术学报, 2007, 21(3): 214-218. Zhao Jin and Ni Jin-ping. A Method for measuring the initial velocity of fragment group of warhead with light screens[J]. Journal of Test and Measurement Technology, 2007, 21(3): 214-218.( 1) 1) |
| [2] | 王泽, 童幼堂, 李立纬. 防空导弹战斗部破片飞散运动的仿真分析[J]. 战术导弹技术, 2010(6): 93-96. Wang Ze, Tong You-tang, and Li Li-wei. Dispersion process simulation of warhead fragments of anti-air missile[J]. Tactical Missile Technology, 2010(6): 93-96.( 1) 1) |
| [3] | 林茂庸, 柯有安. 雷达信号理论[M]. 北京: 国防工业出版社, 1981: 12-13. Lin Mao-yong and Ke You-an. Radar Signal Theory[M]. Beijing: National Defence Industry Press, 1981: 12-13.( 1) 1) |
| [4] | 涂友超, 赵惠昌, 周新刚. 伪码体制引信抗瞄准式噪声调幅干扰性能研究[J]. 南京理工大学学报(自然科学版), 2008, 32(3): 350-355. Tu You-chao, Zhao Hui-chang, and Zhou Xin-gang. Performance of anti-noise AM spot jamming of pseudo-random code fuzes[J]. Journal of Nanjing University of Science and Technology(Natural Science), 2008, 32(3): 350-355.( 1) 1) |
| [5] | 周新刚, 赵惠昌, 涂友超, 等. 基于多普勒效应的伪码调相及其与PAM复合引信的抗噪声性能分析[J]. 电子与信息学报, 2008, 30(8): 1874-1877. Zhou Xin-gang, Zhao Hui-chang, Tu You-chao, et al.. Performance analysis concerning anti-noise for pseudo-random code phase modulation and pulse amplitude modulation combined fuze based on Doppler effect[J]. Journal of Electronics & Information Technology, 2008, 30(8): 1874-1877.( 1) 1) |
| [6] | 徐庆, 徐继麟, 周先敏, 等. 线性调频-二相编码雷达信号分析[J]. 系统工程与电子技术, 2000, 22(12): 7-8, 87. Xu Qing, Xu Ji-lin, Zhou Xian-min, et al.. A discussion of performance of hybrid waveform of radar[J]. Systems Engineering and Electronics, 2000, 22(12): 7-8, 87.( 1) 1) |
| [7] | 郝新红, 白钰鹏, 崔占忠. 一种复合调制波形的测距性能分析[J]. 北京理工大学学报, 2008, 28(4): 297-301. Hao Xin-hong, Bai Yu-peng, and Cui Zhan-zhong. Analysis of range resolution for a new combined modulation waveform[J]. Transactions of Beijing Institute of Technology, 2008, 28(4): 297-301.( 1) 1) |
| [8] | 熊刚, 杨小牛, 赵惠昌. 伪码调相与线性调频复合探测系统的抗噪性能分析[J]. 兵工学报, 2008, 29(10): 1177-1182. Xiong Gang, Yang Xiao-niu, and Zhao Hui-chang. Analysis on antinoise performances of pseudo-random phase modulation and linear frequency modulation combined detecting system[J]. Acta Armamentarii, 2008, 29(10): 1177-1182.( 1) 1) |
| [9] | 向崇文, 黄宇, 王泽众, 等. 基于FrFT的线性调频-伪码调相复合调制雷达信号截获与特征提取[J]. 电讯技术, 2012, 52(9): 1486-1491. Xiang Chong-wen, Huang Yu, Wang Ze-Zhong, et al.. Interception and feature extraction of LFM-PRBC combined modulation radar signal based on FrFT[J]. Telecommunication Engineering, 2012, 52(9): 1486-1491.( 1) 1) |
| [10] | 张淑宁, 朱航, 赵惠昌, 等. 基于周期模糊函数的伪码调相与正弦调频复合引信信号参数提取技术[J]. 兵工学报, 2014, 35(5): 627-633. Zhang Shu-ning, Zhu Hang, Zhao Hui-chang, et al.. Parameter extraction technique based on periodic ambiguity for PRCPM-SFM compound fuze signal[J]. Acta Armamentarii, 2014, 35(5): 627-633.( 2) 2) |
| [11] | 何丹娜, 张天骐, 高丽, 等. 二次调频-伪码调相复合信号的伪码盲估计[J]. 电子技术应用, 2013, 39(5): 100-103. He Dan-na, Zhang Tian-qi, Gao Li, et al.. Blind estimation for PN code of reconnaissance signal combined with quadratic frequency modulated and pseudo-random binary phase code[J]. Application of Electronic Technique, 2013, 39(5): 100-103.( 1) 1) |
| [12] | 朱航, 张淑宁, 赵惠昌. 单通道多分量伪码复合线性调频信号分离及参数估计[J]. 兵工学报, 2014, 35(9): 1363-1374. Zhu Hang, Zhang Shu-ning, and Zhao Hui-chang. Single Channel source separation and parameters estimation of multi-component PRBC-LFM signal[J]. Acta Armamentarii, 2014, 35(9): 1363-1374.( 1) 1) |
| [13] | 李军伟, 张天骐, 朱洪波, 等. 基于聚类的多进制扩频伪码序列盲估计方法[J]. 科学技术与工程, 2014, 14(2): 32-36. Li Jun-wei, Zhang Tian-qi, Zhu Hong-bo, et al.. Clustering based blind estimation of PN sequences in mary spread spectrum system[J]. Science Technology and Engineering, 2014, 14(2): 32-36.( 1) 1) |
| [14] | 陈略, 唐歌实, 韩松涛, 等. 深空测控再生伪码测距技术研究[J]. 飞行器测控学报, 2012, 31(3): 11-15. Chen Lüe, Tang Ge-shi, Han Song-tao, et al.. Regenerative PN ranging technology for deep space applications[J]. Journal of Spacecraft TT&C Technology, 2012, 31(3): 11-15.( 1) 1) |
| [15] | 高述涛. 基于时延控制的伪码多普勒补偿算法[J]. 计算机工程与应用, 2014, 50(12): 198-201. Gao Shu-tao. Code Doppler compensation algorithm based on delay control[J]. Computer Engineering and Applications, 2014, 50(12): 198-201.( 1) 1) |
| [16] | 刘小强. 伪码-线性调频高精度参数估计新方法[J]. 无线电工程, 2014, 44(2): 34-37, 41. Liu Xiao-qiang. High-precision parameters estimation algorithm of combined PRBC and LFM[J]. Radio Engineering, 2014, 44(2): 34-37, 41.( 1) 1) |
| [17] | Levanon N and Freedom A. Periodic ambiguity function of CW signals with perfect periodic autocorrelation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(2): 387-395.( 1) 1) |
| [18] | Levanon N. The periodic ambiguity function-its validity and value[C]. 2010 IEEE Radar Conference, Washington DC, 2010: 204-208.( 1) 1) |
| [19] | Getz B and Levanon N. Weight effects on the periodic ambiguity function[J]. IEEE Transactions on Aerospace and Electronic Systems, 1995, 31(1): 182-193.( 1) 1) |
| [20] | Yang Y X and Niu X X. Periodic ambiguity functions of EQC-based TFHC[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 194-199.( 1) 1) |


