②(中国科学院大学 北京 100049)
②(University of Chinese Academy of Sciences, Beijing 100049, China)
无源雷达是一种本身不发射电磁波,利用广播、电视等信号作为辐射源的被动雷达系统,具有无辐射、反隐身、抗摧毁能力强、研制和维护成本低、设备体积小、机动性强等诸多优势,是国内外研究的热点[1, 2, 3, 4, 5]。无源雷达研究的核心问题是在强干扰中检测弱目标,杂波抑制是无源雷达需要解决的关键技术之一,现有的方法都是在时域进行的[6, 7, 8, 9, 10]。文献[11]提出了扩展相消批处理算法(ECA-B),该算法通过分块最小二乘(LS)处理降低了杂波子空间的维数,并在多普勒维加宽了零陷宽度。
随着数字化技术的发展,具有更稳定频率特性和更优良抗干扰能力的数字调制信号正逐步取代传统的模拟信号,其大带宽能够提高系统的分辨率,提高目标的定位精度。然而信号带宽的增大将导致回波信号信噪比进一步降低,对消阶数增加,数据率急剧增大。以DTTB信号为例,1 s时间的数据信号长度8×106,每个数据占8 B(double型),假设我们对消1000距离单元杂波,分段数为m,根据文献[11]中的公式,每一段至少需要60/m GB的内存来构造一个1000行、8×106/m 列的矩阵,复乘次数为8×1012/m+107,这时就需要分更多的段来减小存储空间和提高处理效率。
ECA-B算法对数据进行分段处理,多普勒分辨率降低,会在对消距离单元的多普勒方向产生一个零陷凹槽,而且分段数越大,凹槽越宽,凹槽深度越深。凹槽会消弱对消单元的低速目标的信噪比,随着分段数的增加,低速目标受到的影响越大,甚至会影响到高速目标的检测,这成为限制分段数的一个重要因素。同样以DTTB信号为例,假设分段数为400时,会对300多普勒单元(径向速度约为 240 km/h)内的目标产生影响。针对这个问题,还没有公开文献提出解决方法。
文献[12]提出,采用LS算法处理每块监测信号,由于该算法会抑制相消距离元内信号的零频分量,当分段数过大或者不合适时,会对目标产生调制作用,产生虚警,影响目标检测。同样分段数越大,越高速的目标受到调制。文章中提出了相应的补偿算法,但是需要真实目标的先验知识。
针对上述问题,本文提出一种频域ECA-B算法,将参考信号与回波信号利用傅里叶变换到频域进行对消。本文方法特点是通过时频转换将凹槽展宽到距离方向,利用凹槽进行杂波对消。本文方法不仅避免了由于多普勒方向的凹槽对目标的消弱,而且间隔地选择距离单元参数也大大降低了处理的运算量。该方法只会在零多普勒方向产生调制作用,不会影响动目标检测。文章先简单介绍了ECA-B算法,然后介绍了频域ECA-B算法的基本原理,并用仿真来确定参数选择,最后用仿真和实测数据验证了该方法的有效性。
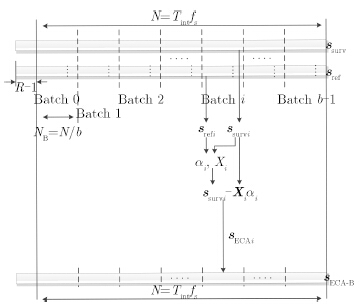
2 频域ECA-B算法 2.1 ECA-B算法介绍ECA算法就是利用最小二乘(LS)估计出多径杂波信号,然后从回波信号中减去杂波信号,从而去除杂波旁瓣的影响,凸显出目标。ECA-B算法是为了提高计算效率提出的一种分块的ECA算法。ECA-B算法的原理如图 1所示,其中N为数据长度,NB为每段的长度,i=0,1,…,b-1为分段数,R为对消的距离单元,第i段参考、回波信号表达式:
| \[{s_{{\rm{surv}}i}} = {[{s_{{\rm{surv}}}}(i{N_{\rm{B}}}){\mkern 1mu} {\kern 1pt} {\mkern 1mu} {\kern 1pt} {s_{{\rm{surv}}}}(i{N_{\rm{B}}} + 1) \cdots {s_{{\rm{surv}}}}((i + 1){N_{\rm{B}}} - 1)]^{\rm{T}}}\] | (1) |
| \[{s_{{\rm{ref}}i}} = {[{s_{{\rm{ref}}}}(i{N_{\rm{B}}} - R + 1)\;\;{s_{{\rm{ref}}}}(i{N_{\rm{B}}} - R) \cdots {s_{{\rm{ref}}}}((i + 1){N_{\rm{B}}} - 1)]^{\rm{T}}}\] | (2) |
| \[{s_{{\rm{ECA}}i}}{\rm{ = }}{s_{{\rm{surv}}i}} - {X_i}{\alpha _i}\] | (3) |
| \[{\alpha _i} = {(X_i^{\rm{H}}{X_i})^{ - 1}}X_i^{\rm{H}}{s_{{\rm{surv}}i}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \] | (4) |
| \[{X_i} = B[{s_{{\rm{ref}}i}}(n)\;\;{s_{{\rm{ref}}i}}(n - 1)\; \cdots \;{s_{{\rm{ref}}i}}(n - R + 1)]\quad \] | (5) |
| \[ B = {\left\{ {{b_{ij}}} \right\}_{i = 1,\cdots {N_B};\;j = 1,\cdots ,\;{N_B} + R - 1}},\quad {b_{ij}} = \{ _{0,\;{\rm{otherwise}}}^{1,\;i = j - R{\rm{ + }}1}\] | (6) |
 | 图 1 ECA-B算法框图 Fig. 1 Sketch of ECA-B approach |
假设参考信号refr(t)=s(t),回波信号${\rm{echo}}(t) = s(t - {\tau _1}){{\rm{e}}^{{\rm{j}}2\pi {f_1}t}}$。分别对其进行傅里叶变换得到:
| \[{\rm{Refr}}(f) = {\rm{FFT}}\left\{ {{\rm{refr}}(t)} \right\} = S(f)\quad \quad \quad \quad \quad \quad \quad \quad \] | (7) |
| \[{\rm{Echo}}(f) = {\rm{FFT}}\left\{ {{\rm{echo}}(t)} \right\} = {{\rm{e}}^{{\rm{j}}2\pi {\tau _1}{f_1}}}S(f - {f_1}){{\rm{e}}^{ - {\rm{j}}2\pi {\tau _1}f}}\] | (8) |
对于零多普勒的多径杂波${f_1}{\rm{ = }}0$,则上述公式变为:
| \[{\rm{Refr}}(f) = S(f)\quad \quad \quad \;\] | (9) |
| \[{\rm{Echo}}(f) = S(f){{\rm{e}}^{ - {\rm{j}}2\pi {\tau _1}f}}\] | (10) |
通过时频对比发现,在频域同样可以利用ECA-B算法进行杂波对消,其中时域的多普勒单元变为频域的距离单元,时域的距离单元变为频域的多普勒单元的相反数,也就是说当我们要对消$({\tau _1},{f_1})$距离多普勒的杂波时,在频域需要对消$({f_1},- {\tau _1})$ 单元的杂波。利用这个原理将多普勒方向的凹槽展宽利用到距离方向,该方法具体实现框图如图 2。
 | 图 2 频域ECA-B实现框图 Fig. 2 Sketch of ECA-B approach |
频域ECA-B方法虽然多了FFT与IFFT这两个步骤,但是该方法会带来以下优点:
(1) 我们将原来的多普勒方向的凹槽展宽利用到距离方向,这样在距离方向就不需要逐个距离单元的对消,而是可以每隔一定的距离单元对消一个单元,这样就可以极大地减小子空间维数,减小计算量。
(2) 该方法不仅避免了由于多普勒方向的凹槽展宽对对消单元内的低速目标的消弱,而且还会对零多普勒的更远的距离单元的杂波产生一定的抑制作用。
(3) ECA-B算法由于分段不合适,会在多普勒方向对目标和杂波产生调制,从而出现虚警,而本文方法只会在零多普勒的距离方向产生调制,对于动目标检测不会带来影响。
2.3 参数选择ECA-B算法分段由于多普勒分辨率下降会导致多普勒方向的零陷凹槽,随着分段数的增多凹槽宽度越宽。本文方法的优势是利用凹槽进行对消,分段数可以根据硬件的性能(如线程数、内存等)尽可能地选择大一些,而主要的参数是单元间隔的选择。下面利用仿真分析了分段数与凹槽之间的关系,相邻凹槽的相互影响,以便选择一个理想的参数。
为了只是观察凹槽情况,我们完全随机地生成了两个噪声信号分别作为参考信号和回波信号,对其进行ECA-B算法处理,仿真结果如图 3所示。从图 3(a)中可以看出分段数越大,凹槽展宽越宽,距离中心处越近,凹槽越深;选取不同的段数得到的凹槽宽度画成一条曲线,如图 3(b)中的蓝线所示,曲线比较接近y=3b/2,也就是说当分段数为b时,会对左右3b/4的单元产生影响。
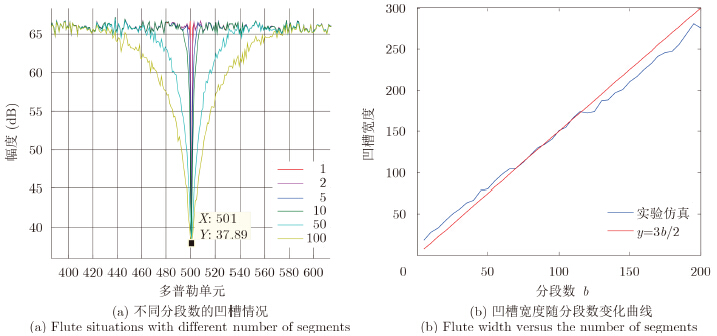 | 图 3 不同分段数凹槽情况 Fig. 3 Flute situations with different number of segments |
为了确定间隔数的选取,做了以下仿真:参考通道数据为长度为105 的高斯白噪声,回波通道数据在参考的基础上加入了0-200距离单元的多径杂波和一个弱目标,以目标的信噪比做为评判对消结果的依据,利用本文方法进行对消,分段数200,仿真结果如图 4所示。图 4(a)和图 4(b)分别为对消前情景设置和目标理想结果;图 4(c)为不同间隔下的目标的信噪比曲线,通过曲线可以发现,当间隔取50时,基本就可以达到理想的对消结果;图 4(d)为间隔为50的3D结果,和图 4(b)基本一致。
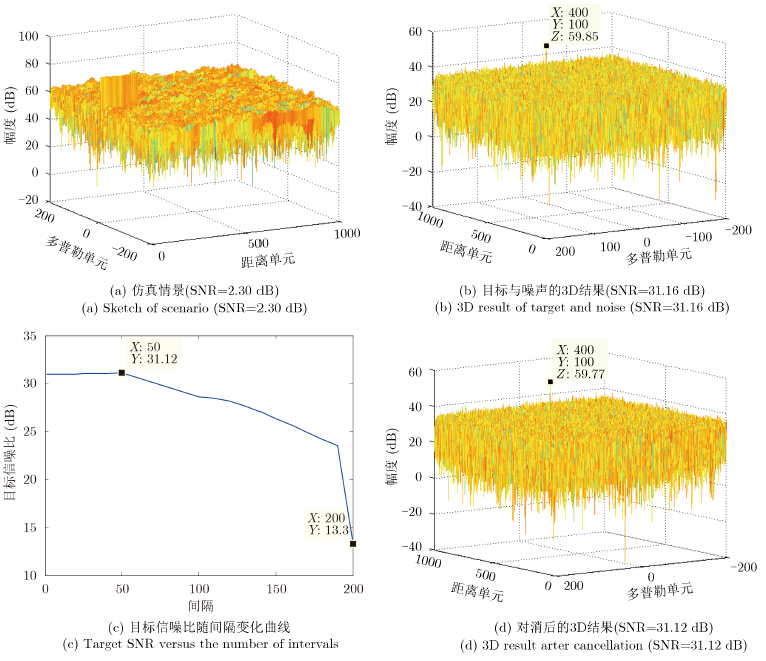 | 图 4 不同间隔的仿真结果 Fig. 4 Simulation results with different intervals |
假设分段数为b,信号长度为n,需要对消的距离单元m,则每一段中信号长度为nb=n/b 。则对于ECA-B方法,需要对对消的距离单元数为md=m,而频域ECA-B需要对消的距离单元数为${m_{\rm{f}}} = \frac{{4m}}{b} + 1$,ECA-B方法的主要计算量表现在$X_i^{\rm{H}}{X_i}$ 的计算和求逆,而频域ECA-B方法还需要两次傅里叶变换和一次逆傅里叶变换,两种方法的复乘次数如表 1所示,可以发现,分段数越大,频域ECA-B降低的计算量也越多。
| 表 1 复乘次数对比 Tab. 1 Complex products comparison |
综上所述,在进行频域ECA-B处理时,根据数据长度和对消阶数确定分段数,兆级数据一般以2048或4096最佳,从对消单元的两端以分段数的1/4等间隔地选取参数,就可以达到理想的对消结果,实测数据杂波较强或者较复杂时,可适当减小间隔。
3 仿真及实测数据处理 3.1 仿真数据处理对本文方法进行了仿真验证,仿真中参考通道数据为长度为 105的高斯白噪声,回波通道数据在参考的基础上加入了0-100距离单元的多径杂波,加入了两个近距离单元的强目标,两个远距离单元的弱目标,目标参数设置如表 2所示。仿真情景如图 5(a)所示,仿真时加入40 dB噪声,对消前模糊函数如图 5(b),图 5(c)所示,由于直达波和杂波的加入,底噪被抬高20 dB,目标被淹没。理想目标与噪声情况如图 5(d)所示,用于结果的对比。
| 表 2 目标参数设置 Tab. 2 Target parameters |
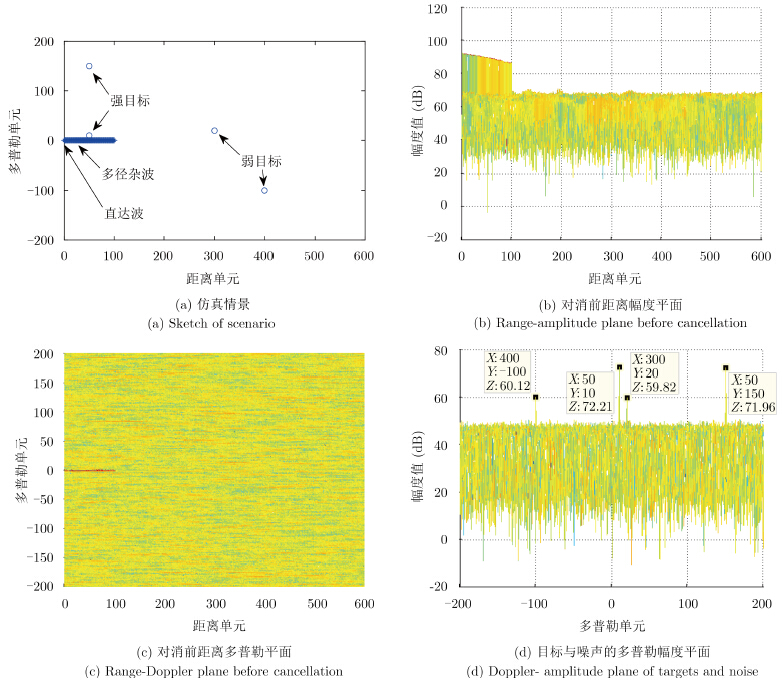 | 图 5 对消前参数设置 Fig. 5 Sketch of reference scenario before cancellation |
然后分别用20段和100段的ECA-B和频域ECA-B方法进行处理,结果如图 6所示:分段20时,ECA-B方法对消单元中的低多普勒目标被削弱(如图 6(a)中(50,10)单元的目标),而且这个目标由于调制产生了虚警(如图 6(b)所示);100段时ECA-B方法(50,10)单元的强目标已经被削弱到底噪以下(如图 6(e)所示),由于分段数过多导致(50,150)处的目标产生了虚警(如图 6(f)所示);而本文方法都达到了理想的效果(如图 6(c),图 6(d),图 6(g),图 6(h)所示)。
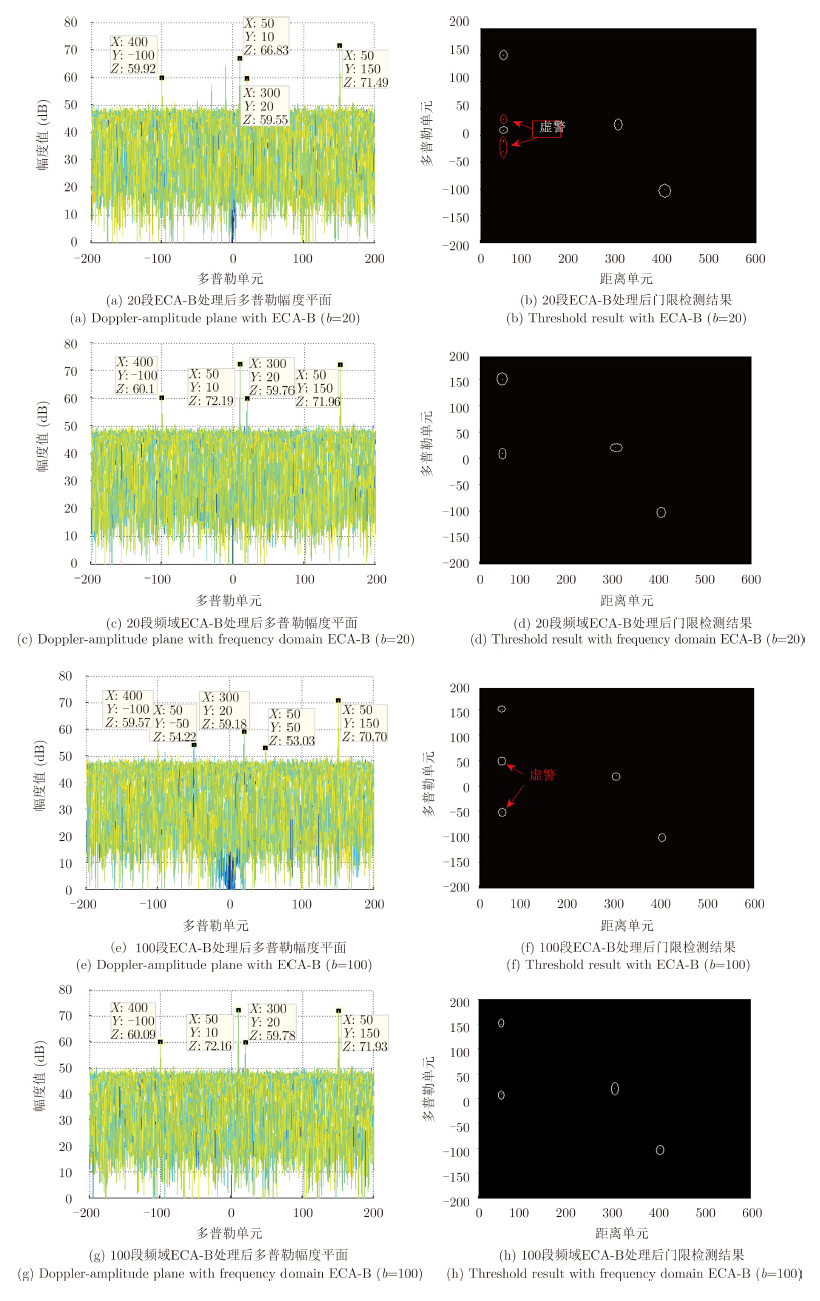 | 图 6 仿真结果 Fig. 6 Simulation results |
测试系统采用密云台信号,信号形式为cmmb信号,中心频率530 MHz,采样率10 MHz,带宽7.512 MHz,对消单元2000,分段数2000,处理结果如图 7所示。其中图 7(a)为对消前模糊函数,远距离单元底噪209 dB,目标都被淹没在其中;图 7(b)为频域ECA-B算法处理后的模糊平面图,底噪降低了约30 dB,目标可以凸显出来,其中1000-1500距离单元的矩形框是特殊场景引起的,并不是处理所带来的结果;图 7(c)是零多普勒切面图,紫色(ECA-B)虽然挖得最深,但是对于远距离单元的底噪降低并没有更显著的效果,绿色(频域ECA-B)不仅对消了0-2000的杂波,也由于其凹槽影响对消了2000-3000单元的杂波;图 7(d)为两种对消方法复乘次数的比较图,利用本文方法可以将计算量降低2-3个数量级;图 7(e),图 7(f)分别为两种方法0-2000距离单元的模糊平面,可以发现由于凹槽的影响,ECA-B方法在2000单元内的目标和杂波都被对消掉了,而频域ECA-B方法的目标都凸显出来;图 7(g),图 7(h)分别为两种方法2000-4000距离单元的多普勒幅度图,通过对比可以发现频域ECA-B方法不仅找到了目标,还由于其凹槽对2136单元杂波的影响,避免了(2136,±212) 处的虚警;图 7(i),图 7(j)为两种方法最远目标(约105 km)的3维图。通过以上对比结果,频域ECA-B是一种可行、高效的杂波对消方法。
 | 图 7 实测数据处理结果 Fig. 7 Real-time results |
本文针对信号带宽变大所带来的分段数增大,低速单元目标损失增大,调制加剧的问题,提出了一种频域ECA-B算法,阐述了频域ECA-B算法的原理,并用仿真和实测数据验证了该方法的有效性,不仅降低了计算量,而且还解决了低速目标的损失和调制问题,是一种实时高效的杂波对消方法,还可以为运动平台无源雷达杂波对消提供指导。
| [1] | Griffiths H D and Baker C J. Passive coherent location radar systems. Part 1: Performance prediction[J]. IEE Proceedings-Radar, Sonar and Navigation, 2005, 152(3): 153-159.( 1) 1) |
| [2] | 万显荣. 基于低频段数字广播电视信号的外辐射源雷达发展现状与趋势[J]. 雷达学报, 2012, 1(2): 109-123.Wan Xian-rong. An overview on development of passive radar based on the low frequency band digital broadcasting and TV signals[J]. Journal of Radars, 2012, 1(2): 109-123.( 1) 1) |
| [3] | 赵耀东, 吕晓德, 李纪传, 等. 无源雷达多普勒谱分析实现动目标检测的方法[J]. 雷达学报, 2013, 2(2): 247-256.Zhao Yao-dong, Lv Xiao-de, Li Ji-chuan, et al. Detection of moving targets based on doppler spectrum analysis technique for passive coherent adar[J]. Journal of Radars, 2013, 2(2): 247-256.( 1) 1) |
| [4] | 赵永科, 吕晓德. 一种联合优化的无源雷达实时目标检测算法[J]. 雷达学报, 2014, 3(6): 666-674.Zhao Yong-ke and Lv Xiao-de. A joint-optimized real-time target detection algorithm for passive radar[J]. Journal of Radars, 2014, 3(6): 666-674.( 1) 1) |
| [5] | 关欣, 胡东辉, 仲利华, 等. 一种高效的外辐射源雷达高径向速度目标实时检测方法[J]. 电子与信息学报, 2013, 35(3): 581-588.Guan Xin, Hu Dong-hui, Zhong Li-hua, et al. An effective real-time target detection algorithm for high radial speed targets in passive radar[J]. Journal of Electronics & Information Technology, 2013, 35(3): 581-588.( 1) 1) |
| [6] | 王桁. 外辐射源雷达的杂波抑制技术研究[J]. 军事通信技术, 2009, 30(3): 80-85.Wang Heng. Cancellation of clutter in passive radar based on opportunity transmitters[J]. Journal of Military Communications Technology, 2009, 30(3): 80-85.( 1) 1) |
| [7] | 王俊, 水鹏朗, 保铮, 等. 基于分数迟延估计的外辐射源雷达杂波相消算法[J]. 西安电子科技大学学报(自然科学版), 2005, 32(3): 378-382.Wang Jun, Shui Peng-lang, Bao Zheng, et al. External illuminator based continuous wave radr clutte canceling algorithm using arrival time estimtion by fractional interpolation[J]. Journal of Xidian University, 2005, 32(3): 378-382.( 1) 1) |
| [8] | Zhao Y D, Zhao Y K, Lu X D, et al. Block NLMS cancellation algorithm and its real-time implementation for passive radar[C]. IET International Radar Conference 2013, Xi'an, 2013: 1-5.( 1) 1) |
| [9] | 陈伟, 万显荣, 张勋, 等. 外辐射源雷达多通道时域杂波抑制算法并行实现[J]. 雷达学报, 2014, 3(6): 686-693.Chen Wei, Wan Xian-rong, Zhang Xun, et al. Parallel implementation of multi-channel time domain clutter suppression algorithm for passive radar[J]. Journal of Radars, 2014, 3(6): 686-693.( 1) 1) |
| [10] | 李纪传, 吕晓德, 向茂生, 等. 等效凹槽滤波器及其在无源相关定位雷达中的应用[J]. 雷达学报, 2014, 3(6): 675-685.Li Ji-chuan, Lv Xiao-de, Xiang Mao-sheng, et al. Notch filter analysis and its application in passive coherent location radar[J]. Journal of Radars, 2014, 3(6): 675-685.( 1) 1) |
| [11] | Colone F, O'hagan D, Lombardo P, et al. A multistage processing algorithm for disturbance removal and target detection in passive bistatic radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 698-722.( 2) 2) |
| [12] | 方亮, 万显荣, 易建新, 等. 外辐射源雷达扩展相消批处理杂波抑制算法的调制补偿[J]. 电子与信息学报, 2014, 36(1): 209-214.Fang Liang, Wan Xian-rong, Yi Jian-xin, et al. Modulation compensation of the batch version of the extensive cancellation algorithm for clutter mitigation in passive radar[J]. Journal of Electronics & Information Technology, 2014, 36(1): 209-214.( 1) 1) |
 2016, Vol. 5
2016, Vol. 5
