1 引言
合成孔径雷达(Synthetic Aperture Rader,SAR)全天时、全天候、大范围观测成像的特点使其在灾害应急监测、环境安全监测、海洋观测、资源勘探评估、农作物估产、森林资源调查、测绘和军事侦察等领域的应用具有独特优势,甚至是极端气象条件下唯一可靠的观测数据来源。充分利用SAR图像中蕴含的目标与场景特性信息,实现SAR图像的有效理解与认知,是提高SAR图像应用水平的关键。
然而,由于SAR的电磁成像机理与人类视觉系统和光学遥感的成像机理有着本质差异,导致SAR图像的特征分析和认知解译非常困难。SAR系统接收的是组成地物目标的每一个独立单元形成的散射能量,呈现在SAR图像上的地物目标是散射单元构成的集合体,多表现为离散的点、线组合。SAR系统独特的成像方式会造成相干斑、透视收缩、叠掩、阴影等现象[1],导致SAR图像在视觉特性上与光学图像有明显差异,表现为“所见非所知”特点。图 1给出了巴黎电信大楼光学遥感图像和SAR图像的对比[2],其中光学遥感图像来自于Google Earth,SAR图像来自于TerraSAR-X。在SAR图像上,地物目标边界以点、短线条为主,连续性和完整性差,图像结构缺失、几何变形严重。
 | 图 1 法国电信大楼光学遥感图像与SAR图像对比 Fig. 1 Comparison of optical image and SAR image for the Maison de la Radio France,Paris |
压缩采样(Compressed Sampling)理论[3, 4, 5, 6]是应用数学界近年来提出的一种新型信号采样与恢复理论,它利用信号表示的稀疏性,通过新的线性综合采样方式,可以在远低于Nyquist采样率的条件下完全恢复原信号。基于压缩采样的信息获取是在新的信号模型、新的采样方式和新的重构理论上开展的。2007年,Rice大学的Baraniuk和Steeghs[7]首先将压缩采样理论与SAR成像相结合,开展了点目标成像仿真。Herman和Strohmer[8]研究了利用压缩采样理论提高传统雷达分辨率的技术,通过对探测时频平面的离散化实现目标信号的稀疏表示,并从理论上给出了目标稀疏度的上界要求。Gurbuz等人[9]开展了基于压缩采样的探地成像雷达研究,Suksmono等人[10]将压缩采样理论用于步进频连续波探地雷达中提高数据获取效率。YANG等人[11]在步进频SAR成像技术的基础上,利用压缩采样理论提出了一种随机频率信号SAR成像技术,克服了步进频信号成像时宽测绘带与高分辨率之间的矛盾。Alonso等人[12]将压缩采样与传统SAR成像过程相结合,距离向处理仍采用传统匹配滤波,而方位向处理使用压缩采样技术降低数据量要求,仿真和实测数据表明50%降采样后仍能获得高质量SAR图像。Alonso等人的方法没有充分利用SAR信号距离向的稀疏性,Patel等人[13]通过建立距离和方位2维稀疏重构模型,在进一步降低采样数据量要求的条件下实现了稀疏SAR成像。Nguyen等人[14]针对超宽带SAR,提出了一种时域稀疏表示模型及相应的稀疏重构算法,大幅度减少了存储量和计算量要求。Batu和Certin[15]研究了稀疏SAR成像中算法参数的自动选择问题,提出了基于Stein无偏估计、广义互验证以及L-曲线技术的处理流程。进一步,Onhon和Certin[16]综合利用目标场景的稀疏性及相位误差因素的稀疏性,实现了成像和相位误差校正的联合处理。Stojanovic等人[17]讨论了不同观测几何下,稀疏SAR成像的性能,提出了一种t%平均互相关评价指标。Fang等人[18]针对稀疏SAR成像图像重构时计算量巨大的缺陷,将压缩采样和匹配滤波纳入统一的稀疏约束框架下,并设计了快速迭代阈值求解算法实现快速成像。2010年,Potter等人[19]对基于压缩采样的雷达成像技术进行了总结和梳理,并对相关理论及应用研究的趋势进行了展望。2012年8月,中国科学杂志F辑出版专刊较全面介绍了国内相关研究进展。2014年,Certin等
人[20]进一步对稀疏SAR成像技术进行了综述,讨论了宽角度成像、成像与自聚焦联合处理、运动目标成像等。综上所述,稀疏微波成像体制有望克服现有微波成像体制存在的系统实现困难、成像处理方法复杂、海量数据传输难以实现、信息冗余但特征提取困难等瓶颈问题。然而,在稀疏微波成像体制下,图像的获取和表征均发生了变化,需要在雷达图像理解现有理论和方法的基础上,研究新的特征分析和认知解译理论与方法。图 2给出了基于RADARSAT-Ⅰ卫星数据,分别使用传统CS (Chirp Scaling)算法和稀疏成像算法对加拿大温哥华英吉利湾的成像结果,从中看出图像特性发生变化。
 | 图 2 传统SAR成像与稀疏微波成像结果对比 Fig. 2 Comparison of tradional SAR imaging and sparse microwave imaging |
对SAR图像特征分析与认知解译相关理论与方法研究的历史由来已久,电磁散射机理是SAR解译研究的基础,目标和场景统计模型是SAR解译研究的前提,图像特性分析是SAR解译研究的必备环节,而具体的SAR解译理论与方法则涉及到图像处理、模式识别、机器学习、人工智能等诸多方面。对于稀疏SAR成像和传统SAR成像,二者电磁散射机理是相同的。在传统SAR图像统计建模研究方面,1976年提出的相干斑模型奠定了理论基础,1981年提出的乘积模型有力推动了该方向发展。近年来,随着SAR图像分辨率的不断提高,图像所表现出的异质特性和不均匀性愈加明显,统计特性更为复杂。针对高分SAR图像,提出了K分布[21]、G0分布、Alpha-Stable分布、Nakagmi-Rice分布、Fisher分布[22]、广义Gamma分布[23]以及基于字典集的混合分布等统计模型。一般来说,单视SAR图像可选择负指数分布,多视图像可选择Gamma分布,大视数处理时可选择高斯分布。某些情况下具有较长拖尾的分布如K分布、Alpha-Stable分布等能更好地描述海杂波,加拿大海洋监测系统(OMW)[24, 25]使用K分布进行舰船目标检测,在RADARSAT-Ⅰ上获得了较好的检测性能;WANG等人[26]研究了基于Alpha-Stable分布的海上舰船目标检测,使用RADARSAT-Ⅰ数据得到了比传统高斯分布和K分布更好的结果。此外,Frery等人[27]利用L,C波段全极化SAR影像数据,研究了基于G0分布及其推广模型的地物分类,认为精确的统计分布模型对获得高精度的分类效果具有重要作用。GAO等人[28]研究了包含K分布和G0分布在内的针对高海况海洋杂波和极不均匀地物杂波等高分辨率SAR图像的统计建模,在城市区域建筑物、军事目标等人造目标检测识别方面取得了较好结果。综上所述,SAR图像统计模型是目标检测识别、地物分类等应用的前提和基础,发挥着关键支撑作用。然而,不同体制、不同类型SAR传感器所获得图像的统计特性是不同的,必须开展针对性的研究,如K分布适用于RADARSAT-Ⅰ图像,但不适用于CCRS C/X SAR数据和Envisat A SAR的交替极化数据等[29]。对于稀疏SAR成像这种新体制,图像统计模型的研究是首先需要开展的工作。
SAR图像目标特征分析与提取的目的是将目标图像用简单明确的数值、符号等来描述,是目标检测识别、地物分类等应用的关键环节。SAR图像目标特征可分为几何结构特征、灰度统计特征、变换域特征和电磁散射特征等几大类[30, 31]。几何结构特征可分为几何特征、结构特征和地形学特征等,具体包括目标的长宽高、面积、质心、边缘、轮廓、阴影、目标峰值、凹陷、脊等;灰度统计特征可分为对比度特征和纹理特征,具体包括最强值、平均强度、标准偏差、灰度共生矩阵、权重序列填充率等;变换域特征通过纯粹的数据处理工具对图像进行分析,不一定具有实际的物理意义,常用的变换包括主成分分析、独立成份分析、离散傅里叶变换、小波变换、超完备字典等;电磁散射特征的提取依赖于特定的电磁散射模型,如利用属性散射中心模型[32]可得到散射中心的距离向坐标、方位向坐标、散射中心幅度、散射中心类型等。SAR图像特征种类和提取方法多样,但点、线、面是各种特征的基础,是最底层和最重要的特征,相应的边缘提取和区域分割是图像处理的基本操作。稀疏SAR成像体制下图像特性发生变化,不能将传统SAR图像的特征分析与提取方法直接搬移过来使用。目前,对稀疏SAR图像特征研究的工作较少,Certin等人[33]最早于2001年研究了结合目标先验知识实现分辨率提升、旁瓣和相干斑抑制等特征增强的SAR成像,采用的图像重构正则化模型与压缩采样信号重构模型原理相似。进一步,Certin等人在文献[34]中详细分析了这种利用先验约束实现特征增强的SAR成像技术,所获得SAR图像特征的精度和鲁棒性,以及ATR识别性能。2013年,Certin等人[35]提出利用组合字典进行稀疏表示,实现多种特征同时增强的SAR成像技术。
2 稀疏微波成像原理[36]
基于压缩感知理论的稀疏微波成像技术在成像模型和处理方法上与传统SAR体制有较大不同,这是稀疏微波SAR图像目标特征不同于传统SAR图像特征的根源。下面从稀疏微波成像的模型与方法出发,分析目标特征变化情况。
考虑雷达发射如下的LFM信号:
| ${s_0}(\tau ) = {w_{\rm{r}}}(\tau ){{\rm{e}}^{{\rm{j}}2\pi {f_0}\tau + {\rm{j}}\pi {K_{\rm{r}}}{\tau ^2}}}$ |
其中${f_0}$为载频,${K_r}$为调频率,${w_{\rm{r}}}(\tau )$为发射信号包络。点目标回波经解调后可表示为:
| $\begin{array}{*{20}{l}} {{s_0}(\tau ,\eta ) = {A_0}{w_{\rm{r}}}\left( {\tau - \frac{{2R(\eta )}}{{\rm{c}}}} \right){w_{\rm{a}}}\left( {\eta - {\eta _{\rm{c}}}} \right)}\\ {\quad \quad \quad \quad \cdot \exp \left\{ { - {\rm{j}}\frac{{4\pi {f_0}R(\eta )}}{{\rm{c}}}} \right\}}\\ {\quad \quad \quad \quad \cdot \exp \left\{ {{\rm{j}}\pi {K_{\rm{r}}}{{\left( {\tau - \frac{{2R(\eta )}}{{\rm{c}}}} \right)}^2}} \right\}} \end{array}$ | (1) |
其中h为方位时间,${A_0}$为点目标后向散射系数,R(h)为点目标方位斜距,${w_{\rm{a}}}\left( \eta \right)$为由天线方向图决定的方位回波信号能量窗函数,hc为方位中心时刻。忽略${A_0}$,式(1)即为单位点目标的冲激响应$h(\tau ,\eta )$。设观测场景的后向散射函数为$g(\tau ,\eta )$,则SAR基带回波信号可表示为:
| ${s_{\rm{r}}}(\tau ,\eta ) = g(\tau ,\eta ) \otimes h(\tau ,\eta ) + n(\tau ,\eta )$ | (2) |
其中$n(\tau ,\eta )$为系统噪声。
使用强散射点回波模型对2维成像场景离散化,同时对回波信号在距离和方位时间域离散化,SAR雷达接收到的场景基带回波可表示为:
| $\begin{array}{l} \begin{array}{*{20}{l}} {{s_{\rm{r}}}(m,n) = \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {{\sigma _{ij}}{w_{\rm{r}}}\left( {{\tau _m} - \frac{{2{R_{ij}}({\eta _n})}}{{\rm{c}}}} \right)} } }\\ {\quad \quad \quad \quad \cdot {w_{\rm{a}}}\left( {{\eta _n} - {\eta _{\rm{c}}}} \right) \cdot \exp \left\{ { - {\rm{j}}\frac{{4\pi {f_0}{R_{ij}}({\eta _n})}}{{\rm{c}}}} \right\}}\\ {\quad \quad \quad \quad \cdot \exp \left\{ {{\rm{j}}\pi {K_{\rm{r}}}{{\left( {{\tau _m} - \frac{{2{R_{ij}}({\eta _n})}}{{\rm{c}}}} \right)}^2}} \right\}} \end{array}\\ \quad \quad \;m = 1,2,\cdots ,M;\;\;n = 1,2,\cdots ,N \end{array}$ | (3) |
成像场景尺寸为I×J, sij为第ij个地面单元的后向散射系数。定义回波信号向量${y} = \left[{{s_{\rm{r}}}(m,n)} \right] \in {{\rm{C}}^{MN \times 1}}$,场景后向散射系数向量$\sigma = \left[{{\sigma _{ij}}} \right] \in {{\rm{C}}^{IJ \times 1}}$,系统噪声向量${n} = \left[{n({\tau _m},{\eta _n})} \right] \in {{\rm{C}}^{MN \times 1}}$以及信号接收矩阵${H} = \left[{{h_{i,j}}({\tau _m},{\eta _n})} \right] \in {{\rm{C}}^{MN \times IJ}}$,则SAR回波信号接收模型为:
| $y = H\sigma + n$ | (4) |
由式(4)直接求解$\sigma $即可获得场景的2维SAR图像,这也是传统BP算法的处理思路。
在模型式(4)的基础之上,若能进一步利用成像场景的稀疏性等先验信息,则有望在降低距离和方位向采样数据量的条件下实现SAR成像。$\sigma $的稀疏性可表现在空域、频域、极化域等中,设$\Psi \in {{\rm{C}}^{IJ \times P}}$表示矩阵,$x$表示系数,即$\sigma = \Psi x$,则$\sigma $的稀疏性体现为${\left\| {x} \right\|_0} \lt \lt P\,$。根据处理域的不同,表示矩阵$\Psi$可为单位阵、傅里叶阵、超完备字典等。稀疏SAR成像通过线性综合测量方式获得降采样后的数据,即
| ${y_{\rm{r}}} = \Psi H\Psi x + n$ | (5) |
${\Phi} \in {{\rm{R}}^{L \times MN}},\;L \lt \lt MN$可选择为随机抽取矩阵、高斯随机矩阵或特殊形式的确定性矩阵等。令$A = \Phi H\Psi \in {{\rm{C}}^{L \times P}}$,则通过求解下述优化问题能有效恢复$\sigma $,实现稀疏SAR成像。
| $\left\{ {\begin{array}{*{20}{l}} {\hat x = \mathop {\arg \min }\limits_x {{\left\| x \right\|}_0},\;\;{\rm{s}}.{\rm{t}}.\;\;{{\left\| {{y_{\rm{r}}} - Ax} \right\|}_2} \le \varepsilon }\\ {\sigma = \Psi \hat x} \end{array}} \right.$ | (6) |
问题式(6)是NP-难题,无法直接求解。目前的求解方法主要包括:贪婪算法、最小${\ell _1}$范数凸优化模型、最小${\ell _p},\;0 \lt p \lt 1$范数非凸优化模型和一些基于特殊形式A矩阵的算法[37]。
3 稀疏微波SAR图像统计特性分析
目前对传统SAR图像相干斑噪声的统计建模及特性分析研究主要从图像数据出发,因为从SAR成像过程角度研究相干斑噪声的形成机理十分困难,涉及到目标、环境、传感器以及处理算法等诸多环节,影响因素多、建模复杂。稀疏微波SAR图像统计特性的研究也将从图像数据出发,但面临图像数据匮乏的实际问题。本文的研究思路是:以传统SAR图像统计建模为基础,通过分析稀疏微波SAR成像相对于传统SAR成像引起图像结果的变化,实现建模分析。
稀疏微波SAR成像结果不仅取决于采样方式$\Phi $,而且与优化重构算法密切相关。首先考虑贪婪算法,目前主要有OMP(Orthogonal Matching Pursuit)、Stagewise OMP(StOMP)、Regularized OMP(ROMP)以及CoSaMP(Compressive Sampling Matching Pursuit)等,其基本思想为根据残差向量与测量矩阵列相关性大小,逐步找到原始信号的支撑集$\Omega$,然后在与支撑集对应的子矩阵${A_{\Omega }}$上进行最小二乘的计算得到${{{x}}_{\Omega } } = $${\left( {{{A}}_{\Omega } ^{\rm{T}}{{{A}}_{\Omega } }} \right)^{ - 1}}{{A}}_{\Omega } ^{\rm{T}}{{{y}}_{\rm{r}}}$,最终恢复的稀疏表示系数${\hat {x}}$为:
| $\left\{ {\begin{array}{*{20}{l}} {\hat x{|_Ω} = {x_Ω}}\\ {\hat x{|_{{Ω^{\rm{c}}}}} = 0} \end{array}} \right.$ | (7) |
支撑集W的大小一般远小于信号长度,即${\hat {x}}$中大部分元素为零。对于空域稀疏场景,表示矩阵$\Psi $为单位阵,此时稀疏SAR图像即为${\hat {x}}$,在视觉表现上除少量强散射点外,背景像素值为零。对于频域稀疏场景,表示矩阵$\Psi $可选择离散傅里叶变换阵、小波变换阵等,重构SAR图像在频域上表现为仅含少量大的表示系数,在空域上表现为滤波平滑效果。其次考虑最小${\ell _1}$-范数凸优化模型,Donoho等人在文献[38]中证明,当感知矩阵A为随机抽取单位阵时,优化模型的解为:
| $\left\{ {\begin{array}{*{20}{l}} {\hat x{|_\Omega }\max \left\{ {{y_{\rm{r}}} - \lambda ,0} \right\}}\\ {\hat x{|_{{\Omega ^0}}} = 0} \end{array}} \right.$ | (8) |
此处$\Omega $为yr的支撑集,$\lambda $为大于零的常数,用于平衡${\ell _1}$优化模型中逼近项和稀疏项的权重。由式(8)可以看出,${\ell _1}$优化模型求解获得的向量${\hat {x}}$中大部分元素为零。使用${\ell _p},\;0 \lt p \lt 1$非凸优化模型能获得比${\ell _1}$更稀疏的解。对于频域稀疏场景,成像结果与贪婪算法类似。此外,从统计估计的角度,使用${\ell _p}$-范数对图像进行约束进而实现图像重构的处理模型${\rm{min}}_{{x}} \left\{ {{{\left\| {{{{y}}_{\rm{r}}} - {{Ax}}} \right\|}_2} + \lambda {{\left\| {{x}} \right\|}_p}} \right\}$等价于MAP(Maximum A Posteriori)估计[39]。不同的范数p对应于使用不同的先验分布描述SAR图像,p=2对应于经典的高斯先验,p=1对应于Laplacian先验,0<p<1对应于具有更长拖尾的先验分布。从MAP估计的角度,先验模型的使用在重构图像上表示为像素能量集中,使得目标主要散射点得到加强,而旁瓣和噪声受到抑制。
下面具体分析经${\ell _1}$惩罚后SAR图像背景像素统计特性的变化。根据式(8),稀疏SAR图像背景各像素值$\hat {σ} $可近似为:
| $\left\{ {\begin{array}{*{20}{l}} {x = {\Psi ^ {†} }\sigma }\\ {\hat x = \max \left\{ {{\rm{abs}}(x) - \lambda ,0} \right\}}\\ {\hat σ = \Psi \hat x} \end{array}} \right.$ | (9) |
其中${\Psi ^{†} }$为$\Psi $的伪逆。设成像场景各散射点后向散射系数是服从概率密度$f(t;\theta )$的随机变量,其中$\theta$为分布函数的参数。将$\sigma $看作由$IJ$个独立同分布随机变量构成的随机向量,则其密度为$\prod\nolimits_{i = 1}^{IJ} {f({t_i};\;\theta )} $。$\Psi $给定的情况下,通过式(9)可推导得到$\hat \sigma $的概率分布,设其每个分量的密度函数分别为g1(t),g2(t)…,gIJ(t),则稀疏SAR图像的统计分布可近似为:
| $g(t) = \frac{{{g_1}(t) + {g_2}(t) + \cdots + {g_{IJ}}(t)}}{{IJ}}$ | (10) |
对于空域稀疏场景,$\Psi$为单位矩阵,此时$\hat \sigma = \max \{ \sigma - \lambda ,0\} $,容易计算得到g(t)。此时稀疏SAR图像背景统计分布不再是连续的,其分布函数为:
| $G(t) = \left\{ {\begin{array}{*{20}{l}} {\int_{ - \infty }^{t + \lambda } {f(u)} {\rm{d}}u{\mkern 1mu} ,\;\;\;t > 0}\\ {}\\ {\int_{ - \infty }^\lambda {f(u)} {\rm{d}}u{\mkern 1mu} ,\;\;\;t = 0}\\ {}\\ {0,\quad \;\quad \;\;\;\;\;\;\;\;\;\;t < 0} \end{array}} \right.$ | (11) |
背景像素值中有$\int_{ - \infty }^\lambda {f(u)} {\rm{d}}u$取值为零,分布退化。对于在频域、时频域、极化域或超完备字典域等稀疏的情况,也可通过类似方法推导得到稀疏SAR图像的分布函数。
下面将通过计算机仿真验证上述分析结论。对于设定的目标场景,根据相干斑噪声的统计模型如高斯分布、Gamma分布、K分布等生成仿真SAR图像,以此作为目标场景后向散射系数s的近似,进而通过求解模型式(6)获得稀疏SAR图像$\hat \sigma $。考虑包含9个点目标的空域稀疏场景,场景尺寸64×64,背景平均灰度值为50,目标尺寸2×2,平均灰度值为200。使用Gamma分布的相干斑噪声模型,仿真获得的SAR图像及其背景统计分布分别如图 3(a)和图 3(b)所示。使用稀疏SAR成像方法,在随机采集40%数据的情况下恢复得到的SAR图像如图 3(c)所示,其背景噪声的统计分布如图 3(d)所示。可以看出,稀疏SAR图像背景大部分为零,分布退化。
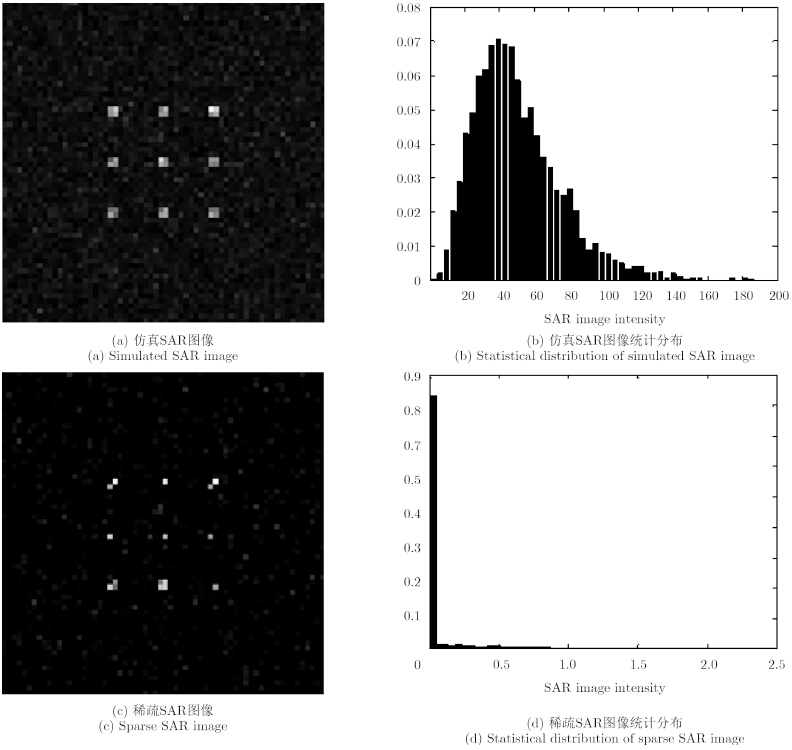 | 图 3 空域稀疏场景仿真SAR图像及其背景统计分布 Fig. 3 Simulated SAR images and statistical distributions for a space-domain sparse scene |
下面以图 2中加拿大温哥华英吉利湾场景为例,统计传统SAR图像与稀疏SAR图像的背景分布情况,结果如图 4所示。可以看出,对于空域稀疏场景,稀疏微波SAR成像后的图像背景干净,统计分布退化,验证了前面理论与仿真分析的结论。
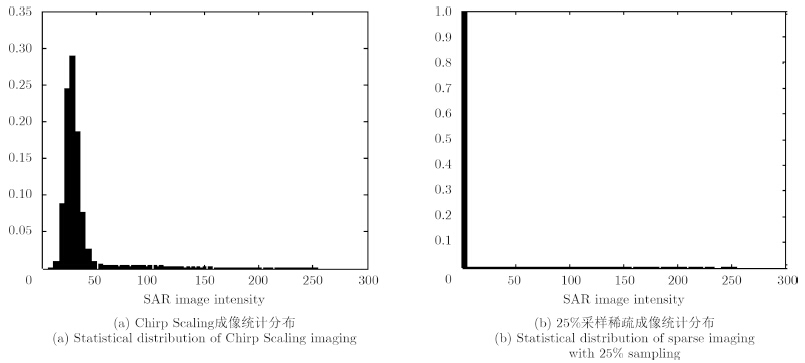 | 图 4 实测数据稀疏SAR图像与传统SAR图像背景统计分布对比 Fig. 4 Comparison between statistical distributions of sparse SAR image and traditional SAR image with real-measured data |
进一步,分析频域稀疏场景情况。成像场景如图 5(a)所示,场景尺寸64×64,背景平均灰度值为50,目标尺寸16×16,平均灰度值为200。考虑Gamma分布的相干斑噪声,仿真得到的SAR图像如图 5(b)所示,背景噪声的统计分布如图 5(c)所示。
 | 图 5 频域稀疏场景仿真SAR图像及其统计分布 Fig. 5 Simulated SAR image and statistical distribution for a frequency-domain sparse scene |
针对图 5中的目标场景,仿真不同降采样率下获得的稀疏SAR图像,通过求解模型式(6)实现,稀疏表示矩阵选用傅里叶变换矩阵。采样率分别为80%、60%、40%和20%时的稀疏SAR图像及其统计分布如图 6(a)-图 6(h)所示,当采样率较高时,稀疏成像算法的滤波平滑效果发挥主导作用,使得背景统计分布退化集中;当采样率较低时,稀疏成像算法的重构误差变大,使得背景统计分布趋于发散。
 | 图 6 频域稀疏场景不同采样率下仿真稀疏SAR图像及其统计分布 Fig. 6 Simulated sparse SAR images and statistical distributions for a frequency-domain sparse scene with different sampling rates |
4 稀疏微波SAR图像目标特征分析
SAR图像中的点、线、面是最基本和底层的图像特征,下面将分析稀疏SAR图像中这些基本特征的变化情况。
4.1 强散射点位置和幅度的恢复误差分析
仍以空域稀疏场景为例,点、线位置的恢复误差来自于对稀疏信号支撑集的恢复误差。对于K稀疏信号,当测量矩阵满足一定的RIP条件时,利用OMP算法或子空间追踪(Subspace Pursuit,SP)等算法,能通过有限步迭代准确恢复稀疏信号支撑集。相关定理如下:
定理4[40] 对K稀疏信号x进行压缩采样y=Ax+w,噪声满足${\left\| w \right\|_2} \le {\varepsilon _1}$,若矩阵A满足如下的RIP条件:
| ${\delta _{K + 1}} \le \frac{{\sqrt {4K + 1} - 1}}{{2K}}$ | (12) |
且信号的最小值满足
| $\mathop {\min }\limits_{i \in T} \left| {{{(x)}_i}} \right| > \frac{{\left( {\sqrt {1 + {\delta _{K + 1}}} + 1} \right){\varepsilon _1}}}{{1 - {\delta _{K + 1}} - \sqrt {1 - {\delta _{K + 1}}} \sqrt K {\delta _{K + 1}}}}$ | (13) |
时,利用OMP算法通过有限步迭代能准确恢复x的支撑集。
当矩阵A存在误差或信号x近似稀疏时,文献[41]的研究表明若A满足一定的RIP条件利用OMP算法仍能准确恢复x的最大K支撑集,且信号恢复均方误差受控。
虽然理论分析表明稀疏SAR成像对强散射点位置和幅度的恢复是精确的,然而实际成像过程中矩阵A和噪声w很难满足理论条件,使得图像恢复存在误差。下面以MSTAR数据集BMP2步兵战车SAR图像为例,分析不同降采样率稀疏SAR成像对目标属性散射中心提取的影响(提取方法来自于文献[42])。图 7为采用频域稀疏模型在不同采样率下恢复的稀疏SAR图像以及对应的属性散射中心提取结果。
 | 图 7 BMP2目标SAR图像属性散射中心提取结果 Fig. 7 Results of attributed scattering centers extraction from SAR images of BMP2 target |
部分属性散射中心提取的具体情况见表 1,其中A,x,y,L分别表示散射中心的幅度,横坐标,纵坐标和长度。可以看出,对强散射中心位置和长度的提取比较准确,即使20%采样率下仍能得到比较满意的结果;由于稀疏重构算法的原因,散射中心幅度发生了变化,且某些尺寸较大的分布散射中心被重构为多个尺寸较小的分布散射中心。此外,采样率降低会影响目标阴影的重构,这对某些情况下的目标解译处理是不利的。
| 表 1 稀疏SAR图像属性散射中心提取结果 Tab. 1 Results of attributed scattering centers extraction from sparse SAR images |
4.2 SNR的变化分析
考虑随机背景下的点目标,设点目标的幅值为x0,背景杂波的统计分布为f(t),相应的SNR为:
| ${\rm{SN}}{{\rm{R}}_0} = \frac{{{E_{\rm{s}}}}}{{{E_{{\rm{cn}}}}}} = \frac{{x_0^2}}{{{\rm{E}}\left[{{c^2}(t)} \right]}} = \frac{{x_0^2}}{{\int_0^\infty {{t^2}f(t){\rm{d}}t} }}$ | (14) |
使用空域稀疏成像模型,根据式(11),稀疏SAR图像的SNR为:
| ${\rm{SN}}{{\rm{R}}_{{\rm{CS}}}} = \frac{{{{\left( {{x_0} - \lambda } \right)}^2}}}{{\int_0^\infty {{t^2}f(t + \lambda ){\rm{d}}t} }}$ | (15) |
以高斯杂波为例,设$f(t) \sim {\rm{N}}\left( {\mu ,{\sigma ^2}} \right)$,那么有
| $\left\{ \begin{array}{l} {\rm{SN}}{{\rm{R}}_0} = \frac{{x_0^2}}{{{\mu ^2} + {\sigma ^2}}}\\ {\rm{SN}}{{\rm{R}}_{{\rm{CS}}}} = \frac{{{{\left( {{x_0} - \lambda } \right)}^2}}}{{{\textstyle{ 1 \over {\sqrt {2\pi }}}}\sigma (\mu - \lambda ) + {\textstyle{ {{1}} \over {{2}}}}\left[{{\sigma ^2} + {{(\mu - \lambda )}^2}} \right]{\rm{Erfc}}\left( {(\lambda - \mu )/(\sqrt 2 \sigma )} \right)}} \end{array} \right.$ | (16) |
其中${\rm{Erfc}}(z) = 1 - \frac{2}{{\sqrt {{\rm{ }}\pi } }}\int_0^z {{{\rm{e}}^{ - {t^2}}}{\rm{d}}t} $为广义误差函数。特别地,当选取$\lambda = \mu $时,有${\rm{SN}}{{\rm{R}}_{{\rm{CS}}}} = \frac{{{{\left( {{x_0} - \mu } \right)}^2}}}{{{\sigma ^2}/2}}$。一般情况下,背景杂波的灰度范围比目标暗得多,此时有${\rm{SN}}{{\rm{R}}_{{\rm{CS}}}} > {\rm{SN}}{{\rm{R}}_0}$。对于其他分布也可以得到类似的结论,图 8给出背景为高斯或Gamma分布时SNRcs随不同l的变化情况,当l=0时即为SNR0。可以看出,随着l的增加信噪比逐渐增加。但需要指出的是对于稀疏SAR成像,并非l越大越好,因为还需考虑到目标像素值的变化情况。此外,对于使用频域、梯度域等稀疏表示模型的情况,SNR的变化将更加复杂。
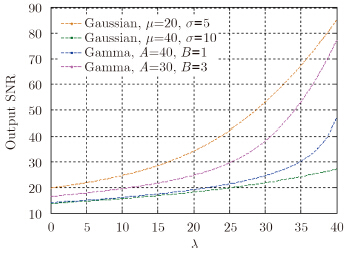 | 图 8 稀疏SAR成像点目标SNR变化情况 Fig. 8 SNR variations of sparse SAR imaging of point target |
4.3 实测稀疏SAR图像边缘与区域特征分析
利用中科院电子所研制的机载稀疏微波成像雷达获得的盐田SAR图像进行边缘和区域特性分析,比较不同采样率下,稀疏微波成像雷达的边缘及区域保持能力。利用传统Chirp Scaling算法获得的SAR图像见图 9(a),相应的边缘提取结果及人工标注的边缘真值见图 9(b)和图 9(c)。从图中可以看出,受相干斑噪声影响,边缘提取有一定误差。进一步,在不同的采样率下使用稀疏微波成像,并进行边缘提取和区域分割,结果见图 10。
 | 图 9 CS成像SAR图像及边缘提取结果 Fig. 9 Chirp Scaling SAR image and edge extraction results |
 | 图 10 不同采样率下稀疏SAR图像边缘提取及区域分割结果 Fig. 10 Edge extraction and segmentation results of sparse SAR images with different sampling rates |
以图 9(c)中的手动标注真值图像为基础,采用Precision-Recall指标评估不同降采样率下稀疏SAR图像的边缘提取性能。对于某次边缘提取结果,通过式(17)计算对应的Precision和Recall值。
| ${\rm{Precision}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FP}}}},\quad {\rm{ Recall}} = \frac{{{\rm{TP}}}}{{{\rm{TP}} + {\rm{FN}}}}$ | (17) |
其中TP为由降采样图像检测出的边缘像素点中为真实边缘的个数,FP为检测出的边缘像素点中非真实边缘像素点的个数,FN为漏检的边缘像素点个数。Precision衡量了边缘检测的正确率情况,Recall衡量了边缘检测的虚警情况。改变边缘提取算法的参数可获得一组Precision-Recall值,当Precision-Recall曲线越靠近坐标点(1,1)时,表明由该图像提取的边缘漏检和虚警都很低,边缘保持性能越好。不同采样率下稀疏SAR图像的Precision-Recall曲线如图 11所示。可以看出,随着采样率的适当降低,边缘检测结果中的虚警和漏检明显减少,这主要是由于稀疏微波SAR图像旁瓣和噪声低,能够很好地保持图像中有强散射特性的点、线目标。但是如果采样率过低,图像重构误差带来的干扰(图中贯穿的横向亮线等)会占据主导地位,造成边缘检测的漏检和虚警急剧上升。从不同采样率下稀疏SAR图像分割的结果看,分割对象块的轮廓形状发生了较大变化,但多个相邻对象块组成的大片同质性区域的外围轮廓变化较小,进一步可分析同一区域平均灰度和纹理系数等指标的变化情况。
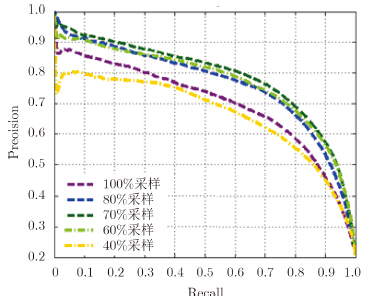 | 图 11 不同采样率下边缘提取性能对比 Fig. 11 Comparison of edge extraction performance with different sampling rates |
5 稀疏微波SAR图像目标检测
从两个方面研究稀疏微波SAR图像的目标检测问题。首先,基于仿真稀疏SAR图像研究采样率的降低对目标检测性能的影响,具体使用Precision-Recall曲线评估图像的目标检测性能;其次,针对稀疏微波SAR图像目标特性,基于实测SAR图像研究海上舰船目标检测的具体算法流程。
5.1 基于仿真稀疏SAR图像的目标检测性能分析
针对图 5中的仿真场景和目标真值,计算图 6中不同降采样率稀疏SAR图像目标检测的Precision-Recall曲线,结果如图 12所示。可以看出,随着采样率的降低,稀疏SAR图像的目标检测性能变化并不是单一的。采样率为60%和40%的稀疏SAR图像能获得较好的目标检测性能,但随着采样率的进一步降低,噪声对图像重构的影响变大,图像恢复质量变差,目标检测性能下降。
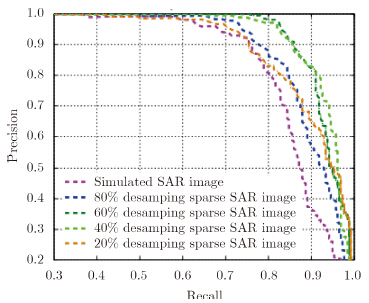 | 图 12 稀疏SAR图像目标检测性能分析 Fig. 12 Sparse SAR image target detection performance analysis |
5.2 基于实测稀疏SAR图像的海上舰船目标检测
由于使用不同数据域稀疏表示模型获得的稀疏SAR图像在背景统计分布、图像特性等方面表现不同,因此应分别设计相应的目标检测算法流程。此处以在空域稀疏的海上舰船目标场景为例,给出相应的目标检测流程,对于其他数据域稀疏场景的目标检测可参照设计。
传统高分SAR目标检测一般包括图像预处理、CFAR检测、虚警抑制、目标鉴别后处理等步骤,过程如图 13所示。
 | 图 13 SAR图像目标检测流程 Fig. 13 Flow of target detection for SAR images |
图像预处理的目的是将不同类型SAR图像的灰度、分辨率、视数等归一化到同一范围内,为后续处理提供统一标准的图像,具体通过增强、重采样和滤波等操作实现;CFAR处理是目标检测流程的核心,具体包括背景统计模型的建模与估计、检验统计量的构造和计算等;虚警抑制是SAR图像目标检测流程的重要和独特部分,SAR图像相干斑噪声严重,CFAR处理后虚警高,虚警抑制可结合SAR图像空域等信息完成,或使用目标先验信息实现鉴别,如结合舰船目标的长、宽、长宽比、面积、质心等先验知识剔除形状非常不合理的备选目标点;后处理的主要目的是利用各种辅助信息,对检测结果进一步鉴别和确认,提高检测结果的可靠性,如利用AIS等数据源对备选目标进一步确认等。
对于空域稀疏场景,稀疏成像结果中背景噪声和旁瓣能量得到极大抑制,统计分布退化,图像中的目标表现为一系列强散射点的集合,灰度层次变弱。此时,目标检测的具体实现上与传统流程有所不同,具体表现为CFAR和虚警抑制两个步骤上。稀疏SAR图像背景干净,使用自适应阈值分割算法比传统双参数CFAR更方便有效。稀疏SAR图像中目标表现为一系列强散射点的集合,虚警抑制时需将目标各强散射点关联起来,进而实现目标特征参数的估计。具体的对阈值分割结果图像进行聚类,然后对聚类结果使用椭圆、长方形等轮廓拟合,进而实现舰船长、宽、质心等参数的估计。
考虑最小误差自适应阈值分割算法,设原始SAR图像目标和背景服从高斯分布$N \left( {{m_i},\sigma _i^2} \right)$,mi和$\sigma _i^2$分别为均值和方差,i=0,1分别对应于背景和目标,根据式(11)可获得稀疏SAR图像的背景分布。进而通过下述步骤可确定最小误差分割的阈值,具体推导过程参见文献[43]。
步骤1 将SAR图像灰度等级量化为$\left\{ {0,1,\cdots } \right.,Z - 1$,计算归一化直方图 $\left\{ {h(z)} \right.:z = 0,\cdots ,\left. {Z - 1} \right\}$。
步骤2 设定分割阈值t,估计均值、方差以及先验概率
| $\left\{ {\begin{array}{*{20}{l}} {{{\hat m}_{i\tau }} = \frac{{\sum\limits_{z \in {R_{i\tau }}} {zh(z)} }}{{\sum\limits_{z \in {R_{i\tau }}} {h(z)} }}}\\ {{{\hat \sigma }_{i\tau }} = \frac{{\sum\limits_{z \in {R_{i\tau }}} {h(z){{(z - {{\hat m}_{i\tau }})}^2}} }}{{\sum\limits_{z \in {R_{i\tau }}} {h(z)} }}}\\ {{P_{0\tau }} = h(0) + \sum\limits_{z \in {R_{0\tau }}} {h(z)} }\\ {{P_{1\tau }} = \sum\limits_{z \in {R_{1\tau }}} {h(z)} n} \end{array}} \right.$ | (18) |
其中${R_{0\tau }} = \left\{ {1,\cdots ,\tau } \right\},{R_{1\tau }} = \left\{ {\tau + 1,\cdots ,Z - 1} \right\}$。
步骤3 计算代价函数
| $J(\tau ) = \sum\limits_{i = 0}^1 {{P_{i\tau }}\left( {{\rm{ln}}{{\hat \sigma }_{i\tau }} - \ln {P_{i\tau }}} \right)} $ | (19) |
| ${\tau ^*} = \arg \min \left\{ {J(\tau ),\tau = 0,1,\cdots ,Z - 1} \right\}$ |
以图 2中加拿大温哥华英吉利湾场景为例,传统SAR图像与不同采样率下稀疏微波SAR图像舰船目标检测的结果如图 14所示(其中传统SAR检测使用课题组开发的软件自动完成,图像显示时进行了对比度处理;稀疏SAR图像没有进行对比度处理,不能显示灰度低的陆地区域)。从中可以看出,对于稀疏微波SAR成像体制,即使获得10%的采样数据仍能实现海上舰船目标的有效检测。
 | 图 14 传统SAR图像与稀疏微波SAR图像目标检测结果对比 Fig. 14 Comparison of target detection for traditional SAR images and sparse microwave SAR images |
6 小结
相比于传统的雷达成像结果,在稀疏微波成像体制下,成像结果的获取和表征均发生了变化,因而需要在现有理论和方法的基础上,研究稀疏微波成像体制下的图像理解问题。本文主要从图像背景统计特性、目标特征变化以及目标检测算法等3个方面对稀疏SAR图像理解问题进行了初探,使用的稀疏表示模型以空域稀疏和频域稀疏为主。根据压缩感知理论,可构造更加复杂的稀疏表示模型,如与应用问题相结合的稀疏表示,有望实现成像处理与图像解译的一体化,此时稀疏SAR图像的理解将会以新的方式呈现。
致谢论文中部分思想和处理结果来自于承担的973课题“稀疏微波成像数据压缩及特征理解(2010CB731904)”,在此向参与该课题的上海交通大学王军锋教授、中国科技大学刘发林教授、张荣副教授,上海交通大学吕文涛博士、柳彬博士、胡昊博士生等表示感谢。此外,感谢中科院电子所提供稀疏微波SAR图像实测数据,感谢国防科技大学计科峰副教授提供SAR图像属性散射中心提取程序。
| [1] | Oliver C and Quegan S. Understanding Synthetic Aperture Radar Images[M]. Raleigh, NC, SciTech Publishing, 2004: 1-512.( 1) 1) |
| [2] | Auer S J. 3D synthetic aperture radar simulation for interpreting complex urban reflection scenarios[D]. [Ph.D. dissertation], Technische Universität München, 2011: 13-15.( 1) 1) |
| [3] | Candes E J. Compressive sampling[C]. International Congress of Mathematics, Madrid, Spain, 2006: 1433-1452.( 1) 1) |
| [4] | Baraniuk R G. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121.( 1) 1) |
| [5] | Candes E J and Wakin M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30.( 1) 1) |
| [6] | Baraniuk R G. More is less: signal processing and the data deluge[J]. Science, 2001, 331(6018): 717-719.( 1) 1) |
| [7] | Baraniuk R G and Steeghs P. Compressive radar imaging[C]. IEEE Radar Conference, Waltham, Massachusetts, 2007: 128-133.( 1) 1) |
| [8] | Herman M A and Strohmer T. High resolution radar via compressed sensing[J]. IEEE Transactions on Signal Processing, 2009, 57(6): 2275-2284.( 1) 1) |
| [9] | Gurbuz A C, McClellan J H, and Scott W R Jr. GPR imaging using compressed measurements[C]. International Geoscience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 2008, 2: II-13-II-16.( 1) 1) |
| [10] | Suksmono A B, Bharata E, Lestari A A, et al. Compressive stepped-frequency continuous-wave ground penetrating radar[J]. IEEE Geoscience and Remote Sensing Letters, 2010, 7(4): 665-669.( 1) 1) |
| [11] | YANG J, Thompson J, HUANG X, et al. Random-frequency SAR imaging based on compressed sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(2): 983-994.( 1) 1) |
| [12] | Tello M, Lopez-Dekker P, and Mallorqui J J. A novel strategy for radar imaging based on compressive sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(12): 4285-4295.( 1) 1) |
| [13] | Patel V M, Easley G R, Healy D M, et al. Compressed synthetic aperture radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 244-254.( 1) 1) |
| [14] | Nguyen L H, Tran T, and Thong D. Sparse models and sparse recovery for ultra-wideband SAR applications[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 940-958.( 1) 1) |
| [15] | Batu O and Certin M. Parameter selection in sparsity-driven SAR imaging[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 3040-3050.( 1) 1) |
| [16] | Onhon N O and Certin M. A sparsity-driven approach for joint SAR imaging and phase error correction[J]. IEEE Transactions on Imaging Processing, 2012, 21(4): 2075-2088.( 1) 1) |
| [17] | Stojanovic I, Certin M, and Karl W C. Compressed sensing of monostatic and multistatic SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(6): 1444-1448.( 1) 1) |
| [18] | FANG J, XU Z, ZHANG B, et al. Fast compressed sensing SAR imaging based on approximated observation[J]. IEEE Journal of Selected Topics in Applied Earth Observation and Remote Sensing, 2014, 7(1): 352-363.( 1) 1) |
| [19] | Potter L C, Ertin E, Parker J T, et al. Sparsity and compressed sensing in radar imaging[J]. Proceedings of the IEEE, 2010, 98(6): 1006-1020.( 1) 1) |
| [20] | Certin M, Stojanovic I, Onhon N O, et al. Sparsity-driven synthetic aperture radar imaging: reconstruction, autofocusing, moving targets, and compressed sensing[J]. IEEE Signal Processing Magazine, 2014, 31(4): 27-40.( 1) 1) |
| [21] | JIANG Q, WANG S, Ziou D, et al. Ship detection in RADARSAT SAR imagery[C]. IEEE International Conference on Systems, Man and Cybernetics, San Diego, California, USA, 1998, 5: 4562-4566.( 1) 1) |
| [22] | Tison C, Nicolas J-M, Tupin F, et al. A new statistical model for Markovian classification of urban areas in high-resolution SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 42(10): 2046-2057.( 1) 1) |
| [23] | LI H, HONG W, WU Y, et al. On the empirical-statistical modeling of SAR images with generalized Gamma distribution[J]. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(3): 386-397.( 1) 1) |
| [24] | Henschel M D, Rey M T, Campbell J W M, et al. Comparison of probability statistics for automated ship detection in SAR imagery[C]. International Conference on Applications of Photonic Technology, Ottawa, Canada, 1998, 3491: 986-991.( 1) 1) |
| [25] | Wackerman C C, Friedman K S, Pichel W G, et al. Automatic detection of ships in RADARSAT-I SAR imagery[J]. Canadian Journal of Remote Sensing, 2001, 27(5): 568-577.( 1) 1) |
| [26] | WANG C, LIAO M, and LI X. Ship detection in SAR image based on the Alpha-stable distribution[J]. Sensors, 2008, 8(8): 4948-4960.( 1) 1) |
| [27] | Frery A C, Correia A H, and Freitas C D. Classifying multifrequency fully polarimetric imagery with multiple sources of statistical evidence and contextual information[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(10): 3098-3109.( 1) 1) |
| [28] | GAO G, LIU L, ZHAO L, et al. An adaptive and fast CFAR algorithm based on automatic censoring for target detection in high-resolution SAR image[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(6): 1685-1697.( 1) 1) |
| [29] | Yeremy M L, Geling G, Rey M, et al. Results from the Crusade ship detection trial: polarimetric SAR[C]. International Geoscience and Remote Sensing Symposium (IGARSS), Toronto, Ontario, Canada, 2002, 2: 711-713.( 1) 1) |
| [30] | 丘昌镇. 高分辨率SAR图像目标分类特征提取与分析[D]. [硕士论文],国防科技大学, 2009: 2-4. QIU C. Feature extraction and analysis of high-resolution SAR images for target classification[D]. [Master dissertation], National University of Defense Technology of China, 2009: 2-4.( 1) 1) |
| [31] | 贺志国, 陆军, 匡纲要. SAR图像特征提取与选择研究[J]. 信号处理, 2008, 24(5): 813-823. HE Z, LU J, and KUANG G. A survey on feature extraction and selection of SAR images[J]. Signal Processing, 2008, 24(5): 813-823.( 1) 1) |
| [32] | 计科峰. SAR图像目标特征提取与分类方法研究[D]. [博士论文],国防科技大学, 2003: 35-56. JI K Targets feature extraction and classification methods for SAR images[D]. [Ph.D. dissertation], National University of Defense Technology of China, 2003: 35-56.( 1) 1) |
| [33] | Çertin M. Feature-enhanced synthetic aperture radar imaging[D]. [Ph.D. dissertation], Boston University, 2001: 38-206.( 1) 1) |
| [34] | Certin M, Karl W C, and Castanon D A. Feature enhancement and ATR performance using nonquadratic optimization-based SAR imaging[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1375-1395.( 1) 1) |
| [35] | Samadi S, Certin M, and Masnadi-Shirazi M A. Multiple feature-enhanced SAR imaging using sparsity in combined dictionaries[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(4): 821-825.( 1) 1) |
| [36] | ZHANG B, HONG W, and WU Y. Sparse microwave imaging: principles and applications[J]. SCIENCE CHINA Information Science, 2012, 55(8): 1722-1754.( 1) 1) |
| [37] | Tropp J A and Wright S J. Computational methods for sparse solution of linear inverse problems[J]. Proceedings of the IEEE, 2010, 98(6): 948-958.( 1) 1) |
| [38] | Donoho D L, Johnstone I M, Koch J C, et al. Maximum entropy and the nearly black object[J]. Journal of the Royal Statistical Society, Series B, 1992, 54(1): 41-81.( 1) 1) |
| [39] | Bouman C and Sauer K. A generalized Gaussian image model for edge-preserving MAP estimation[J]. IEEE Transactions on Image Processing, 1993, 2(3): 296-310.( 1) 1) |
| [40] | CHANG L and WU J. An improved RIP-based performance guarantee for sparse signal recovery via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2014, 60(9): 5702-5715.( 1) 1) |
| [41] | DING J, CHEN L, and GU Y. Perturbation analysis of orthogonal matching pursuit[J]. IEEE Transactions on Signal Processing, 2013, 61(2): 398-410.( 1) 1) |
| [42] | 张爱冰. 高分辨率SAR图像复杂目标属性散射中心特征提取[D]. [硕士论文],国防科技大学, 2009: 9-48. ZHANG A. Attributed scattering center feature extraction of complex target from high resolution SAR imagery[D]. [Master dissertation], National University of Defense Technology of China, 2009: 9-48.( 1) 1) |
| [43] | Cho S, Haralick R, and Yi S. Improvement of Kittler and Illingworths's minimum error thresholding[J]. Pattern Recognition, 1989, 22(5): 609-617.( 1) 1) |


