②(南京航空航天大学雷达成像与微波光子技术教育部重点实验室 南京 210016)
②(Radar Imaging & Microwave Photonics Technology Key Laboratory of Ministry of Education, Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China)
合成孔径雷达[1, 2](Synthetic Aperture Radar,SAR)成像中,由于雷达平台非理想运动、传播介质不均匀等因素使得回波延迟误差不可避免,这种误差随散射点的空间位置变化而变化,即误差具有空变性。回波延迟误差不仅在方位向引入相位误差,导致图像发生方位向散焦;还会产生额外的距离徙动,在成像过程中无法得到校正,导致图像在距离向发生散焦。一般而言,SAR成像的初步环节先利用惯导系统记录的数据进行运动补偿。当惯导精度无法满足要求时,必须从回波数据中提取并补偿相位误差,即自聚焦处理。当观测场景比较小,残留距离徙动不超过一个距离分辨单元时,可以忽略误差的空变性和残留距离徙动效应,可以直接利用传统自聚焦方法,典型如相位梯度自聚焦[3, 4](Phase Gradient Autofocus,PGA)算法进行自聚焦处理。随着成像分辨率的提高,合成孔径长度的增加,残留距离徙动往往会跨越多个距离单元,这时必须考虑残留距离徙动和方位相位误差同时补偿,即2维自聚焦方法。文献[5]将PGA扩展成2维,提出2-D PGA算法试图解决这一问题,但该方法由于没有足够的数据冗余度,相位误差估计性能很难得到保证,还无法像1维PGA那样实用。而文献[6, 7]将2维误差近似成残留距离徙动和方位相位误差,分别对其进行估计和补偿。以上自聚焦方法都认为2维相位误差是完全未知的,并没有考虑2维相位误差的内部解析关系,属于对2维相位误差的盲估计。这种盲估计主要有两个缺陷:首先它没有足够的冗余度来保证估计精度,其次它估计的参数多,计算量相比1维自聚焦成倍增加,算法实时性能较差。文献[8]分析了在极坐标格式(Polar Format Algorithm,PFA)下残留2维相位误差的解析结构,利用这种先验信息将2维相位误差估计问题进行降维处理,从而减少计算量同时提高2维估计精度。
另一方面,由于SAR成像算法复杂度高、数据吞吐量大,如何实时有效处理数据是一个热门课题。随着工艺的发展,现场可编辑门阵列(Field Programmable Gate Array,FPGA)的集成度越来越高,功耗、价格也不断降低,用FPGA实现信号处理成为一个有效手段。自2004年Sandia实验室MiniSAR系统采用FPGA实现了PFA聚束SAR实时成像[9],FPGA以其并行、流水线、可重构等优势逐渐在实时SAR成像领域占据重要地位。目前基于FPGA平台的SAR成像系统处理的大多数是SAR预处理和成像处理,如文献[10]介绍了利用FPGA实现了2 GB SAR信号的多通道、大规模存储管理、FIR滤波与降采样等预处理功能。文献[11]提出了一种用FPGA实现星载SAR实时成像处理的方法,利用7片FPGA以100 MHz的系统时钟33 s左右处理了16K×16K个星载样本点的成像处理。文献[12]介绍了基于FPGA的机载高分辨聚束式SAR实时成像系统,利用经典的极坐标格式算法在2维波数域完成了运动误差估计及补偿,并以100 MHz的时钟在11 s内处理了16K×32K点8 bits数据的成像处理。
而基于FPGA的自聚焦算法的研究较少,如文献[13]在一片Xilinx Virtex-IV芯片上实现了128×128大小4 bits仿真数据的运动补偿和成像,其将雷达数据全部存储在FPGA的片内RAM中, 几乎占用了全部存储资源,难以在实际中得到应用。文献[14]为了减少PGA算法的迭代,在同一个距离单元选取多个孤立的强散射点,在75 MHz的时钟下完成一次迭代校正,处理图像大小为2K×4K。然而选取孤立强点需要判断杂波和混叠干扰,选取过程过于复杂,且对于没有多个好的孤立强点的图像,其仅进行一次迭代的聚焦效果受到很大限制。另外一点,它们自聚焦的场景都比较小,可将相位误差近似成空不变进行处理,但无法适用于空变误差场合。
针对残留距离徙动无法忽略和大场景观测中相位误差的空变性这两种情况,并兼顾处理效率,本文提出了一种基于FPGA的2维自聚焦处理方案。该方案主要包括空不变粗补偿和分块PGA精细补偿。粗补偿主要利用先验的解析结构将估计的方位相位误差映射到2维相位误差,完成残留距离徙动校正和粗略相位补偿,即2维自聚焦;然后采用分块PGA和子图拼接的方法补偿空变误差。本文详细论述了该2维自聚焦处理方案的FPGA实现过程,并对资源占用、运算速度精度和聚焦效果进行了分析。系统工作频率为200 MHz,可在5.7 s内完成了8K×8K单精度复图像的自聚焦处理和存储,并在Xilinx KC705开发板上得到验证。实验结果表明该处理方案自聚焦处理效果显著,满足实时性要求,具有一定的民用和军事工程实践价值。
2 自聚焦算法原理 2.1 相位梯度自聚焦相位梯度自聚焦(Phase Gradient Autofocus,PGA)是一种非参数模型算法,能够有效估计和补偿低阶和高阶相位误差,是一种稳健性良好的自聚焦算法。PGA算法主要包括以下几个步骤:
(1) 选择大能量的距离单元
对于复杂场景,可以选取部分能量较大的距离单元进行处理,这样可以极大减少运算量,带来的误差也可以忽略。
(2) 圆周移位
在SAR复图像域,寻找每一个距离门的最强散射点,将其循环移位到零频率处,使所有最强点位于图像中心。
(3) 加窗
保留最强点包含的模糊信息,同时去除背景杂波和其他散射点对相位估计的干扰,提高信噪比。
(4) 相位误差估计
对圆周移位和加窗后图像数据做IFFT到距离压缩相位历史域,相位差的最大似然估计表达式为:
| \[\Delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Phi } \left( m \right) = \arg \left[ {\sum\limits_{n = 0}^{N - 1} {g_n^*} \left( m \right) \cdot {g_n}\left( {m + 1} \right)} \right]\] | (1) |
对$\Delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Phi } \left( m \right)$进行积分(求和)就可以算出整个孔径上的相位误差,如式(2):
| \[\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Phi } \left( m \right) = \sum\limits_{i = 1}^m {\Delta \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Phi } \left( i \right)} ,\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Phi } \left( 0 \right) = 0\] | (2) |
(5) 迭代校正
校正后新图像距离单元中的强散射点的点散布函数会变得尖锐,因此下一次迭代中减少窗宽以进一步提高信噪比。一般迭代4~6次可达到收敛。
2.2 2维自聚焦算法随着误差的增大,成像分辨力的提高,残留距离徙动跨越距离单元变得不可避免,因此有必要考虑同时补偿残留距离徙动和方位相位误差。文献[8]详细分析了PFA极坐标格式转换对残留误差的影响,得到2维相位误差和方位相位误差之间存在如下映射关系:
| $\phi \left( \bar{t},{{{\bar{f}}}_{\tau }} \right)=\frac{{{f}_{0}}+{{{\bar{f}}}_{\tau }}}{{{f}_{0}}}{{\phi }_{0}}\left( \frac{{{f}_{0}}}{{{f}_{0}}+{{{\bar{f}}}_{\tau }}}\bar{t} \right)$ | (3) |
其中$\phi \left( \bar{t},{{{\bar{f}}}_{\tau }} \right)$为2维相位误差,${{\phi }_{0}}\left( {\bar{t}} \right)$为方位1维相位误差,${{f}_{0}}$为载频,${{\bar{f}}_{\tau }}$为距离频率,$\bar{t}$为方位时间。实际中,${{\phi }_{0}}\left( {\bar{t}} \right)$可以通过常规自聚焦算法(如PGA)估计得到。然后根据式(3)计算出2维相位误差计算。
2.3 自聚焦处理方案流程图
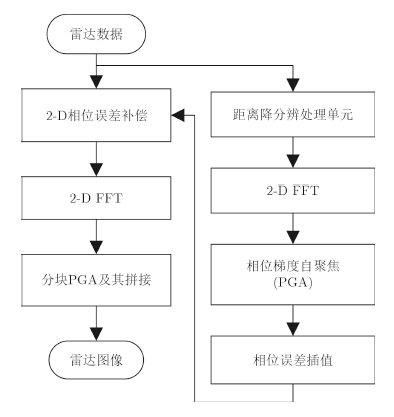
通过前面的分析,我们知道2维相位误差与方位1维相位误差之间的映射关系,利用这种先验知识实现进行2维自聚焦,同时考虑到PFA形式下残留误差的空变性,采用分块PGA和拼接的方法进一步补偿空变误差。整个基于FPGA的2维自聚焦算法处理流程如图 1所示。
|
图 1 2维自聚焦处理流程 Fig.1 Flow of 2-D autofocus processing |
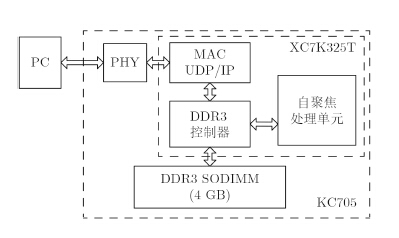
其板级结构如图 2,该方案处理的数据为成像处理后的2维数据域数据(经2维FFT后可得到散焦的复图像),场景大小为8K×8K,每个采样点实部虚部分别以32位单精度数表示。数据通过上位机从PC经RJ45接口传送到处理板上并存储在DDR3中,之后自聚焦处理单元控制DDR数据总线,对原始数据进行处理,得到重新聚焦的图像,最后再将数据发送回PC机显示重聚焦的图像。
|
图 2 自聚焦处理系统的整体结构 Fig.2 Overall structure of autofocus processing system |
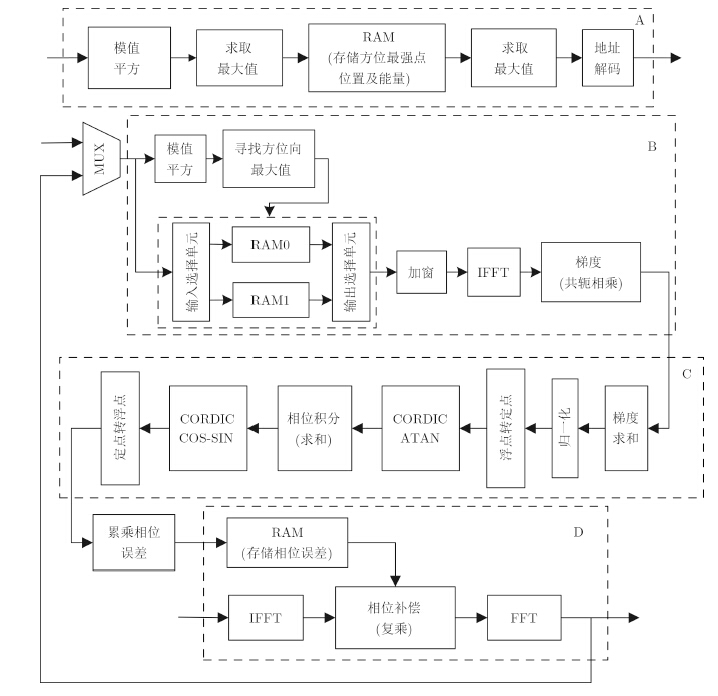
本文实现了PGA模块的参数化设计,用户只需在顶层设置PGA的相关参数,如聚焦场景大小,选择的距离单元数,迭代次数。方位向点数越大,其消耗的资源越多,考虑到误差的空变性,PGA聚焦场景也不能过大;方位向点数越小,资源消耗少,但对于散焦程度较大的情况可能无法包含足够的散焦信息,从而影响估计精度。选择适当的距离单元数来估计相位误差能够减少运算量,同时也需要考虑保留足够的冗余度以保证估计精度。权衡估计精度、运算量和资源耗用,并辅以经验知识,本文选择自聚焦场景大小为${N_{\rm r}}{\rm{ = 1}}024,{N_{\rm a}}= 1024$,距离单元数${N_{\rm Sel}}{\rm{ = 256}}$。由于迭代次数并不影响资源消耗,只会稍微影响处理时间,为保证收敛,本文迭代次数设置为6。本文设计的PGA模块的结构框图如图 3所示。该模块主要包括4个子模块,距离单元选择模块(A)、相位梯度估计模块(B)、积分相位误差(C)和相位误差补偿模块(D),下面将详细介绍每个子模块。
|
图 3 相位梯度自聚焦(PGA)模块结构图 Fig.3 Structure diagram of PGA module |
A模块选择出能量最大的${N_{\rm Sel}}\left( {0 < {N_{\rm Sel}}{\rm{ < 1}}0{\rm{24}}} \right)$
个距离单元,用户控制DDR3 Controller遍历输入散焦图像的每一个距离门,把得到每个距离门模值的最大值存放在RAM里,然后再从RAM选出最大值,通过地址解码后,把地址读取此大能量距离门,一方面送入B模块,一方面把挑选的子图像(${{N}_{\rm Sel}}\times {{N}_{\rm a}}$)存放到一块新的内存空间。清除RAM中的最大值后,类似地再选择出最大值,直到所需要选择的${{N}_{\rm Sel}}$个距离门全部选择完毕。
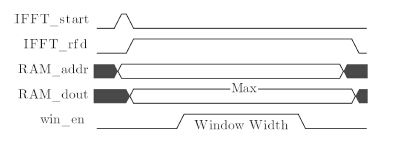
B模块计算每一个距离门的相位梯度。由于要循环移位操作,首先先把数据缓存在RAM中,待寻找出方位向的最大值的位置索引$\text{inde}{{\text{x}}_{\text{max}}}$后,设置RAM的读地址indexmax-Na/2,同时启动IFFT模块的start信号,如图 4。indexmax-Na/2利用了无符号的循环特性,使得RAM的移位输出$\text{ra}{{\text{m}}_{\rm out}}$的最大值位于IFFT模块输入数据流的中心。再根据当前迭代的窗体宽度来设置使能$\text{wi}{{\text{n}}_{\rm en}}$,实现加窗操作。为了实现流水操作,我们设置了两个RAM,RAM0(1)移位输出时,RAM1(0)缓存下一个距离门数据,这样用于估计相位误差的距离门就可以连续不断地输入B模块了。
|
图 4 中心移位、加窗时序图 Fig.4 Timing of circular shifting and windowing |
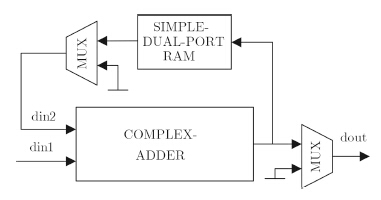
C模块中梯度求和接收模块B计算出来的相位误差梯度(一条方位线$\text{din1}$),与从双口RAM中取出的上一条方位线进行累加求和,并把累加结果存储到双口RAM中,直至求出所选的${{N}_{\rm Sel}}$条方位线之和,结构如图 5。输入第1条方位线时,$\text{din2}$置零,输出最后一个累加结果时$\text{dout}$选通。双口RAM具有2组地址/数据线,只要双口读写地址不冲突即能同时进行读写操作。从图 6可以看出,经过复数加法器的延迟,双口RAM的读写地址总是处于不同位置。
|
图 5 梯度求和模块 Fig.5 Structure of Grad_Sum module |
|
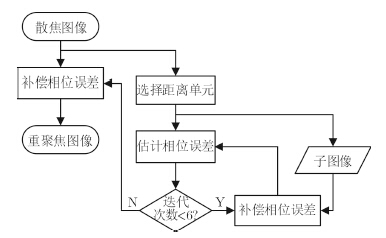
图 6 相位梯度自聚焦(PGA)模块处理流程图 Fig.6 Flow chart of PGA module |
为了求得相位误差,必须对相位误差梯度积分(求和)。求和的实现可以通过对单位模值的复数求积得到,也可以利用CORDIC对复数求相角再求和得到。前者由于复乘的延迟比较大,而求取相位误差须做${{N}_{\rm a}}-1$次复乘,耗费资源大、时间长。后者先把数据转换成定点格式,再求取相角,然后定点求和得到相位误差,最后再转换成浮点数。定点加法可以在每个时钟周期输出一个求和结果同时保持较高的综合频率。本文采用的是第2种方式。
D模块补偿相位,补偿结果输入到B模块进行下一迭代。补偿模块前有一个相位误差累乘模块,其结构与图 5类似。它输出第i次迭代的相位误差之积。这样每次补偿时,只需输入${{N}_{\rm Sel}}\times {{N}_{\rm a}}$的原始子图像进行补偿,而不需要考虑存储中间迭代补偿的结果。连续5次子图像补偿后,再经过相位误差估计就能得到6次迭代的总相位误差,最后再输入${{N}_{\rm r}}\times {{N}_{\rm a}}$的原始散焦图像进行补偿得到最后的重聚焦的图像,把结果存储到DDR3。PGA模块的处理流程图如图 6。
PGA模块的输入输出位宽为64 bits,时钟为200 MHz,可得输入输出带宽分别为1.6 GB/s,模块可以连续不断输入输出数据流,因此处理时间主要取决于处理的数据量。通过选择一定的距离单元数,累乘相位误差补偿等操作可有效减少需要处理的数据量。与原始PGA相比,本文读写操作量大为减少,如表 1。
| 表 1 运算量比较 Tab. 1 Comparison of computation |
要实现2维自聚焦需要把PGA估计出方位向相位误差根据式(3)映射到2维相位误差,该映射可以通过插值实现。权衡计算精度和运算量,SAR数据处理中常使用8点的加权Sinc插值。FPGA实现插值时一般将升采样的插值核存储在表格中,本设计Sinc系数量化位移为采样间隔的1/16,利用8个深度为16,位宽为32的ROM来存储此系数表。8个ROM相同地址位置对应的数据为一组Sinc卷积核系数。偏移量为0的一组系数放在地址0,偏移量为15/16的系数存储在ROM的高地址位置。
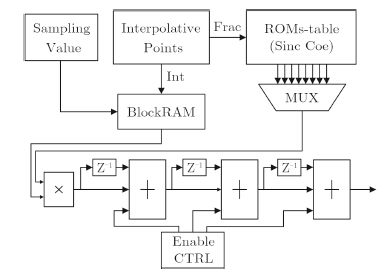
Sinc插值主要有2个子模块:待插值点判断模块和Sinc卷积模块。首先是一个的预处理,通过浮点数IP核将待插值点转化为定点数格式。因为数据是均匀采样且待插值点已经归一化,所以整数部分就是定位位置,而小数部分则指示了所需一组Sinc系数的偏移量。下一步将8个采样数据和一组Sinc系数对应相乘,然后累加起来得到插值结果。值得指出的是,对于那些处于采样样本边界而找不到8个点或者边界外的待插值点,本设计采用两个标识信号来指示这两种特殊情况。只要这两个标识其一有效,则把数据RAM的输出置为0,让其继续进入乘法和加法模块。这样带来一个好处,特殊点和正常点的处理一体化,使得模块设计简单、稳定。Sinc插值模块框图如图 7。
|
图 7 Sinc插值模块框图 Fig.7 Structure diagram of Sinc interpolation module |
本文通过场景中心区域估计出来的方位相位误差,并以此来计算2维相位误差,然后补偿整个场景。这一步的主要作用是校正残留距离徙动和粗略地补偿相位误差,但由于整个场景的相位误差是空变的,因此有必要对图像进行分块PGA,进一步校正误差。只要子块的大小足够小,则小块内方位相位误差可近似成空不变。为消除相邻子块边界目标散焦问题,相邻子块选取会有部分重叠。如果重叠的部分越小,则子块数(运算量)越少,子块边界目标聚焦效果越差,反之相反。本文选择子块的大小为1K×1K,方位向重叠部分为512,这样一方面能够复用前述的PGA模块以减少资源耗用,另一方面也可以保证子块边界目标聚焦效果,同时能够刚好将方位向8K分成整数块。有必要指出,PGA无法估计出线性误差,故聚焦后的图像会有一个方位向的线性位移,此位移如果不加处理会使整张图像发生错位。此位移量可以通过对聚焦前后的子图像进行方位向互相关求得,如图 8。按顺序依次输入两个子图的同一距离频率单元,第1个缓存在FIFO里($\text{Flag=0}$),等第2个输入时($\text{Flag=1}$),两者共轭相乘,再IFFT到时域得到相关峰图,并利用距离向的冗余数据来提高峰值的精确度。在IFFT阶段不需要将峰值移到中心,对其求最大值得到的即是相对左偏移量。

|
图 8 方位向互相关 Fig.8 Cross-correlation in azimuth direction |
本节对自聚焦处理模块在板卡上进行验证。验证平台选用Xilinx公司的KC705评估板。该板集成了一片Kintex-7 XC7K325T-2FFG900C FPGA,4 GB DDR3内存条,三态以太网PHY和200 MHz差分时钟。数据从上位机通过千兆网发送数据到板卡上的内存中,再进行自聚焦处理,处理结果存储在内存中,最后发送回PC机上显示出雷达图像。
当系统工作的时钟频率为200 MHz时,自聚焦处理单元在5.7 s内完成了8K×8K散焦图像的2维自聚焦处理。由于网络不稳定对数据传输速率的影响、数据传输方式的多样性(如以太网、PCIe等),数据传输的时间就不能准确确定。所以本文不对数据传输时间作记录。
整个自聚焦处理系统在一片XC7K325T芯片上实现,系统包括了DDR3内存控制器和千兆以太网MAC、UDP/IP协议栈和自聚焦处理单元,表 2给出了系统的FPGA资源占用情况。
| 表 2 资源使用率 Tab. 2 Resource utilization |
图 9为FPGA对实测数据处理的结果。如图 9(a),图 9(b),由于运动测量单元精度限制和介质传播不均匀性的影响,PFA直接成像的图像散焦程度较大,特别是远离场景中心的地方几乎无法成像。图 9(c),图 9(d)给出了FPGA自聚焦的处理结果。对比处理前后图像,可以看出聚焦效果很显著,在远离场景中心的地方也能聚焦成像。图 10(a)给出了PFA处理后的距离压缩图像(局部),可以明显看出残留距离徙动仍有跨距离单元走动,越远离中心徙动弯曲程度越大。2维自聚焦处理后,如图 10(b),残留的距离徙动得到了有效补偿。

|
图 9 实测数据处理结果 Fig.9 Processing results of measured data |

|
图 10 距离压缩图像(局部) Fig.10 Range-compressed image (partial) |
同时,我们将FPGA上计算得到的相位误差与Matlab处理的结果进行了比较,如图 11。可以看出两者基本上是重合的,这说明FPGA上浮点运算的准确性,系统处理的精度能够满足要求。

|
图 11 FPGA与Matlab估计的相位误差 Fig.11 Comparison of phase error estimated by FPGA and Matlab |
本文讨论了一种2维自聚焦算法的FPGA实现,能够实现对8K×8K场景的散焦复图像的2维自聚焦处理,并在KC705评估板通过验证。文章首先介绍了自聚焦算法原理,然后详细陈述主要子模块的设计过程。相位梯度自聚焦模块能准确估计方位向1维相位误差,通过Sinc插值实现了1维相位误差到2维相位误差的映射,在2维数据域上补偿2维相位误差,能够有效地校正残留距离徙动并重聚焦图像,分块PGA校正空变误差,进一步聚焦图像。实测数据处理结果表明此2维自聚焦算法聚焦效果显著,处理时间和精度都能满足要求。在后续工作中,可以结合基本的成像算法模块使之成为一个完整的实时SAR成像系统。
| [1] | 保铮, 刑孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 186-220. Bao Zheng, Xing Meng-dao, and Wang Tong. Radar Imaging Technology[M]. Beijing: Publishing House of Electronics Industry, 2005: 186-220.( 1) 1) |
| [2] | Zhou Hui, Zhao Feng-jun, Yu Wei-dong, et al.. SAR imaging of ground moving targets with non-ideal motion error compensation[J]. Journal of Radars, 2015, 4(3): 265-275.( 1) 1) |
| [3] | Wahl D E, Eichel P H, Ghiglia D C, et al.. Phase gradient autofocus-a robust tool for high resolution SAR phase correction[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(3): 827-835.( 1) 1) |
| [4] | 卿吉明, 徐浩煜, 梁兴东, 等. 一种可用于实时成像的改进PGA算法[J]. 雷达学报, 2015, doi: 10.12000/JR15037. Qing Ji-ming, Xu Hao-yu, Liang Xing-dong, et al.. An improved phase gradient autofocus algorithm used in real-time processing[J]. Journal of Radars, 2015, doi: 10.12000/JR15037.( 1) 1) |
| [5] | Warner D W, Ghiglia D C, Fitzgerrel A, et al.. Two-dimensional phase gradient autofocus[C]. Proceedings of SPIE Image Reconstruction from Incomplete Data, 2000, 4123: 162-173.( 1) 1) |
| [6] | Zhu Dai-yin. SAR signal based motion compensation through combining PGA and 2-D map drift[C]. 2009 2nd Asian-Pacific Conference on Synthetic Aperture Radar, 2009: 435-438.( 1) 1) |
| [7] | Kirk J C, Lefevre R, Van Dalen Wetters, et al.. Signal based motion compensation (SBMC)[C]. IEEE Radar Conference, 2000: 463-468.( 1) 1) |
| [8] | 毛新华, 朱岱寅, 朱兆达. 一种超高分辨率机载聚束SAR 2维自聚焦算法[J]. 航空学报, 2012, 33(7): 1289-1295. Mao Xin-hua, Zhu Dai-yin, and Zhu Zhao-da. 2-D autofocus algorithm for ultra-high resolution airborne spotlight SAR imaging[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(7): 1289-1295.( 2) 2) |
| [9] | Sandia National Laboratories. A Publication Featuring What's New in Remote Sensing Technology at Sandia National Laboratories. http://www.sandia.gov/radar/ sar.html, 2004, 7.( 1) 1) |
| [10] | Xie Yi-zhuang and Long Teng. Storage and pretreatment of SAR signal based on FPGA[C]. 9th International Conference on Signal Processing, 2008: 2380-2383.( 1) 1) |
| [11] | 熊君君, 王贞松, 等. 星载SAR实时成像处理器的FPGA实现[J]. 电子学报, 2006, 33(6): 1070-1072. Xiong Jun-jun, Wang Zhen-song, et al.. The FPGA design of on board SAR real time imaging processor[J]. Acta Electronica Sinica, 2006, 33(6): 1070-1072.( 1) 1) |
| [12] | 周芳, 唐禹, 张佳佳, 等. 机载高分辨聚束式SAR实时成像处理系统的FPGA实现[J]. 电子与信息学报, 2011, 33(5): 1248-1252. Zhou Fang, Tang Yu, Zhang Jia-jia, et al.. Real-time image formation for airborne high resolution spotlight SAR based on FPGA[J]. Journal of Electronics & Information Technology, 2011, 33(5): 1248-1252.( 1) 1) |
| [13] | 郑晓双, 禹卫东, 李早社. 机载SAR实时运动补偿和成像的FPGA实现[J]. 数据采集与处理, 2008, 23(5): 614-618. Zheng Xiao-shuang, Yu Wei-dong, and Li Zao-she. Real-time motion compensation and image formation for airborne SAR based on FPGA[J]. Journal of Data Acquisition & Processing, 2008, 23(5): 614-618.( 1) 1) |
| [14] | 郝智泉, 王贞松, 刘波. FPGA实时实现PGA算法的研究[J]. 计算机研究与发展, 2008, 45(2): 342-347. Hao Zhi-quan, Wang Zhen-song, and Liu Bo. Research on real-time realizing PGA algorithm in FPGA[J]. Journal of Computer Research and Development, 2008, 45(2): 342-347.( 1) 1) |


