雷达自动目标识别(Radar Automatic Target Recognition,RATR)技术是指通过获取并分析雷达发射并经过目标反射回来的电磁波特性,从中提取出所包含的目标属性信息,从而自动识别目标的类型、类别[1]。在战场日趋透明的现代信息化战争中,RATR系统可以实现目标类型、真假和属性识别,完成战略预警和战场监视,从而对目标威胁度以及战场全局环境有准确的预判,因此,RATR技术成为现代雷达技术的重要发展方向之一。
基于高分辨距离像(High Resolution Range Profile,HRRP)的目标识别由于其所含目标信息量丰富、对存储量要求低、算法设计简单等优点使其近几年来越来越受到青睐。而调频步进频雷达信号通过发射一系列载频线性跳变的调频信号,将接收回波进行脉内脉冲压缩及脉间IFFT的方法合成高分辨1维距离像,是一种重要的距离向高分辨信号形式。因其具有高的距离分辨率,同时又能大幅度降低信号处理机的带宽需求等优势,因此被广泛用在雷达系统中。
频率步进信号的信号处理算法,也即1维高分辨像成像算法的选择决定了最终1维距离像的成像质量好坏,不同的信号处理算法有着各自的优缺点,目前较常用的高分辨成像算法有3类,分别是目标抽取算法[2, 3, 4]、时域合成算法[5]和频域合成算法[6]。它们的计算流程及运算复杂度各不相同,但其共同本质都在于利用匹配滤波的原理得到场景的清晰1维像。本文在此基础上,提出了一种快速匹配滤波1维高分辨像成像算法,利用匹配滤波原理使信噪比达到最优,用FFT快速算法进行计算,并利用Type-II型NUFFT快速算法一步完成从2维回波信号(脉内距离维,脉间频率维)到1维高分辨距离像的脉冲压缩高分辨成像过程,可以获得满意的处理结果。
为满足实时处理需要,较低的算法复杂度是衡量成像算法好坏的重要因素。本文经过仔细分析与仿真验证,论证了本文成像算法可以保证目标上各个散射中心的信噪比,并给出了算法的计算性能分析。
文章的最后采用雷达仿真数据验证了理论分析的正确性。
2 非均匀FFT理论传统的傅里叶变换(FFT)算法要求输入数据是等间隔采样的,当输入数据非均匀采样时,传统傅里叶变换算法失效。非均匀采样快速傅里叶变换(Non-Uniform Discrete Fourier Transform,NUDFT)[7, 8]是解决这一问题的有效手段,NUFFT算法是在非均匀分布的数据域内进行快速计算的一系列方法[9, 10, 11, 12, 13, 14, 15]。一类典型的问题是由给定的频域N个非均匀采样点重建对应的时域函数。非均匀傅里叶变换自从诞生以来,已经在很多领域得到应用,应用领域从医学成像、射电天文学到求偏微分方程的数值解。本质上,NUFFT是FFT与插值运算的结合,其理论形式有两种:一种是从非均匀采样的域变到另一个均匀采样域,另一个是其逆过程。在本文中,两次用到NUFFT算法,一是调频步进频雷达回波的模拟,二是1维高分辨成像,因此在本节为简单起见,将简要介绍1-D 情况下的NUFFT算法原理。
传统的DFT算法用数学语言描述如下:
| \[\tilde h(\omega ) = \sum\limits_{n = 0}^{N - 1} {{h_n}{{\rm{e}}^{ - {\rm{j}}\omega n}}} \] | (1) |
当输入数据在时域和频域的采样点都为N时,式(1)可用快速傅里叶变换算法来实现:
| \[\begin{array}{l} \tilde h\left( {{\omega _{n'}}} \right) = \sum\limits_{n = 0}^{N - 1} {{h_n}\exp \left( { - {\rm{j}}\frac{{2\pi nn'}}{N}} \right)} ,\\ \quad \quad \quad n = 0,1, \cdots ,N - 1 \end{array}\] | (2) |
但是,在很多应用场合中数据是不等间隔采样的,通常的FFT算法不再适用。非等间距傅里叶变换(NUDFT)是解决这一问题的有效方法,类似于FFT与DFT的关系,NUFFT是NUDFT的快速算法。它的精度取决于所用的窗函数的类型及长度。在这里我们用到的是Type-II型2-D 逆NUFFT快速算法,它是由非均匀的频域采样数据求解均匀时域采样数据的过程。
| \[\begin{array}{l} {h_n} = \sum\limits_{m = 0}^{M - 1} {\tilde h\left( {{\omega _m}} \right)\exp ({\rm{j}}{\omega _m}n)} ,\\ \quad \quad n\; = 0,1, \cdots ,N - 1 \end{array}\] | (3) |
大多数NUFFT算法采用过采样技术,由窗函数计算得出,这样在时域和频域都有很好的聚焦特性,因此,式(3)的计算步骤总结如下:
(1) 格网化(插值):
| \[{H_k} = \sum\limits_{m = 0}^{M - 1} {{\upsilon _{mk}}\tilde h\left( {{\omega _m}} \right)} ,\;k = 1, \cdots ,K\] |
(2) K点DFT变换:
| \[{x_n} = \sum\limits_{k = 0}^{K - 1} {{H_k}\exp ({\rm{j}}2\pi kn/K)} \] |
(3) 将${x_n}$ 用变标因子$s_n^*$ 进行加权,其中${s_n}$ 是加权因子,“ $^*$”表示共轭操作,这样就可以得到时域的均匀采样数据 ${h_n}$。其中,常用到的变标因子有:余弦变标因子${s_n} = \cos \frac{{\pi n}}{{Nm}},n = - \frac{N}{2}, \cdots ,\frac{N}{2} - 1$ ;高斯变标因子${s_n} = {{\rm{e}}^{ - b{{\left( {\frac{{2\pi n}}{{Nm}}} \right)}^2}}},n = - \frac{N}{2}, \cdots ,\frac{N}{2} - 1$ ;三角变标因子 ${s_n} = {\rm{1}},n = - \frac{N}{2}, \cdots ,\frac{N}{2} - 1$等。
NUFFT总的算法复杂度为$O\left( {JM} \right) + O(K{\log _2}N)$,通常选取$K = 2N$和$J \le 10$ 。因此,NUFFT的算法复杂度除了一个常数项外与FFT相差不大,NUFFT算法更详细的细节请参见文献[14]。
3 基于NUFFT的快速匹配滤波成像算法 3.1 调频步进频雷达调频步进频信号是一系列载波频率等间隔线性跳变的线性调频脉冲串。记单个基带脉冲信号波形为:
| \[\begin{array}{l} {u_0}(t) = {\rm{rect}}\left( {\frac{t}{{{T_0}}}} \right)\exp \left( {{\rm{j}}\pi {K_0}{t^2}} \right)\\ {\rm{rect}}\left( t \right) = \left\{ {\begin{array}{*{20}{l}} {1,\; - 0.5 \le t < 0.5}\\ {0,\;{\rm{else}}} \end{array}} \right. \end{array}\] |
| \[x(t) = \sum\limits_{n = 0}^{N - 1} {{u_0}\left( {t - n{T_{\rm{r}}}} \right){{\rm{e}}^{{\rm{j}}2\pi {f_n}t}}} \] | (4) |
假设距离雷达位置为r处存在散射系数为${\sigma _0}$ 的静止目标,则该目标的雷达回波可以写成:
| \[y(t) = {\sigma _0}\sum\limits_{n = 0}^{N - 1} {{u_0}\left( {t - n{T_{\rm{r}}} - \frac{{2r}}{{\rm{c}}}} \right){{\rm{e}}^{{\rm{j}}2\pi {f_n}\left( {t - \frac{{2r}}{{\rm{c}}}} \right)}}} \] | (5) |
| \[s(t) = {\sigma _0}\sum\limits_{n = 0}^{N - 1} {{u_0}\left( {t - n{T_{\rm{r}}} - \frac{{2r}}{{\rm{c}}}} \right){{\rm{e}}^{ - {\rm{j}}2\pi {f_n}\frac{{2r}}{{\rm{c}}}}}} \] | (6) |
| \[{s_n}(t) = \int {{u_0}(t - \frac{{2r}}{{\rm{c}}})\sigma (r){{\rm{e}}^{ - {\rm{j}}2\pi {f_n}\frac{{2r}}{{\rm{c}}}}}} {\rm{d}}r\] | (7) |
调频步进频雷达的回波是时-频域的2维回波信号,其中脉内可看作场景的时域回波信号,脉间是载频线性跳变的频域信号。在将每个子脉冲变换到频域并完成匹配滤波之后,由于两个维度的采样率不同,而最终所成的1维距离像(HRRP)是时域均匀采样信号,因此由2维频域回波数据到1维像的成像过程可以看作是由非均匀的频域数据到均匀时域数据的非均匀傅里叶变换(NUDFT),因此可以由NUFFT快速算法来实现。下面将从回波模拟与成像两个过程介绍NUFFT调频步进频成像算法,两个过程互为共轭。
(1) 步进频回波模拟算子构建
式(7)为步进频回波信号的简单模型,其中积分核函数表征了步进频雷达测量与目标场景后向散射率之间的线性依赖关系可以用线性算子A来表示。下面用NUFFT快速算法来求解式(7)的积分。
首先,对式(7)作傅里叶变换得到频域表达式,
| \[{\tilde s_n}(f) = {\tilde u_0}(f)\int {\sigma (r){{\rm{e}}^{ - {\rm{j}}2\pi f\frac{{2r}}{{\rm{c}}}}}{{\rm{e}}^{ - {\rm{j}}2\pi {f_n}\frac{{2r}}{{\rm{c}}}}}} {\rm{d}}r\] | (8) |
| \[{\tilde u_0}(f) \approx \frac{1}{{\sqrt {{K_0}} }}{\rm{rect}}\left( {\frac{f}{{{K_0}{T_0}}}} \right)\exp \left( { - {\rm{j}}\pi \frac{{{f^2}}}{{{K_0}}} + {\rm{j}}\frac{\pi }{4}} \right)\] |
数据处理时通常用离散化来表示,令场景的距离分辨单元大小为$\Delta r$ ,距离像采样坐标为 ${r_l} = l\Delta r,l = 0,1,\cdots ,L - 1,{\sigma _l} = \sigma ({r_l})$。令回波的频域采样间隔为$\Delta {f_m}$ ,频域采样点可写成${f_m} = m\Delta {f_m},m = 0,1,\cdots ,M - 1$ 。另记 ${\tilde s_{nm}} = {\tilde s_n}({f_m}),{\tilde u_{0m}} = {\tilde u_0}({f_m})$ 。则式(8)的离散形式可表示成:
| \[\begin{array}{*{20}{l}} {{{\tilde s}_{nm}} = A{\bf{\sigma }} = {{\tilde u}_{0m}}\exp \left( { - {\rm{j}}2\pi n\Delta f{\tau _0}} \right)}\\ {\quad \quad {\rm{ }} \cdot \sum\limits_{l = 0}^{L - 1} {{\sigma _l}\exp \left( { - {\rm{j}}2\pi \Delta {f_m}\frac{{2\Delta r}}{{\rm{c}}}ml} \right.} }\\ {\quad \quad {\rm{ }}\left. { - {\rm{j}}2\pi \Delta f\frac{{2\Delta r}}{{\rm{c}}}nl} \right)} \end{array}\] | (9) |
| \[\begin{array}{*{20}{l}} {A = {{\left[ {{a_{nm,l}}} \right]}_{NM \times L}},\;\;\sigma = {{\left[ {{\sigma _l}} \right]}_{L \times 1}}}\\ {{a_{nm,l}} = {{\tilde u}_{0m}}\exp \left( { - {\rm{j}}2\pi n\Delta f{\tau _0}} \right)}\\ {\quad \quad \cdot \exp \left( { - {\rm{j}}2\pi \Delta {f_m}\frac{{2\Delta r}}{{\rm{c}}}ml - {\rm{j}}2\pi \Delta f\frac{{2\Delta r}}{{\rm{c}}}nl} \right)} \end{array}\] |
| \[\left. {\begin{array}{*{20}{l}} {{n_1} = l}\\ {{n_2} = l'}\\ {F({n_1},{n_2}) = \sigma (l)\delta (l - l')}\\ {j = (n - 1)M + m}\\ {{x_j} = - 2\pi \Delta {f_m}\frac{{2\Delta r}}{{\rm{c}}}m}\\ {{y_j} = - 2\pi \Delta {f_n}\frac{{2\Delta r}}{{\rm{c}}}n} \end{array}} \right\}\] | (10) |
| \[\begin{array}{*{20}{l}} {{{\tilde s}_{nm}} = f({x_j},{y_j})}\\ {\;\;\;\;\; = \sum\limits_{{n_1} = - {N_1}/2}^{{N_1}/2 - 1} {\sum\limits_{{n_2} = - {N_2}/2}^{{N_2}/2 - 1} {F({n_1},{n_2}){{\rm{e}}^{ - {\rm{j}}{n_1}{x_j}}}{{\rm{e}}^{ - {\rm{j}}{n_2}{x_j}}}} } }\\ {\;\;\;\;\;\;\;\;\;\;\;{x_j},{y_j} \in [0,2\pi ]} \end{array}\] | (11) |
对于静止场景,频率域仍然是均匀采样,因此式(11)所描述的回波模拟算子只是实现了距离均匀采样到快慢时间频率域的快速插值操作。以此为基础,可以扩展出非均匀频率步进,或动目标场景步进频成像的快速成像方法。
(2) 步进频快速成像算子构建
回波模拟算子A的共轭算子AH,可以看做是成像算子,将式(9)进行共轭操作,可以得到场景的后向散射系数,也即目标RCS的计算公式:
| \[\begin{array}{*{20}{l}} {{\sigma _l} = {A^{\rm H}}{{\tilde s}_{nm}} = \sum\limits_{n = 0}^{N - 1} {\sum\limits_{m = 0}^{M - 1} {{{\tilde s}_{nm}}{{\tilde u}_{0m}}} } }\\ {}\\ {\quad \quad \cdot \exp \left( {{\rm{j}}2\pi \Delta {f_m}\frac{{2\Delta r}}{{\rm{c}}}ml} \right)\exp \ge \left( {{\rm{j}}2\pi \Delta {f_n}\frac{{2\Delta r}}{{\rm{c}}}nl} \right)} \end{array}\] | (12) |
| \[\left. {\begin{array}{*{20}{l}} {{n_1} = n}\\ {{n_2} = m}\\ {F({n_1},{n_2}) = {{\tilde s}_{nm}}\tilde u_{0m}^*}\\ {j = l}\\ {{x_j} = 2\pi \Delta {f_m}\frac{{2\Delta r}}{{\rm{c}}}l}\\ {{y_j} = 2\pi \Delta {f_n}\frac{{2\Delta r}}{{\rm{c}}}l} \end{array}} \right\}\] | (13) |
| \[\begin{array}{*{20}{l}} {{\sigma _l} = f({x_j},{y_j})}\\ {\;\;\;\; = \sum\limits_{{n_1} = - {N_1}/2}^{{N_1}/2 - 1} {\sum\limits_{{n_2} = - {N_2}/2}^{{N_2}/2 - 1} {F({n_1},{n_2}){{\rm{e}}^{ - {\rm{j}}{n_1}{x_j}}}{{\rm{e}}^{ - {\rm{j}}{n_2}{x_j}}}} } ,}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{x_j},{y_j} \in [0,2\pi ]} \end{array}\] | (14) |
成像信噪比和计算复杂度往往是衡量成像算法好坏的两个重要因素,下面从这两个方面对新算法的性能进行评估。
根据第2节对NUFFT算法计算流程的分析,NUFFT成像方法的计算复杂度是数据维度以及加权函数长度的函数。因此,可以根据场景回波 ${\tilde s_{nm}}$维度和成像算子AH的相关参数来评估算法的计算量。本小节将从算法的工作流程切入,对算法计算复杂度各组成部分进行分析。同时,在此基础上,分析比对了新成像算法和传统成像算法的复杂度。
从图 1可知,原始回波数据的脉内脉冲压缩是4种算法共有的计算过程,因此为了计算量分析的方便,只比较4种算法其它计算步骤之间计算量的区别。假设雷达回波信号是P个子脉冲的回波,每个子脉冲回波进行N点采样(粗分辨单元)。
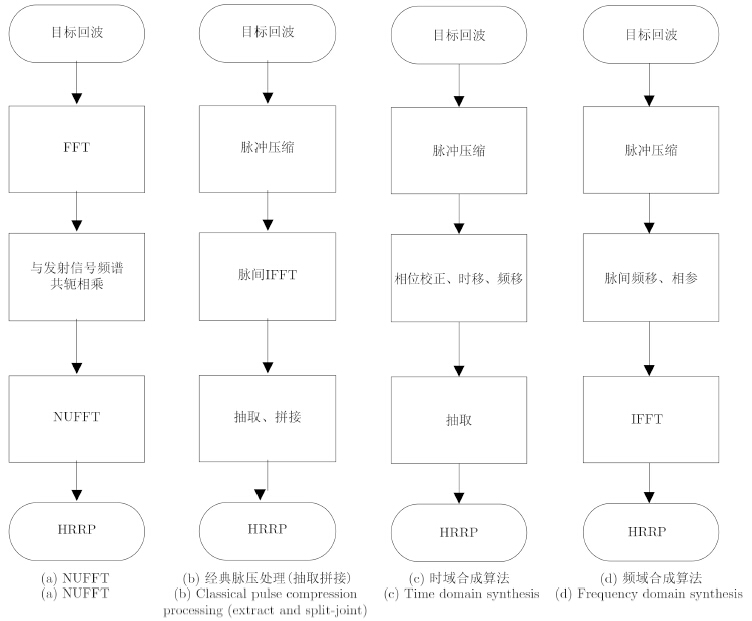 | 图 1 4种算法的计算流程分析 Fig. 1 Calculation flowchart of four algorithms |
(1) NUFFT方法
每个子脉冲内匹配滤波并变换到频域,所需计算量 $O(PN + PN{\log _2}N)$;格网化(插值)所需计算量$O(JP)$ ,其中 $J = I(p)/p$;
\[\begin{array}{*{20}{l}}
{O(PN + PN{{\log }_2}N + JP + NK{{\log }_2}I(p) + NI(p))}\\
{\quad = O(PN + PN{{\log }_2}N + I(p)}\\
{\quad \quad + NK{{\log }_2}I(p) + N \cdot I(p))}
\end{array}\]
(2) 抽取拼接法
计算量主要在于IFFT步骤,为了快速计算,通常在每个粗分辨单元上做2的整数倍IFFT运算,因此先将每列P个数据补零成为2的整数倍。定义函数I(P),其中 $I(p) = \left\lfloor {{{\log }_2}P} \right\rfloor + 1$,若P为2的整数幂;$I(p) = \left\lfloor {{{\log }_2}P} \right\rfloor $ ,若P为2的非整数幂;也即每列数据补零成I(P)个数据;整个算法的计算复杂度约为:
| \[O\left( {NI(p){{\log }_2}I(p)} \right)\] |
(3) 时域合成法
由于基带采样频率${f_s}$ 远小于大时宽带宽重构信号的带宽,为防止重构信号混叠,需要对子脉冲信号进行升采样(采样倍数为脉冲数P),用快速插值方法进行线性内插,即先对信号进行FFT变换,所需计算量 $O(PN{\log _2}N)$,在频谱补零后做IFFT变换得到插值后的时域波形,所需计算量 $O({P^2}N{\log _2}PN)$;每个插值后的子脉冲乘以相位因子${\phi _n} = \exp ({\rm{j}}2\pi \delta {f_n}t)$ 来完成频移,所需计算量 $O({P^2}N)$;相位校正,乘以补偿因子 ${\phi _n} = \exp ({\rm{j}}\pi k{(\delta {\tau _n})^2}$,其中 $\delta {\tau _n} = [n - (N - 1)/2]\tau $,由于其只与n有关,故所需计算量$O(P)$ ;匹配滤波与IFFT,所需计算量$O({P^2}N + {P^2}N{\log _2}PN)$ ;总计算量为:
| \[\begin{array}{*{20}{l}} {O(PN{{\log }_2}N + {P^2}N{{\log }_2}PN + {P^2}N + P + {P^2}N}\\ {}\\ {\quad + {P^2}N{{\log }_2}PN)}\\ {}\\ { \approx O({P^2}N(2{{\log }_2}PN + 2) + PN{{\log }_2}N + P)} \end{array}\] |
(4) 频域合成法
频域合成算法,各子脉冲做FFT得到频谱以进行频移和相参叠加,所需计算量 $O(PN{\log _2}N)$;构造滤波器 $H(f)$进行幅度补偿使各子脉冲的频谱幅度成为理想矩形,所需计算量$O(PN)$ ;大带宽信号做IFFT得到时域信号,所需计算量 $O(PN{\log _2}PN)$;总计算量为:
| $O(PN{\log _2}PN + PN{\log _2}N + PN)$ |
4种方法的计算量分析总结如表 1所示。4种算法的计算量均为距离像采样点数(N)和脉冲数(P)的函数,令距离向采样点数在N=64~512,脉冲数在P=100~500之间变化,绘出其与计算量的函数关系曲线,如图 2所示。在NUFFT算法中,通常取K=2N,$J \le 10$,在本文的应用中,K为比子脉冲数P大的2的整数次幂,即 $K = I(p)$。
| 表 1 4种算法的计算量比较 Tab. 1 Computational complexity compare of four algorithms |
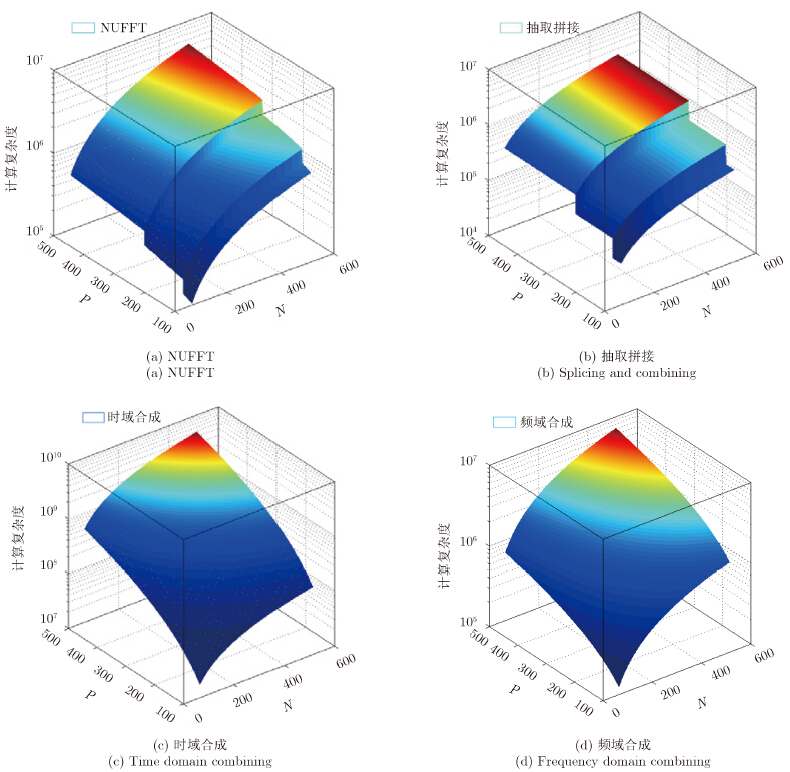 | 图 2 4种算法的“计算量-采样点数(N)-脉冲数(P)”曲线 Fig. 2 Four algorithms “Computational complexity-sampling point (N)-pulse number (P)” curve |
上述实验结果表明计算量受数据维度的影响,而且随着数据维度的增加成指数函数增加。在4种算法中,NUFFT、抽取拼接、频域合成算法的计算量相当,均在107量级,时域合成算法的计算量最高,约为1010量级,这是由于其为避免频谱混叠而进行的高倍升采样操作造成的结果。
图 3(a)和图 3(b)分别给出了固定脉冲数和固定距离向采样点数情况下计算量随另一变量的函数关系曲线,对比4种算法的曲线可以发现抽取拼接算法的计算过程最简单,因此计算量最低,本文的NUFFT方法和传统的频域合成方法计算量相当,甚至稍好于后者,而时域合成方法相比其它算法高出了近3个数量级。
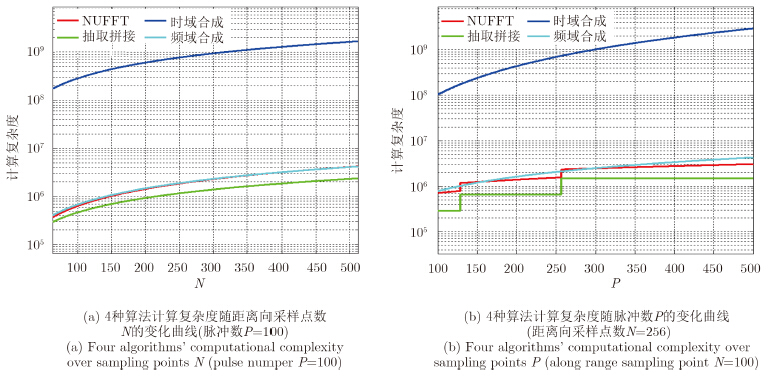 | 图 3 计算复杂度分析 Fig. 3 Analysis of the computational complexity |
需要指出的是,图 3(b)中的阶梯型函数是由于做 $I(p)$列IFFT运算导致的,而在时域合成和频域合成方法中,是将每个子脉冲在时域和频域做合成操作处理,不涉及按列的脉冲间运算,因此不会仍然是一条平滑的对数函数曲线。在跳变点处,2的整数次幂点IFFT操作的目的是加快傅里叶变换的速度,但脉冲数(横轴)的微小变化会导致计算量(纵轴)的成倍增加这一不利后果,实际中其最终效应是使得算法速度提升还是降低,有待于进一步论证。
4 仿真验证本节中利用仿真数据验证本文所提方法的有效性。仿真中采用的线性调频信号的参数为(表 2):脉冲宽度 ${T_{\rm p}}$=5 μs,调频率${K_{\rm r}}$ =1013 Hz/s,信号带宽B=30 Hz,相应的距离分辨率为5 m,依据奈奎斯特采样定理,${f_{\rm s}}$=80 MHz,脉冲个数100,频率跳变间隔6.25 MHz。在目标场景中放置M1坦克模型,其长约7 m,根据雷达波长与一般目标(飞机、坦克、舰船等)尺寸的相对大小关系,可知雷达工作在光学区。由散射中心理论可知,目标的散射可以等效为若干个散射中心组成的散射源。对于坦克目标,强散射中心的位置主要分布于炮筒前端、主炮与机身连接处、机身边缘位置,其它部位如弹药架、履带等位置也可能产生若散射回波。将坦克建模为如图 4所示的主要散射点分布图,散射中心的位置及幅度列于表 2中,定义目标散射点的散射强度为归一化幅度(从0~1不等)。雷达平台位于目标正前方500 m处,雷达与目标均处于静止状态。
| 表 2 M1坦克主要散射中心位置与幅度分布 Tab. 2 M1 tank main scattering points’ location and amplitude |
 | 图 4 目标主要散射点分布示意图 Fig. 4 Target’s main scatter points distribution illustration |
采用NUFFT方法进行成像处理,其中主要参数的选取依据3.3节的分析,K = I(p),p = 100~500,J=6,其最终1维高分辨像如图 5所示。
 | 图 5 目标场景1维高分辨像 Fig. 5 HRRP of the target scene |
从图 4与实际算法成像结果图 5的对比中可以看出NUFFT成像算法的有效性,图 5中各散射点的位置和幅度列于表 3中。对比表 2与表 3可以看出,NUFFT还原结果与仿真预设值基本吻合,误差在2%~5%范围内。该偏差是由于采样峰值点的位置不在sinc函数的峰值处以及理想冲激函数的回波展宽导致的能量泄露引起的。
| 表 3 成像结果各散射中心位置与幅度分布 Tab. 3 Each scattering points’ location and amplitude in imaging result |
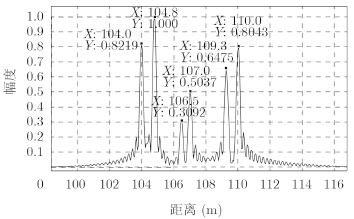
从图 5的成像结果中可以看到各个点目标的回波基本为一sinc函数,符合模型中对雷达回波进行脉冲压缩的理论结果,个别点目标的旁瓣不对称是由于相邻散射点的影响所致。取104.8 m处的散射点2进行分析(图 6)可见,其第1副瓣水平约为-13.3dB,同样符合理想点目标的成像结果,且第2,第3旁瓣也与理想sinc函数吻合的较好,由此验证了NUFFT方法在1维高分辨成像中的有效性。
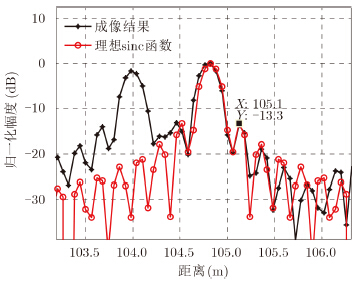 | 图 6 104.8 m散射点成像结果与理想sinc函数对比 Fig. 6 Comparison of imaging result and ideal sinc function of scattering point at 104.8 m |
基于上述成像方法,为验证此方法在目标识别中的有效性。本文仿真了两类地面目标(M1坦克,防空单元)相对于雷达5种静止姿态情况下(目标轴线与雷达视线方向夹角:迎头(0°)、前斜(45°)、正侧(90°)、后斜(135°)、尾追(180°),见图 7)的雷达回波,并用NUFFT方法快速成像,根据1维像的成像结果提取目标特征进行识别。
 | 图 7 M1坦克车和防空单元相对于雷达的5种姿态 Fig. 7 Five positions of M1 tank and air defense units |
用上文的仿真参数,对每种目标每个姿态各200帧的数据进行NUFFT成像,共产生11×200个1维像,在成像结果的基础上,提取目标散射点数和目标长度两个特征进行分类识别。
如图 8所示,从目标的2维特征分布可以看出,两类目标的各个姿态下由于其散射点和长度区分度较大,基本可以区分。但相同姿态不同目标的特征会有交叉重叠,类间区分度不大。需要提取目标其他特征进行辅助识别。
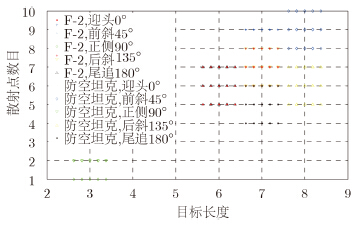 | 图 8 目标散射点数-1维像长度2维特征分布图 Fig. 8 Target’s scattering points-HRRP length 2-D diagram of distribution |
本文提出了一种基于非均匀傅里叶变换的调频步进频信号高分辨成像方法,利用非均匀快速傅里叶变换代替常规算法中复杂的时移、频移等操作,有效降低了成像算法的计算复杂度,加快了信号处理的速度。理论分析与仿真实验表明,基于非均匀快速傅里叶变换的快速成像算法能对目标场景进行清晰准确地成像,为后续的目标识别步骤提供了保障。
| [1] | Jacobs S P. Automatic target recognition using high-resolution radar range profiles[D]. [Ph.D. dissertation], Washington University, 1999.( 1) 1) |
| [2] | Long T, Li D, and Wu Q Z. Design methods for step frequency waveform and the target pick-up algorithm[J]. Systems Engineering and Electronics, 2001, 23(6): 26-31.( 1) 1) |
| [3] | Li D and Long T. Target's redundance removed algorithms of step frequency radar[J]. Acta Electronica Sinica, 2000, 28(6): 60-63.( 1) 1) |
| [4] | Long T, Han Y, and Mao E. Digital signal processing of stepped frequency radar[J]. Acta Aseronqutica et Astronautica Sinica, 2001, 22(S1): 16-25.( 1) 1) |
| [5] | Bai X, Mao S Y, and Yuan Y N. Time domain synthetic bandwidth methods: A 0.1 m resolution SAR technique[J]. Acta Electronica Sinica, 2006, 34(3): 472-477.( 1) 1) |
| [6] | Wilkinson A J, Lord R T, and Inggs M R. Stepped-frequency processing by reconstruction of target reflectivity spectrum[C]. Proceedings of the 1998 South African Symposium on IEEE Communications and Signal Processing, COMSIG'98, 1998: 101-104.( 1) 1) |
| [7] | Potts D, Steidl G, and Tasche M. Fast Fourier Transforms for Nonequispaced Data: A Turorial[M]. Benedetto J J and Ferreira P, Modern Sampling Theory: Mathmatics and Applications, Boston: Birkhauser, 2001: 247-270.( 1) 1) |
| [8] | Fessler J A and Sutton B P. Nonuniform fast Fourier transforms using min-max interpolation[J]. IEEE Transactions on Signal Processing, 2003, 51(2): 560-574.( 1) 1) |
| [9] | Dutt A and Rokhlin V. Fast Fourier transforms for nonequispaced data[J]. SIAM Journal on Scientific Computing, 1993, 14(6): 1368-1393.( 1) 1) |
| [10] | Liu Q H and Nguyen N. An accurate algorithm for nonuniform fast Fourier transforms (NUFFT's)[J]. IEEE Microwave and Guided Wave Letters, 1998, 8(1): 18-20.( 1) 1) |
| [11] | Nguyen N and Liu Q H. The regular Fourier matrices and nonuniform fast Fourier transforms[J]. SIAM Journal on Scientific Computing, 1999, 21(1): 283-293.( 1) 1) |
| [12] | Fessler J and Sutton B P. Nonuniform fast Fourier transforms using min-max interpolation[J]. IEEE Transactions on Signal Processing, 2003, 51(2): 560-574.( 1) 1) |
| [13] | Schaller S, Flohr T, and Steffen P. An efficient Fourier method for 3-D radon inversion in exact cone-beam CT reconstruction[J]. IEEE Transactions on Medical Imaging, 1998, 17(2): 244-250.( 1) 1) |
| [14] | Sarty G E, Bennett R, and Cox R W. Direct reconstruction of non-Cartesian k-space data using a nonuniform fast Fourier transform[J]. Magnetic Resonance in Medicine, 2001, 45(5): 908-915.( 2) 2) |
| [15] | Song J, Liu Q H, Kim K, et al. High-resolution 3-D radar imaging through nonuniform fast Fourier transform (NUFFT)[J]. Communications in Computational Physics, 2006, 1(1): 176-191.( 1) 1) |
 2015, Vol. 4
2015, Vol. 4
