②(陕西省计量科学研究院 西安 710065)
②(Shaanxi Institute of Metrology, Xi'an 710065, China)
合成孔径雷达(Synthetic Aperture Radar,SAR)地面运动目标指示(Ground Moving Target Indication,GMTI)技术可实现地面匀速和匀加速运动目标的有效检测[1]。然而该技术很难实现对地面微动目标(如旋转的雷达天线、振动的车辆引擎等)的有效检测与识别。地面目标的微小运动会对雷达回波产生附加的频率调制,这种现象被称为微多普勒(micro-Doppler,m-D)效应[2]。微动特征蕴含着反映目标身份标识的精细信息,通过对目标微动特征的分析与提取,可为地海面目标的分类与识别提供更为丰富的特征信息。2009年,国防科学技术大学的邓彬等人首次提出了SAR微动目标指示(Micro-Motion Target Indication,MMTI)技术的概念[3],将对地海面微动目标的检测、参数估计与成像技术或实现该技术的SAR统称为SAR MMTI技术,并对SAR MMTI技术展开了一系列的研究工作[4, 5, 6, 7]。
作为SAR GMTI技术的推广,SAR MMTI技术一直受到世界各国的广泛关注。在振动目标特征分析及提取技术研究方面,文献[8]用APY-6雷达采集的两个振动角散射器的回波数据,采用时频分析的方法提取了振动目标的振动频率及振幅,但是振幅的估计误差较大;文献[9]采用毫米波段SAR系统,对旋转和振动目标的微多普勒特征进行了分析;进一步地,文献[10, 11]采用时频分析的方法分别对双基SAR和MIMO SAR系统中振动目标特征进行了分析。上述研究工作均未考虑强地杂波对振动目标检测与特征提取的影响,受强地杂波的影响,微弱的振动目标通常会被淹没在强地杂波背景中难以被检测。文献[12]和文献[13]分别将相位中心偏置天线(Displaced Phase Center Antenna,DPCA)技术应用于单基双通道SAR和固定接收机的双基SAR中,有效地抑制了地杂波,通过时频分析方法获得了目标振动特征。然而,上述工作忽略了采用DPCA技术进行杂波对消后回波信号引入的慢时间包络(Slow Time Envelope,STE)项对振动目标回波能量的影响。
调频连续波(Frequency Modulated Continuous Wave,FMCW)SAR通过在较长的脉冲持续时间内发射连续的线性调频信号,可降低系统的峰值发射功率[14];接收端采用去调频处理体制,回波信号与参考信号进行混频,产生较小的差频带宽,能够降低对视频接收通道、后端A/D采集设备和信号处理速度的要求[15, 16]。总的来讲,FMCW SAR相比传统的脉冲式SAR,具有体积小、重量轻、成本低、功耗低等优势,在无人机等小型飞行平台中具有较大的应用潜力,近年来受到越来越广泛的关注。由于单基FMCW SAR受系统收发隔离度的限制,其作用距离一般比较近,采用收发天线分置于两个独立平台的双基FMCW SAR系统,能够有效地克服收发隔离度限制,进而提高作用距离。同时双基FMCW SAR具有更高的机动性、隐蔽性以及更好的抗干扰和抗截获能力[17]。一站固定式双基SAR是一种特殊的双基模式,该模式是将双基的一个基站固定,另一个基站运动。这种模式的双基SAR组建起来比较容易,而且应用灵活,具有广阔的应用前景[18]。
基于上述分析,本文研究一站固定式双基FMCW SAR的地面振动目标检测与特征提取方法。采用发射机固定接收机运动的双基FMCW SAR工作模式,通过DPCA技术在数据域完成杂波对消处理进而检测地面振动目标。对回波信号的分析表明,由DPCA处理引入的STE项会对振动目标m-D时频曲线的能量分布产生影响,导致无法获取完整的m-D时频曲线。进一步地,利用STE项与振动特征之间的关系,实现了振动目标的特征提取。最后仿真实验验证了理论分析与特征提取方法的有效性。
2 振动目标检测与回波分析一站固定式双基FMCW SAR即一个基站是固定不变的,一个基站是运动的双基形式,既可以采用发射机固定也可以采用接收机固定的形式。采用这种构型的双基FMCW SAR进行地面运动目标检测与特征提取时,通常要求运动平台具备两个发射或接收通道,以实现DPCA杂波抑制。如果运动平台搭载发射机,则需要两个发射天线交替地发射信号,等效地降低了系统的脉冲重复频率[13];而运动平台搭载接收机,可对回波信号进行全孔径接收。基于以上考虑,本文在后续的分析中采用发射机固定接收机运动的双基FMCW SAR构型进行分析。
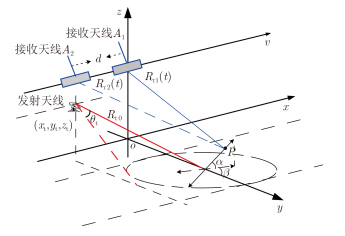
固定发射机的双基FMCW SAR几何构型如图 1所示。固定发射机坐标为(xt,yt,zt),斜视角为${\theta _{\rm{t}}}$,载机配置两个接收天线,两个接收天线间距为d,飞行高度为h,沿x轴正方向以速度v匀速直线飞行。为实现DPCA杂波抑制,两个接收天线间距d需满足:
| $d = M{T_{\rm{P}}}v$ | (1) |
|
图 1 一站固定式双基FMCW SAR/DPCA几何模型 Fig. 1 Geometry of one-stationary bistatic FMCW SAR/DPCA |
其中,M为正整数,TP为FMCW信号脉冲持续时间。可见,天线A1在t时刻接收到的回波信号与天线A2在t+$\tau {_{\rm{d}}}$=MTP)时刻接收到的回波信号相位中心恰好重合,即两天线在空间中同一位置发射和接收信号。这样,两个接收通道接收的静止地面目标的回波信号能够完成对消,振动目标的信息得以保留。
假设成像场景中存在一振动目标点P,振动中心坐标为(xc,yc,zc),振幅为Av,振动频率为fv(角频率${\omega _{\rm{v}}} = 2\pi {f_{\rm{v}}})$,初始相位为${\theta _0}$,目标振动方向与xoy平面的夹角为$\alpha $,振动方向在xoy平面的投影与y轴夹角为$\beta $。
由于FMCW SAR是在一个脉冲持续时间内连续的发射信号,且脉冲持续时间较长,通常脉冲持续时间内载机连续运动引起的距离变化不能忽略。设接收天线A1位于(0,0,h)时为时间起点,振动点P与接收天线Ai (i=1,2)之间的瞬时斜距可表示为:
| $\begin{aligned} {R_{{\rm{r}}i}}\left( t \right) \approx & {R_{{\rm{r}}0}} + {A_{\rm{r}}}\sin \left( {{\omega _{\rm{v}}}t + {\theta _0}} \right)\\ & + \frac{{{{ \big( {vt - \left( {i - 1} \right)d - {A_{\rm{a}}}\sin \left( {{\omega _{\rm{v}}}t + {\theta _0}} \right)} \big)}^2}}}{{2{R_{{\rm{r}}0}}}} \end{aligned}$ | (2) |
其中,${R_{{\rm{r0}}}} = \sqrt {x_{\rm{c}}^{\rm{2}} + y_{\rm{c}}^{\rm{2}} + {{\left( {{z_{\rm{c}}} - h} \right)}^2}} $,t=tk+tm为全时间,tk和tm分别表示快时间和慢时间。${A_{\rm{r}}} = {A_{\rm{v}}}\cos \alpha \cos \beta $表示振动点在y轴方向的振幅,${A_{\rm{a}}} = {A_{\rm{v}}}\cos \alpha \sin \beta $表示振动点在x轴方向的振幅。
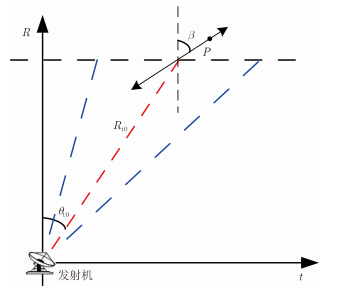
根据图 2给出的固定发射机与振动目标的2维几何关系,可得固定发射机到振动点P的瞬时斜距[19]为:
| $\begin{aligned} {R_{\rm{t}}}\left( t \right) \approx & {R_{{\rm{t0}}}} + {A_{\rm{r}}}\cos {\theta _{{\rm{t0}}}}\sin \left( {{\omega _{\rm{v}}}t + {\theta _0}} \right)\\ & + {A_{\rm{a}}}\sin {\theta _{{\rm{t0}}}}\sin \left( {{\omega _{\rm{v}}}t + {\theta _0}} \right)\\ & + \frac{{{{\cos }^2}{\theta _{{\rm{t0}}}}}}{{2{R_{{\rm{t0}}}}}}{\big( {{A_{\rm{a}}}\sin \left( {{\omega _{\rm{v}}}t + {\theta _0}} \right)} \big)^2} \end{aligned}$ | (3) |
|
图 2 固定发射机与振动目标几何关系 Fig. 2 Geometrical relationship between stationary transmitter and vibration target |
其中,${R_{{\rm{t0}}}} = \sqrt {{{\left( {{x_{\rm{t}}} - {x_{\rm{c}}}} \right)}^2} + {{\left( {{y_{\rm{t}}} - {y_{\rm{c}}}} \right)}^2} + {{\left( {{z_{\rm{t}}} - {z_{\rm{c}}}} \right)}^2}} $。为简化分析,设振动目标初始相位${\theta _0} = 0$,振动目标与天线A1和固定发射机的双程距离可表示为:
| $\begin{aligned} {R_{{\rm{tr1}}}}\left( t \right) & = {R_{\rm{t}}}\left( t \right) + {R_{{\rm{r1}}}}\left( t \right)\\ & \approx {R_{{\rm{tr0}}}} \! + \! {A_{\rm{e}}}\sin \left( {{\omega _{\rm{v}}}t} \right) \! + \! \frac{{{{\big( {vt - {A_{\rm{a}}}\sin \left( {{\omega _{\rm{v}}}t} \right)} \big)}^2}}}{{2{R_{{\rm{r0}}}}}}\\ & \quad + \frac{{A_{\rm{a}}^{\rm{2}}{{\cos }^2}{\theta _{{\rm{t0}}}}{{\sin }^2}\left( {{\omega _{\rm{v}}}t} \right)}}{{2{R_{{\rm{t0}}}}}} \end{aligned}$ | (4) |
其中,Rtr0=Rt0+Rr0,Ae=Arcos$ {\theta _{{\rm{t0}}}}$+Aasin$ {\theta _{{\rm{t0}}}}$+Ar,为叙述简便,此处称Ae为等效振幅,该等效振幅也是一站固定式双基FMCW SAR与单站式FMCW SAR的区别所在。经时延${\tau _{\rm{d}}}$后,振动目标与天线A2和固定发射机的双程距离可表示为:
| $\begin{aligned} {R_{{\rm{tr2}}}}\left( {t + {\tau _{\rm{d}}}} \right) & = {R_{\rm{t}}}\left( {t + {\tau _{\rm{d}}}} \right) + {R_{{\rm{r2}}}}\left( {t + {\tau _{\rm{d}}}} \right)\\ & \approx {R_{{\rm{tr0}}}} + {A_{\rm{e}}}\sin \left( {{\omega _{\rm{v}}}\left( {t + {\tau _{\rm{d}}}} \right)} \right)\\ & \quad + \frac{{{{\big( {vt - d - {A_{\rm{a}}}\sin \left( {{\omega _{\rm{v}}}\left( {t + {\tau _{\rm{d}}}} \right)} \right)} \big)}^2}}}{{2{R_{{\rm{r0}}}}}}\\ & \quad + \frac{{A_{\rm{a}}^{\rm{2}}{{\cos }^2}{\theta _{{\rm{t0}}}}{{\sin }^2}\left( {{\omega _{\rm{v}}}\left( {t + {\tau _{\rm{d}}}} \right)} \right)}}{{2{R_{{\rm{t0}}}}}} \end{aligned}$ | (5) |
由于振动点的振动远小于Rt0,因此在后面的分析中忽略了式(4)和式(5)中的最后一项。进一步地,将式(4)和式(5)展开为关于快时间tk的1次项:
| $\begin{aligned} {R_{{\rm{tr1}}}}\left( t \right) \approx & {R_{{\rm{tr}}0}} + {A_{\rm{e}}}\sin \left( {{\omega _{\rm{v}}}{t_{\rm{m}}}} \right) + {A_{\rm{e}}}{\omega _{\rm{v}}}\sin \left( {{\omega _{\rm{v}}}{t_{\rm{m}}}} \right){t_{\rm{k}}}\\ & + \frac{{{v^2}{t_{\rm{m}}}}}{{{R_{{\rm{r0}}}}}}{t_{\rm{k}}} + \frac{{{{\big( {v{t_{\rm{m}}} - {A_{\rm{a}}}\sin \left( {{\omega _{\rm{v}}}{t_{\rm{m}}}} \right)} \big)}^2}}}{{2{R_{{\rm{r0}}}}}} \end{aligned}$ | (6) |
| $\begin{aligned} {R_{{\rm{tr2}}}}\left( {t + {\tau _{\rm{d}}}} \right) \approx & {R_{{\rm{tr}}0}} + {A_{\rm{e}}}\sin \left( {{\omega _{\rm{v}}}\left( {{t_{\rm{m}}} + {\tau _{\rm{d}}}} \right)} \right)\\ & + {A_{\rm{e}}}{\omega _{\rm{v}}}\sin \left( {{\omega _{\rm{v}}}\left( {{t_{\rm{m}}} + {\tau _{\rm{d}}}} \right)} \right){t_{\rm{k}}} + \frac{{{v^2}{t_{\rm{m}}}}}{{{R_{{\rm{r0}}}}}}{t_{\rm{k}}}\\ & + \! \frac{{{{\big( {v\left( {{t_{\rm{m}}} \!\! + \! {\tau _{\rm{d}}}} \right) \!\! - \!\! d \!\! - \! {A_{\rm{a}}}\sin \left( {{\omega _{\rm{v}}} \! \left( {{t_{\rm{m}}} \!\! + \! {\tau _{\rm{d}}}} \right)} \right)} \big)}^2}}}{{2{R_{{\rm{r0}}}}}} \end{aligned}$ | (7) |
式(6)和(7)中第3项和第4项为FMCW SAR中特有的,其中第3项为目标点振动引起的脉内多普勒频移项;第4项为载机连续运动引起的脉内多普勒频移项,在后续的处理可通过在方位多普勒频域构造多普勒频移补偿函数对该项进行补偿[14]。
雷达发射FMCW信号,两个接收天线接收的回波信号经去调频处理后,分别表示为:
| $\begin{aligned} {s_{{\rm{tr}}1}}\left( t \right) = & {\sigma _{\rm{P}}}\exp \left( { - {\mathop{\rm j}\nolimits} \left( {\frac{{2{π} \mu }}{\rm c}\left( {{t_{\rm{k}}} - \frac{{2{R_{{\rm{ref}}}}}}{\rm c}} \right)} \right.} \right.{R_{\Delta {\rm{tr1}}}}\left( t \right)\\ & \left. { + \left. {\frac{{2{π} }}{\lambda }{R_{\Delta {\rm{tr}}1}}\left( t \right)} \right)} \right)\exp \left( {{\rm{j}}\frac{{2{π} \mu }}{{{{\rm c}^2}}}R_{\Delta {\rm{tr}}1}^2\left( t \right)} \right) \end{aligned}$ | (8) |
| $\begin{aligned} {s_{{\rm{tr2}}}}\left( {t + {\tau _{\rm{d}}}} \right) = & {\sigma _{\rm{P}}}\exp \left( { - {\rm{j}}\left( {\frac{{2{π} \mu }}{\rm c}\left( {{t_{\rm{k}}} - \frac{{2{R_{{\rm{ref}}}}}}{\rm c}} \right)} \right.} \right.\\ & \cdot \left. {\left. {{R_{\Delta {\rm{tr}}2}}\left( {t + {\tau _{\rm{d}}}} \right) + \frac{{2{π} }}{\lambda }{R_{{\rm{tr2}}}}\left( {t + {\tau _{\rm{d}}}} \right)} \right)} \right)\\ & \cdot \exp \left( {{\rm{j}}\frac{{2{π} \mu }}{{{{\rm c}^2}}}R_{\Delta 21}^2\left( {t + {\tau _{\rm{d}}}} \right)} \right) \end{aligned}$ | (9) |
其中,${\sigma _{\rm{P}}}$为目标点散射系数,Rref为参考距离,且${R_{\Delta {\rm{tr}}1}} \! \left(t \right) \! = \! {R_{{\rm{tr1}}}} \! \left( t \right) \! - \! 2{R_{{\rm{ref}}}}$,${R_{\Delta {\rm{tr2}}}}\left( {t \! + \! {\tau _{\rm{d}}}} \right) \!\! = \!\! {R_{{\rm{tr2}}}}\left( {t \! + \! {\tau _{\rm{d}}}} \right) \! -$$ 2{R_{{\rm{ref}}}}$。式(8)和式(9)中最后一个指数项为剩余视频相位(RVP)项,在FMCW SAR成像中通常忽略该项的影响,或在方位多普勒频域对其进行补偿[14],本文在后续的分析处理中,忽略该项的影响。经距离压缩后两通道的回波差频信号可表示为:
| $\begin{aligned} {S_{{\rm{tr1}}}}\left( {{f_{\rm{r}}},{t_{\rm{m}}}} \right) = & {\sigma _{\rm{P}}}{\rm{sinc}}\big( {{T_{\rm{P}}}\left( {{f_{\rm{r}}} + {\psi _{{\rm{tr}}1}}\left( {{t_{\rm{m}}}} \right)} \right)} \big)\\ & \cdot \exp \big( { - {\rm{j}}{{2{π} {R_{\Delta {\rm{tr}}1}}\left( {{t_{\rm{m}}}} \right)} \mathord{\left/ {\vphantom {{2{π} {R_{\Delta {\rm{tr}}1}}\left( {{t_{\rm{m}}}} \right)} \lambda }} \right.} \lambda }} \big) \end{aligned}$ | (10) |
| $\begin{aligned} {S_{{\rm{tr2}}}}\left( {{f_{\rm{r}}},{t_{\rm{m}}} + {\tau _{\rm{d}}}} \right) = & {\sigma _{\rm{P}}}{\rm{sinc}}\left( {{T_{\rm{P}}}\left( {{f_{\rm{r}}} + {\psi _{{\rm{tr}}2}}\left( {{t_{\rm{m}}} + {\tau _{\rm{d}}}} \right)} \right)} \right)\\ & \cdot \exp \left( { - {\rm{j}}{{2{π} {R_{\Delta {\rm{tr}}2}}\left( {{t_{\rm{m}}} \! + \! {\tau _{\rm{d}}}} \right)} \mathord{\left/ {\vphantom {{2{π} {R_{\Delta {\rm{tr}}2}}\left( {{t_{\rm{m}}} + {\tau _{\rm{d}}}} \right)} \lambda }} \right. } \lambda }} \right) \end{aligned}$ | (11) |
| ${\psi _{{\rm{tr1}}}}\left( {{t_{\rm{m}}}} \right) = \frac{\mu }{\rm c}\left( {{R_{{\rm{tr}}0}} - 2{R_{{\rm{ref}}}} + F\sin \left( {{\omega _{\rm{v}}}{t_{\rm{m}}} + \psi } \right)} \right)$ | (12) |
| $\begin{aligned} {\psi _{{\rm{tr2}}}}\left( {{t_{\rm{m}}} + {\tau _{\rm{d}}}} \right) = & \frac{\mu }{c}\left( {{R_{{\rm{tr0}}}} - 2{R_{{\rm{ref}}}} } \right.\\ & + F\sin \left. {\left( {{\omega _{\rm{v}}}{t_{\rm{m}}} + {\omega _{\rm{v}}}{\tau _{\rm{d}}} + \psi } \right)} \right) \end{aligned}$ | (13) |
其中,$F = \sqrt {A_{\rm{e}}^{\rm{2}} + {a^2}} $,$a = {{{\omega _{\rm{v}}}{A_{\rm{e}}}{f_{\rm{c}}}} \mathord{\left/ {\vphantom {{{\omega _{\rm{v}}}{A_{\rm{e}}}{f_{\rm{c}}}} \mu }} \right. } \mu }$,$\psi = $ $\arctan \left( {{a \mathord{\left/ {\vphantom {a {{A_{\rm{e}}}}}} \right. } {{A_{\rm{e}}}}}} \right)$。与脉冲式SAR不同,FMCW SAR中振动点距离峰值位置不仅与振动中心和振幅有关,还与振动点的等效振幅、振动频率及信号载频有关。现实中,由于振动目标的振幅通常较小(一般为毫米级),振动频率一般在十几或几十赫兹,因此同样满足:$F \ll {\rho _{\rm{r}}}$,其中,${\rho _{\rm{r}}}$为距离分辨率,因此式(10)和式(11)可化简为:
| ${S_{{\rm{tr1}}}}\left( {{f_{\rm{r}}},{t_{\rm{m}}}} \right) = {\sigma '\! _{\rm{P}}}\exp \left( { - {\rm{j}}{{2{π} {R_{\Delta {\rm{tr}}1}}\left( {{t_{\rm{m}}}} \right)} \mathord{\left/ {\vphantom {{2{π} {R_{\Delta {\rm{tr}}1}}\left( {{t_{\rm{m}}}} \right)} \lambda }} \right. } \lambda }} \right)$ | (14) |
| $\hspace{15.5pt} {S_{{\rm{tr}}2}}\left( {{f_{\rm{r}}},{t_{\rm{m}}} + {\tau _{\rm{d}}}} \right) \\ \qquad \quad = {\sigma '\! _{\rm{P}}}\exp \left( { - {\rm{j}}{{2{π} {R_{\Delta {\rm{tr}}2}}\left( {{t_{\rm{m}}} + {\tau _{\rm{d}}}} \right)} \mathord{\left/{\vphantom {{2{π} {R_{\Delta {\rm{tr}}2}}\left( {{t_{\rm{m}}} + {\tau _{\rm{d}}}} \right)} \lambda }} \right. } \lambda }} \right)$ | (15) |
其中${\sigma '\! _{\rm{P}}}$为常数。这样,经距离压缩后,振动目标在距离-慢时间谱图中表现为沿方位向的直线。为抑制地杂波,将两通道回波差频信号作DPCA对消[13],即
| $\begin{aligned} {S_{{\rm{DPCA}}}}\left( {{f_{\rm{r}}},{t_{\rm{m}}}} \right) = & {S_{{\rm{tr1}}}}\left( {{f_{\rm{r}}},{t_{\rm{m}}}} \right) - {S_{{\rm{tr2}}}}\left( {{f_{\rm{r}}},{t_{\rm{m}}} + {\tau _{\rm{d}}}} \right)\\ = & {{\sigma '}_{\rm{P}}}P\left( {{t_{\rm{m}}}} \right)\exp \left( {{\rm{j}}\left( {{π} \left( {{R_{\Delta {\rm{tr1}}}}\left( {{t_{\rm{m}}} + {\tau _{\rm{d}}}} \right)} \right.} \right.} \right.\\ & + \left. {\left. {\left. {{R_{\Delta {\rm{tr}}2}}\left( {{t_{\rm{m}}}} \right)} \right)/\lambda } \right)} \right) \end{aligned}$ | (16) |
其中,
| $\begin{aligned} P\left( {{t_{\rm{m}}}} \right) = & - 2\sin \bigg( \left( {\frac{{2{π} {A_{\rm{e}}}}}{\lambda } - \frac{{{π} v{t_{\rm{m}}}{A_{\rm{a}}}}}{{\lambda {R_{{\rm{r0}}}}}}} \right) \\ & \cdot \sin \phi \cos \left( {{\omega _{\rm{v}}}{t_{\rm{m}}} \! + \phi } \right) \bigg) \end{aligned}$ | (17) |
$\phi = {{{\omega _{\rm{v}}}{\tau _{\rm{d}}}} \mathord{\left/ {\vphantom {{{\omega _{\rm{v}}}{\tau _{\rm{d}}}} 2}} \right.} 2}$。实际受载机运动误差等的影响,采用DPCA技术很难完全抑制杂波,这将影响后续的振动目标特征提取,对此可采用相应的运动补偿方法尽量减少杂波的影响[20]。两通道回波差频信号经DPCA处理后,包含一个与慢时间tm有关的包络项P(tm)即STE项,如式(17)所示。该项将影响杂波对消后的回波差频信号的能量分布,且当$\sin \phi = 0$,即fv=nv/d,$n = 1,2,3 \cdots $时,包络项为零。即当振动点振动频率满足上述关系式时将与静止地杂波同时被抑制,即所谓的“盲速”。为避免这种情况的发生,应尽量提高载机速度v,减小收发天线之间的距离d。在远场条件下,有如下关系式:
| $\frac{{2{π} {A_{\rm{e}}}}}{\lambda } \gg \frac{{{π} v{t_{\rm{m}}}{A_{\rm{a}}}\sin \phi }}{{\lambda {R_{{\rm{r0}}}}}} \approx 0$ | (18) |
根据式(18)所示,对一站固定式双基FMCW SAR的地面振动目标的微多普勒特征分两种情况进行讨论:
(1) Ae≠0;
此时,STE项可近似为:
| $P\left( {{t_{\rm{m}}}} \right) \approx - 2\sin \left( {{{{\rm{2}}{π} {A_{\rm{e}}}\sin \phi \cos \left( {{\omega _{\rm{v}}}{t_{\rm{m}}} + \phi } \right)} \mathord{\left/ {\vphantom {{{\rm{2}}{π} {A_{\rm{e}}}\sin \phi \cos \left( {{\omega _{\rm{v}}}{t_{\rm{m}}} + \phi } \right)} \lambda }} \right. } \lambda }} \right)$ | (19) |
式(16)经补偿载机运动引起的线性调频多普勒项后,其m-D频率为:
| ${f_{{\rm{m {\Large {\text -}} D}}}} \approx - \frac{{{A_{\rm{e}}}{\omega _{\rm{v}}}\cos \phi \cos \left( {{\omega _{\rm{v}}}{t_{\rm{m}}} + \phi } \right)}}{\lambda }$ | (20) |
在这种情况下,地面振动目标引起的m-D频率表现为随慢时间变化的余弦(正弦)形式,其m-D频率通常采用时频分析的方法获取振动特征。但是,与传统的振动点m-D时频曲线不同,受随慢时间变化的STE项影响,回波信号能量也随慢时间而变化,这也将影响振动点m-D时频曲线的能量分布。且m-D频率变化趋势与STE变化趋势相同,当m-D频率为零时,其回波能量也为零。且当$\cos \phi = 0$时,m-D频率为零。即当振动点振动频率满足$\cos \phi = 0$时,同样无法采用时频分析的方法检测到振动目标。
(2) Ae=0;
此时,振动点振动方向$\beta$满足:$\beta = {{π} \mathord{\left/{\vphantom {{π} 2}} \right.} 2} + {{{\theta _{\rm{t}}}} \mathord{\left/{\vphantom {{{\theta _{\rm{t}}}} 2}} \right.} 2}$。STE项可近似为:
| $P\left( {{t_{\rm{m}}}} \right) \approx \frac{{2{π} v{t_{\rm{m}}}{A_{\rm{a}}}}}{{\lambda {R_{{\rm{r0}}}}}}\sin \phi \cos \left( {{\omega _{\rm{v}}}{t_{\rm{m}}} + \phi } \right)$ | (21) |
其m-D频率为:
| ${f_{{\rm{m {\Large {\text -}} D}}}} = \frac{{2v{A_{\rm{a}}}{\omega _{\rm{v}}}\cos \phi {t_{\rm{m}}}\cos \left( {{\omega _{\rm{v}}}{t_{\rm{m}}} + \phi } \right)}}{{\lambda {R_0}}}$ | (22) |
在这种情况下,地面振动目标引起的m-D频率表现为非周期变化的形式,同时STE项也表现为非周期变化的形式。然而,由于P(tm)近似为零,导致很难检测到这种振动情况下的振动目标。基于此,本文在后续讨论振动目标特征提取方法时,主要针对Ae≠0时的振动目标。
3 振动目标特征提取本节根据对消后回波差频信号的特点,依据STE项与目标振动特征的关系,来进行振动特征的提取。根据上一节的分析可知,回波差频信号经DPCA处理后,STE项中包含了振动目标的特征信息,对式(16)取模得:
| $\begin{aligned} \left| {{S_{{\rm{DPCA}}}}\left( {{f_{\rm{r}}},{t_{\rm{m}}}} \right)} \right| & \approx {{\sigma '} \! _{\rm{P}}}\left| {P\left( {{t_{\rm{m}}}} \right)} \right|\\ & = 2{{\sigma '} \! _{\rm{P}}}\Big| {\sin \left( {{A_{\rm{e}}}C\cos \left( {{\omega _{\rm{v}}}{t_{\rm{m}}} + \phi } \right)} \right)} \Big| \end{aligned}$ | (23) |
其中,${{C = 2{π} \sin \phi } \mathord{\left/ {\vphantom {{C = 2{π} \sin \phi } \lambda }} \right. } \lambda }$。经取模处理后,振动点所在距离单元的STE为周期信号,因此可表示为傅里叶级数的形式:
| $\begin{aligned} \left| {{S_{{\rm{DPCA}}}}\left( {{f_{\rm{r}}},{t_{\rm{m}}}} \right)} \right| = & \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{a_n}\cos \left( {n\omega {t_{\rm{m}}}} \right)} \\ & + \sum\limits_{n = 1}^\infty {{b_n}\sin \left( {n\omega {t_{\rm{m}}}} \right)} \end{aligned}$ | (24) |
其中,an,bn为傅里叶级数的系数:
| \[{a_n} = \frac{{{\kern 1pt} 2}}{{T{\mkern 1mu} {\kern 1pt} }}\int_{ - \frac{T}{2}}^{\frac{T}{2}} {\left| {{S_{{\rm{DPCA}}}}\left( {{f_{\rm{r}}},{t_{\rm{m}}}} \right)} \right|\cos \left( {n\omega {t_{\rm{m}}}} \right){\rm{d}}{t_{\rm{m}}}} \] | (25) |
| \[{b_n} = \frac{{{\kern 1pt} 2}}{{T{\mkern 1mu} {\kern 1pt} }}\int_{ - \frac{T}{2}}^{\frac{T}{2}} {\left| {{S_{{\rm{DPCA}}}}\left( {{f_{\rm{r}}},{t_{\rm{m}}}} \right)} \right|\sin \left( {n\omega {t_{\rm{m}}}} \right){\rm{d}}{t_{\rm{m}}}} \] | (26) |
T和w分别为式(23)的周期和1次谐波角频率,且w=2wv。因此,振动点振动频率可通过对取模后的STE进行FFT,提取1次谐波频率即为振动点频率的2倍。式(23)的离散形式可表示为:
| $\left| {{S_{{\rm{DPCA}}}}\left( m \right)} \right| = 2{\sigma ' \! _{\rm{P}}}\left| {\sin \left( {{A_{\rm{e}}}C\cos \left( {{\omega _{\rm{v}}}m{T_{\rm{P}}} + \phi } \right)} \right)} \right|$ | (27) |
其中m为整数。
由式(27)可知,STE模值为正弦函数与余弦函数组成的复合函数,受余弦函数调制的影响,正弦函数内的值在$[{ - {A_{\rm{e}}}C\quad {A_{\rm{e}}}C}] $之间变化,因此STE曲线形式与AeC的取值有关。对振动点振幅的提取,主要指对其等效振幅的提取。下面分两种情况讨论振动点等效振幅的提取方法:
(1) $\left| {{A_{\rm{e}}}C} \right| \le {{π} \mathord{\left/ {\vphantom {{π} 2}} \right. } 2}$
在这种情况下,STE模值的最大值为:
| ${\left| {{S_{{\rm{DPCA}}}}\left( {{m_1}} \right)} \right|_{\max }} = 2{\sigma ' \! _{\rm{P}}}\left| {\sin \left( {{A_{\rm{e}}}C} \right)} \right|$ | (28) |
其中最大值点位置${m_1}$满足$\cos \left( {{\omega _{\rm{v}}}{m_1}{T_{\rm{P}}} + \phi } \right) = \pm 1$,且在STE 1个周期内仅包含1个最大值点。提取STE另一位置点m2的值:
| $\begin{aligned} {\left| {{S_{{\rm{DPCA}}}}\left( {{m_2}} \right)} \right|_{{\rm{mid}}}} & = 2{{\sigma '}\! _{\rm{P}}}\left| {\sin \left( {{A_{\rm{e}}}C\cos \left( {{\omega _{\rm{v}}}{m_2}{T_{\rm{P}}} + \phi } \right)} \right)} \right|\\ & = \! 2{{\sigma '}\! _{\rm{P}}}\left| {\sin \left( {{A_{\rm{e}}}C\cos \left( {{\omega _{\rm{v}}}{m_1}{T_{\rm{P}}} \!\! + \!\! \phi \!\! + \!\! \varphi } \right)} \right)} \right| \\ & = 2{{\sigma '}\! _{\rm{P}}}\left| {\sin \left( {{A_{\rm{e}}}C\cos \left( \varphi \right)} \right)} \right| \end{aligned}$ | (29) |
其中$\varphi = {\omega _{\rm{v}}}{T_{\rm{P}}}\left( {{m_2} - {m_1}} \right)$。取$\varphi = {{π} \mathord{\left/ {\vphantom {{π} 3}} \right. } 3}$,则${m_2} = $ $\left[{{m_1} + {{π} \mathord{\left/ {\vphantom {{π} {\left( {3{\omega _{\rm{v}}}{T_{\rm{P}}}} \right)}}} \right. } {\left( {3{\omega _{\rm{v}}}{T_{\rm{P}}}} \right)}}} \right]$,[·]表示近似取整运算。定义m2的位置为STE的中值点。式(28)与式(29)的比值为:
| $\begin{aligned} {S_{{\rm{ratio}}}} & = \frac{{{{\left| {{S_{{\rm{DPCA}}}}\left( {{m_2}} \right)} \right|}_{\max }}}}{{{{\left| {{S_{{\rm{DPCA}}}}\left( {{m_1}} \right)} \right|}_{{\rm{mid}}}}}} = \frac{{2{{\sigma '} \! _{\rm{P}}}\left| {\sin \left( {{A_{\rm{e}}}C} \right)} \right|}}{{2{{\sigma '} \! _{\rm{P}}}\left| {\sin \left( {{{{A_{\rm{e}}}C} \mathord{\left/ {\vphantom {{{A_{\rm{e}}}C} 2}} \right. } 2}} \right)} \right|}}\\ & = 2\cos \left( {{{{A_{\rm{e}}}C} \mathord{\left/ {\vphantom {{{A_{\rm{e}}}C} 2}} \right. } 2}} \right) \end{aligned}$ | (30) |
根据式(30),振动点等效振幅可通过下式进行计算:
| ${A_{\rm{e}}} = {{2\arccos \left( {{{{S_{{\rm{ratio}}}}} \mathord{\left/ {\vphantom {{{S_{{\rm{ratio}}}}} 2}} \right. } 2}} \right)} \mathord{\left/ {\vphantom {{2\arccos \left( {{{{S_{{\rm{ratio}}}}} \mathord{\left/ {\vphantom {{{S_{{\rm{ratio}}}}} 2}} \right. } 2}} \right)} {\left| C \right|}}} \right. } {\left| C \right|}}$ | (31) |
(2) $\left| {{A_{\rm{e}}}C} \right| > {{π} \mathord{\left/ {\vphantom {{π} 2}} \right. } 2}$
在这种情况下,STE模值的最大值点为:
| ${\left| {{S_{{\rm{DPCA}}}}\left( {{m_k}} \right)} \right|_{\max }} = 2{\sigma ' \! _{\rm{P}}}$ | (32) |
其中,最大值点位置mk满足:${A_{\rm{e}}}C\cos \left( {{\omega _{\rm{v}}}{m_k}{T_{\rm{P}}} \! + \! {{\theta '} \! _0}} \right) $$=\pm {{\left( {2k \! - \! 1} \right){π}} \mathord{\left /{ \vphantom {{\left( {2k \! - \! 1} \right){π}} 2}} \right.} 2}$,$k \! = \! 1,2 \cdots $。在1个周期内,除最大值点外,STE曲线中还包含1个极小值点(或极大值点),假设该点的位置为${m_0}$,则满足$\cos \left( {{\omega _{\rm{v}}}{m_0}{T_{\rm{P}}} + \phi } \right) = \pm 1$。m0与mk之间的关系如图 3所示。

|
图 3 m0 与 mk 关系示意图 Fig. 3 The relationship between m0 and mk |
根据以上分析有如下关系式:
| $\Big| {{A_{\rm{e}}}C\cos \left( {{\omega _{\rm{v}}}{m_\Delta }{T_{\rm{P}}}} \right)} \Big| = {{\left( {2k - 1} \right){π} } \mathord{\left/ {\vphantom {{\left( {2k - 1} \right){π} } 2}} \right. } 2}$ | (33) |
其中,${m_\Delta } = {m_k} - {m_0}$。因此,振动点等效振幅可通过下式进行计算:
| ${A_{\rm{e}}} = \frac{{\left( {2k - 1} \right){π} }}{{2\left| {C\cos \left( {{\omega _{\rm{v}}}{m_\Delta }{T_{\rm{P}}}} \right)} \right|}}$ | (34) |
对于以上两种情况的判定,可通过对提取的STE曲线最大值点之间的时间间隔进行判断。当相邻两个最大值点之间的时间间隔与STE的周期相等时,则判定为第1种情况;如果小于STE的周期,则判定为第2种情况。上述分析表明,STE中包含了振动点的振动特征,对STE进行FFT可有效提取振动点振动频率,通过提取STE曲线某些特殊位置点,可实现对等效振幅的有效提取。
4 仿真验证与分析固定发射机的双基FMCW SAR系统仿真参数设置采用如图 1所示的几何模型。发射机坐标为(-10,1,6) km,相应的斜视角约为27°,FMCW信号载频为35 GHz,带宽为150 MHz,脉冲持续时间为1 ms;搭载双通道接收天线的运动平台运动速度为30 m/s,飞行高度为10 km,两接收天线的间距为0.51 m,对差频信号的采样频率为0.4 MHz,合成孔径时间为0.8 s,场景中包括3个振动点目标和7个随机分布的静止点目标,3个振动点的各项参数如表 1所示。
| 表 1 振动点参数 Tab. 1 Parameters of vibration point |
其中振动点P的等效振幅为0,因此其回波幅度近似为零,为有效检测到等效振幅为0的振动点,进而验证本文理论分析的正确性,振动点P的散射系数设定为振动点Q和R的200倍。
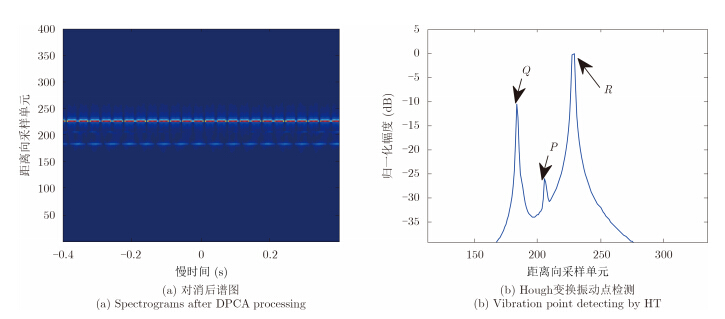
图 4给出了DPCA杂波抑制后回波差频信号距离-慢时间谱图以及采用Hough变换进行振动目标检测结果。其中图 4(a)为经DPCA杂波抑制处理后回波差频信号的距离-慢时间谱图,经DPCA处理后静止目标信息被消除,仅剩振动目标点信息。振动目标回波在距离-慢时间谱图中表现为沿方位向的直线,其幅度受STE的影响,随慢时间周期变化。且图 4(a)中仅能直观地观测到两条直线,即目标点Q和R,由于目标点P的等效振幅为0,虽然其散射系数是目标点Q和R的200倍,其回波能量仍然很弱。采用Hough变换对谱图中的直线进行检测,获取振动目标点所在距离单元位置,如图 4(b)所示。可以看出,经Hough变换后目标点P的归一化幅度与目标点Q和R的归一化幅度相差近20 dB,当系统存在一定噪声时,目标点P的回波很容易被淹没在噪声中难以检测。
|
图 4 DPCA杂波抑制及振动目标检测 Fig. 4 DPCA clutter suppression and vibration target detection |
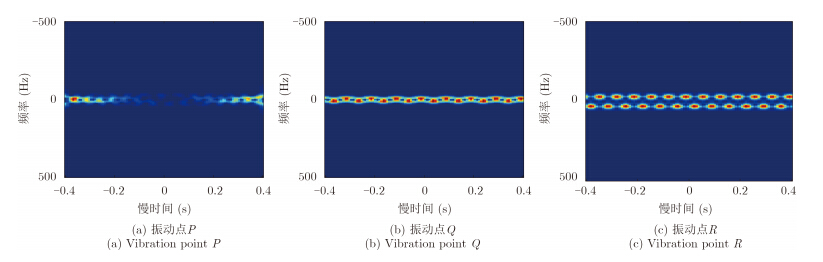
分别抽取振动点所在距离单元位置进行时频分析,3个振动点的m-D时频曲线如图 5所示。振动点P的m-D时频曲线表现为随时间非周期变化的特点,且其多普勒频偏很微弱;Q和R则表现为周期变化的特点。但是受STE的影响,只能获得3个目标点不连续的m-D时频曲线。
|
图 5 振动目标m-D时频曲线 Fig. 5 The m-D curves of vibration point |
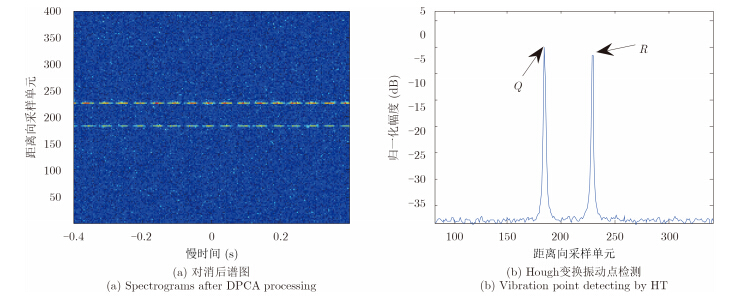
在振动目标特征提取的仿真实验中,为更好地验证本文给出的特征提取方法的有效性,每个接收通道加入信噪比为-3 dB的高斯白噪声。图 6给出了DPCA杂波抑制后回波差频信号距离-慢时间谱图以及采用Hough变换进行振动目标检测结果。可以看出,振动点P的回波已完全淹没在噪声中,即使采用能量累加方法进行直线检测的Hough变化也无法实现对该类振动目标的检测。
|
图 6 DPCA杂波抑制及振动目标检测 Fig. 6 DPCA clutter suppression and vibration target detection |
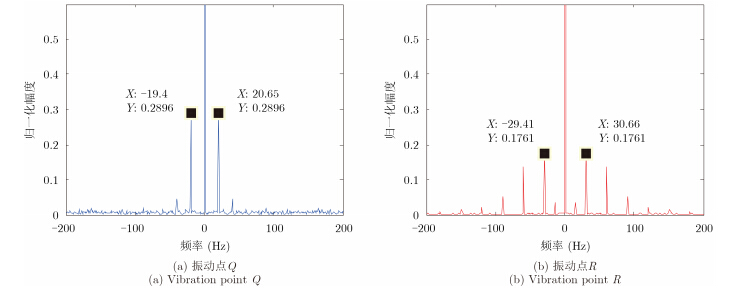
提取振动点Q和R所在距离单元位置的STE,对提取的振动目标点STE模值进行FFT以提取其振动频率,如图 7所示。其中图 7(a)为目标点Q的回波STE模值谱图,图 7(b)为目标点R的回波STE模值谱图。谱图中一次谐波对应的频率点的二分之一即为两个目标点的振动频率,同时由于STE项为双边带调制,提取上下边带的一次谐波频率模值求其均值再计算相应的振动目标频率。提取的振动目标点Q和R的振动频率分别为10.01 Hz和15.02 Hz。
|
图 7 振动频率的提取 Fig. 7 Extraction of the vibration frequency |
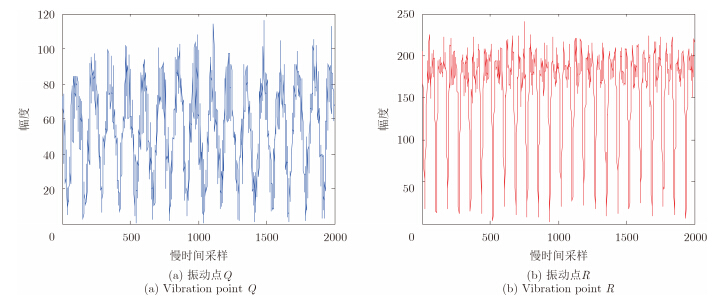
2个目标点的STE模值曲线如图 8所示,为提高提取精度,对STE模值曲线进行了2.5倍的插值处理。由于回波信号存在高斯白噪声且无法通过杂波对消进行抑制,STE的幅值受到一定的影响,无法直接进行振动目标振幅的提取,但是整个STE曲线的变化趋势并未受到太大影响。
|
图 8 振动目标STE模值曲线 Fig. 8 STE curves of vibration target |
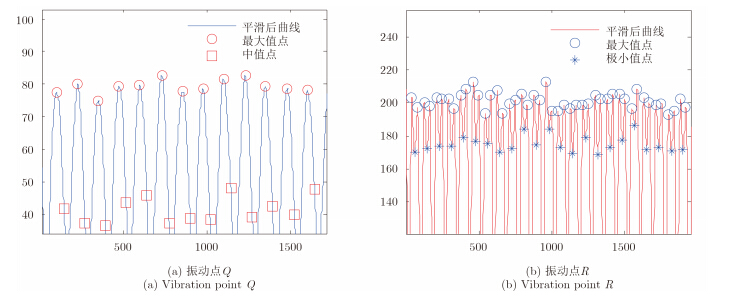
本文采用卷积平滑处理的方法,对STE曲线进行平滑处理,以提取曲线的最大值点和极小值点(或极大值点)等信息,如图 9所示。图 9(a)为平滑处理后Q点的STE模值曲线,提取曲线的最大值点,计算相邻两个最大值点之间的时间间隔约为0.05 s,等于Q 点STE模值周期0.05 s,因此判定为第3节中所述的第1种情况。进一步提取曲线中值点位置及幅值信息,根据式(31)计算Q点等效振幅均值为1.18 mm。图 9(b)为平滑处理后R点的STE模值曲线,提取曲线最大值点,计算相邻两个最大值点之间的时间间隔约为0.015 s,R点STE模值周期0.033 s,因此判定为第3节中所述的第1种情况。进一步提取曲线的极小值点位置,根据式(34)计算得R点振幅的均值为3.93 mm。经计算获得的两个振动点等效振幅均与理论值较为接近。
|
图 9 等效振幅提取 Fig. 9 Extraction of the equivalent vibration amplitudes |
同时可以看出振动点R的振幅估计值比振动点Q的振幅估计值精度更高,这是由于在计算R点振幅时只需提取最大值点和极小值点的位置信息,而计算Q点振幅时不仅需要提取最大值点和中值点位置信息,还需要其幅度值,而STE幅度受噪声的影响很难提取到其真实的幅度值,因此,提取精度受到一定的限制。根据式(31)和式(34),采用本文方法提取振动目标的等效振幅值,可采用提高信号载频的方法,时振动目标回波尽量满足第3节所述的第2种情况,以提高振动目标振幅的提取精度。
5 结论FMCW SAR由于其自身的优越性,必将受到越来越广泛的关注。论文开展了一站固定式双基FMCW SAR振动目标检测与特征提取方法的研究。进一步分析了STE对振动目标微多普勒时频曲线的影响,同时给出了一种基于STE的振动目标特征提取方法,所提提取方法能够完成对振动点振动频率及一站固定式双基SAR模式下振动目标特有的等效振幅的有效提取。对于本文所述采用慢时间包络进行振动特征提取的方法,仍存在一定的局限性,就是在1个距离单元处存在多个振动频率不同的振动目标时,将很难完成振动特征的提取,这也是下一步研究工作的重点。
| [1] | Entzminger J N. Joint STARS and GMTI: past, present and future[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(2): 748-761.( 1) 1) |
| [2] | Chen V C, Li F Y, Ho S S, et al.. Micro-Doppler Effect in Radar: Phenomenon, Model and Simulation Study[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 2-21.( 1) 1) |
| [3] | Deng B, Wu G Z, Qin Y L, et al.. SAR/MMTI: an extension to conventional SAR/GMTI and a combination of SAR and micromotion techniques[C]. IET RADAR Conference, Guilin, China, 2009: 42-45.( 1) 1) |
| [4] | Deng B, Wang H Q, Li X, et al.. Generalised likelihood ratio test detector for micro-motion targets in SAR raw signals[J]. IET Radar, Sonar and Navigation, 2011, 5(5): 528-535.( 1) 1) |
| [5] | Deng B, Wang H Q, Wu C G, et al.. SAR micromotion target detection based on gapped sine curves[C]. IGARSS Munich, Germen, 2012: 29-32.( 1) 1) |
| [6] | 邓彬. 合成孔径雷达微动目标指示(SAR/MMTI)研究[D]. [博士论文], 国防科技大学, 2011.Deng Bin. Study on the Synthetic Aperyure Radar Micro-Motion Target Indication (SAR/MMTI)[D]. [Ph.D. dissertation], School of Electronic Science and Engineering, 2011.( 1) 1) |
| [7] | 邓彬, 吴称光, 秦玉亮, 等. 合成孔径雷达微动目标指示(SAR/MMTI)研究进展[J]. 电子学报, 2013, 41(12): 2436-2442.Deng Bin, Wu Cheng-guang, Qin Yu-liang, et al.. Advances in Synthetic Aperture Radar Micro-Motion Target Indication (SAR/MMTI)[J]. Acta Electronica Sinica, 2013, 41(12): 2436-2442.( 1) 1) |
| [8] | Sparr T and Krane B. Micro-Doppler analysis of vibrating targets in SAR[J]. IEE Proceedings-Radar, Sonar and Navigation, 2003, 150(4): 277-283.( 1) 1) |
| [9] | Rüegg M, Meier E, and Nüesch D. Vibration and rotation in millimeter-wave SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(2): 293-304.( 1) 1) |
| [10] | Clemente C and Soraghan J J. Vibrating target micro-Doppler signature in bistatic SAR with a fixed receiver[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8): 3219-3227.( 1) 1) |
| [11] | Zhao G, Zhang C, and Fu Y W, et al.. Micro-Doppler analysis of vibrating target in MIMO SAR[C]. EUSAR Conference, Berlin, Germany, 2014: 624-627.( 1) 1) |
| [12] | 张伟, 童创明, 张群, 等. 基于DPCA杂波抑制的地面振动目标微多普勒提取[J]. 系统工程与电子技术, 2011, 33(4): 738-741.Zhang Wei, Tong Chuang-ming, Zhang Qun, et al.. Micro-Doppler extraction of ground vibrating targets based on SAR/DPCA technique[J]. Systems Engineering and Electronics, 2011, 33(4): 738-741.( 1) 1) |
| [13] | Zhang W, Tong C, and Zhang Q, et al.. Extraction of vibrating features with dual-channel fixed-receiver bistatic SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(3): 507-511.( 3) 3) |
| [14] | Meta A, Hoogeboom P, and Ligthart L P. Signal processing for FMCW SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3519-3532.( 3) 3) |
| [15] | Liu Y, Deng Y, Wang R, et al.. Efficient and precise frequency-modulated continuous wave synthetic aperture radar raw signal simulation approach for extended scenes[J]. IET Radar, Sonar and Navigation, 2012, 6(9): 858-866.( 1) 1) |
| [16] | Stove A G. Linear FMCW radar techniques[J]. IEE Proceedings F: Radar and Signal Processing, 1992, 139(5): 343-350.( 1) 1) |
| [17] | 梁毅, 李燕平, 邢孟道, 等. 一种平行航线双基聚束式FMCW SAR的两步处理方法[J]. 电子学报, 2013, 41(10): 1975-1982.Liang Yi, Li Yan-ping, Xing Meng-dao, et al.. A two-step processing approach for parallel bistatic spotlight FMCW SAR focusing[J]. Acta Electronica Sinica, 2013, 41(10): 1975-1982.( 1) 1) |
| [18] | 金日初, 王宇, 邓云凯, 等. 改进的一站固定式双基SAR频域成像方法[J]. 雷达学报, 2014, 3(2): 192-200. doi: 10.3724/SP.J.1300.2014.13115. Jin Ri-chu, Wang Yu, Deng Yun-kai, et al.. A modified frequency domain imaging method for one-stationary bistatic SAR[J]. Journal of Radars, 2014, 3(2): 192-200. doi: 10.3724/SP.J.1300.2014.13115.( 1) 1) |
| [19] | 梁毅, 王虹现, 邢孟道, 等. 基于FMCW的大斜视SAR成像研究[J]. 电子与信息学报, 2009, 31(4): 776-780. doi: 10.3724/SP.J.1146.2007.01851.Liang Yi, Wang Hong-xian, Xing Meng-dao, et al.. Imaging study of high squint SAR based on FMCW[J]. Journal of Electronics & Information Technology, 2009, 31(4): 776-780. doi: 10.3724/SP.J.1146.2007.01851.( 1) 1) |
| [20] | 刘向阳, 廖桂生, 杨志伟, 等. 机载多通道雷达DPCA误差补偿及稳健的杂波抑制[J]. 电子学报, 2009, 37(9): 1982-1988.Liu Xiang-yang, Liao Gui-sheng, Yang Zhi-wei, et al.. DPCA error compensation and robust clutter suppression for multi-channel airborne radar[J]. Acta Electronica Sinica, 2009, 37(9): 1982-1988."( 1) 1) |
 2015, Vol. 4
2015, Vol. 4
