②(海军航空工程学院信息融合研究所 烟台 264001)
②(Institute of Information Fusion, Naval Aeronautical and Astronautical University, Yantai 264001, China)
雷达作为对海上目标探测的主要手段,在海上维权、海洋监视等公共安全以及国防安全领域应用广泛[1, 2]。然而,随着海上威胁的日益增多,雷达在复杂海洋环境下的探测性能难以满足实际需求。一方面是由于海面电磁散射形成的海杂波严重影响了雷达目标检测,回波信杂比(Signal-to-Clutter Ratio,SCR)低,因此,对海杂波特性分析和杂波抑制技术的研究尤为重要,也是国内外学者重点关注的研究热点[3, 4, 5]。另一方面,目标本身复杂的运动引起雷达回波的多普勒调制效应,导致回波信号具有非平稳和时变特性,使得雷达对海杂波背景下微弱目标,尤其是“低(低掠射角)、慢(慢速运动目标)、小(小尺寸目标)、快(机动目标)、隐(隐身目标)”目标的探测难度越来越大[6, 7]。因此,更加亟需从目标特性角度出发,深入研究目标运动状态和回波特性之间的关系,进而设计相应的匹配增强和滤波算法,改善SCR,提高对海雷达探测性能。
近年来,微多普勒(micro-Doppler,m-D)理论为非平稳信号的分析和处理提供了新的思路[8, 9]。研究表明,由于风浪等环境因素的影响,也由于螺旋桨、舵等海洋运动体自身的各种推动和控制作用,会产生复杂的运动,导致姿态变化,引起雷达回波功率调制效应,不仅存在平动,舰船还绕参考点作3轴转动(滚动、俯仰和偏航),导致散射点的多普勒频率随时间非线性变化,因此,采用微多普勒理论分析海杂波以及海上目标回波信号是非常适合的,拓展了信号维度,从而有助于进一步提升雷达对海上微弱目标的检测和识别能力[6, 10]。微多普勒理论的“创始人”Victor C. Chen教授在文献[11]中将海面目标的复杂运动作为微多普勒特性分析的重要研究内容,值得深入研究。目前,海上目标微多普勒的理论研究及应用仍处在起步阶段,首先需要掌握海上目标的微动特征,并对其进行特性分析。本文对海杂波中刚体目标微动特性及信号模型进行了深入的研究,建立了海面非匀速平动目标、转动目标以及长时间观测条件下的微动目标回波模型。采用雷达实测数据分析微动特征并验证模型的正确性。研究成果可为后续的海杂波抑制、海上目标检测和识别提供技术支撑[12, 13]。
2 微多普勒效应概念和内涵 2.1 微动和微多普勒效应目标相对于雷达存在径向运动,则雷达回波的频率将偏离发射信号的频率,这就是常见的多普勒现象,产生的频移量就是多普勒频率。若目标相对于雷达存在径向运动的同时,目标或目标上的结构还伴随着微运动(振动、自转、旋动、翻滚),会在雷达回波中规则的多普勒频移上引起额外的频率调制,即在多普勒频率附近产生边带,这种微动对雷达回波的调制称为微多普勒现象[8]。目标微动状态常常是独一无二的,反映了目标的精细特征和姿态,可用于目标检测、目标成像和目标识别等[6, 14]。近年来,人们将微多普勒的概念推广为目标或目标组成部分在径向相对雷达径向距离的小幅非匀速运动或运动分量,其回波频谱存在旁瓣或展宽。微多普勒是频率的瞬时特性的反映,表征了目标的瞬时微动速度,具有非平稳和时变特性,对微动特征分析和处理最本质的问题是时变信号处理。
2.2 海面目标微动特征类型本文主要研究海面刚体目标,即在目标运动过程中,目标所有质元之间的距离、内部各部分相对位置始终保持不变。因此,常用“刚体的质心”来研究刚体的运动。海面目标的运动是在3维空间中的复合运动,包括沿3个坐标轴的平动和围绕3个坐标轴的旋转运动,即六自由度运动。根据微多普勒的定义,海面目标的微动特征表现为平动中的非匀速运动以及3轴转动(俯仰、偏航和横滚),归纳起来可分为如下3类:(1)低空掠海飞行目标,如掠海飞行的巡航导弹和飞机等,通常具有很强的机动能力,表现为非匀速运动,并且由于贴近海面飞行,使得雷达照射目标后的回波信号受海杂波影响,回波SCR低;(2)高海况条件下的大目标,但由于距离远、杂波背景强等因素导致目标单元中SCR很低,例如预警雷达对舰船和航母等的远程探测和监视,船体随海面起伏而绕3轴转动;(3)海面快速机动目标,如海面快艇等。
3 海杂波中目标微多普勒模型 3.1 坐标系定义假设雷达与目标近似处在同一水平面内。对海雷达观测海面目标几何关系如图 1所示[10],包括目标固定参考坐标系Cref=(X, Y, Z)、目标运动坐标系Cmov=(x, y, z)以及雷达至海面目标的视线距离(Radar Line of Sight,RLOS)坐标系Crlos=(q, r, h)。参考坐标系的坐标原点假定与雷达始终保持相同距离且位于目标船体中心。目标运动坐标系的原点为o,纵轴ox平行于目标横滚轴并指向舰船的船首,横轴oy平行于俯仰轴并指向左舷,垂直轴oz指向目标的上部。为了分析问题方便,常把原点o设在舰船质心上,并认为坐标轴ox, oy和oz分别为目标的横滚轴、俯仰轴和偏航轴,(x, y, z)坐标绝对值分别表示目标的长度、宽度和高度。RLOS坐标系中的r沿视线方向在XOY平面内,h轴垂直于r轴,并且q满足右手法则。
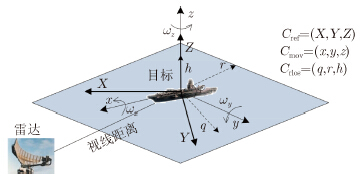 | 图 1 对海雷达观测海面目标几何关系 Fig. 1 Geometry of radar and target at sea |
采用向量形式分析海面微动目标模型,如图 2所示,其中雷达位于原点O,RLOS为rs(tm),tm表示在相参处理间隔(Coherent Processing Interval,CPI)内脉冲-脉冲间的慢时间。在tm=t0时刻,海面微动目标质心位于O1点,点散射体D1在tm=t1时运动到D3点,目标质心运动到O2点。根据图 2的几何关系,则RLOS距离OD3可分解为初始距离r0,以速度v从D1平动到D2,然后以角速度$\omega = {\rm{ }}{\left( {{\omega _x},{\omega _y},{\omega _z}} \right)^{\rm{T}}}$转动到D3,
| \[\begin{array}{*{20}{l}} {{r_{\rm{s}}}_{({t_{\rm{m}}})} = O{D_3} = O{D_1} + {D_1}{D_2} + {D_2}{D_3}}\\ {\quad \quad \quad \; = {r_0} + v{t_{\rm{m}}} + {R_\rm{t}}{R_0}} \end{array}\] | (1) |
 | 图 2 雷达和微动目标观测模型 Fig. 2 Observation model of radar and micromotion target |
为了获得高分辨率和远探测距离,假设雷达发射LFM信号 \rm c
| \[{s_{\rm{t}}}\left( t \right) = {\rm{rect}}\left( {t/{T_{\rm{p}}}} \right)\exp \left( {{\rm{j2}}\pi {f_{\rm{c}}}t + {\rm{j}}\pi \gamma {t^2}} \right)\] | (2) |
| \[\begin{array}{*{20}{l}} {{s_{\rm{r}}}(t) = {\sigma _{\rm{r}}}{\rm{rect}}\left( {\frac{{t - \tau }}{{{T_{\rm{p}}}}}} \right)}\\ {\quad \quad \quad \cdot \exp \left\{ {{\rm{j2}}\pi \left[ {{f_{\rm{c}}}(t - \tau ) + \frac{\gamma }{2}{{(t - \tau )}^2}} \right]} \right\}} \end{array}\] | (3) |
雷达通常采用相对应的LFM信号作为回波解调的参考信号
| \[\begin{array}{*{20}{c}} {{s_{{\rm{ref}}}}(t,{t_{\rm{m}}}) = \exp \left\{ {{\rm{j}}2\pi {{\left[ {{f_{\rm{c}}}\left( {t - \frac{{2{r_{{\rm{ref}}}}\left( {{t_{\rm{m}}}} \right)}}{{\rm{c}}}} \right)} \right]}^2}} \right.}\\ {\quad \left. { + \frac{1}{2}\gamma \left( {t - \frac{{2{r_{{\rm{ref}}}}({t_{\rm{m}}})}}{{\rm{c}}}} \right)} \right\}} \end{array}\] | (4) |
| \[\begin{array}{*{20}{l}} {s(t,{t_{\rm{m}}}) = {\sigma _{\rm{r}}}{\rm{rect}}\left( {\frac{{t - 2{r_{\rm{s}}}\left( {{t_{\rm{m}}}} \right)/{\rm{c}}}}{{{T_{\rm{p}}}}}} \right)}\\ {\quad \quad \quad \quad \cdot \exp \left[ { - {\rm{j}}\frac{{4\pi }}{{\rm{c}}}\gamma \left( {t - \frac{{2{r_{{\rm{ref}}}}\left( {{t_{\rm{m}}}} \right)}}{{\rm{c}}}} \right)\Delta {r_{\rm{s}}}\left( {{t_{\rm{m}}}} \right)} \right]}\\ {\quad \quad \quad \quad \cdot \exp \left( { - {\rm{j}}\frac{{4\pi }}{{\rm{c}}}{f_{\rm{c}}}\Delta {r_{\rm{s}}}\left( {{t_{\rm{m}}}} \right)} \right)} \end{array}\] | (5) |
| \[\begin{array}{*{20}{l}} {s(t,{t_{\rm{m}}}) = {\sigma _{\rm{r}}}B{\rm{sinc}}\left[ {\frac{{2B}}{{\rm{c}}}(r - \Delta {r_{\rm{s}}}({t_{\rm{m}}}))} \right]}\\ {\quad \quad \quad \quad \cdot \exp \left( { - {\rm{j}}\frac{{{\rm{4}}\pi {f_{\rm{c}}}}}{{\rm{c}}}\Delta {r_{\rm{s}}}({t_{\rm{m}}})} \right)} \end{array}\] | (6) |
| \[\Delta {r_{\rm{s}}}\left( {{t_{\rm{m}}}} \right) = \int_0^{{T_{\rm{n}}}} {\left[ {\left( {v + \omega \times {R_{\rm{t}}}{R_0}} \right) \cdot n} \right]{\rm{d}}{t_{\rm{m}}}} \] | (7) |
对于短时间观测,可暂不考虑目标的距离走动,即得到的目标回波为同一距离单元内的回波数据。因此可不考虑式中的sinc函数项。由文献[15]可知,对于非匀速平动目标,其雷达回波经过解调和脉压运算后,动目标回波信号受速度和加速度调制,可近似为1阶多项式信号,即线性调频(Linear Frequency Modulation,LFM)信号,频率具有时变特性,可看作微动信号的一种。
| \[\begin{array}{*{20}{l}} {{f_{\rm{t}}} = - \frac{2}{\lambda }\frac{{{\rm{d}}({r_0} - {v_0}{t_{\rm{m}}} - {a_{\rm{s}}}t_{\rm{m}}^2/2)}}{{{\rm{d}}{t_{\rm{m}}}}}}\\ {\quad = \frac{2}{\lambda }({v_0} + {a_{\rm{s}}}{t_{\rm{m}}})} \end{array}\] | (8) |
对于做横滚、俯仰或偏航运动的3轴转动目标,其RLOS距离可由目标绕中心做旋转运动的旋转矩阵 Rz-y-x=R(θx)R(θy)R(θz)来描述,其中R(θx),R(θy),R(θz)分别为横滚、偏航和俯仰矩阵,θx, θy和θz为对应的旋转角度[10]
| \[\left. {\begin{array}{*{20}{l}} {R({\theta _x}) = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos {\theta _x}}&{ - \sin {\theta _x}}\\ 0&{\sin {\theta _x}}&{\cos {\theta _x}} \end{array}} \right]}\\ {R({\theta _y}) = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _y}}&0&{\sin {\theta _y}}\\ 0&1&0\\ { - \sin {\theta _y}}&0&{\cos {\theta _y}} \end{array}} \right]}\\ {R({\theta _z}) = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _z}}&{ - \sin {\theta _z}}&0\\ {\sin {\theta _z}}&{\cos {\theta _z}}&0\\ 0&0&1 \end{array}} \right]} \end{array}} \right\}\] | (9) |
根据雷达和微动目标的几何关系,可得到RLOS距离[10]:
| \[\begin{array}{*{20}{l}} {{r_{\rm{s}}}({t_{\rm{m}}}) = \sin \varphi ({a_{11}}x + {a_{12}}y + {a_{13}}z)}\\ {\quad \quad \quad + \cos \varphi ({a_{21}}x + {a_{22}}y + {a_{23}}z)} \end{array}\] | (10) |
| \[{f_{\rm{r}}} = \frac{{2{v_{\rm{r}}}({t_{\rm{m}}})}}{\lambda } = \frac{2}{\lambda }\frac{{{\rm{d}}{r_{\rm{s}}}({t_{\rm{m}}})}}{{{\rm{d}}{t_{\rm{m}}}}}\] | (11) |
若同时存在横滚、偏航和俯仰运动,微多普勒为三者的线性组合:
| \[\begin{array}{*{20}{l}} {{f_{\rm{r}}} \approx \frac{2}{\lambda }\cos \varphi \left[ {3\omega x - {\omega _x}z + {\omega _z}x} \right.}\\ {\quad \quad + \left. {\left( {\omega {\omega _y}z - \omega {\omega _z}y - \omega _x^2y - \omega _z^2y} \right){t_{\rm{m}}}} \right]} \end{array}\] | (12) |
在雷达信号处理中,通常可以延长积累时间以增加目标的能量,达到提高SNR/SCR的目的[13, 14]。然而,对于长时间观测目前主要面临以下两个方面的难题:一方面由于雷达距离分辨力的不断提高和目标的高速运动,目标回波包络在不同脉冲周期之间走动和弯曲,目标的峰值位置会随慢时间变化而偏移,当偏移量大于雷达距离单元时,将产生距离徙动效应(Across Range Unit,ARU),使得目标能量在距离向分散,对于此种回波模型,不能忽略式中的sinc函数包络项;另一方面在长观测时间内,目标的加速运动、高阶运动以及转动等会引起回波相位变化,使雷达回波信号具有时变特性并表现为高阶相位形式,目标的多普勒频率将跨越多个多普勒单元,称为多普勒徙动效应(Doppler Frequency Migration,DFM),使得目标能量在频域分散,降低了相参积累增益。此外,对于高速运动目标,其距离和多普勒频率在较短的积累时间内仍会有较大的变化,同样会出现距离和多普勒徙动。
仅考虑径向速度分量,可得海面目标的微多普勒频率:
| \[\begin{array}{*{20}{l}} {{f_{{\rm{m - D}}}}({t_{\rm{m}}}) = \frac{2}{\lambda } \cdot \frac{{\rm{d}}}{{{\rm{d}}{t_{\rm{m}}}}}{R_{\rm{s}}}({t_{\rm{m}}})}\\ {\quad \quad \quad \;\begin{array}{*{20}{l}} { = \frac{2}{\lambda } \cdot {{\left[ {\nu + \frac{{\rm{d}}}{{{\rm{d}}{t_{\rm{m}}}}}({R_{\rm{t}}}{R_0})} \right]}^{\rm{T}}} \cdot n}\\ { = {f_{\rm{t}}}({t_{\rm{m}}}) + {f_{\rm{r}}}({t_{\rm{m}}})} \end{array}} \end{array}\] | (13) |
| \[\begin{array}{*{20}{l}} {{f_{\rm{r}}}({t_{\rm{m}}}) = \;\frac{2}{\lambda } \cdot ({v_{\rm{r}}} \cdot n)}\\ {\quad \quad \;\; \approx {f_0} + \mu {t_{\rm{m}}} + \frac{k}{2}t_{\rm{m}}^2} \end{array}\] | (14) |
| \[\begin{array}{*{20}{l}} {{f_{\rm{r}}}({t_{\rm{m}}}) = \;\frac{2}{\lambda }(\omega \times {R_{\rm{t}}}{R_0}) \cdot n}\\ {\begin{array}{*{20}{l}} {\quad \quad \;\; \approx \frac{2}{\lambda }\left[ {{\omega _0} \cdot ({R_{\rm{t}}}{R_0} \times n)} \right.}\\ {\quad \quad \quad \begin{array}{*{20}{l}} { + {\omega _1}({R_{\rm{t}}}{R_0} \times n){t_{\rm{m}}}}\\ { + {\omega _2}\left. {({R_{\rm{t}}}{R_0} \times n)\frac{{t_{\rm{m}}^2}}{2}} \right]} \end{array}} \end{array}} \end{array}\] | (15) |
| \[\begin{array}{*{20}{l}} {{R_{\rm{s}}}({t_{\rm{m}}}) = \int_0^{{T_{\rm{n}}}} {[(v + \omega } \times {R_{\rm{t}}}{R_0}) \cdot n]{\rm{d}}{t_{\rm{m}}}}\\ {\quad \quad \quad \approx {r_0} - {v_0}{t_{\rm{m}}} - {a_{\rm{s}}}t_{\rm{m}}^2/2 - {g_{\rm{s}}}t_{\rm{m}}^3/6} \end{array}\] | (16) |
对于高海况下的海面目标而言,由于受非线性策动力和非线性阻尼力的作用,其在海浪的作用下各维度的摆动将呈现多倍周期和随机性的特点。此时,船体的偏航、俯仰和横滚角为时间的周期函数,周期与振幅的大小与海况、船型、船速和航向有关,则目标与雷达的径向距离表示为:
| \[{R_{\rm{s}}}({t_{\rm{m}}}) = {r_0} + {A_{\rm{r}}}\cos ({\omega _{\rm{r}}}{t_{\rm{m}}} + {\varphi _{\rm{r}}})\] | (17) |
| \[{f_{\rm{r}}} = \frac{2}{\lambda }{A_{\rm{r}}}{\omega _{\rm{r}}}mr\sin \left( {{\omega _{\rm{r}}}{t_{\rm{m}}} + {\varphi _{\rm{r}}}} \right)\] | (18) |
由上述刚体目标微多普勒调制模型的讨论中得知,目标的微多普勒频率由非匀速平动和3维转动引起,其幅度和频率受海况和目标运动状态影响。微动目标在一段短的时间范围内,可用LFM信号作为调频信号的1阶近似,包括幅度、初速度和加速度3个参数。
| \[\begin{array}{*{20}{l}} {x(t) = s(t) + c(t) = \sum\limits_i {{A_i}(t)\exp \left( {{\rm{j}}2\pi {f_i}t + {\rm{j}}\pi {\mu _i}{t^2}} \right)} }\\ {\quad \quad \;\; + c(t)\;,\;\;\left| t \right| \le T/2} \end{array}\] | (19) |
海面微动目标在较长的观测时间,运动变得较为复杂,对于以非匀速平动为主要运动方式的海面目标,如低空掠海飞行目标、快艇、潜望镜等,回波仍可建模为LFM信号;而对于以转动为主要运动方式或者高机动的海面目标,如高海况海面起伏目标、大型舰船、反舰导弹等,其回波具有周期调频性,可建模为多分量QFM信号,具有2次调频的多普勒频率,由于正弦调频信号在一个周期内仍可由3次多项式很好地近似,因此,长时间微动目标观测模型可统一建模为:
| \[\begin{array}{*{20}{l}} {x(t,{t_{\rm{m}}}) = s(t,{t_{\rm{m}}}) + c(t,{t_{\rm{m}}})}\\ {\begin{array}{*{20}{l}} {\quad \quad \;\;\; = {A_{\rm{r}}}{\rm{sinc}}\left[ {B\left( {t - \frac{{2{R_{\rm{s}}}({t_{\rm{m}}})}}{{\rm{c}}}} \right)} \right]}\\ {\quad \quad \quad \quad \cdot \exp \left[ {{\rm{j2}}\pi \left( {{f_0}{t_{\rm{m}}} + \frac{1}{2}\mu t_{\rm{m}}^2 + \frac{1}{6}kt_{\rm{m}}^3} \right)} \right]}\\ {\quad \quad \quad \quad + c(t,{t_{\rm{m}}}),\left| {{t_{\rm{m}}}} \right| \le {T_{\rm{n}}}/2} \end{array}} \end{array}\] | (20) |
X波段对海实验雷达毗邻渤海,方便观测海面航道和空中航道,水面和空中目标众多。该雷达为全相参高分辨率雷达,对海掠射角约为0.9°,海况约为2级。在此条件下,降低了海杂波的影响,能够获得高SCR的海面目标回波数据,有利于算法的验证和分析海面目标微动特性。图 3为航行中的船式起重机照片。
 | 图 3 海上目标照片 Fig. 3 Picture of marine target |
距离向脉压后的雷达回波如图 4(a)所示,能够得到清晰的目标高分辨率距离像。对船首部分的雷达回波进一步做时频分析,得到图 4(b)的短时傅里叶变换(Short-Time Fourier Transform,STFT)谱,可发现目标的多普勒主要由两部分组成,一部分由船体本身径向运动分量产生的平动分量(约为-490 Hz),另一部分为海面起伏导致的船体的转动分量(约为140 Hz)。同时从图 4(b)可知,在较短的观测时间内,两个多普勒信号分量均受频率调制,从而验证了3.2节中的目标模型。
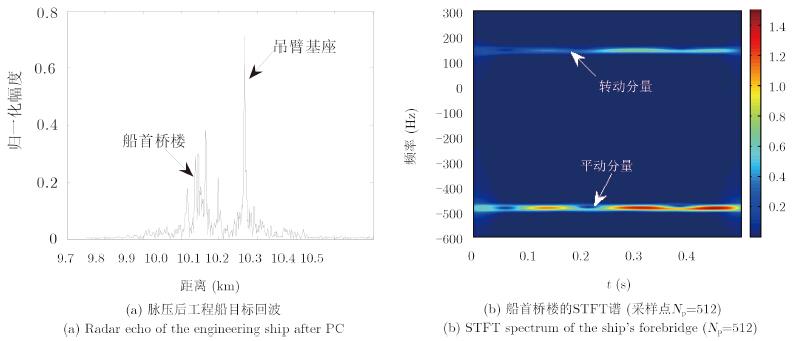 | 图 4 目标回波时频分析 (X波段对海雷达数据) Fig. 4 Time-frequency analysis of the radar returns (Data recorded by an X-band marine radar) |
分数阶傅里叶变换(FRactional FT,FRFT)作为一种统一的时频变换,将信号分解在一组正交的chirp基上,更适于分析或处理时变的非平稳信号,尤其是LFM信号,能够反映多普勒的变化规律。图 5比较了船首微多普勒信号的频谱和FRFT谱,图中又给出了两个微动分量的局部放大图。根据FRFT域峰值搜索结果,得到两者的最佳变换阶数为popt1=1.007和popt2=1.006,而不是频域的p=1,表明目标的平动和转动分量均可近似建模为LFM信号。对比图 5(a)和图 5(b)也可以发现,FRFT谱的峰值较频谱尖锐,并且旁瓣较低,表明在FRFT域能量更为集中。最后,采用文献[10]中的滤波方法提取微动信号分量,得到微动特征如图 6(c)所示,与图 4(b)相比,高斯短时分数阶傅里叶变换(Gaussian Short-Time FRFT,GSTFRFT)对微动特征的提取结果优于STFT方法。
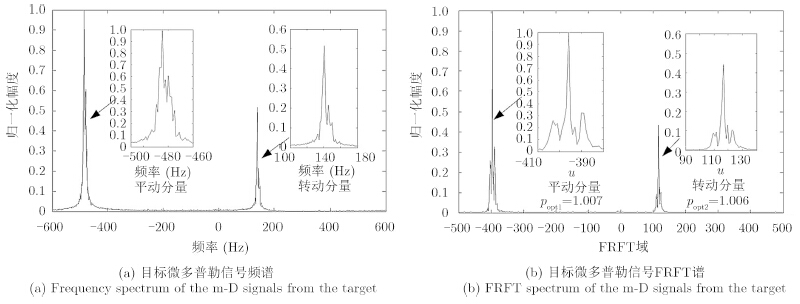 | 图 5 微多普勒信号的频谱和FRFT谱比较 (Np=512) Fig. 5 Comparison of frequency and the best FRFT spectrum of the m-D signals (Np=512) |
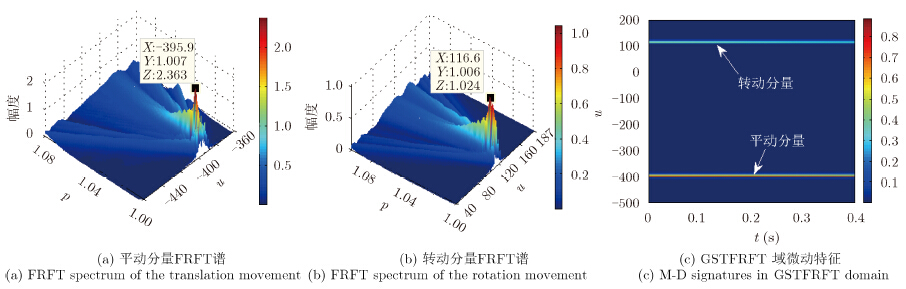 | 图 6 船首微动特征提取结果 (Np=512) Fig. 6 Extraction result of m-D signatures from the ship’s forebridge (Np=512) |
采用南非科学与工业研究理事会(Council for Scientific and Industrial Research,CSIR)[17]采集的对海雷达数据对海面目标微动特性进行分析。试验由位于南非开普敦西部的奥弗比格试验场(Overberg Test Range,OTB)的Fynmeet雷达完成。在实验中,CSIR研究团队还记录了其它辅助信息,如天气(风速、气温和雨雪)、波浪向、显著波高以及目标的GPS位置信息,其中利用GPS可将目标实际位置与GPS位置进行比对,从而易于获得目标的雷达回波数据,帮助算法的比对和开发。同时,雷达天线上加装了高分辨率视频摄像机,能够随时准确地记录海面环境以及目标的运动姿态等。数据包含不同类型大小的合作目标数据,非常适合海面微动目标信号的分析和算法验证。CSIR数据库及数据描述参见表 1。
| 表 1 数据描述 Tab. 1 Data description |
雷达地理位置及周边环境如图 7(a)所示,图 7(b)对海杂波的特性进行了分析,包括距离-时间信息、时频分析以及相关性分析。由图 7(b)和图 7(c)可知,雷达对海观测时间约为67 s,观测区域覆盖90个距离单元,明显看出由风速产生的周期性海面起伏,根据显著波高判断试验时的海况等级约为5级,为高海况数据,其频谱具有时变特性,多普勒分布在50~150 Hz,谱宽较宽,表明观测方向为逆风向。
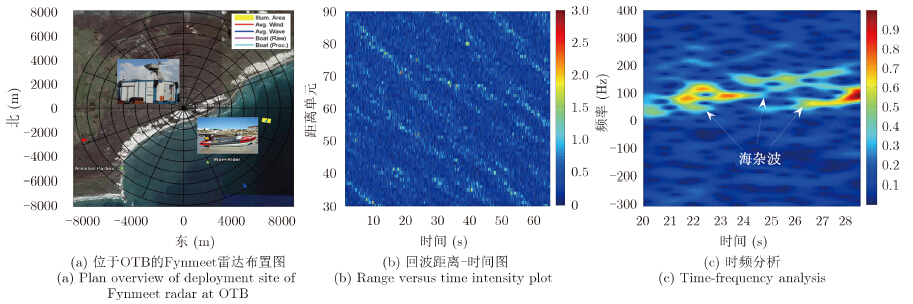 | 图 7 CSIR海杂波数据描述及特性分析 (CSIR-TFC15-038) Fig. 7 Description and property analysis of the CSIR dataset (CSIR-TFC15-038) |
采用CSIR数据库中的TFC17-006数据验证所提算法,在高海况条件下由Fynmeet雷达采集合作目标乘浪者号充气橡皮艇(WaveRider Rigid Inflatable Boat,RIB)的回波数据,试验参数如表 2所示。
| 表 2 CSIR-TFC17-006数据参数 Tab. 2 Parameters of CSIR-TFC17-006 |
图 8为CSIR-TFC17-006的回波数据分析,其中图 8(a)的雷达回波距离-时间图表明雷达观测时间为100 s,观测范围覆盖约45个距离单元,仅通过幅度难以从强海杂波中发现WaveRider RIB目标。图 8(b)为目标距离走动、GPS轨迹和多项式拟合曲线示意图,可知目标在观测时间内跨越了多个距离单元,并且采用3次多项式函数能够很好地拟合目标运动轨迹,验证了3.3节长时间观测目标模型的正确性。进一步分析回波的时频特性(图 8(c)),可以看出目标多普勒随时间变化,近似有周期振荡性,证明目标具有微动特性,利用微动特征可区分海杂波和目标。
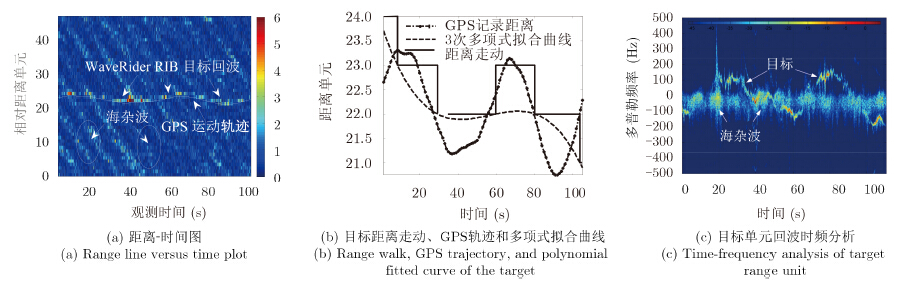 | 图 8 CSIR-TFC17-006回波数据分析 Fig. 8 Data analysis of CSIR-TFC17-006 |
由以上分析可知:(1)受海况和目标本身运动状态影响,海面刚体目标的微动特征表现为平动中的非匀速运动以及3轴转动,当观测时间较短,且目标在同一距离单元内时,可用LFM信号作为调频信号的1阶近似,包括幅度、初速度和加速度3个参数;(2)转动目标的微动参数需要由旋转矩阵求得,并与俯仰、偏航和横滚角速度有关;(3)长时间观测可获得目标更多的能量和信息,故有利于检测性能的提高,但受ARU,DFM和距离弯曲等效应的影响,微动目标回波能量分散在多个距离和多普勒单元,同时,回波信号中出现高阶相位,具有2次调频特性或周期调频性,但在适当的相参积累时间内可建模为多分量QFM信号。
5 结束语微多普勒描述了海面目标运动的精细特征,成为区分海杂波和目标的有用特征之一,有助于提高雷达目标探测和识别能力。本文对海杂波中刚体目标微动特性及信号模型进行了深入的研究,建立了海面非匀速平动目标、转动目标以及长时间观测条件下的微动目标回波模型,表明海上目标具有微动特性,其多普勒具有周期或调频特性,表现为回波信号具有时变和非平稳特性。根据观测时间的长短,可采用LFM,QFM或周期调频信号来近似,在长时间观测条件下,回波信号易产生距离和多普勒徙动效应,需要在后续的信号处理中补偿,以提高相参积累增益。实测数据验证模型的有效性。海面目标微动特征已为海杂波背景下微弱目标的检测和识别提供了新的途径,有助于提高雷达的探测性能和识别能力。
| [1] | Ward K D and Watts S. Use of sea clutter models in radar design and development[J].IET Radar, Sonar & Navigation, 2010, 4(2): 146-157.( 1) 1) |
| [2] | Chen X L, Guan J, Liu N B, et al. Detection of a low observable sea-surface target with micromotion via the Radon-linear canonical transform[J].IEEE Geoscience and Remote Sensing Letters, 2014, 11(7): 1225-1229.( 1) 1) |
| [3] | Greco M, Stinco P, Gini F, et al. Impact of sea clutter nonstationarity on disturbance covariance matrix estimation and CFAR detector performance[J].IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(3): 1502-1513.( 1) 1) |
| [4] | 黄勇, 陈小龙, 关键. 实测海尖峰特性分析及抑制方法[J]. 雷达学报, 2015, 4(3): 334-342.Huang Y, Chen X L, and Guan J. Property analysis and suppression method of real measured sea spikes[J]. Journal of Radars, 2015, 4(3): 334-342.( 1) 1) |
| [5] | Al-Ashwal W A, Woodbridge K, and Griffiths H D. Analysis of bistatic sea clutter—part I: average reflectivity[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 1283-1292.( 1) 1) |
| [6] | 陈小龙, 关键, 何友. 微多普勒理论在海面目标检测中的应用及展望[J]. 雷达学报, 2013, 2(1): 123-134.Chen X L, Guan J, and He Y. Applications and prospect of micro-motion theory in the detection of sea surface target[J]. Journal of Radars, 2013, 2(1): 123-134.( 3) 3) |
| [7] | Shui P L, Li D C, and Xu S W. Tri-feature-based detection of floating small targets in sea clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 1416-1430.( 1) 1) |
| [8] | Chen V C, Fayin Li, Ho S-S, et al. Micro-Doppler effect in radar: phenomenon, model, and simulation study[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 2-21.( 2) 2) |
| [9] | 罗迎, 张群, 王国正, 等. 基于复图像OMP分解的宽带雷达微动特征提取方法[J]. 雷达学报, 2012, 1(4): 361-369.Luo Y, Zhang Q, Wang G Z, et al. Micro-motion signature extraction method for wideband radar based on complex image OMP decomposition[J]. Journal of Radars, 2012, 1(4): 361-369.( 1) 1) |
| [10] | Chen X L, Guan J, Bao Z H, et al. Detection and extraction of target with micro-motion in spiky sea clutter via short-time fractional Fourier transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(2): 1002-1018.( 5) 5) |
| [11] | Chen V C, David Tahmoush, and William J Miceli. Radar Micro-Doppler Signature: Processing and Applications[M]. UK: IET, 2014.( 1) 1) |
| [12] | Chen X L, Guan J, Li X Y, et al. Effective coherent integration method for marine target with micromotionvia phase differentiation and radon-Lv’s distribution[J]. IET Radar, Sonar & Navigation, 2015, 9(9): 1284-1295.( 1) 1) |
| [13] | Chen X L, Guan J, Huang Y, et al. Radon-linear canonical ambiguity function-based detection and estimation method for marine target with micromotion[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(4): 2225-2240.( 2) 2) |
| [14] | 李彦兵, 杜兰, 刘宏伟, 等. 基于微多普勒效应和多级小波分解的轮式履带式车辆分类研究[J]. 电子与信息学报, 2013, 35(4): 894-900.Li Y B, Du L, Liu H W, et al. Study on classification of wheeled and tracked vehicles based on micro-Doppler effect and multilevel wavelet decomposition[J]. Journal of Electronics & Information Technology, 2013, 35(4): 894-900.( 2) 2) |
| [15] | Chen X L, Guan J, Liu N B, et al. Maneuvering target detection via Radon-fractional Fourier transform-based long-time coherent integration[J]. IEEE Transactions on Signal Processing, 2014, 62(4): 939-953.( 1) 1) |
| [16] | Wang Y. Inverse synthetic aperture radar imaging of maneuvering target based on range-instantaneous-Doppler and range-instantaneous-chirp-rate algorithms[J]. IET Radar, Sonar & Navigation, 2012, 6(9): 921-928.( 1) 1) |
| [17] | De Wind H J, Cilliers J E, and Herselman P L. Dataware: sea clutter and small boat radar reflectivity databases[J]. IEEE Signal Processing Magazine, 2010, 27(2): 145-148.( 1) 1) |
 2015, Vol. 4
2015, Vol. 4
