②(北京遥感设备研究所 北京 100854)
②(Beijing Remote Sensing Equipment Research Institute, Beijing 100854, China)
合成孔径雷达(Synthetic Aperture Radar,SAR)能够在复杂的气象条件下全天时工作,获得高分辨率图像。随着SAR系统的发展,设计了多种新的工作模式以满足不同观测需求,如滑聚、圆迹、环扫等。环扫模式是指天线波束中心绕着一条轴进行旋转扫描,可以在短时间内获得环状目标区域的信息[1, 2, 3, 4, 5, 6]。随着环扫SAR分辨率的提高、测绘带的增宽,对成像算法精度提出更高的要求。而高精度成像算法研究所需的模拟回波数据也海量增加,对计算效率提出了更高的要求。传统的串行回波模拟方法效率低,因此有必要利用高性能计算技术加速回波模拟过程,为环扫SAR成像算法研究、系统设计提供有力支撑。
高性能计算在各种计算密集型科研问题领域得到广泛应用,很多研究者也把SAR回波模拟和高性能计算进行了结合,比如利用OpenMP(Open Multiprocessing)的多核并行方法实现机载SAR回波仿真[7],基于MPI的多CPU并行方法实现星载SAR回波仿真[8],基于网格计算的多计算机并行方法实现SAR回波模拟[9],以及基于GPU(Graphics Processing Unit,图形处理器)的众核并行回波仿真[10, 11, 12, 13, 14, 15, 16, 17, 18]等。但是,以上文献的并行加速均未针对环扫SAR回波模拟,此外,虽然速度相比于传统的回波模拟串行方法有了很大的提升,但是与成像处理的时间差距依然很大。因此有必要在前期研究基础上,结合环扫成像几何、回波生成的特点,进行环扫SAR回波的多GPU快速模拟研究,为成像算法研究提供支持。
高分辨率、宽测绘带条件下的回波数据海量增加,给环扫SAR多GPU回波仿真带来两方面的问题。首先是冗余计算问题,在判断波束脚印内的有效目标回波时,需要计算整个场景的目标信息,但实际贡献回波的目标点只有很小一部分,从而产生大量的冗余计算。其次是由于冗余计算带来的冗余存储问题,波束脚印计算中需要存储整个场景的大小,虽然大显存的GPU能够解决这一问题,但硬件成本也会增加。因此,有必要对冗余计算及其引发的冗余存储问题进行深度优化,加快多GPU的环扫回波仿真效率。
针对环扫SAR回波模拟有待解决的问题,本文提出了一种基于冗余计算约简的环扫SAR回波多GPU快速模拟方法。采用MPI进程控制不同的GPU卡,对原始数据进行分块,使得每个进程在进行回波仿真时只需要开辟私有的存储空间,对照射范围外目标斜距历史的冗余计算进行约简,然后通过不同的GPU对相应块数据并行地进行回波模拟计算,最后通过回波数据收集,得到最终的模拟回波数据。该方法能够更好的应用于大场景环扫SAR回波模拟,相对传统串行方法可以达到2个数量级以上的加速并有效地降低硬件需求,为工程应用提供了指导。
2 环扫SAR回波模拟算法 2.1 成像几何模型环扫SAR在运动过程中,天线在保持入射角不变的同时,绕地面垂线做环形扫描,从而形成近似环状的扫描区域,其成像几何如图 1所示,其中SAR平台沿X轴正方向做直线运动,天线波束以固定的中心视角β0绕地面垂线做逆时针圆周扫描,B为波束中心点,Q(x1,y1,z1)为SAR载荷位置,βmin为波束起始视角,βmax为波束终止视角,θmin和θmax分别表示波束脚印方位角的最小值和最大值。假定SAR天线从X正半轴开始绕Z轴做圆周扫描,由于SAR平台沿X轴正方向前进,经过完整一周的扫描,在地面会产生一个不闭合的圆环扫描区域,如图 1所示。
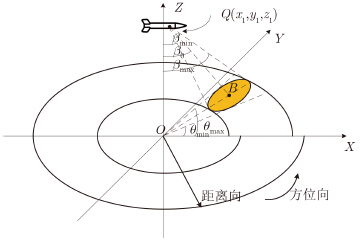 | 图 1 环扫SAR成像几何 Fig. 1 Circular scanning SAR imaging geometry |
成像几何主要用于计算目标和SAR之间的斜距、角度等几何信息。其中角度信息用来进行波束脚印范围判断,斜距信息用来计算回波延迟、相位,下面以场景内某点P(xi,yi,zi)为例,介绍成像几何的解算过程:
首先,点P的斜距Ri及水平投影${R'_i}$的计算公式如下。
| ${R_i} = \sqrt {{{({x_1} - {x_i})}^2} + {{({y_1} - {y_i})}^2} + {{({z_1} - {z_i})}^2}} $ | (1) |
| ${R'_i}=\sqrt {{{({x_1} - {x_i})}^2} + {{({y_1} - {y_i})}^2}} $ | (2) |
接着,点P的波束视角bi和方位向角qi求解如下。
| ${{\beta }_{i}}=\arccos \left(\frac{{{z}_{1}}-{{z}_{i}}}{{{R}_{i}}}\right)$ | (3) |
| ${\theta _i} = \arccos \left( {\frac{{{{\rm{x}}_1} - {x_i}}}{R'_i}} \right)$ | (4) |
然后,需要根据点P的角度信息进行波束脚印范围判断。波束脚印范围计算包括距离向、方位向两个方面的角度约束。距离向角度约束是指根据βmin和βmax对所有点波束视角进行判断,可以在整个场景中筛选出一个环状区域。在此基础上,根据θmin和θmax进行方位向角度约束得到最终的波束脚印范围内的目标点。因此,如果点P在波束范围内,则需满足如下条件:
| ${\beta _{\min }} \le {\beta _i} \le {\beta _{\max }}$ | (5) |
| ${\theta _{\min }} \le {\theta _i} \le {\theta _{\max }}$ | (6) |
回波模拟算法从处理域角度可以划分为距离时域、距离频域、2维频域等3类,其中时域模拟算法由于能够较好地考虑各种系统误差和运动误差,常应用于算法研究、系统设计过程。本节主要针对所采用的距离时域快速模拟方法[19]进行介绍。
SAR发射的chirp信号表达式如下:
| $s(\tau ) = {\rm{rect}}\left( {\frac{\tau }{{{T_{\rm{p}}}}}} \right)\exp \left( {{\rm{j2}}\pi {f_{\rm{c}}}\tau + {\rm{j}}\pi {k_{\rm{r}}}{\tau ^2}} \right)$ | (7) |
经过相干接收,SAR回波信号表达式如下:
| $\begin{array}{*{20}{c}} {{s_{\rm{r}}}(t,\tau ) = \underbrace {\left\{ {{\rm{rect}}\left( {\frac{t}{{{T_{\rm{a}}}}}} \right) \cdot \exp \left( { - {\mathop{\rm j}\nolimits} \frac{{4\pi }}{\lambda }r(t)} \right)} \right\}}_{方位向}}\\ { \cdot \underbrace {\left\{ {{\rm{rect}}\left( {\frac{{\tau - \frac{{2r(t)}}{{\mathop{\rm c}\nolimits} }}}{{{T_{\rm{p}}}}}} \right) \cdot \exp \left[{{\mathop{\rm j}\nolimits} \pi {k_{\rm{r}}}{{\left( {\tau - \frac{{2r(t)}}{{\mathop{\rm c}\nolimits} }} \right)}^2}} \right]} \right\}}_{距离向}} \end{array}$ | (8) |
由式(8)可知,每个方位时刻的回波信号看作由一系列狄拉克函数和发射信号的卷积,并通过傅里叶变换的方法在频域完成混叠的方位回波信号与距离向信号的卷积过程实现回波快速模拟,如式(9)所示。
| $\begin{array}{*{20}{c}} {{s_{\rm{r}}}({t_n},\tau ) = \sum\limits_{n = 0}^T {{s_{\rm{a}}}({t_n},\tau )} \otimes s(\tau )}\\ { = \sum\limits_{n = 0}^T {{{\rm{F}}^{ - 1}}\left\{ {\left. {{\rm{F}}[{s_{\rm{a}}}({t_n},\tau )] \cdot S(\xi )} \right\}} \right.} } \end{array}$ | (9) |
| ${s_{\rm{a}}}({t_n},\tau ) = \sum\limits_i {\exp } \left\{ { - {\rm{j}}\frac{{4\pi }}{\lambda }{r_i}({t_n})} \right\} \cdot \left[{\delta \left( {\tau - \frac{{2{r_i}({t_n})}}{{\mathop{\rm c}\nolimits} }} \right)} \right]{\rm{ }}$ | (10) |
根据式(9),式(10),可以得到回波模拟步骤如图 2所示。首先,根据环扫SAR成像几何解算,得到某一个方位时刻场景中目标点的斜距、视角、方位角信息;接着,进行波束脚印判断,对于范围内的目标方位向回波进行计算,并叠加到对应的距离门中;然后,将叠加的方位向信号和距离向信号通过频域乘法的方式完成卷积处理,得到一个方位时刻的回波数据;最后,遍历所有方位向时刻得到完整的回波数据。
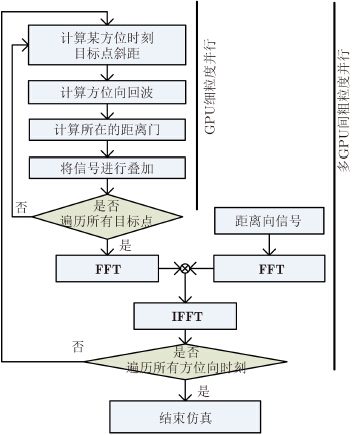 | 图 2 SAR回波模拟仿真流程图 Fig. 2 Flowchart of SAR raw data simulation |
CUDA (Compute Unified Device Architecture)是由显卡厂商英伟达推出的一种通用的并行计算架构,能够方便地将通用数值问题映射到GPU并行解决,因此GPU和传统算法的结合成为一个热点问题。
GPU与CPU在硬件架构上有着很大的不同,主要体现在逻辑控制、数据计算和存储体系方面。首先,由于芯片表面放置较少的逻辑控制单元,GPU的逻辑处理能力较差,因此在CPU+GPU异构系统中的逻辑控制部分通常由CPU完成。其次,GPU芯片表面比CPU芯片表面放置了更多的计算单元,因此GPU的计算能力优于后者。然后,GPU具有更加丰富的存储体系,每个线程都有自己的寄存器和本地存储器,多个线程构成一个线程块,每个线程块中的线程有共享的存储空间,多个线程块构成一个网格,网格中线程可以共享全局存储器、常量存储器和纹理存储器中的数据,GPU的存储模型如图 3所示。
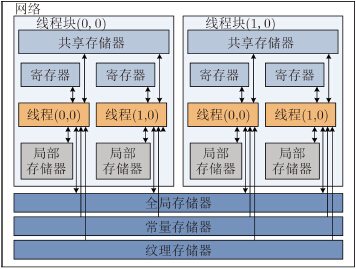 | 图 3 GPU存储器模型 Fig. 3 GPU memory hierarchy |
根据以上分析介绍,在环扫SAR多GPU回波仿真中,CPU主要用来完成输入输出、数据和参数分配、数据收集等任务,GPU主要用来完成计算密集度大的回波计算部分。
3.2 MPI并行编程库CUDA用于完成单GPU卡的回波计算,对于多GPU卡的控制、任务调度,可以通过MPI完成。MPI全称消息传递接口,是一个并行的编程库,可以实现多机多核并行编程。在多GPU回波仿真中,任务的分发、收集都需要通过信息传递完成,而MPI是解决这一问题的最佳方法。MPI是基于消息传递机制的,可以灵活地进行仿真状态信息传递、仿真数据传输、多GPU计算进程控制等任务,便于进行不同粒度的并行,可以扩展到更多的GPU卡进行回波模拟工作,如图 4所示。
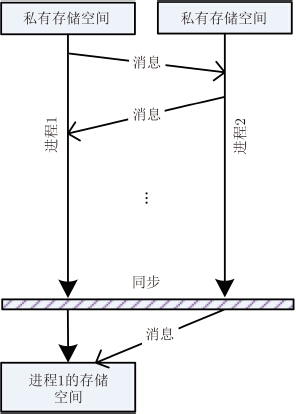 | 图 4 MPI消息传递简图 Fig. 4 MPI message-passing diagram |
3.3 多GPU并行回波模拟方法
随着分辨率提高、测绘带宽变宽、观测场景增大,需要进行模拟的回波数据量海量增加,虽然通过单GPU实现回波仿真已经在速度上有了很大的提升,但是大场景回波模拟与成像处理之间还是有着很大的时间差,影响成像算法研究进程,因此有必要引入多GPU进行快速仿真。
根据stop-and-go模型,在SAR进行环扫时,各个方位向时刻的回波仿真过程是独立的。此外,在信号相干积累过程中,各个目标点的信号散射也可以看作是相互独立的。因此,可以从这两个层面进行并行化设计,以每个方位时刻的回波仿真作为粗粒度并行单位,分发给各个GPU进行计算;在每个方位时刻内,以单个目标点回波模拟作为细粒度并行单位,分发给单个GPU卡中的各个线程进行计算,如图 2所示。
因此,可以对整个方位向仿真时间进行划分,分配给每一块GPU卡相应的仿真时间范围,GPU卡收到计算任务之后开始进行计算,不同卡之间是并行执行的,直到最后所有的计算任务都已经完成,CPU负责将计算任务进行收集整理,得到最后的回波数据,如图 5所示,具体的步骤如下:
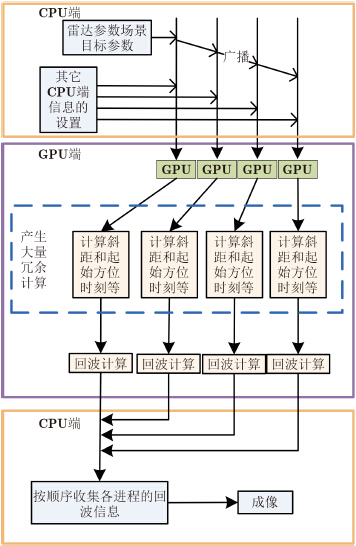 | 图 5 多GPU的SAR回波模拟仿真流程 Fig. 5 Flowchart of multi-GPUs based SAR raw data simulation |
(1) 读入雷达参数、场景目标参数等仿真基本信息;
(2) 将存入内存中的参数信息通过MPI主进程广播到其他MPI进程中;
(3) 通过不同的进程控制不同的GPU,并将各自内存空间中的参数信息和进程号传送到GPU显存中;
(4) 在GPU进行计算时,通过进程号、总进程数与总的方位向点数计算出该GPU卡在计算回波时的起始方位时刻和结束方位向时刻,也就是将整个方位向长度划分成了若干个小的方位向范围;
(5) 计算场景目标的斜距等成像几何信息,进而计算在该方位时刻的回波;
(6) 遍历该GPU所需遍历的所有方位向时刻,得到仿真回波数据子块;
(7) 计算完成后,将各自回波通过消息传递给主进程,CPU主进程进行回波的收集整理。
3.4 基于MPI的冗余计算约简
分析上述回波仿真过程,可以看出波束脚印判断步骤需要计算场景内所有目标点的成像几何信息,但是波束脚印内的目标点只是其中一部分,对于波束脚印外目标点的成像几何计算是冗余的,这样就产生了两个问题:
(1) 一个合成孔径范围相对于整个场景较小,但在进行波束脚印范围判断时却要计算场景中所有点的斜距、角度等成像几何信息,这样就产生了很大的冗余计算。
(2) 如果需要计算场景中所有点的成像几何信息,那么就需要将所有点的信息拷贝到GPU显存中,但实际上需要的只有该GPU计算任务中对应照射区域内的点信息,这样就产生了显存的浪费。
综上可知,传统回波并行模拟方法中在成像几何计算部分出现计算冗余和存储冗余,因此可以根据以上分析对这两个问题提出解决措施,即通过MPI进行分块的方法约简计算量和减少显存的使用量。为了减少在分块时产生的计算量,分块的处理原则是尽量取内存中连续的数据,减少不连续数据的存取。所以对于环扫SAR这种特殊的扫描方式,可以采取4块划分。如图 6,沿X轴和Y轴将环状区域划分为4块。
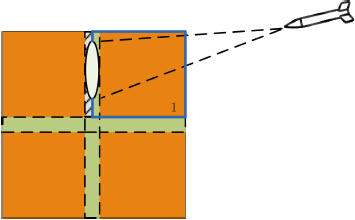 | 图 6 雷达扫描分块边缘平面图 Fig. 6 Block edge diagram of radar scanning |
但进行分块划分之后,又出现了新的问题,假如在某个方位时刻进行回波仿真时,合成孔径超出了该块,使得在场景块边缘的点并没有扫到,如图 6。蓝色边线区域为场景块,黄色区域为已经经过的区域,在该方位时刻,由于雷达在扫描时已经到了场景的边缘,所以有一部分场景目标信息没有扫描到,如图 6的1区域中斜线部分,所以在回波计算时会产生能量积累不完全的情况。
雷达在沿方位向前进时,扫描到的区域是连续的,所以在该场景边缘,最多有半个合成孔径距离没有扫描到,在进行目标场景分块时,需要将图中斜线区域的场景目标信息加进来,这样就避免了在某个方位向时刻出现扫描场景不完全的情况,如图 7所示。图中黄色部分为需要回波仿真的场景,淡蓝色区域为1个合成孔径距离,也就是左右或者上下两块各多占大于半个合成孔径的距离。对仿真场景的分块处理需要4个MPI进程获取自己的场景块信息,因为在仿真开始前,主进程已经将场景信息通过广播发送给了各个进程,所以每个进程中有各自独立的场景信息。场景的大小可用如下公式计算:
| $\begin{array}{*{20}{r}} {S = \left( {\frac{{{\rm{height}}}}{{{\rm{MPI}}\_{\rm{NUM}}}}*2 + \frac{d}{2}} \right)}\\ {{\rm{*}}\left( {\frac{{{\rm{width}}}}{{{\rm{MPI}}\_{\rm{NUM}}}}*2 + \frac{d}{2}} \right)} \end{array}$ | (11) |
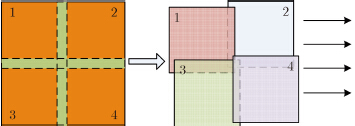 | 图 7 MPI分块示意图 Fig. 7 MPI partitioning diagram |
在未进行MPI分块时,GPU显存中需要存储整个的场景信息,在计算斜距和波束脚印范围时,GPU需要对计算整个场景数据进行计算。假设单位面积内目标点在进行斜距和波束脚印范围计算时所需要的运算量为Cpt,每个方位时刻的回波运算量为echo_Cpt,而目标点在场景中都是均匀分布的,所以Cpt跟场景的面积成正比。MPI分块前后的每个方位向时刻的回波总运算量Cpt_total和Cpt_total_pieces如式(12)和式(13),MPI分块前后的回波总运算量的比值Ni如式(14)。
| ${\rm{Cpt\_total = (height}} * {\rm{width)}} * Cpt + echo\_Cpt$ | (12) |
| ${\rm{Cpt}}\_{\rm{total}}\_{\rm{pieces}} = \left( {\frac{{{\rm{height}}}}{{{\rm{MPI}}\_{\rm{NUM}}}}*2 + \frac{d}{2}} \right){\rm{*}}\left( {\frac{{{\rm{width}}}}{{{\rm{MPI}}\_{\rm{NUM}}}}*2 + \frac{d}{2}} \right){\rm{*Cpt}} + {\rm{echo}}\_{\rm{Cpt}}$ | (13) |
| $\begin{array}{*{20}{c}} {{N_{\rm{i}}} = \frac{{{\rm{Cpt}}\_{\rm{total}}}}{{{\rm{Cpt}}\_{\rm{total}}\_{\rm{pieces}}}} \approx \frac{{({\rm{height*width}}){\rm{*Cpt + echo}}\_{\rm{Cpt}}}}{{\frac{{{\rm{height*width}}}}{{{\rm{MPI}}\_{\rm{NU}}{{\rm{M}}^{\rm{2}}}}}{\rm{*4*Cpt + echo}}\_{\rm{Cpt}}}}}\\ { = {{\left( {\frac{{{\rm{MPI}}\_{\rm{NUM}}}}{{\rm{2}}}} \right)}^{2}} - \frac{{\left( {{{(\frac{{{\rm{MPI}}\_{\rm{NUM}}}}{{\rm{2}}}{\rm{)}}}^4} - {{(\frac{{{\rm{MPI}}\_{\rm{NUM}}}}{{\rm{2}}}{\rm{)}}}^2}} \right){\rm{*echo}}\_{\rm{Cpt}}}}{{({\rm{height*width}}){\rm{*Cpt}} + {{(\frac{{{\rm{MPI}}\_{\rm{NUM}}}}{{\rm{2}}})}^2}*{\rm{echo}}\_{\rm{Cpt}}}}} \end{array}$ | (14) |
从式(12)和式(13)可以看出总的回波运算量近似的与场景块的面积成正比,而d相对于整个场景的height和width而言是很小的,所以在计算Ni时忽略了d的影响。假设启动了4个MPI进程,并且在实验过程中场景为6000×6000时,计算整个场景的斜距及波束脚印范围的运算量约为计算1个方位向时刻的回波运算量的2倍,那么上式中Ni的值约等于2。在相同波束宽度的前提下,如果场景小于6000×6000,则Ni<2,如果场景大于6000×6000,则Ni>2,并且随着场景的增大,Ni会变大,也就是MPI分块方法的优势会随着场景的增大而更加显著。
通过图 7的分块方法每个进程可以从场景中获取与自己进程号相关的场景块,例如主进程将获取1号场景块,然后将场景块信息发送到GPU端进行各自的回波仿真处理。最终当所有的场景块都仿真完成,也就是所有的方位向时刻点都仿真完成的时候,除主进程外的其他进程会向主进程发送回波结果,由主进程进行整合,完成整个回波过程。
从图 7中可以看出,在计算斜距等信息时每个进程只需要对本进程对应的场景块进行处理,而不需要对全部的场景进行计算,减少了将近3/4的斜距等信息的计算量,增加的是MPI进程在进行分块时的计算量,由于分块时尽量取连续内存中的数据,所以在分块时带来的计算量相对是非常小的。而且由于每个进程只需要获取本场景块的信息,使用的显存空间也大大减少了,原来需要将整个场景信息都传送到显存中,而现在只需要传送稍大于1/4原场景的信息量,对显卡的显存要求也会降低,从而降低系统构建经济成本。
4 实验结果分析 4.1 实验条件为了验证本文方法的有效性,需要设计大场景回波模拟实验进行比较分析。回波仿真参数如表 1所示,并采用美国MSTAR数据[20]作为场景散射系数图进行模拟计算。本次试验的硬件环境如下,CPU型号是Intel(R) Xeon(R) CPU E5-2630 v2,2.6 GHz,GPU共4块,型号为Nvidia Tesla C2070(显存6 G),使用的CUDA版本为CUDA 4.0,MPI版本为MPICH 2.0。
| 表 1 回波仿真参数 Tab. 1 Simulation parameters |
以CPU串行计算作为基准算例,在此基础上进行多GPU、基于MPI分块的多GPU并行回波模拟实验,对比并行仿真的加速效果。
为了验证多GPU并行方法和基于冗余计算约简的多GPU并行方法的优势,分别针对4000×4000,5000×5000,6000×6000以及7000×7000等4个场景进行环扫SAR回波仿真,结果如表 2、表 3所示。从计算结果可以看出来,经过4块GPU卡的并行加速,运算时间大大减少,相对CPU的加速比可达160倍左右,但是仿真时间仍需要17 min;在此基础上,进行冗余计算约简,仿真时间缩短,加速比可以提升至352倍。可见在多GPU并行仿真基础上,进行冗余计算约简,能够有效地提高环扫SAR回波仿真效率。
| 表 2 不同场景下3种方法的计算时间对比 Tab. 2 Simulation time comparison of three algorithms in different scenes |
| 表 3 不同场景下多GPU和MPI分块的多GPU方法的加速比 Tab. 3 Speedup comparison of the multi-GPUs based method and the proposed method |
为了分析MPI分块方法在速度上的优势,测试了MPI分块时间以及分块后的多GPU计算总时间及加速情况,如表 4所示。从计算结果可以看出,利用MPI在CPU端进行并行分块的冗余计算约简,可以在多GPU并行仿真基础上,提高2.2倍。该方法虽然相对多GPU方法具有一定的复杂度,但是时间消耗较少。通过较少的时间消耗,减少大量的冗余数值计算,从而提高整体并行计算效率,是一种并行计算的优化思路。图 8给出了MPI分块约简冗余计算的加速效果对比,从图中的柱状信息可以看出,用MPI分块的方法进行回波模拟仿真相比于未分块的多GPU来说,仿真的速度快了近2倍。此外,从折线信息可以看出,多GPU的仿真时间的增长率要大于MPI+多GPU的增长率,也就可以预测,随着仿真场景的增大,MPI分块方法的优势会越来越明显。
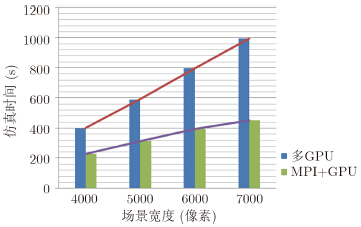 | 图 8 多GPU和MPI+GPU的仿真总时间对比图 Fig. 8 Total simulation time comparison of the multi-GPUs based method and the proposed method |
| 表 4 不同场景下冗余计算约简的计算时间及加速比 Tab. 4 Performance analysis of the proposed method in time and speedup |
此外,实验还分析了场景大小为7000×7000的情况下,整个环扫SAR回波仿真过程中,输入/输出时间、CPU串行程序时间、MPI分块时间和GPU并行回波模拟时间,如图 9所示。可以看出,针对回波模拟这种计算密集型的数值计算,即使经过优化的多GPU并行加速,核心回波计算部分仍然占据了95%的执行时间,可见针对大场景、乃至长条带场景的回波仿真,可以扩大GPU并行的数量,通过更多的并行计算资源,来加快环扫SAR回波仿真,并逐步减少与成像处理之间的时间差距。
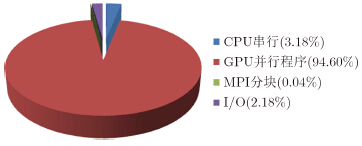 | 图 9 7000×7000场景大小的运行时间比例图 Fig. 9 The running time scale map of the proposed method in 7000×7000 simulation area |
最后,为了验证MPI分块的多GPU并行回波仿真的正确性,采用CS成像算法对多GPU,MPI+多GPU仿真的回波数据进行成像验证,两者的回波数据、成像结果完全一致,可以看出这种基于数据分块的冗余计算约简方法对成像精度没有影响,成像结果如图 10所示。
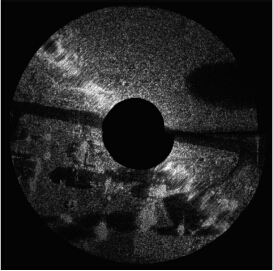 | 图 10 本文方法仿真回波的成像结果 Fig. 10 The imaging result of the simulated raw data by the proposed method |
此外,还需要进一步比较MPI+多GPU仿真方法和CPU仿真方法的计算精度。论文[16, 17, 18]和本文采用相同回波仿真算法,其结合点目标指标对GPU和CPU的回波仿真精度进行分析,结论是两者计算结果差别很小,在成像精度允许的范围内。因此,这里主要从回波数据、面目标指标角度对两者的仿真精度进行比较分析,如表 5所示。从回波数据来看,两种方法的差别较小,表现在均值误差为1e-7,方差误差为2.6e-5,以CPU结果为参考值计算出来的均方根误差(RMSE)为1e-5;从成像结果来看,辐射分辨率误差仅为1e-4,均值、方差误差较小,在成像精度允许的范围内。总之,基于MPI分块的多GPU回波仿真方法,虽然在做浮点数运算、FFT运算时与CPU相比存在微小差别,但是都在误差允许范围内,能够满足回波仿真精度的需要。
| 表 5 CPU方法和MPI分块的多GPU方法的仿真精度对比 Tab. 5 Accuracy analysis of the proposed methods |
在进行回波模拟时间对比的同时,也对硬件成本做了对比分析。经过冗余计算约简,每块GPU卡存储的数据量减少,大场景回波模拟对于显存的需求降低了,因此在计算能力相当的前提下,可以选用显存较小的GPU计算卡。
以Nvidia的Tesla C2070和C2050为例进行分析,前者硬件成本是后者的1.5倍左右,其配置如表 6所示。从表中可以看出两种处理器的差别只有显存大小不同,当计算场景大小为30000×30000的回波时,在没有分块之前需要的显存空间是3.35 G,所以如果从上面两种GPU中选择时,只能选择C2070;而如果运用分块的方法,在GPU进行运算时所需要的显存空间仅为0.84 G,所以可以选择C2050显卡。以本文实验所采用4块GPU为例,进行冗余存储约简后的硬件成本相比之前节省了大约50%。
| 表 6 相关硬件配置对比表 Tab. 6 Hardware configuration comparison |
本文实现了基于冗余计算约简的环扫SAR多GPU快速模拟仿真算法,通过MPI进行分块处理,约简了波束范围外目标的成像几何计算,减少仿真计算量的同时节省大量存储空间。实验结果表明,基于冗余计算约简的多GPU环扫SAR回波仿真方法可以满足精度要求,在时间上相比于多GPU并行模拟提升2倍以上,硬件成本也有了明显降低。基于本文算法,采用4块GPU卡的环扫SAR回波数据模拟相对CPU串行仿真的速度提升可达350倍,极大缩短成像算法的研究历程。此外,通过实验发现,CPU在GPU计算过程中一直处于空闲状态,造成计算资源浪费,因此在下一步研究中,会尝试通过多CPU结合多GPU的异构计算方式,充分利用计算机的计算资源,进一步提升回波模拟速率,为成像算法研究奠定基础。
| [1] | 李天池, 周荫清, 蔡世学, 等. 机载环扫成像雷达数据处理方法研究[J]. 系统工程与电子技术, 2002, 24(7): 1-3. Li Tianchi, Zhou Yinqing, Cai Shixue, et al.. Study on the data processing methods for airborne circular scanning imaging radar[J]. Systems Engineering and Electronics, 2002, 24(7): 1-3.(  1) 1) |
| [2] | 李静, 黄培康, 潘旭东, 等. 雷达下视环扫成像分辨率研究[J]. 系统工程与电子技术, 2009, 31(2): 315-318. Li Jing, Huang Peikang, Pan Xudong, et al.. Study on resolution for circular scanning imaging radar[J]. Systems Engineering and Electronics, 2009, 31(2): 315-318.(  1) 1) |
| [3] | 李勇, 朱岱寅, 朱兆达. 环视 SAR 成像处理中的几何失真校正算法[J]. 南京航空航天大学学报, 2009, 41(2): 232-237. Li Yong, Zhu Daiyin, and Zhu Zhaoda. Geometric distortion correction algorithm for circular-scanning SAR imaging[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2009, 41(2): 232-237.(  1) 1) |
| [4] | 毛新华, 朱岱寅, 李勇, 等. 环视 SAR 几何失真校正误差分析及补偿技术研究[J]. 电子与信息学报, 2007, 30(11): 2706-2709.doi:10.3724/SP.J.1146.2007.00679. Mao Xinhua, Zhu Daiyin, Li Yong, et al.. Study on error analysis of geometric distortion correction and compensation techniques for circular-scan SAR[J]. Journal of Electronics & Information Technology, 2007, 30(11): 2706-2709. doi:10.3724/SP.J.1146.2007.00679.(  1) 1) |
| [5] | 赵亮, 毛新华, 吴迪. 基于回波信号的环视 SAR 成像运动参数估计[J]. 数据采集与处理, 2014, 29(4): 590-596. Zhao Liang, Mao Xinhua, and Wu Di. Motion parameter estimate of circular-scanning SAR imaging based on echo signal[J]. Journal of Data Acquisition and Processing, 2014, 29(4): 590-596.(  1) 1) |
| [6] | 孙兵, 周荫清, 李天池, 等. 环扫 SAR 的快速聚焦成像算法[J]. 北京航空航天大学学报, 2007, 33(7): 803-806. Sun Bing, Zhou Yinqing, LI Tianchi, et al.. Fast focused imaging algorithm for circular scanning SAR[J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(7): 803-806.(  1) 1) |
| [7] | 苏宇, 齐向阳. 基于OpenMP的星载SAR回波信号并行仿真[J]. 中国科学院研究生院学报, 2008, 25(1): 129-135. Su Yu and Qi Xiangyang. OpenMP based space-borne SAR raw signal parallel simulation[J]. Journal of Graduate School of the Chinese Academy of Sciences, 2008, 25(1): 129-135.(  1) 1) |
| [8] | 王曦爽, 黄立胜, 王贞松. 分布式星载SAR回波仿真的并行化计算研究[J]. 系统仿真学报, 2006, 18(8): 2097-2100. Wang Xishuang, Huang Lisheng, and Wang Zhensong. Research on parallel arithmetic of distribute spaceborne SAR ground target simulation[J]. Journal of System Simulation, 2006, 18(8): 2097-2100.(  1) 1) |
| [9] | 张帆, 林殷, 洪文. 基于网格计算的SAR回波分布式仿真[J]. 系统仿真学报, 2008, 20(12): 3165-3167. Zhang Fan, Lin Yin, and Hong Wen. SAR echo distributed simulation based on grid computing[J]. Journal of System Simulation, 2008, 20(12): 3165-3167.(  1) 1) |
| [10] | Yu L, Xie X, and Xiao L. GPU-accelerated circular SAR echo data simulation of large scenes[C]. XXXIth URSI General Assembly and Scientific Symposium, Beijing, China, 2014: 1-4.( 1) 1) |
| [11] | Chapman W, Ranka S, Sahni S, et al.. Parallel processing techniques for the processing of synthetic aperture radar data on GPUs[C]. IEEE International Symposium on Signal Processing and Information Technology, 2011: 573-580.( 1) 1) |
| [12] | Zhu H, Xu H, and Feng L. Application of GPU for missile-borne SAR raw signal simulation[C]. International Conference on Artificial Intelligence, Management Science & Electronic Commerce, Zhengzhou, China, 2011: 2816-2820.( 1) 1) |
| [13] | Sheng H, Zhou M, Wang K, et al.. SAR echo simulation from numerous scattering cells based on GPU[C]. IET International Radar Conference, 2013: 1-5.( 1) 1) |
| [14] | 秦洁, 张志敏. 基于图形处理单元架构的合成孔径雷达回波仿真实现与优化[J]. 科学技术与工程, 2014, 14(13): 85-89. Qin Jie and Zhang Zhimin. Implementation and optimization of SAR echo simulation based on GPU[J]. Science Technology and Engineering, 2014, 14(13): 85-89.(  1) 1) |
| [15] | Wang B, Zhang F, and Xiang M. SAR raw signal simulation based on GPU parallel computation[C]. IEEE Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 2009: 617-620.( 1) 1) |
| [16] | Zhang F, Wang B, and Xiang M. Accelerating InSAR raw data simulation on GPU using CUDA[C]. IEEE Geoscience and Remote Sensing Symposium, Honolulu, Hawaii, USA, 2010: 2932-2935.( 2) 2) |
| [17] | Zhang F, Li Z, Wang B, et al.. Hybrid general-purpose computation on GPU (GPGPU) and computer graphics synthetic aperture radar simulation for complex scenes[J]. International Journal of Physical Sciences, 2012, 7(8): 1224-1234.( 2) 2) |
| [18] | Zhang F, Hu C, Li W, et al.. Accelerating time-domain SAR raw data simulation for large areas using multi-GPUs[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(9): 3956-3966.( 2) 2) |
| [19] | 黄立胜, 王贞松, 郑天垚. 基于FFT的快速SAR分布目标回波模拟算法[J]. 遥感学报, 2004, 8(2): 128-136. Huang Lisheng, Wang Zhensong, and Zheng Tianyao. A fast algorithm based on FFT used in simulation of SAR return wave signal[J]. Journal of Remote Sensing, 2004, 8(2): 128-136.(  1) 1) |
| [20] | Moving and Stationary Target Acquisition and Recognition (MSTAR) Public Dataset[OL]. https://www.sdms.afrl.af.mil/datasets/mstar/.( 1) 1) |


