合成孔径雷达(Synthetic Aperture Radar,SAR)不受气候的影响,能全天时、全天候、高分辨率、大区域对地观测,成为空间信息遥感技术飞速发展时代的主旋律之一[1]。随着高分辨率SAR影像数据的不断获取,以及其在土地覆盖/土地资源监测[2, 3]、目标检测[4]、环境与灾害监测[5, 6]等方面上应用需求的增加,给SAR影像的变化检测技术研究带来了新的时机和挑战。
SAR图像变化检测目的是根据对不同时段的同一目标或场景进行变化分析[7]。根据变化检测目标对象的不同,可将其分为基于像素级的变化检测、基于特征级的变化检测和基于目标级的变化检测[8]。这些传统的变化检测方法包括基于代数运算的方法,如:差值法、比值法、回归法、变化向量法等;基于影像变换的方法,如:主成分分析法、基于小波的方法、人工神经元网络法、交叉相关分析法等,以及基于影像分类、人工智能和神经元网络分类等方法。但传统变化检测方法往往只运用了SAR影像的单一特征(如强度或幅度),因此难以取得令人满意的结果。
针对以上问题,本文考虑融合高分辨率SAR图像中的相干/非相干信息进行变化检测。目前一些研究者将纹理信息、干涉相干信息引入到SAR影像变化检测中,多特征融合受到越来越多的关注。廖明生等[9]利用ERS-1/2 SAR影像中的强度和相干特征对上海地区的城区变化进行检测取得了不错的效果。公茂果等[10]充分考虑到SAR图像中的纹理结构和强度信息,用多时相SAR数据中的纹理和强度信息进行变化检测。Dierking等由极化SAR数据发现交叉极化通道的相关系数和相位的区分度大于传统的强度[11]。干涉相干性表征两复数数据的相似程
度,而不同的地物目标具有不同的时间去相干特性,InSAR在观测地表形变等领域的应用已获得成功[12]。随着SAR干涉测量技术的发展,融合高分辨率SAR相干/非相干特性的变化检测已成为一大研究趋势。
变化检测的方法总的来说分为三大步:预处理、差异图构造、变化区域提取[13]。本文提出了多尺度、多特征融合的SAR影像变化检测方法,分别从强度图像和相干影像序列中提取局部区域变化特征、多时相差异特征、相干变化特征,使用合适的差异算子得到多特征差异图后,经D-S证据理论(Dempster-Shafer evidence theory)融合差异特征,进而得到最终的变化检测结果。
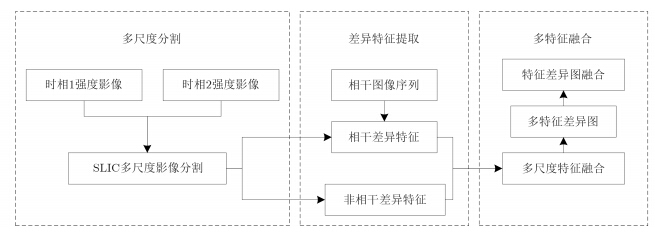
2 基于特征信息融合的变化检测原理框架本文所提出的算法可以分为多尺度分割、差异度特征提取、多特征融合3个部分。算法的流程如图 1所示,最终通过特征差异图得到变化检测结果。
|
图 1 基于多尺度多特征融合SAR影像变化检测流程 Fig.1 Flow chart of change detection for SAR image based on multi-scale and multi-feature fusion |
随着变化检测由像素级向对象级发展,多尺度分割成为面向对象的变化检测研究方法的有力工具。本文选用Achanta[14]等提出的简单线性迭代聚类(Simple Linear Iterative Clustering,SLIC)作为超像素分割算法,该算法形成的图斑形状规则,排列紧密,分割迅速的同时可较好地保持区域边界。本文使用经滤波处理的对数比值图像作为输入图像完成图像分割,然后再将分割边界分别应用到双时相图像中,既可以保证分割的同质性约束而又避免了分别分割产生细小碎片。
2.2 变化特征提取 2.2.1 非相干信息特征本文选取高分辨率SAR影像中4种非相干信息特征来进行分析。这4种特征包括单时相纹理差异特征[15]、多时相强度差异特征和联合降噪差异特征,估算表达式如表 1所示。
| 表 1 选取的非相干信息特征 Tab.1 The selected features of incoherent information |
半方差系数(Semi-Variance Coefficient,SVC)从局部信息量和纹理分布角度出发,包含较多的图像细节信息,表达式中xi和xi+h为距离为h的像素对,N为像素对的数目。修正归一化标准差|dB(LNSD)和局部最大最小比(MTCD)能较好地刻画图像纹理的波动程度,修正归一化标准差|dB表达式中μx为影像的图斑均值,局部最大最小值比表达式中min(μi)和max(μj)为N景影像中像素邻域的时相最小和最大强度值。联合似然比和KL距离[16]的GLR-KL特征在充分利用局部信息的同时降低相干斑的不利影响,表达式中,SGLR为噪声影像x与x*的广义似然比,SKL为降噪影像间的KL距离,h和h*为SGLR和SKL的规范化参数,依据局部邻域计算的SGLR表示为:
| $\begin{array}{l} \begin{array}{*{20}{l}} {{S_{{\rm{GLR}}}}\left( {{y_1},{y_2}} \right) = \sum\limits_{k \in K} {\left[{\left( {{L_{1,k}} + {L_{2,k}}} \right)} \right.}} \end{array}\!\!\!\! \log \left( {{L_{1,k}}{y_{1,k}}\left. { + {L_{2,k}}{y_{2,k}}} \right)} \right. - \left( {{L_{1,k}} + {L_{2,k}}} \right)\\ \quad \quad \quad \quad \quad \quad \quad \cdot \log \left( {{L_{1,k}}} \right.\left. { + {L_{2,k}}} \right)\left. { - {L_{1,k}}\log {y_{1,k}} - {L_{2,k}}\log {y_{2,k}}} \right] \end{array}$ | (1) |
| $\begin{array}{l} {S_{\rm{KL}}}\left( {{{\hat x}_1},{{\hat x}_2}} \right) = \sum\limits_{k \in K} {\left\{ {{L_{1,k}}\frac{{{{\hat x}_{2,k}}}}{{{{\hat x}_{1,k}}}} + {L_{2,k}}\frac{{{{\hat x}_{1,k}}}}{{{{\hat x}_{2,k}}}} - {L_{1,k}} - {L_{2,k}} + {L_{1,k}}\left[{\psi \left( {{L_{1,k}}} \right) \\- \psi \left( {{L_{2,k}}} \right) + \ln {{\hat x}_{1,k}} + \ln {{\hat x}_{2,k}}} \right]} \right.} \\ \quad \quad \quad\quad\quad\quad- {{L_{2,k}}\left[{\psi \left( {{L_{1,k}}} \right) - \psi \left( {{L_{2,k}}} \right) + \ln {{\hat x}_{1,k}} + \ln {{\hat x}_{2,k}}} \right]} \bigg\} \end{array}$ | (2) |
SAR复数影像的相似性和稳定程度可以使用相干系数g表示,定义为:
| \[\gamma = \frac{{|E\left[ {{s_1}\left( x \right) \cdot s_2^*\left( x \right)} \right]|}}{{\sqrt {E\left[ {{{\left| {{s_1}\left( x \right)} \right|}^2}} \right]E\left[ {{{\left| {{s_2}\left( x \right)} \right|}^2}} \right]} }}\] | (3) |
| $ \kappa = \frac{{{\gamma _{\rm{pre}}} - {\gamma _{\rm{co}}}}}{{{\rm{mean}}\left( {{\gamma _{\rm{pre}}},{\gamma _{\rm{co}}}} \right)}}$ | (4) |
| ${\kappa ^*} = \frac{{{\mu _{{\gamma _{\rm{pre}}}}} - {\mu _{{\gamma _{\rm{co}}}}}}}{{{\rm{mean}}\left( {{\mu _{{\gamma _{\rm{pre}}}}},{\mu _{{\gamma _{\rm{{co}}}}}}} \right)}}$ | (5) |
本文所选取的差异特征取值与差异性均呈正相关,由此可选择Mean算子进行多尺度差异融合,取各图斑的差异指数平均值作为融合的差异特征值。不同时相的SAR影像由各图斑提取半方差系数特征后,可得到多幅特征图,对短时间间隔的特征图作时相平均后,可得到两幅特征图像${\bar I_{\rm{fea1}}}$和${\bar I_{\rm{fea2}}}$,使用比值法[17]作为差异特征算子:
| ${r_{\rm{d\_fea}}} = 1 - \min \left( {\frac{{{{\bar I}_{\rm{fea1}}}(i,j)}}{{{{\bar I}_{\rm{fea2}}}(i,j)}},\frac{{{{\bar I}_{\rm{fea2}}}(i,j)}}{{{{\bar I}_{\rm{fea1}}}(i,j)}}} \right)$ | (6) |
在充分利用不同特征信息的同时,需完成多特征的优化融合以生成融合差异图。在融合前可进行归一化处理,以便使不同的特征存在可比性。本文选择D-S证据理论[18, 19]完成该特征融合过程。
在证据理论中,一组互斥而完备的命题组成假设空间,记作${θ}$,假设空间的命题子集构成的集合记为$2 ^ {θ}$,假设空间的子命题置信度记为m(A),对于集合$2 ^ {θ}$中的任意子命题,有:
| $\left\{ {\begin{array}{*{20}{c}} {0 \le m(A) \le 1}\\ {\!\!\!\!\!\!\!\!\!\!\!\! m(\varnothing) = 0}\\ {\sum\limits_{A \subseteq {2 ^ {θ} }} {m(A) = 1} } \end{array}} \right.$ | (7) |
| $\left. {\begin{array}{*{20}{l}} {{\rm{bel}}(B) = \sum\limits_{A \subseteq B} {m(A)} }\\ {{\rm{pl}}(B) = \sum\limits_{A \cap B \ne \emptyset } {m(A)} } \end{array}} \right\}$ | (8) |
| $\left. {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {\quad \ \ m\left( A \right) = {m_1} \oplus {m_2} \oplus \cdots \oplus {m_n}\left( A \right)}\\ {\qquad \qquad \; = \frac{1}{{1 - K}}\sum\limits_{{A_1} \cap \cdots \cap {A_n} = A} {\prod\limits_{i = 1}^n {{m_i}\left( {{A_i}} \right)} } ,} \end{array}}\\ \quad \quad \,K = \sum\limits_{{A_1} \cap \cdots \cap {A_n} = \varnothing } {\prod\limits_{i = 1}^n {{m_i}\left( {{A_i}} \right)} } \end{array}} \right\}$ | (9) |
对于本文的变化检测任务,命题分为“变化”C和“非变化”U两种,Θ={C,U},C∩U=$\varnothing$,2Θ={C,U,Θ,$\varnothing$}。对于置信函数,可定义为:
| $\left. \begin{array}{l} m\left( C \right) \! = \! \left\{ {\begin{array}{*{20}{c}} {\!\!\! 0.5 \! \times \! \left[{1{\rm{ + }}{{\left( {x - {\overline T \,}} \right)} \mathord{\left/ {\vphantom {{\left( {x \! - \! \overline T \,} \right)} {\left( {1 - \overline T \,} \right)}}} \right. } {\left( {1 \! - \! \overline T \,} \right)}}} \right],\ x \! \ge \! \overline T \,}\\ { \!\!\! 0.5 \! \times \! \left[{1{\rm{ + }}{{\left( {x - \overline T \,} \right)} \mathord{\left/ {\vphantom {{\left( {x \!\! - \!\! \overline T \,} \right)} {\overline T \,}}} \right. } {\overline T \,}}} \right],\quad\quad\quad x \! < \! \overline T \,} \end{array}} \right.\\ m\left( U \right) \! = \! \frac{{1 - m\left( C \right)}}{{1 + m\left( C \right)}}\\ m\left( {Θ} \right) = m\left( C \right)m\left( U \right)\\ m\left( \varnothing \right) = 0 \end{array} \!\!\!\! \right\} \hspace{100pt}$ | (10) |
本文选取两组美国旧金山地区港口附近的TerraSAR-X数据切片进行实验[23]。数据集Ⅰ的实验区域的影像大小为1000×1000像素(如图 2所示),分辨率为1 m。数据集Ⅱ的切片大小为600×600(如图所示),分辨率和采集时间与数据集Ⅰ相同,如图 3所示。

|
图 2 数据集Ⅰ影像 Fig.2 The images in dataset Ⅰ |

|
图 3 数据集Ⅱ影像 Fig.3 The images in datasetⅡ |
两组数据的强度数据采集自2007年12月5日和2011年10月2日,采用与强度数据生成时间相差11天影像组成数据对生成干涉相干数据。用成像于2007年11月11日分辨率为0.6 m的QuickBird和成像于2011年10月9日分辨率为0.5 m的WorldView光学遥感数据作为参考光学影像。数据集Ⅰ和数据集Ⅱ的参考真值图(Ground truth)如图 4所示。

|
图 4 数据集参考真值图 Fig.4 Ground truth of dataset |
在提取区域差异特征之前,本文使用4个尺度的区域大小参数对多时相SAR影像进行联合分割,区域大小尺度参数S设置为7,10,13,15。参数l平衡特征向量中空间和纹理关系,一般取为0.1。分别在4个尺度水平上提取各分割区域的差异特征,典型的差异特征如图 5所示,选用的特征为局部最大最小比(MTCD)。

|
图 5 MTCD多尺度特征差异图 Fig.5 Multi-scale difference maps by feature MTCD |
我们选择以下检测指标对检测结果进行评估:变化检测正检率(Pc)、负检率(Pu)、全精度(OA)和Kappa系数。Pc为正确检测的变化像素占变化像素的比例;Pu为正确检测的背景像素占背景像素的比例;OA为正确检测的像素占全部像素的比例;Kappa系数对正确检测像素及由虚警和漏检造成的错误检测综合考虑,是关键性的评估指标。可以看出,Pc和Pu分别从正反两方面反映了漏检和虚警的程度。
3.1 数据集Ⅰ结果与分析获得多尺度差异特征后,可使用Mean算子对多尺度差异特征进行融合,得到多尺度融合特征,获得更稳定的差异特征。在进行D-S证据理论特征融合之前,需对各特征进行归一化处理,消除特征值域对融合的不利影响。对得到的特征差异图进行阈值分割,阈值为各个特征差异图各自通过基于广义高斯分布的KI阈值法、基于瑞利分布的恒虚警率阈值法和FTC直方图分割法选取得到的阈值T1,T2,T3的均值$\overline T \,$ 。获得的变化区域如图 6所示。

|
图 6 数据集Ⅰ特征差异图变化检测结果 Fig.6 The result of change detection by feature different maps in datasetⅠ |
图 6中,从左至右,由上而下,依次为半方差系数(SVC)、归一化标准差(LNSD)、局部最大最小比(MTCD)、GLR-KL、相干特征变化度k和D-S融合特征得到的检测图。观察数据集Ⅰ的检测结果图可以发现,各特征在检测出主要变化区域的同时,对不同区域的细节变化把握能力各不相同。MTCD和相干特征对变化最为敏感,但前者具有很高的虚警,对变化的细节把握能力不好。在所选的强度特征中,LNSD和GLR-KL特征表现最好,后者在保持较高的检测率的同时,较好地控制了虚警数,但该特征的区域连续性不是特别理想。经D-S证据理论融合的融合特征,对噪声的抑制明显强于单一特征,表 2支持了上述结论,尽管融合特征的正检率和负检率都不是最优的,但其在保持较高的正检率的同时,具有最高的全精度和Kappa指数,说明该融合策略能集合各特征自身的优势,避免单个特征的错误决策。
| 表 2 多特征变化检测结果(数据集Ⅰ) Tab.2 The result of change detection by multi-features (dataset Ⅰ) |
对于数据集Ⅱ,其检测图和定量检测结果如图 7和表 3所示。得到的结论与数据集Ⅰ相似:不同特征对语义变化的鉴别能力存在很大的差异,而与数据集Ⅰ不同的是,不同特征之间检测能力随着数据集的不同而有所变化。当面对不同的变化类型时,表现尤为明显,对于左侧的“弱变化类”,MTCD和相干特征k对该类变化检测能力弱于其他特征,这种由异物同谱造成的小强度差异是变化检测的一个难点所在;而在数据集Ⅰ中,主要的变化类型为“强变化”,相干特征k具有很高的检测率。

|
图 7 数据集Ⅱ特征差异图变化检测结果 Fig.7 The result of change detection by feature different maps in datasetⅡ |
| 表 3 多特征变化检测结果(数据集Ⅱ) Tab.3 The result of change detection by multi-features (datasetⅡ) |
由此可见,单一特征并不能保证获得稳定的检测结果,而使用D-S融合特征,可在综合各差异特征长处的同时,有效地降低虚警,在检测率和虚警之间获得更好的平衡,得到更均衡稳定的检测结果。
4 结束语
对于高分辨率SAR影像,单一尺度和单一特征往往不能得到稳健的变化检测结果。本文提出使用D-S证据理论融合高分辨率SAR图像的相干/非相干信息以得到更为鲁棒的变化检测结果。实验表明尽管多特征融合后变化监测的正检率和负检率指标有小幅度提升,并且在保持较高的正检率的同时,Kappa指数有较大的提升。未来的工作中,拟进一步探索分级的相干/非相干信息融合方法,以得到更为精确的变化检测结果。
致谢 作者感谢美国数字地球公司(DigitalGlobe)、法国阿斯特里姆地理信息服务公司(Astrium Services)和美国地质调查局官网(USGS)为本研究提供相应的数据集,并向电气和电子工程师协会地球科学与遥感学会(IEEE GRSS)图像分析和数据融合委员会致以诚挚的感谢。
| [1] | 李春升, 杨威, 王鹏波. 星载SAR成像处理算法综述[J]. 雷达学报, 2013, 2(1): 111–122.Li Chun-sheng, Yang Wei, and Wang Peng-bo. A review of spaceborne SAR algorithm for image formation[J]. Journal of Radars, 2013, 2(1): 111–122.( 1) 1) |
| [2] | Evans T L and Costa M. Landcover classification of the lower nhecolandia subregion of the brazilian pantanal wetlands using ALOS/PALSAR, RADARSAT-2 and ENVISAT/ASAR imagery[J]. Remote Sensing of Environment, 2013, 128: 118–137.( 1) 1) |
| [3] | 田维, 徐旭, 卞小林, 等. 环境一号C卫星SAR图像典型环境遥感应用初探[J]. 雷达学报, 2014, 3(3): 339–351.Tian Wei, Xu Xu, Bian Xiao-lin, et al.. Applications of environmental remote sensing by HJ-1C SAR imagery[J]. Journal of Radars, 2014, 3(3): 339–351.( 1) 1) |
| [4] | 尤红建, 付琨. 合成孔径雷达图像精准处理[M]. 北京: 科学出版社, 2011: 1–27.( 1) 1) |
| [5] | Refice A, Capolongo D, Lepera A, et al.. SAR and InSAR for flood monitoring: examples with COSMO/SkyMed data[C]. IEEE Geoscience and Remote Sensing Symposium, Melbourne, VIC, 2013: 703–706.( 1) 1) |
| [6] | Federica B, Luigi T, Claudio P, et al.. Shoreline detection: capability of COSMO-SkyMed and high-resolution multispectral images[J]. European Journal of Remote Sensing, 2013, 46: 837–853.( 1) 1) |
| [7] | 浮瑶瑶, 柳彬, 张增辉, 等. 基于词包模型的高分辨率SAR图像变化检测与分析[J]. 雷达学报, 2014, 3(1): 101–110.Fu Yao-yao, Liu Bin, Zhang Zeng-hui, et al.. Change detection and analysis of high resolution synthetic aperture radar images based on bag-of-words model[J]. Journal of Radars, 2014, 3(1): 101–110.( 1) 1) |
| [8] | 周启鸣. 多时相遥感影像变化检测综述[J]. 地理信息世界, 2011, (2): 28–33.Zhou Qi-ming. Review on change detection using multi-temporal remotely sensed imagery[J]. Geomatics World, 2011, (2): 28–33.( 1) 1) |
| [9] | Liao M, Jiang L, Lin H, et al.. Urban change detection based on coherence and intensity characteristics of SAR imagery[J]. Photogrammetric Engineering & Remote Sensing, 2008, 74(8): 999–1006.( 1) 1) |
| [10] | Gong M, Li Y, Jiao L, et al.. SAR change detection based on intensity and texture changes[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2004, 93(7): 123–135.( 1) 1) |
| [11] | Dierking W and Skriver H. Change detection for thematic mapping by means of airborne multitemporal polarimetric SAR imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(3): 618–636.( 1) 1) |
| [12] | Lefort A, Grippa M, Walker N, et al.. Change detection across the Nasca pampa using spaceborne SAR interferometry[J]. International Journal of Remote Sensing, 2004, 25(10): 1799–1803.( 1) 1) |
| [13] | Bazi Y, Bruzzone L, and Melgani F. An unsupervised approach based on the generalized Gaussian model to automatic change detection in multitemporal SAR images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(4): 874–887.( 1) 1) |
| [14] | Achanta R, Shaji A, Smith K, et al.. SLIC superpixels compared to state-of-the-art superpixel methods[[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2012, 34(11): 2274–2282.( 1) 1) |
| [15] | Dekker R J. Texture analysis and classification of ERS SAR images for map updating of urban areas in The Netherlands[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(9): 1950–1958.( 1) 1) |
| [16] | Su X, Deledalle C A, Tupin F, et al.. SAR image change detection by likelihood ratio test in multi-temporal time series[C]. IEEE International Geoscience and Remote Sensing Symposium, Melbourne, VIC, 2013: 3439–3442.( 1) 1) |
| [17] | Bazi Y, Bruzzone L, and Melgani F. Automatic identification of the number and values of decision thresholds in the log-tatio image for change detection in SAR images[J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(3): 349–353.( 1) 1) |
| [18] | Smarandache F and Dezert J. Advances and Applications of DSmT for Information Fusion[M]. New Mexico: American Research Press, 2004: 3–31.( 1) 1) |
| [19] | Golino G, Graziano A, Farina A, et al.. Comparison of identity fusion algorithms using estimations of confusion matrices[C]. IEEE 17th International Conference on Information Fusion, 2014: 1–7.( 1) 1) |
| [20] | Kittler J. Minimum error thresholding[J]. Pattern Recognition, 1986, 19(1): 41–47.( 1) 1) |
| [21] | Kuttikkad S and Chellappa R. Non-Gaussian CFAR techniques for target detection in high resolution SAR images[C]. IEEE International Conference on Image Processing, 1994, 1: 910–914.( 1) 1) |
| [22] | Delon J, Desolneux A, Lisani J L, et al.. A nonparametric approach for histogram segmentation[J]. IEEE Transactions on Image Processing, 2007, 16(1): 253–261.( 1) 1) |
| [23] | 2012 IEEE GRSS Data Fusion Contest. Online:http://www.grss-ieee.org/community/technical-committees/data-fusion.( 1) 1) |


