②(内蒙古工业大学雷达技术研究所 呼和浩特 010051)
②(Radar Research Institute, Inner Mongolia University of Technology, Hohhot 010051, China)
全极化合成孔径雷达(Polarimetric Synthetic Aperture Radar, PolSAR)数据可提取地物目标的完整散射矩阵、几何结构的细节特性和地物目标的介电常数信息,极大地增强了成像雷达对目标信息的获取能力[1]。极化SAR遥感为对地观测提供了更丰富的场景和目标信息(如目标的几何形状等),但同时也对极化图像的解译提出了新的挑战。其中,如何从极化SAR数据中有效地提取表达地物的特征信息是提高极化SAR图像解译性能的关键问题之一。
文献[2]中周晓光等人对极化SAR图像分类中应用的各种极化特征进行了详细的论述。目前,极化特征主要包括基于测量数据及其简单变换组合的特征和基于极化目标分解的特征。Cloude等人[3]将极化散射矩阵的分解方法分为3类:基于Mueller矩阵和斯托克斯矢量的方法、利用协方差或相干性矩阵的特征向量分析方法和采用相干散射矩阵模型的分解方法,并从不同角度分析了地物的散射特性。Freeman等人[4]提出三分量散射分解模型来刻画极化SAR数据中地物的散射机制,并取得了较好的建模效果。继Freeman之后,Yamaguchi等人[5]将螺旋散射功率组合到Freeman的散射机制中,增强了对密集建筑区的描述准确率。自此,通过极化分解的方式获取极化SAR数据中地物的极化特征在极化SAR图像处理中被广泛应用[6, 7, 8, 9]。但是,对于复杂场景的分析,仅靠几种散射模型难以准确提取极化SAR数据中的地物特征信息。
近年来,原型理论(Prototype Theory)被广泛应用于图像分类领域[10, 11]。K-prototype算法在数据聚类分析中也取得了很好的实验效果[12, 13]。Crammer等人[14]的研究理论表明基于原型理论的分类器比最近邻分类器更准确。其中,最主要的原因是这种代表数据间本质差异的样本数据集——原型集,以图像子集间相互映射的方式表现了各类数据之间的差异,减少了传统分类器中易出现的模型过拟合情况。Martin等人[15]利用一定数量具有判别力的原型集来描述数据集,以提高分类表达与处理的效率。Dai等人[16]利用最大-最小采样方法构造原型集,并结合集成投影方法构建特征表达应用于半监督的图像分类,获得了满意的分类结果。另外,由于利用原型树或稀疏原型集能够准确学习并描述目标特征,达到快速匹配识别的效果,原型理论也被成功应用于目标跟踪与动作识别[17, 18]等领域。
本文针对极化SAR图像解译中的特征描述问题,尝试将原型理论引入极化SAR图像处理中,提出一种新的极化特征提取算法。不同于光学图像中原型理论的应用,极化SAR数据表现的极化特性增加了原型集构建的难度。特别是,在衡量图像区域相似度方面,适用光学图像的欧氏距离或马氏距离在极化SAR数据上难以取得令人满意的结果。本文算法在考虑极化SAR数据散射特性的同时,利用图像区域间基于协方差矩阵数据的相似度计算构建多组原型集,并以原型理论构建图像中匀质区域之间的映射关系。最后,用主成分分析方法进行特征降维,并通过非监督分类展示最终特征描述子的应用效果。
2 极化散射特征极化SAR图像的解译通常依赖于极化数据中所含的丰富信息。极化SAR测量数据利用极化散射矩阵S表示,
| \[S = \left[ {\begin{array}{*{20}{l}} {{S_{{\rm{HH}}}}\quad {S_{{\rm{HV}}}}}\\ {{S_{{\rm{VH}}}}\quad {S_{{\rm{VV}}}}} \end{array}} \right]\] | (1) |
| \[\begin{array}{l} C = \left\langle {X{X^{\rm{H}}}} \right\rangle \\ \quad = \left[ {\begin{array}{*{20}{c}} {\left\langle {{{\left| {{S_{{\rm{HH}}}}} \right|}^2}} \right\rangle {\rm{ }}\sqrt 2 \left\langle {{S_{{\rm{HH}}}}S_{{\rm{HV}}}^*} \right\rangle {\rm{ }}\left\langle {{S_{{\rm{HH}}}}S_{{\rm{VV}}}^*} \right\rangle }\\ {\sqrt 2 \left\langle {{S_{{\rm{HV}}}}S_{{\rm{HH}}}^*} \right\rangle {\rm{ }}2\left\langle {{{\left| {{S_{{\rm{HV}}}}} \right|}^2}} \right\rangle {\rm{ }}\sqrt 2 \left\langle {{S_{{\rm{VV}}}}S_{{\rm{HH}}}^*} \right\rangle }\\ {\left\langle {{S_{{\rm{VV}}}}S_{{\rm{HH}}}^*} \right\rangle {\rm{ }}\sqrt 2 \left\langle {{S_{{\rm{VV}}}}S_{{\rm{HV}}}^*} \right\rangle {\rm{ }}\left\langle {{{\left| {{S_{{\rm{VV}}}}} \right|}^2}} \right\rangle } \end{array}} \right] \end{array}\] | (2) |
以散射矩阵为主,基于SAR测量数据及其数学变换的方式可作为基本的极化特征提取方式。这些特征包括后向散射强度与强度比、相位差以及去极化比等[19](参见表 1)。每种对极化SAR测量数据的数学处理都能够表达出地物固有的极化信息。但是在某些情况下,同类地物可能表现出不同的极化信息,不同类别地物也可能表现出相似的极化信息,即同物异谱或异物同谱。这使得纯粹依赖于对极化SAR测量数据进行数学处理的极化特征描述方法出现描述不准确或特征不具辨别力的情况。
| 表 1 基本极化特征表达 Tab. 1 Fundamental polarimetric feature representation |
基于极化目标分解的散射特征提取方法更清楚地表达了极化SAR数据中目标的散射机制。以目标散射机制的稳定性为依据,可将极化目标分解方法分为两种类型:相干分解与非相干分解。前者适用于具有确定的或稳态的散射特性的目标,散射回波是相干的,其针对Sinclair矩阵的分解;后者适用于散射特性不确定、需多视处理的目标,散射回波是部分或非相干的,其针对Mueller矩阵、相干矩阵和协方差矩阵的分解。Pauli分解[20]是一种经典的相干极化目标分解方法,它将目标的极化散射矩阵分解成3个基本矩阵的加权组合。而非相干极化目标分解中基本的分解方法是Cloude分解[3],它以特征值分解方式将相干矩阵分解为3个独立矩阵。另一种常用的非相干分解方法是Freeman-Durden分解[4],以3种散射类型描述了目标的散射机制(具体参数参见表 2)。基于目标分解的极化特征各有侧重,但仍不足以全面描述整个雷达检测场景中的地物。因此,发展新的极化特征表达方法是极化SAR图像的解译的研究重点。
| 表 2 基于目标分解的极化特征表达 Tab. 2 Target decomposition based polarimetric feature representation |
在极化SAR图像的特征分析中,以匀质的图像区域作为分析对象,不仅可避免以像素点为单元分析导致的特征表达模糊,而且能提高地物极化特征表达的准确度与效率。文中利用简单线性迭代聚类算法[21](SLIC)将极化SAR图像分割为多个匀质区域,并借鉴文献[16]中的基本思想,以基于原型理论的特征编码模型对图像的原始特征进行编码,以期获取更全面、更具分辨力的图像极化特征。算法的完整流程图如图 1所示。
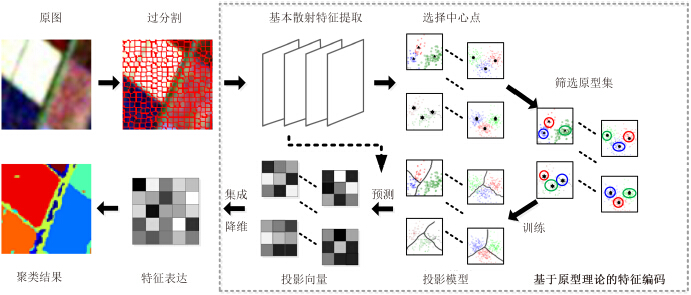 | 图 1 基于原型理论的极化SAR图像特征提取算法流程图Fig.1 Framework of feature extraction algorithm based on prototype theory for PolSAR image |
基于原型理论的特征编码通过从图像中选取一部分具有代表性的样本集——原型集进行特征分析,从而将原始图像特征映射到另一个特征空间,得到更为准确的图像表达。这种仅针对图像中被选原型集的分析方式避免了对图像整体场景的细致分析,有效地降低了图像分析的复杂度。为提高编码后特征的辨别力与描述的全面性,选择合适的原型集是该编码模型的重点。
原型集的选取有两个约束条件:
(1) 原型集内不同类别代表样本之间的差异性较大;
(2) 同类别代表样本之间的差异性较小。
同时,各原型集内部及原型集之间均需保持一定的多样性。否则,仅处理几个或几组样本,即便这些样本都具有很高的代表性也不能确保其囊括图像的所有特征。虽然,这将消耗更多计算时间,但是相应得到的特征描述子质量也会有显著的提高。
在选取合适的原型集的基础上,原型理论中图像原始特征到另一个特征空间的映射方式也是影响最终特征表达效果的一个重要因素。在分类问题中,将一系列分类器单独决策结果以某种方式组合(一般为加权或非加权投票的方式)去决定新样本的分类结果比使用单个分类器进行决策得到的结果更好。这一思想可应用于图像的特征编码,即以集成多个子编码器的特征学习方式对图像原始特征进行映射以得到新的特征表达。本文正是利用这种集成映射的方式从多个不同的角度对基本极化特征进行分析,挖掘更深层的信息。
3.2 基于原型理论的特征表达多样化原型集描述能够全面且深入地表达图像极化信息,有鉴如此,本文引入原型理论获取新的极化SAR特征描述子。通过利用SLIC过分割算法将极化SAR图像I分割为N块匀质区域。假设F为图像I在某尺度SLIC分割下各区域的d维原始散射特征集合,$F = [{f_1} \cdots {f_n} \cdots {f_N}] \in {\mathbb{R}^{d \times N}}$。
为准确选取原型集,首先需要确定其中心点。中心点是原型集中各组样本集合的中心,确定了样本描述的对象。中心点的选择需满足条件(1),使得各组样本尽量描述不同的对象或对象的不同方面。中心点的选取算法如算法1[16]所示。在超像素分割块中以随机游走的方式选取T个初始图像区域的集合S后,以匀质区域之间协方差信息的相似度为研究对象,多次迭代,选取相互之间差异性最大的一组中心点作为输出。协方差矩阵之间的相似度利用Bartlett距离公式[22]衡量。具体地,令$\overline {{C}} $为各匀质图像区域协方差信息的均值,$\overline C = [{\overline c _1} \cdots {\overline c _n} \cdots {\overline c _N}] \in $
${\mathbb{R}^{3 \times 3 \times N}}$,任意两个样本点的协方差信息之间的距离为:
| \[{D_B}({\overline c _i},{\overline c _j}) = \ln \left( {\frac{{{{\left| {{{\overline c }_i} + {{\overline c }_j}} \right|}^2}}}{{\left| {{{\overline c }_i}} \right|\left| {{{\overline c }_j}} \right|}}} \right) - 2q{\rm{ln}}2,1 \le i,j \le N\] | (3) |
| 算法 1:选取中心点 | 算法 2:筛选原型集 |
| 输入:N个匀质区域的协方差信息均值$\overline C $ | 输入:中心点集合S与协方差信息均值$\overline C $ |
| 初始化:$\widehat e$=0, | 初始化:$l(n) = 0,n \in [1,N]$, |
| 迭代计算:当迭代次数≤m时, | 距离计算:$D(n) = \{ {D_B}({\overline c _n},{\overline c _j}),j \in S\} $ |
| S={随机选择的T个图像区域}, | $D(n,t) = \min D(n),l(n) = t$, |
| $e = \sum\nolimits_{i \in \Sigma {\bf{S}}} {\sum\nolimits_{j \in \Sigma {\bf{S}}} {{D_{\rm{B}}}({{\bar c}_i},{{\bar c}_j})} } $ | t为标签,$t \in [1,T \,]$ |
| 如果$e > \widehat e$, | 选取原型样本: |
| 那么$\hat e = e$, $\widehat S = S $ | for t=1 to T |
| 当迭代次数>m, | st=M个最小D(n, t)对应的{n} |
| $S = \widehat S $ | ${l^t} = [t \cdots t \cdots t] \in {\mathbb{R}^n}$ |
| 输出:一组中心点集合S | 输出:一组原型集${P = \{ {p^t}\} = \{s^t},{l^t}\} $ |
其次,筛选原型集中的样本。原型集中同一类别样本描述了该类别的信息。为保证类别信息的准确清晰,样本筛选需要满足条件式(2),具体如算法2所示。先通过Bartlett距离最小化划分匀质区域的类别,对于划分为同类别的样本,再选取离中心最近的M个样本作为原型集的类别样本。由于图像中每类地物所占的面积不同,用于描述它们的图像区域数量不同,因此不能保证每个类别中样本量相等。
再次,为确保原型集样本的多样性需要选取多组中心点,生成多组原型集。单组原型集数据仅具有一定的类别区分能力。从集成投影的角度看,可在较宽松的约束条件下提取多组原型集,并利用这些原型集获取多个子分类函数以弥补单组原型集的不足。假设重复算法1和算法2构建Num组原型集$P = [{P_1}\;\;{P_2}\; \cdots \;{P_{{\rm{Num}}}}]$,每组原型集Pnum中都包含了T类样本,且均以d维散射特征F描述。以T×d维的原型集信息以及原型样本在集合中的标签l为输入对象,本文利用逻辑回归模型分别对Num组原型集进行训练,构建Num组图像特征编码器,将图像原始特征的编码转换为图像中子区域之间的相互映射,图像区域标签L归为类t的概率为:
| \[p\left( {L = t|f;W,b} \right) = \frac{{\exp \left( {w_t^Tf + {b_t}} \right)}}{{\sum\limits_{t = 1}^T {\exp \left( {{b_t} + w_t^Tf} \right)} }}\] | (4) |
| \[\arg \min \sum\limits_c {{{\left\| {{w_c}} \right\|}_1}} - \gamma \sum\limits_i {\log } \left( {\frac{{\exp \left( {{b_{{l_i}}} + w_{{l_i}}^T{f^i}} \right)}}{{\sum\limits_{t = {l_i}}^T {\exp \left( {{b_t} + w_t^Tf} \right)} }}} \right)\] | (5) |
式中${\left\| \cdot \right\|_1}$表示L1正则化,γ是一个正则化系数,并且第i次实验是在特征向量fi与标签li的训练样本上进行的。对Num组原型集进行训练后得到Num个不同的投影函数H。对于新输入的对象x,每个投影函数hnum都可将其映射到一个T维空间中,ynum=hnum(x)即为映射向量。
最后,集成x在所有投影函数H上得到的映射向量{y1···ynum···yNum},即可得到新的对象特征表达。特征矢量的集成方式有很多,为不丢失任一组投影结果,试验中选取的集成方式是向量串联。值得注意的是,由于最终投影向量的组成方式是串联,很可能导致极化特征描述维度过高。为准确有效地降低特征维度并尽可能保留特征信息的主要成分,在完成极化特征提取后可采用主成分分析算法进行降维。
4 实验结果与分析为验证本文方法的有效性,使用荷兰Flevoland地区的AIRSAR数据和德国Oberpfaffenhofen地区的ESAR数据进行极化特征分析,并与Lee等人提出的Freeman-Wishart非监督算法[24]进行对比,从定性与定量两方面评估实验结果。
4.1 实验1荷兰Flevoland地区获取的AIRSAR图像大小为1279×1024像素,包含地物种类较多。为对聚类结果进行细致分析,选取原数据中大小为340×200像素的区域进行极化特征分析(见图 2(a))。
 | 图 2 AIRSAR数据与本文特征的聚类结果Fig.2 Original AIRSAR image and Clustering results of the proposed features |
试验中,设定SLIC的最小分割块尺寸为5×5像素,得到2720个匀质区域。将这些匀质区域划分为T=17类,以d=23维原始极化特征(第2节)为信息筛选每类中距离中心点最近的M=60%的区域构成一组原型集。本组实验中,原型集组数设置为Num=70,正则化逻辑回归训练后,针对整幅图像映射得到17×70维极化特征。由于特征维度较高,利用PCA取精度为99%对上述极化特征进行降维,并利用K均值聚类算法对降维后的21维特征描述子进行聚类,聚类类别数为10类,结果见图 2(b)。为说明实验中参数——原型集组数Num对本文中提出的极化特征的影响,图 2(c)和图 2(d)显示了其他参数(T与M)不变的情况下,原型集组数分别为Num=50与Num=100的聚类结果。经实验对比,映射得到的极化特征维数的改变不会对本文所提出的极化特征的表达特性有明显的影响。但是,当上述维度过低时,该极化特征的描述能力将会降低以致不能准确分辨地物;而当上述维度过高时,将会增加特征提取的计算量,而且特征描述过于精准也可能造成聚类结果中同质区域纯净度降低。算法中,初始类别数T和区域选取比例值M,与原型集组数Num值在对特征描述的影响上具有类似的特性,因此实验中,我们依据图像场景中地物特性以及图像处理经验选取相应参数值。
为比较基于原型理论的特征编码与PCA降维算法的特征映射效果,图 3(b)给出了未经PCA降维的(17×70维)映射得到的极化特征的K均值聚类结果。对比图 3(a)与图 3(b)可见,除了降低特征的维度,PCA降维算法并未对映射得到的极化特征的表达能力造成明显影响,仅在极少部分区域使得表达结果更纯净(图 3(a)与图 2(b)相同)。
 | 图 3 AIRSAR数据与聚类结果Fig.3 Original AIRSAR image and Clustering results |
为有效评估新的极化特征的聚类效果,本文将文中提出的极化特征聚类表达结果与Freeman-Wishart算法的非监督分类结果(聚为10类)进行对比。同时,为进一步说明基于原型理论的特征编码的有效性,定性和定量分析未编码的特征与编码后的特征在相同参数下的聚类结果。由于该地区缺乏完整的对应的地面参照资料,文中取图像中4块均质子区域(见图 4)进行聚类纯净度[25]比较,
 | 图 4 纯净度评估子区域Fig.4 Selected regions for purity evaluation |
| \[{\rm{Purity}} = \sum\limits_{r = 1}^{{\rm{Num}}} {\frac{1}{n}} {\max _i}(n_r^i)\] | (6) |
| 表 3 子区域聚类结果的纯净度(%) Tab. 3 Purity(%) of the experimental results for sub image regions |
实验2提取德国柏林机场的ESAR全极化数据为研究区域,图像分辨率为3 m×3 m,大小为1200×1500像素。实验截图以及对应的地面参照分别显示在图 5(a)与图 5(b)中,是一幅大小为500×500像素的数据,地物类型包括林地、农田、建筑区和道路等。
 | 图 5 ESAR数据与聚类结果Fig.5 Original ESAR image and clustering results |
本组试验中,设定SLIC的最小分割块尺寸为10×10像素,得到10000个匀质区域。其他参数为:原型集有Num=70组,每组类别数T=15,特征维数d=23,每类样本量为距离中心点最近的M=60%的区域。PCA降维后K均值的聚类结果显示在图 5(e)和图 5(h)中。文中选取道路与农田的聚类效果进行分析。
本文分别利用3种算法对实验区域进行5类与8类两组聚类实验,结果显示在图 5(c)~图 5(h)中。由图 5(e)和图 5(h)可见,无论是聚类为5类还是8类,本文算法能够准确表达道路和农田区域。而其他两种算法中在以5类表达图像时完全无法完成道路区域聚类,甚至在8类聚类时也不能准确描述道路区域,存在较为严重的错误分类现象。利用纯净度Purity和错误聚类率Pe分别对8类聚类中农田与道路区域的聚类结果进行评估。Pe则是聚类中属于某类而实际数据中不属于该类别的像素占实际数据中属于该类的像素的比例:
| \[{\rm{P}}{{\rm{e}}_i} = \frac{{{C_i} - T{C_i}}}{{{G_i}}}\] | (7) |
| 表 4 农田与道路区域聚类结果的定量分析(8类) Tab. 4 Quantitative evaluation of the experimental results for farmland and road regions (8 classes) |
定性和定量的分析均显示,在该组数据上,虽然Freeman-Wishart算法聚类结果的纯净度较高,均在90%左右,但是它易将不属于同类的数据划分为同一类别,导致错误聚类率高达77%。这样的聚类结果将给后续的极化SAR图像解译带来困难。本文提出的聚类算法在保证纯净度的同时,以更全面准确的极化特征进行表达,显著降低了错误聚类率。在两类地物上的聚类错误率不到Freeman-Wishart算法的1/3,这在很大程度上提高了此聚类结果的解译准确度。与原始极化特征的表达效果相比,本文算法编码后的极化特征在聚类纯净度与准确度上均有明显的提高。聚类结果的视觉观感与定量分析都说明了本文基于原型理论的特征提取算法的可行性与有效性。
5 结论本文提出一种基于原型理论的特征编码方法,利用原型理论分析图像数据点之间极化信息的差异度映射关系,构建多组原型集,并以正则化逻辑回归函数进行训练得到多组投影函数,从而获得对地物目标特征信息的更准确、全面的表达。两组极化SAR数据的聚类实验的定性与定量评估分析均表明了该方法的有效性。
| [1] | Cloude S. Polarisation: Applications in Remote Sensing[M]. London, U.K.: Oxford University Press, 2009.( 1) 1) |
| [2] | 周晓光, 匡纲要, 万建伟. 极化SAR图像分类综述[J]. 信号处理, 2008, 24(5): 806-812. Zhou Xiao-guang, Kuang Gang-yao, and Wan Jian-wei. A review of polarimetric SAR image classification[J]. Signal Processing, 2008, 24(5): 806-812.( 1) 1) |
| [3] | Cloude S R and Pottier E. A review of target decomposition theorems in radar polarimetry[J]. IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(2): 498-518.( 2) 2) |
| [4] | Freeman A and Durden S L. A three-component scattering model for polarimetric SAR data[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 963-973.( 2) 2) |
| [5] | Yamaguchi Y, Moriyama T, Ishido M, et al.. Four-component scattering model for polarimetric SAR image decomposition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(8): 1699-1706. ( 1) 1) |
| [6] | 闫剑, 李洋, 尹嫱, 等. 引入有取向二面角散射的Freeman-Durden分解[J]. 雷达学报, 2014, 3(5): 574-582. Yan Jian, Li Yang, Yin Qiang, et al.. Freeman-Durden decomposition with oriented dihedral scattering[J]. Journal of Radars, 2014, 3(5): 574-582.( 1) 1) |
| [7] | 滑文强, 王爽, 侯彪. 基于半监督学习的SVM-Wishart极化 SAR 图像分类方法[J]. 雷达学报, 2015, 4(1): 93-98. Hua Wen-qiang, Wang Shuang, and Hou Biao. Semi-supervised learning for classification of polarimetric SAR images based on SVM-Wishart[J]. Journal of Radars, 2015, 4(1): 93-98.( 1) 1) |
| [8] | 李洪忠, 程劲松, 王超, 等. 基于相似性的POLSAR 占优散射归类及非监督聚类[J]. 电子与信息学报, 2012, 34(6): 1501-1505. Li Hong-zhong, Cheng Jin-song, Wang Chao, et al.. POLSAR dominant scattering mechanism clustering and unsupervised classification based on similarity[J]. Journal of Electronics & Information Technology, 2012, 34(6): 1501-1505.( 1) 1) |
| [9] | 陈博, 王爽, 焦李成, 等. 利用0-1矩阵分解集成的极化SAR图像分类[J]. 电子与信息学报, 2015, 37(6): 1495-1501. Chen Bo, Wang Shuang, Jiao Li-cheng, et al.. Polarimetric SAR image classification via weighted ensemble based on 0-1 matrix decomposition[J]. Journal of Electronics & Information Technology, 2015, 37(6): 1495-1501.( 1) 1) |
| [10] | Wohlhart P, Kostinger M, Donoser M, et al.. Optimizing 1-Nearest prototype classifiers[C]. 2013 IEEE Conference on Computer Vision and Pattern Recognition, 2013: 460-467.( 1) 1) |
| [11] | Quattoni A, Collins M, and Darrell T. Transfer learning for image classification with sparse prototype representations[C].IEEE Conference on Computer Vision and Pattern Recognition, 2008: 1-8.( 1) 1) |
| [12] | 王宇, 杨莉. 模糊k-prototypes聚类算法的一种改进算法[J]. 大连理工大学学报, 2003, 43(6): 849-852. Wang Yu and Yang Li. An improved algorithm for fuzzy k-prototypes algorithm[J]. Journal of Dalian University of Technology, 2003, 43(6): 849-852. ( 1) 1) |
| [13] | 陈韡, 王雷, 蒋子云. 基于K-prototypes的混合属性数据聚类算法[J]. 计算机应用, 2010, 30(8): 2003-2005. Chen Wei, Wang Lei, and Jiang Zi-yun. K-prototypes based clustering algorithm for data mixed with numeric and categorical values[J]. Journal of Computer Application, 2010, 30(8): 2003-2005.( 1) 1) |
| [14] | Crammer K, Gilad-Bachrach R, Navot A, et al.. Margin analysis of the LVQ algorithm[C]. Advances in Neural Information Processing Systems, 2002: 462-469.( 1) 1) |
| [15] | Kostinger M, Wohlhart P, Roth P M, et al.. Joint learning of discriminative prototypes and large margin nearest neighbor classifiers[C]. IEEE International Conference on Computer Vision, 2013: 3112-3119.( 1) 1) |
| [16] | Dai D and Gool L V. Ensemble projection for semi-supervised image classification[C]. IEEE International Conference on Computer Vision, 2013: 2072-2079.( 2) 2) |
| [17] | Wang D. Online object tracking with sparse prototypes[J]. IEEE Transactions on Image Process, 2013, 22(1): 314-325.( 1) 1) |
| [18] | Lin Z, Jiang Z, and Davis L S. Recognizing actions by shape-motion prototype trees[C]. 2009 IEEE 12th International Conference on Computer Vision, 2009: 444-451.( 1) 1) |
| [19] | Molinier M, Laaksonen J, Rauste Y, et al.. Detecting changes in polarimetric SAR data with content-based image retrieval[C]. IEEE International on Geoscience and Remote Sensing Symposium, 2007: 2390-2393.( 1) 1) |
| [20] | Lee J S and Pottier E. Polarimetric Radar Imaging: From Basics to Applications[M]. Boca Raton, FL: CRC Press, 2009.( 1) 1) |
| [21] | Achanta R, Shaji A, Smith K, et al.. SLIC superpixels compared to state-of-the-art superpixel methods[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(11): 2274-2282.( 1) 1) |
| [22] | Kersten P R, Lee J S, and Ainsworth T L. Unsupervised classification of polarimetric synthetic aperture radar images using fuzzy clustering and EM clustering[J]. IEEE Transactions on Geoscience and Remote Sensing, 2005, 43(3): 519-527.( 1) 1) |
| [23] | Collins M, Schapire R E, and Singer Y. Logistic regression, adaboost and bregman distances[J]. Machine Learning, 2002, 48(1): 253-285.( 1) 1) |
| [24] | Lee J S, Grunes M R, Pottier E, et al.. Unsupervised terrain classification preserving polarimetric scattering characteristics[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(4): 722-731.( 1) 1) |
| [25] | Zhao Y and Karypis G. Criterion functions for document clustering: experiments and analysis[R]. Technical Report, 2001, 1: 40.( 1) 1) |
 2016, Vol. 5
2016, Vol. 5
